Evolution of domain structure and frequency effect on

ferroelectric properties in BIT ferroelectrics

 ZHENG Xue-jun(郑学军)^{1, 2}, LU Jia(卢佳)¹, ZHOU Yi-chun(周益春)^1,2,

WU Bo(吴波)¹, CHEN Yi-qiang(陈义强)¹

1. Faculty of Materials, Optoelectronic and Physics, Xiangtan University, Xiangtan 411105, China;

2. Key Laboratory for Low Dimensional Materials and Application Technology, Ministry of Education,

Xiangtan University, Xiangtan 411105, China

Received 15 July 2007; accepted 10 September 2007

Abstract: Based on the time-dependent Ginzburg-Landau (TDGL) equation, the temporal evolution of the domain structure and hysteresis loops of polarization versus electric field were simulated by a phase-field model for Bi₄Ti₃O₁₂ (BIT) ferroelectric single crystal under an applied electric field. In the static electric energy induced by an applied alternating electric field, the effects of field frequency on the ferroelectric properties of BIT ferroelectrics were investigated. The results show that the evolution of ferroelectric domain structure is a gradual process including domain nucleation, domain wall motion, domain growth and domain combination. In the boundary regions of ferroelectric domain, the new domain nucleations occur and the old domains disappear. The coercive field increases with the field frequency, and it is in good agreement with the previous experiment.

Key words: ferroelectrics; phase field theory; domain; polarization; frequency

                                                                                                                                                                          
1 Introduction

Much attention has been attached to ferroelectrics in recent years, because the pronounced properties of ferroelectric, pyroelectric, piezoelectric, electric-optical, dielectric and nonlinear photonic can be used in designing many devices[1-2]. The coercive field is an important factor for the properties of the ferroelectric random access memory (FRAM). LOHSE et al[3] have found that the coercive field increases with frequency in PZT thin films, this phenomenon obeys the Curie–von Schweidler law which is applicable to all kinds of ferroelectrics as well as nonferroelectrics[4]. So, further research is needed to understand the effect of frequency on the properties of ferroelectrics.

The decline of the capability for the polarization switching under the applied electric filed is of great importance for the fatigue properties in ferroelectric thin films and devices. Phase field theory is widely used to simulate ferroelectric domain structure and polarization switching of BaTiO₃ (BT) and PbTiO₃ (PT) ferroelectrics under an applied field. AHLUWALIA and CAO[5-6] have investigated the domain pattern formation and the ferroelectric domain switching of ferroelectrics. The phase field model of two-dimensional domain structure was used to study the temporal evolution of PT single crystal and size effect on domain configuration and polarization switching of PT thin films[7-9], and the model of three-dimensional domain structures was constructed to study the effect of substrate constraint and temperature on the stability of domain structure for PT and BT ferroelectric thin films[10-11]. A realistic electro-mechanical boundary conditions were used to predict the domain switching in an ideal single BT crystal[12], and the effect of grain boundaries and defect pinning on domain switching was discussed in bicrystals[13]. Few of literatures were concerned on the evolution of domain structure and frequency effect on ferroelectric properties of BIT thin film under an applied electric field, as far as we know.

In this study, the phase field theory based on time-dependent Ginzburg-Landau (TDGL) equation was used to study the dynamic process of the polarization switching under an applied electric field. Because the time-dependence of polarization switching could limit the erasure/rewrite speed of memory devices[14], the relationship between the remnant polarization and coercive field on the hysteresis loop of BIT thin film was understood via the simulated curves of average polarization and electric field versus time. In order to investigate the change of remnant polarization and coercive field with different frequency, the hysteresis loop of BIT thin film was simulated at the normalized frequencies of 0.05, 0.02 and 0.0063. It may offer useful guidelines to research the dynamic process of the polarization switching, and frequency effect on ferroelectric properties for the design of memory capability of ferroelectric device.

2 Methodology

2.1 Model of phase field theory

(1)                             

where  L denotes the kinetic coefficient, F is the total free energy of the system, ?F/?P_i(r, t) is the thermodynamic drive force, t is time.  is the polarization, and the subscript i denotes the three directions of the polarization field, P=(P₁, P₂, P₃), to depict the domain structure[10]. r denotes the spatial vector  r=( x₁, x₂, x₃), where x₁, x₂ and x₃ are the horizontal and vertical direction in the plane, and vertical direction out of plane (see Fig.1).

According to Landau-Devenshire thermodynamic theory, the total free energy F can be expressed as[15]

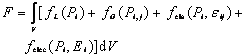
(2)

where  f_L(P_i), f_G(P_{i, j}), f_ela(P_i, ε_ij)and f_elec(P_i, E_i) denote the local free-energy density[9], domain wall energy density[10], elastic energy density[11], and additional electrical energy density[14], respectively. ε_ij and E_i are the elastic strain and applied electric field.

2.2 Two-dimensional polarization switching under alternative electric field  

Two-dimensional simulations are conducted under the plane-polarization and plane-strain conditions, namely P₃=0 and ε₃₃=ε₂₃=ε₃₂=ε₁₃=ε₃₁=0. For the simulated region boundary, the strain-free is assumed, and the polarization dP/dn=0, where n refers to a unit length in the outward normal direction of the surface. The extrapolation length approaches infinity, and the intrinsic size effect vanishes because in this case, there is no difference for polarization in the media between the surface and the interior[16].

To conveniently interpret domain structures and to identify numerical issues, the variables in Eqn.(2) are normalized as in Ref.[7]. With the dimensionless variables, each expression of the energy density in Eqn.(2) is substituted into TDGL Eqn.(1), the 2D time-dependent Ginzburg-Landau equations are rewritten as follows:

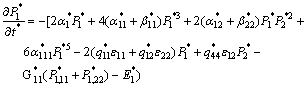
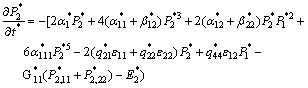
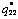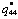where , (i=1, 2),  and  are the amplitude and frequency of the applied electric field. The constants, ,  and  are the expansion constants of the local free energy density. , , , , , ,  and are the polynomial expressions of elastic constants , , and electrostrictive constants, , 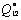.  denotes the gradient energy coefficient of the domain wall energy density. The superscript * denotes the dimensionless values of the corresponding variables.

For bismuth titanate ferroelectrics, the expansion constants, elastic constants and electrostrictive coefficients are obtained from Refs.[17-19], and listed in Table 1. Due to the lack of experimental data, isotropic domain wall energy was assumed and 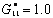 in this study[8].

The finite difference method for spatial derivations and the Runge-Kutta method of order four for temporal derivations are employed to solve Eqn.(3). We used 32×32 discrete grid points with a cell size of 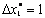, .The time step is set at , and the total number of time steps is 2 000, which can ensure that the domain structure reaches its steady state. In each grid, the sum of  and  is the polarization vector, where the length and direction of an arrow denote the magnitude and the direction of each polarization vector,  and  are the polarizations along the horizontal and vertical directions. The average polarizations  and  were taken as the macroscopic polarizations of the entire simulated region to the x₁ and x₂ directions.

3 Results and discussion

3.1 Polarization switching under applied sinusoidal alternative electric field

At first, no applied electric field conditions were considered, namely,  and  were zero. At the beginning of the evolution, a Gaussian random fluctuation was introduced to initiate the polarization
evolution process. Because the initial state is in a non- equilibrium random configuration, the domainstructure changes to the configuration of minimal of the free energy. These domains interact with one another elastically and electrostatically and evolve until a steady state is reached. Fig.1(a) shows the final steady state without applied loading. At this state, the 180°domain structure is shown, and the polarization point to the right at A, C region, left at B.

The final state of the spontaneous polarization shown in Fig.1(a) was used as the starting state of the domain structure. Electric field 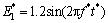 was then applied along the x₁ direction, the frequency f* is 0.006 2，while  equals zero. Figs.1-3 show the process of domain switching, the curve of the polarization

Table 1 Expansion constants at 25 ℃ electrostrictive constants and elastic constants

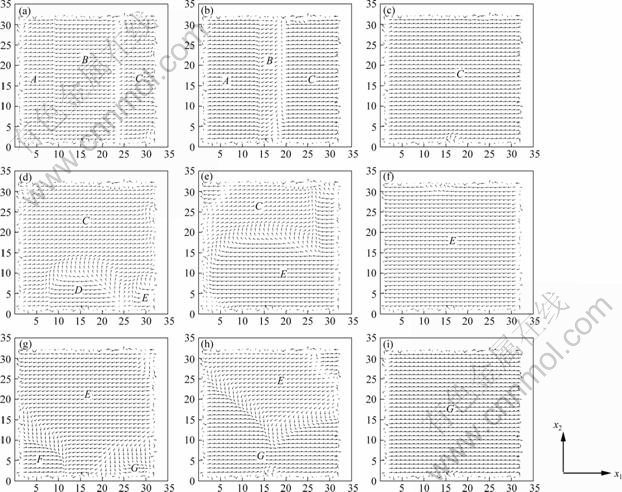
Fig.1 Domain structures corresponding to point a-i in Figs.2 and 3: (a) 0; (b)120; (c)150; (d)900; (e)950; (f) 1 000; (g) 1 700;      (h) 1 750; (i) 2 000 time steps

Fig.2 Simulated curves of dimensionless average polarization versus dimensionless time, and dimensionless electric field versus dimensionless time

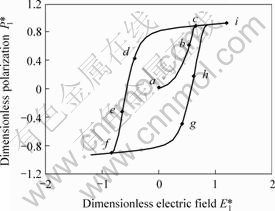
Fig.3 Hysteresis loop of dimensionless average polarization versus dimensionless applied electric field

versus time and the hysteresis loop under the applied alternative electric field. Figs.1(b)-(c) show that the opposite polarization to the electric field  shrunk in region B, and then gradually disappeared as the strength of the electric field increased. At the state of Fig.1(c), the polarizations in region C are all along the x₁ direction, indicating that the domain structure reaches a saturated state with only a single domain. While the applied electric field varied from Fig.1(a) to Fig.1(c), the average polarization increases smoothly, which is attributed to the smooth domain wall motion, as shown by points a-c in Fig.2. Then, the applied electric field changes its sign to negative and the smooth changes in the average polarization with the applied field continue until point e in Fig.2 is reached, at which jumps occur. The jump in the average polarization reverses the direction of the average polarization. The jumps are also attributed to a great change in the domain structure, which is shown in Figs.1(d) and (e). Fig.1(d) shows the left-side polarization firstly occurred in the bottom boundary D and the right corner E. The region D merged into E and then gradually expanded to the top as the negative electric field is increased, as shown in Fig.1(e). Fig.1(f) shows the domain structure reaches a saturated state with the polarization points to the left side. Comparing Fig.1(f) with Fig.1(c), the polarization turns to the opposite side. By further increasing of the field strength from the negative maximum to the positive maximum, the domain structure repeats the reversal from the left to the right, which is demonstrated in Figs.1(g)- (i). Fig.1(g) shows the new domain nuclei also appear in the bottom corner of regions F and G, and the previous polarization in region E disappeared on the top boundary, as shown in Fig.1(h). Fig.1(i) shows the polarization back to the right side in region F combined in region G, and completes a cycle of the polarization switching.

Fig.2 shows the polarization changes periodically with the sinusoidal alternating electric field. It is shown that the absolute value of  is lager than that of  under an applied electric field in x₁ direction. This indicates that the polarization vector leans to the direction of the applied electric field. At 805 steps, when the electric field firstly decreases to zero, the polarizations are not zero due to the nonlinear ferroelectric property. The polarization is called the remnant polarization at this time. When the electric field continues to decrease to a negative value at 933 steps, the average polarization reverses at the applied electric filed equal to -0.57, the absolute strength of the applied electric field is called the coercive field. While the electric field changes from negative to positive, the polarization switching process repeats again. Fig.3 shows the hysteresis loop of the average polarization  along x₁ direction versus the electric field . The details of domain structures corresponding to the points a-i in Figs.2 and 3 are shown in Fig.1.

In summary, the polarization switches with the direction of the applied electric field, and the new domain nucleation and the old domain disappearance occur at the boundary. The evolution of ferroelectric domain structure is a gradual process including domain nucleation, domain wall motion, domain growth and domain combination. We assume that the simulated region boundary is an anti-phase boundary, the new domain nucleation as well as the old domain disappearance occurs at such boundary. It can be inferred that the anti-phase boundaries (APBs) can supply additional nucleation sites of polarization domains in switching process, and can avoid fatigue behavior when the nucleation at the electrode is seriously depressed[20]. Therefore, it makes nucleation easier and accelerates the speed of the polarization reversal.

3.2 Effect of frequency on ferroelectric properties

The process of polarization switching in ferroelectric needs a period of time, so the coercive field is related to the frequency. Fig.4 shows the hysteresis loop in different frequency. Electric fields 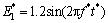 and 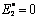 are applied on the ferroelectric. The frequencies equal 0.05, 0.02 and  0.006 3, respectively, and the cycle, τ*=1/f^*, equals 20, 50 and 158. On the one hand, it can be seen from Fig.4 that the hysteresis loop becomes narrow with decreasing frequency. This indicates that the coercive field will decrease with frequency. And the values of the coercive fields are 1.15, 0.95 and 0.63, respectively. One reason for this could be that the polarization switched under a low field frequency experiences a period of time, while in the high frequency, there is not enough time to experience switching process, which leads to a high coercive field. On the other hand, there is no obvious difference in the remnant polarization in Fig.4. That may be caused by the range of the simulated frequency chosen to be too narrow, which leads to the remnant polarization of one frequency being little different from the other. The area of the hysteresis loop increases with the frequency. The area of the hysteresis loop is in direct proportion to the energy loss. This part of energy transforms into thermal energy, so hysteresis loop is usually measured in low frequency. LOHSE et al[3] have observed that the coercive field increases with the frequency in PZT thin films. We can see that the trend of the coercive field versus the frequency in our simulation agrees with the experimental results.

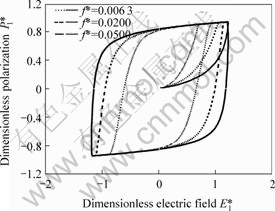
Fig.4 Hysteresis loops with different dimensionless frequencies

4 Conclusions

1) Domain structure turns to the saturated state with only a single domain at the maximum of the electric field. It can be found that the polarization switches to the direction of the electric field, and the new domain nucleation and the old domain disappearance occur at the boundary of the simulated region.

2) The coercive field increases with the frequency. The phase field simulation explains the experimental results, and the trend of the coercive field changing with the frequency is in agreement with the experimental results.

References

[1] SCOTT J F. Application of modern ferroelectrics[J]. Science, 2007, 315: 945-959.

[2] SETTER N, DAMJANOVIC D, ENG L, FOX G, GEVORGIAN S, HONG S. Ferroelectric thin films: Review of materials, properties, and applications[J]. J Appl Phys, 2006, 100: 051606-1-46.

[3] LOHSE O, GROSSMANN M, BOETTGER U, BOLTEN D, WASER R. Relaxation mechanism of ferroelectric switching in Pb(Zr,Ti)O₃ thin films[J]. J Appl Phys, 2001, 89(4): 2332-2336.

[4] ISHIWARA H, OKUYAMA M, ARIMOTO Y. Ferroelectric random access memories, Topics in applied physics[M]. New York: Springer-Verlag, 2004: 31-45.

[5] AHLUWALIA R, CAO Wen-wu. Effect of surface induced nucleation of ferroelastic domains on polarization switching in constrained ferroelectrics[J]. J Appl Phys, 2003, 93(1): 537-544.

[6] AHLUWALIA R, LOOKMAN T, SAXENA A, CAO Wen-wu. Domain-size dependence of piezoelectric properties of ferroelectrics[J]. Phys Rev B, 2005, 72: 014102-1-13.

[7] WANG Jie, SHI San-qiang, CHEN Long-qing, LI Yu-lan, ZHANG Tong-yi. Phase field simulation of ferroelectrtic/ferroelastic polarization switching[J]. Acta Mater, 2004, 52: 749-764.

[8] WANG Jie, LI Yu-lan, CHEN Long-qing, ZHANG Tong-yi. The effect of mechanical strains on the ferroelectric and dielectric properties of a model single crystal-phase field simulation[J]. Acta Mater, 2005, 53: 2495-2507.

[9] WANG Jie, ZHANG Tong-yi. Size effects in epitaxial ferroelectric islands and thin films[J]. Phys Rev B, 2006, 73: 144107-1-13.

[10] LI Y L, HU S Y, LIU Z K, CHEN L Q. Effect of substrate constraint on the stability and evolution of ferroelectric domain structures in thin films[J]. Acta Mater, 2002, 50: 395-411.

[11] LI Y L, CHEN L Q. Temperature-strain phase diagram for BaTiO3 thin films[J]. Appl Phys Lett, 2006, 88: 072905-1-3.

[12] ZHANG W, BHATTACHARYA K. A computational model of ferroelectric domains. Part I: Model formulation and domain switching[J]. Acta Mater, 2005, 53: 185-198.

[13] ZHANG W, BHATTACHARYA K. A computational model of ferroelectric domains. Part II: Grain boundaries and defect pinning[J]. Acta Mater, 2005, 53: 199-209.

[14] LU Xiao-mei, LI Li-ben, QIAN Dong, LI Wei, YE Yu-da, WU Xiao-shan, ZHU Jin-song. Switching properties of Nd- and La-doped Bi₄Ti₃O₁₂ thin films under applied stress[J]. Phys Rev B, 2005, 72: 212103-1-4.

[15] ZHONG Wei-lie. The physics of ferroelectric[M]. Beijing: Science Press, 2000: 74-94.

[16] ZHONG W L, WANG Y G, ZHANG P L, QU B D. Phenomenological study of the size effect on phase transitions in ferroelectric particles[J]. Phys Rev B, 1994, 50(2): 698-703.

[17] WATANABE Y. Theoretical stability of the polarization in insulating ferroelectric/semiconductor structures[J]. J Appl Phys, 1998, 83(4): 2179-2193.

[18] GU Hao-shuang, ZHOU You-hua, TIAN Hu-yong. Thermodynamical analysis of bismuth titanate[J]. J Hubei Univ: Natural Science, 1997, 19(3): 227-232.

[19] GOSPODINOV M, HAUSS?HL S, SVESHTARCV P, DOBREVA S, SAMPIL A. Growth and physical properties of bismuth titanate crystals[J]. Mat Res Bull, 1992, 27: 1415-1421.

[20] DING Y, LIU J S, QIN H X, ZHU J S, WANG Y N. Why lanthanum-substituted bismuth titanate becomes fatigue free in a ferroelectric capacitor with platinum electrodes[J]. Appl Phys Lett, 2001, 78(26): 4175-4177.

Foundation item: Projects (10472099, 10672139) supported by the National Natural Science Foundation of China; Project (207079) supported by the Key Project of Ministry of Education of China; Project (05FJ2005) supported by the Key Project of Scientific, Technological Department of Hunan Province, China; Project (06A072) supported by the Key Project of Education Department of Hunan Province, China

Corresponding author: ZHENG Xue-jun; Tel: +86-732-8293648; E-mail: zhengxuejun@xtu.edu.cn

(Edited by YANG You-ping)