Trans. Nonferrous Met. Soc. China 24(2014) 217-223
Experimental and simulation research on thermal stamping of carbon fiber composite sheet
Qi ZHANG, Qiang GAO, Jin CAI
School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China
Received 20 October 2012; accepted 19 October 2013
Abstract: To improve the manufacture efficiency and promote the application of composites in the automobile industry, a new composite forming method, thermal stamping, was discussed to form composite parts directly. Experiments on two typical stamping processes, thermal bending and thermal deep drawing, were conducted to investigate the forming behavior of composite sheets and analyze the influence of forming temperature on the formed composite part. Experimental results show that the locking angle for woven composite is about 30°. The bending load is smaller than 5 N in the stamping process and decreases with the increase of temperature. The optimal temperature to form the carbon fiber composite is 170 °C. The die temperature distribution and the deformation of composite sheet were simulated by FEA software ABAQUS. To investigate the fiber movement of carbon woven fabric during stamping, the two-node three-dimension linear Truss unit T2D3 was chosen as the fiber element. The simulation results have a good agreement to the experimental results.
Key words: thermal stamping; carbon fiber composite sheet; shear angle; bending; deep drawing
1 Introduction
Compared with other commonly used materials such as metals and alloys, fiber composites possess excellent features such as low weight, high specific strength, high modulus, high stiffness and outstanding designability. Therefore, they have been widely used in the fields such as aerospace, automobile manufacture, shipping, building reinforcing, sports, energy development [1,2]. But the commonly used composites forming technologies, such as hand lay-up, spray-up, resin transfer molding, filament winding and autoclave molding, cannot overcome problems, such as high operation complexity, low efficiency and high cost. As composite parts are widely used in manufacturing fields, especially in automobile manufacturing, a high- efficiency, low-cost, mass-production forming method for composite parts is in urgent need [3-5].
Thermal stamping was one of the most effective ways to fabricate composite sheets. This method was proposed to form composite parts directly by the isothermal die set. As shown in Fig. 1, the forming process is composed of three stages. First, die set is heated up, and the punch moves downward until it contacts with the blank. Second, the resin in the blank becomes soft because it is heated by contact heat transfer with the heated punch and die, then the composite blank is stamped as the punch moves downward. Finally, the resin in the composite resolidifies in the cooling die set, and the part is obtained.
Since thermal stamping has great advantages over traditional forming method, a lot of studies have been conducted to investigate the forming property and deformation mechanism of thermal stamping [6-8]. HOU and FRIEDRICH [9,10] heated the composites to 180 °C by contact heat transfer, then put the sample in the die set to stamp and resolidify to get orthopaedic part. ZHU et al [11] measured the strain of the workpiece in the thermal stamping process. The results show the shape of the die set and the initial distribution of the fiber may affect the forming property. CABRERA et al [12] studied the thermal stamping process of polypropylene self-reinforcement composites. The results show that shear deformation is the dominant mechanism of deformation for composites thermal forming and thermal stamping is an efficient way to form complex parts.
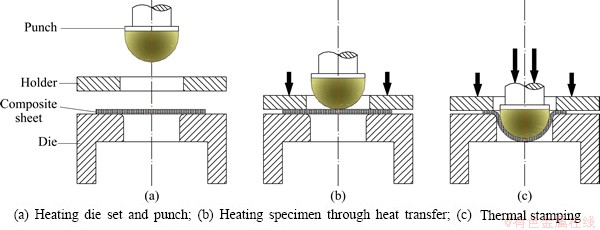
Fig. 1 Illustration of thermal stamping process
In this study, we investigated the deformation mechanism of thermal stamping by bias extension test and picture frame test, and also obtained the reasonable temperature range. In order to obtain the load- displacement curve of the stamping process, thermal bending and thermal deep drawing experiments were conducted, the temperature distribution and fiber movement was simulated by ABAQUS software.
2 Shear properties of reinforcement
2.1 Shear angle
Carbon fiber reinforced polymer matrix composites consist of woven fiber reinforcement and polymer matrix. Woven fabric plays a vital role in composites forming. In thermal forming process, resin matrix turns into the viscous state, so the constraint between fiber reinforcement and polymer matrix reduces greatly. The specific mechanical properties and deformation mechanisms of fiber-reinforced polymer matrix composites are influenced by the characteristic of fiber reinforcement.
Shear deformation is the dominant mechanism of deformation for composites thermal forming. A 3D deformation of fabric is required at corners or over spherical regions [13]. When textile composites are subjected to deep drawing, in-plane shear will occur. This primarily corresponds to the relative sliding of parallel tows with fabric layer or composite ply, and to rotation of tows at their crossovers. The change of angle between the warp and weft yarns is defined as shear angle, and it is equal to the difference of the enclosed angle between the two yarn directions before and after deformation. Since the warp and weft yarns are perpendicular to each other before deformation, so shear angle can be defined as follows:
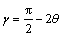 (1)
(1)
In thermal forming process, fiber bundles are extruded and twisted, and when the angle between two crossover fiber bundles comes to its crucial value ‘locking angle’, wrinkle will occur gradually. To investigate the forming properties of carbon fiber reinforced matrix composites, picture-frame test and bias extension test are often used to study the forming phenomenon of carbon fiber.
2.2 Testing methods
Experimental equipments for picture frame test and bias extension test are shown in Fig. 2. Carbon woven fabric specimens are clamped by testing device. With moving up of the testing machine slide, the displacement and force of the woven fabric are measured.

Fig. 2 Experimental set-ups for picture frame test (a) and bias extension test (b)

Fig. 3 Experimental principles for picture frame test (a) and bias extension test (b)
Experimental principles for picture frame test and bias extension test are shown in Fig. 3, from which the equations to measure the shear angle for the two tests can be deducted as Eqs. (2) and (3).
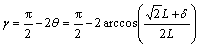 (2)
(2)
where θ is the frame angle, L is the side length measured between the centers of the bearings and δ is the displacement of crosshead.
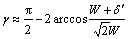 (3)
(3)
where W is the initial width of the specimen and δ′ is the vertical displacement.
2.3 Normalized shear stress
As we can see from the two testing methods above, experimental set-up and sample size used in picture frame test are different from those of bias extension test, so as to the testing results. To compare and analyze the testing results, HARRISON et al [14] proposed a method to normalize the shear force, which related the shear force with material area in the shear zone. Shear force increases with the increase of material area in the shear zone. However, this method assumed that the size of the sample is as same as that of the shear frame. Based on the energy method, LEE et al [15,16] improved the normalized shear force method, and applied it to different sample sizes and shear frame. In their research, shear force can be normalized through the following equation:
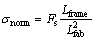 (4)
(4)
where σnorm is the normalized shear stress, Fs is the force, Lframe is the length of the frame and Lfab is the length of the fiber composites.
In order to obtain the normalized shear force of the bias extension test, Eq. (4) can be written as Eq. (5).
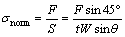 (5)
(5)
where σnorm is the normalized shear stress of bias extension test, F is the force, S is the area and t is the thickness of the specimen.
Normalizing the data obtained in the bias extension test and the picture frame test according to Eq. (4) and Eq. (5), the normalized shear force-shear angle curve can be acquired, as shown in Fig. 4.
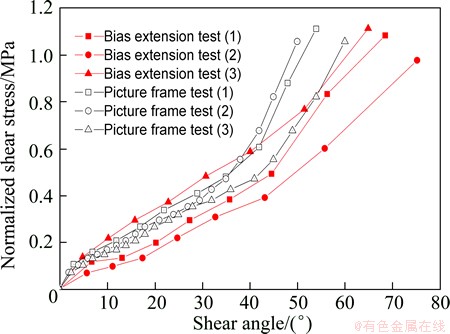
Fig. 4 Normalized shear stress-shear angle curves
As we can see from the normalized shear force-shear angle curves, for both bias extension test and picture frame test, shear force increases with the increase of shear angle. When shear angle is below 30°, shear force increases slowly; and when shear angle is above 30°, shear force increases greatly. So, 30° is the locking angle for the composite sheet.
3 Thermal bending
3.1 Experimental set-up
Thermal bending was one of the typical forming processes and the experimental set-up was designed to conduct the bending experiments. The experimental set-up consisted of tensile testing machine, temperature control unit and thermal bending die set. A tensile testing machine was utilized, and an aluminum die set was manufactured. According to the calculation results, a heating rod of 100 W was used to heat up the punch. And a thermal couple was placed 5 mm away from the punch surface to feedback the temperature. The heating rod was monitored by the temperature control unit to provide accurate temperatures, which can reach ±1 °C. The experimental set-up used in this study is shown in Fig. 5.

Fig. 5 Thermal bending experimental set-up
3.2 Temperature field simulation
In the thermal bending process, temperature distribution of the die set and the location of heating rod in the punch should be confirmed. To study the temperature distribution of the mould, FEA software ABAQUS was used to simulate the temperature distribution. As shown in Fig. 6, surfaces of the punch and die, which contact with the deformation region of the bending workpiece, show a relatively high temperature.
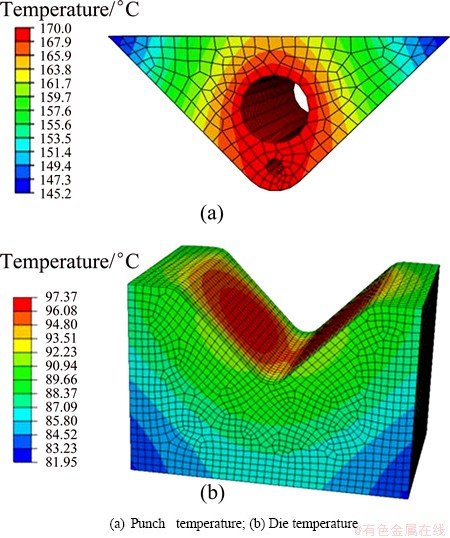
Fig. 6 Temperature distribution on punch and die
As shown in Fig. 7, workpieces were heated to the preassigned temperature through contact heat transfer with the punch. So, the deformation regions of the workpiece that contacts with the punch directly, show the maximum temperature and reach the steady temperature first. Temperature was usually low in undeformation regions, which were far away from the high temperature region of the punch.
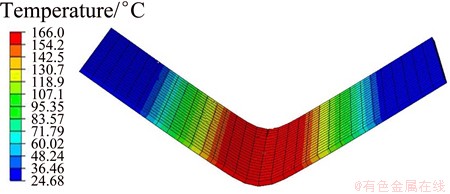
Fig. 7 Workpiece temperature field
3.3 Experimental results
Experiments under different forming parameters were conducted. A group of workpieces were obtained as shown in Fig. 8. The bending angles of the workpieces were different from each other. In the thermal bending process, the deformation region on the workpiece was heated, so the constraints between the fiber reinforcement and resin matrix were greatly reduced. In the same bending process, the forming resistance increased with the increase of stamping speed. When stamping speed is too fast, crack will occur (see Fig. 9).

Fig. 8 Bending workpice

Fig. 9 Surface qualities of workpieces
Experimental results show that forming force is relevant to the forming parameters. It can be seen from Fig. 10 that the thermal bending load of composite sheet is quite small, which is less than 5 N. As the punch moves, the forming force increases. Meanwhile, forming force deceases when a high forming temperature or a relatively low stamping speed is applied. When the forming temperature is lower than 70 °C, or loading speed is higher than 100 mm/min, brittle fracture will occur. According to the load curve, fracture in the composite sheet will lead to a significant reduction of forming load.
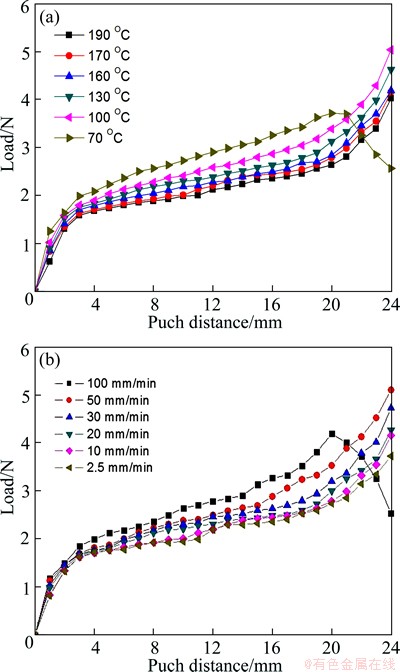
Fig. 10 Loading curves under different forming temperatures (a) and stamping speeds (b)
4 Thermal deep drawing
4.1 Experimental set-up
As shown in Fig. 11, deep drawing die consisted of mold base, punch, blankholder and die. Hemispherical punch with a radius of 30 mm was connected to the upper base with bolts and between the punch and upper base, there was a layer of asbestos board to reduce the heat conduction. The punch was heated by one heating rod. The blankholder was heated by four heating rods and die by six rods, which distributed uniformly alongthe circumference. The composite specimens were circle with a diameter of 100 mm and since they were heated by contact heat transfer between the heated die and the sheet. The punch, blankholder and die were manufactured by aluminum alloy with high thermal conductivity.

Fig. 11 Deep drawing die
4.2 Temperature field simulation
The temperature distribution of the die set is shown in Fig. 12. We can see that the temperature on the surface, which contacts with the deformation regions of workpiece directly, is nearly 170 °C evenly. The surface consists of spherical head of the punch, the lower surface of the black holder, and the bending fillet of the die. Therefore, the forming region of workpiece can be heated to the temperature by the die set.
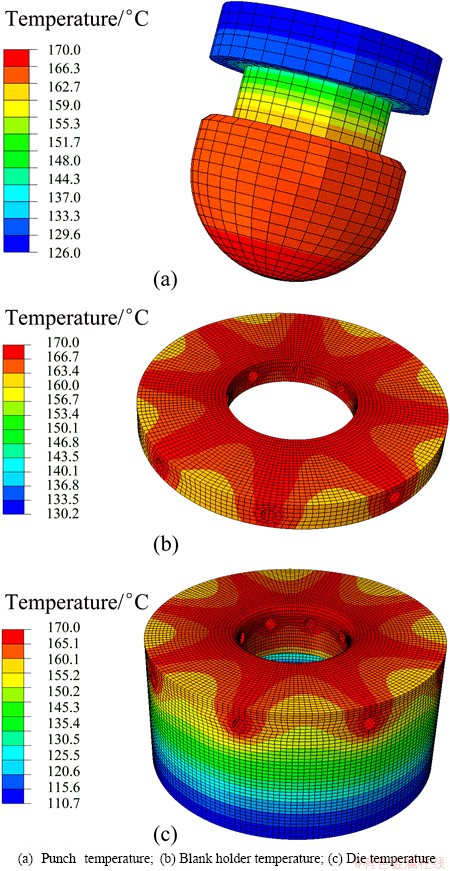
Fig. 12 Die set temperature field
The workpiece is heated up through contact heat transfer with the die set, so regions that contacts with the die set first are heated up earlier and reach a relatively high temperature. As shown in Fig. 13, three nodes are chosen and the temperature variation curves in the thermal deep drawing process are given in Fig. 14.
As can be seen from Fig. 14, temperatures of nodes No. 1 and No. 3 increase faster than node No. 2, and the steady temperatures are relatively high. This is because nodes No. 1 and No. 3 contact with the heated punch earlier.
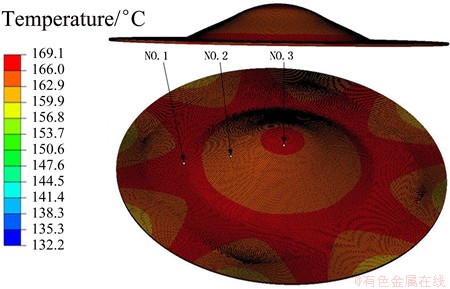
Fig. 13 Specimen temperature field
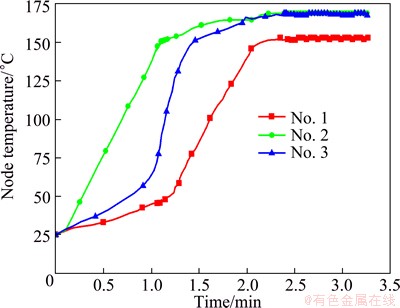
Fig. 14 Temperature variation curves
4.3 Experimental results
The deformation process of the workpiece is shown in Fig. 15. The thermal forming process consists of the deformation of the composite sheet resin and the relocation of the fibre bundles. It can be seen that the circular outline of workpiece is drawn to nearly square one. This is because the force, which acts along the fiber direction, can pull the fiber into the semisphere.

Fig. 15 Workpiece deformation process
The deformation process of fiber is simulated by FEA software ABAQUS, and the fiber is meshed as the two-node three-dimension linear Truss unit T2D3. We can see from Fig. 16 that in the tensile deformation region, the fiber flows faster. In the shear deformation region, the fiber flows slower. Measuring the shear angle of the deformed fiber, shear angle-deep drawing distance curves are obtained. As can be seen in Fig. 17, shear angle increases with the increase of the deep drawing distance. This is consistent with the experimental result.

Fig. 16 Workpiece deformation
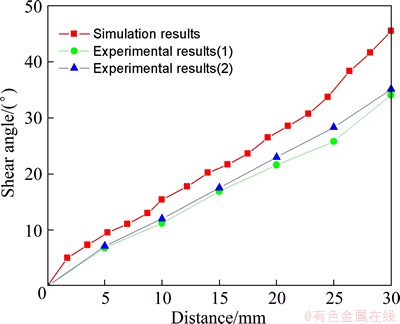
Fig. 17 Shear angle-deep drawing distance curves
5 Conclusions
1) The locking angle for woven composite is about 30°. When conducting composite sheet thermal stamping, the shear angle should be below 30°.
2) Load for composite thermal bending is smaller than 5 N in the stamping process and increases with the increase of bending speed.
3) 170 °C is the optimal temperature to form carbon fiber composites and the temperature in deformation regions of the deep drawing workpiece is relatively higher than other regions.
4) Shear angle increases with the increase of the deep drawing distance. The fiber movement, simulated by ABAQUS software, has a good agreement with experimental result.
References
[1] CHE Jian-fei, HUANG Jie-wen, YANG Juan. Composite materials and its engineering application [M]. Beijing: Mechanical Industry Press, 2006: 138-330. (in Chinese)
[2] WAKEMAN M D, ZINGRAFF L, BOURBAN P E. Stamp forming of carbon fibre/PA12 composites—A comparison of a reactive impregnation process and a commingled yarn system [J]. Composites Science and Technology, 2006, 66: 19-35.
[3] LIM T C, RAMAKRISHNA S. Modelling of composite sheet forming: A review [J]. Composites Part A, 2002, 33: 515-537.
[4] ALLAOUI S, LAUNAY J, SOULAT D. Experimental tool of woven reinforcement forming [J]. Int J Mater Form, 2008, 1: 815-818.
[5] CAO J, AKKERMAN R, BOISSE P. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark result [J]. Composite Part A, 2008, 39: 1037-1053.
[6] LONG A C, RUDD C D, BLAGDON M. Characterizing the processing and performance of aligned reinforcements during preform manufacture [J]. Composites Part A, 1996, 27: 247-253.
[7] LOMOV S V, VERPOEST I. Model of shear of woven fabric and parametric description of shear resistance of glass woven reinforcements [J]. Composites Science and Technology, 2006, 66: 919-933.
[8] BUET-GAUTIER K, BOISSE P. Experimental analysis and modeling of biaxial mechanical behavior of woven composite reinforcements [J]. Experimental Mechanics, 2001, 41(3): 260-269.
[9] HOU M, FRIEDRICH K. Adjustable forming of thermoplastic composites for orthopaedic applications [J]. Journal of Material Science: Material in Medicine, 1998, 9: 83-88.
[10] HOU M, FRIEDRICH K. 3-D stamping forming of thermoplastic matrix composites [J]. Applied Composite Materials, 1994, 1: 135-153.
[11] ZHU B, YU TX, ZHANG H. Experimental investigation of formability of woven textile composite preform in stamping operation [J]. Int J Mater Form, 2008, 1: 969-972.
[12] CABRERA N O, REYNOLDS C T, ALCOCK B. Non-isothermal stamp forming of continuous tape reinforced all-polypropylene composite sheet [J]. Composites Part A, 2008, 39: 1455-1466.
[13] LEBRUN G, BUREAU M N, DENAULT J. Evaluation of bias-extension and picture-frame test methods for the measurement of intraply shear properties of PP/glass commingled fabrics [J]. Composite Structures, 2003, 61: 341-352.
[14] HARRISON P, CLIFFORD M J, LONG A C. Shear characterisation of viscous woven textile composites: A comparison between picture frame and bias extension experiments [J]. Composites Science and Technology, 2004, 64: 1453-1465.
[15] LEE W, CAO J, BADEL P. Non-orthogonal constitutive model for woven composites incorporating tensile effect on shear behaviour [J]. Int J Mater Form, 2008, 1: 891-894.
[16] LEE W, UM M K, BYUN J H. Numerical study on thermal-stamping of woven fabric composites based on double-dome stretch forming [J]. Int J Mater Form, 2010, 3: 1217-1227.
碳纤维编织复合材料板材热冲压成形的实验和模拟研究
张 琦,高 强,蔡 进
西安交通大学 机械工程学院,西安 710049
摘 要:提出一种新型的复合材料成形工艺,即热冲压成形,来直接成形复合材料。为了研究复合材料板的成形行为,分析了成形温度对零件的影响,进行了热弯曲和热拉深实验。实验结果表明,编织复合材料板的锁止角为30°,在成形过程中,变形载荷一般小于5 N,并且变形载荷随着温度的升高而降低。成形碳纤维复合材料板的最佳温度是170 °C。采用有限元分析软件ABAQUS对模具的温度场分布和复合材料板的变形进行了数值模拟。为了研究碳纤维在成形过程中的运动,采用两节点的三维Truss 单元T2D3对纤维进行网格剖分,模拟结果与试验结果相吻合。
关键词:热冲压;碳纤维复合板;剪切角;弯曲;拉深
(Edited by Hua YANG)
Foundation item: Project (51375369) supported by the National Natural Science Foundation of China; Project (SYG201137) supported by the Science and Technology Development Program of Suzhou, China
Corresponding author: Qi ZHANG; Tel: +86-29-82668607; E-mail: henryzhang@mail.xjtu.edu.cn
DOI: 10.1016/S1003-6326(14)63050-8