
DOI: 10.11817/j.issn.1672-7207.2020.12.025
盾构下穿既有地铁隧道环向围压及受力变化
魏纲1,齐永洁2,吴华君3,华鑫欣4,张苑竹1
(1. 浙大城市学院 土木工程系,浙江 杭州,310015;
2. 安徽理工大学 土木建筑学院,安徽 淮南,232001;
3. 义乌工商职业技术学院,浙江 义乌,322000;
4. 中铁二院华东勘察设计有限责任公司,浙江 杭州,310004)
摘要:为研究盾构近距离下穿对既有隧道管片环向内力的影响,综合考虑盾构正面附加推力、侧摩阻力、盾尾附加注浆力及土体损失4个因素在水平及竖直方向上产生的附加应力,提出一种既有隧道在附加应力作用下的围压重分布模型,推导了既有隧道环向围压的计算公式,利用修正惯用法计算了相应围压作用下的衬砌内力。结合具体工程案例,研究了盾构下穿前后既有隧道的环向围压、弯矩、轴力及剪力的变化,分析了下穿盾构埋深、盾构掘进位置及研究断面变化对环向围压的影响规律。研究结果表明:盾构下穿会引起既有隧道环向围压、弯矩、剪力和轴力减小;随着盾构埋深增加,既有隧道受到的附加围压及弯矩的影响逐渐减弱,且减小速度逐渐放缓;在穿越过程中,既有隧道受到的影响先增大、后减小,且在隧道上下拱顶位置的附加围压及弯矩变化较大;当既有隧道上的断面逐渐远离穿越中心点时,环向附加围压的分布模式由“竖椭圆分布”逐渐变为“横椭圆分布”。
关键词:盾构下穿;既有隧道;附加围压;内力变化;修正惯用法
中图分类号:TU452 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)12-3515-13
Changes in circumferential pressure and stresses in existing tunnels caused by tunnel crossing
WEI Gang1, QI Yongjie2, WU Huajun3, HUA Xinxin4, ZHANG Yuanzhu1
(1. Department of Civil Engineering, Zhejiang University City College, Hangzhou 310015, China;
2. School of Civil Engineering and Architecture, Anhui University of Science and Technology,Huainan 232001, China;
3. Yiwu Industrial & Commercial College, Yiwu 322000, China;
4. CREEC East China Survey and Design Co. Ltd., Hangzhou 310004, China)
Abstract: In order to study the influence of shield tunneling on the annular internal force of the existing tunnel segments, the influence of additional stress on the horizontal and vertical direction caused by four factors including frontal thrust, lateral friction resistance, shield tail grouting force and soil loss was comprehensively considered. A re-distribution model of confining pressure for existing tunnel under the action of additional stress was presented. The internal force of lining under the appropriate confining pressure was calculated by the modified conventional method. The changes of circumferential confining pressure, bending moment, axial force and shear force of the existing tunnel before and after shield tunneling were studied. The influence of the buried depth, the tunneling position and the study section on the circumferential confining pressure of the existing tunnel was analyzed. The results show that shield tunneling can reduce the annular confining pressure, bending moment, shear force and axial force of the existing tunnel. With the increase of the buried depth of shield, the effects of additional confining pressure and bending moment on the existing tunnel are gradually weakened, and the reduction speed gradually slows down. In the process of crossing, the influences on the existing tunnel increase firstly and then decrease, and the additional confining pressure and bending moment at the top and bottom of the tunnel change greatly. When the section on the existing tunnel is gradually away from the crossing center, the distribution mode of circumscribed additional confining pressure changes from vertical elliptical distribution to horizontal elliptical distribution.
Key words: shield tunneling underneath; existing tunnels; additional confining pressure; internal force change; modified routine method
随着城市地铁建设的蓬勃发展,有限的城市浅地层空间出现了越来越多的盾构近距离穿越既有地铁隧道的工况。地铁隧道变形控制要求严格,而盾构的近距离穿越施工风险大,极易损伤和危害既有隧道。因此,研究盾构近距离穿越影响下既有隧道的应力及变形规律变得十分必要。目前,已有国内外学者通过理论解法研究盾构掘进施工引起的土体附加应力及其对既有管线和隧道产生影响等问题[1-7]。齐静静等[2-3]结合Mindlin解,推导了盾构正面附加推力、摩擦力以及土体损失引起的土体附加应力计算公式;王涛等[4]应用镜像法原理,推导了土体损失影响下3个方向上的附加应力公式;张琼方等[5]基于Mindlin解,将既有隧道视为Winkler地基梁,在综合考虑刀盘附加推力、盾构摩擦、附加注浆压力及土体损失共同作用的情况下,计算了盾构下穿对已建隧道的附加应力及变形影响;魏纲等[6-7]在此基础上,结合“剪切错台模型”,分别研究了盾构垂直上穿和下穿工况下既有隧道的竖向附加应力及纵向变形。综上所述,大多学者主要研究既有隧道所受的竖向附加应力和纵向沉降,还未见针对既有隧道围压和内力变化的研究报道。
本文以盾构垂直下穿既有隧道为研究工况,根据建立的盾构下穿既有隧道的力学模型,基于Mindlin解,综合考虑盾构切口附加推力q、盾壳摩擦力f、注浆附加应力p和土体损失作用,计算了既有隧道受到的水平及竖向附加荷载,提出了隧道横向受力位移再平衡的附加围压重分布模型,推导了附加围压的计算公式,通过叠加隧道初始围压算出盾构穿越后的最终围压,并根据修正惯用法计算了管片的环向内力。结合工程案例,研究了盾构近距离下穿工况下既有隧道的围压和内力变化规律。
1 力学模型的建立
1.1 现有力学模型的不足
1) 目前针对盾构掘进引起土体附加应力计算的理论研究中,大多的学者均假定盾壳摩擦力和附加注浆压力沿环向均匀分布。但由于盾构环向各点埋深不同,其表面压力并非均匀分布,故盾壳摩擦力呈均匀分布的模式不合理。另外,由于浆液本身具有重力,若采用均匀分布的附加注浆压力模式,则浆液会在重力作用下向下集中渗流,造成盾构环向注浆出现不均匀,严重时可能导致上部出现注浆空洞,影响隧道的结构受力安全[8]。
2) 在求解环向不均匀摩擦的研究中,梁荣柱等[9]通过盾构环向受到的径向正应力求解盾壳摩擦,但在计算中没有考虑盾构本身质量。本文作者认为随着盾构推进,原本位置的土体被排出,而由盾构本身质量对下方土体进行挤压,故在计算盾构下部产生的径向正应力的过程中,需要考虑盾构本身质量,而非原本土体质量。而朱合华等[10]提出的方法中,虽然考虑了盾构本身的质量影响,但并未精确计算盾构外径向应力,而是进行了简化,仅仅推导了总的盾壳摩擦力计算公式,无法计算环向不均匀的盾壳摩擦力。
3) 目前还未见新建盾构穿越对既有隧道造成的环向附加围压计算模型。
1.2 针对不足进行修改的说明
1) 将目前采用的均匀盾壳摩擦力分布模式,改为更合理的非均匀分布模式。在梁荣柱等[9]提出的盾壳摩擦力计算方法的基础之上,考虑土体置换和盾构本身质量的影响,优化与改进计算公式。
2) 在不少实际工程中,已开始采用“上小下大”的附加注浆压力模式,如图1所示。因此,本文采用该模式进行土体附加应力计算。参照张长强等[8]的变动附加压力设定法,确定隧道拱顶、拱腰和拱底的附加注浆压力分别为40,120和180 kPa。
3) 分析盾构穿越工况下既有隧道的围压变化规律,建立了隧道横向受力位移再平衡的附加围压重分布模型,并推导了附加围压的计算公式。
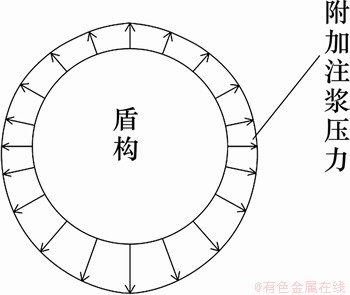
图1 盾构环向附加注浆压力分布示意图
Fig. 1 Distribution diagram of additional grouting pressure in ring direction of shield
1.3 力学计算模型
图2所示为新建隧道下穿既有隧道的力学模型。新建隧道和既有隧道的轴线埋深分别为h和H,既有隧道半径为Rs,新建隧道半径为R。其中,盾构沿着x轴正方向掘进,既有隧道沿着y轴方向,盾构切削面的位置随着盾构推进不断发生变化。为了研究方便,令切削面暂位于yoz平面上。盾构掘进过程中,刀盘正面附加推力q作用于盾构前端切削面,方向沿x轴正方向;盾壳侧摩阻力f沿着盾构四周环向分布,方向沿x轴正方向;盾尾附加注浆压力p作用于盾构尾部,沿径向分布,作用宽度为m。
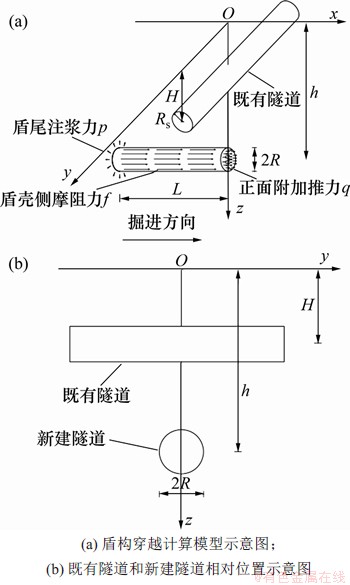
图2 新建隧道下穿既有隧道力学模型图
Fig. 2 Mechanical model diagram of new tunnel underpassing existing tunnel
1.4 建立计算公式
根据梁荣柱等[9]研究,盾壳上任意位置的摩擦力f可表示为
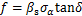 (1)
(1)
式中: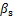 为残余摩阻力和极限摩阻力的比值;
为残余摩阻力和极限摩阻力的比值;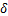 为盾壳与周围地层的界面摩擦角;
为盾壳与周围地层的界面摩擦角;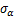 为盾构表面受到的法向压力。
为盾构表面受到的法向压力。
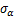 可表示为
可表示为
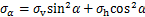 (2)
(2)
式中: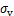 和
和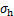 分别为计算位置的竖向和水平土压力;
分别为计算位置的竖向和水平土压力;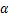 为计算点与水平方向的夹角。
为计算点与水平方向的夹角。
分析认为,在考虑土体置换和盾构本身质量挤压的情况下,盾构环向围压的分布模式如图3所示,由于上下竖向土压力的计算公式存在差异,故需将盾构分为上下2部分进行讨论,并计算各自范围的土压力。
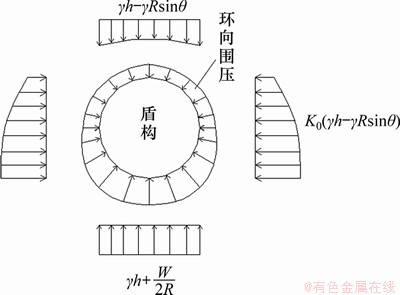
图3 盾构环向围压分布示意图
Fig. 3 Distribution diagram of shield circumferential confining pressure
当0≤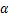 ≤
≤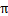 时,竖向和水平土压力计算如下:
时,竖向和水平土压力计算如下:
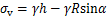 (3)
(3)
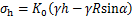 (4)
(4)
当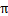 <
<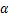 <
<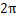 时,竖向和水平土压力计算如下:
时,竖向和水平土压力计算如下:
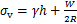 (5)
(5)
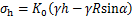 (6)
(6)
式中: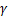 为土体重度;W为盾构单位自重kN/m;K0为侧向静止土压力系数。
为土体重度;W为盾构单位自重kN/m;K0为侧向静止土压力系数。
2 计算公式推导
2.1 盾构掘进引起的附加应力
由于盾构隧道和既有隧道垂直相交,盾构掘进对既有隧道的影响主要考虑竖直(沿z轴)及水平(沿x轴)2个方向的附加应力。参考文献[11]和[7]的方法,基于Mindlin弹性解,对荷载q,f,p及土体损失因素造成的既有隧道在x轴和z轴方向的附加应力进行推导。令点(x0,y0,z0)为应力作用点,点(x,y,z)为应力求导点。
2.1.1 刀盘附加推力q引起的附加应力
盾构切削面位于yoz平面上,故刀盘推力q的应力作用点坐标满足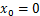 ,
,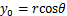 ,
,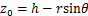 。如图4所示,在盾构前端刀盘处任取微元体
。如图4所示,在盾构前端刀盘处任取微元体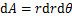 ,荷载q沿x方向,根据Mindlin公式积分可得荷载q在(x,y,z)点处的水平应力
,荷载q沿x方向,根据Mindlin公式积分可得荷载q在(x,y,z)点处的水平应力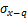 和竖向应力
和竖向应力 分别为:
分别为:
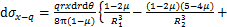
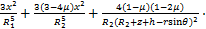
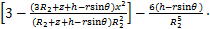
 (7)
(7)
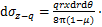
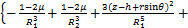
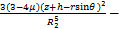
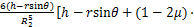
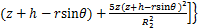 (8)
(8)
通过积分可得:
 (9)
(9)
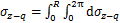 (10)
(10)
式中: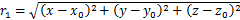 ;
;
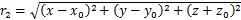 ;
;
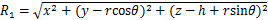 ;
;
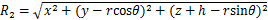 ;
;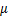 为土的泊松比。
为土的泊松比。
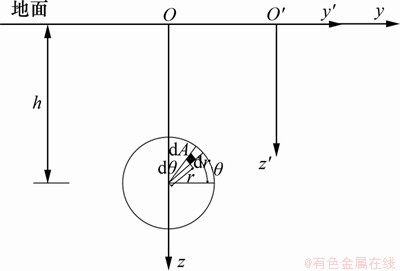
图4 刀盘附加推力积分示意图
Fig. 4 Integral diagram of additional thrust of cutter head
2.1.2 盾壳侧摩阻力f引起的附加应力
盾壳侧摩阻力f采用非均匀分布模式,计算方法参照1.4节进行分段求解,应力作用点坐标满足 ,
, ,
,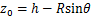 。图5所示为盾壳侧摩阻力积分示意图,在盾壳壁上任取一微元体
。图5所示为盾壳侧摩阻力积分示意图,在盾壳壁上任取一微元体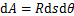 ,荷载f沿x方向,根据Mindlin公式积分可得荷载f在(x,y,z)点处的水平应力
,荷载f沿x方向,根据Mindlin公式积分可得荷载f在(x,y,z)点处的水平应力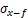 和竖直应力
和竖直应力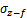 分别为:
分别为:
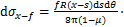
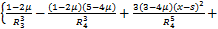
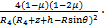
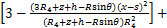
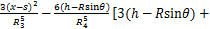
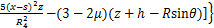 (11)
(11)
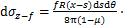
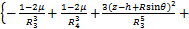
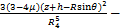
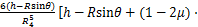
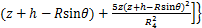 (12)
(12)
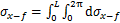 (13)
(13)
 (14)
(14)
式中:L为盾构机长度;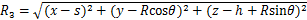 ;
;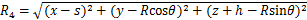 。
。
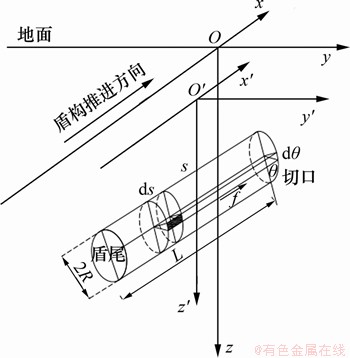
图5 盾壳侧摩阻力积分示意图
Fig. 5 Integral diagram of side friction integral of shield shell
2.1.3 附加注浆压力p引起的附加应力
附加注浆压力p位于盾尾注浆面,沿径向扩散,采用“上小下大”的附加注浆压力模式,分别取拱顶、拱腰和拱底等位置的附加注浆压力进行计算,并通过取平均值的方式求得因附加注浆压力p引起的最终土体附加应力。为了便于计算分析,将荷载p分为竖向荷载p1和水平荷载p2。荷载p1和p2又将分别对既有隧道产生x方向和z方向的附加应力影响,需分别计算。荷载p应力作用点坐标满足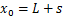 ,
,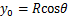 ,
,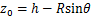 。如图6所示,在盾尾注浆处任取一微元体
。如图6所示,在盾尾注浆处任取一微元体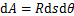 ,荷载p1沿z方向,荷载p2沿y方向。
,荷载p1沿z方向,荷载p2沿y方向。
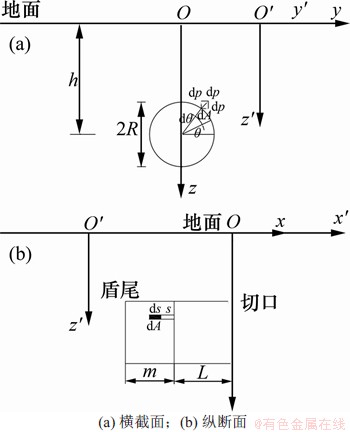
图6 盾尾注浆力积分示意图
Fig.6 Integral diagram of grouting force of shield tail
根据Mindlin公式积分可得荷载p1和p2在(x,y,z)点处的水平应力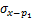 ,
,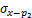 和竖直应力
和竖直应力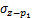 ,
,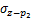 分别为:
分别为:
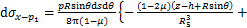
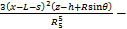
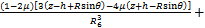
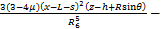
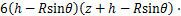
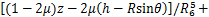
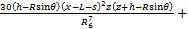

 (15)
(15)
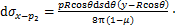
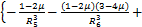
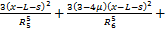
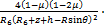
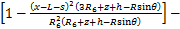
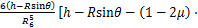
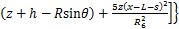 (16)
(16)
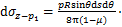
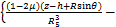
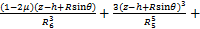
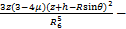
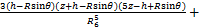
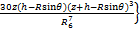 (17)
(17)
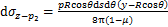
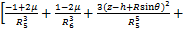

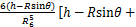
 (18)
(18)
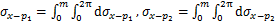 (19)
(19)
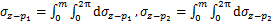 (20)
(20)
式中: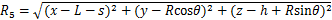 ;
;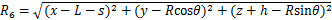 。
。
2.1.4 土体损失引起的附加应力
本文根据文献[12-13]和[4],基于镜像法,采用椭圆形非等量径向土体移动模式,可求得(x0,y0,z0)点处半径为a的空隙在点(x,y,z)处产生水平应力及竖向应力,其中水平应力包括应力分量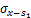 和
和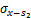 ,竖向应力分量包括
,竖向应力分量包括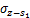 和
和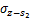 ,各应力分量的表达式如下:
,各应力分量的表达式如下:
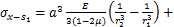
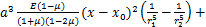
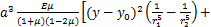
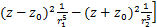 (21)
(21)

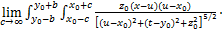
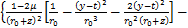
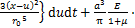
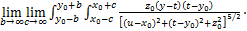
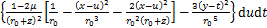 (22)
(22)
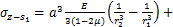
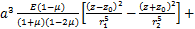
 (23)
(23)
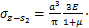
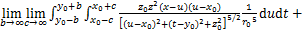
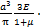
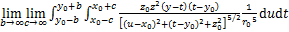 (24)
(24)
单位体积空隙引起的x和z方向的附加应力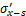 和
和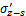 分别为:
分别为:
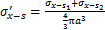 (25)
(25)
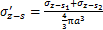 (26)
(26)
盾构掘进造成的最终土体损失应力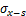 和
和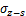 分别为:
分别为:
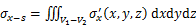 (27)
(27)
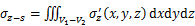 (28)
(28)
式中: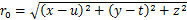 ;E为土体弹性模量;
;E为土体弹性模量; 为损失土体的体积。
为损失土体的体积。
将刀盘附加推力q、盾壳侧摩阻力f、附加注浆压力p和土体损失引起的附加应力叠加,可以得到盾构穿越引起既有隧道在水平x方向和竖直z方向的总附加应力为:
 (29)
(29)
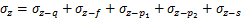 (30)
(30)
2.2 盾构穿越引起的既有隧道围压
盾构近距离穿越引起的附加荷载会破坏既有隧道的初始围压平衡,导致隧道和土体发生协调位移变形,围压实现应力重分布,最后隧道受力再次平衡,变形趋于稳定。
以下穿为例,假设盾构从左向右穿越既有隧道下部,导致既有隧道左侧和下侧受到附加荷载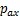 和
和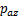 作用发生整体位移,从而挤压另一侧土体,土体反作用引起隧道另一侧围压增加。设附加荷载在水平及竖直方向上的增量为
作用发生整体位移,从而挤压另一侧土体,土体反作用引起隧道另一侧围压增加。设附加荷载在水平及竖直方向上的增量为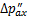 和
和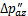 。而位移反方向侧,即隧道左侧和下侧的土体应力得到释放,在附加荷载
。而位移反方向侧,即隧道左侧和下侧的土体应力得到释放,在附加荷载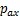 和
和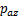 的基础上有所下降,设减小量分别为
的基础上有所下降,设减小量分别为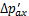 和
和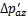 。假设隧道环向不发生变形,隧道横截面发生整体位移,故两侧位移数值相等,两侧的附加荷载变化量相等,即
。假设隧道环向不发生变形,隧道横截面发生整体位移,故两侧位移数值相等,两侧的附加荷载变化量相等,即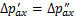 ,
,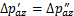 。最终,初始附加应力作用一侧(左侧和下侧)的土体附加应力分别由
。最终,初始附加应力作用一侧(左侧和下侧)的土体附加应力分别由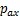 和
和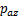 减小为
减小为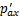 和
和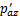 ,另一侧(右侧和上侧)的土体附加应力由0增大到
,另一侧(右侧和上侧)的土体附加应力由0增大到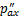 和
和 ,隧道两侧的附加应力再次趋于平衡。
,隧道两侧的附加应力再次趋于平衡。
上述各附加应力满足以下条件:
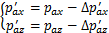 (31)
(31)
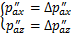 (32)
(32)
考虑隧道纵向位移,管片环与管片环之间存在错台变形,每1片管片环在发生横截面位移的过程中均会受到相邻管片的剪切约束,受到水平剪切力 及竖向剪切力
及竖向剪切力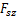 的作用。而隧道沿纵向的力远远小于水平和竖向剪切力,故在此忽略隧道纵向力的影响。
的作用。而隧道沿纵向的力远远小于水平和竖向剪切力,故在此忽略隧道纵向力的影响。
由于盾构穿越造成的既有隧道围压变化最终都将平衡,故在水平及竖直方向均满足:
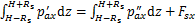 (33)
(33)
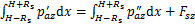 (34)
(34)
再将式(31)和(32)代入式(33)和(34)可得:
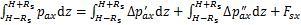 (35)
(35)
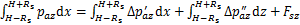 (36)
(36)
为了便于计算非线性附加荷载作用下的隧道围压及内力,本文将既有隧道横断面(y=0)单侧受到的附加荷载简化成n段线性荷载分布单元(n≥1),每段长度为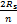 ,除了单边两侧的端点荷载之外,分别计算单边的n-1个位置的附加应力为
,除了单边两侧的端点荷载之外,分别计算单边的n-1个位置的附加应力为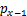 ,
,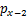 ,
,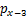 ···
···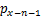 和
和 ,
,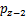 ,
,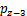 ···
···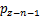 ,作为每1个荷载单元的平均值。
,作为每1个荷载单元的平均值。
由于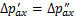 ,
,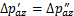 ,则有:
,则有:
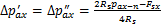 (37)
(37)
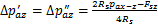 (38)
(38)
将式(38)代入式(25)和(26)即得
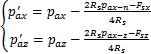 (39)
(39)
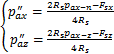 (40)
(40)
通过环向各点的附加应力,可以求得沿既有隧道环向的附加围压为
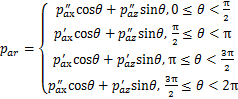 (41)
(41)
根据魏纲等[7]的研究成果可知,盾构隧道下穿既有隧道引起的隧道纵向下沉在穿越线路中轴线处(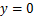 )位移最大,但管片环间错台量为0,故剪切约束力
)位移最大,但管片环间错台量为0,故剪切约束力 和
和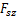 均为0。代入式(39)和(40)可得既有隧道在下部盾构穿越中轴线处截面(
均为0。代入式(39)和(40)可得既有隧道在下部盾构穿越中轴线处截面(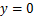 )的附加荷载分布为
)的附加荷载分布为
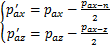 (42)
(42)
 (43)
(43)
2.3 盾构穿越引起的既有隧道内力
在盾构未施工前,既有隧道衬砌受到水土压力、自重力及环间作用力的作用,形成一个初始应力状态。图7所示为隧道初始荷载组合示意图,环向初始应力在衬砌自重G、竖向土压力Pe、侧向土压力qe,竖向静水压力Pw、侧向静水压力qw、横向土层抗力pk及拱底反力Pg的共同作用下形成。
参照文献[14],利用水土分算法及修正惯用法来求解既有隧道环向初始围压。再通过上文所述的方法求出盾构穿越对既有隧道造成的环向附加围压,两者叠加即为隧道穿越造成的最终围压。运用曙光盾构隧道设计分析软件,计算衬砌环的弯矩、剪力和轴力变化,研究盾构隧道垂直下穿对既有隧道环向受力的影响。
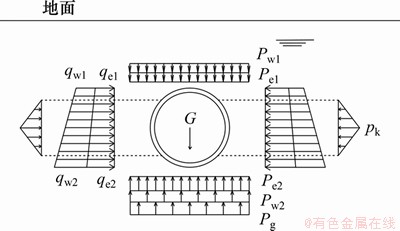
图7 隧道初始荷载组合示意图
Fig. 7 Schematic diagram of initial load combination of tunnel
3 算例分析
3.1 算例工况
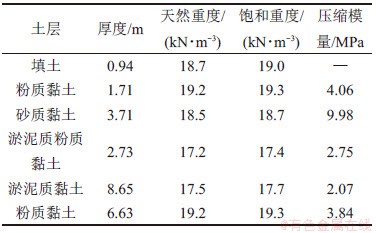
以上海某新建隧道下穿已建隧道工程作为实际案例[15]。其中,H=9.1 m,h=20.1 m,R=3.1 m,Rs=3.1 m,E=16.49 MPa,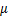 =0.35,土体损失率为1.5%。参照文献[7]和[14]及工程经验确定其他相关参数,其中,q=45 kPa,m=8.4 m,L=9 m,既有隧道衬砌混凝土为C60,弹性模量为34.5 GPa,管片厚度为0.35 m,混凝土密度为2.6 t/m3,弯曲刚度有效率为0.7,地层反力系数为5 000 kN/m3。地下水位高为地下1 m处,相关土层参数详见表1。经过本文方法计算可得f=42.7 kPa,p=115 kPa。
=0.35,土体损失率为1.5%。参照文献[7]和[14]及工程经验确定其他相关参数,其中,q=45 kPa,m=8.4 m,L=9 m,既有隧道衬砌混凝土为C60,弹性模量为34.5 GPa,管片厚度为0.35 m,混凝土密度为2.6 t/m3,弯曲刚度有效率为0.7,地层反力系数为5 000 kN/m3。地下水位高为地下1 m处,相关土层参数详见表1。经过本文方法计算可得f=42.7 kPa,p=115 kPa。
表1 算例各土层相关参数
Table 1 Relevant parameters of each soil layer from calculation
3.2 计算结果及分析
3.2.1 盾构掘进过程中附加荷载变化
图8(a)所示为既有隧道左侧端点(-3.1,0和 9.1 m)随着盾构切削面从x=-50 m掘进到x=50 m过程中受到的水平附加应力变化曲线,其中负号和正号分别表示盾构切削面位于穿越前或穿越后。当盾构切削面在(-20 m,-10 m)区间掘进时,左侧端点受到的水平附加荷载变化幅度较大,从-1.29 kPa变化到0.91 kPa,其余区段多表现为波动变化,变幅较小。从影响因素上分析,影响水平附加荷载的最大因素为盾壳侧摩阻力和土体损失,且土体损失影响水平附加荷载的规律与盾壳侧摩阻力的相反,而附加注浆力和附加推力的影响较小。
图8(b)所示为既有隧道下端点(0,0,12.2 m)受到的竖直附加应力变化曲线。由图8(b)可知:下端点受到的附加荷载开始趋近于0,当盾构切削面到达x=-20 m左右时,其值急剧增加;在切削面正好经过下端点正下方时,竖向附加荷载接近最大,其值约为7 kPa;之后受到的附加荷载开始下降,于x=10 m处其值达到最小,约为5.2 kPa;紧接着竖向附加荷载开始回升,并最终稳定在7.62 kPa左右。从影响因素分析,在-50 m到-20 m的区域,竖向附加荷载变化较小;在-20 m到20 m的区域,盾壳侧摩阻力、土体损失和盾尾附加注浆力共同影响竖向附加荷载;在20 m右侧的区域,土体损失逐渐成为影响竖向附加荷载的主要因素。其中,随着盾构掘进,土体损失对既有隧道造成的竖向附加荷载变化规律与文献[16-17]研究成果类似,总应力的变化规律及影响范围与文献[18]研究成果类似,进一步验证了本文方法的可靠性。
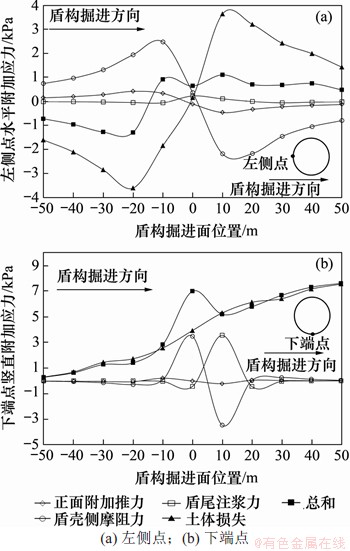
图8 既有隧道左侧点和下端点附加应力随盾构掘进变化曲线
Fig. 8 Curve of additional stress at left point and lower end point of existing tunnel with shield tunneling
3.2.2 既有隧道衬砌围压及内力计算
从上述关于盾构掘进对既有隧道的附加荷载影响曲线可知:当盾构切削面掘进到x=50 m时,既有隧道受到的附加荷载趋于稳定状态,故定义此处的附加荷载状态作为盾构穿越后的应力状态。
图9所示为案例中盾构下穿前后既有隧道在y=0处横断面的围压变化。由图9可知:在盾构穿越前,则既有隧道所受到的围压呈现左右对称;若以水平向右为0°,则沿逆时针方向,环向围压在45°,135°,225°和315°位置较大,围压分别为143.60,143.60,224.02和224.02 kPa;而在0°,90°,180°和270°处较小,围压分别为101.19,113.75,101.19和203.77 kPa。盾构穿越后,环向围压总体均有所减少,但分布规律未变。
图10所示为盾构下穿后既有隧道在y=0处横截面的附加围压,图10中环向虚线为附加围压为0 kPa的参照基准线。由图10可知:环向附加围压近似呈现“竖椭圆形”,大致呈对称分布,且在隧道拱顶和拱底的位置降低幅度最大,达到 -3.82 kPa,靠近左右侧拱腰处降低幅度逐渐趋于0 kPa。出现该分布规律的原因可能是当盾构掘进至x=50 m处时,既有隧道面受到的竖向附加荷载值大于横向附加荷载,成为影响围压的主要因素。
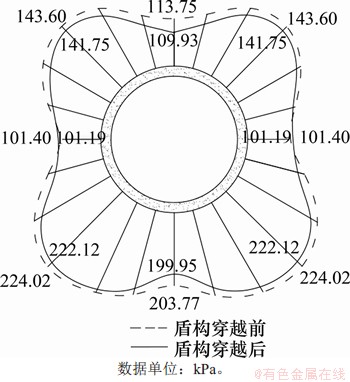
图9 盾构穿越前后的围压变化
Fig.9 Diagram of changes of confining pressure before and after shield crossing
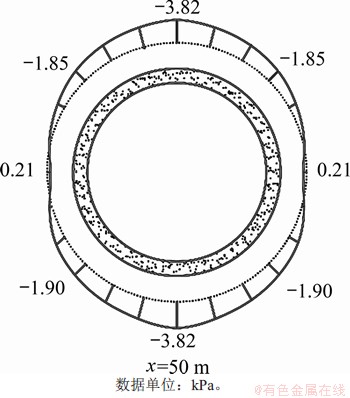
图10 盾构下穿后附加围压
Fig. 10 Diagram of additional confining pressure after shield penetration
根据修正惯用法,利用曙光盾构软件研究管片内力。图11所示为盾构穿越前后既有隧道环向弯矩、剪力及轴力的对比分析。
由图11(a)可见:1) 在盾构穿越前,盾构环向附加弯矩呈左右对称分布,两侧拱腰受到负弯矩作用,拱顶和拱底受到正弯矩作用。最大弯矩分别出现在90°以及270°位置处,分别为153.93 kN·m和117.00 kN·m,而左右两侧拱腰弯矩均为-133.82 kN·m。2) 在盾构穿越后,环向弯矩的分布规律基本保持不变,但整体的正弯矩和负弯矩数值均有所减小,90°和270°处的正弯矩分别减小为147.29 kN·m和110.39 kN·m,分别降低了4.3%和5.6%;0°和180°处的负弯矩减小为-127.28 kN·m,减小幅度为4.9%。
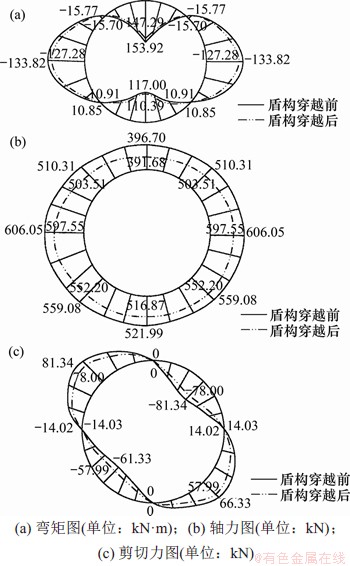
图11 盾构穿越前后衬砌内力变化
Fig. 11 Changes of lining internal forces before and after shield crossing
由如图11(b)可见:环向轴力在穿越前和穿越后分布规律一致:在水平方向上,左右侧受到的轴力相等,呈对称分布;在竖向方向上,上部受到的轴力要明显小于下部所受的轴力,呈“上小下大”分布;盾构穿越后,环向轴力均有所减小,在0°,90°,180°和270°位置处内力分别由穿越前的606.05,396.70,606.05和521.99 kN减小为597.55,391.68,597.55和516.87 kN,依次减小了1.4%,1.3%,1.4%和1.0%。
由如图11(c)可见:盾构穿越前后的剪切力分布规律大致相同。在0°,90°,180°和270°位置处,穿越前后的剪切力较小且变化不大。在45°和225°位置处隧道受到的剪切力为负值,穿越前剪切力依次为-81.34 kN和-61.33 kN,穿越后分别变为-78.00 kN和-57.99 kN,分别减小了4.1%和5.4%。在135°和315°位置处隧道受到正向剪切力作用,变化规律相同。
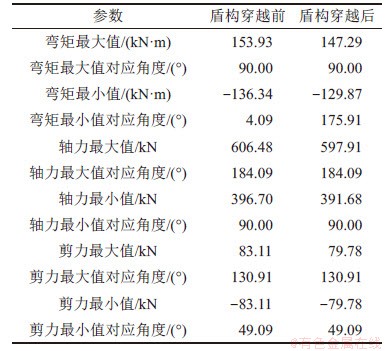
表2所示为盾构穿越前后衬砌内力极值及分布位置,由表2可见:既有隧道环向弯矩、轴力和剪力的最大值、最小值分布位置基本上未发生改变。弯矩最大值位于90°位置处,弯矩最小值位于两侧拱腰位置附近,分别为175.91°和4.09°;轴力最大值位于拱腰部分,角度为184.09°,轴力最小值位于拱顶,角度为90.00°;剪力的最大值位于130.91°,剪力的最小值位于49.09°。参照文献[19]利用有限元模拟得到的结果,本文得到的环向弯矩、轴力分布图及穿越前后的变化规律与之相似。
表2 盾构穿越前后衬砌内力极值及分布位置
Table 2 Extreme internal force and distribution location of shield tunnel lining before and after crossing
3.3 影响因素分析
利用本文方法可以进一步研究盾构在不同埋深和掘进位置处对既有隧道不同横断面产生的围压及内力影响。
取案例中的既有隧道埋深h=20.1 m,与h为25和30 m工况下既有隧道受到的附加荷载进行对比研究。研究的既有隧道横断面为y=0 m处,盾构掘进面位置取为x=0 m。研究结果显示:下穿盾构埋深h增大会减少对既有隧道的围压影响,但影响下降趋势逐渐减缓;随着埋深h变化,附加围压和附加弯矩的分布模式基本保持一致。
针对掘进面离既有隧道不同距离情况下对既有隧道的不同影响展开研究。取案例中盾构切削面依次在x=-50,-20,0,20和50 m处,对既有隧道所受的环向附加围压及弯矩进行对比研究。研究的既有隧道断面为y=0 m处,且盾构埋深为20.1 m,其余参数不变。
研究结果显示:
1) 随着盾构掘进,既有隧道受到的影响先增大、后减小,且在隧道上下拱顶位置的附加围压及弯矩变化较大,两侧拱腰位置变幅相对较小。其附加围压分布模式由“横椭圆分布”逐渐转换为最终稳定的“竖椭圆分布”。参照文献[20],本文关于环向最大附加围压分布的描述与之相似,从侧面验证了本文得到的附加围压变化规律的可靠性;
2) 附加弯矩在0°,90°,180°和270°这4个位置变化较大。随着盾构逐渐靠近既有隧道,附加弯矩逐渐增长为最大。在盾构穿越既有隧道后,切削面逐渐远离既有隧道,受到的附加弯矩先较快下降,后又逐渐回升直至趋于稳定。该变化规律主要是因为当盾构靠近既有隧道的过程中,既有隧道受到水平及竖向附加荷载的作用,管片表现为“加载”状态,环向弯矩明显增大;当盾构穿过既有隧道后,土体损失的影响逐渐加大,既有隧道受到“卸载”作用,环向弯矩减小;随着盾构逐渐远离,“卸载”作用减弱,环向弯矩回升。该环向弯矩随盾构掘进面移动的变化规律与文献[21-22]通过有限元方法得到的变化规律相似。
针对盾构下穿对既有隧道纵向不同横断面的影响规律进行研究。取案例中既有隧道依次在y为0,5和10 m处的环向附加围压进行对比研究。研究的盾构隧道埋深h=20.1 m,切削面位于x=0 m处。研究结果显示:随着研究断面逐渐远离穿越中心点,环向附加围压的分布模式由“竖椭圆分布”逐渐变为“横椭圆分布”,而附加弯矩先是大幅减小,后略有增加。
4 结论
1) 盾构穿越前既有隧道的环向围压呈左右对称分布,其值在45°,135°,225°和315°处较大,在0°,90°,180°和270°处较小。盾构近距离下穿会减小既有隧道环向围压,且减小的附加围压总体呈“竖椭圆形”分布。
2) 盾构下穿会引起既有隧道的环向弯矩、剪力和轴力有所减小,且弯矩和剪力的变化幅度更加显著,而轴力变化影响较小。
3) 随着下穿盾构埋深增加,既有隧道受到的附加围压和弯矩的影响逐渐减小,且减小速度逐渐放缓;盾构切削面从逐渐靠近到逐渐远离的整个穿越过程中,隧道在上下拱顶及拱底部分的附加围压、弯矩变化较大,而在左右两侧拱腰部分的影响相对较小;在靠近穿越中心点的横断面上附加围压呈“竖椭圆形”分布,随着研究断面距离中点的y逐渐增大,环向受到的附加围压逐渐呈“横椭圆形”分布。
4) 本文在计算既有隧道附加荷载时对管片环的荷载分布和土层性质进行了简化,在求解隧道环向围压及内力过程中,将受到的附加荷载简化为4段线性荷载分布单元,有待后续进一步精细化研究。另外,管片本身的形状和分块对内力分布有重要影响,后续可以加强对这方面研究。
参考文献:
[1] MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Physics, 1936, 7(5): 195-202.
[2] 齐静静, 徐日庆, 魏纲, 等. 隧道盾构法施工引起周围土体附加应力分析[J]. 岩土力学, 2008, 29(2): 529-534, 544.
QI Jingjing, XU Riqing, WEI Gang, et al. Analysis of superimposed stress of surrounding soil due to shield tunneling[J]. Rock and Soil Mechanics, 2008, 29(2): 529-534, 544.
[3] 齐静静, 徐日庆, 魏纲. 双线平行盾构法隧道施工附加荷载的计算分析[J]. 岩土力学, 2009, 30(6): 1665-1670.
QI Jingjing, XU Riqing, WEI Gang. Analysis and calculation of superimposed load induced by double parallel shield tunnelling[J]. Rock and Soil Mechanics, 2009, 30(6): 1665-1670.
[4] 王涛, 徐日庆, 齐静静, 等. 盾构掘进引起的土体附加应力场分析[J]. 浙江大学学报(工学版), 2008, 42(11): 2009-2014.
WANG Tao, XU Riqing, QI Jingjing, et al. Additional stress field of surrounding soil due to shield tunneling[J]. Journal of Zhejiang University(Engineering Science), 2008, 42(11): 2009-2014.
[5] 张琼方, 林存刚, 丁智, 等. 盾构近距离下穿引起已建地铁隧道纵向变形理论研究[J]. 岩土力学, 2015, 36(S1): 568-572.
ZHANG Qiongfang, LIN Cungang, DING Zhi, et al. Theoretical analysis of vertical deformation of existing metro tunnel induced by shield tunneling under-passing in a short distance[J]. Rock and Soil Mechanics, 2015, 36(S1): 568-572.
[6] 魏纲, 俞国骅, 杨波. 新建隧道上穿既有隧道引起的剪切错台变形研究[J]. 自然灾害学报, 2018, 27(4): 50-58.
WEI Gang, YU Guohua, YANG Bo. Study on shearing dislocation platform deformation of existing tunnel due to construction of above-crossing new tunnel[J]. Journal of Natural Disasters, 2018, 27(4): 50-58.
[7] 魏纲, 俞国骅, 杨波. 新建盾构隧道下穿既有隧道剪切错台变形计算[J]. 湖南大学学报(自然科学版), 2018, 45(9): 103-112.
WEI Gang, YU Guohua, YANG Bo. Calculation of existing shield tunnel shearing dislocation platform deformation due to undercrossing new shield tunnel undercrossing[J]. Journal of Hunan University(Natural Sciences), 2018, 45(9): 103-112.
[8] 张长强, 翟志国, 陈明娟, 等. 富水砂卵石地层中大直径泥水盾构同步注浆技术[J]. 中国工程科学, 2010, 12(12): 75-78, 88.
ZHANG Changqiang, ZHAI Zhiguo, CHEN Mingjuan, et al. Synchronous grouting of large diameter slurry shield in water-rich sandy gravel stratum[J]. Engineering Sciences, 2010, 12(12): 75-78, 88.
[9] 梁荣柱, 夏唐代, 林存刚, 等. 盾构推进引起地表变形及深层土体水平位移分析[J]. 岩石力学与工程学报, 2015, 34(3): 583-593.
LIANG Rongzhu, XIA Tangdai, LIN Cungang, et al. Analysis of ground surface displacement and horizontal movement of deep soils induced by shield advancing[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 583-593.
[10] 朱合华, 徐前卫, 廖少明, 等. 土压平衡盾构施工的顶进推力模型试验研究[J]. 岩土力学, 2007, 28(8): 1587-1594.
ZHU Hehua, XU Qianwei, LIAO Shaoming, et al. Experimental study on thrust force during tunnel excavation with earth pressure balance shield machine[J]. Rock and Soil Mechanics, 2007, 28(8): 1587-1594.
[11] 林存刚. 盾构掘进地面隆陷及潮汐作用江底盾构隧道性状研究[D]. 杭州: 浙江大学建筑工程学院, 2014: 111-128.
LIN Cungang. Research on shield tunnelling-induced ground surface heave and subsidence and behavior of underwater shield-driven tunnels subject to tidal bores[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2014: 111-128.
[12] SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Geotechnique, 1987, 37(3): 301-320.
[13] 姜忻良, 赵志民. 镜像法在隧道施工土体位移计算中的应用[J]. 哈尔滨工业大学学报, 2005, 37(6): 801-803.
JIANG Xinliang, ZHAO Zhimin. Application of image method in calculating tunneling-induced soil displacement[J]. Journal of Harbin Institute of Technology, 2005, 37(6): 801-803.
[14] 魏纲, 洪文强, 魏新江, 等. 偏心堆载引起的盾构隧道横向受力理论计算[J]. 中南大学学报(自然科学版), 2019, 50(7): 1645-1654.
WEI Gang, HONG Wenqiang, WEI Xinjiang, et al. Theoretical calculations of transverse force on shield tunnel caused by eccentric load[J]. Journal of Central South University(Science and Technology), 2019, 50(7): 1645-1654.
[15] 张冬梅, 宗翔, 黄宏伟. 盾构隧道掘进引起上方已建隧道的纵向变形研究[J]. 岩土力学, 2014, 35(9): 2659-2666.
ZHANG Dongmei, ZONG Xiang, HUANG Hongwei. Longitudinal deformation of existing tunnel due to underlying shield tunneling[J]. Rock and Soil Mechanics, 2014, 35(9): 2659-2666.
[16] 魏纲, 洪杰, 魏新江. 双圆盾构隧道施工对平行既有隧道的影响分析[J]. 岩土力学, 2012, 33(S2): 98-104.
WEI Gang, HONG Jie, WEI Xinjiang. Analysis of influence of DOT shield tunneling on existed adjacent tunnel[J]. Rock and Soil Mechanics, 2012, 33(S2): 98-104.
[17] 洪杰. 双圆盾构隧道施工扰动及对周边构筑物影响研究[D]. 杭州: 浙江大学建筑工程学院, 2013: 67-71.
HONG Jie. Study on DOT shield tunnel construction disturbance and its impact on surrounding structures[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2013: 67-71.
[18] 华珊珊. 新建隧道上跨或下穿施工对既有隧道力学响应研究[D]. 徐州: 中国矿业大学土木学院, 2018: 40-58.
HUA Shanshan. Study on the mechanical response of above-crossing or under-crossing tunnelling on the existing tunnel[D]. Xuzhou: China University of Mining and Technology. Civil Engineering College, 2018: 40-58.
[19] 赵青. 盾构隧道三维数值分析方法与衬砌力学特性研究[D]. 成都: 西南交通大学土木工程学院, 2017: 49-59.
ZHAO Qing. Study on three dimensional numerical modeling method of shield tunnel and mechanical properties of lining[D]. Chengdu: Southwest Jiaotong University. Civil Engineering College, 2017: 49-59.
[20] 康佐, 代光辉. 地铁盾构法隧道正交下穿施工对既有隧道影响分析[J]. 隧道建设, 2014, 34(10): 931-936.
KANG Zuo, DAI Guanghui. Shield boring of metro tunnel perpendicularly crossing underneath existing tunnel: analysis on influence of shield boring on existing tunnel[J]. Tunnel Construction, 2014, 34(10): 931-936.
[21] 方勇, 何川. 盾构法修建正交下穿地铁隧道对上覆隧道的影响分析[J]. 铁道学报, 2007, 29(2): 83-88.
FANG Yong, HE Chuan. Analysis of influence of undercrossing subway shield tunneling construction on the overlying tunnel[J]. Journal of the China Railway Society, 2007, 29(2): 83-88.
[22] 方晓慧, 王星华. 盾构隧道近距离正交下穿复杂地下结构的影响分析[J]. 铁道科学与工程学报, 2014, 11(1): 60-66.
FANG Xiaohui, WANG Xinghua. The impact analysis of shield tunnel close undercrossing complex underground structure[J]. Journal of Railway Science and Engineering, 2014, 11(1): 60-66.
(编辑 秦明阳)
收稿日期: 2020 -02 -09; 修回日期: 2020 -04 -27
基金项目(Foundation item):浙江省公益技术应用研究计划项目(LGF19E080002) (Project(LGF19E080002) supported by the Public Technology Application Research Program of Zhejiang Province)
通信作者:张苑竹,博士,副教授,从事隧道混凝土研究;E-mail:zhangyz@zucc.edu.cn