文章编号：1004-0609(2012)03-0934-06
物探数据三角网逆生长网格化方法
李瑞雪1, 2，张道军3，黄 龙3，席振铢1, 2，王 鹤1, 2，冯万杰1, 2
(1. 中南大学 有色金属成矿预测教育部重点实验室，长沙 410083；
2. 中南大学 地球科学与信息物理学院，长沙 410083；2. 长沙五维地科勘察技术有限责任公司，长沙 410205)
摘 要：针对矩形网格化方法和传统三角网格化方法的不足，提出一种三角网逆生长网格化方法。该方法首先根据离散物探数据的特点提取数据边界，然后以边界作为基础由外向内逆向生长构建三角网。应用某测区的EH4电磁测深数据进行网格化及可视化分析。实验结果表明：该方法能够在当前数据条件下智能地生成高质量的不规则三角网，且边界拟合算法简单精确，可以为后续的数据可视化和资料处理解释提供良好的基础。
关键词：物探数据；网格化；三角网；生长算法
中图分类号：P623.6 文献标志码：A
Inverse growth algorithm for
creating triangular mesh of geophysical data
LI Rui-xue1, 2, ZHANG Dao-jun3, HUANG Long3, XI Zhen-zhu1, 2, WANG He1, 2, FENG Wan-jie1, 2
(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,
Central South University, Changsha 410083, China;
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Changsha 5D Geo-survey & Technical Co., Ltd., Changsha 410205, China)
Abstract: To solve those problems existed in rectangular grid and triangular mesh method, an inverse growth algorithm for the geophysical data was presented. According to the characteristics of discrete geophysical data, the data boundary was extracted first, and then triangular mesh was generated from outside to inside by using the boundary as the basis. This algorithm was used to triangulation and visualization analysis of an EH4 sounding profile data. The result states that, high-quality irregular triangular mesh can be generated automatically, and the data boundary is fitted easily and accurately, a good foundation is provided for data visualization and data processing.
Key words: geophysical data; gridding; triangular mesh; growth algorithm
目前，常用于物探数据成图的软件有Surfer、Grapher、AutoCAD和MapGIS等，其中Surfer和Grapher属于科学绘图软件，有良好的成图功能但图件的编辑能力相对较弱；AutoCAD是辅助设计软件，在图件编辑方面有极强优势但不具备物探数据成图功能；MapGIS等是地理信息系统软件，可用于物探数据的处理但通常需要与其他软件结合使用，这些软件都不是针对物探专业开发。专用于物探数据可视化的软件开发具有重要意义，而数据的网格化是其可视化的基础，所以，很有必要研究适用于物探数据的网格化方法。
所谓网格化就是将平面区域划分为规则或不规则的格网，然后通过一定的方法得到网格节点处的物理量值。网格化方法广泛应用于有限元计算、计算机辅助几何设计及可视化分析。早期出现的网格化主要采用矩形网格化方法，但因其网格单元结构简单，在对复杂地形的拟合方面灵活性较差，逐步发展到四边形网格化方法[1]，1970年后开始出现了以三角形为网格单元的网格化方法。目前，Delaunay三角网是公认的最优三角网，已有许多专家学者对此进行了深入的研究和相应的改进[2-9]。1975年到1978年，SHAMOS和HOEY[2]、LAWSON[3]以及GREEN和SIBSON[4]先后提出了分治算法、逐点插入算法及生长算法等主流三角网格化算法，1987年CHEW[5]提出了Delaunay细化算法并成功应用于均匀二维网格，改进了网格质 量，但未提及边界的拟合问题，1998年杨钦等[6]解决了平面任意域离散点集的三角网格化问题，解决了边界拟合的问题，但计算过程复杂。
在地球物理学领域，国内外研究学者越来越关注三角网格化方法[10-15]。1986年，WANNAMAKER 等[10]在研究有限元二维电磁响应时用三角网格化方法剖分了带地形的二维模型，1999年，阮百尧等[11]采用三角网格对激发极化数据进行了二维反演，2000年，李桐林等[12]研究了规则边界地震模型的三角网格化方法，2006年，汤井田等[13]介绍了任意复杂地球物理模型的三角剖分。可见，三角网格化方法在地球物理学领域的应用集中在正反演计算的模型剖分，而应用到物探数据的可视化分析则较少。例如，2010年，刘兆平等[16]对于物探数据网格化的研究仍集中在矩形网格化方法上。
基于上述分析，本文作者拟在三角网生长法的基础上，充分考虑物探数据既有的分布离散但不趋于平均以及边界点明确等特点，提出一种三角网逆生长网格化方法。有别于传统的三角网生长法首先生成一个三角形作为生长基础再向外扩展构建三角网，本算法在构网时首先计算边界，再由边界作为基础进行扩展，通过距离和最小原则保证三角网质量，自外向内逆向生长构建三角网。
1 三角网逆生长网格化方法原理
三角网逆生长网格化方法区别于普通生长法的特点是构网时先处理边界。其实现步骤是首先根据物探数据的特点提取边界点，生成边界边；然后以这些边界边为基础，逐一选取其最佳第三点，构建新边及三角形；再以新生成的边为基础重复上述过程，直到所有离散点都成为三角网的节点，整个三角网构建完毕。
1.1 地球物理数据边界提取
三角网逆生长网格化方法是以边界边为基础进行生长的，在构网时必须首先提取边界。
地球物理数据的每一个数据点都包括坐标信息及属性信息。物探测深数据在纵向上成列分布，横向上与地形及地下构造相关，一般浅部数据密集，深部相对稀疏，在整个空间上分布离散且不均匀；一条测线上的边界数据点包括最小号、最大号测点的全部数据以及其他号测点的最浅部和最深部数据，这些数据点信息明确，易识别提取。对于物探平面数据，其规律更加明确，边界数据仅由测线测点号即能识别。边界点的提取可以由任意一点开始，为了便于生成边界边及扩展边界边，确定第一个边界点后，按照顺时针或逆时针的顺序顺次提取相邻的边界点；得到全部边界点并依次连接，从而得到整个离散数据集的闭合边界。
1.2 点线位置关系判断
对三角网中的任意一边进行扩展时，并不是离散点集内的任意一点都有成为该边最佳第三点的可能，最佳的第三点只存在于一定的范围内。如图1所示，边P1P2已存在于三角形P1P2P3中，因此，有可能成为该边的最佳第三点的点只可能存在于P1P2所在直线的右侧。在扩展过程中，对任何一条边的扩展都需要先通过判断点线位置关系求取符合这一范围要求的点。目前常用的点线位置关系的判断通常利用直线判别正负区的原理[12]，即首先建立直线判别式，然后将待扩展边的两端点代入方程判别式计算系数，最后将第三点代入直线方程判别式，根据所得值的符号判断该点位于待扩展边的哪一侧。该判别方法计算过程比较复杂，而利用向量方法则可以大大简化这一过程。
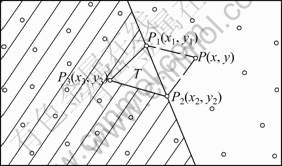
图1 向量叉积判断点线位置关系
Fig. 1 Judgment of position relationship of point and edge using vector cross product
对于某一内部边，需要判断一点是否位于该边所在三角形的对顶点的异侧，对于边界边，需要判断一点是否位于该边的内侧。利用向量叉积，可以简单地实现二者的判断。如图1所示，判断任意点P与点P3位于边P1P2的同侧或异侧，只需将边P1P2、P1P3和P1P分别看作向量，首先根据式(1)和式(2)计算向量P1P2与P1P3以及向量P1P2与P1P的叉积，根据向量叉积的右手法则，可知向量P1P2与P1P3的叉积为负，向量P1P2与P1P的叉积为正；然后将两叉积的结果相乘，所得数值如果小于0，则点P位于点P3的异侧，大于0则点P位于点P3的同侧，若等于0，则点P位于边P1P2所在的直线上。对于边界边的扩展，同样可以利用该方法判断点线位置，如果构造边界时是顺时针方向连接边界，则取点时只取位于边界右侧的点。在图1中假设边P1P2是离散数据集的一段边界，取其左侧的点，假设为P3，根据式(1)计算向量P1P2与P1P3的叉积，为负值就可以满足要求。
(1)
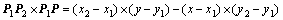(2)
1.3 最佳三角形的构建
尽管对不均匀的离散数据进行网格化只能生成不规则的三角网，但是在实际应用中仍希望网格单元尽量趋近于饱满，即每个三角形尽量接近正三角形。网格质量的好坏将直接影响后续计算的精度。三角形外接圆半径与内切圆半径的比值称为三角形的横纵比(Aspect radio)。用三角形的横纵比来衡量三角形的质量，具有大的横纵比的三角形至少有一个小角且三个顶点接近共线。如图2所示，有两种质量差的三角形单元，没有短边的Blade和有一个短边的Dagger。
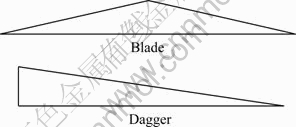
图2 两种畸形三角形单元
Fig. 2 Two kinds of deformed triangle element
在进行网格化时，利用距离和最小准则能保证离散点集中最邻近的三点构成三角形，避免生成畸形三角形单元及三角形的交叉。第三点的确定，是通过使用三角形边角关系的余弦定理来进行的：三角形中任意两边的平方和减去此两边与其夹角的余弦值等于第三边的平方，即：
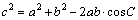(3)
由式(3)可得
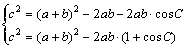(4)
对于固定的c，C角越大，cosC值越小，-2ab· (1+cosC)越大，a+b也就越小。如图1所示，如果某点P的角C在每个满足条件的点与待扩展边所构成的三角形中是最大的，那么点P距离待扩展边两端点P1、P2的距离之和最小，该三点是离散点集中最邻近的三点，选该点P为第三点满足最小距离和准则，所生成的三角形符合最佳三角形条件。
2 三角网逆生长网格化方法实现
本算法的实现采用C Sharp语言，算法流程图如图3所示，生长示意图如图4所示。
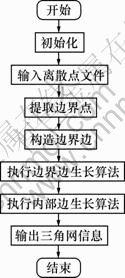
图3 程序流程图
Fig. 3 Program flow chart
具体实现步骤：
Step 1: 如图4(a)所示，对于给定的点集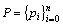
，首先按次序提取其边界点并加入边界点集
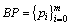。如图4(b)所示，利用边界点集构造边界边并加入边界边集
。
for (int i=0; i＜m-1; i++)
{Edge edge=new Edge (BP[i], BP[i+1]);
BE. Add(edge);}
Edge edge=new Edge (BP[m], BP[0]);
BE. Add(edge);
图4 三角网逆生长示意图: (a) 离散点集; (b) 边界提取; (c) 边界边生长; (d) 内部边生长
Fig. 4 Triangular mesh inverse growth sketch: (a) Discrete points set; (b) Boundary extraction; (c) Boundary growth; (d) Inner boundary growth
Step 2: 如图4(c)所示，对边界执行生长算法，判断边界边的三角形数量，若等于0，对该边进行扩展，查找其最佳第三点，构造新边，判断该边是否存在，若不存在，加入内部边集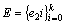
。
for (int i=0; i＜m+1; i++)
{ if (BE[i]. TriangleCount == 0)
{ Point p=Findpoint(BE[i], P);
Edge e=new Edge (BE[i]. p[1], p);
if(!Checkexist(e)) {E.Add(e);}
Edge e=new Edge (BE[i]. p[0], p);
if( !Checkexist(e)) {E.Add(e);}
}
}
Step 3: 如图4(d)所示，对内部边执行生长算法，判断内部边的三角形数量，若等于1，对该边进行扩展，查找其最佳第三点，构造新边，判断该边是否存在，若不存在，加入内部边集。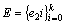
for (int i = 0; i ＜ E.Count; i++)
{ if (E[i].TriangleCount==1)
{ Point p=Findpoint(E[i], P);
Edge e=new Edge(E[i].p[1], p);
if(!Checkexist(e)) {E.Add(e);}
Edge e=new Edge(E[i].p[0], p);
if(!Checkexist(e)) {E.Add(e);}
}
}
3 实例
应用某测区的EH4电磁测深数据，分别用传统三角网生长法及三角网逆生长法进行处理，得到如图5和6所示实验结果。由图5可见，图5(a)和图5(b)所示分别为应用传统三角网生长法和三角网逆生长法得到的不规则三角网，图5(a)中虚线部分为未被正确拟合的边界。由图6可见，图6(a)和图6(b)所示分别为应用两个不规则三角网进行可视化分析得到的等值线图，图6(a)中，①处的等值线在地表处并不存在，是虚假等值线，②处的等值线超出数据区域，不合理。通过对比分析可知，三角网逆生长网格化方法得到的不规则三角网边界拟合更准确，效果更好，应用于可视化分析所绘制的等值线均位于数据范围以内，在地表以上没有形成虚假的等值线，深部也未存在不合理的等值线。
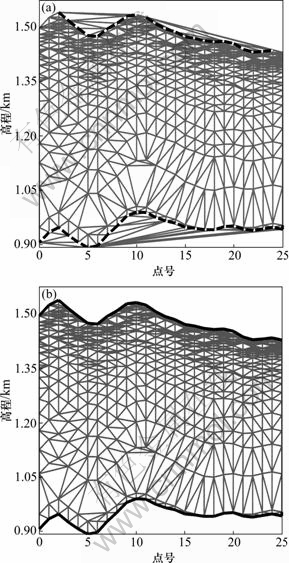
图5 三角网格化结果对比: (a) 生长法三角网格化结果; (b) 逆生长法三角网格化结果
Fig. 5 Comparison of triangulation results: (a) Triangulation result of growth algorithm; (b) Triangulation result of inverse growth algorithm
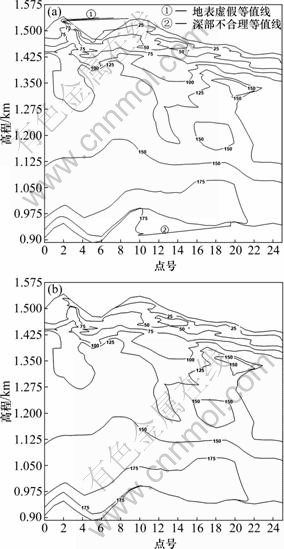
图6 可视化结果对比: (a) 生长法可视化结果; (b) 逆生长法可视化结果
Fig. 6 Comparison of visualization results: (a) Visualization result of growth algorithm; (b) Visualization result of inverse growth algorithm
4 结论
1) 三角网逆生长网格化方法思路简单，算法稳定，生成的三角网符合Delaunay准则，质量最优且唯一，能简单而精确地拟合物探数据的复杂边界。
2) 相比于常用的矩形网格化方法，三角网逆生长网格化方法得到的网格节点值全部是原始数据，避免了大量的数值计算以及由此引起的误差；相比于传统的三角网生长算法，恰当地应用了物探数据的特点进行边界处理，避免了复杂的边界计算，应用于物探数据处理及资料解释符合实际情况，以此为基础的可视化计算得到的等值线图不产生非法等值线。
REFERENCES
[1] 李海生. Delaunay三角剖分理论及可视化应用研究[M].哈尔滨: 哈尔滨工业大学出版社, 2010: 4-7.
LI Hai-sheng. Study of Delaunay triangulation theory and visualization applications [M]. Harbin: Harbin Institute of Technology Press, 2010: 4-7.
[2] SHAMOS M I, HOEY D. Closest-point problems[C]//IEEE Computer Society. Proceedings of the 16th Annual Symposium on the Foundations of Computer Science. New York: ACM Press, 1975: 151-162.
[3] LAWSON C L. Software for C1 surface interpolation [C]// RICE J R. Mathematical software Ⅲ. New York: Academic Press, 1977: 161-194.
[4] GREEN P J, SIBSON R. Computing dirichlet tessellations in the plane [J]. The Computer Journal, 1978, 21(2): 168-173.
[5] CHEW L P. Constrained Delaunay triangulations [C]// SIGGRAPH. Proceedings of the Third Annual Symposium on Computational Geometry. New York: ACM Press, 1987: 215- 222.
[6] 杨 钦, 徐永安, 陈其明, 谭建荣. 任意平面域离散点集的三角化方法[J]. 软件学报, 1998, 9(4): 241-245.
YANG Qin, XU Yong-an, CHEN Qi-ming, TAN Jian-rong. Triangulation algorithm of scattered data on arbitrary planar domain [J]. Journal of Software, 1998, 9(4): 241-245.
[7] 刘少华, 程朋根, 赵宝贵. 约束数据域的Delaunay三角剖分算法研究及应用[J]. 计算机应用研究, 2006(3): 26-28.
LIU Shao-hua, CHENG Peng-gen, ZHAO Bao-gui. A study on algorithm of Delaunay triangulation for the constrained data set and application [J]. Application Research of Computers, 2006(3): 26-28.
[8] 高晓枫. 2D-Delaunay三角网格的数据结构与遍历[J].天津理工大学学报, 2006, 22(2): 66-69.
GAO Xiao-feng. Data structure and traverse of 2D-Delaunay triangulation [J]. Journal of Tianjin University of Technology, 2006, 22(2): 66-69.
[9] 周佳文, 薛之昕, 万 施. 三角剖分综述[J]. 计算机与现代化, 2010(7): 75-79.
ZHOU Jia-wen, XUE Zhi-xin, WAN Shi. Survey of triangulation methods [J]. Computer and Modernization, 2010(7): 75-79.
[10] WANNAMAKER P E, SYODT J A, RIJO L. Two dimensional topographic responses in magnetollurics modeled using finite elements [J]. Geophysics, 1986, 51(11): 2131-2144.
[11] 阮百尧, 村上裕, 徐世浙. 激发极化数据的最小二乘二维反演方法[J]. 地球科学: 中国地质大学学报, 1999, 24(6): 619-624.
RUAN Bai-yao, YUTAKA Murakami, XU Shi-zhe. Least square 2-D inversion method for induced polarization data [J]. Earth Science: Journal of China University of Geosciences, 1999, 24(6): 619-624.
[12] 李桐林, 齐守奎, 赵海珍. 有限元金属矿地震波场模拟中三角网的自动剖分与模型编辑[J]. 铀矿地质, 2000, 16(1): 42-45.
LI Tong-lin, QI Shou-kui, ZHAO Hai-zhen. Automatic area dividing and editing techniques for finite element ore deposit seismic modeling [J]. Uranium Geology, 2000, 16(1): 42-45.
[13] 汤井田, 任政勇, 化希瑞. 任意地球物理模型的三角形和四面体有限单元剖分[J]. 地球物理学进展, 2006, 21(4): 1272-1280.
TANG Jing-tian, REN Zheng-yong, HUA Xi-rui. Triangle and tetrahedral finite element meshing fromarbitrary geophysical model data [J]. Progress in Geophysics, 2006, 21(4): 1272-1280.
[14] KERRY K, CHESTER W. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example [J]. Geophysics, 2006, 71(6): 291-299.
[15] TANG Jing-tian, WANG Fei-yan, REN Zheng-yong. 2.5-D DC resistivity by adaptive finite-element method with unstructured triangulation [J].Chinese Journal of Geophysics, 2010, 53(3): 708-716.
[16] 刘兆平, 杨 进, 武 炜. 地球物理数据网格化方法的选取[J]. 物探与化探, 2010, 34(1): 93-97.
LIU Zhao-ping, YANG Jin, WU Wei. The Choice of gridding methods for geophysical data [J]. Geophysical and Geochemical Exploration, 2010, 34(1): 93-97.
(编辑 何学锋)
基金项目：国家“十一五”科技支撑计划资助项目(2006BAB01B07)
收稿日期：2011-12-01；修订日期：2012-01-04
通信作者：席振铢，教授；电话：13873150690；E-mail: xizhenzhu@163.com
