圆钢管混凝土梁柱节点变形性能分析
宋彬彬1,付功义2
(1. 湖南理工学院 土木建筑工程学院,湖南 岳阳,414006;
2. 上海交通大学 船舶海洋与建筑工程学院,上海,200030)
摘要:基于梁柱节点是保证圆柱钢管混凝土结构工作性能的重要部位,对15个圆钢管混凝土结构梁柱节点局部构件单向及双向的静载试验结果进行分析,研究柱-钢梁节点的变形性能及延性系数计算方法。以试验结果为基础,采用线性回归分析方法得到的延性系数计算公式考虑了屈强比、试验参数及实验误差等因素影响。研究结果表明:节点具有较好的延性性能,达到全塑性强度后还有较大的变形能力以实现延性破坏;极限变形值与对应全塑性强度时的变形值之比为2.49~10.12;由线性回归分析方法所得延性系数计算式误差较小,可用于具体节点延性性能的量化计算。
关键词:圆钢管混凝土;梁柱节点;变形性能;延性系数;线性回归
中图分类号:TU398 文献标志码:A 文章编号:1672-7207(2013)08-3479-07
Deformation properties of connection between steel beam and concrete-filled circular column tube
SONG Binbin1, FU Gongyi2
(1. College of Civil Engineering and Architecture, Hunan Institute of Science and Technology, Yueyang 414006, China;
2. School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai 200030, China)
Abstract: Because beam-to-column connection is important component to fufill service behavior of concrete-filled circular column tube structures, the test results of 15 specimens of local models to connection between steel beam and concrete-filled circular column tube which were applied with unidirectional loading and bidirectional loading was analyzed, and the deformation properties and calculating method to ductility coefficient were studied. The calculation formulas to ductility coefficient which was based on experimental results and linear regression method were used. The ratio of ultimate strength to plastic strength was considered. The results show that the beam-to-column connection has good ductility performance and it has better deformation ability to perform ductile fracture. The ratio of ultimate deformation to plastic deformation is in 2.49 to 10.12. The calculation formulas to ductility coefficient can satisfy the use of calculation to ductility properties of connections.
Key words: concrete-filled circular column tube; beam-to-column connection; deformation properties; ductility coefficient; linear regression
钢管混凝土结构由于其具有良好的工作性能,在公路桥梁、地下、高层结构等领域如重庆巫山长江大桥、深圳赛格广场等[1]得到了广泛应用。钟善桐等[1-8]对钢管混凝土结构进行研究,提出了相应的设计方法和理论。在实心钢管混凝土结构中,常见的截面形式为方形钢管、圆形钢管。圆钢管由于在圆形截面钢管中内填混凝土,使其处于三向受压状态,充分发挥了混凝土材料的性能,同时也有利于钢管在荷载作用下受力性能的改善,因此得到了广泛应用。在圆钢管混凝土结构体系中,节点是重要的组成构件,节点设计对整体结构安全至关重要,日本对此研究起步较早,提出了依据实际内力和依据等强原则进行设计的基本方法,对平面及空间框架的节点进行了大量研究[9-10]。Yu等[11-14]对节点的强度进行了分析比较,提出了相应的强度计算方法。除了强度以外,节点变形性能直接影响到结构体系的整体性、稳定性以及传递荷载、耗能能力等。目前,对变形性能的研究通常通过延性系数(即将达到极限承载力时的变形值与构件进入屈服阶段时的变形值之比)来表征,没有具体的量化公式,且延性系数的影响因素通常集中在构件长细比、轴压比、含钢量等方面。而实际上,圆钢管混凝土结构中构件本身的因素如柱钢管外径与壁厚比、梁翼缘宽度与钢管外径比、加强板直径等对节点延性系数均有重要影响。为此,本文作者通过对15个构件的荷载-位移试验结果进行分析,研究圆钢管混凝土结构梁柱节点的变形性能,并且通过线性分析方法,考虑构件等相关影响因素,建立节点延性系数的计算方法,以便对圆钢管混凝土梁柱节点变形进行估算。
1 试验
1.1 局部简化模型及试件
图1所示为实际工程中的圆钢管混凝土梁柱节点模型。图1中:柱为钢管混凝土圆形截面柱;梁为H型钢梁;梁端弯矩考虑了竖向恒荷载、风载及水平荷载地震作用的影响。由于圆柱的填充混凝土可以抵抗H型钢梁受压翼缘处的很大部分压力,从而使节点受压区的总强度比受拉区总强度高,因此,只取图中虚线范围内所表示的受拉翼缘部分作为分析对象。研究对象为无横隔板及有贯通横隔板加强的2种节点模型,受载形式为单向及双向2种受力状况,对无横隔板加强节点的单向试件采用编号UMN,双向试件采用编号BMN;而贯通横隔板加强的节点单向试件采用编号UMD,双向试件采用编号BMD,试件编号及构件相关参数见表1和表2。表1和表2中:Ds为钢管外径;tc为钢管厚度;Bb为梁翼缘宽度;tf为梁翼缘厚度;Lb为梁翼缘长度;Dd为加强板内径;td为加强板厚度。

图1 节点的局部简化模型
Fig.1 Model simplification
表1 单向试件编号及参数
Table 1 Dimensions of specimens with unidirectional loading mm

表2 双向试件编号及参数
Table 2 Dimensions of specimens with bidirectional loading mm

1.2 试验方法及结果
用液压千斤顶对试件施加荷载,对单向试件在梁翼缘处施加单侧(x方向)的拉伸荷载,双向试件则在一侧(x方向)的梁翼缘处受拉、在另一侧(y方向)的梁翼缘处受压,加载方式如图2和图3所示。荷载均按比例增加,节点处的局部变形值则通过在梁翼缘轴线上圆柱钢管壁处安装的测量装置测得。由于柱管壁与梁翼缘通过对接焊缝连接,所测得的变形包括焊缝处变形。试验测得的受拉侧荷载、位移见表3和表4。表3和表4中:Pu为节点受拉侧加载至破坏时对应的最大抗拉强度;Pp为依据General Yield Point方法[10]确定的节点全塑性抗拉强度;△u和△p分别为荷载达Pu和Pp时对应的变形值。为了研究变形随荷载的变化规律,以UMD1,UMD2,UMD3,BMD1,BMD2和BMD3试件为例,绘制受拉侧荷载-变形曲线,如图4所示。由图4可知:无论单向受力试件还是双向受力试件,在进入屈服阶段后,还有较大的安全储备,荷载-变形曲线较好地反映了试件的延性特征。由表3和表4可知:UMN1试件最大强度与全塑性强度比值达到1.52,而BMD1试件最大强度与全塑性强度比值则达到1.56;单向试件△u/△p最大达到5.82,双向试件△u/△p最大则达到10.12;所有试件中△u/△p的最小值也有2.49,说明节点具有较好的延性性能,在进入屈服阶段后仍有较大的变形能力,有助于耗散荷载作用能量,实现构件的延性破坏,能够满足“强节点”的延性设计要求。图4所示的荷载-变形曲线也较好地反映了试件的延性特征。加载过程结束后,从试验构件中取出的内填混凝土试件如图5所示。从图5可以观察到节点无论在受拉侧或受压侧区域均出现比较明显的椭圆形变形痕迹。
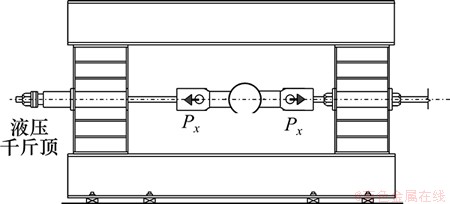
图2 单向试件加载方法
Fig.2 Applying method of unidirectional specimens

图3 双向试件加载方法
Fig.3 Applying method of bidirectional specimens
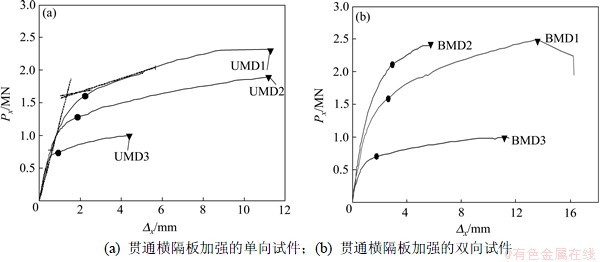
图4 荷载-变形曲线
Fig.4 Relationship between P and △
表3 单向试件试验结果
Table 3 Results of specimens with unidirectional loading
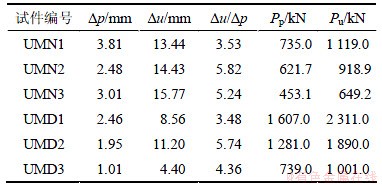
表4 双向试件试验结果
Table 4 Results of specimens with bidirectional loading


图5 内填混凝土的变形
Fig.5 Deformation of concrete
2 节点延性系数计算公式
2.1 无横隔板节点延性系数
无横隔板节点局部模型延性系数μ的影响因素主要考虑以下几个:N(即节点最大抗拉强度Pu与全塑性抗拉强度Pp的比值)、柱钢管外径与壁厚比Ds/tc、梁翼缘宽度与钢管的外径比Bb/Ds。除上述主要影响因素以外,还有一些其他因素,如钢管的制造方法及试验过程中的随机因素等。这些随机因素影响较复杂,通过对试件BMN4,BMN5和BMN6进行分析发现:对于径厚比小而屈强比大的试件,与相同参数的无缝钢管相比,冷成型的钢管由于在材料冷弯和焊接过程中的机械性质不均匀而造成的试验结果偏低程度较大,且若把随机因素作为变量考虑,会造成方程中未知量过多,加大求解难度;对于不同试件,试验器材、条件、方法均相同,因此,可将相关随机因素在试验范围内均假定为常数。通过设定幂函数的形式来考虑主要因素N,Ds/tc和Bb/Ds对延性系数μ的影响,则可设定延性系数方程为
 (1)
(1)
其中: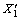 ,X2,X3和X4为幂函数的待求解参数。通过对式(1)两边取对数,使之变换成为与原始参数对数相关的多元线性公式,将各参数对数设为:
,X2,X3和X4为幂函数的待求解参数。通过对式(1)两边取对数,使之变换成为与原始参数对数相关的多元线性公式,将各参数对数设为: ,
,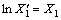 ,
, ,
, ,
, 则方程(1)写为:
则方程(1)写为:
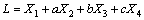 (2)
(2)
表5所示为式(1)中的各原始参数值,简化方程(2)中各系数,计算结果如表6所示。
表5 无横隔板试件参数
Table 5 Specimens’ experimental parameters

表6 无横隔板试件系数计算结果
Table 6 Specimens’ calculation results
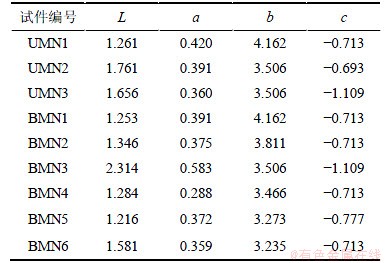
通过分析试验数据,可得到如下观测方程式:
 (3)
(3)
用Li和Pi分别表示L的测定值和权,用 ,
,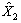 ,
, 和
和 表示X1,X2,X3和X4的最佳或然值,依据残差定义,则有:
表示X1,X2,X3和X4的最佳或然值,依据残差定义,则有:
 (4)
(4)
误差式(4)中的方程数目多于未知量的数目,通过最小二乘法来计算,可设
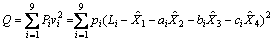
若取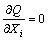 ,则可得到残差平方和最小。因此,计算出标准方程式如下(方程中i=1, …, 9的标示省略):
,则可得到残差平方和最小。因此,计算出标准方程式如下(方程中i=1, …, 9的标示省略):
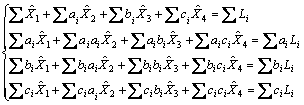 (5)
(5)
可得到方程式数目等于未知量数目的标准方程,通过求解线性方程组可计算出各未知量的最佳或然值。依据表6中的参数值写出标准方程后,再求解即可得到式中各未知量值:
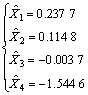
计算出 ,则可得到无横隔板加强节点局部模型延性系数的函数方程:
,则可得到无横隔板加强节点局部模型延性系数的函数方程:
 (6)
(6)
2.2 贯通横隔板加强节点延性系数
分析无横隔板节点局部模型延性系数函数方程的方法同样可适用于有贯通横隔板加强的节点局部模型,其延性系数μ的主要影响因素同样考虑节点最大抗拉强度Pu与全塑性抗拉强度Pp的比值N、柱钢管外径与壁厚比Ds/tc、梁翼缘宽度与钢管的外径比Bb/Ds以及作为常数考虑的相关随机因素。此外,还需考虑贯通横隔板直径与钢梁翼缘的影响,为此,引入钢梁翼缘宽度与贯通横隔加强板的内圆半径比Bb/Dd,则可设定延性系数方程为
 (7)
(7)
其中: ,Y2,Y3,Y4和Y5为幂函数的待求解参数。
,Y2,Y3,Y4和Y5为幂函数的待求解参数。
通过对式(7)两边取对数,使之变换成为与原始参数对数相关的多元线性公式,将各参数对数设为: ,
,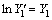 ,
, ,
,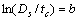 ,
, ,
,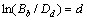
则方程(7)写为:
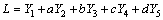 (8)
(8)
表7所示为方程(7)中的各原始参数值,简化方程(8)中各系数,计算结果如表8所示。通过分析试验数据,可得到如下观测方程式:
表7 贯通横隔板加强试件参数
Table 7 Specimens’ experimental parameters with through diaphragm

表8 贯通横隔板加强试件系数计算结果
Table 8 Specimens’ calculation results with through diaphragm

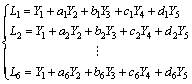 (9)
(9)
用Li和Pi分别表示L的测定值和权,用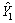 ,
, ,
, ,
,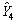 和
和 分别表示Y1,Y2,Y3,Y4和Y5的最佳或然值。依据残差定义,则有:
分别表示Y1,Y2,Y3,Y4和Y5的最佳或然值。依据残差定义,则有:
 (10)
(10)
误差方程式(10)中的方程数目多于未知量的目,通过最小二乘法来计算,可设

若取 ,则可得到残差平方和最小。因此,计算出标准方程式如下(方程中i=1, …, 6的标示省略):
,则可得到残差平方和最小。因此,计算出标准方程式如下(方程中i=1, …, 6的标示省略):
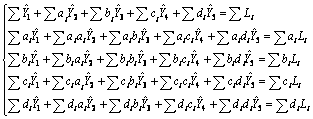 (11)
(11)
则可得到方程式数目等于未知量数目的标准方程,通过求解线性方程组可计算出各未知量的最佳或然值。依据表8中的参数值写出标准方程后,再求解即可得到式中各未知量值:

计算出 ,则贯通横隔板加强节点局部模型延性系数的函数方程为:
,则贯通横隔板加强节点局部模型延性系数的函数方程为:

 (12)
(12)
3 结果检验
3.1 无横隔板节点延性系数方程检验
若上述求解 ,
,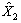 ,
, 和
和 过程及结果正确,则可进一步求出无横隔板试件残差Vi(i=1, …, 9)的正确值且应该满足下式:
过程及结果正确,则可进一步求出无横隔板试件残差Vi(i=1, …, 9)的正确值且应该满足下式:
 (13)
(13)
由已求解得到的 ,
,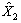 ,
, ,
, ,可得无横隔板试件残差为:
,可得无横隔板试件残差为:

 (14)
(14)
依据式(14)可依次算出V1, V2, V 3, …, V9,于是,可以得到无横隔板试件的检测结果:
 (15)
(15)
3.2 贯通横隔板加强节点延性系数方程检验
若上述求解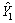 ,
, ,
, ,
,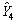 和
和 过程及结果正确,则可进一步求出贯通横隔板加强试件的残差Vi (i=1, …, 6)的正确值而且应该满足下式:
过程及结果正确,则可进一步求出贯通横隔板加强试件的残差Vi (i=1, …, 6)的正确值而且应该满足下式:
 (16)
(16)
由已求解得到的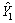 ,
, ,
, ,
,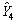 和
和 ,可得贯通横隔板加强试件残差为:
,可得贯通横隔板加强试件残差为:
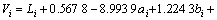
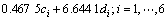 (17)
(17)
依据式(17)可依次算出V1, V2, V 3, …, V6,于是,可以得到贯通横隔板加强试件的检验结果:
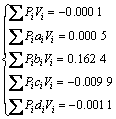 (18)
(18)
由计算结果式(15)和(18)可以判断延性系数计算方程(6)和(12)可行。
4 结论
(1) 圆钢管混凝土结构梁柱节点具有较强的变形能力,在达到极限承载力之前有明显的变形过程,可实现延性破坏。
(2) 节点延性系数与构件尺寸参数、试件屈强比等因素相关,建立在试验结果基础上的延性系数计算公式误差非常小,可用于衡量变形性能的初步量化计算。
(3) 由于钢管壁与钢梁翼缘采用对接焊缝连接,延性性能及延性系数计算公式考虑焊缝的影响。
参考文献:
[1] 钟善桐. 钢管混凝土结构研究新进展:《空心钢管混凝土结构设计技术规程》简介[J]. 钢结构, 2009, 24(5): 54-58.
ZHONG Shantong. New development of research work for concrete-filled steel tubular structures: Brief introduction of the technical specification for design of hollow concrete-filled steel tubular structures[J]. Steel Construction, 2009, 24(5): 54-58.
[2] 钟善桐. 钢管混凝土结构[M]. 3版. 北京: 清华大学出版社, 2003: 8-30.
ZHONG Shantong. Concrete-filled steel tubular structures[M]. 3rd ed. Beijing: Tsinghua University Press, 2003: 8-30.
[3] HAN Linhai. Tests on stub columns of concrete-filled RHS sections[J]. Journal of Constructional Steel Research, 2002, 58(3): 353-372.
[4] 丁发兴, 李刚, 龚永智, 等. 钢骨-圆钢管混凝土轴压短柱力学性能分析[J]. 中南大学学报: 自然科学版, 2012, 43(9): 3625-3630.
DING Faxing, LI Gang, GONG Yongzhi, et al. Behavior of tubular stub columns of axially loaded steel-reinforced concrete-filled circular steel[J]. Journal of Central South University: Science and Technology, 2012, 43(9): 3625-3630.
[5] 周凌宇, 王海波, 贺桂超. 采用PBL连接件的组合桁架节点受力性能[J]. 中南大学学报: 自然科学版, 2012, 43(7): 2762-2767.
ZHOU Lingyu, WANG Haibo, HE Guichao. Experiment for mechanical properties on steel-concrete composite truss joints with PBL connectors[J]. Journal of Central South University: Science and Technology, 2012, 43(7): 2762-2767.
[6] 蔡建国, 朱洪进, 冯健, 等. 世构体系框架中节点抗震性能试验研究[J]. 中南大学学报: 自然科学版, 2012, 43(5): 1894-1901.
CAI Jianguo, ZHU Hongjin, FENG Jian, et al. Experimental study on seismic behavior of middle joints of SCOPE system[J]. Journal of Central South University: Science and Technology, 2012, 43(5): 1894-1901.
[7] 李永学, 刘贵位. 钢筋混凝土矩形桥墩的延性抗震分析[J]. 公路, 2010, 10(10): 20-27.
LI Yongxue, LIU Guiwei. Anti-seismic analysis of ductility of reinforced concrete bridge piers with rectangle section[J]. Highway, 2010, 10(10): 20-27.
[8] 陈誉, 彭兴黔, 赵宪忠. 圆钢管搭接节点延性分析[J]. 兰州理工大学学报, 2007, 33(4): 122-125.
CHEN Yu, PENG Xingqian, ZHAO Xianzhong. Ductility analysis of overlapped joints in circular steel tubes[J]. Journal of Lanzhou University of Technology, 2007, 33(4): 122-125.
[9] 日本钢结构协会. 钢结构技术总览:建筑篇[M]. 陈以一, 付功义, 译. 北京: 中国建筑工业出版社, 2003: 119-127.
Japan UNI Agency Inc. Steel structure technology overview: Construction[M]. CHEN Yiyi, FU Gongyi, trans. Beijing: China Construction Industry Press, 2003: 119-127.
[10] FU Gongyi, Morita K, et al. Mechanical properties of connection between steel beam flange and concrete-filled circular column tube[C]// Assembly documents for design and construction of AIJ. Tokyo: Architectural Institute of Japan, 1998: 157-164.
[11] YU Xiaowen, FU Gongyi, LIU Bing, et al. Local tensile strength of connection between H-steel beam flange and concrete-filled circular column tube with through diaphragm[J]. Journal of Shanghai Jiaotong University: Science, 2004, E-9(3): 11-16.
[12] 虞晓文. 贯通横隔板加强圆形钢管混凝土柱—H型钢梁节点局部抗弯强度的研究[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2004: 5-28.
YU Xiaowen. Local tensile strength of connection between -steel beam flange and concrete-filled circular column tube with through diaphragm[D]. Shanghai: Shanghai Jiaotong University. School of Naval Architecture, Ocean & Civil Engineering, 2004: 5-28.
[13] 刘兵. 圆形钢管混凝土结构梁柱节点抗弯强度的研究[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2003: 10-20.
LIU Bing. Local tensile strength of connection between steel beam flange and concrete-filled circular column tube[D]. Shanghai: Shanghai Jiaotong University. School of Naval Architecture, Ocean & Civil Engineering, 2003: 10-20.
[14] LIU Bing, FU Gongyi, REN Tao, et al. Local tensile strength of connection between steel beam flange and concrete-filled circular column tube[C]// The Fourth Shanghai-Seoul Forum on Urban Environmental Science and Technology. Shanghai: Shanghai Jiaotong University, 2002: 9-15.
(编辑 陈灿华)
收稿日期:2013-03-28;修回日期:2013-05-12
基金项目:湖南省教育厅科学研究项目(09C475)
通信作者:付功义(1962-),男,浙江义乌人,博士,教授,从事空间结构研究;电话:13762017604;E-mail: 47463410@qq.com