DOI: 10.11817/j.ysxb.1004.0609.2020-37592
随机森林回归分析在激光熔覆形貌预测中的应用
梁旭东，王 炜，赵 凯，郝云波，杨 萍，朱忠良
(上海航天设备制造总厂有限公司，上海 200245)
摘 要：激光熔覆修复过程中单道熔覆层形貌极大地影响修复效果，但多工艺参数对熔覆层影响的耦合作用机制尚未被研究清楚，因此，获得不同工艺参数组合与熔覆层尺寸的定量关系是亟待解决的难题。以Inconel 625合金的激光熔覆修复为背景，采用随机森林(Random Forest，RF)算法构建了激光熔覆工艺参数(激光功率、扫描速度、送粉速率)到单道熔覆层尺寸的回归模型，将模型用于特定熔覆参数组下单道尺寸的预测；同时在给定期望的单道熔覆层尺寸参数时，基于Gini不纯度选择强关联因子构建了工艺参数预测模型。结果表明，激光熔覆工艺参数预测模型的预测误差小于4%，能够准确地估计加工特定单道熔覆层截面几何形状所需的激光熔覆工艺参数。
关键词：随机森林；激光熔覆；特征筛选；参数预测
文章编号：1004-0609(2020)-07-1644-09 中图分类号：TG665 文献标志码：A
近些年来，在汽车、能源、航空等高端制造领域，零件装备呈现出加工技术先进、结构复杂等特征[1]，对零件的维修保障难度大为增加，这已成为制约装备制造业整体效能的关键因素。作为一种经济效益较高的再制造加工技术，激光熔覆技术能够在破损零件表面熔覆异种材料，使其达到甚至超过原有的性能[2]。将激光熔覆技术应用于高附加值零件的修复，不仅产生了巨大的经济效益，而且为战场等极端情况下的现场修复带来可能，具有重要的军事效益。
激光熔覆过程是一个复杂的冶金过程，过程中激光束、粉末材料与基材交互耦合作用，全过程的持续稳定进行受诸多因素影响[3]。除却人为因素情况外，其他因素之间也存在交互耦合及干扰，因此激光增材制造过程也必然受到影响，并具有一定非预期性[4]。若工艺参数选择不当，不仅严重影响成型精度，导致加工结果难以预测，更可能产生熔覆层内部孔隙[5]、表面粗糙等现象[6]，这已然成为熔覆成形、修复等技术产业化的瓶颈。
激光熔覆通常涉及多个变量的非线性相互作用，研究熔覆参数间的耦合关系以及各参数对单道熔覆的影响规律，实现不同参数输入下熔覆形貌的预测，从而更好地指导熔覆过程以提高成型质量[7]。在以往的研究中，多采用有限元模拟计算方法[8-9]对熔覆过程进行分析，其中需要设置许多假设条件，这些条件往往不能很好涵盖熔覆过程中的实际情况，导致仿真结果很难对实际加工过程产生有意义的指导。
对激光熔覆过程来说，熔覆参数(如激光功率、送粉速度、扫描速度)之间互相影响，熔覆参数的预测是一个多元非线性回归问题[10]。以往的研究中多关注于分析单个变量对熔覆结果的影响。现在的研究多采用多变量统计分析和数据挖掘方法来试图理解变量系统之间的复杂相互作用。例如有些研究[11-12]使用响应曲面法分析了熔覆参数对熔覆层的作用机理以及各参数间的耦合机制，并建立了激光熔覆工艺参数与单道尺寸间的多项式回归方程。但该模型预测的单道尺寸误差较大，多项式拟合模型的精度不高，因此难以应用到实际生产。
随着人工智能理论的高速发展，机器学习算法在多元非线性回归问题上逐渐体现出其特有的优越性[13-14]。例如神经网络可以有多个非线性的层，对非常适合对比较复杂的非线性关系建模[15]，因此，CAIAZZO等[16]开发了一种基于人工神经网络的机器学习方法，以找出激光熔覆工艺参数与2024铝合金板上单道熔覆层尺寸参数之间的相关性。但该方法需要多次调参，才能实现较好的预测精度，同时易产生过拟合现象。
随机森林(Random forest，RF)作为目前预测效果最好的非参数回归模型之一，与参数回归方法相比，该算法无需对变量的正态性和独立性等假设条件进行检验，同时也不需要考虑多变量的共线问题[17]。与神经网络等其他机器学习算法相比，RF用于回归预测不仅不需要多次调参，同时能够度量每个参数对响应的重要性[18-19]，这个特点可以方便深入对激光熔覆过程的理解。综合以上，本文作者将采取RF算法构建激光熔覆参数组与熔覆的单道尺寸的关联模型，并将模型用于特定熔覆工艺参数组下单道熔覆层尺寸的预测以及估计能实现期望单道熔覆层的工艺参数组。
1 实验设计
采用自主研制的激光熔覆系统进行球形Inconel 625粉末在不锈钢基体上的单道熔覆实验。激光熔覆原理如图1所示，金属粉末随高纯氩气流动经熔覆头送粉喷嘴汇聚于一点。激光束由熔覆头镜组汇聚于工作平面并在基体表面形成熔池，同时合金粉末输送入熔池发生冶金反应。当激光熔覆头移动熔池迅速凝固并形成熔覆层，经层层扫描堆叠形成具有一定厚度的修复层。
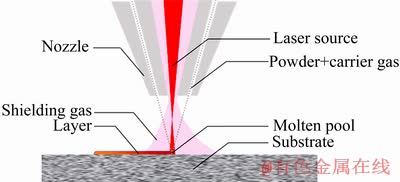
图1 激光熔覆原理图
Fig. 1 Laser cladding schematic diagram
为构建激光熔覆参数与单道熔覆层尺寸的预测模型，需要构建模型的训练组。现有研究认为激光功率、扫描速度和粉末流速是影响熔覆层形貌的最主要的工艺参数[20-21]，因此在实验设计时只需要改变这3个参数。对于随机森林回归模型(Random forest regressor，RFR)来说，训练时可参考的实验结果越多，模型的拟合效果就越好，但也同时增加了实验的复杂性。本文设计了20组三因子的Inconel 625粉末激光熔覆单道实验，并将其同时作为多项式模型和RF模型的训练组。
将实验得到的单道熔覆层做成金相工艺试验件，分别测定了单道熔覆层的尺寸参数，包括熔高(Clad height)、熔宽(Clad width)、熔深(Clad depth)、热影响区深(HAZ depth)。熔覆时激光加工头并不与基板垂直，因此，熔池受力发生流淌，导致熔覆层截面不对称。本实验测量的是熔覆层截面中较小的润湿角(Wetting angle)，如图2所示。
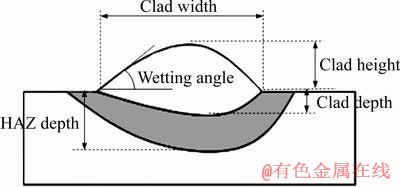
图2 熔覆单道截面尺寸参数
Fig. 2 Schematic view of selected responses of laser clad
熔覆层截面的形状可以由稀释率(Dilution)来反映，稀释率对零件修复的质量至关重要。按定义熔覆层的稀释率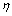
可由式(1)计算：
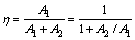(1)
式中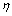：为稀释率；A1为母材熔化区域截面积；A2为熔覆层截面积。通过大量的实验发现，截面积A1和A2变化主要体现在熔覆层高度h与基材熔深d，因此，可用式(2)近似表示熔覆层的稀释率[2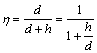2]：
(2)
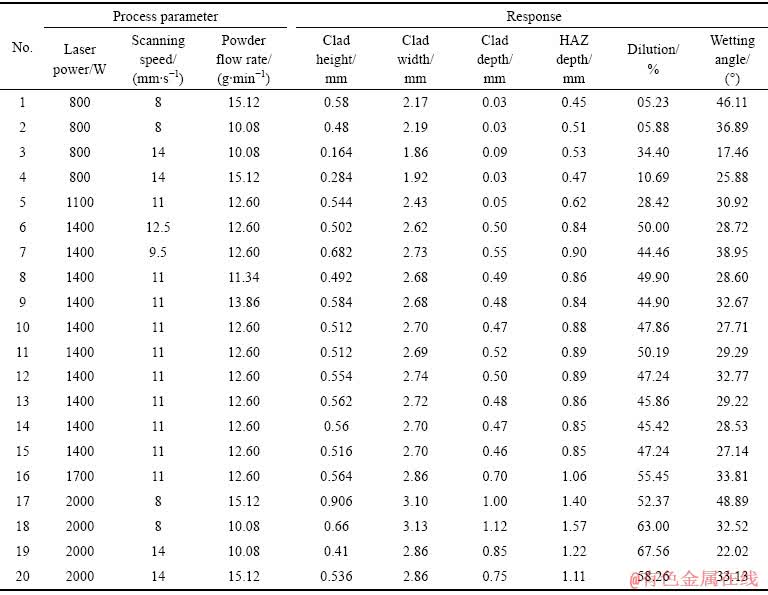
对得到的20个实验样本进行切割并将截面打磨至轮廓清晰，借助高倍显微镜测得的实验数据见表1。这些数据将作为训练RF模型的样本。
2 单道熔覆层尺寸预测
2.1 模型建立
作为集成学习算法(Ensemble learning)领域中典型的多分类器，随机森林算法已经被证实在一些小样本情形下的预测性能比神经网络、支持向量机更为优异。本文对建立激光熔覆尺寸预测模型的过程可以分为如下几个步骤。
1) 用有抽样放回的方法(Bootstrap)从激光熔覆参数组合样本集中选取n个样本作为一个训练集；
2) 用抽取的样本集生成一棵决策树。在生成的每一个结点上，随机不重复地选择d个特征，然后利用这d个特征分别对样本集进行划分；
表1 实验设计与结果
Table 1 Experimental design and corresponding experimental responses
3) 重复步骤1到步骤2共X次，其中X为随机森林中决策树的数量；
4) 用训练得到的随机森林对测试样本进行预测，并用票选法决定预测的结果。
从RF算法的构建过程可以看出，RF算法的随机性主要体现在样本的随机性，以及节点分裂属性的选择随机性。有了这些随机性的保证，RF算法便不会产生过拟合的现象，这使得RF在性能上更优于神经网络。本章用设计的20组实验来训练RF模型，因为要实现对不同熔覆参数的熔覆结果的预测，故设计的输入(Xi)是：
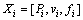(i=1, …, n) (3)
式中：Pi代表激光功率；vi代表扫描速度；fi代表粉末流速。
对于每一组确定的输入，都有对应的输出响应组(Yi)：
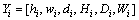(i=1, …, n) (4)
式中：hi、wi、di、Hi、Di、Wi分别代表熔高、熔宽、熔深、热影响区深度、稀释率与润湿角度。
本文在构建RF时，考虑了影响RF性能和效率的因素：RF中决策树的数量X和叶节点的最小样本数Y。当X较小时，RF的分类回归误差大，性能也比较差。另一方面，RF具有不过拟合性质，因此可使X尽量大，以保证集成分类器的多样性。但是构建RF的复杂度与X成正比，X过大会使得RF构建效率降低。同时森林的规模达到一定程度时，将导致森林的可解释性减弱。因此，针对X对RF性能、可解释性和复杂性之间的平衡问题，经多次调整选择了X=200。至于叶节点的最小样本数Y，RF的性能对其不敏感。通常情况下，随机森林用于回归时设定Y=5。
2.2 结果与检验
采用该方法分别对熔高、熔深、熔宽、HAZ深度、稀释率和润湿角度建立预测模型，对得到的模型进行准确性检验，即将原始的20组实验数据作为输入，经过模型预测后与真实值进行比较。图3所示为几个RF模型的预测值与真实值的比对结果。
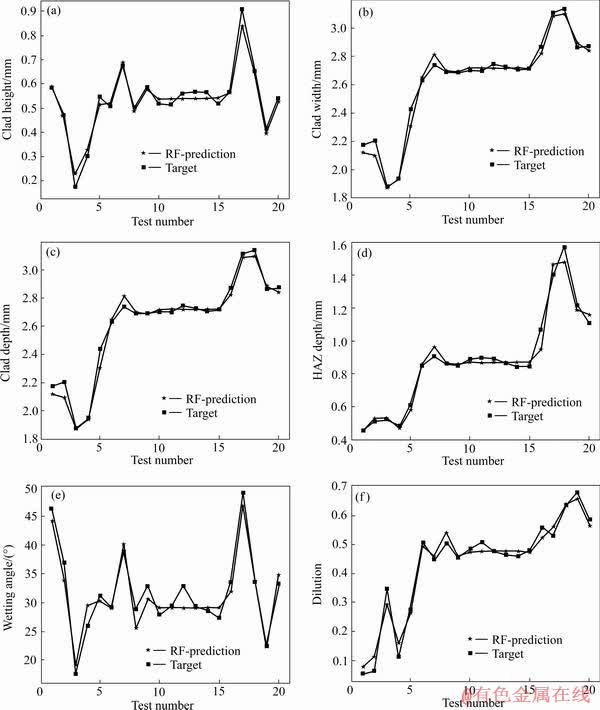
图3 预测模型的对样本集的拟合效果图
Fig. 3 Experimental (blue marks) and RF-estimated (red marks) values, for each of p=20 experimental conditions
为了验证模型具有一定的优越性，本文采用多项式回归方法与RF方法进行对比。在典型的多输入多响应实验过程中，多项式回归方法即是将响应建模为所有的主要因子和相互作用效应因子的函数模型。对于主要输入变量之间存在多种相互作用的单道激光熔覆模型，通常选择二阶多项式函数，如式(5)所示：
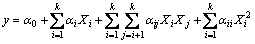(5)
式中：k是输入变量的个数；Xi (i=1，2，3)在本文中是三个工艺参数激光功率(LP)、扫描速度(SS)和送粉速率(PFR)；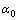
是常数项；
、
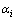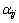和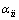
分别是分别是线性系数，变量相互作用系数和二次项系数。
为了保证的模型的准确性，采用方差分析分析(Analysis of variance，ANOVA)来确定回归多项式中每一项的重要程度，从而在方程拟合时消除不重要的项。ANOVA中如果p值(显着概率值)小于置信水平[18]，则
认为每个项都是显着的。在本文中，置信水平达到95%以上时认为模型是可信的。分别对HAZ深度、稀释率、熔宽等响应值建立多项式回归模型进行拟合，其中一些不重要的项将通过ANOVA方法进行剔除。
通过计算R2(R-Squared)值来比较分析两种方法的预测精度。R2值用于检查预测数据和测量数据之间的拟合效果。对于所有输出响应，R2值接近于1显示实验和预测结果之间具有高度相关性，模型拟合效果也越好。R2的计算方法如下：
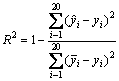(6)
对HAZ深度、稀释率、熔宽等响应值建立的多项式模型和RF预测模型测定的R2值结果见表2。
通过对比可以看出，RF回归预测模型的R2普遍要比多项式回归模型更接近1，这说明了用RF模型预测激光熔覆参数结果的准确性更高。
3 特定单道熔覆层尺寸下的激光熔覆参数预测
3.1 基于重要性评估的模型建立
除了预测不同激光熔覆参数组合下的熔覆形貌以外，建立的随机森林回归模型也可以在给定期望的单道熔覆层尺寸参数时，估计与之相匹配的工艺参数。据此模型的输入因子应为
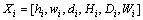(i=1, …, n) (7)
与前一节相似，每组输入对应特定的响应组，定义为
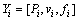(i=1, …, n) (8)
可见模型的因子数量较多，并且存在强相关因子(稀释率与熔高、熔深)，这些冗余信息对RF模型的建立具有不利影响，因此需要进行特征筛选，即保留重要性较高的因子。用RF进行特征重要性评估(Variable importance measures，VIM)的原理是：计算每个特征在随机森林中的每棵树上做的贡献，然后比较各因子贡献的大小。RF回归分析中一般用基尼指数(Giniindex，GI)或者袋外数据(OOB)错误率来量化特征对模型的贡献。本文采取用Gini指数的方法，假设m个特征x1，x2，x3，…，xm，则每个特征xj的Gini指数评分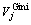
，亦即第j个特征在RF所有决策树中节点分裂不纯度的平均改变量。Gini指数的计算公式为
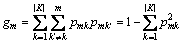(9)
式中：K表示有K个类别；pmk表示节点m中类别k所占的比例。特征xj在节点m的重要性，即节点m分枝前后的GI变化量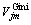
为
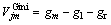(10)
其中：gl和gr分别表示分枝后两个新节点的Gini指数。假设建立的RF模型中共有n颗树，那么
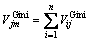(11)
最后，将各因子所有求得的重要性评分做归一化处理：
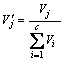(12)
对建立的RF预测模型进行重要性检验，即分别对激光功率、扫描速度、粉末流速进行重要性评估，结果如图4所示。本文中重要性超过0.15被认为该因子对响应具有显著影响。由此可以看出，受到激光功率变化影响最大的尺寸参数是单道的熔覆深度，而激光功率变化对于润湿角度与熔覆高度几乎没有影响；扫描速度变化影响的尺寸参数主要是熔覆高度和润湿角度；受到粉末流速变化影响较多的尺寸参数是单道的熔覆高度、润湿角度、热影响区深度和熔覆深度，熔覆宽度和稀释率受粉末流速变化的影响很小。
表2 训练集拟合结果比较
Table 2 Fitting results performance comparison of training set
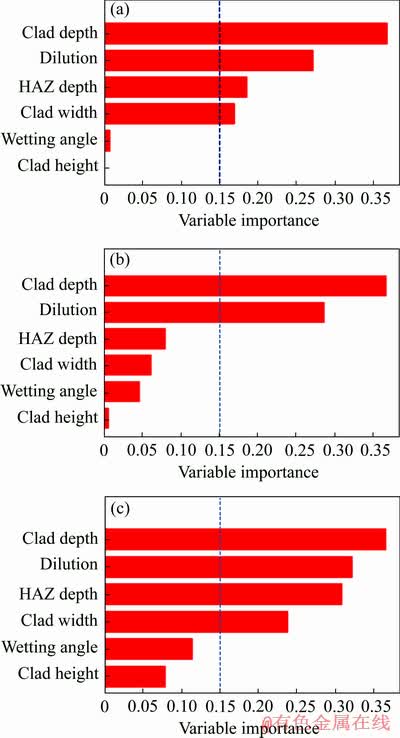
图4 激光功率、预测扫描速率和粉末流速预测的因子重要性评估
Fig. 4 Variable importance measures of laser power prediction(a), scan rateprediction(b) and powder flow rate prediction(c)
基于以上分析，筛选掉影响度在0.15以下的因子后，激光功率的预测过程需要4个因子：熔深、稀释率、HAZ深、熔宽；扫描速度的预测需要2个因子：熔高和润湿角度；粉末流速的预测需要4个因子：熔高、润湿角度、HAZ深度、熔深。
3.2 模型预测结果
为了检验经过特征筛选后的RF模型预测性能，设计了7组实验，以验证模型对特定尺寸下的激光熔覆参数预测的准确性。对7条单道切割后，抛光、腐蚀至截面轮廓线清晰，电镜下的结果图如图5所示。
图5 验证组的实验结果图
Fig. 5 Experimental results of verification group
RF模型预测出的激光功率、扫描速度、粉末流速与实际值的对比如图6所示。
RF模型对3个响应的预测误差分别为1.17%、3.43%、3.51%。由此可见，经过Gini不纯度进行特征筛选后的RF预测模型，可以对熔覆工艺参数组进行精确地预测，从而制定满足生产需要的目标熔覆层截面尺寸与形状。
4 结论
1) 以高端装备修复为背景，对熔覆参数(激光功率、扫描速度、送粉速率)与多个响应(熔高、熔宽等)进行了建模并对比分析了两种预测模型的效果。多元回归分析往往不能得到很好的模型。究其原因是激光熔覆的响应模型较为复杂，建模一般选择的二次回归曲线难以完成高精度的拟合，导致模型的误差保持在8%以内。而随机森林对非线性关系的映射能力很强，在解决复杂多元非线性问题时体现出其优势，本文搭建的RF模型正向预测误差均小于4%，该模型可以实现特定熔覆参数组合下的熔覆形貌预测。
2) 在反向预测时通过求解节点处的Gini不纯度来评定各参量的重要性，若要改变单道熔覆层的熔深，最有效的方法是调整激光功率的大小，同时激光功率也是控制激光熔覆单道稀释率的最关键的因素。增大熔覆过程中激光的扫描速度与送粉量都能增加熔覆层的高度，同时也会使熔覆层的形状更加饱满。配合调整激光功率与送粉速度可以有效降低基体的热影响区，提高成形质量。该结论可以对熔覆成形过程稳定控制中工艺参数的调整提供依据。
3) 基于Gini不纯度对其筛选掉不必要的项，建立了熔覆层尺寸参数到激光熔覆参数的RF模型。经过实验证明了该模型具有良好的预测效果，因此，在加工过程中可以基于此预测模型定制熔覆层的尺寸。RF模型预测结果对研究机器学习方法在同轴送粉激光熔覆工艺参数预测乃至性能优化等方面具有一定的参考价值和现实意义。
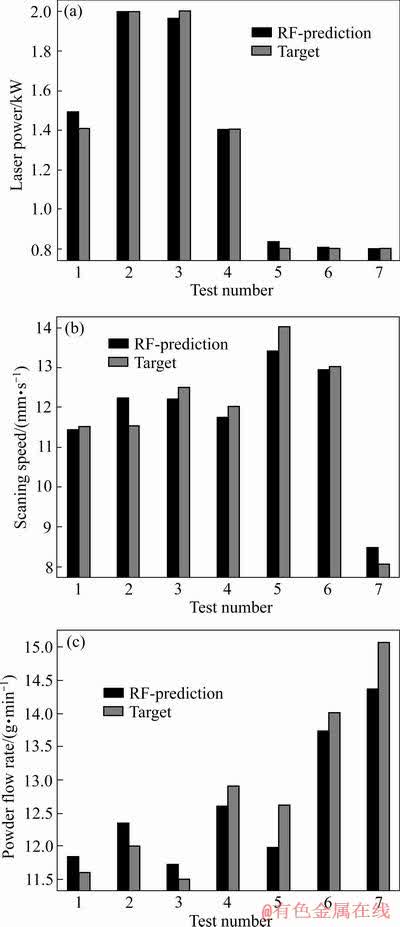
图6 激光功率、扫描速度和粉末流速RF预测结果
Fig. 6 Comparison of RF prediction and target results of laser power(a), scanning speed(b) and powder flow rate(c)
REFERENCES
[1] 伏 琳. 智能制造新模式下“中国制造”面临的机遇和挑战[J]. 机床与液压, 2016, 44(9): 161-164, 89.
FU Lin. Opportunities and challenges facing Chinese manufacturing under new model of intelligent manufacturing[J]. Machine Tool & Hydraulics, 2016, 44(9): 161-164, 89.
[2] 张 坚, 吴文妮, 赵龙志. 激光熔覆研究现状及发展趋势[J]. 热加工工艺, 2013, 42(6): 131-134, 139.
ZHANG Jian, WU Wen-ni, ZHAO Long-zhi. Research progress and development trend of laser cladding[J]. Hot Working Technology, 2013, 42(6): 131-134, 139.
[3] 蒋厚峰, 乌日开西·艾依提, 安鹏芳. 激光熔覆成形的熔池形貌及熔池温度研究综述[J]. 热加工工艺, 2019, 48(10): 10-14.
JIANG Hou-feng, AIYITI Wurikaixi, AN Peng-fang. Review on study of molten pool geometry and molten pool temperature of laser cladding forming[J]. Hot Working Technology, 2019, 48(10): 10-14.
[4] 任维彬, 董世运, 徐滨士, 王玉江, 闫世兴. 激光再制造闭环控制系统的研究现状及发展[J]. 激光技术, 2016, 40(1): 103-108.
REN Wei-bin, DONG Shi-yun, XU Bin-shi, WANG Yu-jiang, YAN Shi-xing. Research advance and development of laser remanufacture closed-loop control systems[J]. Laser Technology, 2016, 40(1): 103-108.
[5] YAN Z, LIU W, TANG Z, LIU X, ZHANG N. Review on thermal analysis in laser-based additive manufacturing[J]. Optics and Laser Technology, 2018: 427-441.
[6] 魏娟娟, 米国发, 许 磊, 王有超. 激光增材制造铝合金及其复合材料研究进展[J]. 热加工工艺, 2019, 48(8): 27-31.
WEI Juan-juan, MI Guo-fa, XU Lei, WANG You-chao. Research progress on laser additive manufacturing of aluminum alloy and its composite[J]. Hot Working Technology, 2019, 48(8): 27-31.
[7] YAKOUT M, CADAMURO A, ELBESTAWI M A, VELDHOIS S C. The selection of process parameters in additive manufacturing for aerospace alloys[J]. The International Journal of Advanced Manufacturing Technology, 2017: 2081-2098.
[8] LI C J, TSAI T W, TSENG C. Numerical simulation for heat and mass transfer during selective laser melting of titanium alloys powder[J]. Physics Procedia, 2016: 1444-1449.
[9] 郭 卫, 张亚普, 柴蓉霞. 单道次激光熔覆304不锈钢数值模拟与实验研究[J]. 激光与光电子学进展, 2019, 56(9): 163-169.
GUO Wei, ZHANG Ya-pu, CHAI Rong-xia. Numerial simulation and experimental study of Single-track laser cladding of 304 stainless steels[J]. Laser & Optoelectronics Progress, 2019, 56(9): 163-169.
[10] 雷凯云, 秦训鹏, 刘华明, 冉 渊. 基于神经网络的宽带激光熔覆熔池特征参数预测[J]. 光电子·激光, 2018, 29(11): 1212-1220.
LEI Kai-yun, QIN Xun-peng, LIU Hua-ming, NI Mao. Prediction on characteristics of molten pool in wide-band laser cladding based on neural network[J]. Journal of Optoelectronics Laser, 2018, 29(11): 1212-1220.
[11] FARAHMAND P, KOVACEVIC R. Parametric study and multi-criteria optimization in laser cladding by a high power direct diode laser[J]. Lasers in Manufacturing and Materials Processing, 2014, 1(1/4): 1-20.
[12] 许向川, 温海骏, 王俊元, 苗 苗. 基于响应面的装备零件再制造激光熔覆工艺参数优化[J]. 真空科学与技术学报, 2018, 38(7): 615-620.
XU Xiang-chuan, WEN Hai-jun, WANG Jun-yuan, MIAO Miao. Optimization of laser cladding conditions in response surface method for repairing damaged alloy parts[J]. Chinese Journal of Vacuum Science and Technology, 2018, 38(7): 615-620.
[13] 郑伟达, 张惠然, 胡红青, 刘 尧, 李盛洲, 丁广太, 张金仓. 基于不同机器学习算法的钙钛矿材料性能预测[J]. 中国有色金属学报, 2019, 29(4): 803-809.
ZHENG Wei-da, ZHANG Hui-ran, HU Hong-qing, LIU Yao, LI Sheng-zhou, DING Guang-tai, ZHANG Jin-cang. Performance prediction of perovskite materials based on different machine learning algorithms[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(4): 803-809.
[14] GARCIAGUTIERREZ J, MARTINEZALVAREZ F, TRONCOSO A, RIQUELME J. A comparative study of machine learning regression methods on LiDAR data: A case study[C]. Spain: International Joint Conference SOCO’13-CISIS’13-ICEUTE’13, 2014: 249-258.
[15] KONG W, DONG Z Y, JIA Y, RIQUELME J C. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 841-851.
[16] CAIAZZO F, CAGGIANO A. Laser direct metal deposition of 2024 Al alloy: Trace geometry prediction via machine learning[J]. Materials, 2018, 11(3): 444-455.
[17] NGUYEN H, BUI X. Predicting blast-induced air overpressure: A robust artificial intelligence system based on artificial neural networks and random forest[J]. Natural Resources Research, 2019, 28(3): 893-907.
[18] ZHU X, XIN Y, GE H. Recursive random forests enable better predictive performance and model interpretation than variable selection by LASSO.[J]. Journal of Chemical Information and Modeling, 2015, 55(4): 736-746.
[19] SMITH P F, GANESH S, LIU P. A comparison of random forest regression and multiple linear regression for prediction in neuroscience[J]. Journal of Neuroscience Methods, 2013, 220(1): 85-91.
[20] GOODARZI D M, PEKKARINEN J, SALMINEN A. Analysis of laser cladding process parameter influence on the clad bead geometry[J]. Welding in The World, 2017, 61(5): 883-891.
[21] HOU X, DU D, CHANG B, MA N. Influence of scanning speed on microstructure and properties of laser cladded Fe-based amorphous coatings[J]. Materials, 2019, 12(8): 1279-1294.
[22] 洪 鑫, 于爱兵, 魏金龙, 何 源, 吴毛朝. 工艺参数对激光熔覆断屑台稀释率的影响[J]. 激光杂志, 2018, 39(5): 70-73.
HONG Xin, YU Ai-bing, WEI Jin-long, HE Yuan, WU Mao-chao. Influence of processing parameters on dilution rate of laser cladded chip breaking dot[J]. Laser Journal, 2018, 39(5): 70-73.
Application of random forest regression analysis in trace geometry prediction of laser cladding
LIANG Xu-dong, WANG Wei, ZHAO Kai, HAO Yun-bo, YANG Ping, ZHU Zhong-liang
(Shanghai Aerospace Equipments Manufacturer Co., Ltd., Shanghai 200245, China)
Abstract: The shape of the single cladding layer in the laser cladding repair process greatly affects the quality of the repair. It is necessary to control the morphology of the cladding layer to achieve high-quality repair. However, the coupling mechanism of multi-process parameters on the cladding layer was studied clearly. Therefore, obtaining the quantitative relationship between different process parameter combinations and the size of the cladding layer is an urgent problem to be solved. Based on the laser cladding repair of Inconel 625 alloy, a random forest (RF) algorithm was used to construct a regression model of laser cladding process parameter set (laser power, scanning speed, powder feeding rate) to single pass cladding size. The model was used to predict the single track size of a specific cladding parameter group. At the same time, the strong correlation factors were selected based on the Gini impurity and used to build a process parameter prediction model. The results show that the prediction error of the laser cladding process parameter prediction model is less than 4%, which can accurately estimate the laser cladding process parameters required to process the specific single-pass cladding cross-section geometry.
Key words: random forest; laser cladding; feature selection; parameter prediction
Foundation item: Project(51705328) supported by the National Natural Science Foundation of China; Project (17YF1408500) supported by the Shanghai Youth Science and Technology Talent Yangfan Program, China
Received date: 2019-07-19; Accepted date: 2020-04-28
Corresponding author: LIANG Xu-dong; Tel: +86-21-24187143; E-mail: fengshenxiaoxu@163.com
(编辑 李艳红)
基金项目：国家自然科学基金资助项目(51705328)；上海市青年科技英才杨帆资助项目(17YF1408500)
收稿日期：2019-07-19；修订日期：2020- 04 28
通信作者：梁旭东，助理工程师；电话：021-24187143；E-mail：fengshenxiaoxu@163.com
