J. Cent. South Univ. Technol. (2008) 15(s1): 266-270
DOI: 10.1007/s11771-008-360-9

R-T instability model of magnetic fluid and its numerical simulations
ZHENG Qiu-yun(郑秋云), LI Ming-jun(李明军), SHU Shi(舒 适)
(School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, China)
Abstract: The Rayleigh-Taylor(R-T) instability of ferrofluid has been the subject of recent research, because of its implications on the stability of stellar. By neglecting the viscosity and rotation of magnetic fluid, and assuming that the magnetic particles are irrotational and temperature insensitive, we obtain a simplified R-T instability model of magnetic fluid. For the interface tracing, we use five-order weighted essentially non-oscillatory(WENO) scheme to spatial direction and three-order TVD R-K method to time direction on the uniform mesh, respectively. If the direction of the external magnetic field is the same as that of gravity, the velocities of the interface will be increased. But if the direction of the external magnetic field is in opposition to the direction of gravity, the velocities of the interface will be decreased. When the direction of the external magnetic field is perpendicular to the direction of gravity, the symmetry of the interface will be destroyed. Because of the action which is produced by perpendicular external magnetic field, there are other bubbles at the boudaries which parallel the direction of gravity. When we increase the magnetic susceptibility of the magnetic fluids, the effects of external magnetic fields will be more distinct for the interface tracing.
Key words: magnetic fluid; Rayleigh-Taylor instability; weighted essentially non-oscillatory scheme; TVD R-K method
1 Introduction
The conceptual treatment of ferrohydrodynamics was first introduced by YAMAGUCHI[1] and ROSENSWEIG[2]. The magnetic viscosity effects of ferrofluids under magnetic field were researched by SHLIMOIS[3] and ODENBACH[4], et al. The instability of thermomagnetic natural convection was studied by GOTOH and YAMADA[5], and BERKOVSKY[6], et al. did a lot of works about the applications in technology, machine and science.
Rayleig-Taylor (R-T) flow is the motion of the interface of a heavy fluid resting above a lighter fluid in the presence of gravity, which is very basic but important problem. Model equations for the location of interface have been derived[7-8]. XIE[9] studied the existence and uniqueness of analytic solution for R-T problem. LI[10] studied the nonlinear evolution of R-T instability and the SHP simulation. QIN and WANG[11] compared the differences between R-T instabilities of compressible and incompressible fluid. Numerical simulations of R-T instability were performed by ANUCHINA et al[12] with MAH-3 code. SHI et al[13] also simulated the R-T instability problem. The magnetic fluids’ R-T instability was considered by ANJIALI DEVI and HEMAMALINI[14] in theory. KOROVIN and KUBASOV[15] considered the structure of tangential magnetic field in a thin layer of viscous magnetic fluid when developing R-T instability. And MOHAMED et al[16] also studied the R-T instability in magnetic field in the theory.
In this work, neglecting the viscosity and rotation of magnetic fluid, that is to say, assuming that the magnetic particles are irrotational and temperature insensitive, the 2-D Rayleigh-Taylor (R-T) instability of magnetic fluids is inverstigated numerically. The concrete contents are as follows: in section 2, by simplifying the 2-D fluid’s equations, the model of 2-D R-T instability of magnetic fluids is obtained. And five-order weighted essentially non-oscillatory(WENO) and three-order TVD R-K methods to spatial direction and time direction on the uniform mesh, respectively, are used to numerical calculating[17]. The numerical results are also displayed in this section. In section 3, the effects of external magnetic fields and followed woks are discussed simply.
2 Numerical simulations of 2-D R-T instabi- lity of magnetic fluids
2.1 Basic equations
M and H are magnetization vector and magnetic field strength vector, respectively. Their normal numbers are M and N. We suppose the magnetic fluids are diluted suspensions and the time is very short that the magnetic
fluids are magnetized. The magnetization law of magnetic fluids is described by the Langevin function L(ζ) with following formula
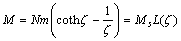
where N is the number of particles per unit volume ζ=mH/kBT (Langevin argument), kB is the Boltzmann constant, m is the magnetic moment and T is Kelvin temperature.
1) The 2-D continuity equation is of the same form for an ordinary fluid
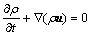
where u=(u, v)T is the velocity vector, ρ is density.
2) The linear momentum equation is as follows
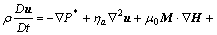
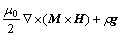
where p* is the total pressure, p*=p0+μ0H2/2; ηa is the apparent viscosity of a suspension in the absence of a magnetic field; g is body force exclusive of magnetic field body force; μ0 is permeability of free space, μ0=4π×10-7H/m ; D/Dt is material derivation.
3) The energy equation
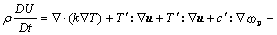
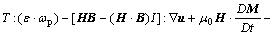

where U is the internal energy exclusive of field energy, T is total stress tensor, ε=eiejekεijk is polyadic alternator, I is second order unit tensor, c is the couple stress tensor, and ωp is the average spin angular velocity of particles about their own center.
4) Maxwell equations
Regarding magnetic fluids as nonconductive, then the Maxwell equations are written as follows
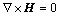 ,
, 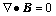
where B is magnetic induction vector, B=μ0(H+M).
2.2 Model of 2-D R-T instability of magnetic fluids after simplified
In this work, the viscosity of the magnetic fluids is neglected, the fluids is irrotational, and the intrinsic rotation of magnetic particles is very small and also neglected. The relaxation time is very short, then M is equal to equlibrium magnetization. The process of magnetized is Langevin process. If the magnetic fluids are temperature insentive and the process can be linear, then magnetic induction vector B=μH, M=χH, where μ and χ are magnetic permeability and magnetic susceptibility, respectively. And magnetic susceptibility is proportion to the particles’ concentration. It is obvious that we have M//H. The total energy exclusive of field energy is written by E, E=U+ρ(u2+v2)/2. Also assume that all heat sources are neglected and the external heat are not introduce, then the based equations of magnetic fluids are simplified as follows:
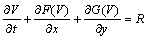
where
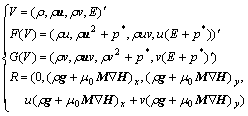
The heavy fluid is below the interface and the light fluid is above the interface with the acceleration in the positive y-direction. So we can get the 2-D R-T instability control equations of magnetic fluids
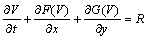
where
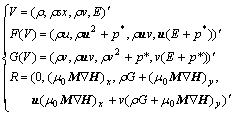
where p=(γ-1)(E-ρ(u2+v2)/2), γ is the ratio of specific heats, G is non-dimensional gravitational acceleration. If the initial values and boundary conditions are given, we can simulate the system. In the following, we will simulate the system under the special initial values and boundary conditions.
2.3 Numerical simulation of R-T instability of magnetic fluid with ratio of density 1?2 and ratio of particles concentration ρ1?ρ2
Our numerical examples are as follows[5]: the computational domain is [0, 1/4]×[0, 1]; the initial interface y=0.5, the heavy fluid ρ=2 below the interface, and the light fluid ρ=1 above the interface with the acceleration in the positive y-direction; a small perturbation is given to the y-direction fluid speed; thus for 0≤y<0.5, ρ=2, u=0, v=-0.025ccos(8πx), p=2y+1, and for 0.5≤y≤1, ρ=1, u=0, p=y+1.5, where c is the sound speed, 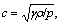 and the ratio of specific heats γ=5/3; non-dimensional gravitational acceleration is G;
and the ratio of specific heats γ=5/3; non-dimensional gravitational acceleration is G;  is kept constant and χ is proportional to ρ; for the left boundary, the right boundary and the upper boundary are all solid boundary, the bottom boundary is free boundary (that is to say, outflow condition). The uniform meshes are 120×480. The final simulation time is t=1.95.
is kept constant and χ is proportional to ρ; for the left boundary, the right boundary and the upper boundary are all solid boundary, the bottom boundary is free boundary (that is to say, outflow condition). The uniform meshes are 120×480. The final simulation time is t=1.95.
2.4 Numerical simulations analysis
The regions of the figures are all [0, 0.25]×[0.2, 0.9]. In Fig.1, we do not consider the extenal magnetic field and if G is equal to 1.0, 1.1, 1.2, we can get Figs.1(a), (b) and (c), respectively. In Fig.2, χ=0.1ρ, G=1 and if the linear external magnetic fields H are equal to
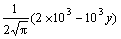 ,
,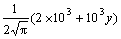 ,
, ,
,
we can get Figs.2(a), (b) and (c), respectively. In Fig.3, χ=0.2ρ, G=1 and if the linear external magnetic fields H are equal to
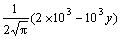 ,
, 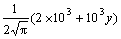 ,
, ,
,
we can get Figs.3(a), (b) and (c), respectively. From Fig.1(a) to Fig.2(a), these figures indicate that if the gravitational acceleration is increased, it will accelerate the fluidity of the interface and increase the instability of the fluid. Fig.2(a) and Fig.3(a) indicate that if the direction of external magnetic field is the same as the gravitational acceleration, the interface will move more quickly and the R-T problem will become more unstable, and if the magnetic susceptibility is increased, the effects of the extenal magnetic field will be more obviously. On the contrary, Fig.2(b) and Fig.3(b) indicate that if the direction of external magnetic field is in opposition to the direction of the gravitational acceleration, the interface will move more slowly, and if the magnetic susceptibility is increased, the effects of the extenal magnetic field will also be more obviously. Fig.2(c) and Fig.3(c) indicate that if the external magnetic field is perpendicular to gravitational acceleration, the velocity vectors will lose the symmetry and the other bubbles will appear, and the larger magnetic susceptibility will make the velocity become more asymmetry. Compared Fig.1, Fig.2(a), Fig.2(b), Fig.3(a), Fig.3(b), the figures indicate the effects of the external magnetic fields are similar to gravity when magnetic fields vectors parallelize gravity. Comparing Fig.2 with Fig.3, we can know that the larger magnetic susceptibility has the larger effects in magnetic fluids. So, in magnetic fluids, if we change the external fields or the magnetic susceptibility of magnetic particles, we will change the velocities of the magnetic fluids.
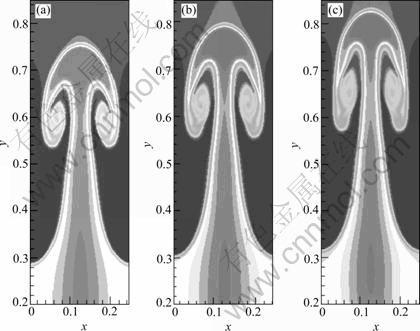
Fig.1 Rayleigh-Taylor instability (Density ρ in subdomain [0, 0.25]×[0.2, 0.9], five order WENO scheme and three-order TVD R-K method with uniform meshes, h=1/480): (a) G=1.0, H=0; (b) G=1.1, H=0; (c) G=1.2, H=0
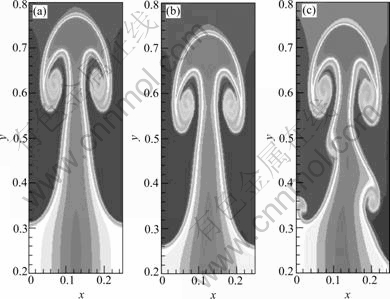
Fig.2 Rayleigh-Taylor instability (Density ρ in subdomain [0, 0.25]×[0.2, 0.9], five order WENO scheme and three-order TVD R-K
method with uniform meshes h=1/480):
(a) G=1.0, χ=0.1ρ, 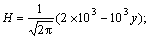 (b) G=1.0, χ=0.1ρ,
(b) G=1.0, χ=0.1ρ, 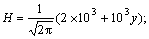 (c) G=1.0, χ=0.1ρ,
(c) G=1.0, χ=0.1ρ,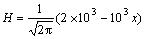
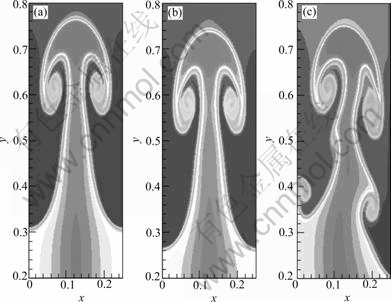
Fig.3 Rayleigh-Taylor instability (Density ρ in subdomain [0, 0.25]×[0.2, 0.9], five order WENO scheme and three-order TVD R-K
method with uniform meshes h=1/480):
(a) G=1.0, χ=0.2ρ, 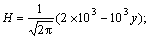 (b) G=1.0, χ=0.1ρ,
(b) G=1.0, χ=0.1ρ, 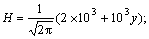 (c) G=1.0, χ=0.2ρ,
(c) G=1.0, χ=0.2ρ,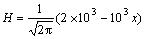
3 Conclusions
As well known, the difference of gravitational forces will affect the instability of interface in 2-D Rayleigh-Taylor instability. According to the results from numerical calculations, the force produced by extenal magnetic fields and magnetic particles will also affect the instability of the interface, which is just an important forcing term. That is to say, if external magnetic field and gravity have the same direction, the external magnetic field will increase the instability of the interface; on the contrary, the external magnetic field will decrease the instability of the interface; if the direction of the external magnetic field is perpendicular to the direction of the gravity, the symmetry of the interface will be changed. And if we increase the magnetic susceptibility of the magnetic particles, the influences of magnetic forces will be enhanced. These results correspond to the physical phenomena. But in this paper, we do not consider the magnetic viscosity and the effects which are produced by variational temperature. There are a lot of work that needs to be done in these aspects.
References
[1] YAMAGUCHI H. Engineering fluid mechanics [M]. Netherlands: Springer, 2008.
[2] ROSENSWEIG R E. Ferrohydrodynamics [M]. New York: Combridge University Press, 1985.
[3] SHLIOMIS M I. Efeective viscosity of magnetc fluid suspensions [J]. Soviet Phys JETP, 1972, 34(6): 1291-1294.
[4] ODENBACH S. Magnetoviscous effects in ferrofluids [M]. Tokyo: Springer, 2002.
[5] GOTOH K, YAMADA M. Thermal convective in a horizontal layer of magnetic fluids [J]. J Phys Soc, 1982, 51(9): 3042-3048.
[6] BERKOVSKY B M, MEDVEDEV V F, KRAKOV M S. Magnetic fluid, engineering application [M]. Oxford Univ Press, 1993.
[7] BAKER G R, CAFLISCH R, SIEGEL M. Singularity formation during Rayleigh-Taylor instability [J]. J Fluid Mech, 1993, 252: 477-501.
[8] MOORE D W. Avortex method applied to interfacial waves [M]. HORNUNG H G, MULLER E A, eds. Vortex Motion, Vieweg & Sons, 1982.
[9] XIE Xu-ming. Existence and uniqueness of analytic solution for Rayleigh-Taylor problem [J]. J Differential Equations, 2007, 237: 116-132.
[10] LI Xu. Nonliear evolution of R-T instability and SPH simulation [D]. Beijing: China Academy of Engineering Physics, 2002.
[11] QIN Cheng-sen, WANG Pei. Comparison beween Rayleigh-Taylor instability of compressible and incompressible fluid [J]. CNIC-01769, IAPCM-0042. (in Chinese)
[12] ANUCHINA N N, VOLKOV V I, GORDEYCHUK V A, ES’KOV N S, ILYUTINA O S, KOZYREV O M. Numerical simulations of Tayleigh-Taylor anf Richtmyer-Meshkov instability using MAH-3 code [J]. Journal of Computational and Applied Mathematics, 2004, 168: 11-20.
[13] SHI Jing, ZHANG Yong-tao, CHU Chi-wang. Resolution of high order WENO schemes for complicated flow structures [J]. Journal of Computational Physics, 2003, 186: 690-696.
[14] ANJIALI DEVI S P, HEMAMALINI P T. Nonlinear Rayleigh-Taylor instability of two superposed magnetic fluids under parallel rotation and a normal magnetic field [J]. Journal of Magnetism and Magnetic Materials, 2007, 314: 135-139.
[15] KOROVIN V M, KUBASOV A A. Tangential magnetic field induced structure in a thin layer of viscous magnetic fluid when developing Rayleigh-Taylor instability [J]. Journal of Magnetism and Magnetic Materials, 1999, 202: 547-553.
[16] MOHAMED A A, EL SHEHAWEY E F, EL-DIB Y O. Electroviscoelastic Rayleigh-Taylor instability of Maxwell fluids (Ⅰ): Effect of a constant tangential electric field [J]. J Phys A, 1994, A27: 3937.
[17] SHU Chi-wang. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws [R]. ICASE Report No.97-65.
(Edited by CHEN Ai-hua)
Foundation item: Projects(10771178, 10676031) supported by National Natural Science Foundation of China; The Project of National High-Tech (863) Program about ICF; Project(20070530003) supported by the Research Fund for the Doctoral Program of Higher Education
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: SHU Shi, Professor, PhD; Tel; +86-732-8293317; E-mail: shushi@xtu.edu.cn