Effect of viscosity on material behavior in friction stir welding process

ZHANG Hong-wu(张洪武), ZHANG Zhao(张 昭),

BIE Jun(别 俊), ZHOU Lei(周 雷), CHEN Jin-tao(陈金涛)

State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics,

Dalian University of Technology, Dalian 116024, China

Received 25 November 2005; accepted 8 May 2006

Abstract: Temperature-dependent elastic viscoplastic material model was used for the numerical simulation of the friction stir welding process. The non-elastic response of the rate-dependent material in the large deformation problems was calculated by using the closest point algorithm. The numerical results show that the shape of the equivalent plastic strain looks like onion rings and the spacing of the rings is approximately equal to the forward movement of the tool in one rotation. The equivalent plastic strain is increased with the increase of viscosity coefficient due to the increase of friction stress in the pin-plate interface. The region which is influenced by the rotating tool is decreased with the decrease of viscosity coefficient. The radial and circumferential stresses in front of the pin are greater than the ones behind the pin. This difference can be reduced with the decrease of viscosity.

Key words: rate-dependent model; constitutive relationship; radial return mapping algorithm; friction stir welding

1 Introduction

Friction stir welding(FSW) is a new solid-state joining process invented by TWI, in which joining of material is achieved without melting. The usual flaws such as slag-inclusions and porosity can be minimized or even can be eliminated in friction stir welds. This new technique is successfully being applied to the aerospace, automobile and ship-building industries. Numerical simulation is important for investigating the mechanism and even optimizing the process parameters of friction stir welding. DENG et al[1] used solid-mechanics based finite element method with adaptive meshing to simulate the friction stir welding process. Two different interface models with rate-independent material were used to study the material flow. SANTIAGO et al[2] simulated the 3D thermally coupled FSW process and presented the temperature field distribution using a general finite element code. The strain hardening and texture evolution in the friction stir welds of stainless steel has been studied by CHO et al[3]. Recently, ZHANG et al[4] studied the stress and strain distributions in FSW by finite element method. LIU et al[5, 6] studied the tensile fracture location characterizations in friction stir welds and the friction stir welding characteristic of aluminum alloy plates with different thicknesses.

As a solid-state joining technique, the material around the pin will generate great thermal plastic strain during FSW. The mechanical properties of the material at high temperature can be related to time. Thus, the understanding of the mechanism of FSW can be improved by use of the visco-plasticity model.

A time-continuous model normally forms the basis for the constitutive equations in the modeling of the elasto-plastic material behavior. In this time-continuous model the relation between strain and stress in the inelastic domain is defined in a rate formulation. So in the numerical solution procedure, it becomes necessary to integrate the constitutive equation to obtain the incremental formulation. It is recognized that the return mapping algorithm is very efficient for large scale inelastic computations[7]. This integration scheme is both inexpensive and accurate[8]. In order to preserve the quadratic rate of asymptotic convergence, it is crucial to ensure the consistency between the tangent modulus and the integration algorithm especially for the widely used iterative schemes based on Newton’s method.

ZHANG[9] presented a method whereby an explicit expression for the tangent moduli consistent with a closest point return mapping algorithm may be developed for generalized pressure-dependent elasto- plasticity models. One significant advantage of this method is that no matrix inversion is necessary in the consistent tangent modulus expression. SERCOMBE et al[10] investigated the consistent return mapping algorithm for chemo-plastic constitutive laws with internal couplings. A closest point project algorithm was developed to preserve the quadratic rate of convergence of the Newton-Raphson iteration scheme.

In the high temperature state, the effect of the viscosity on material behavior becomes important. In FSW, the temperature near the pin is high enough to make the material soft, and it is believed that the temperature ranges 80%-90% of the melting point of the material[11]. So the effect of the viscosity on material behavior becomes more obvious. The study of the effect of the viscosity becomes useful and interesting in the FSW process.

The return mapping algorithm is implemented for the massive computations on the flow properties around the pin in the FSW process. Two methods are used to reduce the computational costs and to complete the simulation in a reasonable short time. One is the use of the experimental temperature field which is applied to the friction stir welds. The temperature field in the simulation keeps the same as the one in the experiments at any instant. The other method is to increase the loading speeds. The combination of the two methods will reduce the computational costs dramatically. The codes developed are combined with the explicit solver in ABAQUS to model the friction stir welding process as a user subroutine (VUMAT).

Fig.1 shows the sketch of the FSW model used in this research. The translational velocity v=2 mm/s is applied to the boundaries of the welding plates, which is equal to the translational velocity of the tool in FSW. The tool is rotated with a certain angular velocity ω=400 r/min. The dimensions of the welding plates are 100 mm in length and 30 mm in width. The plate material to be welded is 1018CR steel. The diameter of the rotating pin is R₀=3 mm. Ro₁θ is a polar coordinate fixed on the pin. The weld can be divided into two parts: the advancing side and the retreating side according to the rotating direction of the pin and to the travel direction.

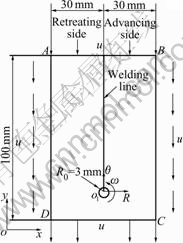
Fig.1 Sketch of friction stir welding

In the FSW process, the rotating pin is in contact with the welding plates, which produces heat transforma-tion and causes the solving difficulty of double non- linearity[12]. In order to solve this problem the temperature field from experiment[13] is used. In the experimental test, the angular velocity of the rotating tool is ω=400 r/min and the translational velocity v=2 mm/s. Fig.2 shows the history of temperature. In the FSW process, the friction force between rotating tool and the welding plates cannot grow without limit. Therefore the modified Coulomb law is used to describe the contact behavior. The limited critical friction stress in the pin-plate interface is defined as follows:

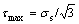                                                                        (1)

where  σ_s is the current yield stress.

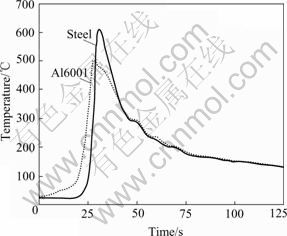
Fig.2 Experimental data used in FSW modeling

The material properties depend on the temperature and are shown in Fig.3[14]. So the material around the pin is soft to make the FSW process continue successfully. The initial yield stress of 1018CR steel  σ(20, 0)=478 MPa and the elastic modulus at room temperature E(20)=210 GPa.

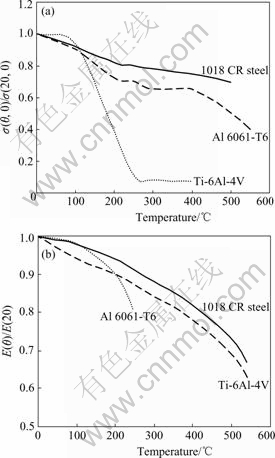
Fig.3 Properties of materials used in FSW modeling: (a) Varia- tion of yield stress with temperature; (b) Variation of elastic modulus with temperature

3 Material constitutive model

The generalization of the classic von Mises criterion for the rate dependent material can be expressed as[8]

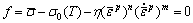                                  (2)

where  σ₀ is the initial yield stress, m is the viscosity exponent, n is the strain hardening exponent, and η is the viscosity coefficient.

The equation can be transformed to idealize elastic-plastic model when η=0. If n=0, the strain rate hardening/softening model can be obtained as follows:

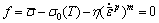                                             (3)

where  η＞0 represents the state of strain rate hardening and η＜0 strain rate softening. Strain rate softening has a remarkable influence on the material distortion in finite element solution. In the same case, plastic strain in the softening model is greater than that in the hardening model[15].

In contrast to the case of rate-independent plasticity, the effective stress is no longer constrained to remain less than or equal to the yield stress. The loading function based on von Mises condition can be defined as

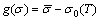                                                                (4)

where 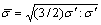 is the equivalent stress.

For Perzyna model, the flow law is given by

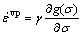                                                                      (5)

where  γ is the slip rate and

                                                                        (6)

where 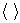 denotes Macauley brackets which is defined by .

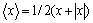The plastic strain has no influence on elastic characteristic tensor, considering thermal strain the stress can be expressed as

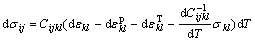             (7)

where  C_ijkl is a material elastic constant tensor, for heat transfer problems in high temperature, C_ijkl=C_ijkl(T) is a function of temperature, 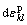 represents the plastic strain and  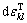is the thermal strain.

4 Return mapping algorithm

For elastic perfectly viscoplastic model, the geometric interpretation of the closest point projection algorithm in stress space is illustrated in Fig.4[16, 17]. In the state of plastic loading,

                                                                          (8)

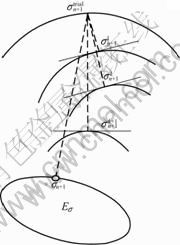
Fig.4 Geometric interpretation of closest point projection algorithm in stress space

The plastic flow residual can be defined as

                                        (9)

where

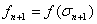                                                                 (10)

Since the total strain is fixed during the elastic-predictor stage, it follows

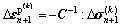                                                         (11)

Linearization of Eqns.(9) and (10) gives

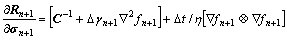
                                                                                                 (12)

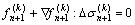                                                    (13)

Hessian matrix can be given by

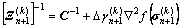                                     (14)

Solving the linearized problem, one can obtain the increment of the viscoplastic strain:

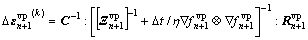(15)

So the plastic strain ε^vp can be updated until the residual is less than a specific tolerance.

5 Computational costs

For the themo-elasto-viscoplastic coupling problem, the time increment is given by

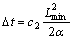                                                                         (16)

where  c₂ is a constant, L_min is the smallest element dimension, α is the thermal diffusivity of the material, and

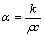                                                                                  (17)

where  k is the heat exchange coefficient, c is the specific heat, and ρ is the density. The iteration number n is defined by the time period of the event being simulated (the natural time) t and the time increment Δt:

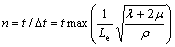                                       (18)

where  L_e is the characteristic length of element. In the present coupled thermal stress calculation the mechanical response will govern the stability limit. The estimate of the time increment is only approximate and in most cases not conservative.

Increasing the loading speed will reduce the natural time of the event being simulated and then reduce the computational costs. The viscosity must be reduced to balance the influence of strain rate increment when the loading speed is increased. The relation of strain rate and slip rate is linear from Eqn.(5). According to Eqn.(3), increasing the strain rate by N times and reducing viscosity coefficient by N times do not affect the material behavior when m=1.

6 Benchmark examples

1) Example 1

The side of the plane is 1 m×1 m, as shown in Fig.5. The elastic modulus is 70 GPa. The Poisson’s ratio is 0.1. The initial yield stress is 200 MPa. The viscosity exponent is m=1 and the viscosity coefficient is η=51.8 MPa. The right side of the plane is subjected to a uniform load of 300 MPa.

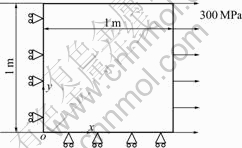
Fig.5 Plate subjected to uniform load

Fig.6 shows the stress-strain curve in x direction as the results of the code developed and ANSYS. The good agreement of the two curves demonstrates the validity of the model established. This means that the closest point return mapping algorithm developed is available in the elastic viscoplastic problems.

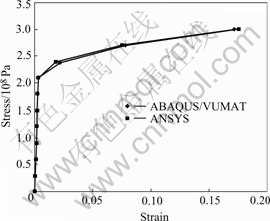
Fig.6 Stress-strain relation of plate subjected to uniform load

2) Example 2

The side of the plane is 1 m×1 m, as shown in Fig.7 and the elastic modulus is 210 GPa. The Poisson’s ratio is 0.1. The initial yield stress is 478 MPa. The viscosity exponent is m=1 and the viscosity coefficient is η=152.8 MPa. The displacement of the right side in the natural time t is 0.005 m, the stress distribution of the plane is calculated when t is different.

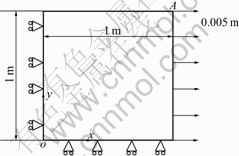
Fig.7 Tension of plate under different load rates

Fig.8 shows the stress under different loading speeds. The displacement of the right side of the plane is 0.005 m in x direction at the end of the natural time t. When t=1 s, σ_x is 502.3 MPa. In another case t=0.1 s in x direction which means that the simulation is accelerated by 10 times, the stress in x direction is 502.3 MPa. The results obtained in the two cases can agree with each other very well. But the calculation time can be reduced from 34 s without considering any computational acce- leration to 3 s in the case in which the loading speed is increased by 10 times. So this method is very essential to reduce the computational costs when the rate dependent constitutive model is used.

Fig.8 Numerical results of tensile plate with given displace- ments

Table 1 shows the history results of the cases mentioned above.  represents the natural time. 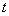 is  1 s for the case without computational acceleration, and  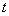is 0.1 s for the case in which the loading speed is increased by 10 times. In the elastic domain, the error ranges from 0.047% to 0.469%. In the initial stage of the plastic state, the error decreases to 0.02% and then decreases to zero with the increase of the plastic strain. This means that the error caused by increasing the loading speeds can be neglected in large deformation problems.

Table 1 Comparison of history results

7 Numerical results of FSW

By using the codes developed, the FSW process is simulated. The results obtained are described as follows.

Figs.9(a) and (b) show the equivalent plastic strain distribution when the viscosity coefficients are 50.3 MPa and 22.9 MPa respectively. As can be seen from the figures, the equivalent plastic strain distribution looks like onions, which shows the nature of the material deformation behavior in the FSW process. Around the pin, the value of the equivalent plastic strain distribution is greater and the maximum value does not occur in welding line but on the advancing side near the welding line. This shows that the material flow on the advancing side and the one on the retreating side are different [18-20], which causes that the deformation of material near the welding line is not strictly symmetric. At the same time the value of equivalent plastic strain around the pin is increased when the viscosity η is increased. Due to the increase of viscosity coefficient, the yield stress in the pin-plate interface is also increased and then the friction stress in the interface is increased. So the deformation of the material near the pin is increased when the viscosity is increased. Fig.9(c) shows the texture of onion rings in friction stir welds which is caused by the rotation and the forward movement of the pin. It is noted that the spacing of the rings is equal to the forward movement of the tool in one rotation[21]. The comparison of Figs.9(a), (b) and (c) shows that the deformation of the material shapes like onion ring when the material is slightly away from the pin in the weld. The deformation is not strictly symmetric along the welding line. The spacing of the rings is equal to the forward movement of the tool in one rotation.

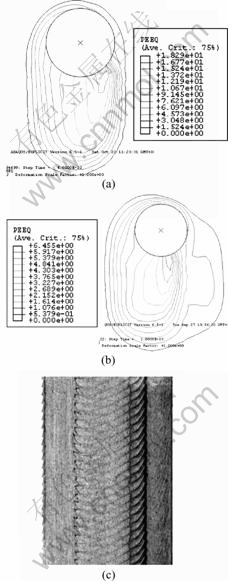
Fig.9 Distribution of equivalent plastic strain and texture of onion rings in friction stir weld: (a) η=50.3 MPa; (b) η=22.9 MPa; (c) Texture of onion rings in friction stir welds

Fig.10 shows the material flow near the pin. Loading speeds, including the translational velocity and the angular velocity of the pin, are accelerated by 1000 times to increase the moving velocity and the rotation velocity in order to accelerate the solving process. It can be seen that the difference of the viscosity coefficient has effect on the material flow. The maximum material flow velocity when η=22.9 MPa in Fig.10(a) is about 18 m/s, while the maximum flow velocity when η=50.3 MPa in Fig.10(a) reaches 22 m/s. When the viscosity is increased, the current yield stress in the pin-plate interface is also increased and then the friction stress in the pin-plate interface is increased. This is the reason for the increase of the velocity near the pin when the viscosity is increased. It should be noticed that the velocities at different radii in Fig.10 when η=50.3 MPa are very similar. This means a thicker fluid bed exists around the pin when the viscosity coefficient is greater. The material flow velocity at R=3.15 mm is reduced more obviously than that at R=3.05 mm when η=22.9 MPa, which means smaller viscosity coefficient causes the decrease of the influence range of the pin. The material flow in the region of 120?＜θ＜250? is faster, which means that the material flow on the retreating side is faster than that on the advancing side.

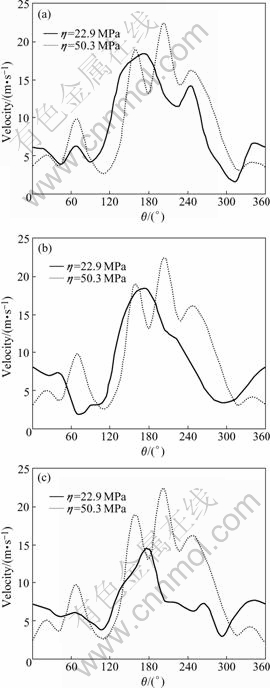
Fig.10 Material flow near pin: (a) R=3.05 mm; (b) R=3.1 mm; (c) R=3.15 mm

Fig.11 shows the distributions of the radial stress around the pin. As can be seen, the radial stress in the front area (θ=0?-180?) of the pin is larger than that behind the pin (θ=180?-360?). This is because that in the FSW process the rotating pin moves forward with rotating, which causes the material in front of the pin to be extruded and to be rotated around the pin. Therefore, the radial stress in front of the pin is greater while the one behind the pin is smaller. The maximum of the radial stress is reduced from 3.86 GPa to 3.78 GPa with the decrease of viscosity coefficient. The radial stress behind the pin (θ=180?-360?) is also increased with the increase of viscosity coefficient.

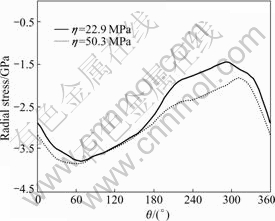
Fig.11 Radial stress distributions around pin at circle of R=0.1mm

Fig.12 shows the distributions of the circumferential stress around the pin with different viscosity coefficients. The maximum of circumferential stress occurs in front of the pin while the minimum behind the pin. The decrease of viscosity coefficient causes that the circumferential stress is decreased from 3.68 GPa to 3.37 GPa. This means the increase of viscosity coefficient may cause the increase of the radial stress and the circumferential stress, although the amplitude is small. But the increase of the stresses behind the pin is greater than the one in front of the pin. ZHANG et al[18] used the model of rate-independent aluminum alloy to investigate the relationship between the distribution of stress and time t around the pin when η=0. The calculating result shows the stress distribution around the pin is more homogeneous. Compared with this result, increasing the viscosity coefficient may cause the differences of the radial stress and the circumferential stress in front of the pin and behind the pin become more obvious.

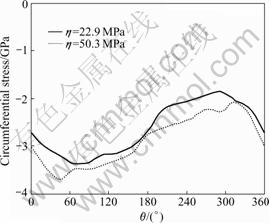
Fig.12 Circumferential stress distributions around pin at circle of R=0.1mm

Fig.13 shows the shear stress distributions near the pin-plate interface. It can be seen that the shear stress around the pin is increased with the increase of the viscosity. In the region near θ=0? the shear stress is very weak. This is the reason for the slower material flow on the advancing side. The increase of the shear stress on the retreating side with the increase of the viscosity is the real cause for the increase of the material flow, as shown in Fig.10.

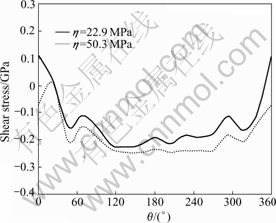
Fig.13 Shear stress distributions around pin at circle of R=0.1mm

8 Conclusions

A two-dimensional model of the FSW process is developed by using the elastic-viscoplastic constitutive relationship and the return mapping algorithm. The stress and deformation of the material around the pin are investigated. The effect of the viscosity coefficient on material behavior and stress distribution is also analyzed. The results demonstrate the validity of the numerical model developed. The main results obtained are summarized below.

1) The distribution of equivalent plastic strain looks like onion ring and the spacing of the rings is equal to the forward movement of the rotating tool in one rotation.

2) The increase of viscosity coefficient causes the increase of the equivalent plastic strain.

3) The influence range of the rotating tool can be decreased with the decrease of the viscosity coefficient.

4) The radial stress and the circumferential stress in front of the pin are greater than those behind the pin.

5) The material flow on the retreating side is faster than that on the advancing side.

The authors would like to thank Prof. DENG Xiao-min and Dr. XU Shao-wen at the University of South Carolina for their invaluable suggestions and helps on the current research.

References

[1] DENG X M, XU S W. Two dimensional finite element simulation of material flow in friction stir welding process [J]. J Manuf Process, 2004, 6(2): 125-133.

[2] SANTIAGO D H, LOMBERA G, URQUIZA S, et al. Numerical modeling of welded joints by “friction stir welding” process [J]. Mater Res, 2004, 7(4): 569-574.

[3] CHO J H, BOYCE D E, DAWSON P R. Modeling strain hardening and texture evolution in friction stir welding of stainless steel [J]. Mater Sci Eng A, 2005, 398: 146-163.

[4] ZHANG H W, ZHANG Z, CHEN J T. Finite element analysis of friction stir welding process [J]. Trans China Weld Insti, 2005, 26(9): 13-18.(in Chinese)

[5] LIU H J, FUJJI H, MAEDA M, NOGI K. Tensile fracture location characterizations of friction stir welded joints of different aluminum alloys [J]. J Mater Sci Technol, 2004, 20(1): 103-105.

[6] LIU H J, FENG J C, CHEN Y C. Friction stir welding characteristics of aluminum alloy plates with different thickness [J]. Trans Nonferrous Met Soc China, 2005, 15(S2): 97-100.

[7] LOF J, VAN DEN BOOGAARD A H. Adaptive return mapping algorithms for J2 elasto-viscoplastic flow [J]. Int J Num Meth Eng, 2001, 51: 1283-1298.

[8] PONTHOT J P. An extension of the radial return algorithm to account for rate-dependent effects in frictional contact and visco-plasticity [J]. J Mater Process Technol, 1998, 80-81: 628-634.

[9] ZHANG Z L. Explicit consistent tangent modulus with a return mapping algorithm for pressure dependent elastoplasticity models [J]. Comput Meth Appl Mech Eng, 1995, 121: 29-44.

[10] SERCOMBE J, ULM F J, MANG H A. Consistent return mapping algorithm for chemoplastic constitutive laws with internal couplings [J]. Int J Num Meth Eng, 2000, 47: 75-100.

[11] TANG W, GUO X, MCCLURE J C, et al. Heat input and temperature distribution in friction stir welding [J]. J Mater Process Manuf Sci, 1998, 7(2): 163-172.

[12] ZHANG H W, LIAO A H, ZHANG Z, CHEN J T. Numerical simulation for heat transfer and contact problems with a thermal-resistant constitutive model [J]. J Mech Strength, 2004, 26(4): 393-399.(in Chinese)

[13] CHEN C M, KOVACEVIC R. Joining of Al 6061 alloy to AISI 1018 steel by combined effects of fusion and solid state welding [J]. Int J Mach Tools Manuf, 2004, 44: 1205-1214.

[14] POTDAR Y K, ZEHNDER A T. Measurements and simulations of temperature and deformation fields in transient metal cutting [J]. J Manuf Sci Eng, 2003, 125: 645-655.

[15] CHEN Z H, TANG C Y, CHAN L C, et al. Simulation of the sheet metal extrusion process by the enhanced assumed strain finite element method [J]. J Mater Process Technol, 1999, 91: 250-256.

[16] SIMO J C, HUGHES T J R. Computational Inelasticity [M]. New York: Springer, 1998.

[17] BELYTSCHKO T, LIU W K, MORAN B. Nonlinear Finite Element for Continua and Structures [M]. New York: John Wiley, 2000.

[18] ZHANG H W, ZHANG Z, CHEN J T. The finite element simulation of the friction stir welding process [J]. Mater Sci Eng A, 2005, 403: 340-348.

[19] ZHANG H W, ZHANG Z, CHEN J T. Effect of angular velocity of the pin on material flow during friction stir welding [J]. Acta Metall Sin, 2005, 41(8): 853-859.(in Chinese)

[20] ZHANG Z, CHEN J T, ZHANG H W. The 3D simulation of friction stir welding process [A]. International Conference on Mechanical Engineering and Mechanics[C]. Nanjing: Science Press & Science Press USA Inc., 2005. 1338-1342.

[21] KRISHNAN K N. On the formation of onion rings in friction stir welds [J]. Mater Sci Eng A, 2002, 327: 246-251.

Foundation item: Porjects(10225212; 10421002; 10302007) supported by the National Natural Science Foundation of China; Project supported by the Program of Changjiang Scholars and the Innovative Research Team in University of China(PCSIRT) and Project(2005CB321704) supported by the National Basic Research Program of China

Corresponding author: ZHANG Hong-wu; Tel/Fax: +86-411-84706249; E-mail: zhanghw@dlut.edu.cn

(Edited by YUAN Sai-qian)