FRP-混凝土界面剥离承载力
俞裕果1,李静1,袁兵2,黄炎生1, 3
(1. 华南理工大学 土木与交通学院,广东 广州,510641;
2. 广东工业大学 土木与交通工程学院,广东 广州,510006;
3. 华南理工大学 亚热带建筑科学国家重点实验室,广东 广州,510641)
摘要:对比已有的各种界面剥离承载力计算模型的优劣。基于国内外多位学者的FRP-混凝土界面面内剪切试验数据,进行多尺度的有限元模拟研究,得到全新的半理论半经验界面本构模型。基于所提出的界面本构模型,提出全新的界面剥离承载力计算模型。与试验数据对比发现:所提出的界面剥离承载力模型除了具有较高的计算精度,且具有更好的计算稳定性,推荐在FRP加固混凝土结构的相关设计中采用。
关键词:FRP-混凝土界面;剥离破坏;有限元模拟;界面本构模型;界面剥离承载力模型
中图分类号:TU37 文献标志码:A 文章编号:1672-7207(2014)11-3986-07
Bonding strength of FRP-to-concrete interface
YU Yuguo1, LI Jing1, YUAN Bing2, HUANG Yansheng1, 3
(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China;
2. School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China;
3. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510641, China)
Abstract: All existing computational models for calculating interfacial bonding strength of FRP-to-concrete were reviewed and analyzed. Based on a large amount of direct pullout test results, a new semi-theoretical and semi-experiential constitutive model for FRP-to-concrete interface was developed to simulate the mechanical behavior of FRP-to-concrete interface. A new computational model for calculating interfacial bonding strength was proposed based on the constitutive model, and multi-scale finite element analysis was carried out to investigate the interface bond behavior between FRP and concrete. The computational model proposed is demonstrated to be accurate and effective and possess excellent computational stability.
Key words: FRP-to-concrete interface; debonding failure; finite element analysis; interfacial constitutive model; computational model for calculating interfacial bonding strength
近年来,外贴纤维增强复合材料(fiber reinforced polymer, FRP)片材加固混凝土结构技术发展非常迅速。在这种加固方式中,FRP和混凝土的界面黏结性能是保证加固效果的重要条件,很多FRP加固混凝土构件都是因为界面剥离而破坏[1]。针对FRP-混凝土界面的力学性能,国内外已有诸多学者展开过相关的试验以及有限元研究[2-7],但各学者研究的侧重点不同,Qu等[5]运用线弹性断裂力学方法进行了FRP与混凝土界面的剥离分析,得到了界面裂纹尖端的应力强度因子计算方法,但是其所采用的线弹性断裂力学方法易导致高估应力强度因子的计算结果。He等[6]基于数值方法研究了FRP黏结长度对界面力学性能的影响,证实了增加FRP黏结长度对于界面黏结强度的提高具有一定上限。此外,更多学者主要是针对FRP-混凝土界面剥离承载力展开研究。自1996年以来,国内外基于混凝土表面粘贴FRP片材的面内剪切试验结果提出了许多界面剥离承载力模型。其中,早期的模型所考虑的影响因素较少,而近期的模型对各种因素的考虑相对全面一些。特别是在FRP有效锚固长度的概念引入之后,剥离承载力的计算精度得到了显著提升。早期未考虑FRP有效锚固长度的界面剥离承载力计算模型有:K. Izumo模型[7]、Hiroyuki & Wu模型[8]、Tanaka模型[9]、Gemert模型[10]、Chaallal等模型[11]。而考虑了FRP有效锚固长度对界面剥离承载力影响的计算模型包括:杨勇新等模型、Chen & Teng模型、陆新征模型、Sato模型、M. Iso模型[7]以及Maeda等模型[12]、Neubauer & Rostasy模型[13]和Khalifa模型[14]。除了FRP有效锚固长度外,上述13个计算模型还不同程度地考虑了影响剥离承载力的其他主要因素,如混凝土强度等级、FRP片材与混凝土试块之间的宽度比、FRP片材刚度等。其中,以冯鹏等[7]基于合理的界面本构模型提出的承载力模型的理论性及计算精度为最优。虽然随着时间的推移,后来所提出的模型所考虑的因素逐渐趋于全面。但是,经本文计算验证,全部13个计算模型对于界面剥离承载力计算结果的离散性均偏大,因此,亟需提出更稳定的剥离承载力计算模型。本文作者以FRP-混凝土界面上的剥离承载力为核心展开分析,基于文献[7]提出的精细有限单元法,对多个面内剪切试验进行数值模拟,同时对模型的多个关键参数进行讨论,以更精确地模拟FRP-混凝土界面的剥离承载力;综合面内剪切试验和精细有限元的模拟结果,提出全新的半理论半经验FRP-混凝土界面黏结-滑移本构模型,建立界面单元法有限元模型以快速计算界面剥离承载力;基于所提出的半理论半经验本构模型,提出全新的界面剥离承载力计算模型并与所收集到的118个面内剪切试验数据进行对比。
1 界面剥离承载力的有限元模拟
1.1 精细有限单元法模拟
在试验或者常规尺度的有限元分析中很难对界面剥离破坏过程进行精确的模拟,但通过精细有限单元法的分析可以得到剥离全过程的各种细节。在没有明确的界面黏结-滑移关系的情况下,采用精细有限元法可以避免设置过多的界面参数,从而使得到的计算结果具有更实际的物理意义。这主要是因为在精细有限元分析中,采用共用节点的方法将FRP单元与对应混凝土单元连接起来,从而通过模拟物理界面下的混凝土单元的开裂直至裂缝贯通,来模拟FRP片材的剥离。本文采用的精细有限元模型的计算简图如图1所示。

图1 精细有限单元法模型计算简图
Fig. 1 Computing diagram of meso-scale finite element model
精细有限元模型在通用有限元软件MSC.MARC中建立,所使用的单元边长为0.5 mm。FRP运用平面四节点加筋单元(143号单元)建立[15],并按理想弹性材料进行模拟。混凝土单元使用平面四节点完全积分单元(3号单元)建立[15],其受压行为直接采用通用有限元软件MSC.MARC提供的混凝土本构模型[16],混凝土受拉行为则采用Subrananian等[17]提出的裂缝带模型(Crack band model),来考虑混凝土单元受拉开裂时显著的尺寸效应。而开裂混凝土裂面上的受剪行为,采用本文提出的全新裂面剪力保持模型进行考虑(式(1))。该式不仅能确保开裂混凝土单元裂面上的剪力传递能力随着裂缝宽度的增加而降低,还能避免由于单元过度开裂而在局部单元节点上出现的奇异性。
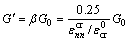 (1)
(1)
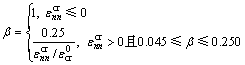 (2)
(2)
式中: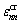 为混凝土开裂正应变;
为混凝土开裂正应变;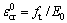 为混凝土临界开裂正应变;
为混凝土临界开裂正应变;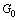 为初始剪切模量;
为初始剪切模量;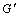 为折减后的剪切模量;
为折减后的剪切模量;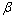 为裂面剪力保持系数。
为裂面剪力保持系数。
该建议模型在形式上类似于Al-Mahaidi裂面剪力模型[1],采用随裂缝宽度变化的裂面剪力保持系数与初始剪切模量的乘积,考虑单元开裂后剪力传递能力的降低。但本模型中混凝土临界开裂正应变取用真实值,而非Al-Mahaidi模型中默认取用的200με。此外,通过控制裂面剪力系数的上下限,能够防止有限元模型中局部单元出现奇异性,从而更好地模拟FRP-混凝土界面黏结性能问题。本文的精细有限元法模拟主要针对谭壮等[2-4]的试验研究展开。
1.2 界面本构模型的推导及界面单元法有限元模拟
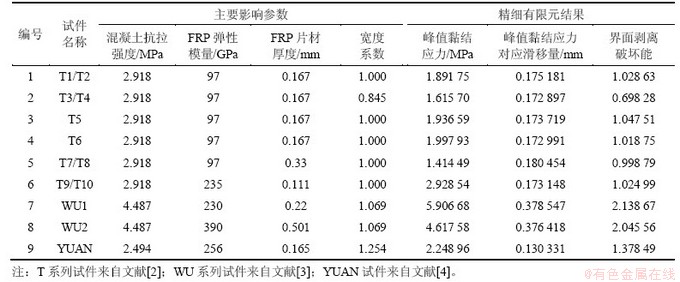
基于精细有限元法的计算结果,可以得到包括FRP-混凝土界面黏结应力分布、FRP片材滑移量以及界面破坏能等在内的各种界面力学特性指标,如表1所示。再以试验承载力指标作为模型检验标准,从而可以推导出半理论半经验的FRP-混凝土界面黏结-滑移本构模型。
现有FRP-混凝土界面黏结性能研究表明,在FRP粘贴长度大于有效锚固长度的情况下,剥离承载力主要取决于界面破坏能,而与具体的曲线形状无关[7]。因此,本文以双线性模型为基础研究界面本构模型。由于本文有限元研究是基于平面应力模型展开的,无法考虑FRP和混凝土试块的宽度比影响,因此,参考文献[5]的宽度系数模型以考虑该因素对剥离承载力的影响。通过对表1进行分析,可以得到界面力学指标的变化规律,从而得到半理论半经验的FRP-混凝土界面本构模型如式(3)~(7)所示。
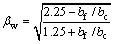 (3)
(3)
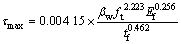 (4)
(4)
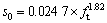 (5)
(5)
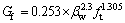 (6)
(6)
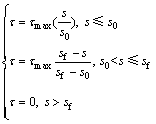 (7)
(7)
式中:bf和bc分别为FRP和混凝土的宽度;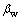 为宽度比系数;ft为混凝土抗拉强度;tf和Ef为FRP片材厚度和弹性模量;
为宽度比系数;ft为混凝土抗拉强度;tf和Ef为FRP片材厚度和弹性模量;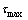 和s0分别为峰值黏结应力及其对应的滑移量;Gf为界面剥离破坏能;
和s0分别为峰值黏结应力及其对应的滑移量;Gf为界面剥离破坏能;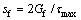 为FRP极限滑移量;
为FRP极限滑移量;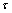 和s为界面黏结应力和滑移量。
和s为界面黏结应力和滑移量。
精细有限元模型的单元尺度很小,分析时需要精确调整混凝土材料的开裂特性,否则易造成计算消耗大和难以收敛等问题。然而,在获得了FRP-混凝土界面本构模型的基础上,可以改用常规尺度有限元方法加以模拟计算。主要的做法是在FRP单元和混凝土单元之间加入界面单元,并将建议的界面本构模型赋予界面单元即可,该方法在本文中称为“界面单元法”。在界面单元法有限元模拟中,除混凝土单元继续采用四节点平面应力完全积分单元(3号单元)[15]以外,FRP片材采用平面二节点桁架单元(9号单元)[15]进行建模,而FRP-混凝土之间的界面采用平面四节点界面单元(186号单元)[15]进行建模。单元的材料性质方面,除FRP-混凝土界面单元的材料性质需应用子程序导入本文的建议双线性本构模型之外,FRP片材以及混凝土单元的材料性质设定与精细有限单元法模型一致。但是,由于界面单元法模型中的混凝土单元尺度发生了改变(单元边长改为5 mm),因此,需要运用裂缝带模型[17],以重新考虑该尺度下混凝土单元开裂时的尺寸效应。
表1 精细有限元计算FRP-混凝土界面主要力学特性指标
Table 1 Major parameters for mechanical behavior of interface acquired by meso-scale FEA
1.3 有限元计算剥离承载力结果对比及界面本构模型验证
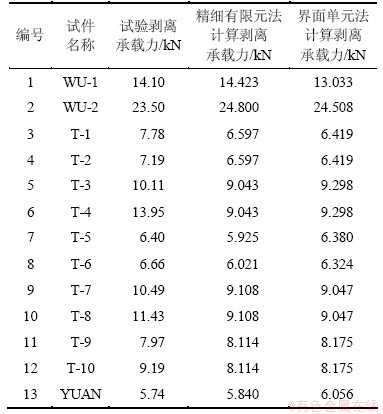
本研究共收集了118个面内剪切试验记录,其中文献[2-4]中所提供的13个试验记录给出了较为具体的试验结果,包括有剥离承载力、FRP有效黏结长度以及FRP片材应变分布曲线等。因此,本文主要对这13个试件展开有限元数值模拟研究,FRP-混凝土界面剥离承载力的2种有限元方法计算结果与对应的双面面内剪切试验结果的对比如表2所示。
表2 剥离承载力计算结果对比
Table 2 Comparison between FE debonding strength and experimental ones
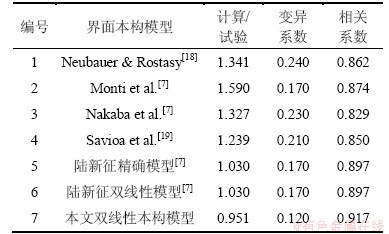
为进一步验证本文所建议的双线性界面本构模型的先进性,分别将6种FRP-混凝土界面本构模型(如表3所示)和本文建议的界面本构模型一同导入通用有限元软件MSC.MARC中生成界面单元、建立相应有限元模型,并对上述13个面内剪切试件进行了有限元分析计算。鉴于篇幅限制,此处仅将各模型所得承载力计算结果的数值统计信息列于表3。此外,运用本文建议的双线性界面本构模型,还能够得到构件自初始受力直至发生剥离后的FRP应变分布情况,如图2所示。由图2可以看出,本文建议的界面本构模型,能够较好地模拟FRP-混凝土界面各阶段的受力性能。在发生剥离破坏后,试验曲线产生了较剧烈的波动,这主要是FRP-混凝土界面剥离裂缝失稳扩展的随机性所致。然而,在有限元模拟中,将混凝土假定为各项同性材料进行建模,因此,有限元结果无法模拟得到实际试验曲线所反映的这一性质。但是,该数值结果依然较好地获得了剥离破坏后FRP片材应变沿黏贴长度方向的大致分布情况。
表3 各黏结-滑移本构模型计算界面剥离承载力对比
Table 3 Comparison of FE debonding strength acquired by using different constitutive models
2 界面剥离承载力计算模型
2.1 界面剥离承载力计算模型
类似于文献[7]所提出的计算模型,本文的界面剥离承载力计算模型同样是依据合理的FRP-混凝土界面黏结-滑移本构模型提出的。根据已有的界面剥离承载力模型的研究,界面的剥离承载力主要与混凝土抗拉强度、FRP片材弹性模量、FRP片材厚度以及界面破坏能等因素有关。通过对上述有限元结果的研究,可以得到FRP-混凝土界面剥离承载力随主要影响参数的变化规律为:
1) 承载力随着混凝土抗拉强度的提高而显著增长;
2) 界面剥离承载力随着FRP片材弹性模量和厚度的乘积的增长略有提高;
3) 由于将FRP片材宽度系数对承载力的影响综合进界面破坏能内进行考虑,因此界面剥离承载力并未按预计的以界面破坏能的增长而提高,而是与界面破坏能呈反比;
4) 界面剥离承载力中的另一个重要指标为有效黏结长度,其取值大致随着FRP片材的弹性模量、厚度以及宽度的乘积的增长而略有提高。
经过大量试算以及模型参数拟合,本文基于半理论半经验的界面本构模型,提出建议FRP-混凝土界
面剥离承载力计算模型如下:
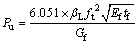 (8)
(8)
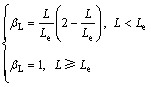 (9)
(9)
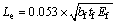 10)
10)
式中:Le为FRP有效锚固长度;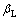 为FRP有效锚固长度系数;Pu为界面剥离承载力。
为FRP有效锚固长度系数;Pu为界面剥离承载力。
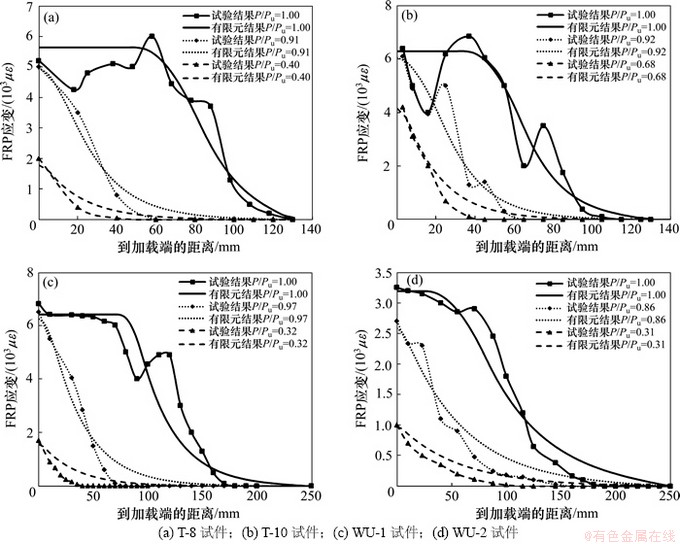
图2 建议界面本构模型计算FRP应变分布和试验结果对比
Fig. 2 Comparison between FE FRP strain distribution and experimental ones
2.2 界面剥离承载力计算模型的验证
运用其他学者所提出的计算模型以及本文推导的界面剥离承载力计算模型,对所收集到的全部118个面内剪切试件分别进行了计算分析。在13个剥离承载力模型中,本文选取了其中计算精度较好的3个模型,以及本文计算模型的计算结果,绘制了计算承载力结果与试验承载力结果的对照图(如图3所示)。其他计算模型的结果、各个剥离承载力模型的计算变异系数以及相关系数等见表4。
表4 不同界面剥离承载力模型的对比
Table 4 Comparison of different bond strength models for interface
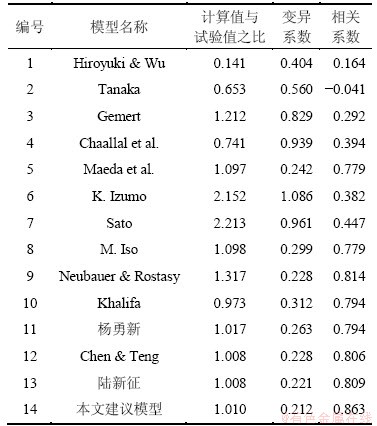
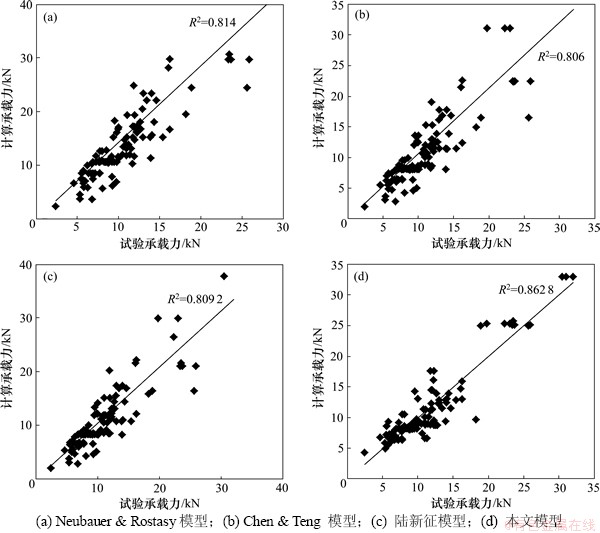
图3 计算剥离承载力结果对比
Fig. 3 Comparison of calculating bond strength
3 结论
1) 基于Al-Mahaidi模型,提出了全新的混凝土裂面剪力保持模型,该模型能够较好地模拟小尺度混凝土单元的开裂受力性能。
2) 基于精细有限元法的分析结果,提出了全新的半理论半经验的FRP-混凝土界面黏结-滑移本构模型,并证明了该模型能够较好地模拟界面各阶段的力学性能。
3) 基于所得到的半理论半经验的界面本构模 型,提出了全新的FRP-混凝土界面剥离承载力计算模型。经与其他学者所提出的计算模型相比,本文模型的计算结果与试验结果的对比具有较大的相关系数以及较小的变异系数,表明具有更强的计算稳定性。
参考文献:
[1] 陆新征, 叶列平, 滕锦光, 等. FRP片材与混凝土黏结性能的精细有限元分析[J]. 工程力学, 2006, 23(5): 74-82.
LU Xinzheng, YE Lieping, TENG Jinguang, et al. Meso-scale finite element analysis of FRP-to-concrete bond behavior [J]. Engineering Mechanics, 2006, 23(5): 74-82.
[2] 谭壮. GFRP布加固混凝土梁受力性能的试验研究[D]. 北京: 清华大学土木学院, 2002: 10-25.
TAN Zhuang. Experimental research for RC beam strengthened with GFRP[D]. Beijing: Tsinghua University. School of Civil Engineering, 2002: 10-25.
[3] WU Zhishen, YUAN Hong, Hiroyuki Y, et al. Experimental or analytical study on interfacial fracture energy and fracture propagation along FRP-concrete interface[J]. ACI International, 2001, SP-201-8: 133-152.
[4] YUAN Hong, TENG Jinguang, Seracino R, et al. Full-range behavior of FRP-to-concrete bonded joints[J]. Engineering Structures, 2004, 26(5): 553-564.
[5] QU Hongchang, CHEN Lingling, ZHANG Shengli. Debonding analysis between FRP-concrete interface with a linear elastic fracture mechanics approach[J]. Advanced Materials Research, 2011(189/ 190/191/192/193): 2306-2311.
[6] HE Zhujie, XU Tao, TANG Chunan. A numerical study on the effect of bond length on the bonding performance of FRP-concrete interface[J]. Advanced Materials Research, 2011(268/269/270): 857-862.
[7] 冯鹏, 陆新征, 叶列平. 纤维增强复合材料建设工程应用技术: 试验、理论与方法[M]. 北京: 中国建筑工业出版社, 2011: 104-116.
FENG Peng, LU Xinzheng, YE Lieping. Application of fiber reinforced polymer in construction: Experiment, theory and methodology[M]. Beijing: China Building Industry Press, 2011: 104-116.
[8] Hiroyuki Y, WU Zhishen. Analysis of debonding fracture properties of CFS strengthened member subject to tension[C]// 3rd International Symposium on Non-Metallic (FRP) Reinforcement for Concrete Structures, Vol. 1. Sapporo, 1997: 284-294.
[9] Tanaka T. Shear resisting mechanism of reinforced concrete beams with CFS as shear reinforcement[D]. Hokkaido: Hokkaido University, 1996.
[10] Van Gemert D. Force transfer in epoxy-bonded steel-concrete joints[J]. International Journal of Adhesion and Adhesives, 1980, 1(2): 67-72.
[11] Chaallal O, Nollet M J, Perraton D. Strengthening of reinforced concrete beams with externally bonded fiber-reinforced-plastic plates: Design guidelines for shear and flexure[J]. Canadian Journal of Civil Engineering, 1998, 25(4): 692-704.
[12] Chajes M J, Finch W J, Januszka T F et al. Bond and force transfer of composite material plates bonded to concrete[J]. ACI Structural Journal, 1996, 93(2): 295-230.
[13] Neubauer U, Rostasy F S. Design aspects of concrete structures strengthened with externally bonded CFRP plates[C]// 7th International Conference on Structural Faults and Repair Vol. 2. Edinburgh, Scotland: ECS Publications, 1997: 109-118.
[14] Khalifa A, Gold W J, Nanni A et al. Contribution of externally bonded FRP to shear capacity of RC flexural members[J]. Journal of Composites for Construction, 1998, 2(4): 195-203.
[15] MSC.MARC. Volume B: Element library[M]. California: MSC.Software Corporation, 2010: 113-661.
[16] MSC.MARC. User’s manual[M]. California: MSC.Software Corporation, 2010: 534-537.
[17] Subramaniam K V, Carloni C, Nobile L. An understanding of the width effect in FRP-concrete debonding[J]. Strain. 2011, 47(2): 127-137.
[18] Neubauer U, Rostasy F S. Bond failure of concrete fiber reinforced polymer plates at inclined cracks-experiments and fracture mechanics model[C]// 4th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures ACI. Michigan: Farmington Hills, 1999: 369-382.
[19] Savioa M, Farracuti B, Mazzotti C. Non-linear bond-slip law for FRP-concrete interface[C]// 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003: 163-172.
(编辑 赵俊)
收稿日期:2013-12-19;修回日期:2014-02-10
基金项目(Foundation item):亚热带建筑科学国家重点实验室开放性课题(2012KB28);住房和城乡建设部科学技术项目(2011-K3-22) (Project(2012KB28) supported by State Key Laboratory of Subtropical Building Science Open Fund; Projcet(2011-K3-22) supported by Science and Technology Program of Ministry of Housing and Urban-Rural Development)
通信作者:黄炎生(1963-),男,广东普宁人,教授,博士生导师,从事结构分析及其可视化、既有建筑物的可靠性评估等研究;电话:13922167183;E-mail: cvyhuang@scut.edu.cn