大型矿山地矿工程三维可视化模型的构建
周智勇,陈建宏,杨立兵
(中南大学 资源与安全工程学院,湖南 长沙,410083)
摘 要:对真三维环境下地矿工程三维立体模型的构建进行研究;采用分形插值算法即改进的中点移位法建立地形模型;建立基于TIN和ARTP的三维数据模型;利用顶板中心线加巷道断面法实现开拓系统的三维实体建模;基于线框法及块段法分别构建矿体的表面模型及内部模型。研究结果表明:采用改进的中点移位法,提高了细分过程的平稳性,使整体形状容易控制;顶板中心线加断面法容易实现,建模速度快,效果较好;线框构模法与块段法相互结合可用于精确表达矿体的边界形态及内部属性。
关键词:地矿工程;三维建模;可视化;三维数据模型;分形
中图分类号:TD672 文献标识码:A 文章编号:1672-7207(2008)03-0423-06
3D visualization modeling on geological and mining engineering in
a large-sized mine
ZHOU Zhi-yong, CHEN Jian-hong, YANG Li-bing
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: 3D modeling for geological and mining engineering was studied under real 3D condition. Fractal interpolation 3D date algorithm, i.e., improved midpoint displacement method, was utilized to set up the terrain model. Based on TIN and ARTP, 3D data model was constituted. 3D entity model of development system was established by the method of placing the roadway section on the roof center line. Surface model and internal model of orebody were established by line-frame and block-section method, respectively. The results show that the improved midpoint displacement method can be used to improve the stationarity of subdivision process, and make the control of whole shape easy. The method in which the roadway section located in roof center line possesses some excellences such as easy realization, fast modeling and good modeling effect. The boundary configuration and internal model of orebody can be established accurately by using line-frame method with block-section method.
Key words: geological and mining engineering; 3D modeling; visualization; 3D data model; fractal
矿井设计是矿井建设和生产中非常关键的环节,若设计不合理,则可能严重降低矿山效益或引发事 故[1]。所以,采用先进的方法和技术来进行矿井规划和设计非常必要。传统的矿井设计是在纸质图上进行或者用Autocad等软件进行辅助设计,都是用二维图形表示三维的地质现象和复杂的井筒巷道的分布,很不直观,且给施工人员准确理解其空间关系和正确施工造成了一定的困难。利用矿山现有测量资料及地质资料,构建矿山地矿工程的三维可视化模型,直观地展示地下巷道与地形地貌、巷道与矿体的关系,是比较理想的解决方案。
许多研究者在这方面进行了大量研究,取得了一定成果,但是也存在一些局限性,实践证明,采用这些方法在大多数情况下不能如实地反映地表的真实自然形态。因为大多数地形模型的建立是基于一些传统的建模方法如趋势面法、距离幂反比法和克立格法,如张建桃等[1]采用虚拟建模软件和仿真软件进行了矿井设计实验;葛永慧等[2]利用巷道网络系统(基本元素为结点、节点及巷道中线)加载巷道断面实现了巷道建模;魏占营等[3]设计了基于巷道断面及顶板中心线的C++算法。从建模效果可以看出,所建巷道模型都过于理想化,对于快速建立大型矿山的复杂巷道具有一定的局限性。徐云和等[4-5]利用钻孔数据绘制剖面,进而建立矿体模型,这对于厚大矿体是适用的,但是,对于某些薄矿脉甚至是极薄矿脉则需要寻找新的技术手段。针对这些情况,本文作者对真三维环境下大型矿山复杂地矿工程三维立体模型的快速构建方法进行研究,建立某大型矿山包含地下巷道、矿体、地质钻孔及地形地貌的三维立体模型,以直观地展示工程之间的空间关系,提高设计的准确性和合理性,有助于正确施工。
1 基于分形插值算法的地形建模
地形模型实际上是一个二维网格化数组,地形建模过程就是根据已知地形数据(坐标及标高)给每一个网格(即单元块)中心赋以1个高程。对于目前许多现有的地形建模插值算法,其应用背景多针对工程几何造型,而且要求所得到的结果应尽量表面光滑平整,故它们不能如实地反映地表的真实自然形态。随着分形几何理论的发展,基于分形特征的自然地表插值技术日益受到人们的重视。许多基于分形维数的表面插值算法应运而生,如泊松阶跃法、傅里叶滤波法、中点位移法、逐次随机增加法、带限噪声累积法和小波变换等[6]。实验表明,利用分形算法得到的地形模型不仅能够如实地反映原数据的总体轮廓,而且还可以较好地再现原始自然地表的粗糙起伏特性,显示较强的逼真性。
1.1 改进的中点移位法
现已广泛采用的“中点移位法”其基本思路是:对规则格网进行递归细分,每次细分产生的新结点的高程除了用相邻点高程进行线性内插计算外,还增加1项由分维特征值H和σ以及递归层次i构成的随机位移?i:

中点移位法尽管算法简单,便于实现,但容易在地形表面产生“折皱痕迹”。为此,提出一种改进算法,即有约束的“中点移位方法”——空间网格的递归细分算法,如图1所示。其中,图1(a)所示为DEM原始网格(X和Y上的平面图),图1(b)所示为细分内插点网格。细分后新的网格结点的高程分别按式(3)~(6)计算[7]。
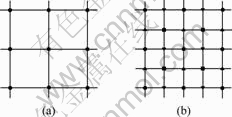
(a) 第k步;(b) 第k+1步
图1 改进的中点移位法示意图
Fig.1 Sketch map of improved midpoint displacement method
对于“■”点的细分:
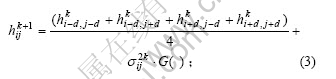
对于“▲”点的细分:
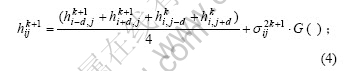
对于“▼”点的细分:
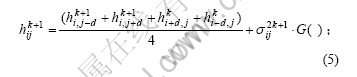
对于“●”点的细分:
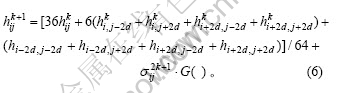
其中:G( )为正态分布的随机噪声,即N(0, 1);d为DEM经(k+1)次细分后网格结点间的距离; 为结点处的根方差:
为结点处的根方差:

1.2 地形模型
采用上述算法建立了矿区地形模型,如图2所示。可见,所建模型与地表的真实自然形态非常接近,如实地反映了矿区地形的总体轮廓。将钻孔数据调入(图3),可以验证所建模型的准确性。

图2 地形模型
Fig.2 Terrain model

图3 地形、钻孔组合图
Fig.3 Combined diagram of terrain and drill
2 三维数据模型
目前,对三维数据模型的研究虽然取得了一些成果,但仍然无法满足实际应用需求。其主要问题是这些研究大多致力于为3DGIS提供一种通用的数据模型,而很少有人进行某个专业领域的数据模型研究,从而导致模型难以实现,无法推广和应用。在这种情况下,有专家提出基于不规则三角网TIN和似直三棱柱(简称ARTP)的三维数据模型[2, 8]。其中,TIN可以用于表达边界和面信息;而ARTP可以用于将空间对象剖分成一系列邻接但不交叉的体元的集合,描述空间对象的内部特征。
2.1 ARTP体元的定义
ARTP是3条棱线垂直水平面、顶底三角形面不一定平行的似直三棱柱体元(见图4)。其中:A1,B1,C1,A2,B2和C2构成一个基本的ARTP体元,△A1B1C1和△A2B2C2 在水平面的投影均为△A0B0C0。此外,ARTP体元还有可能出现像A2,B2,C2,B1,A1,C2,A1,C1和B1这样的特殊形状,分别可以看作是2点和3点重合的特殊情况。

图4 ARTP体元示意图
Fig.4 Sketch map of ARTP volume unit
2.2 基于TIN和ARTP的三维数据模型
在基于TIN和ARTP的三维数据模型(图5)中,将地矿空间对象抽象为点状实体、线状实体、面状实体和体状实体。这4种空间对象类型又通过结点、弧段、三角形边、ARTP棱边、三角形、四边形和ARTP体元共7种基本几何元素来表达[8]。
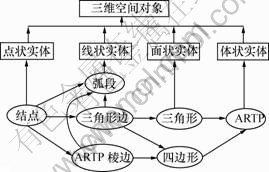
图5 基于TIN和ARTP的三维数据模型
Fig.5 3D data model based on TIN and ARTP
点状实体是零维空间对象,可表示三维空间中 的点状地物,如钻孔点等。点状实体对应于结点元素,具有空间位置信息,即x,y,z坐标。
线状实体是一维空间对象,可表示三维空间中的线状地物,如断层线、钻孔等,可由1个或多个弧段元素组成。弧段由起结点和终结点加一系列有序点集表示,也可由三角形边和ARTP棱边组成。
面状实体是二维空间对象,可表示三维空间中的面状地物,如地层面、断层等,可使用TIN来表达,在几何形态上是不规则的,是三维空间中的曲面。
体状实体是三维空间对象,可表示三维空间中的体状地物,如巷道、矿体等。任意1个体状实体均 可以剖分成一系列邻接但不交叉的ARTP体元的集合。当不需要考虑该实体的内部信息时,可以简单地用构成该实体的边界面来表达。
3 开拓系统建模
3.1 巷道及井筒的三维建模和算法实现
在巷道的几何建模过程中,将巷道分解为点、弧段、巷道断面、局部巷道4个组成部分。巷道是由一系列的局部巷道组成;局部巷道则由巷道中心线弧段和巷道断面来表达[9-10]。巷道断面是巷道几何建模中的重要参数,主要有拱形、矩形、梯形、斜梯形等形态(图6)。为了便于表达,把巷道断面分为上、下、左、右4个弧段,用于描述巷道的断面形态,其中每个弧段又由一系列点组成。

(a) 拱形断面;(b) 矩形断面;(c) 梯形断面
图6 主要巷道断面形态示意图
Fig.6 Sketch maps of main laneway profile
当生成巷道模型时,从二维图上提取巷道顶板中心线和断面参数等数据,若1条巷道断面尺寸基本保持不变,则可利用巷道中心线和断面图来描述它的空间形态(图7)。根据上述思想,设计如下算法:
a. 根据导线测量数据及二维平面图纸确定巷道中心线;
b. 巷道中心线平滑处理;
c. 确定巷道断面数据;
d. 绘制3维巷道实体模型。

图7 巷道实体模型示意图
Fig.7 Sketch map of laneway entity model
3.2 开拓系统三维实体模型的构建
该矿山采用多段斜井开拓,矿内各种井筒、巷道多且复杂。建模根据各井筒断面规格分类进行,见表1。此次建模的内容包括各种开拓工程,如平巷、斜井、竖井、风井及溜井等。建模效果如图8~10所示。
表1 井筒断面规格表
Table 1 Profile standard of shaft
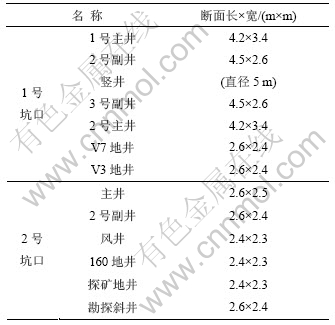

图8 开拓系统整体投影图(X-Z坐标)
Fig.8 Projection drawing of whole development system
(X-Z coordinate)

图9 开拓系统整体投影图(Y-Z坐标)
Fig.9 Projection drawing of whole development system
(Y-Z coordinate)

图10 开拓系统局部立体图
Fig.10 Stereogram of local development system
4 矿体建模
考虑到矿体不仅具有形状、大小及空间位置等信息,而且存在矿体成分、质量、品位等属性,因 此,采用线框法建立矿体表面模型,采用块段法插值建立矿体内部模型。这样既可利用线框构模法精确地识别矿体的边界形态,划分矿体的岩性信息,又可以利用矿体块段属性进行插值的方法来建立矿体的内部模型[11-15]。这2种方法取长补短,可精确地用于表达矿体的三维形态(图11)。

图11 V3矿脉实体模型
Fig.11 Entity model of V3 mine vein
4.1 矿体表面模型的建立
地质数据的获取大都是通过勘探得到的,逐个绘制勘探线剖面图,各剖面间相互平行,每一剖面与实体的交线是实体在该剖面上的轮廓线,即二维平面上一条封闭的无自交线。将一系列剖面上的轮廓线连接起来,形成轮廓三角网,进而构造出地质体的表面模型。
4.2 矿体内部模型的建立
a. 确定块段模型根块的范围。求出表面模型的最小和最大的X,Y和Z,凭借这6个坐标值来确定根块的大小和位置,再分别求出X,Y和Z坐标的差值,取其最大者,以保证矿体表面模型包含在根块之内。
b. 建立块段模型。以与根块相切表面模型上的一点为起始点,一定的长度为棱长,把根块分成若干个用户定义的单元块,对母块和子块分别编号,并存储在数据库中。利用克里格插值方法计算每个单元块的属性。
5 结 论
a. 改进的中点移位法增加了相邻区域间的相关性,且具有连续随机增加的效果,提高了细分过程的平稳性。在上层结点处,采用基于三次样条光滑曲面进行插值,使整体形状容易控制。
b. 基于TIN的数据模型可用于表达边界和面信息;而ARTP数据模型可以用于将空间对象剖分成一系列邻接但不交叉的体元的集合,描述空间对象的内部特征。
c. 巷道或井筒断面尺寸变化不大时,可采用顶板中心线加断面法来建立巷道或井筒的实体模型。实践证明,此种建模方法容易实现,建模速度快,效果好。
d. 采用线框构模法可精确识别矿体的边界形态,划分矿体的岩性信息;采用块段法可对矿体块段属性进行插值,建立矿体的内部模型。将这2种方法相互结合可精确表达矿体的三维形态。
参考文献:
[1] 张建桃, 伏永明. 基于虚拟现实技术的矿井规划与设计[J]. 计算机时代, 2005(3): 22-23.
ZHANG Jian-tao, FU Yong-ming. Planning and designing of mine based on virtual reality technique[J]. Computer Era, 2005(3): 22-23.
[2] 葛永慧, 王建民. 矿井三维巷道建模方法的研究[J]. 工程勘察, 2006(10): 46-49.
GE Yong-hui, WANG Jian-min. Study on the method of 3D laneway modeling[J]. Journal of Geotechnical Investigation & Surveying, 2006(10): 46-49.
[3] 魏占营, 王宝山, 李青元. 地下巷道的三维建模及C++实现[J]. 武汉大学学报: 信息科学版, 2005, 30(7): 60-62.
WEI Zhan-ying, WANG Bao-shan, LI Qing-yuan. Underground laneway modeling and realization by C++[J]. Geomatics and Information Science of Wuhan University, 2005, 30(7): 60-62.
[4] 徐云和, 赵吉先, 程朋根, 等. 地矿3维GIS模型的构建及可视化[J]. 中国矿业, 2003, 12(4): 60-62.
XU Yun-he, ZHAO Ji-xian, CHENG Peng-gen, et al. Construction and visualization of 3D GIS mine mode[J]. China Mining Magazine, 2003, 12(4): 60-62.
[5] 李 艳, 王恩德, 鲍玉斌, 等. 基于钻孔数据的矿体三维可视化研究与实现[J]. 沈阳工业大学学报, 2005, 27(4): 418-421.
LI Yan, WANG En-de, BAO Yu-bin, et al. Study and implementation of borehole data based 3D visualization of orebody[J]. Journal of Shenyang University of Technology, 2005, 27(4): 418-421.
[6] 肖高逾, 周源华. 基于分形几何的空间多面体变形法在三维地表插值中的应用[J]. 中国图像图形学报, 2000, 5(3): 241-243.
XIAO Gao-yu, ZHOU Yuan-hua. Fractal-based special polyhedron model deformation algorithm in terrain surface interpolation[J]. Journal of Image and Graphics, 2000, 5(3): 241-243.
[7] 徐 青. 地形三维可视化技术[M]. 北京: 测绘出版社, 2000.
XU Qing. Three dimension terrain[M]. Beijing: Sino Maps Press, 2000.
[8] 毛善君, 熊 伟. 煤矿虚拟环境系统的总体设计及初步实现[J]. 煤炭学报, 2005, 30(5): 571-575.
MAO Shan-jun, XIONG Wei. Design and primary implementation of coal mine virtual environment system[J]. Journal of China Coal Society, 2005, 30(5): 571-575.
[9] 熊 伟, 毛善君, 马蔼乃, 等. 煤矿虚拟环境的巷道几何建模及关键算法研究[J]. 测绘通报, 2002(8): 15-21.
XIONG Wei, MAO Shan-jun, MA Ai-nai, et al. A research on geometric modeling of roadway and the key algorithm of coalmine in virtual environment[J]. Bulletin of Surveying and Mapping, 2002(8): 15-21.
[10] 王宝山, 魏占营. 煤矿虚拟环境的巷道三维建模研究[J]. 测绘学院学报, 2005, 22(3): 204-211.
WANG Bao-shan, WEI Zhan-ying. A research on three- dimensional modeling of roadway in virtual environment for coalmine[J]. Journal of Institute of Surveying and Mapping, 2005, 22(3): 204-211.
[11] 刘亚静, 李 梅, 姚纪明. 多分辨率扩展八叉树矿体建模研究[J]. 煤炭科学技术, 2006, 34(8): 57-60.
LIU Ya-jing, LI Mei, YAO Ji-ming. Research on orebody model establishment with multi resolution ratio and extended octree[J]. Coal Science and Technology, 2006, 34(8): 57-60.
[12] 李春民, 李仲学, 王云海, 等. 地矿工程三维可视化系统建模[J]. 金属矿山, 2005(12): 44-50.
LI Chun-min, LI Zhong-xue, WANG Yun-hai, et al. Visualization system modeling for geological and mining engineering[J]. Metal Mine, 2005(12): 44-50.
[13] 汪云甲, 伏永明. 矿井巷道三维自动建模方法研究[J]. 武汉大学学报: 信息科学版, 2006, 31(12): 1097-1100.
WANG Yun-jia, FU Yong-ming. On 3D automatic modeling method of mine roadway[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1097-1100.
[14] 李翠平, 李仲学. 矿床的体视化仿真技术与实现[J]. 北京科技大学学报, 2004, 26(6): 579-583.
LI Cui-ping, LI Zhong-xue. Volume visualization approach for modeling mineral deposits[J]. Journal of University of Science and Technology Beijing, 2004, 26(6): 579-583.
[15] 王恩德, 李 艳, 鲍玉斌. 矿体三维可视化建模技术[J]. 东北大学学报: 自然科学版, 2005, 26(9): 890-892.
WANG En-de, LI Yan, BAO Yu-bin. Visualized 3-D modeling of orebodies[J]. Journal of Northeastern University: Natural Science, 2005, 26(9): 890-892.
收稿日期:2007-08-20;修回日期:2007-10-18
基金项目:国家自然科学基金资助项目(50774092);全国优秀博士学位论文专项资金资助项目(200449);中南大学教育创新工程基金项目资助项目(1343-76230)
通信作者:周智勇(1980- ),男,江西上饶人,博士研究生,从事矿床建模、安全预警、采矿仿真及可视化技术研究;电话: 0731-8879889;E-mail: csuzzy@126.comx