J. Cent. South Univ. (2019) 26: 3188-3199

DOI: https://doi.org/10.1007/s11771-019-4245-x

Simulation on flow, heat transfer and stress characteristics of large-diameter thick-walled gas cylinders in quenching process under different water spray volumes

GAO Jing-na(高静娜)^{1, 2}, GAO Ying(高颖)², XU Qin-ran(徐钦冉)¹, WANG Ge(王葛)¹, LI Qiang(李强)^{1, 3}

1. National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Yanshan University, Qinhuangdao 066004, China;

2. School of Materials Science and Engineering, Hebei University of Science and Technology,Shijiazhuang 050018, China;

3. School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300130, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: Cooling strength is one of the important factors affecting microstructure and properties of gas cylinders during quenching process，and reasonable water spray volume can effectively improve the quality of gas cylinders and reduce production costs. To find the optimal water spray parameters, a fluid-solid coupling model with three-phase flow was established in consideration of water-vapor conversion. The inner and outer walls of gas cylinder with the dimensions of d914 mm×38 mm×12000 mm were quenched using multi-nozzle water spray system. The internal pressure, average heat transfer coefficient (h_ave) and stress of the gas cylinder under different water spray volumes during quenching process were studied. Finally, the mathematical model was experimentally verified. The results show that both the internal pressure and h_ave increase along with the increase of spray volume. The internal pressure increases slowly first and then rapidly, but h_ave increases rapidly first and then slowly. To satisfy hardenability of gas cylinders, the minimum spray volume should not be less than 40 m³/(h·m). The results of stress indicate that water spray quenching will not cause deformation of bottle body in the range of water volume from 40 to 290 m³/(h·m).

Key words: large-diameter thick-walled gas cylinders; quenching; water spray volume; heat transfer; stress; numerical simulation

Cite this article as: GAO Jing-na, GAO Ying, XU Qin-ran, WANG Ge, LI Qiang. Simulation on flow, heat transfer and stress characteristics of large-diameter thick-walled gas cylinders in quenching process under different water spray volumes [J]. Journal of Central South University, 2019, 26(11): 3188-3199. DOI: https://doi.org/10.1007/s11771-019- 4245-x.

1 Introduction

Car-mounted gas cylinders are mainly thin-walled, which can be hardened by immersion quenching only on external surface [1]. However, for the thick-walled gas cylinders, the inner wall must also be quenched simultaneously to meet the requirements of microstructure and properties. The current quenching technology inside the cylinder has not been mature yet [2]. The simplest quenching method for gas cylinders with smaller diameters and lengths is to inject water directly into the inner cavity. But for the large-diameter long- tube gas cylinders, e.g. d914 mm×38 mm×12000 mm in this research, the local stress would increase sharply and instantaneously by injecting water directly into the inner cavity. It causes bending or cracking of the bottle wall. Instead, the application of multiple nozzles for water spray quenching can effectively solve the problem of uneven cooling and product quality caused by stress concentration [3, 4]. Meanwhile, higher water flow rate or larger number of nozzle arrangement will be required to obtain comparable cooling rate with the immersion quenching result [5]. Due to the complexity of convective heat transfer inside the gas cylinders, the hardenability of long-tube thick-walled cylinders is an urgent problem to be solved.

When water is sprayed onto hot surfaces, there are three main forms of heat transfer, namely, forced convection, nucleation boiling and membrane boiling [6]. To avoid the increase of heat resistance caused by boiling and make the surface always be forced convection, it is necessary to select appropriate process parameters to improve heat transfer efficiency.

Water spray cooling efficiency is related to many factors such as nozzle size, water droplet diameter, flow rates, workpiece thickness and so on [7-9]. Many researchers have done a lot of experiments on this subject. SURESHKUMAR et al [10] pointed out that a smaller nozzle at higher pressure could produce greater cooling efficiency at a specific water flow rate. NAYAK et al [11] investigated the influences of thickness of plate, distance from nozzle to plate, air and water pressure on the heat transfer coefficients of mild steel plates, and developed a new correlation for optimization of surface heat transfer coefficients. LABERGUE et al [12] demonstrated that the sprays lead a more spatial uniformity of the heat flux and a better cooling efficiency compared to the liquid jet. AAMIR et al [13] studied the effects of water spray characteristics on cooling time and cooling rate at different inlet pressures. CHEN et al [14] showed that as the water flow rate increased, the heat flux increased but the spray cooling efficiency decreased. SOMASUNDARAM et al [15] proposed that full cone nozzles at lower flow rates were more suitable for intermittent spray cooling to enhance cooling efficiency. However, in addition to improving cooling efficiency, the effect of process parameters on the stress of workpiece during water spraying cannot be neglected. Because of the difficulty in testing thermal stress and phase transformation stress, little experiments focused on quenching stress [16].

To solve the problems in testing difficulties, experimental cost, safety and limitation of material composition, numerical methods and neural networks are used in many fields of engineering [17-22]. The problems of convective heat transfer and stress during spray cooling are no exception. The convective heat transfer coefficient is an important parameter affecting cooling efficiency. Generally, it is solved by combining the experiment and simulation [23-27]. While the quenching stress is an important factor affecting the quality of the product. The variation of the stress during quenching process can be determined by simulation, and the location where deformation or cracking may occur could be predicted [28-30].

The previous studies in spray cooling have addressed important issues focusing on the surface heat transfer in the open space, but little work has been done towards the water spray characteristics in semi enclosed space [31, 32]. Large-diameter thick- walled gas cylinder has larger internal space and smaller outlets, approximately in a semi-closed state. When the inner wall is continuously sprayed and quenched, due to the instantaneous accumulation of water vapor, higher pressure is formed, and greatly affects the heat transfer efficiency on the inner wall. It is difficult to obtain the detailed information of spray areas inside the gas cylinder by relying on experiments. To ensure that gas cylinders could satisfy the requirements of microstructure and properties, it is necessary to determine reasonable water spray volume. In this work, the distribution characteristics of pressure, heat transfer and stress of gas cylinder under different water volumes were researched by numerical simulation method. The optimum water volume range was obtained, and the mathematical model was verified by experiments. The research results could provide theoretical guidance for industrial testing and production.

2 Mathematical model and quenching parameter

2.1 Mathematical model

2.1.1 Control equations

The spray quenching process is accompanied by the changes in flow field, heat transfer and stress. The continuity equation and NAVI-STOKES (N-S) equation are respectively expressed as follows:

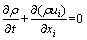                           (1)

 (2)

where ρ is the density of the fluid; t is the time; u_i and u_j are the components of velocity vector; x_i and x_j are the components of each coordinate; 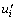and are the components of pulsating velocity tensor; u_i and u_j are the components of velocity tensor; μ is the dynamic viscosity coefficient; f_i is the unit mass force; P is the unit surface force.

The water spraying process is a complex turbulent flow, accompanied by jets and vortices. The realizable k-ε turbulence model could accurately predict the divergence rate of the jet, and achieve good results of rotating flow, boundary laminar flow, flow separation, and complex multiphase flow. The realizable k-ε control equation [33] is:

 (3)

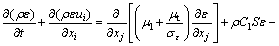
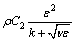                          (4)

where σ_k and σ_ε are the Prandtl numbers of turbulent energy k and dissipation rate ε respectively; G_k is the turbulent kinetic energy generated by an average velocity gradient; μ₁ and μ_t are molecular viscosity coefficient and turbulent viscosity coefficient respectively; S is the user-defined source item; C₁ and C₂ are the empirical constants; ν is the coefficient of kinematic viscosity.

The volume fraction equation of phase K is obtained from the continuity equation of K phase, which is as follows:

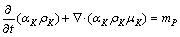              (5)

where α_K is the volume fraction of phase K; ρ_K is phase density of K; μ_K is the dynamic viscosity coefficient of phase K; m_P is the energy source term.

Energy conservation equation is:

 (6)

where T is the temperature; x, y and z are the cartesian coordinate components; u_x, u_y and u_z are the components of velocity vectyor; c_P is the specific heat capacity; λ is the thermal conductivity coefficient; S_T is the internal heat source.

Stress-strain constitutive equation is:

                          (7)

where D_ep is the elastic-plastic matrix; d{σ} is the stress in the elastic stage and plastic stage; d{ε} is the total strain tensor.

2.1.2 Definite conditions

1) Initial conditions

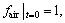
At the initial moment, the gas cylinder is filled with air, and the initial temperature is the austenitizing temperature, as depicted in Eq. (8):

                 (8)

where f_air is the volume fraction of air.

2) Boundary conditions

The boundary conditions of the inlet, outlet and outer wall are set as velocity-inlet, free outflow and convective heat transfer coefficients respectively.

2.2 Material parameters

The gas cylinder is made of hot- expanding seamless steel pipe. The material is ASTM 4130 alloy structural steel (equivalent to 30CrMo of China National Standard), and the initial microstructure is composed of ferrite and pearlite. The chemical composition and mechanical properties are shown in Tables 1 and 2 [34], respectively.

The thickness of the hardened layer of ASTM 4130 steel tested by end quenching method is 22.5 mm and the hardness of semi-martensite is HRC 45. The continuous cooling transition curve (CCT) is determined by DIL805L Thermal Expansion Phase Change Instrument, as shown in Figure 1, where HV is Vickers hardness unit. It can be seen that A_c1 (austenite start temperature when heating) and A_c3 (austenite finish temperature when heating) are 819 °C and 879 °C respectively. M_s (martensite start temperature) and M_f (martensite finish temperature) are 349 °C and 180 °C respectively. The critical cooling rate corresponding to the hardness of semi-martensite is about 4.2 °C/s, which is the minimum cooling rate to satisfy hardenability of gas cylinders.

Table 1 Chemical composition of ASTM 4130 (mass fraction, %)

Table 2 Mechanics performance parameters of ASTM 4130

Figure 1 CCT curve of ASTM 4130 steel

2.3 Quenching process and meshing

The overall size of the gas cylinder is d914 mm×38 mm×12000 mm, and the inner diameter of the outlet at both ends is 152 mm. The inner wall and the outer wall of the cylinder are respectively spray quenched. The schematic diagram of the quenching process is shown in Figure 2. Two water pipes are inserted from two ends of the bottle mouth into the cavity of the gas cylinder respectively.The nozzles are uniformly arranged in the circumferential and axial directions of the water pipe wall, and water is sprayed through the nozzle onto the wall.

Figure 2 Quenching schematic diagram of gas cylinder

In consideration of the geometric symmetry of gas cylinder and the periodicity of water spray distribution, the fluid-solid coupling model with a length of 1 m and 1/8 circle was selected as the calculation area, including a row of multiple nozzles system with a diameter of 5 mm and an axial spacing of 70 mm. The water spray volumes range from 15 to 580 m³/(h·m), referring to the water quantity per hour per meter of gas cylinder.

To reduce the computational period, the following assumptions have been adopted in the model:

1) The effect of the number of nozzles on the strength and deformation of the water pipe is ignored.

2) Assume that the gas cylinder doesn’t rotate; eight nozzles are selected in the circumferential direction of the water pipe in order to satisfy the circumferential quenching uniformity, which are not the actual number.

3) Assume that the outer surface of the gas cylinder is uniformly cooled.

4) Assume that the nozzle velocity along the axial direction is the same, ignoring the influences of the inlet velocity of water pipe on the velocity of each nozzle.

The nozzle entrance was taken as the calculated inlet. The model was divided into hexahedron grids with 482767 elements and 449365 nodes, as shown in Figure 3, where P₁, P₂, and P₃ are the points on the inner wall, the central layer, and the outer wall of the cylinder, respectively.

3 Results and analysis

3.1 Analysis of pressure

When the gas cylinder is quenched by spraying water, the internal water vapor will remain stable after being aggregated. The internal relative pressure distribution (relative to the standard atmospheric pressure) after stabilization is shown in Figure 4. It can be seen that the pressure rises with the increase of the water volume. The maximum pressure difference is located in the transition from the arc section to the port. There are negative pressure zones around the nozzle near the bottle mouth, and the greater the water volume is, the more obvious the negative pressure is. Zone A in Figure 4(c) is enlarged as shown in Figure 5. As can be seen from Figure 5(a), the negative pressure is close to the left of the nozzle, while the pressure on the right is positive, significantly higher than the surroundings, but the velocity is lower than that in the surroundings (in Figure 5(b)). The reason is that the pressure at a lower flow velocity is higher according to Bernoulli’s equation. However, the velocity is lower in the negative-pressure zone. Because the water vapor flows out through the bottle mouth at a certain acceleration under high pressure, and a small dead zone is formed at the left corner of the nozzle where the outflow is smaller than the inflow, resulting in smaller density and negative pressure. Moreover, the velocity of fluid in the gas cylinder increases with the increase of internal pressure, which leads to the increase of turbulence intensity near the bottle mouth, and then produces a greater negative pressure.

Figure 3 Grid model

Figure 6 establishes the relationship between the water volume and the maximum pressure in the cylinder during quenching. The pressure tends to increase gently first, and then rises sharply with the increase of water volume. Especially when the water volume is more than 290 m³/(h·m), the growth rate of pressure is accelerated. It indicates that the instantaneous steam generated during quenching could not be discharged in time. A greater water spray volume results in a faster instantaneous accumulated mass flow rate and a rapid rise of the internal pressure. According to the design requirements, the nominal pressure of the gas cylinder is 25 MPa. As can be seen in Figure 6, when the water spray volume is less than 600 m³/(h·m), the internal pressure is far less than 25 MPa, which would not cause quality problems to the gas cylinder.

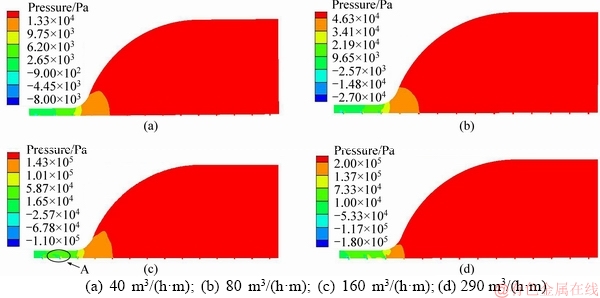
Figure 4 Pressure nephograms under different water volumes:

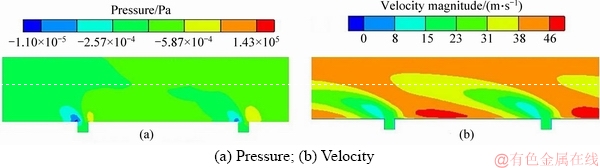
Figure 5 Enlarged view of flow field in zone A:

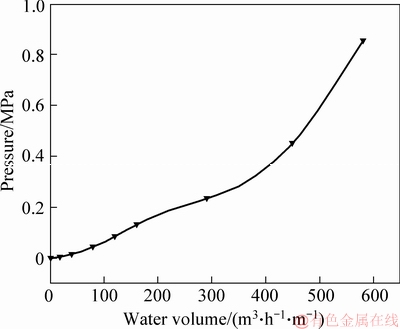
Figure 6 Relationship of water volume and maximum pressure

3.2 Analysis of heat transfer

3.2.1 Analysis of convection heat transfer on inner wall of the cylinder

The variation law of average heat transfer coefficient (h_ave) on the inner wall with different parameters is shown in Figure 7. The relationship between h_ave and water spray volumes was established in Figure 7(a). It can be seen that the larger the water volume is, the greater the h_ave is, but the trend of curves remains basically consistent. With the increase of temperature, the h_ave increases sharply first and then slowly. After 800 °C, it decreases rapidly. Figure 7(b) establishes the relationship between h_ave and water spray volume at 400 and 800 °C, respectively. The h_ave increases rapidly with the increase of the water volume, and the growth rate of h_ave at 800 °C is higher than that at 400 °C until it is more than 290 m³/(h·m). Then the growth rate becomes smooth, and the two curves are approximately parallel, indicating that the water spray volume has less influence on the heat transfer efficiency after it is more than m³/(h·m).

The position where water is directly sprayed is called injection point, and the middle point of the line connecting two adjacent injection points is called midpoint. The curves of the temperature differences between adjacent injection point and midpoint with time are shown in Figure 8. It can been seen that the temperature difference increases sharply first and then decreases rapidly. With the increase of the spray volume, the peak temperature difference increases, but the time for the temperature to be uniform becomes short. The peak temperature difference ranges from 95.1 to 116.5 °C. The temperature difference is below 20 °C after 120 s at the water volume of 40 m³/(h·m). When the water volume is more than 80 m³/(h·m), it is lower than 20 °C after 70 s, and the temperature on the inner wall tends to be uniform.

Figure 7 Curves of average heat transfer coefficient with temperature (a) and water volume (b)

Figure 8 Effect of water spray volumes on temperature difference

3.2.2 Determination of reasonable water spray volume

According to technological requirements, the the bottle mouth and arc transition only need to meet the requirements of thickness, that is, not less than 75% of thickness of the bottle body. Actually, they are thicker than the bottle body, and have satisfied the design requirements. Therefore, the research of hardenability focuses on the bottle body. In order to ensure that the bottle body can be hardened, more than 50% martensite must be obtained, so it is necessary to consider the amount of water spray required for the bottle body.

It can be seen from the foregoing result (Section 2.2) that the minimum cooling rate of gas cylinder should be higher than 4.2 °C/s. Therefore, to ensure that the gas cylinder is hardened, the time to cool to the martensite start temperature (M_s=349 °C) is less than 130 s.

Figure 9 shows the temperature distribution of the minimum cooling point of the bottle body. It can be seen from the fluid-solid coupling nephogram (in Figure 9(a)) that the surface temperature in the water-spraying zone is the lowest, while the point with the slowest cooling rate is located on the side of the central layer of the bottle.

The minimum cooling rate curves under different spray volumes are shown in Figure 9(b). It can be seen that the temperature gradient increases with the increase of cooling water volume. At 130 s, the temperature is 372 °C at the water volume of 20 m³/(h·m), which does not drop to martensite start temperature. It satisfies the condition of hardenability when the temperature is less than 300 °C at the water volume of 40 m³/(h·m). In addition, when the water volume is less than 120 m³/(h·m), the temperature difference is more than 40 °C for water volume difference of 20 m³/(h·m). But when the water volume is more than 160 m³/(h·m), the temperature difference is less than 10 °C for water volume difference of 20 m³/(h·m), indicating that the water quantity has little effect on the cooling efficiency.

In consideration of the cooling efficiency and hardenability, the optimum water volume required for the gas cylinders with the size of d914 mm×38 mm is in the range of 120-160 m³/(h·m).

Figure 9 Simulation nephogram and cooling curves:

3.3 Analysis of stress

The average temperature distributions calculated on the inner wall and outer wall were taken as the boundary conditions. The axial stress and effective stress at different monitoring points of gas cylinders during quenching were calculated as shown in Figures 10 and 11, respectively.

As can be seen from Figure 10, the direction of the axial stress at P₁ and P₃ is the opposite to that at P₂, because the cooling speeds at different points are different, causing the time of phase transition to be different. All the points are affected by thermal stress and phase transformation stress in the quenching process, making the stress state oscillate.

It is apparent from Figures 10 and 11, the peaks of the axial stress and effective stress move to the left as the water volume increases. The larger the water volume is, the larger the peak at P₁ and P₂ is. Compared with the curves at the water quantity of 290 m³/(h·m) and 40 m³/(h·m), the maximum peak difference of axial tensile stress peak is about 91 MPa and the maximum peak difference of effective stress is about 187 MPa. However, the peak stresses at P₂ are less influenced by water volumes because the heat in the center of the bottle is released in the form of heat conduction, and the cooling rate varies little due to the smaller thermal conductivity of the material.

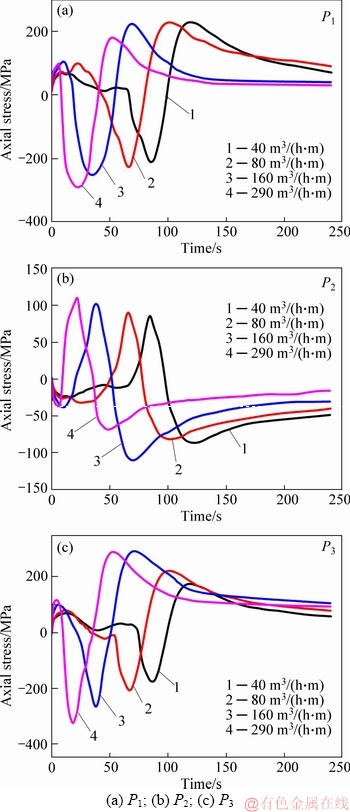
Figure 10 Effect of water spray volume on axial stress of gas cylinder:

In order to determine whether the quenching stress causes deformation of the bottle body, the peak values of effective stress at each monitoring point under different water volumes are compared with the yield strength of the material (Table 2), as shown in Figure 12. It can be seen that all the effective stress peaks are lower than the yield strength at the same temperature. Therefore, there is no risk of deformation for the gas cylinder when the water spray volume is in the range of 40 to 290 m³/(h·m).

Figure 11 Effect of water spray volume on effective stress of gas cylinder:

In general, when other parameters remain unchanged, the cooling strength increases with the increase of spraying volume, and the martensite content increases correspondingly, which is beneficial to increase the tensile strength of the material. Therefore, in the safe range of quenching stress, a larger water volume should be selected. Due to the water volume has little effect on the cooling rate after more than 160 m³/(h·m), in consideration of the economic costs and other influencing factors, the optimal range of water is 120-160 m³/(h·m).

Figure 12 Comparison of yield strength and effective stress

4 Experimental verification

The workpiece used in the verification experiment was taken from a hot-expanding seamless steel pipe, which is used to make gas cylinders. The overall size is d914 mm×38 mm× 800 mm. Two circular flat plates with inner diameter of 150 mm and thickness of 20 mm were respectively welded to the two outlets of the steel pipe, as shown in Figure 13. The material of the workpiece is ASTM 4130. The chemical composition and mechanical properties are shown in Tables 1 and 2, respectively.

The workpiece was heated to the austenitizing temperature (900 °C) in the industrial roller hearth furnace and hold for 45 min, and then the inside and outside of the workpiece were simultaneously subjected to water immersion quenching. After heat treatment, two samples were cut longitudinally in the middle of the quenched workpiece (including point P₁ on inner wall and point P₂ in the center of thickness, respectively). After grinding and polishing, the samples were etched with alcohol solution containing 4% of nitric acid and the micro- structure was observed by Axio Vert.A1 Zeiss optical microscope (Figure 14). The hardness was tested by HV-1000 microhardness tester, and the average value was obtained by five-point measurement. Meanwhile, the flow-solid coupling numerical simulation of the workpiece during quenching was carried out, and the cooling curves of P₁ and P₂ with quenching time were obtained, as shown in Figure 15.

Figure 13 Experimental workpiece

Figure 14 Microstructure of ASTM 4130 after quenching:

It can be observed from Figure 14 that the microstructure of P₁ is mainly composed of martensite, while that of P₂ is mainly composed of martensite and a small amount of bainite. The hardness of P₁ and P₂ are determined as HV618.6 and HV562.2, respectively. In contrast to the hardness of CCT curve (in Figure 1), it can be seen that the cooling rate of P₁ is in the range of 40 to 60 °C/s and that of P₂ is in the range of 10 to 15 °C/s. And the microstructure in the velocity range on the CCT curve is consistent with that of metallographic observation. Furthermore, as shown in Figure 15, the average cooling rates of P₁ and P₂ before martensitic transformation are calculated to be 56.2 and 14.3 °C/s respectively, which are consistent with the cooling speed range assessed by hardness. Since the position of the metallographic observation and the hardness measurement has a certain deviation from that of P₁ and P₂, the result has a certain error. However, the results of the experiment and simulation are basically consistent, proving that the mathematical model is correct.

Figure 15 Simulation results

5 Conclusions

In this work, the fluid-solid coupling mathematical model was established, and the internal pressure, heat transfer and stress of gas cylinder during quenching process were simulated. The mathematical model has been verified by experiments. The main results are as follows:

1) As the water spray volume increases, the internal pressure increases slowly first, then increases rapidly after more than 290 m³/(h·m), while the average heat transfer coefficients show the opposite increasing trend.

2) The peaks of the axial stress and effective stress increases with the increase of water spray volume, but there is no risk of deformation for the gas cylinder in the range of 40-290 m³/(h·m).

3) Based on considerations of the cooling efficiency and economic cost, the reasonable water spray volume is in the range of 120 to 160 m³/(h·m).

Nomenclature

ρ

Density of the fluid

μ

Dynamic viscosity coefficient

μ_t

Turbulent viscosity coefficient

f_i

Unit mass force

P

Unit surface force

x_i , x_j

Components of each coordinate

σ_k

Prandtl number of turbulent energy

σ_ε

Prandtl number dissipation rate

G_k

Turbulent kinetic energy generated by an average velocity gradient

α_K

Volume fraction of phase K

ρ_K

Density of phase K

m_P

Energy source term

t

Flow time of the fluid

T

Temperature of the material

c_P

Specific heat capacity

λ

Thermal conductivity coefficient

S_T

Internal heat source of the material

D_ep

Elastic-plastic matrix

d{σ}

Stress in elastic stage and plastic stage

d{ε}

Total strain tensor

f_air

Volume fraction of air

S

User-defined source item

C₁, C₂

Empirical constants

ν

Coefficient of kinematic viscosity

μ_K

Dynamic viscosity coefficient of phase K

μ₁

Molecular viscosity coefficient

u_i, u_j

Components of velocity tensor

u_i', u_j'

Components of pulsating velocity tensor

References

[1] ZHANG Hong-xing, ZHANG Hua-sheng. Research overview of compressed natural gas cylinder for vehicle [J]. Petroleum and Chemical Equipment, 2011, 14(10): 5-8. DOI: 10.3969/j.issn.1674-8980.2011.10.001. (in Chinese)

[2] ZHAO Jing-mao. Brief description of heat treatment of large volume steel seamless cylinders [C]// Proceedings of the 20th Anniversary Conference of China Industrial Gas Industry Association. Shanghai: China Industrial Gas Industry Association, 2008: 177-182. http://www. wanfangdata.com.cn/details/detail.do?_type=conference&id=6528571. (in Chinese)

[3] WEN Zhe-xi, HE Ya-ling, MA Zhao. Effects of nozzle arrangement on uniformity of multiple impinging jets heat transfer in a fast cooling simulation device [J]. Computers & Fluids, 2018, 164: 83-93. DOI: https://doi. org/10.1016/j. compfluid.2017.05.012.

[4] HOU Yan, TAO Yu-jia, HUAI Xiu-lan, ZOU Yu, SUN Dong-liang. Numerical simulation of multi-nozzle spray cooling heat transfer [J]. International Journal of Thermal Sciences, 2018, 125: 81-88. DOI: 10.1016/j.ijthermalsci. 2017.11.011.

[5] SOEJIMA H, MITSUTAKE Y, ILLIAS S, TSUBAKI K, MONDE M. Application of the spray quenching to T6 heat treatment of thick A6061 hollow cylinders [J]. Procedia Engineering, 2015, 105: 776-786. DOI: https://doi.org/10. 1016 /j.proeng.2015.05.070.

[6] XU Rong, LI Luo-xing, ZHANG Li-qiang, ZHU Bi-wu, LIU Xiao, BU Xiao-bing. Influence of pressure and surface roughness on the heat transfer efficiency during water spray quenching of 6082 aluminum alloy [J]. Journal of Materials Processing Technology, 2014, 214(12): 2877-2883. DOI: https://doi.org/10.1016/j. jmatprotec.2014.06.027.

[7] YAO S C, COX T L. A General heat transfer correlation for impacting water sprays on high-temperature surfaces [J]. Experimental Heat Transfer, 2002, 15(4): 207-219. DOI: https://doi.org/10.1080/08916150290082649.

[8] PATIL V S, VEDULA R P. Local heat transfer for jet impingement onto a concave surface including injection nozzle length to diameter and curvature ratio effects [J]. Experimental Thermal and Fluid Science, 2018, 92: 375- 389. DOI: https://doi.org/10.1016/j.expthermflusci.2017.08. 002.

[9] NAYAK S K, MISHRA P C, PARASHAR S K S. Influence of spray characteristics on heat flux in dual phase spray impingement cooling of hot surface [J]. Alexandria Engineering Journal, 2016, 55(3): 1995-2004. DOI: https://doi.org/10.1016/j.aej.2016.07.015.

[10] SURESHKUMAR R, KALE S R, DHAR P L. Heat and mass transfer processes between a water spray and ambient air–I. Experimental data [J]. Applied Thermal Engineering, 2008, 28(5, 6): 349-360. DOI: https://doi.org/10.1016/j. applthermaleng. 2007.09.010.

[11] NAYAK S K, MISHRA P C. Desirability function based optimization of experimental data for air-water spray impingement cooling [J]. Management Science Letters, 2016: 203-212. DOI: 10. 5267/j.msl.2016.1.007.

[12] LABERGUE A, GRADECK M, LEMOINE F. Comparative study of the cooling of a hot temperature surface using sprays and liquid jets [J]. International Journal of Heat and Mass Transfer, 2015, 81: 889-900. DOI: https://doi.org/ 10.1016/j.ijheatmasstransfer.2014.11.018.

[13] AAMIR M, QIANG L, XUN Z, HONG W, ZUBAIR M. Ultra fast spray cooling and critical droplet diameter estimation from cooling rate [J]. Journal of Power and Energy Engineering, 2014, 2(4): 259-270. DOI: 10.4236/jpee. 2014.24037.

[14] CHEN Hua, CHENG Wen-long, PENG Yu-hang, ZHANG Wei-wei, JIANG Li-jia. Experimental study on optimal spray parameters of piezoelectric atomizer based spray cooling [J]. International Journal of Heat and Mass Transfer, 2016, 103: 57-65. DOI: https://doi.org/10.1016/j.ijheatmasstransfer. 2016.07.037.

[15] SOMASUNDARAM S, TAY A A O. Comparative study of intermittent spray cooling in single and two phase regimes [J]. International Journal of Thermal Sciences, 2013, 74: 174-182. DOI: https://doi.org/10.1016/j.ijthermalsci.2013. 06.008.

[16] ZHANG Yu-xun, YI You-ping, HUANG Shi-quan, DONG Huang-fei. Influence of quenching cooling rate on residual stress and tensile properties of 2A14 aluminum alloy forgings [J]. Materials Science and Engineering A, 2016, 674(12): 658-665. DOI: https://doi.org/10.1016/j. msea.2016. 08.017.

[17] KALTENBACH C, LAURIEN E. CFD simulation of spray cooling in the model containment THAI [J]. Nuclear Engineering and Design, 2018, 328: 359-371. DOI: https:// doi.org/10.1016/j.nucengdes.2017.12.030.

[18] KHALAJ G, NAZARI A, POURALIAKBAR H. Prediction of martensite fraction of microalloyed steel by artificial neural networks [J]. Neural Network World, 2013, 23(2): 117-130. DOI: 10.14311/NNW.2013.23.009.

[19] POURALIAKBAR H, KHALAJ G, JANDAGHI M R, KHALAJ M J. Study on the correlation of toughness with chemical composition and tensile test results in microalloyed API pipeline steels [J]. Journal of Mining and Metallurgy, Section B: Metallurgy, 2015, 51(2): 173-178. DOI:10. 2298/JMMB140525025P.

[20] FAIZABADI M J, KHALAJ G, POURALIAKBAR H, JANDAGHI M R. Predictions of toughness and hardness by using chemical composition and tensile properties in microalloyed line pipe steels [J]. Neural Computing and Applications, 2014, 25(7, 8): 1993-1999. DOI: https://doi. org/10.1007/s00521-014-1687-9.

[21] POURALIAKBAR H, KHALAJ M J, NAZERFAKHARI M, KHALAJ G. Artificial neural networks for hardness prediction of HAZ with chemical composition and tensile test of X70 pipeline steels [J]. Journal of Iron and Steel Research International, 2015, 22(5): 446-450. DOI: https:// doi.org/ 10.1016/S1006-706X(15)30025-X.

[22] KHALAJ G, YOOZBASHIZADEH H, KHODABANDEH A, NAZARI A. Artificial neural network to predict the effect of heat treatments on Vickers microhardness of low-carbon Nb microalloyed steels [J]. Neural Computing and Applications, 2013, 22(5): 879-888. DOI: https://doi.org/10.1007/s00521- 011-0779-z.

[23] CHENG Wen-long, CHEN Hua, HU Lei, ZHANG Wei-wei. Effect of droplet flash evaporation on vacuum flash evaporation cooling: Modeling [J]. International Journal of Heat and Mass Transfer, 2015, 84: 149-157. DOI: https:// doi.org/10.1016/j.ijheatmasstransfer. 2014.12.078.

[24] FENG Ming-jie, WANG En-gang, WANG Hai, LI Yan-dong, LIU Bing. Numerical simulation on boiling heat transfer of evaporation cooling in a billet reheating furnace [J]. Journal of Central South University, 2016, 23(6): 1515-1524. DOI: 10.1007/s11771-016-3203-0.

[25] PENG Liang-gui, LIU Xiang-hua, ZHAO Xian-ming, WU Di. Mathematic modeling on flexible cooling system in hot strip mill [J]. Journal of Central South University, 2014, 21(1): 43-49. DOI: 10.1007/s11771-014-1913-8.

[26] ZHAO Hou-jian, LI Xiao-wei, WU Xin-xin. Numerical investigation of supercritical water turbulent flow and heat transfer characteristics in vertical helical tubes [J]. The Journal of Supercritical Fluids, 2017, 127: 48-61. DOI: https://doi.org/10.1016/j.supflu.2017.03.016.

[27] XIAO Lie-hui, GE Zhi-hua, YANG Li-jun, DU Xiao-ze. Numerical study on performance improvement of air-cooled condenser by water spray cooling [J]. International Journal of Heat and Mass Transfer, 2018, 125: 1028-1042. DOI: https://doi.org/10.1016/j.ijheatmasstransfer.2018.05.006.

[28] LIU Yu, QIN Sheng-wei, ZUO Xun-wei, CHEN Nai-lu, RONG Yong-hua. Finite element simulation and experimental verification of quenching stress in fully through-hardened cylinders [J]. Acta Metallurgica Sinica, 2017, 53(6): 733-742. DOI: 10.11900/0412.1961.2016. 00509.

[29] NING Qin-heng, DONG Jun-yuan, LI Yong-gang, ZUO Xiu-rong, WU Xiang, ZHAO Wei-wei. Finite element simulation of water jet quenching for large NM450 steel plate [J]. Heat Treatment of Metals, 2018, 48(10): 221-226. DOI: 10.13251/j.issn.0254-6051.2018.10.044. (in Chinese)

[30] KAMENICKY R, DOMALAPALLY P K, ARNOULT X. Thermo-mechanical stress analysis of the water cooled DEMO First Wall mock-up components [J]. Fusion Engineering and Design, 2018, 136: 1618-1623. DOI: https://doi.org/10.1016/j.fusengdes.2018.05.072.

[31] WANG Ge, DU Xiong-fei, GAO Jing-na, CUI Ming-ti, LI Qiang. Numerical simulation and experiment on final heat treatment of the large-diameter thick-wall gas cylinder of 30CrMo steel [J]. Transactions of Materials and Heat Treatment, 2016, 37(3): 210-215. DOI: 10.13289/j.issn. 1009-6264.2016.03.036. (in Chinese)

[32] WANG Ge，ZHU Guo-shan，GAO Jing-na, WANG Li-li, DU Xiong-fei, LI Qiang． Numerical simulation of flow and temperature fields in spray quenching process of large-diameter thick-walled 4130X steel gas cylinder [J]. Transactions of Materials and Heat Treatment, 2015, 36(7): 250-256. DOI: 10.13289/j.issn.1009-6264.2015. 07.042. (in Chinese)

[33] XU Qin-ran. Numerical simulation on quenching cooling uniformity of gas storage for gas supply stations [D]. Qinhuangdao: Yanshan University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10216-1017726618.htm. (in Chinese)

[34] DU Xiong-fei. Numerical simulation and experiment on heat treatment process of large diameter and thick wall gas cylinder [D]. Qinhuangdao: Yanshan University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10216-1015901591.htm. (in Chinese)

(Edited by ZHENG Yu-tong)

中文导读

大直径厚壁气瓶淬火时不同喷水量下流动换热及应力特性仿真模拟

摘要：冷却强度是影响气瓶淬火组织性能的重要因素，合理的喷水量可以有效提高气瓶质量，降低生产成本。为了寻找最佳的喷水参数，考虑了水-汽的转化，建立了三相流共存的流-固耦合模型。采用多喷嘴喷水系统对气瓶尺寸为d 914 mm×38 mm×12000 mm的内壁和外壁进行了淬火冷却，研究了气瓶淬火时不同喷水量下内部压强、平均换热系数和瓶体应力的分布规律，并最终对数学模型进行了实验验证。结果表明，随着喷淋量的增大，内部压强和平均换热系数都随之增大。内部压强先缓慢增长，之后迅速增加，而平均换热系数则相反，先急速增加，而后增长速率较平缓。为保证气瓶能被淬透，最小的喷水体积应不小于40 m³/(h·m)。应力结果表明，喷水量在40~290 m³/(h·m)范围内淬火不会使瓶体发生变形。

关键词：大直径厚壁气瓶；淬火；喷水量；传热；应力；数值模拟

Foundation item: Project(51674096) supported by the National Natural Science Foundation of China; Project(E2016203119) supported by Hebei Natural Science Foundation of China; Project(18211045) supported by the Key Research and Development Foundation in Hebei Province of China

Received date: 2018-07-08; Accepted date: 2019-03-02

Corresponding author: LI Qiang, PhD, Professor; Tel: +86-311-81668706; E-mail: liqiang@ysu.edu.cn; ORCID: 0000-0002-6925-0804