Rockburst proneness criteria for rock materials: Review and new insights
来源期刊:中南大学学报(英文版)2020年第10期
论文作者:宫凤强 王云亮 罗松
文章页码:2793 - 2821
关键词:deep rock; rockburst; rockburst proneness; rockburst proneness criterion; rock mechanics
Key words:deep rock; rockburst; rockburst proneness; rockburst proneness criterion; rock mechanics
Abstract: To review the rockburst proneness (or tendency) criteria of rock materials and compare the judgment accuracy of them, twenty criteria were summarized, and their judgment accuracy was evaluated and compared based on the laboratory tests on fourteen types of rocks. This study begins firstly by introducing the twenty rockburst proneness criteria, and their origins, definitions, calculation methods and grading standards were summarized in detail. Subsequently, to evaluate and compare the judgment accuracy of the twenty criteria, a series of laboratory tests were carried out on fourteen types of rocks, and the rockburst proneness judgment results of the twenty criteria for the fourteen types of rocks were obtained accordingly. Moreover, to provide a unified basis for the judgment accuracy evaluation of above criteria, a classification standard (obtained according to the actual failure results and phenomena of rock specimen) of rockburst proneness in laboratory tests was introduced. The judgment results of the twenty criteria were compared with the judgment results of this classification standard. The results show that the judgment results of the criterion based on residual elastic energy (REE) index are completely consistent with the actual rockburst proneness, and the other criteria have some inconsistent situations more or less. Moreover, the REE index is based on the linear energy storage law and defined in form of a difference value and considered the whole failure process, and these superior characteristics ensure its accuracy. It is believed that the criterion based on REE index is comparatively more accurate and scientific than other criteria, and it can be recommended to be applied to judge the rockburst proneness of rock materials.
Cite this article as: GONG Feng-qiang, WANG Yun-liang, LUO Song. Rockburst proneness criteria for rock materials:

J. Cent. South Univ. (2020) 27: 2793-2821
DOI: https://doi.org/10.1007/s11771-020-4511-y

GONG Feng-qiang(宫凤强)1, 2, WANG Yun-liang(王云亮)1, LUO Song(罗松)1
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. School of Civil Engineering, Southeast University, Nanjing 211189, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: To review the rockburst proneness (or tendency) criteria of rock materials and compare the judgment accuracy of them, twenty criteria were summarized, and their judgment accuracy was evaluated and compared based on the laboratory tests on fourteen types of rocks. This study begins firstly by introducing the twenty rockburst proneness criteria, and their origins, definitions, calculation methods and grading standards were summarized in detail. Subsequently, to evaluate and compare the judgment accuracy of the twenty criteria, a series of laboratory tests were carried out on fourteen types of rocks, and the rockburst proneness judgment results of the twenty criteria for the fourteen types of rocks were obtained accordingly. Moreover, to provide a unified basis for the judgment accuracy evaluation of above criteria, a classification standard (obtained according to the actual failure results and phenomena of rock specimen) of rockburst proneness in laboratory tests was introduced. The judgment results of the twenty criteria were compared with the judgment results of this classification standard. The results show that the judgment results of the criterion based on residual elastic energy (REE) index are completely consistent with the actual rockburst proneness, and the other criteria have some inconsistent situations more or less. Moreover, the REE index is based on the linear energy storage law and defined in form of a difference value and considered the whole failure process, and these superior characteristics ensure its accuracy. It is believed that the criterion based on REE index is comparatively more accurate and scientific than other criteria, and it can be recommended to be applied to judge the rockburst proneness of rock materials.
Key words: deep rock; rockburst; rockburst proneness; rockburst proneness criterion; rock mechanics
Cite this article as: GONG Feng-qiang, WANG Yun-liang, LUO Song. Rockburst proneness criteria for rock materials:
Review and comprehensive comparison [J]. Journal of Central South University, 2020, 27(10): 2793-2821. DOI: https://doi.org/10.1007/s11771-020-4511-y.
1 Introduction
With the continuous development and utilization of underground space and mineral resources, more and more underground rock projects are being constructed at increasing depths [1-4]. During the excavation of deep buried caverns or tunnels, many unconventional surrounding rock failure phenomena are often encountered, such as spalling (or slabbing) [5-7], rockburst [8-10]. Different from spalling failure, rockburst is a dynamic geological disaster of deep rock mass, which is usually caused by the sudden and violent release of elastic strain energy stored in rock [9-12]. Due to the massive damage caused by rockburst, more and more attentions have been drawn to the research on rockburst in the past decades from the theoretical analysis [13-17], experimental study [18-22], numerical simulation [23-25] and project case analysis [8, 9, 26], especially the prediction of rockburst [27-34]. The study of rockburst proneness (or tendency) of rock material is one of the basic works of rockburst prediction. After decades of research, based on the laboratory tests, many researchers have put forward a variety of rockburst proneness criteria of rock materials in terms of energy or brittleness. For example, the strain energy storage index (WET) [35, 36], the energy impact index (ACF) [37] and the potential energy of elastic strain (PES) [38, 39] were three typical rockburst proneness criteria considering energy. With the development of related research, many researchers have revised the above criteria. ZHANG et al [40] gave a new rockburst proneness grading standard for WET combining with the experiences in engineering practices. Based on the accurate peak elastic strain energy, GONG et al [41, 42] put forward the peak-strength strain energy storage index  and the peak-strength energy impact index A′CF. Moreover, combining the characteristics of WET and ACF, the effective energy impact index (W) [43] was proposed as a new criterion. Besides, some other criteria are also proposed from the perspective of energy. JIN et al [44] thought that the pre-peak elastic energy can reflect the rockburst proneness and proposed the energy formula of rockburst (E). DENG et al [45] studied the rockburst proneness considering the energy evaluation characteristic of post-peak, and put forward the rockburst energy index (Bq). Moreover, some scholars believed that the remaining elastic energy after the rock failure can directly reflect rockburst proneness degree, and proposed the surplus energy index (WR) [46], and the residual elastic energy index (AEF) [41]. In addition, the rock brittleness is also considered to be closely related to the rockburst proneness, and several criteria were put forward as follows, the brittleness index modified (BIM) [47, 48], the deformation brittleness index (Ku) [49], the brittleness index of rockburst proneness (B) [50], and the strength brittleness index (B1 [38, 51], B2 [49], B3 [40]). Except for the energy and brittleness, the deformation modulus was used to evaluate the rockburst proneness by SINGH et al [52, 53] who proposed the decrease modulus index (DMI). Moreover, based on the load–unload response ratio theory, GONG et al [54] proposed the lag time ratio index (TR) for rockburst proneness evaluation.
and the peak-strength energy impact index A′CF. Moreover, combining the characteristics of WET and ACF, the effective energy impact index (W) [43] was proposed as a new criterion. Besides, some other criteria are also proposed from the perspective of energy. JIN et al [44] thought that the pre-peak elastic energy can reflect the rockburst proneness and proposed the energy formula of rockburst (E). DENG et al [45] studied the rockburst proneness considering the energy evaluation characteristic of post-peak, and put forward the rockburst energy index (Bq). Moreover, some scholars believed that the remaining elastic energy after the rock failure can directly reflect rockburst proneness degree, and proposed the surplus energy index (WR) [46], and the residual elastic energy index (AEF) [41]. In addition, the rock brittleness is also considered to be closely related to the rockburst proneness, and several criteria were put forward as follows, the brittleness index modified (BIM) [47, 48], the deformation brittleness index (Ku) [49], the brittleness index of rockburst proneness (B) [50], and the strength brittleness index (B1 [38, 51], B2 [49], B3 [40]). Except for the energy and brittleness, the deformation modulus was used to evaluate the rockburst proneness by SINGH et al [52, 53] who proposed the decrease modulus index (DMI). Moreover, based on the load–unload response ratio theory, GONG et al [54] proposed the lag time ratio index (TR) for rockburst proneness evaluation.
The above rockburst proneness criteria have been partially summarized in some literatures [32, 55, 56] and their characteristics are analyzed. However, the existing summaries of criteria in these researches are not complete enough, and the characteristics of them are not described in detail. Moreover, few studies focus on evaluating and comparing the judgment accuracy of those criteria according to actual rock experimental phenomenon. The judgment results of some criteria are sometimes inaccurate. For example, TAN [37] pointed out that the overestimates of rockburst proneness degree usually occur compared with the practical situations, when the energy impact index ACF is used for rockburst proneness evaluation. The practical rockburst proneness of a rock can be reflected by the rock failure phenomenon in laboratory tests. In general, the more violent the rock is destroyed, the higher the rockburst proneness is. Thus, it is necessary to comprehensively review the existing rockburst proneness criteria, analyze their characteristics in detail, and evaluate and compare the judgment accuracy of them based on the practical rock failure phenomenon in laboratory tests. In doing so, a reference can be offered for the rockburst proneness evaluation of rock materials in the future.
In this study, twenty criteria for rockburst proneness evaluation were comprehensively summarized, including their origins, definitions, calculation methods and grading standards. Besides, a series of laboratory tests on fourteen types of rocks were conducted to evaluate the judgment accuracy of the twenty criteria according to practical rock failure phenomenon. Moreover, the judgment accuracy of the twenty criteria was compared based on the evaluation results, and then their characteristics were discussed.
2 Overviews of twenty rockburst proneness criteria
Numerous criteria were proposed by scholars from diverse perspectives to evaluate the rockburst proneness of rock materials. In this paper, we first summarize the twenty criteria as follows, and the grading standards of rockburst proneness of these criteria are also summarized in Table 1.
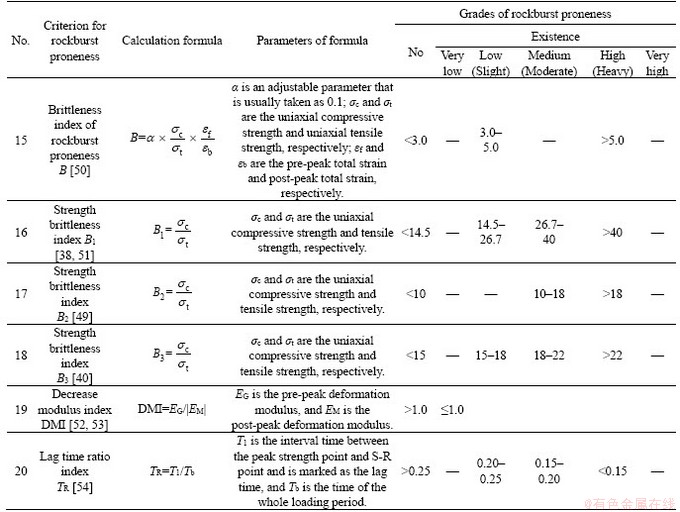
Table 1 Summary of twenty criteria calculation principles and their grading standards of rockburst proneness
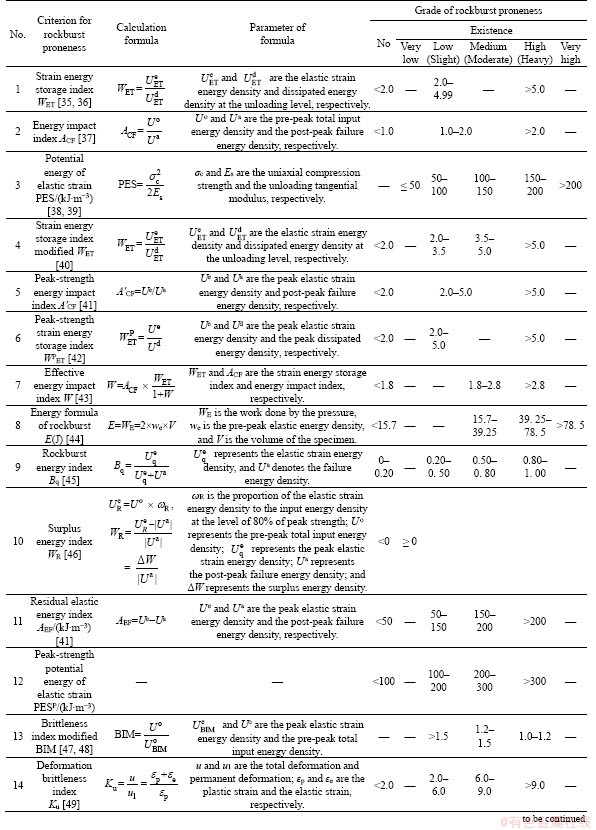
Continued
2.1 Strain energy storage index (WET)
WET [35, 36] is a typical bursting proneness discriminant criterion for rocks, and is widely involved in many literatures [57-59]. The value of WET can be obtained according to the single loading-unloading uniaxial compression test, where the unloading level (the ratio of unloading point stress to the uniaxial compressive strength) ranges from 0.8 to 0.9, as shown in Figure 1.
It is defined as the proportion of the elastic strain energy density to the dissipated energy density at the corresponding unloading level. The formula for calculating the criterion is as follows:
 (1)
(1)
 (2)
(2)
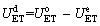 (3)
(3)
 (4)
(4)

Figure 1 Calculation diagram of WET and Ku
where 
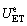 and
and are the input energy densities, the elastic strain energy density and dissipated energy density at the corresponding unloading level, respectively;
are the input energy densities, the elastic strain energy density and dissipated energy density at the corresponding unloading level, respectively;  and ε0 are the strain at the corresponding unloading level, and the residual strain when the stress is unloaded to 0, respectively.
and ε0 are the strain at the corresponding unloading level, and the residual strain when the stress is unloaded to 0, respectively.
2.2 Energy impact index (ACF)
According to the complete stress-strain curve obtained in the uniaxial compression (UC) tests, ACF [37] is defined as the proportion of the pre-peak total input energy density to the post-peak failure energy density. Figure 2 shows the calculating method of ACF, which is expressed as follows:
 (5)
(5)
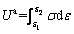 (6)
(6)
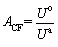 (7)
(7)
where Uo and Ua are the pre-peak total input energy density and post-peak failure energy density, respectively, ε1 is the strain at peak strength and ε2 is the maximum strain of the rock specimen during UC tests, respectively.

Figure 2 Calculation method diagram for ACF and B
2.3 Potential energy of elastic strain (PES)
The elastic strain energy stored in rock is also applied to judge the bursting proneness for rock materials, which is defined as the potential energy of elastic strain PES [38, 39]. As Figure 3 shows, in the single circle loading-unloading uniaxial compression (SCLUC) test, the stress is first loaded to 80% to 90% of peak strength and then unloaded to 0, and the stress is reloaded until the rock specimen is completely destroyed. The tangent of the unloading curve is marked in the figure, whose parallel line is assumed as an unloading curve at the peak strength point (see Figure 3). The area under the assumed unloading curve is considered as the peak elastic strain energy density. Accordingly, the PES is obtained, which can be illustrated by the shaded area shown in Figure 3. The formula is expressed as:
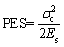 (8)
(8)
where σc and Es are the uniaxial compression strength and the unloading tangential modulus, respectively.
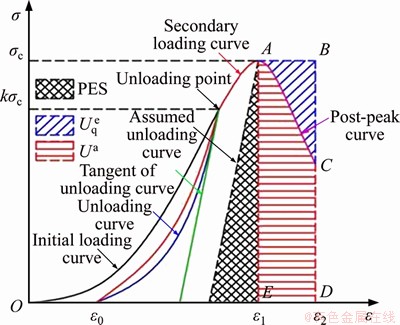
Figure 3 Calculation diagram of PES, WR and Bq
2.4 Strain energy storage index modified 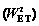
ZHANG et al [40] proposed an improved WET named 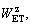 whose definition was the same as WET. However, a new grading standard of rockburst proneness was provided.
whose definition was the same as WET. However, a new grading standard of rockburst proneness was provided.
2.5 Peak-strength energy impact index (A′CF)
The peak elastic energy density plays an important role in the study of rockburst proneness criterion. In order to obtain the peak elastic energy density accurately, GONG et al [41, 60] have carried out a series of SCLUC tests. Based on the test results, GONG et al [41, 60] first found the linear energy storage law in the process of rock uniaxial compression test. The linear energy storage law has also been confirmed in the tensile failure test and shear failure test, which can be regarded as an inherent material property of rock materials [41, 42, 60-63]. According to the linear energy storage law, there is a strong linear relationship between the elastic energy density and the input energy density during the uniaxial compression of rock specimen [41, 42, 60]. The linear energy storage law can be expressed as follows:
 (9)
(9)
where  and
and  are the elastic energy density and input energy density at different unloading level i in SCLUC tests (i is the ratio of preset unloading stress to the peak strength of each rock specimen), which can be calculated by the area integral under the initial loading stress-strain curve and unloading stress-strain curve, respectively.
are the elastic energy density and input energy density at different unloading level i in SCLUC tests (i is the ratio of preset unloading stress to the peak strength of each rock specimen), which can be calculated by the area integral under the initial loading stress-strain curve and unloading stress-strain curve, respectively.
According to the obtained linear energy storage law, the peak elastic strain energy density Ue can be accurately calculated by substituting the pre-peak total input energy density Uo into formula (1):
 (10)
(10)
The peak-strength energy impact index A′CF was defined as the proportion of the peak elastic strain energy density to the post-peak failure energy density (see Figure 4) [41]. The formula is as follows:
A′CF=Ue/Ua (11)
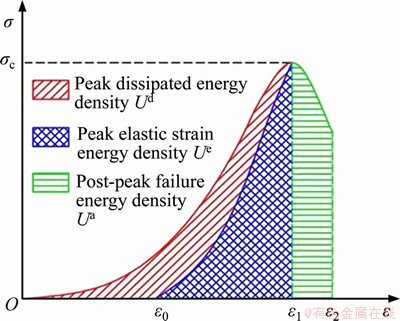
Figure 4 Calculation method diagram for A′CF, 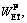 PESpand AEF
PESpand AEF
2.6 Peak-strength strain energy storage index 
As a modification from WET,  [42] was proposed on the basis of the linear storage energy law, which is the proportion of the peak elastic strain energy density to the peak dissipated energy density (see Figure 4). The formula is as follows:
[42] was proposed on the basis of the linear storage energy law, which is the proportion of the peak elastic strain energy density to the peak dissipated energy density (see Figure 4). The formula is as follows:
 (12)
(12)
where Ue and Ud are the peak elastic strain energy density and the peak dissipated energy density, respectively. They can be calculated according to the methods in Section 2.5.
2.7 Effective energy impact index (W)
Considering the characteristics of WET and ACF, W was proposed [43]. Its definition is the proportion of the pre-peak elastic strain energy density to the post-peak failure energy density. The capacity for storing elastic energy ωo is approximated by the following formula:
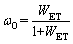 (13)
(13)
After combining with ACF, W is given by
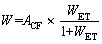 (14)
(14)
2.8 Energy formula of rockburst (E)
Energy formula of rockburst E reflects the pre-peak elastic energy [44]. In an UC test, the pre-peak elastic energy density we is as follows:
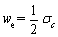 ,
, 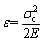 (15)
(15)
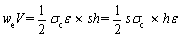
 (16)
(16)
where V is the volume of the specimen; σc is the uniaxial compressive strength; ε is the compressive strain; s is the cross-sectional area of the specimen; h is the height of the specimen; F is the pressure; △h is the displacement under the pressure; and WE is the work done by the pressure. After that, we obtain E as:
E=WE=2×we×V (17)
2.9 Rockburst energy index (Bq)
Rockburst energy index Bq was proposed according to the post-peak section of the complete stress-strain curve [45]. Figure 3 shows the approach for calculating the criterion, and the relevant formula is
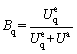 (18)
(18)
where 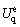 represents the elastic strain energy density, which is the area of ABC, and Ua denotes the failure energy density, which is the area of ACDE.
represents the elastic strain energy density, which is the area of ABC, and Ua denotes the failure energy density, which is the area of ACDE.
2.10 Surplus energy index (WR)
Based on the SCLUC test, WR [46] was proposed. Figure 3 shows the test method of calculating this criterion. The method can be described as follows: the stress is unloaded to 0 when the stress reaches 80% of peak strength; then the reloading starts until the rock specimen is completely destroyed. The criterion is described as
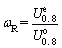 (19)
(19)
 (20)
(20)
 (21)
(21)
where 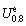 and
and 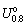 are the elastic strain energy density and the input energy density at the stress level of 80% of peak strength, respectively; ωR represents the elastic energy storage capacity of a rock; U o represents the pre-peak total input energy density calculated by integrating the pre-peak part under stress-strain curve;
are the elastic strain energy density and the input energy density at the stress level of 80% of peak strength, respectively; ωR represents the elastic energy storage capacity of a rock; U o represents the pre-peak total input energy density calculated by integrating the pre-peak part under stress-strain curve; 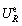 represents the peak elastic strain energy density calculated by Formula (20); Ua represents the post-peak failure energy density; and △W represents the surplus energy density.
represents the peak elastic strain energy density calculated by Formula (20); Ua represents the post-peak failure energy density; and △W represents the surplus energy density.
2.11 Residual elastic energy index (AEF)
Considering the energy evolution law of the whole failure process, GONG et al proposed the residual elastic energy index AEF [41]. The residual elastic energy index is defined as the difference between the peak elastic strain energy density and the post-peak failure energy density, which can be expressed as
AEF=Ue-Ua (22)
where Ue and Ua are the peak elastic strain energy density and the post-peak failure energy density, respectively. They can be obtained according to the methods mentioned in Section 2.5.
2.12 Peak-strength potential energy of elastic strain (PESP)
Based on the linear energy storage law, the peak-strength potential energy of elastic strain PESP was put forward, which represents the peak elastic strain energy density at of rock specimen and is modified from PES. The peak-strength potential energy of elastic strain (shown in Figure 4) can be calculated by the linear energy storage law introduced in Section 2.5 [41]. The grading standard of the rockburst proneness of this criterion is shown in Table 1.
2.13 Brittleness index modified (BIM)
The BIM [47, 48] is defined as the ratio of the total input energy density of the pre-peak to the peak elastic strain energy density. The peak elastic strain energy density is obtained based on the tangential modulus in the elastic loading phase. The parallel line to the elastic part of loading curve is assumed the unloading curve at the peak strength point (presented in Figure 5). The area under the assumed unloading curve is considered the peak elastic strain energy density. Figure 5 illustrates the calculation of the criterion, and the calculation formula is
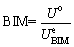 (23)
(23)
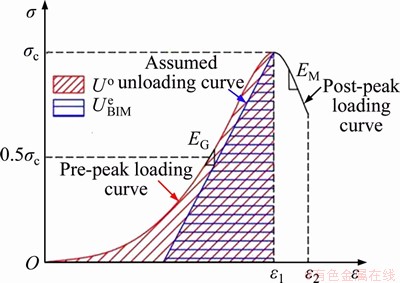
Figure 5 Calculation method diagram for BIM and DMI
2.14 Deformation brittleness index (Ku)
The rockburst proneness of a rock is closely related to the brittleness of the rock. Based on this, Ku [49] was proposed. As Figure 1 shows, the stress is unloaded to 0 when it reaches 80%–90% of the peak strength. Ku is equivalent to the proportion of the total deformation to the permanent deformation. The formula of calculating Ku is as follows:
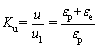 (24)
(24)
where u and u1 are the total deformation and permanent deformation, εp and εe are the plastic strain and the elastic strain, respectively.
2.15 Brittleness index of rockburst proneness (B)
Based on the close relationship between the rock brittleness and rockburst proneness, B [50] (Figure 2) was proposed to judge the bursting proneness for rock materials. B is given as:
 (25)
(25)
where α is an adjustable parameter that is usually taken as 0.1; σc and σt are the uniaxial compressive strength and uniaxial tensile strength, respectively; and εf and εb are the pre-peak total strain and post-peak total strain, respectively.
2.16 Strength brittleness index (B1)
As a classical criterion, strength brittleness index B1 [38, 51] is widely used to evaluate the rock brittleness, and is defined as the proportion of the uniaxial compressive strength to the uniaxial tensile strength, as follows:
 (26)
(26)
where σc and σt are the uniaxial compressive strength and tensile strength, respectively.
2.17 Strength brittleness index (B2)
There is another strength brittleness index B2 [49] whose definition is the same as B1, but a new grading standard of rockburst proneness is proposed and presented in Table 1.
2.18 Strength brittleness index (B3)
ZHANG et al [40] also put forward a new grading standard (Table 1) of rockburst proneness as the strength brittleness index, B3, based on the five-factor comprehensive rockburst criterion. The five factors include the mechanical conditions of rockburst σ1/σc and σθ/σc, the rock brittleness σc/σt, the elastic energy index WET and the rock mass integrity coefficient Kv. σ1 is the maximum principal stress at the tunnel periphery, and σθ is the maximum tangential stress at the tunnel periphery.
2.19 Decrease modulus index (DMI)
The DMI [52, 53] is the proportion of the pre-peak elastic modulus to the post-peak decrease modulus. The calculation of DMI is demonstrated in Figure 5, and the formula is as below:
DMI=EG/|EM| (27)
where EG is the pre-peak elastic modulus obtained by the slope of the linear part of pre-peak stress- strain curve, and EM is the post-peak decrease modulus obtained by the slope of the post-peak decreasing stress-strain curve.
2.20 Lag time ratio index (TR)
The load-unload response ratio (LURR) theory was proposed by YIN [64] to study rock damage precursors and instability prediction. During the pre-peak uniaxial compressive test of rock material, the deformation modulus of loading section is different from that of unloading section except elastic deformation stage. The differences can reflect the deterioration degree of the rock mechanical properties. The differences can be quantified by the formula as follows [64]:
 (28)
(28)
where △R is the response increment, and △P is the load increment. The LURR is defined as
 (29)
(29)
where X+ is the loading response rate and X- is the unloading response rate [65-67].
Using the LURR theory, GONG et al [54, 68] studied the relationship between load–unload response ratio characteristic of rock material and rockburst proneness degree based on the uniaxial step load–unload test, and proposed the lag time ratio index, which is defined as the ratio of the time from the LURR S-R (start rise) point to the peak strength point to the time of the whole loading period (Figure 6). It can be expressed as
TR=T1/Tb (30)
where T1, which is marked as the lag time, is the interval time between the peak strength point and S-R point, and Tb is the time of the whole loading period. The S-R point can be obtained directly by analyzing the data of LURR-strain curves, and it is the last point whose LURR value is smaller than the previous one. Besides, the time corresponding to the LURR S-R point is consistent with the change point of the AE counting rate, and the axial stress corresponding to the LURR S-R point is the same as the rock damage strength [68, 69].

Figure 6 Calculation method diagram for TR
The above 20 rockburst proneness criteria were proposed from diverse perspectives and have different characteristics. However, the judgment accuracy of these criteria lacks a unified evaluation and comparison, so that choosing a suitable criterion for evaluation of rockburst proneness is difficult. To obtain the judgment results of the criteria and compare the judgment accuracy of them, a series of laboratory tests on fourteen types of rocks were conducted.
3 Test procedure and test results
In order to evaluate the rockburst proneness of rock materials using the above criteria, different types of laboratory tests are required to carry out firstly. Generally, UC test, SCLUC test or Brazilian disc (BD) test are involved. In this study, the BD test, UC test and SCLUC test were conducted on fourteen types of rocks to obtain the judgment results of the criteria and compare the judgment accuracy of them, and the details of the tests are as follows.
3.1 Specimen preparation and test instrument
Fourteen types of rocks were selected for the tests, including six types of granite, four types of sandstone, two types of marble, one type of slate, and one type of limestone (Figure 7).
The rocks were processed into cylindrical with two specifications: d50 mm×50 mm specimens were prepared for the BD test, and d50 mm×100 mm specimens were used for the UC and SCLUC tests. The density and P-wave velocity of the fourteen types of rocks are measured and listed in Table 2.
The BD tests were conducted on the MTS 322 test system (Figure 8), and a loading module was used in the tests. The UC and SCLUC tests were carried out by INSTRON 1346 test system (Figure 8), whose maximum axial loading force can reach 2000 kN. The loading module and rock specimen installation in the two test systems above are shown in Figure 8. The instantaneous failure process of each kind of rock under compression was recorded by a high-speed camera.
3.2 Test procedure
The BD test on a rock specimen merely comprised a sustained loading process, during which the specimen was loaded until destruction by force control with a loading rate of 10 kN/min. The rock tensile strength can be obtained through the BD tests.

Figure 7 Fourteen types of rock specimens (d50 mm×100 mm)
Table 2 Basic properties of fourteen types of rocks


Figure 8 MTS 322 test system (a), loading module and specimen installation in the BD tests (b), specimen installation in the UC and SCLUC tests (c) and INSTRON 1346 test system (d)
During the UC tests, the rock specimen was loaded by pressure heads until it was completely destroyed; the axial force and displacement were recorded in real time. The tests were conducted by force control with a loading rate of 120 kN/min, and the control mode was transformed into displacement control with a loading rate of 0.065 mm/min when the stress reached about the 80% of peak strength. Based on the UC tests, the complete stress-strain curves and the uniaxial compressive strength (σc) of the specimen tested were attained.
The SCLUC tests are usually used to study the energy evolution and storage characteristics of rock specimens during uniaxial loading and unloading [41, 42, 60, 70-72]. The SCLUC tests were performed following the procedures hereinafter. First, the initial loading was conducted on a rock specimen until the stress reached kσc (k=0.1, 0.3, 0.5, 0.7 and 0.9), and then the specimen was unloaded until the stress reached 0.02σc. Finally, the secondary loading was performed until the specimen was totally destroyed. During the loading process, the loading mode was the same as that in UC tests, besides, the unloading process was conducted by force control with a loading rate of 120 kN/min. The associated loading path in a SCLUC test is depicted in Figure 9.

Figure 9 Loading path of SCLUC tests
3.3 Test results
After the tests, the average tensile strength, average uniaxial compressive strength, average elastic modulus (shown in Table 2), stress-strain curves (shown in Figures 10 and 11) and other necessary parameters of fourteen types of rocks were obtained, which are the key factors for obtaining the judgment results of rockburst proneness using the criteria. From Figure 10, it can be seen that the characteristics of these stress-strain curves are different from each other. Some rock specimens have complete stress-strain curves, such as marble, white marble and yellow rust granite, and their curves are flat, which shows that they have obvious plasticity. However, some other rock specimens like red sandstone and Yueyang granite have incomplete post-peak curves and the stress of these specimens drop sharply after peak, which indicates that they have strong brittleness. Besides, the stress-strain curves of three typical rock specimens (Yellow granite, Green sandstone and Marble) in SCLUC tests are shown in Figure 11. It can be observed that the unloading curve is below the initial loading curve for the existence of energy dissipation during loading process, the irreversible permanent deformation will occur in the load-unloading process. The secondary loading curve is between the initial loading curve and unloading curve, and it develops as the trend of the initial loading curve after going through the unloading point.
Figure 12 shows the relationships between the elastic strain energy density and input energy density of yellow granite, green sandstone and marble in SCLUC tests, and the calculation results of other eleven types of rocks are shown in Table 3.

Figure 10 Stress-strain curves of fourteen rocks in UC tests

Figure 11 Stress-strain curves of three rocks in SCLUC tests:
The results show that there is a very obvious linear function relationship between the elastic energy and the input energy of rock specimens during uniaxial compression, indicating that the linear energy storage law is applicable to all kinds of rocks. By using the linear energy storage law, the peak elastic energy density can be accurately calculated by substituting the peak total input energy density into the calculation formula, and the calculation results are shown in Table 3.
4 Classification standard for rockburst proneness in laboratory tests
Using the test data in Section 3, the rockburst proneness grade of the 14 kinds of rocks can be evaluated according to the definition of each rockburst proneness criterion in Section 2 and the grading standards in Table 1.
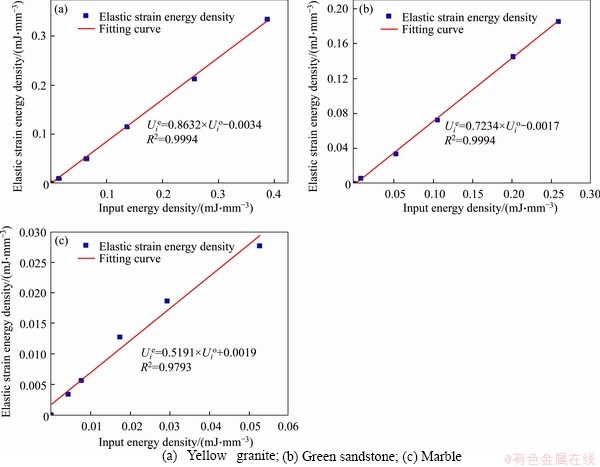
Figure 12 Relationships between elastic strain energy density and input energy density of three rocks in SCLUC tests:
Table 3 Calculations of average peak elastic strain energy density based on linear energy storage law

As mentioned above, the judgment results of some criteria are sometimes inconsistent with the actual state of rock specimens after failure. Therefore, the judgment results need to be analyzed based on the practical experimental phenomenon to evaluate and compare the judgment accuracy of the criteria. To complete it, the classification standard of rockburst proneness based on the practical experimental phenomenon was introduced in this section that was used as the basis for evaluating the judgment accuracy of the criteria.
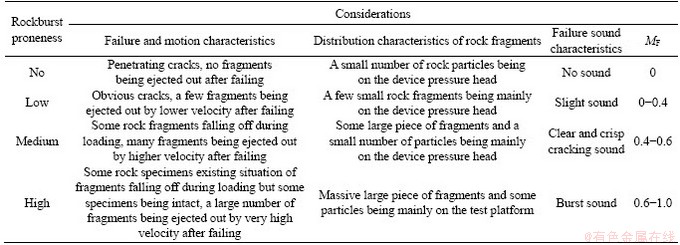
Similar to the rockburst occurring in deep in-site engineering, the rock specimen failure in the laboratory tests was generally accompanied by an ejection phenomenon of rock fragments. The rockburst proneness of the rocks is closely related to the kinetic energy of the ejected rock fragments. The most ideal method of judging the rockburst proneness of a rock specimen is to obtain the mass and velocity of each rock fragment and calculate its kinetic energy precisely. However, there are numerous rock fragments being ejected in diverse directions in a very short time during rock failure, as shown in Figure 13 (the failure process of Yueyang granite recorded by the high-speed camera). In Figure 13, it is impossible to track the path of each rock fragment and calculate its velocity. Collecting and weighing each rock fragment are also hard to achieve. Therefore, the ideal method will not work under the current technical conditions. Under this circumstance, the factors such as the ejection distance of rock fragments, failure and motion characteristics are considered to comprehensively judge the rockburst proneness. In this study, a classification standard for rockburst proneness in laboratory tests (Sr) [41] was introduced considering four factors (ejection distance of rock fragments, failure and motion characteristics, distribution characteristics of rock fragments and failure sound characteristics) from qualitative and quantitative aspects by analyzing the practical failure processes (recorded by the high-speed camera) and failure characteristics of the rock specimens. The rockburst proneness degree is divided into four grades (no, low, medium, and high). The details of the classification standard are as follows.

Figure 13 Failure process of Yueyang granite
Firstly, the rockburst proneness of the rock materials is analyzed from the quantitative perspective, and the far-field ejection mass ratio (MF) was introduced [41]. In view of the difficulty of rockburst proneness evaluation with the ideal method, an approximate calculation method was proposed considering the ejection distance and mass of rock fragments. Kinetic energy includes two parameters, i.e., mass and velocity. The farther the rock fragments eject, the greater the velocity. Thus, the more rock fragments eject into a wider range, the greater the kinetic energy. Accordingly, the rockburst proneness could be judged quantitatively by collecting and counting the rock fragments ejecting in different distances. To simplify the calculation, the rock specimen tested was taken as the center, and the distribution area of rock fragments was divided into two parts: the area in the device pressure head range, and the area beyond the device pressure head range and in the test platform (Figure 14). This method was defined as MF which is the ratio of the mass of the rock fragments falling outside the device pressure head range to the total mass of rock fragments separated from the rock sample. The formula is as follows:
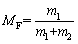 (31)
(31)
where m1 and m2 are the mass of rock fragments falling outside the device pressure head range but within the test platform range, and the mass of rock fragments falling within the scope of pressure head,respectively.
By comprehensively considering the practical failure characteristics and the value of MF, a specific grading standard for rockburst proneness of MF is obtained as follows [41]:
 (32)
(32)
There are two typical states: 1) m1=0, namely no rock fragments fell outside the device pressure head range, and MF=0 at this state, which corresponds to no rockburst proneness. 2) m2=0, all the rock fragments separated from the rock sample and fell outside the device pressure head range but within the test platform range, and MF=1; in this state, the rock is subjected to high rockburst proneness.
Secondly, the rockburst proneness is analyzed from the qualitative perspective based on the failure and motion characteristics, the distribution characteristics of rock fragments, and the failure sound characteristics. The detailed analyses are described as follows.
No rockburst proneness: A small number of particles of rock fell around the specimen after it failed. There are penetrating cracks on the surface of the rock specimen, and no fragments separated from the specimen during the failure process. Moreover, there is no sound when the specimen is destroyed. These situations appeared in the marble, white marble and yellow rust granite, as shown in Figures 15(a)–(c).
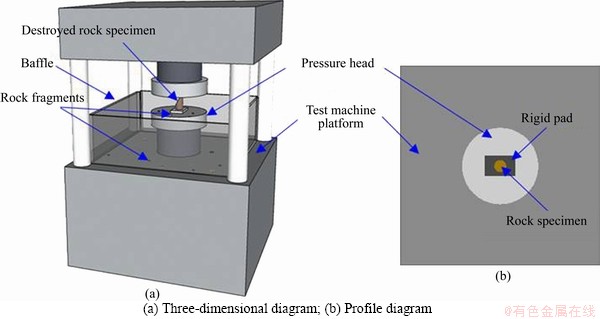
Figure 14 Diagrammatic sketch for MF:

Figure 15 State of white marble, marble, yellow rust granite and black sandstone after failure:
Low rockburst proneness: As the failure of black sandstone shown in Figure 15(d), after the specimen failure, a few small fragments are distributed in the area around the specimen, including the areas of the device pressure head and test platform. Some fragments are ejected down obliquely from the specimen with a lower velocity when the specimen is totally destroyed. This can be observed from the failure process of black sandstone, as shown in Figure 16. There is a slight sound when the specimen is destroyed.
Medium rockburst proneness: After the failure of the rock specimen, some large pieces of fragments and a small number of particles distribute around the specimen and most of them are on the device pressure head (see the failures of red sandstone, red granite, green sandstone, and yellow sandstone shown in Figure 17). Many fragments are ejected down obliquely from the specimen with a higher velocity when the specimen totally fails, e.g., the failure of red granite shown in Figure 18. There is a clear and crisp cracking sound when the specimen is destroyed.
High rockburst proneness: Massive pieces of fragments and some particles are distributed around the specimen, and most of them are on the test platform (see the failures of Fine granite, Yueyang granite, Yellow granite, Slate, Limestone, and Qingshan granite shown in Figure 19). When the specimens totally fail, a large number of fragments with some particles are ejected nearly along the horizontal direction from the specimen at a very high velocity, as can be observed from Figure 20. There is a burst sound when the specimen is destroyed.
Thus, by combining the above quantitative and qualitative analyses of rockburst proneness of rock materials, the classification standard for rockburst proneness (Sr) in laboratory tests is obtained, as shown in Table 4.
It is noted that the Sr is a comprehensive empirical classification standard for rockburst proneness considering diverse factors based on the practical experimental phenomenon. The judgment standard will vary if the testing condition changes, and it will take a lot of work if Sr is directly used for the judgment of rockburst proneness degrees of rock specimens. Therefore, Sr is not suitable to be popularized as a discriminant criterion for the judgment of rockburst proneness in laboratory conditions; Sr is merely used as a basis of evaluating the judgment accuracy of rockburst proneness criteria in this study.

Figure 16 Failure process of black sandstone

Figure 17 Situation of rock specimens after failure for medium rockburst proneness:

Figure 18 Failure process of red granite

Figure 19 Situation of rock specimens after failure for high rockburst proneness:

Figure 20 Failure process of Qingshan granite
Table 4 Classification standard for rockburst proneness of rock materials [41]
5 Judgment accuracy analysis of twenty criteria
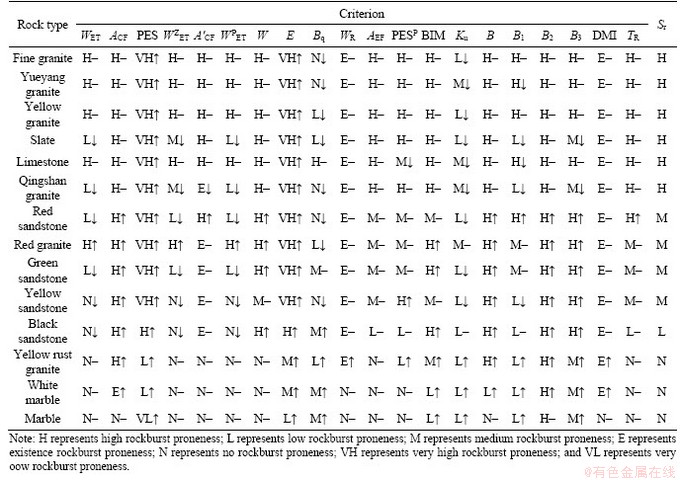
According to the rockburst proneness grading standards of the twenty criteria and the test results of the fourteen types of rocks, the judgment results of the rockburst proneness for each type of rock regarding every specific criterion were obtained. The calculation results of the criteria are listed in Table 5, and the judgment results of the criteria are shown in Table 6. It can be seen that the results of different criteria for one type of rock are different from each other, as each criterion has its own limitation. This also indicates that the judgement accuracies of these criteria are worth analyzing.
In this study, Sr is taken as the standard to evaluate the judgment results of the twenty criteria of rockburst proneness to obtain their judgment accuracies. To achieve it, the judgment results of the fourteen rocks by Sr are obtained and presented in Table 6. Besides, the applicability and validity of Sr are explained as follows based on the judgment results in Table 6 and the actual rockburst proneness. Taking yellow rust granite, white marble and marble as examples and according to the actual state of rock failure (shown in Figure 15), these three kinds of rocks have no rockburst proneness, but only the judgment results of six criteria (WET,W ZET, W, A′CF, W PET, AEF) and Sr (Table 6) accord with this situation. Moreover, the black sandstone has low rockburst proneness (Figure15(d)) and red granite has medium rockburst proneness (Figure 17(b)) according to the actual situation of rock failure. However, the judgment results (Table 6) of WET, W ZET, W and W PET for these two rocks are evidently wrong. The result of A′CF is not precise, which cannot distinguish the rockburst proneness in low and medium degrees. Only the judgment results of AEF and Sr are consistent to the actual situation. Similarly, the other rocks are also analyzed as the above way. It is found that the judgment results of Sr totally conform the actual rockburst proneness, which indicates that Sr is appropriate and effective to be an evaluation standard for the judgment accuracy of the twenty criteria.
The preliminary evaluation of the accuracy regarding the judgment results of the twenty criteria are shown in Table 6. There, the “↑” represents that the judgment result of the criterion is higher than the judgment result of Sr for the same type of rock, the “↓” represents that the judgment result of the criterion is lower than the judgment result of Sr for the same type of rock, and the “–” represents that the judgment results of the criterion and Sr for the same type of rock are the same. The detailed analysis for the judgment accuracy of the twenty criteria, according to Sr, is as follows.
Table 5 Calculation results of the twenty criteria and MF

Table 6 Judgment results of the twenty criteria and Sr
Three indexes were put forward to further analyze the judgment accuracy of the twenty criteria of rockburst proneness: misjudgment rate, high-judgment rate and low-judgment rate. These three indexes were obtained by comparing the judgement results of the twenty criteria to the judgment results of Sr for each rock specimen. The misjudgment rate is defined as the ratio of the number of rocks that are misjudged to the total amount of rocks. The high-judgment rate is the ratio of the number of the rocks that are higher than the practical rockburst proneness to the total number of rocks. The low-judgment rate is defined as the ratio of the number of the rocks that are lower than the practical rockburst proneness to the total number of rocks. The calculation results for these three indexes are presented in Figure 21. From Figure 21(a), we can see that the criteria are ranked by the misjudgment rate from high to low. As can be seen in Figure 21(a), the misjudgment rates of thirteen criteria are greater than or equal to 50%, the misjudgment rates of six criteria are less than 50%, and there is only one criterion AEF whose misjudgment rate is 0.
The criteria are ranked by the high-judgment rate from high to low, as shown in Figure 21(b). From Figure 21(b), we can see that all of the criteria have some judgment results that are higher than the practical rockburst proneness, excluding AEF. Moreover, the high-judgment rates of seven criteria are greater than 40%, and it is also worth noting that the high-judgment rates of PES and E are 100%. However, as the judgment results of the criteria are higher, the supporting strength in the practical projects is stronger, and can guarantee safety.
Figure 21(c) presents the criteria that are ranked by the low-judgment rate from high to low. From Figure 21(c), we can see that nine criteria have some judgment results lower than the actual rockburst proneness, whose low-judgment rates range from 7% to 64 %. The lower judgment results would not allow the supporting work to achieve the desired effects in practical projects, and could be dangerous for people and equipment. Therefore, these cases should be avoided.
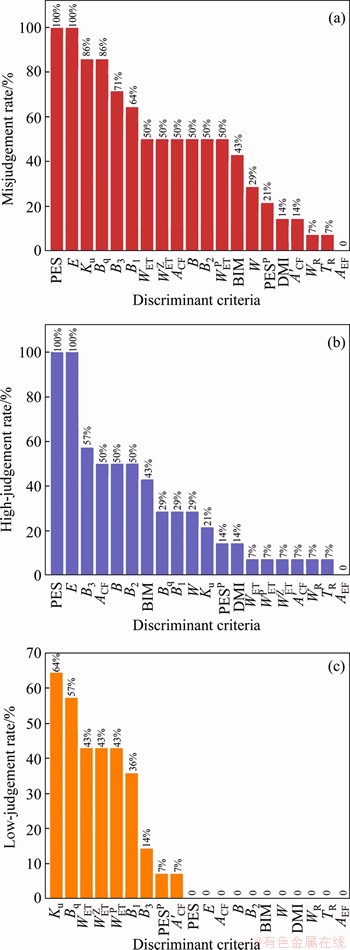
Figure 21 Calculation results for misjudgment rate (a), high-judgment rate (b) and low-judgment rate (c) of each criterion for rockburst proneness
The judgment accuracy of the twenty criteria has been evaluated and compared above. It can be observed from the analyses that all the criteria except AEF can result in some misjudgments, and the judgment results of AEF are completely consistent with Sr’s. In addition, Figure 22 illustrates the corresponding relationship between the judgment results of four criteria (WET, Ku, B1 and AEF) and the judgment results of MF, in which the “H, M, L, N” represent high rockburst proneness, medium rockburst proneness, low rockburst proneness, no rockburst proneness, respectively. It can be seen that AEF yields the completely consistent judgment results with MF, and the other remaining criteria show some discrepancies in their judgment results. Therefore, compared to other criteria, AEF is believed to be more accurate and scientific in evaluating the rockburst proneness of the rock materials.
6 Discussion
The rockburst proneness criteria summarized in this study are widely used for rockburst proneness evaluation, and they exist different characteristics due to the various considerations when being proposed. Besides, the obtaining methods of the parameters in the calculation formulas of different criteria also exist differences. The differences of the two aspects will affect the judgment accuracy of the criteria, therefore, the different characteristics of the criteria and the different obtaining methods of the parameters in criteria are analyzed and discussed to study their influences on the judgment accuracy of criteria.
6.1 Characteristics of rockburst proneness criteria
The characteristics differences of the various criteria are mainly reflected in theoretical bases, definition forms, and research objects.
In terms of theoretical bases, the twenty rockburst proneness criteria involve energy (e.g., WET, ACF, PES, WR and AEF), brittleness (e.g., Ku, B, B1), rigidity (DMI), and LURR theory (TR). It is known to all that rockburst happens accompanied by the release of energy accumulated in rock mass. The occurrence of rockburst is closely related to the energy evolution of rock mass, including energy storage, dissipation and release. Hence, the criteria based on energy can more directly reflect the rockburst proneness than others. The brittleness, rigidity and LURR indeed have some connections with rockburst proneness of rock materials, whereas it is difficult to use them to evaluate the rockburst proneness degree accurately. As shown in Figure 21(a), among the criteria whose misjudgment rate are lower than 50%, most of them are proposed based on energy. Thus, the energy- based criteria are more suitable and scientific for the evaluation of the rockburst proneness of rock materials.
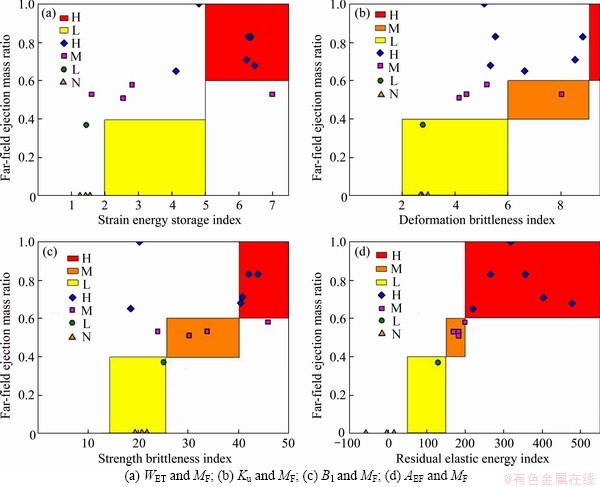
Figure 22 Relationship between judgment results of four criteria and MF (H represents high rockburst proneness;M represents medium rockburst proneness; L represents low rockburst proneness; N represents no rockburst proneness):
The definition forms of the criteria can also affect their judgment accuracies. A′CF is modified from ACF based on the linear energy storage law, according to which the peak elastic energy can be precisely obtained to make the criterion more accurate [41]. However, A′CF still has some misjudgment situations as presented in Figure 21(a) and the misjudgment rate of AEF is 0. When comparing the two criteria following the description in Sections 2.5 and 2.11, it can be observed that both the criteria involve the peak elastic energy and the failure energy. However, the defined forms of them are different: A′CF is defined in the form of ratio value, and AEF is defined in the form of a difference value. The form of ratio value for criteria such as A′CF can only reflect the relative grade of rockburst proneness to some extent; they can’t reflect the absolute grade of rockburst proneness. Taking the judgment results of A′CF in Tables 5 and 6 for an example, the results show that both the black sandstone and red granite exist rockburst proneness, and the value of black sandstone for A′CF is greater than that of the red granite. However, it is observed that the red granite (Figure 17(b)) has more violent rock fragments ejections than the black sandstone (Figure 15(d)). Moreover, the judgment results of AEF show that the red granite has higher rockburst proneness than the black sandstone and that the AEF value of red granite is greater than that of the black sandstone. The above analyses confirm that the criteria in the form of a difference value can evaluate the rockburst proneness grades more accurately.
Rockburst is related to the whole rock failure process, and it should be considered in the rockburst proneness criteria. The pre-peak stage involves the energy storage and dissipation, and the stored elastic energy is the main source of the kinetic energy of rock fragments ejection. The post-peak stage involves the energy dissipation and release. A part of the elastic strain energy is used for rock failure, and the remaining elastic strain energy can drive the rock fragments flying out. Therefore, both of pre-peak and post-peak stages are significant for analyzing the rockburst proneness and the whole rock failure process should be considered for the criteria of rockburst proneness.
From the above analyses, it is found that the criteria that are energy-based, defined in the form of a difference value and involving the whole rock failure process are more scientific and accurate.
6.2 Calculation method of peak elastic energy density
As mentioned above, the energy-based criteria are more scientific relative to the others. Additionally, the calculation method of energy parameters, especially the peak elastic strain energy density Ue, can also affect the judgment accuracy of criteria. However, owing to the indeterminacy of the peak strength of rock, it is impossible to unload promptly at the peak strength point during the UC test. Thus, the peak elastic strain energy density could not be directly obtained by integral according to the stress-strain curve. Under this circumstance, some approximate calculation methods for peak elastic strain energy density were used in criteria such as PES, BIM, WR, and W. There is a typical approximate calculation method that was widely used [38, 43, 59], and its formula is
 (33)
(33)
where σc is the uniaxial compression strength, and Eu is the linear modulus of an ideal unloading curve at the peak strength point as presented in Figure 23 [41]. Two methods are usually applied to calculate Eu: 1) Eu is regarded as the unloading tangential modulus Es (Figure 23(a)); 2) Eu is regarded as the elastic modulus of the loading curve E1 (Figure 23(b)).
The approximate calculation methods will inevitably lead to inaccurate judgment results of criteria, and the four criteria mentioned above all have some misjudgment situations as presented in Figure 21(a).
To solve the above problem and obtain the peak elastic strain energy density precisely, GONG et al [41, 42, 62] found the linear energy storage law, which indicates that there is a linear relationship between the elastic strain energy density and input energy density, and their functional relationship can be obtained by SCLUC tests.
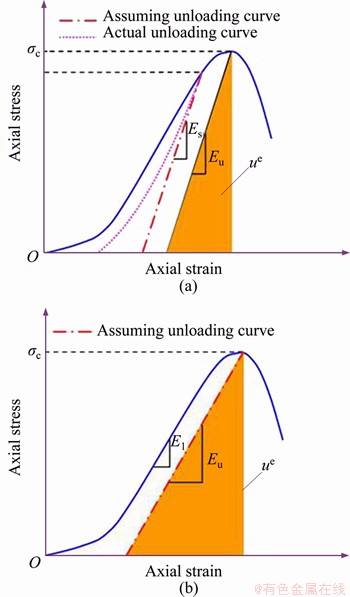
Figure 23 Schematic drawing of calculation of Eu [60]
The pre-peak total input energy density could be easily obtained by integrating based on the stress-strain curve. Then, the elastic energy density could be precisely calculated by the functional relationship between the elastic strain energy density and the input energy density.
According to the linear energy storage law, PES was modified into PESP that reflect the peak elastic strain energy more precisely. It is evident that the value of PESP is greater than that of PES as Figure 24 shows.
This can also be confirmed by the test data (Figure 25), the values of PESP for the fourteen rocks are greater than PES’s. Moreover, the judgment results of PESP are more accurate than PES’s (Figure 21(a)), which indicates the significance of calculating the peak elastic strain energy density precisely.
Overall, the above analyses indicate that the criteria that are energy-based, defined in the form of a difference value, involving the whole rock failure process, and based on the linear energy storage law to calculate the peak elastic strain energy are more scientific and accurate. Among the summarized twenty criteria, AEF meets all of the above characteristics, which indicates AEF is a scientific and reliable rockburst proneness criterion.
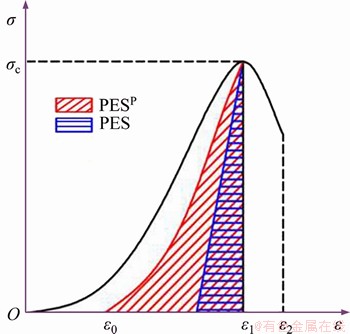
Figure 24 Comparison of PES and PESP

Figure 25 Comparison of PES and PESP according to tests for fourteen rock materials
7 Conclusions
1) Twenty criteria for rockburst proneness were summarized in detail, including their origins, definitions, calculation methods and grading standards. The detailed summaries provide convenience for evaluating the rockburst proneness of rock materials.
2) The judgement results of the twenty criteria were obtained by a series of laboratory tests on fourteen types of rocks. The results show that different criteria have diverse judgment results even for the same rock type, which implies the accuracy of them is worth evaluating and comparing.
3) The judgement accuracy of the twenty criteria was evaluated based on a classification standard for the rockburst proneness in laboratory tests (Sr) obtained from qualitative and quantitative aspects according to the practical test phenomena. The result shows that the judgment results of AEF are completely consistent with the actual rockburst proneness. In contrast, all the other criteria have some inconsistencies.
4) The characteristics of the criteria were analyzed. The results show that the criteria that are energy-based, defined in the form of a difference value, involving the whole rock failure process, and based on precise methods to calculate parameters are more scientific and can evaluate the rockburst proneness accurately. AEF meets all these characteristics, which further demonstrates the superiority of AEF. Thus, we conclude that AEF is relatively more accurate and scientific than other criteria and it is recommend to evaluate the rockburst proneness of rock materials.
Contributors
GONG Feng-qiang provided the idea of the study, developed the overarching research goal, and led the research activity planning and execution. GONG Feng-qiang also made great contribution to the improvement of manuscript after the initial draft finished. WANG Yun-liang conducted the experiments, analyzed the test data, and wrote the initial draft of the manuscript. LUO Song offered some valuable suggestions for the contents of the manuscript and polished the language of the manuscript. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
GONG Feng-qiang, WANG Yun-liang and LUO Song declare that they have no conflict of interest.
References
[1] LI X B, YAO J R, GONG F Q. Dynamic problems in deep exploitation of hard rock metal mines [J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2551-2563. DOI: 10.19476/j.ysxb.1004.0609.2011.10.022. (in Chinese)
[2] LI X B, ZHOU J, WANG S F, L B. Review and practice of deep mining for solid mineral resources [J]. The Chinese Journal of Nonferrous Metals, 2017, 27(6):1236-1262. DOI: 10.19476/j.ysxb.1004.0609.2017.06.021. (in Chinese)
[3] CAI M F, BROWN E T. Challenges in the mining and utilization of deep mineral resources [J]. Engineering, 2017, 3(4): 432-433. DOI: 10.1016/J.ENG.2017.04.027.
[4] DONG L J, TONG X J, LI X B, ZHOU J, WANG S F, LIU B. Some developments and new insights of environmental problems and deep mining strategy for cleaner production in mines [J]. Journal of Cleaner Production, 2019, 210: 1562-1578. DOI: 10.1016/j.jclepro.2018.10.291.
[5] DIEDERICHS M S. The 2003 Canadian geotechnical colloquium: Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling [J]. Canadian Geotechnical Journal, 2007, 44(9): 1082-1116. DOI: 10.1139/T07-033.
[6] GONG F Q, LUO Y, LI X B, SI X F, TAO M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels [J]. Tunnelling and Underground Space Technology, 2018, 81: 413-427. DOI: 10.1016/j.tust.2018.07.035.
[7] DU K, TAO M, LI X B, ZHOU J. Experimental study of slabbing and rockburst induced by true-triaxial unloading and local dynamic disturbance [J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3437-3453. DOI: 10.1007/s00603-016-0990-4.
[8] LI S J, FENG X T, LI Z H, CHEN B R, ZHANG C Q, ZHOU H. In situ monitoring of rockburst nucleation and evolution in the deeply buried tunnels of Jinping II hydropower station [J]. Engineering Geology, 2012, 137-138(7): 85-96. DOI: 10.1016/j.enggeo.2012.03.010.
[9] ZHANG C Q, FENG X T, ZHOU H, QIU S L, WU W P. Case histories of four extremely intense rockbursts in deep tunnels [J]. Rock Mechanics and Rock Engineering, 2012, 45(3): 275-288. DOI: 10.1007/s00603-011-0218-6.
[10] ZHOU H, MENG F Z, ZHANG C Q, LU J J, XU R C. Review and status of research on physical simulation test for rockburst [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 915-923. DOI:10.13722/j.cnki. jrme.2014.0339. (in Chinese)
[11] MARTIN C D, CHRISTIANSSON R. Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 219-228. DOI: 10.1016/j.ijrmms.2008.03.001.
[12] GONG F Q, WU W X, LI T B, SI X F. Experimental simulation and investigation of spalling failure of rectangular tunnel under different three-dimensional stress states [J]. International Journal of Rock Mechanics and Mining Science, 2019, 122: 104081. DOI: 10.1016/j.ijrmms.2019. 104081.
[13] LI X B, GONG F Q, TAO M, DONG L J, DU K, MA C D, ZHOU Z L, YIN T B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(4): 767-782. DOI: 10.1016/j.jrmge. 2017.04.004.
[14] LI X B, GONG F Q, WANG S F, LI D Y, TAO M, ZHOU J, HUANG L Q, MA C D, DU K, FENG F. Coupled static-dynamic loading mechanics mechanism and dynamic criterion of rockburst in deep hard rock mines [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 708-723. DOI: 10.13722/j.cnki.jrme.2018.1496. (in Chinese)
[15] ORTLEPP W D, STACEY T R. Rockburst mechanisms in tunnels and shafts [J]. Tunnelling and Underground Space Technology, 1994, 9: 59-65. DOI: 10.1016/0886-7798(94) 90010-8.
[16] FENG X T, CHEN B R, ZHANG C Q, LI S J, WU S Y. Mechanics, waring and dynamic control of rockburst development processes [M]. Beijing: Science Press, 2013. ISBN: 978-7-03-036465-4. (in Chinese)
[17] HE M C, REN F Q, LIU D Q. Rockburst mechanism research and its control [J]. International Journal of Mining Science and Technology, 2018, 28(5): 829-937. DOI: 10.1016/j.ijmst.2018.09.002.
[18] GONG F Q, LI X B, LIU X L, ZHAO J. Experimental study of dynamic characteristics of sandstone under one- dimensional coupled static and dynamic loads [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2076-2085. http://www.cnki.com.cn/Article/CJFDTOTAL-Y SLX201010019.htm.htm. (in Chinese)
[19] HE M C, JIA X N, COLI M, LIVI E, LUIS S. Experimental study of rockbursts in underground quarrying of Carrara marble [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 52: 1-8. DOI: 10.1016/j.ijrmms. 2012.02.006.
[20] SU G S, JIANG Q, ZHAI S B, ZHANG G L. Influence of tunnel axis stress on strainburst: An experimental study [J]. Rock Mechanics and Rock Engineering, 2017, 50(6): 1551-1567. DOI: 10.1007/s00603-017-1181-7.
[21] GONG F Q, SI X F, LI X B, WANG S Y. Experimental investigation of strain rockburst in circular caverns under deep three-dimensional high-stress conditions [J]. Rock Mechanics and Rock Engineering, 2019, 52: 1459-1474. DOI: 10.1007/s00603-018-1660-5.
[22] SI X F, GONG F Q. Strength-weakening effect and shear-tension failure mode transformation mechanism of rockburst for fine-grained granite under triaxial unloading compression conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 131: 104347. DOI: 10.1016/j.ijrmms.2020.104347.
[23] WAND S Y, LAM K C, AU S K, TANG C A, ZHU W C, YANG T H. Analytical and numerical study on the pillar rockbursts mechanism [J]. Rock Mechanics and Rock Engineering, 2006, 39(5): 445-467. DOI: 10.1007/s00603- 005-0075-2.
[24] ZHU W C, LI Z H, ZHU L, TANG C A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance [J]. Tunnelling and Underground Space Technology, 2010, 25(5): 587-599. DOI: 10.1016/j.tust.2010. 04.004.
[25] GAO F Q, KAISER P K, STEAD D, EBERHARDT E, ELMO D. Strainburst phenomena and numerical simulation of self-initiated brittle rock failure [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 116: 52-63. DOI: 10.1016/j.ijrmms.2019.03.021.
[26] TANG C A, WANG J M, ZHANG J J. Preliminary engineering application of microseismic monitoring technique to rockburst prediction in tunneling of Jinping II project [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(3): 193-208. DOI: 10.3724/SP.J.1235. 2010.00193.
[27] GONG F Q, LI X B. A distance discriminant analysis method for prediction of possibility and classification of rockburst and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 1012-1018. DOI: 10.3321/j. issn:1000-6915.2007.05.021. (in Chinese)
[28] ZHANG J J, FU B J. Rockburst and its criteria and control [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 2034-2042. DOI: 10.1121/1.4754966. (in Chinese)
[29] GONG F Q, LI X B, ZHANG W. Rockburst prediction of underground engineering based on Bayes discriminant analysis method [J]. Rock and Soil Mechanics, 2010, 31(S1): 370-377. DOI: 10.1109/VETECS.2006.1683241. (in Chinese)
[30] ADOKO A C, GOKCEOGLU C, WU L, ZUO Q J. Knowledge-based and data-driven fuzzy modeling for rockburst prediction [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 86-95. DOI: 10.1016/j.ijrmms.2013.02.010.
[31] CAI M F. Prediction and prevention of rockburst in metal mines-A case study of Sanshandao gold mine [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(2): 204-211. DOI: 10.1016/j.jrmge.2015.11.002.
[32] AFRAEI S, SHAHRIAR K, MADANI S H. Statistical assessment of rockburst potential and contributions of considered predictor variables in the task [J]. Tunnelling and Underground Space Technology, 2018, 72: 250-271. DOI: 10.1016/j.tust.2017.10.009.
[33] FARADONBEH R S, TAHERI A. Long-term prediction of rockburst hazard in deep underground openings using three robust data mining techniques [J]. Engineering with Computers, 2019, 35(2): 659-675. DOI: 10.1007/s00366- 018-0624-4.
[34] ZHOU J, LI X B, MITRI H S. Evaluation method of rockburst: State-of-the-art literature review [J]. Tunnelling and Underground Space Technology, 2018, 81: 632-659. DOI: 10.1016/j.tust.2018.08.029.
[35] KIDYBINSKI A. Bursting liability indices of coal [J]. International Journal of Rock Mechanics and Mining Sciences, 1981, 18(6): 295-304. DOI: 10.1016/0148-9062 (81)91194-3.
[36] SINGH S P. The influence of rock properties on the occurrence and control of rockbursts [J]. Mining Science and Technology, 1987, 5: 11-18. DOI: 10.1016/S0167-9031(87) 90854-1.
[37] TAN Y A. Discussion on the energy impact index of rockburst [J]. Hydrogeology & Engineering Geology, 1992, 19(2): 10-12. http://www.cnki.com.cn/Article/CJFDTOTAL- SWDG199202005.htm. (in Chinese)
[38] WANG J A, PARK H D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks [J]. Tunnelling and Underground Space Technology, 2001, 16: 49-57. DOI: 10.1016/S0886-7798(01)00030-X.
[39] TAJDUS A, CIESLIK J, TAJDUS K. Rockburst hazard assessment in bedded rock mass: Laboratory tests of rock samples and numerical calculations [J]. Archives of Mining Sciences, 2014, 59(3): 591-608. DOI: 10.2478/amsc-2014- 0042.
[40] ZHANG J J, FU B J, LI Z K, SONG S W, SHANG Y J. Criterion and classification for strain mode rockbursts based on five-factor comprehensive method [C]// The 12th ISRM International Congress on Rock Mechanics, Harmonising Rock Engineering and the Environment. 2011: 1435-1440. DOI: 10.1201/b11646-272.
[41] GONG F Q, YAN J Y, LI X B. A new criterion of rockburst proneness based on the linear energy storage law and the residual elastic energy index [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 1993-2014. DOI: 10.13722/j.cnki.jrme.2018.0232. (in Chinese)
[42] GONG F Q, YAN J Y, LI X B, LUO S. A peak-strength strain energy storage index for bursting proneness of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 117: 76-89. DOI: 10.1016/j.ijrmms.2019.03. 020.
[43] ZHU F C, PAN C L, GUO R. A new rockburst proneness index–effective impact energy index [J]. Ground Pressure and Strata Control, 2002(3): 83-84. DOI: CNKI:SUN: KSYL.0.2002-03-037. (in Chinese)
[44] JIN X C, ZHOU Z H. Energy formula of rockburst [J]. Metal Mine, 2012(8): 40-43. DOI: CNKI:SUN:JSKS.0.2012-08- 012. (in Chinese)
[45] DENG L, WU J, LU Y. Study on rockburst energy index method based on the rock stress-strain curve [J]. Railway Standard Design, 2012(7): 108-111. DOI: 10.13238/j.issn. 1004-2954.2012.07.002. (in Chinese)
[46] TANG L Z, PAN C L, WANG W X. Surplus energy index for analyzing rockburst proneness [J]. Journal of Central South University of Technology, 2002, 33(2): 129-132. DOI: 10.3969/j.issn.1672-7207.2002.02.005. (in Chinese)
[47] AUBERTIN M, GILL D E, SIMON R. On the use of the brittleness index modified (BIM) to estimate the post-peak behavior of rocks [C]// 1st North American Rock Mechanics Symposium. Balkema: ARMA, 1994: 945-952. https:// www.onepetro.org/conference-paper/ARMA-1994-0909.
[48] KENETI A, SAINSBURY B A. Review of published rockburst events and their contributing factors [J]. Engineering Geology, 2018, 246(28): 361-373. DOI: 10.1016/j.enggeo.2018.10.005.
[49] LI S L, FENG X T, WANG Y J, YANG N G. Evaluation of rockburst proneness in a deep hard rock mine [J]. Journal of Northeastern University (Natural Science), 2001, 22(1): 60-63. DOI: 10.1111/j.1751-1097.1988.tb02873.x. (in Chinese)
[50] FENG T, XIE X B, WANG W X, PAN C L. Brittleness of rocks and brittleness indexes for describing rockburst proneness [J]. Mining and Metallurgical Engineering, 2000, 20(4): 18-19. DOI: 10.3969/j.issn.0253-6099.2000.04.006. (in Chinese)
[51] QIAO C S, TIAN Z Y. Possibility of rockburst occurrence in dongguashan copper deposit [J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(S): 917-921. http:// cpfd.cnki.com.cn/Article/CPFDTOTAL-ZYSY199810001017.htm. (in Chinese)
[52] SINGH S P. Classification of mine workings according to their rockburst proneness [J]. Mining Science and Technology, 1989(8): 253-262. DOI: 10.1016/S0167- 9031(89)90404-0.
[53] SIMON R. Analysis of fault-slip mechanisms in hard rock mining [D]. Montreal: McGill University, 1999. DOI: 10.1016/S0021-9290(06)83383-X.
[54] GONG F Q, WU C, LUO S, YAN J Y. Load–unload response ratio characteristics of rock materials and their application in prediction of rockburst proneness [J]. Bulletin of Engineering Geology and the Environment, 2019, 78: 5445-5466. DOI: 10.1007/s10064-019-01474-6.
[55] ZHANG C Q, LU J J, CHEN J, ZHOU H, YANG F J. Discussion on rock burst proneness indexes and their relation [J]. Rock and Soil Mechanics, 2017, 38(5): 1397-1404. DOI: 10.16285/j.rsm.2017.05.022. (in Chinese)
[56] LI P X, CHEN B R, ZHOU Y Y, XIAO Y X, FENG G L, ZHU G Q. Review of the research progress of rockburst prediction and early warning in hard rock underground engineering [J]. Journal of China Coal Society, 2019, 44(S2): 447-465. DOI: 10.13225/j.cnki.jccs.2019.0665. (in Chinese)
[57] TARASOV B G, POTVIN Y. Absolute, relative and intrinsic rock brittleness at compression [J]. Mining Technology, 2012, 121(4): 218-225. DOI: 10.1179/1743286312Y.0000000015.
[58] AKSOY C O. Performance prediction of impact hammers by block punch index for weak rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(8): 1383-1388. DOI: 10.1016/j.ijrmms.2009.02.008.
[59] MUNOZ H, TAHERI A, CHANDA E K. Rock drilling performance evaluation by an energy dissipation based rock brittleness index [J]. Rock Mechanics and Rock Engineering, 2016, 49(8): 3343-3355. DOI: 10.1007/s00603-016-0986-0.
[60] GONG F Q, YAN J Y, LUO S, LI XB. Investigation on the linear energy storage and dissipation laws of rock materials under uniaxial compression [J]. Rock Mechanics and Rock Engineering, 2019, 52: 4237-4255. DOI: 10.1007/s00603- 019-01842-4.
[61] GONG F Q, LUO S, YAN J Y. Energy storage and dissipation evolution process and characteristics of marble in three tension-type failure tests [J]. Rock Mechanics and Rock Engineering, 2018, 51(11): 3613-3624. DOI: 10.1007/s00603 -018-1564-4.
[62] LUO S, GONG F Q. Linear energy storage and dissipation laws during rock fracture under three-point flexural loading [J]. Engineering Fracture Mechanics, 2020, 234: 107102. DOI: 10.1016/j.engfracmech.2020.107102.
[63] LUO S, GONG F Q. Energy storage and dissipation laws of rocks under preset angle shear conditions [J]. Rock Mechanics and Rock Engineering, 2020, 53: 3303-3323. DOI: 10.1007/s00603-020-02105-3.
[64] YIN X C. The new approach of earthquake prediction [J]. Earthquake Research in China, 1987, 3(1): 1-7. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD198701000.htm. (in Chinese)
[65] YIN X C, CHEN X Z, SONG Z P. A new approach to earthquake prediction-the load/unload response ratio (LURR) theory [J]. Pure and Applied Geophysics, 1995, 145(3, 4): 701-715. DOI: 10.1007/BF00879596.
[66] YIN X C, YIN C. The precursor of instability for nonlinear systems and its application to earthquake prediction [J]. Science China Chemistry, 1991, 34(8): 977-986. http:// www.cnki.com.cn/Article/CJFDTotal-JBXG199108001.htm.
[67] DUAN M K, JIANG C B, XING H L, ZHANG D M, PENG K, ZHANG W Z. Study on damage of coal based on permeability and load-unload response ratio under tiered cyclic loading [J]. Arabian Journal of Geosciences, 2020, 13(6): 250. DOI: 10.1007/s12517-020-5249-4.
[68] GONG F Q, WU C. Identifying crack compaction and crack damage stress thresholds of rock using load–unload response ratio (LURR) theory [J]. Rock Mechanics and Rock Engineering, 2020, 53(2): 943-954. DOI: 10.1007/s00603- 019-01936-z.
[69] WU C, GONG F Q, LUO Y. A new quantitative method to identify the crack damage stress of rock using AE detection parameters [J]. Bulletin of Engineering Geology and the Environment, 2020. DOI: 10.1007/s10064-020-01932-6.
[70] CHEN Y, ZUO J P, LI Z H, DOU R. Experimental investigation on the crack propagation behaviors of sandstone under different loading and unloading conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 130: 104310. DOI: 10.1016/j.ijrmms.2020. 104310.
[71] WANG C L, HE B B, HOU X L, LI J Y, LIU L. Stress–energy mechanism for rock failure evolution based on damage mechanics in hard rock [J]. Rock mechanics and Rock Engineering, 2020, 53(3): 1013-1027. DOI: 10.1007/ s00603-019-01953-y.
[72] DUAN M K, JIANG C B, GAN Q, LI M H, PENG K, ZHANG W Z. Experimental investigation on the permeability, acoustic emission and energy dissipation of coal under tiered cyclic unloading [J]. Journal of Natural Gas Science and Engineering, 2020, 73: 103054. DOI: 10.1016/ j.jngse.2019.103054.
(Edited by HE Yun-bin)
中文导读
岩石材料的岩爆倾向性判据研究:综述与新观点
摘要:为了对岩石材料的岩爆倾向性判据的判别准确性进行综合比较,本文归纳了现有的20种岩爆倾向性判据,并利用14种岩石进行了一系列实验室测试,根据试验结果综合评估这20种岩爆倾向性判据的判别准确性。文中首先详细介绍了20种岩爆倾向性判据,包括其文献出处、定义、计算方法和具体的判据分级标准。随后,对14种岩石进行了一系列的实验室测试,包括单轴压缩试验、一次加卸载单轴压缩试验和巴西劈裂试验等,利用所得试验数据计算了20种判据针对每种岩石的岩爆倾向性判别结果。此外,为了统一评估上述判别结果的准确性,引入了一种基于室内实验室测试岩石试样破坏结果和现象的岩爆倾向性分级标准。将依据该分级标准得出的各岩石的实际岩爆倾向性与20种判据的判别结果进行对比,结果表明,基于剩余弹性能指数这一判据的判别结果与14种岩石的实际岩爆倾向性完全一致,其他判据的结果均存在误判的情况。剩余弹性能指数以线性储能规律为基础,而且以差值的形式进行定义,并考虑了岩石破坏全过程的能量转化。上述特点确保了其判别准则的科学性和准确性。根据以上分析可以得出,基于剩余弹性能指数的岩爆倾向性判据相对于其他判据更加科学、准确,在对岩石材料的岩爆倾向性进行评价时推荐优先使用该判据。
关键词:深部岩石;岩爆;岩爆倾向性;岩爆倾向性判据;岩石力学
Foundation item: Project(41877272) supported by the National Natural Science Foundation of China; Project(2020zzts715) supported by the Fundamental Research Funds for the Central Universities of Central South University, China; Project(2242020R10023) supported by the Fundamental Research Funds for the Central Universities of Southeast University, China
Received date: 2020-06-21; Accepted date: 2020-08-31
Corresponding author: GONG Feng-qiang, PhD, Professor; Tel: +86-18175973819; E-mail: fengqiangg@126.com; ORCID: https:// orcid.org/0000-0002 -2040-4294

