J. Cent. South Univ. (2018) 25: 2438-2450

DOI: https://doi.org/10.1007/s11771-018-3927-0

SLC-index: A scalable skip list-based index for cloud data processing

HE Jing(何婧)^{1, 2}, YAO Shao-wen(姚绍文)^{1, 2}, CAI Li(蔡莉)^{1, 2}, ZHOU Wei(周维)^{1, 2}

1. National Pilot School of Software, Yunnan University, Kunming 650091, China;

2. Key Laboratory in Software Engineering of Yunnan Province, Kunming 650091, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Due to the increasing number of cloud applications, the amount of data in the cloud shows signs of growing faster than ever before. The nature of cloud computing requires cloud data processing systems that can handle huge volumes of data and have high performance. However, most cloud storage systems currently adopt a hash-like approach to retrieving data that only supports simple keyword-based enquiries, but lacks various forms of information search. Therefore, a scalable and efficient indexing scheme is clearly required. In this paper, we present a skip list-based cloud index, called SLC-index, which is a novel, scalable skip list-based indexing for cloud data processing. The SLC-index offers a two-layered architecture for extending indexing scope and facilitating better throughput. Dynamic load-balancing for the SLC-index is achieved by online migration of index nodes between servers. Furthermore, it is a flexible system due to its dynamic addition and removal of servers. The SLC-index is efficient for both point and range queries. Experimental results show the efficiency of the SLC-index and its usefulness as an alternative approach for cloud-suitable data structures.

Key words: cloud computing; distributed index; cloud data processing; skip list

Cite this article as: HE Jing, YAO Shao-wen, CAI Li, ZHOU Wei. SLC-index: A scalable skip list-based index for cloud data processing [J]. Journal of Central South University, 2018, 25(10): 2438–2450. DOI: https://doi.org/10.1007/ s11771-018-3927-0.

1 Introduction

Emerging cloud computing [1] systems can provide users with cheap and powerful facilities for communication. Existing cloud computing systems include Amazon’s Elastic Compute Cloud (EC2) [2], IBM’s Blue Cloud [3], Microsoft’s Azure [4], etc. These adopt flexible resource management mechanisms and perform well. Users share a “black-box” known as the cloud that consists of a large number of interconnected virtual machines. They can tailor the computing resources for their own purposes from an infinite amount of resources that cloud systems can provide.

Being synonymous with the cloud computing movement, the amount of data generated by people shows signs of growing faster than ever before [5, 6]. Without efficient large-scale data processing, cloud computing systems cannot provide services for millions of users. Therefore, distributed data processing infrastructures play an essential part in cloud systems. Most cloud data storage systems, however, currently adopt a hash-like approach to retrieve data that only supports simple keyword- based enquiries, but lacks various forms of information search. For example, Hadoop operates on key-value pairs and serially reads data blocks. If users want to find videos within a given date range in a cloud video system, Hadoop will completely scan the dataset and find only a few relevant records for further consideration. Recent studies have shown that indexes can improve the performance of cloud storage systems dramatically. To support range queries, an auxiliary index is produced offline by running a MapReduce job. However, this offline approach is time-consuming and does not guarantee timeliness. Newly inserted keywords cannot be queried until the offline batch task completes the scanning and the index is updated. Based on the analysis above, it is clear that a gap exists and there is a need for a novel index structure that can dynamically handle different types of queries.

In this paper, we present a skip list-based cloud index (SLC-index) as an auxiliary indexing scheme for cloud data processing. This paper makes the following contributions:

1) Extending skip lists to provide a two- layered architecture for large-scale cloud data process indexing, which facilitates better throughput. By combing the local index and global index, the scanning of the data nodes that do not contain the query results can be mostly avoided.

2) Proposing scaling strategies with splitting and merging algorithms that could dynamically migrate index’s nodes for balancing loads. Querying and updating algorithms are also discussed. The SLC-index is efficient for both point and range queries.

3) Mathematical analysis of the SLC-index’s two-layered architecture. An expression is deduced to estimate the benefit of nodes published from the lower layer to the upper layer. An adaptive publishing algorithm is also developed to integrate the gap between the upper layer and the lower layer, based on which the SLC-index achieves better performance.

4) A simulator extended from Peersim is developed to evaluate the effectiveness of the SLC-index.

This paper is organized as follows: Section 2 introduces related work. Section 3 presents the overview of the SLC-index. Section 4 gives the analysis of the SLC-index’s adaptive publishing strategy. Section 5 presents the SLC-index’s process details. Section 6 shows experimental evaluations of the SLC-index. Section 7 summarizes the paper.

2 Related work

Some existing cloud storage systems include: Google’s Bigtable [7], GFS [8] and its open-source implementation Hadoop [9], Amazon’s Dynamo [10] and Facebook’s Cassandra [11]. As a de facto standard for cloud storage systems, Hadoop has been widely used in many business companies, including Yahoo, LinkedIn, and Twitter. Being large scale, Hadoop allows multiple petabytes of data storage across hundreds or thousands of physical storage servers or nodes. However, some inherent weaknesses of Hadoop affect its high-performance operations, such as range queries and dynamic selections.

Recent studies have shown that an index can improve the performance of a cloud storage system dramatically. In general, there are two approaches to implementing a cloud storage index, the embedded-index model and the bypass-index model. The embedded-index model refers to setting up an index directly within cloud storage systems. There have been several studies focusing on efficient index access in Hadoop [12–17]. DITTRICH et al [12] proposes a Trojan index to improve runtime performance. It injects technology at the right places through UDFs (User Defined Functions) only and affects Hadoop from inside. YANG et al [13] explores ways to build tree indexes. It also incorporates a new algorithm into the Map-Reduce- Merge framework. In general, the embedded-index model is a kind of tight coupling solution. It integrates the index itself into the Hadoop framework closely for achieving high-performance block selection. In order to decouple the index and the storage system, a generalized search tree for MapReduce systems is designed in Ref. [15]. However, there are also some weaknesses in these indexing approaches. For example, all of the above approaches require changing some bottom-level operations concerning the file store systems or job schedules, which makes them difficult to implement and not scalable. If there is a new Hadoop release version, such as YARN, a considerable amount of further work needs to be done. Another problem is that these approaches do not always maintain a full index in memory, but adopt a run-time index creation strategy. This leads to a high index creation cost, especially when users only aim to find a few relevant records for further consideration and quickly change their queries.

The bypass-index model is another kind of approach. It builds the index outside the cloud storage system and always maintains it in memory. The index can communicate with the cloud storage system through an application program interface (API). Recent studies, such as [18–25], attempt to propose a dynamic auxiliary cloud indexing. In Ref. [18], a global distributed B-tree index is built to organize large-scale cloud data. This method has high scalability and fault tolerance, while it takes up a lot of memory to cache index information in the client. HUANG et al [19] and ZHOU et al [20] present improved B+ tree indexes. A local B+ tree index is built for each compute node. Further, these computer nodes are organized as a structured overlay and a portion of the local B+ tree nodes are published to the overlay for efficient query processing. In Ref. [21], a multi-dimensional indexing, called RT-CAN (R-tree-based index in content addressable networks), is proposed. Local R-tree servers are indexes and the global index is organized as a logical CAN-based overlay network. Similar to RT-CAN, a VA-file and CAN-based index framework is presented in Ref. [22], which improved query performance by eliminating the false positive queries in RT-CAN. LU et al [23] adopt a compressed bitmap index to construct the cloud index, which can save a lot of storage costs than other index structures. In practice, a parallel positional inverted index is proposed to improve graph queries [24]. HE et al [25] utilize the randomized idea to construct a hierarchal Octree index for three dimensional data. Comparing with the embedded-index model, the bypass-index model may be not as fast due to its loose coupling characteristics. However, it is more flexible and easier to maintain such a dynamic index system.

The SLC-index is a kind of bypass-index model. But unlike other previous approaches, we have developed a novel skip list-based dynamic index. The SLC-index adopts a two-layered architecture (the upper layer and the lower layer). In the upper layer, a global server acts as a main controller to ensure the integrity and consistency of the whole index. In the lower layer, each local server maintains a subset of the global skip list. The SLC-index is flexible and can be employed with systems such as GFS and Hadoop, among cluster nodes.

3 Overview of SLC-index

3.1 Skip lists

A skip list [26] is a randomized, ordered list of keys with additional parallel links. Each key is first inserted into the base layer and then it randomly promotes itself to the upper layer with probability of 1/2. If successful, the key will leave a logical node copy in the previous layer and try to promote itself again in the upper layer until it fails or a MaxLayer is met. When a search operation is executed, the highest layer’s node will first be compared. If the search key is less than the compared node’s key, it will follow the top layer’s link to quickly skip over unnecessary nodes. Otherwise, it will move down to a lower layer and execute the compare operation again until it reaches the base layer, and then it will perform a linear search to finish the search operation. Figure 1 shows the processing to find node 17 in a skip list of 12 nodes. Compared to balanced binary search trees, a skip list is more efficient with its auxiliary lists.

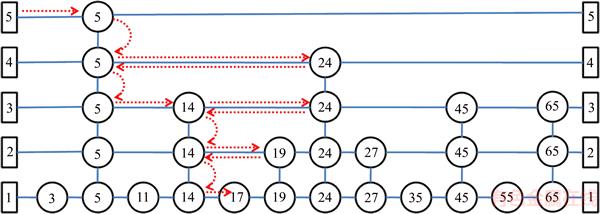
Figure 1 A regular skip list of 12 nodes to find 17

3.2 SLC-index architecture

The SLC-index is logically composed of a very large skip list (referred to as the global skip list), which is divided into several pieces and stored in local servers. Figure 2 depicts the overall architecture of the SLC-index. As shown above, the SLC-index adopts a two-layered architecture (the upper layer and the lower layer). In the upper layer, a global server acts as a main controller to ensure the integrity and consistency of the whole index. In the lower layer, each local server maintains a subset of the global skip list, while the index boundaries of each local server are not overlapped. The distributed data stored in the cloud storage system can be uniquely mapped to the nodes of the skip lists in the local servers.

To expedite queries, the global index in the upper layer is fully buffered in the memory of the global server. However, due to limited memory, the global server stores only meta-indexes that are published by the local servers. The meta-index is denoted as a triple in the form of (key, ip, blk), where key refers to the search key in the local skip list node, ip is the IP address of the computer node that really holds the local skip list node, and blk is the disk block number to locate the local skip list node. Moreover, local servers selectively publish some of their nodes to a global server based on the adaptive publishing strategy discussed in Section 4 below. To guarantee the integrality of the indexing, each local server publishes at least one node that must contain the first node as a stub to identify the boundary of its index.

The SLC-index stores a set of key-value pairs (k, v) that is spread over multiple servers and supports the standard dictionary operations (Insert, Update, Lookup, and Delete). The request process in the SLC-index is illustrated in the sequence of numbers denoted in black in Figure 2. Hence, for a typical request, query processing can be divided into two phases: locating a relative local index server in the upper layer and processing the request on the selected local server in the lower layer.

In contrast to the benefits of the SLC-index’s two-layered architecture, the global server may be overloaded if the lower layer contains too many local servers. To address this potential problem, the SLC-index uses a replica strategy to disperse the loading on the global server. Basically, there are two replicas of the global server; any update process will actively engage all replicas. In the global server, the replication involved in this strategy may increase costs in the global server for ensuring the consistency of the update process. However, this cost is well worth the expenditure due to the benefit that is evident in the scalability of the SLC-index.

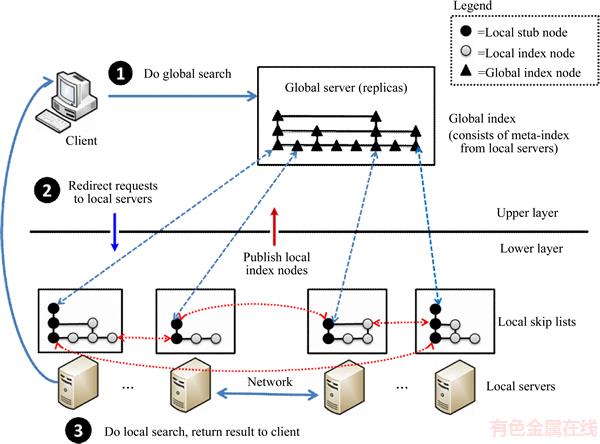
Figure 2 SLC-index system overview

4 Analysis of adaptive publishing

As discussed in above section, the SLC-index is designed to support large-scale data processing with dynamic changing volumes of data. The nature of the two-layer architecture requires that the index must be synchronized across both the lower layer and the upper layer. Such frequent data updating and information synchronization causes challenges for index maintenance in the SLC-index. Besides, only a proportion of the local nodes can be published into the upper layer due to limited memory. If the local server publishes larger numbers of the lower nodes’ meta-indexes, then the query process can be expedited in the local server. However, this increases the memory consumption in the global server. Hence, we need to estimate the benefits of such node publishing.

4.1 Cost model

In the SLC-index, the query process involves cooperation of both global servers and local servers. The total query cost (refers to cost_global) of the SLC-index must be a function that involves the query cost of the global server (refers to cost_global) and the query cost of the local servers (refers to cost_local). The relationship can be defined as follows:

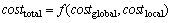              (1)

The SLC-index’s adaptive publishing strategy needs to calculate the variation of cost_total in order to make a decision between publishing or removing nodes from the local servers. First, let us differentiate between two types of variation: variation of cost_global (refers to P_global) and variation of cost_local (refers to P_local). In order to calculate this, it is necessary to have an expression that can indicate the query cost in a skip list that starts search from any median node. Based on analysis of skip lists in Ref. [26], given n nodes in the bottom level of a skip list, there are 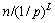nodes expected in the L level. Hence, the highest level L in a skip list with n nodes can be presented as follows:

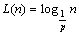                            (2)

Furthermore, PUGH [26] uses backward traversing to estimate a skip list’s search cost, the expression is as follows:

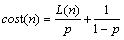                      (3)

By Eq. (3), 1/(1–p) may be taken as a constant, and the time cost of a skip list could be simplified as 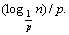Based on this, now we can estimate the variation of the query cost of the global server (P_global) and the variation of the query cost of the local server (P_local).

In the following, we define P_global. Suppose that the skip list in the global server represents n_m nodes, and each local server represents n_s nodes. After new nodes are published, there would be n_m nodes in the global skip list, and the number of nodes in the local server is also n_s. Putting the results together, we get the increment of the global server’s query cost P_global as follow:

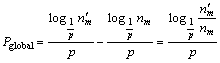         (4)

Let k denote the published layers in the local server. When new nodes are published in the global server, the SLC-index not only redirects to the local server but also starts search in the median node in level k. Similarly, the decrement of the local server’s query cost P_local can be deduced as follows:

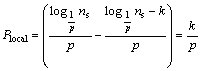            (5)

In the SLC-index, we expect that use of the published nodes at the local server will improve the overall performance. Assume P_total as the saved time cost when the local server’s nodes are published to the global server. P_total can be defined as follows:

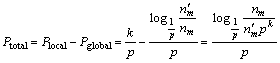 (6)

In order to achieve the best performance of searching in a skip list, the probability p must be set to 1/e [26]. In Eq. (6), let p=1/e, intuitively P_total increase by k, where k is the local server’s published level that must be between 1 and lnn_m (the highest level defined in Eq. (2)). To ensure the local server’s publishing benefit for the SLC-index, P_total is must greater than 0 in that the publishing can expedite queries. Hence, a further limitation of k is needed in Eq. (6) as follows:

 (7)

Based on Limitation (7), it ensures that nodes published in the SLC-index always result in a positive benefit. On the other hand, if it dynamically changes the probability p of a skip list, the best performance of the SLC-index can be estimated by the following expression:

            (8)

The optimized value of P_total with dynamically changing probability of p in a skip list can also be calculated by taking a derivation from Eq. (6):

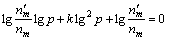                (9)

Based on Limitation (8) and Equation (9), we can find that when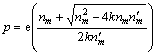and 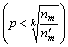, the SLC-index can achieve its best performance theoretically. In practice, the probability of p in a skip list is usually set to a constant, because dynamic changing of p may lead to the overhead of nodes adjusting. Hence, Limitation (8) and Equation (9) are not practical; in this paper, the SLC-index’s adaptive publishing strategy is actually based on Equation (6) and Limitation (7), and will be discussed below.

4.2 Adaptive publishing strategy

In the SLC-index, the publishing of the nodes from the local server to the global server will affect both the system’s query efficiency and the global server’s memory load. In Section 4.1, we have analyzed the query process in the SLC-index, and derived its benefit predictive expression (Eq. (6)). Figure 3 shows the variation tendency of the SLC-index’s query benefit, based on Eq. (6). We can see that the overall query efficiency increases with published levels in local servers. However, the growth rate of the overall query efficiency progressively decreases. On the other hand, based on the feature of the skip list that a node’s level increases progressively with probability p, the number of nodes using top-down publishing approach will increase exponentially. Therefore, Figure 4 shows the variation tendency of the global server’s memory loads with same conditions as in Figure 3. It shows that although the SLC-index’s publishing enhances the overall query efficiency, the memory loads of the global server also increase exponentially.

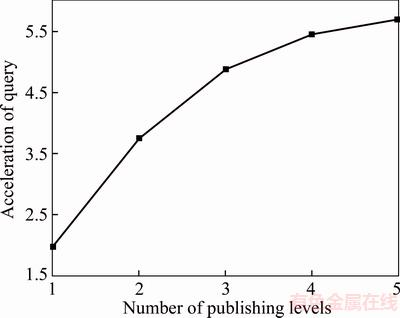
Figure 3 Variation of query benefit

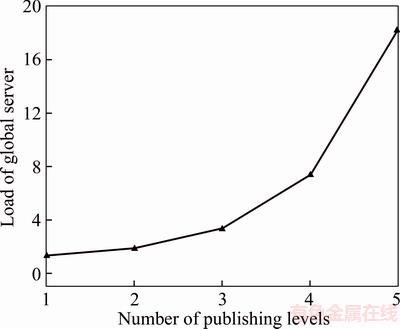
Figure 4 Variation of memory load

Therefore, the adaptive publishing strategy in the SLC-index must balance the query efficiency and memory cost. The SLC-index uses the incremental ratio as the identifier to decide whether publishing is beneficial. Specifically, before publishing the next level’s node, the local server will calculate the current incremental ratio of the query benefit and the global server’s memory load. Let Q_old be the query benefit before publishing the next level’s nodes, Q_new is the predictive query benefit after publishing the next level’s nodes. The incremental ratio of query efficiency is defined as A_query=(Q_new–Q_old)/Q_old. The incremental ratio of the global server’s memory load A_{mem_load}=(M_new–M_old)/ M_old is defined similar to A_query, in which M_new denotes the memory load after publishing the next level’s nodes and M_old is the original load. Based on the two incremental ratios, the judgment condition of adaptive publishing can be defined as:

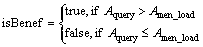
This expression is used in the LocalIndexPublish() algorithm that is discussed in the next section. It guarantees the positive and optimal performance of the SLC-index’s adaptive publishing strategy.

5 SLC-index process details

5.1 Local index publishing algorithm

As described above, the local server selectively and adaptively publishes the meta-index of other nodes to expedite the query process. Due to the feature that a skip list’s nodes in higher levels decline exponentially, the SLC-index’s local servers adopt a top-down approach to publish their meta-index. First, nodes at the highest level (must contain stub nodes) in the local server will be published into the global index, then each local server periodically calculates its publishing benefit prediction with the expression defined in Section 4. If the local server finds that publishing the next level’s nodes can achieve better performance, it will publish these nodes into the global index. This publishing procedure will repeat until it cannot achieve better performance.

Figure 5 gives an example of one local server changing its top-down publishing approach from level 3 to level 2. Obviously, a decrease of publishing level in a local server requires that more nodes insert into the global server. It is significant that the lower level nodes always contain all the replicas of the upper level nodes in a skip list. As the local server publishes nodes level by level, only new nodes (i.e., those that have not been included in the last level) are now inserted into the global server.

Algorithm 1: LocalIndexPublish(S_i)

Input: S_i — local server that needs to publish its local skip list nodes

1: S_i publishes the stub node of its local skip list

2: l := Level(S_i)

3: while true do

4:  S_i checks its published local skip list nodes

5:   if isBeneficial(l–1) then

6:   S_i additionally publishes the meta-index at level l–1

7:   else

8:     if benefit(l) < maintenanceCost(l) then

9:       S_i remove meta-index at level l which is published in the global meta-index of the global server

10: wait for a time

Algorithm 1 shows the details of how a local server publishes its nodes’ meta-index into the global server. Initially, only the index of a stub node is published (line 1). Then it will decide if it is beneficial to publish the meta-index at the next level. If the meta-index at the next level can improve search efficiency, the next level meta-index will be added to the global server (lines 4–6). In contrast, if the meta-index is published at the current level with low benefit and high maintenance cost, these indexes will be removed from the global node-indexes server (lines 8–9). The checking process described above will be invoked periodically.

5.2 Range querying and update strategy

A typical range query processing in the SLC-index can be divided into two phases: 1) locating the relevant local index server in the upper layer, and 2) processing the request to the selected local server in the lower layer. The sequences of the numbers are identified in black in Figure 2. If the client invokes a query request with any key, it will first send the query request to the global server which covers the entire index boundary (Step 1). Next, the global server uses these matched meta- indexes to redirect to some specific local servers (Step 2). Finally, the local servers invoke a local searching and return the query results to the client (Step 3). The procedure can be expressed as Algorithm 2.

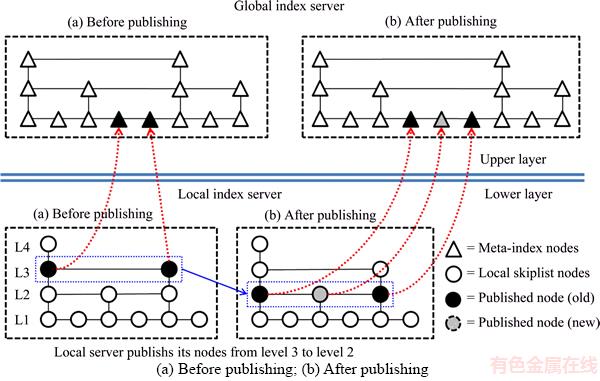
Figure 5 Details of local server’s node publishing:

Algorithm 2: Rangequery (Q=[l, u])

Input: Q – keys map to data that range from l to u

Output: S_result – set contains data that maps to keys in search range

1: S_i := lookup(l)

2: Ni := localSearch(Si, l)

//if it is a range query, performs a linear search to get others

3: while Niàforward exists and Ni.key < u do

4:   local search on Ni and put the indexed nodes overlapping with Q into set S_result

5:   Ni := Niàforward

6: forward S_result to query requestor

Algorithm 2 shows the overall query process in the SLC-index. Initially, the client uses lookup() to access the global server in order to get the result of local server redirection (line 1). After locating a local server with lookup(), a local search is performed in that local server (line 2). For a range query, a linear search is performed from the first node as the lower bound to the end of the node in the upper bound. Further search results will be added to the read set of transactions (lines 3–5), until the search process has been completed. Finally, the data are output directly to the client (line 6).

The performance of data insertions and deletions are a major consideration for index maintenance. In the SLC-index, the process of insertion is in two stages that require both location and addition. The locating phase is similar to a search process as discussed above. In the adding phase, new data are stored as a skip list node in a local server. The new node is given a random level l with probability. Then, the local server will publish the new node to the global server if its level l is greater than current published level. Otherwise, the process of this insertion is complete and returns the state of the code to the client.

Algorithm 3: Insert(key, value)

Input: key – entry to get index

Input: value – index that maps to distributed file system

1: S_i := lookup(key)

2: lv := randomLevel(S_i.StubLevel)

3: txn := BeginTx()

4: node := store(txn, lv, key, value)

5: if Si’s current published level <= lv then

6:   metaIndex := getMeta(node);

7:   publishToGlobal(S_i, metaIndex);

8: Commit(txn)

9: EndTx(txn)

Algorithm 3 is the process of insertion in the SLC-index. The operation of insertion is executed with key-value pairs, in which the key used to locate the server and decide where to store the value. Due to the characteristic that every server has its first node at the highest level, a helper function randomLevel() is used to ensure that a new node that is being inserted is always lower than the first node (also called the stub node). In the insert algorithm, the client first uses lookup() as the method to locate which server will accept the add request (line 1). Then, the client sends information to the server. When the server accepts an insert request, it first undertakes a local search with the insert key to locate where the new value will be inserted. If it finds the position, a new node will be created to store the key-value pairs (line 4). A transaction actually stores the new value to ensure consistency. Specifically, if the new node is created with a level higher than the publishing level of the server, the meta-index of new node must also be published to the global server (lines 5–7). The deletion process is similar to the insertion process.

5.3 Dynamic load balancing

Load balancing is significant in distributed systems. The migration process in the SLC-index allows the local servers to split part of their data to other servers or merge together some local servers’ data. The SLC-index uses a statistical approach to monitor the status of the system load. Here, each local server saves information as it accesses and periodically sends the statistics to the global server. Statistics from the local servers are calculated at the global server to identify the loading factor at each local server, and the global server will decide whether some migrations need to be invoked.

In the SLC-index, an overloaded local server can split its local skip list, then migrate part of the skip list to a new server or adjacent server. Here we give some definitions used in the splits as follows:

S is a non-empty skip list consisting of several non-empty sorted linked lists. All the items are stored in the list of level 1. Some of them also belong to the list of level 2 and so forth.

key(x) denotes the key of each item x in S.

level(x) denotes the height of each item x in S. We write level(S) to denote the maximum level among the levels of its items.

wall(x, l)=“the first node y to the right of x, i.e., key(x)l”. Given a skip list S and a node x≠NIL and some integer 0≤l≤level(x), we can get wall(x, l). For instance, in Figure 6, wall(5, 3) is the node having key 24, and wall(5, 2) is the node having key 14.

The SLC-index has a stub node as the first node and also identifies the highest level in each server. With the stub node, the splitting of the local skip list can be done locally without communicating with neighbor servers. The splitting algorithm can be described as follows:

Algorithm 4 Split (S₁, S₂, l)

Input: S₁ – server which needs to split its local skip list

Input: S₂ – server which accepts the back part of the split local skip list

Input: l – argument to decide split span

1:   //validate whether wall(S₁, l) exists, if not adjust l

2: for i := l downto 1 do

3:   if wall(S₁, i) exists then break;

4: l := i

5:   //record the links which need to be updated after splitting

6: local updateLink[1…S₁. StubLevel]

7: x := S₁.list→header

8: for i := S₁.StubLevel downto 1 do

9:   while x→forward[i] < wall(x, l) do

10:    x := x→forward[i]

11:  updateLink[i] := x

12:  x := x→forward[1]

13:  //migrate nodes and relink two servers

14: if x == wall(x, l) then

15:  for i := l+1 to S1. StubLevel do

16: x→forward[i] := updateLink[i]→forward[i]

17:   updateLink[i]→forward[i] := x

18: migrate(S₁, S₂, x);

Algorithm 4 splits the local skip list of server S₁ into two parts, then migrates the back part into server S₂. The argument l is configured to decide the splitting span. If the l is near the stub level, after splitting, more nodes will remain in S₁. In contrast, if the l is far from the stub level, more nodes will migrate to S₂. Figure 6 is an example of splitting with level(S)=5 and l=4, the skip list of server S₁ is divided into two parts from node 24 which is the first node in level 4, then the back part of the original skip list is migrated to server S₂.

The splitting algorithm initially checks if a node is at a level l that can be used as the splitting node. If not, it will adjust l until a splitting node can successfully be found (lines 2–4). The nodes that link to the splitting node will then be recorded in order to update the links after splitting (lines 6–12). When all the preparatory work is finished, the back part from the splitting node will be migrated to a new server, and the nodes in the front part that link to the migrated splitting node will update their pointers to link to new server (lines 14–18).

Figure 6 Migration with splitting:

The SLC-index also provides a merging algorithm as a process to support migration between existing servers or to deal with a server crash.

Algorithm 5: Merge(S₁, S₂)

Input: S₁ – server that needs to migrate its local skip list

Input: S₂ – server that accepts the migrated local skip list

Output: whether merge operation is successful

1: // get all data from S₁, buffered them in migrateList

2: migrateList := extractIndexData(S₁);

3: foreach index in migrateList do

4:   // use insert interface of skip list to save migrated index at a proper location in S₂

5:   insert(S₂, index);

6:   node := getNodeInfo(S₂, index);

7:   // if the new inserted node is in a published level, it must be updated to the global server

6:   if node.level >= S₂. publisedLevel then

7:       metaIndex := getMeta(node);

8:       updateToGlobal(S₂, metaIndex);

The merging algorithm migrates the local skip list of server S₁ into server S₂. First, all the index data in S₁ are extracted and buffered in a list (line 2). Then the list is sent to S₂. When S₂ receives the buffered list, it invokes the insert() interface of the skip list to store the index data in proper locations (lines 3–5). To guarantee indexing correctness, after the insertions of each migrated data, if the inserted node’s level is greater or equal to S₂’s published level, S₂ needs to publish its meta-index into the global server because the newly inserted node might have changed S₂’s indexing range (lines 6–8).

6 Experimental evaluations

To evaluate the performance of the SLC-index, we developed a simulator extended from Peersim [27]. The testing computer had an Intel Core i3-350M 2.26 GHz CPU, 2 GB RAM, and 320 GB disk space, and ran CentOS 6.0 (64-bit). It was used to simulate different sizes of cloud computing systems, ranging from 32 nodes to 256 nodes. In the simulator, each node manages 5000 resource files with sizes from 32 kB to 64 kB. For comparison, we also implemented a distributed B+ tree index, described in Ref. [18].

Figure 7 shows the performance of point query in the SLC-index. We can see that the ScalableBTree is faster than the SLC-index. By analyzing the experiment data, we discovered two reasons for this result. The first one is that the SLC-index adopts a two-layered architecture, for each query process. Consequently, additional routing cost may arise due to the routing from the global server to a local server. The second one is that although a skip list can provide query performance of O(logN) in theory, it does however under-perform a little compared with B-tree, in practice.

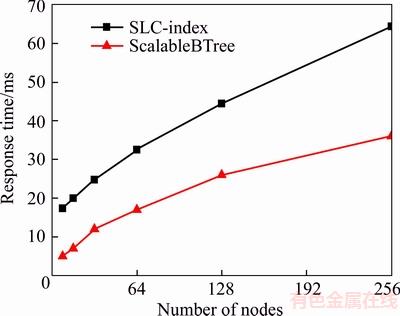
Figure 7 Performance of point query in SLC-index

Figure 8 illustrates a comparison of range-query performance between the SLC-index and the ScalableBTree. We can see that the SLC-index performs better than the ScalableBTree as systems are scaled up. The SLC-index benefits from the indexing boundary distribution that data are sequentially located in local servers. Hence, it can reduce routing cost as the indexing range covers more servers. Conversely, the randomly dispersed nodes in ScalableBTree also affect its range-query performance due to the need for more hops per range-query.

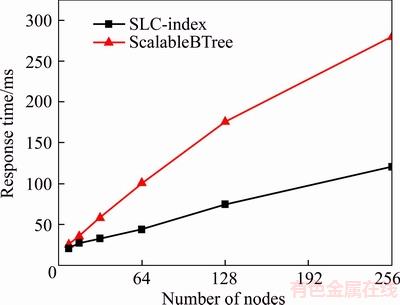
Figure 8 Comparison of range query performance between SLC-index and scalable BTree

System scalability is an essential indicator for distributed systems. We dynamically and randomly insert keys to test SLC-index performance in scale-up. From Figure 9, we can see that the SLC-index performs stably as the system is scaled up. This is because the SLC-index adopts a two-layered architecture, and most of the key insertions can be completed in a local server without any adverse impact on the global server. As discussed in Section 3.3, the SLC-index’s local server publishes only some higher level nodes to the global server. Hence, if a new key is inserted into the SLC-index, only the new inserted node whose level is higher than published level needs to be sent to the global server. The two-layered architecture is a prominent feature that reduces the cost of indexing boundary adjustment.

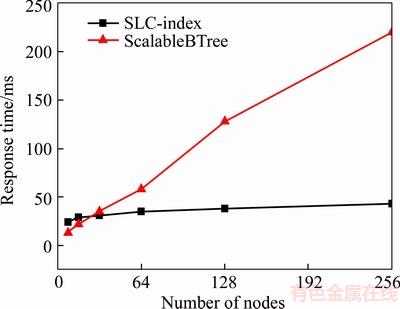
Figure 9 System scalability

The dynamic splitting and merging of local servers for load-balancing are also interesting features of the SLC-index. In Figure 10, we test the splitting and merging cost of the SLC-index with different scale-ups of the system. We can see that the adjusting time increases with system scale-up with effects of splitting or merging that can result in affecting the indexing boundary adjustment in the system. In the SLC-index, the global server maintains consistency across the indexing boundary as a whole. After splitting or merging, the level of moved nodes may change because a skip list is a probabilistic data structure. To guarantee correctness of the indexing boundary at the local server, the SLC-index must decide for each moved node whether or not it needs to be published to the global server.

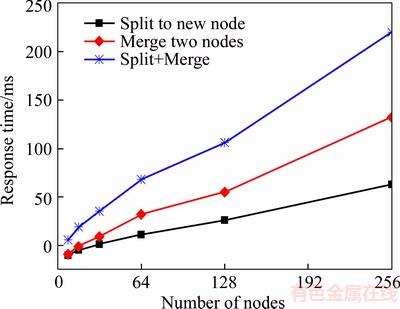
Figure 10 Load adjusting performance

7 Conclusions

We have presented the design and implementation of a skip list-based indexing scheme for cloud data processing. We analyze the profit and cost arising from the publishing of nodes at local servers. We illustrate that the SLC-index can achieve better performance with dynamic adjusting. Moreover, the SLC-index also provides system scaling strategies that support dynamic splitting and merging for online migrations. The SLC-index is a flexible, dynamic and easily maintainable index system. It is efficient for both point and range queries, and can help to filter relative block selection. The SLC-index can also be employed with cloud storage systems with cluster nodes.

References

[1] ARMBRUST M, FOX A, GRIFFITH R. A view of cloud computing [J]. Communications of the ACM, 2010, 53(4): 50–58. DOI: 10.1145/1721654.1721672.

[2] BEN-YEHUDA O A, BEN-YEHUDA M, SCHUSTER A, TSAFRIR D. Deconstructing Amazon EC2 spot instance pricing [J]. ACM Transactions on Economics and Computation, 2013, 1(3): 16. DOI: 10.1145/2509413. 2509416.

[3] WANG Li-zhe, von LASXEWSKI G, YOUNGE A. Cloud computing: A perspective study [J]. New Generation Computing, 2010, 28(2): 137–146. DOI: 10.1007/s00354- 008-0081-5.

[4] CALDER B, WANG J, OGUS A W. Windows Azure storage: A highly available cloud storage service with strong consistency [C]// ACM Symposium on Operating Systems Principles. Cascais: ACM, 2011: 143–157. DOI: 10.1145/2043556. 2043571.

[5] LIU An-feng, LIU Xiao, LI He. MDMA: A multi-data and multi-ACK verified selective forwarding attack detection scheme in WSNs [J]. IEICE Transactions on Information and Systems, 2016, E99-D(8): 2010–2018. [2016-08-01] https:// search.ieice.org/bin/summary.php?id=e99-d_8_2010.

[6] DING Y S, HAO K R. Multi-objective workflow scheduling in cloud system based on cooperative multi-swarm optimization algorithm [J]. Journal of Central South University, 2017, 24(5):1050-1062. DOI: 10.1007/s11771- 017-3508-7.

[7] CHANG F, DEAN J, GHEMAWAT S. Bigtable: A distributed storage system for structured data [J]. ACM Transactions on Computer Systems, 2008, 26(2): 1–26. DOI: 10.1145/1365815.1365816.

[8] GHEMAWAT S, GOBIOFF H, LEUNG S T. The Google file system [C]// ACM Symposium on Operating Systems Principles. Bolton landing: ACM, 2003, 37(5): 29–43. DOI: 10.1145/1165389. 945450.

[9] VAVILAPALLI V K, MURTHY A C, DOUGLAS C. Apache hadoop yarn: Yet another resource negotiator [C]// ACM Annual Symposium on Cloud Computing. Santa clara: ACM, 2013(5): 1–16. DOI: 10.1145/2523616.2523633.

[10] DECANDIA G, HASTORUN D, JAMPANI M. Dynamo: Amazon’s highly available key-value store [C]// ACM Symposium on Operating Systems Principles. Stevenson: ACM, 2007, 41(6): 205–220. DOI: 10.1145/1323293. 1294281.

[11] LAKSHMAN A, MALIK P. Cassandra: A decentralized structured storage system [J]. ACM SIGOPS Operating Systems Review, 2010, 44(2): 35–40. DOI: 10.1145/ 1773912.1773922.

[12] DITTRICH J, QUIANERUIZ J, JINDAL A. Hadoop++: Making a yellow elephant run like a cheetah (without it even noticing) [J]. Proceedings of The VLDB Endowment, 2010, 3(1, 2): 515–529. DOI: 10.14778/1920841.1920908.

[13] YANG H C, PARKER D S. Traverse: Simplified indexing on large map-reduce-merge clusters [C]// International Conference on Database Systems for Advanced Applications. Brisbane: Springer, 2009: 308–322. DOI: https://doi.org/ 10.1007/978-3-642-00887-0_27.

[14] LIN J, RYABOY D, WEIL K. Full-text indexing for optimizing selection operations in large-scale data analytics [C]// The Second International Workshop on Map Reduce and Its Applications. San Jose: ACM, 2011: 59–66. DOI: 10.1145/1996092. 1996105.

[15] LU Peng, CHEN Guang, OOI B C. ScalaGiST: Scalable generalized search trees for mapreduce systems [innovative systems paper] [J]. Proceedings of the VLDB Endowment, 2014, 7(14): 1797–1808. DOI: 10.14778/2733085.2733087.

[16] RICHTER S, QUIANERUIZ J, SCHUH S. Towards zero-overhead static and adaptive indexing in Hadoop [J]. Proceedings of the VLDB Endowment, 2014, 23(3): 469–494. DOI: https://doi.org/10.1007/s00778-013-0332-z.

[17] CHANG B R, TSAI H F, HSU H T. Secondary Index to big data NoSQL database–Incorporating solr to HBase approach [J]. Journal of Information Hiding and Multimedia Signal Processing, 2016, 7(1): 80–89. http://bit.kuas.edu.tw/~ jihmsp/2016/vol7/JIH-MSP-2016-01-009.pdf.

[18] AGUILERA M K, GOLAB W, SHAH M A. A practical scalable distributed B-Tree [J]. Proceedings of the VLDB Endowment, 2008, 1(1): 598–609. DOI: 10.14778/ 1453856.1453922.

[19] HUANG Bin, PENG Yu-xing. An efficient two-level bitmap index for cloud data management [C]// IEEE International Conference on Communication Software and Networks. Xi’an: IEEE, 2011: 509–513. DOI: 10.1109/ICCSN.2011. 6014776.

[20] ZHOU Wei, LU Jin, LUAN Zhong-zhi. SNB-index: A SkipNet and B+ tree based auxiliary Cloud index [J]. Cluster Computing, 2014, 17(2): 453–462. DOI 10.1007/s10586- 013-0246-y.

[21] WANG Jin-bao, WU Sai, GAO Hong. Indexing multi- dimensional data in a cloud system [C]// ACM SIGMOD International Conference on Management of Data. Indianapolis: ACM, 2010: 591–602. DOI: 10.1145/1807167. 1807232.

[22] CHENG Chun-lin, SUN Chun-ju, XU Xiao-long. A multi-dimensional Index structure based on Improved VA-file and CAN in the cloud [J]. International Journal of Automation and Computing, 2014, 11(1): 109–117. DOI: https://doi.org/10.1007/s11633-014-0772-y.

[23] LU Peng, WU Sai, SHOU Li-dan. An efficient and compact indexing scheme for large-scale data store [C]// IEEE International Conference on Data Engineering. Brisbane: IEEE, 2013: 326–337. DOI: 10.1109/ICDE.2013.6544836.

[24] DINARI H, NADERI H. A method for improving graph queries processing using positional inverted index (PII) idea in search engines and parallelization techniques [J]. Journal of Central South University, 2016, 23(1): 150–159 DOI: 10.1007/s11771-016-3058-4.

[25] HE Jing, WU Yue, DONG Yun-yun. Dynamic multidimensional index for large-scale cloud data [J]. Journal of Cloud Computing Advances Systems & Applications, 2016, 5(1): 1–12. DOI: 10.1186/s13677-016-0060-1.

[26] PUGH W. Skip lists: A probabilistic alternative to balanced trees [J]. Communications of The ACM, 1990, 33(6): 668–676. DOI: 10.1145/78973.78977.

[27] JESI G. P. Peersim HOWTO: Build a new protocol for the PeerSim 1.0 simulator [EB/OL]. [2011-08-04] http://peersim. sourceforge.net/.

(Edited by HE Yun-bin)

中文导读

SLC：基于跳表的可扩展云数据索引

摘要：随着基于云平台的应用的增加，云存储系统中的数据呈现出爆炸式增长的趋势，要求云数据处理系统具备高效的海量数据处理能力，然而，现有的云存储系统大多采用哈希方法检索数据，主要提供针对键值的查询，范围查询效率较低。因此，有必要为云存储系统构建辅助数据索引。提出了一种基于跳表的云数据索引结构，简称SLC索引。SLC索引采用双层体系结构，该索引结构契合云存储系统的分布式存储特性，易于在多个服务器节点上灵活扩展。局部索引节点基于查询耗费计算模型向全局索引节点发布索引信息，保证SLC索引结构的整体高效性。通过动态的索引节点分裂与合并机制，降低数据倾斜带来的性能影响，实现索引结构负载均衡。实验结果表明，SLC索引能够支持高效的单点查询和范围查询，是一种适用于云计算系统的具有高可扩展性的辅助数据索引。

关键词：云计算；分布式索引；云数据处理；跳表

Foundation item: Projects(61363021, 61540061, 61663047) supported by the National Natural Science Foundation of China; Project(2017SE206) supported by the Open Foundation of Key Laboratory in Software Engineering of Yunnan Province, China

Received date: 2017-07-11; Accepted date: 2018-01-09

Corresponding author: ZHOU Wei, PhD, Professor; E-mail: zwei@ynu.edu.cn; ORCID: 0000-0002-5881-9436