DOI： 10.11817/j.issn.1672-7207.2020.09.011

熔融沉积成形制件表面粗糙度预测模型

胡伟岳^{1, 2}，廖文和^{1, 2}，刘婷婷^{1, 2}，肖行志^{1, 2}，顾明飞^{1, 2}，李仕博^{1, 2}

(1. 南京理工大学 机械工程学院，江苏 南京，210094；

2. 数控成形技术与装备国家地方联合工程实验室，江苏 南京，210094)

摘要：针对熔融沉积成形的制件表面较为粗糙这一问题，通过试验方法分析关键工艺参数对表面粗糙度的影响，重点分析层厚和挤出宽对制件表面粗糙度的影响，研究成形过程中丝材截面的变化情况与侧表面轮廓的形成过程，建立表面粗糙度预测模型，并进行试验验证。研究结果表明：2组试验中，模型预测的表面粗糙度和实际测得的表面粗糙度的平均相对误差分别为6.25%和5.04%，证明了该模型的可行性。

关键词：熔融沉积成形；表面粗糙度；轮廓曲线；预测模型

中图分类号：TH162                    文献标志码：A

文章编号：1672-7207（2020）09-2460-11

Prediction model of surface roughness of fused deposition modeling parts

HU　Weiyue^{1, 2}, LIAO　Wenhe^{1, 2}, LIU　Tingting^{1, 2}, XIAO　Xingzhi^{1, 2}, GU　Mingfei^{1, 2}, LI　Shibo^{1, 2}

(1. College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;

2. National and Local Joint Engineering Laboratory of CNC Forming Technology and Equipment,Nanjing 210094, China)

Abstract: Aiming at the problem on surface roughness of fused deposition modeling parts, the influence of key process parameters on surface roughness was analyzed by experimental method, and the influence of layer thickness and extrusion width on surface roughness was analyzed emphatically. The change of wire section and the formation process of side surface profile were studied in the process of forming, and the prediction model of surface roughness was established and verified by experiments. The results show that the average relative errors of the predicted surface roughness and the measured surface roughness are 6.25% and 5.04%, respectively, which proves the feasibility of the model.

Key words: fused deposition modeling; surface roughness; contour curve; predictive model

熔融沉积成形技术(fused deposition modeling, FDM)可以实现复杂模型的个性化生产，而且FDM设备成本较低，使用的耗材较为清洁，打印制件的后处理相对简单。这些都使得FDM技术易于推广。目前，FDM技术已经广泛应用于产品开发、零件加工、生物医疗、教育等方面^[1-2]。2018年，全球3D打印机的销量超过200万台，其中FDM打印机约占60%。FDM是一种典型的逐层打印技术，成形件由加工成丝状的热塑性耗材在熔融挤出之后层层黏结堆积形成的。在堆积过程中，制件表面层与层结合处会有明显的不连续现象，即“台阶效应”，这使得制件表面粗糙，极大地影响了FDM制件的应用范围^[3]。因此，近年来国内外的研究者对如何提升FDM制件表面质量进行了较多研究，这些研究主要从化学处理、机械处理、热处理、工艺参数优化、数学模型预测等方面展开。SINGH等^[4]使用丙酮对ABS制件进行表面处理，首先将制件暴露在45~50 ℃的丙酮蒸汽中20 s，然后，将制件在0~4 ℃的环境中冷却15 min。试验结果表明，ABS制件的表面粗糙度由10 μm左右降低到0.1 μm以下。PANDEY等^[5]使用热切割技术对ABS制件进行后处理，通过设置合理的切割速度、切割方向和刀具前角，使得制件的表面粗糙度降低到0.3 μm。LIAN等^[6]研究了热处理方式对PMMA表面粗糙度的影响，发现最佳热处理工艺条件为于60 ℃恒温30 min，可以将制件的表面粗糙度从4.7 μm降低到1 μm以下。但后处理方法增加了额外的设备成本，而且需要大量的试验才能给出最优的后处理工艺参数。参数优化和数学模型预测可以在FDM成形过程中完成，无需额外的设备，相对容易实现。CAMPBELL等^[7]提出表面粗糙度取决于微观形貌，并通过试验数据建立了层厚和成形角相关的侧表面粗糙度数学预测模型。但该模型以“台阶效应”为基础，成形角在0°~45°和135°~170°范围时预测结果较准确，但不能预测成形角为90°时的粗糙度。AHN等^[8-10]也开发了根据工艺参数预测制件表面粗糙度的模型，但仅从数值上建立了工艺参数与表面粗糙度的关系。本文作者研究喷嘴温度、打印速度、层厚和挤出宽等工艺参数对制件表面粗糙度的影响程度，选择影响显著的工艺参数并分析其在制件表面轮廓形成过程中的作用，建立预测制件表面粗糙度的预测模型。

1  试验

1.1　试验机器和耗材

本试验使用Mass Portal公司提供的Pharaoh ED FDM打印机，该型打印机采用Delta结构，其直径×高为200 mm×200 mm。喷头温度可以加热到300 ℃，基板温度最高为120 ℃。该设备使用直径为0.2 mm和0.4 mm的喷头，在使用直径为0.4 mm的喷头打印PLA材料时，默认工艺参数为：层厚0.20 mm，挤出宽0.4 mm，挤出倍率100%，喷嘴温度210 ℃，基板温度60 ℃。

使用的耗材为Polymaker公司生产的PolyMax^TM PLA耗材，材料的直径为1.75 mm。

1.2　试验设计

在FDM成型过程中，喷嘴温度、基板温度、首层层厚、正常层层厚、挤出宽、成形角、物体壁厚、回抽距离、填充率、光栅角、喷头移动速度、环境温度等工艺参数均影响成型质量，其中喷嘴温度、打印速度、层厚以及挤出宽直接影响表面粗糙度^[11]。

本文考虑喷嘴温度、打印速度、层厚以及挤出宽对表面粗糙度的影响，设计3组试验，试验1为喷嘴温度单因素试验，参数设置如表1所示；试验2为成型速度单因素试验，参数设置如表2所示。

表1　喷嘴温度单因素试验

Table 1　Single factor test of nozzle temperature

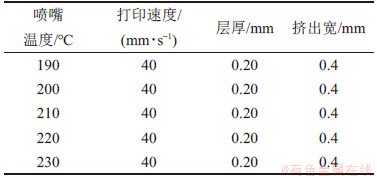
表2　打印速度单因素试验

Table 2　Single factor test of printing speed

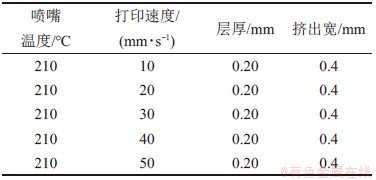
考虑层厚和挤出宽数值相互影响，且共同决定挤出丝材的截面形状，设计试验3，如表3所示。

表3　层厚和挤出宽为变量的工艺参数组合

Table 3　Combination of process parameters with variable layer thickness and extrusion width

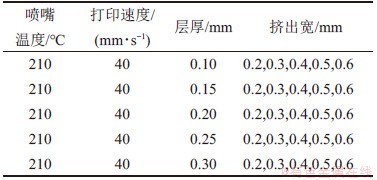
试样是长×宽×高为15 mm×15 mm×10 mm的长方体，其中Z方向高度为10 mm。设置基板温度为60 ℃，填充率为100%，成形角度为90°即竖直打印，内部填充的光栅角^[12]，即堆积路径方向与成型室X轴正方向的夹角为0°，挤出倍率为100%。

1.3　测量试样表面粗糙度的方法

使用VK-X200K激光扫描显微镜观察试样的表面形貌并测量试样侧表面粗糙度。将样件侧表面朝上摆放后，在平面上取6个位置，其中边缘4个，中央2个。如图1所示，对每个位置测量4组垂直于光栅方向的线条粗糙度，取平均值作为该位置的侧表面粗糙度；取6个位置的侧表面粗糙度的平均值作为试样的侧表面粗糙度，方法见文献[13]。

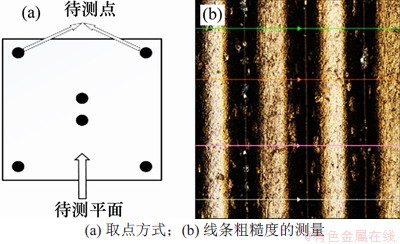
图1　粗糙度测量方式

Fig. 1　Roughness measurement method

1.4　截面拍摄

根据AHN等^[14]提出的处理方法，对需要处理的试样截面使用砂纸进行打磨，然后用金刚石抛光膏进行抛光。再使用歌能清洗设备有限公司提供的G-080S超声清洗机在40 kHz的超声波频率下对试样超声清洗10 min后，对截面进行喷金处理，最后使用FEI Quanta 250F场发射环境扫描电镜观察截面形貌。

2  测量结果

图2所示为试验1中不同喷嘴温度对应的试样表面粗糙度，所有试样的表面粗糙度分布在15~20 μm这一较小的范围内，测量结果如表4所示。

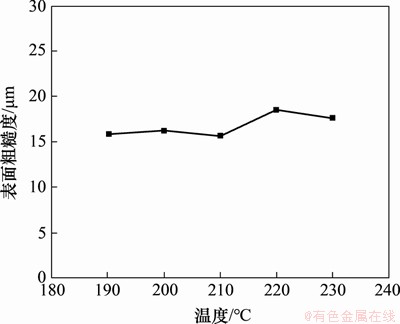
图2　不同喷嘴温度下试样的表面粗糙度

Fig. 2　Surface roughness of specimens at different nozzle temperatures

依据JJF 1105—2003“触针式表面粗糙度测量仪校准规范”，激光扫描显微镜引入的不确定度分量u₁取1.00%^[15]。测量重复性引入的不确定度分量u₂的计算方式为

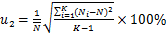(1)

其中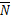：为表面粗糙度的均值；K为测量次数；N_i为第i次测量的粗糙度。

取包含因子k=2，得扩展不确定度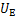为

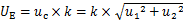(2)

表4　不同喷嘴温度对应的表面粗糙度测量结果

Table 4　Surface roughness measurement results at different nozzle temperatures

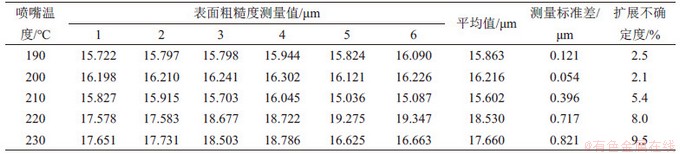
图3所示为试验2中不同打印速度对应的试样表面粗糙度，随着打印速度的变化，试样表面粗糙度的变化范围与图2中的相似，分布在15~20 μm这一区间内。

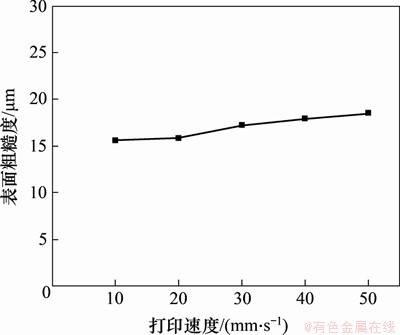
图3　不同打印速度下试样的表面粗糙度

Fig. 3　Surface roughness of samples at different printing speeds

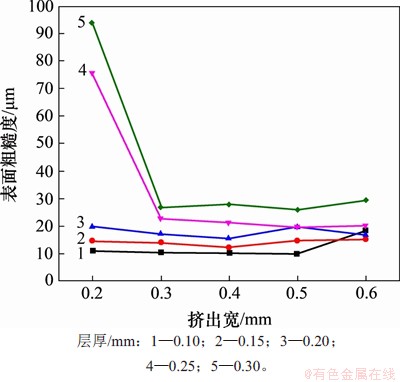
图4　不同层厚和挤出宽组合下试样的表面粗糙度

Fig. 4　Surface roughness of specimens with different layer thicknesses and extrusion widths

不同打印速度对应的表面粗糙度具体测量结果如表5所示。

表5　不同打印速度对应的表面粗糙度测量结果

Table 5　Surface roughness measurement results at different printing speeds

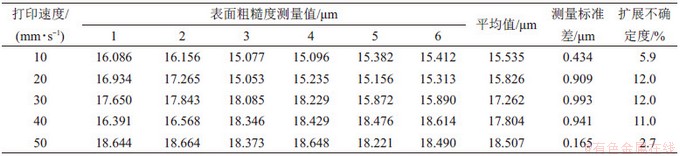
图4所示为试验3中不同的层厚和挤出宽组合对应的试样表面粗糙度。大多数层厚和挤出宽组合对应的试样表面粗糙度分布在10~30 μm。只有层厚0.25 mm、挤出宽0.2 mm以及层厚0.30 mm、挤出宽0.2 mm这2个参数组合对应的试样表面粗糙度远超过30 μm，分别达到75 μm和93 μm。总体上，当挤出宽相同时，层厚越大，试样的表面粗糙度越大，只有层厚0.10 mm、挤出宽0.6 mm这一组合对应的试样表面粗糙度超过层厚为0.15 mm和0.20 mm试样的表面粗糙度，不符合这一规律；当层厚相同时，若不考虑几个特殊点，则试样的表面粗糙度在一个相对较小的范围内波动，每一组层厚理论上对应1个最优的挤出宽使得表面粗糙度最小。

表6所示为不同层厚和挤出宽对应的表面粗糙度测量结果。对表6中的测量结果进行双因素无重复方差分析^[16]，结果如表7所示。层厚(t)对应的检验水平P为0.032，小于显著性水平0.05，表明统计学上层厚和表面粗糙度的相关性较为显著；而挤出宽(w)对应的P为0.067，大于0.05，表明统计学上挤出宽和侧表面粗糙度相关性较小。

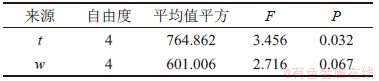
表6　不同层厚和挤出宽对应的表面粗糙度测量结果

Table 6　Surface roughness measurement results for different layer thickness and extrusion width

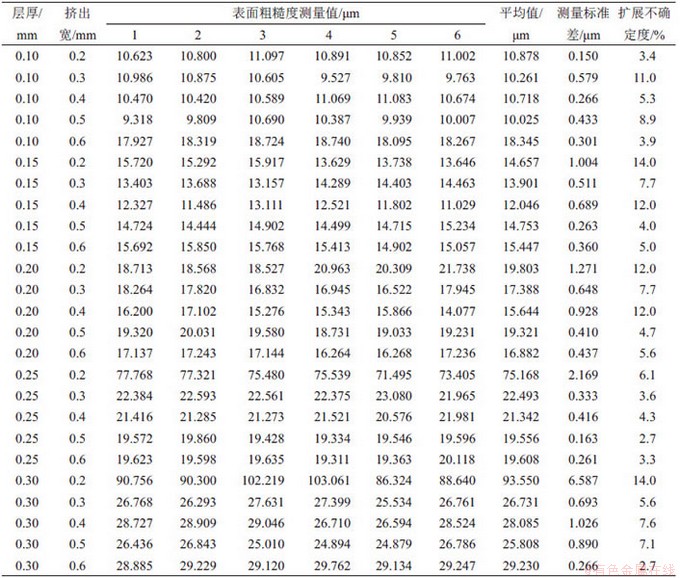
表7　双因素无重复方差分析结果

Table 7　Results of two-way analysis of variance

对3组试验得到的结果进行比较，发现喷嘴温度和打印速度对试样表面粗糙度的影响非常小，而层厚和挤出宽的组合对试样表面粗糙度的影响较大；再对试验3的测量结果进行方差分析，结果表明层厚对试样表面粗糙度的影响相较挤出宽的影响更加显著。

3  分析与建模

3.1　轮廓曲线形状分析

试样表面形貌直接影响表面粗糙度，为具体分析层厚和挤出宽对试样表面粗糙度的影响，对试验3中所有试样的表面形貌进行比较分析，总体上，各试样呈现一致的表面形貌。选取所有试样待测平面的中央位置进行观察，代表性的表面形貌图像如图5所示(照片放大倍率为200倍)。从图5可知：各工艺参数下，试样的侧表面形貌均呈现为垂直于光栅方向具有周期性的连续波浪形态；随着层厚从0.10 mm增加至0.30 mm，周期从0.10 mm 增加到0.30 mm，周期内峰值和谷值的高度差从71.245 μm增加到129.405 μm。这可以解释层厚增加时试样的表面粗糙度显著增大的原因。

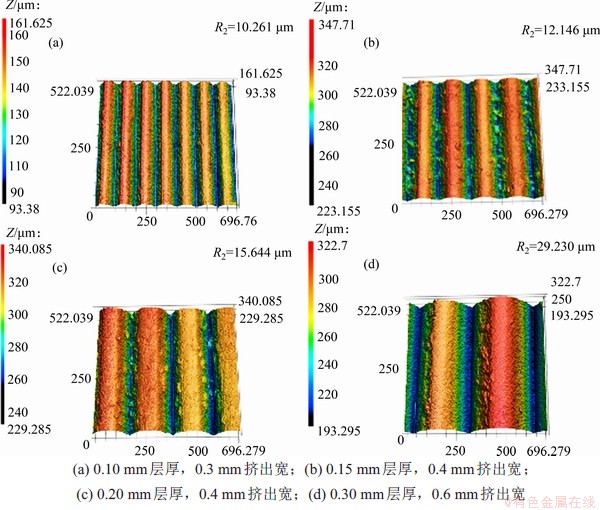
图5　具有代表性的侧表面轮廓形貌图像

Fig. 5　Representative side surface profile images

试验3中层厚0.25 mm、挤出宽0.2 mm，层厚0.30 mm、挤出宽0.2 mm以及层厚0.10 mm、挤出宽0.6 mm这3组试样表面粗糙度过大，存在异常。对这3组试样的表面形貌进行分析，结果如图6所示。从图6发现试样表面形貌呈现出明显的凸起和塌陷，在相同的拍摄面积下没有周期性。这可能是因为层厚0.25 mm、挤出宽0.2 mm与层厚0.30 mm、挤出宽0.2 mm这2个试样，挤出宽与层厚的比值小于1，比其他试样的小；而层厚0.10 mm、挤出宽0.6 mm试样，挤出宽与层厚的比值为6，比其他试样的大。当挤出宽与层厚的比值小于1或者挤出宽与层厚的比值为6时，堆积过程中丝材截面形状的变化不稳定，甚至发生塌陷，导致表面形貌异常。因此，在建立表面粗糙度预测模型时，将这3个工艺参数组合对应的奇点剔除。

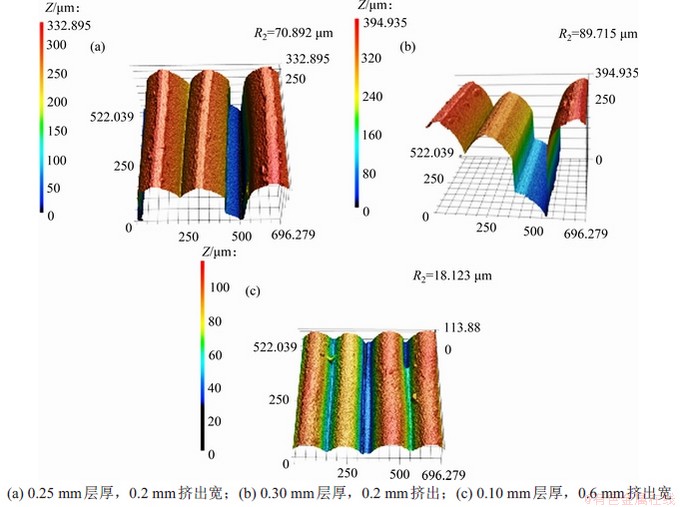
图6　特殊情况下的侧表面轮廓形貌图像

Fig. 6　Side surface profile image in a special situation

对剔除异常试样后的其他试样进行分析，以层厚0.20 mm、挤出宽0.4 mm打印的试样为例(图5(c))，当测量垂直于光栅方向的线条粗糙度时，截取出的轮廓曲线如图7所示。

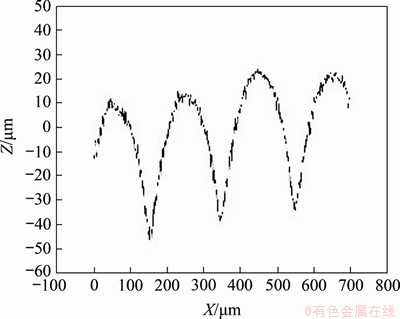
图7　某一点轮廓曲线图像

Fig. 7　A contour curve image of a certain point

将其理解成1个周期函数曲线，周期约等于200 μm，接近试样的层厚。取连续曲线中所有点的坐标，采用二次曲线模型拟合其中一段周期内的函数曲线，结果如式(3)所示，对应的拟合相关系数R²为0.977 4，拟合性较好。

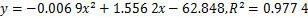  (3)

对待测平面其余点做相同处理，得到每一段函数对应的二次曲线。再对得到的所有二次曲线进行水平方向平移，使其关于X=0对称，得到处理后的二次函数。

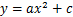(4)

将处理得到的所有的a和c去掉最大与最小值后，取平均值，作为该工艺参数组合下得到的轮廓曲线对应的二次函数的参数值。对其他工艺参数组合下测量得到的轮廓曲线用相同方法进行处理，得到各工艺参数组合下，侧表面上1个周期内的轮廓曲线。再根据表面粗糙度计算公式(5)，求出二次函数曲线的中心线并计算出这些轮廓曲线对应的表面粗糙度R_a，所得结果如表8所示。

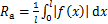(5)

表8　表面轮廓曲线拟合结果

Table 8　Surface contour curve fitting results

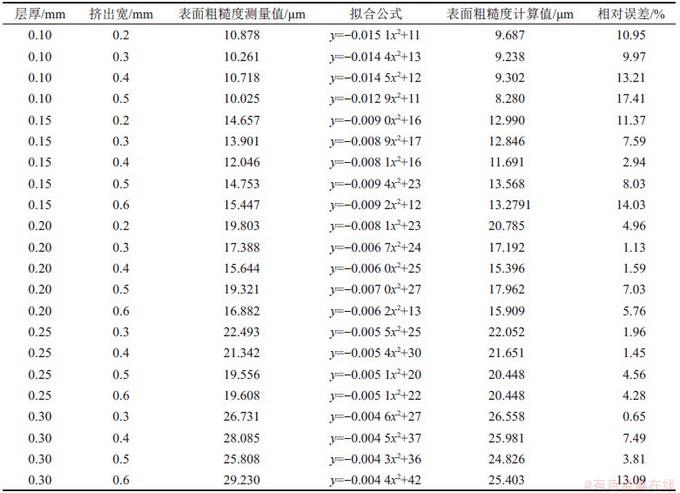
从表8可以看出：整体上拟合得到的二次曲线计算出的侧表面粗糙度与测量值相比偏小，且平均相对误差为6.97%。

3.2　表面粗糙度形成过程分析

为分析表面形貌形成原理，设计长和宽均为20 mm、高为15 mm的薄壁件，壁厚由两圈轮廓构成，不封底，顶层铺设一层单丝，如图8所示。设置层厚为0.20 mm、挤出宽为0.4 mm并进行打印。试样去除底板后，将侧面插入镶嵌膏中，等待镶嵌膏冷却固化后，对镶嵌膏的底面进行打磨和抛光，使顶层单丝和侧壁轮廓的剖面露出镶嵌膏，再经过超声洗和喷金后，用扫描电子显微镜拍摄截面。拍摄结果如图9所示。图9中，A代表理论上丝材的截面形状，B代表丝材结合位置的孔隙。在不受约束的情况下，单丝截面形状接近于椭圆形(图9(a))；当层层叠加时，由于丝材在水平和垂直方向的相互作用，丝材截面的形状变为近似矩形，层与层结合位置出现孔隙，丝材外侧连结成试样的外轮廓，并呈现出周期性(图9(b))。

图8　获取单丝截面和双层轮廓截面的试验模型

Fig. 8　Experimental model for obtaining a monofilament section and a double profile section

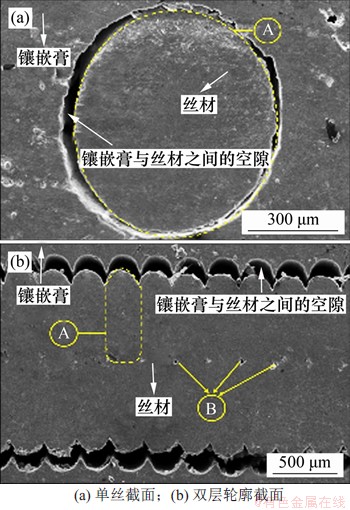
图9　单道丝材和轮廓的SEM图像

Fig. 9　SEM images of a single wire and profile

取试验3中层厚0.15 mm、挤出宽0.3 mm和层厚0.20 mm、挤出宽0.4 mm的试样，沿垂直于填充丝材轴向的方向，从各边中点铣削出截面后，对截面进行打磨、抛光、超声洗、喷金等处理，用扫描电子显微镜观测，结果如图10所示。图10中，B代表丝材结合位置的孔隙。

图10　完整截面的SEM图像

Fig. 10　SEM images of a complete cross-section

从图10可见：内部丝材熔合状况较好，看不出丝材原有的形状，截面上存在孔隙，分布在丝材结合的位置；丝材在经过成形过程后，截面形状趋向于宽为挤出宽w、高为层厚t的矩形。

经分析认为，打印完成前和打印完成后，材料处在相同的环境温度下，若不考虑丝材在挤出机构中的损失，则挤入丝材的体积等于打印出的丝材体积，如下式所示：

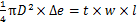(6)

其中：D为丝材直径；Δe为打印1条线段时挤出齿轮转动的距离；t为层厚；w为挤出宽；l为该线段的长度^[17]。

不论最终形成的截面形状如何变化，理论上截面的面积不变，等于理想矩形的面积。而对于直接构成侧表面轮廓的每一层最外圈的丝材，水平方向上一侧受到相互作用，一侧不受相互作用，竖直方向仍然与相邻层发生挤压，最终形成的形状可以形成图11所示的形状。靠近内部填充的一侧为矩形，靠近外部的一侧接近于平椭圆，且理论上截面积不变，等于理想矩形的面积^[18]。而每一层的外侧曲线在打印过程的层层堆叠中连结成试样侧表面的轮廓曲线。

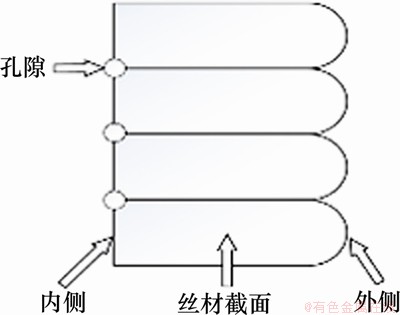
图11　丝材截面的形状和外轮廓的形成

Fig. 11　A cross-sectional view of wire and formation of an outer profile

3.3　建立数学预测模型

考虑到喷嘴温度和打印速度对试样表面粗糙度的影响相对较小，不会直接改变轮廓形貌，因此，本文建立数学预测模型时只考虑层厚和挤出宽。

根据截面积不变，理想矩形截面的竖直边即为实际截面形状外侧的二次曲线的中心线，将x轴平移至理想矩形的竖直边，y轴平移至中心(图12)。令此时二次曲线的方程为y=ax²+c，根据中心线两侧二次曲线与x轴围成的面积相等，在这一坐标系下，可以推出：

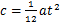(7)

其中：t为层厚，也是侧表面轮廓曲线的周期。

根据表8中各层厚和挤出宽组合对应的拟合公式，对层厚t、挤出宽w和a的关系进行二元非线性回归^[19]。回归分析结果如表9所示。

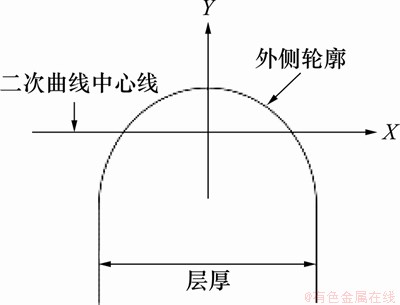
图12　新坐标系下的外侧轮廓曲线

Fig. 12　Outside profile curve in a new coordinate system

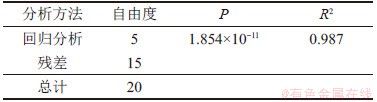
表9　回归分析的方差分析结果

Table 9　ANOVA results for regression analysis

回归方程如下：

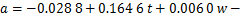
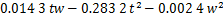(8)

R²为0.987，接近1；P为1.854×10^-11，小于显著性水平0.05。因此，可以认为这一回归方程拟合程度较好。对1个周期即1个层厚内的二次函数y=ax²+c取中心线，然后根据表面粗糙度计算公式(5)，求出二次函数曲线对应的表面粗糙度，结果如式(9)和(10)所示。

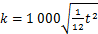(9)

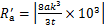(10)

其中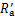：为初步计算出的表面粗糙度，μm。拟合的二次函数曲线求出的侧表面粗糙度与测量值的平均相对误差p=6.97%，所以，最终得到的预测结果为

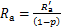(11)

3.4　验证

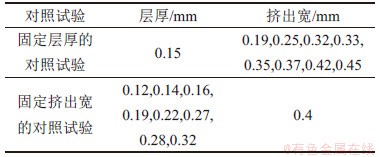
前面通过理论推导和对试验数据的拟合，得到根据层厚和挤出宽预测制件表面粗糙度的经验公式。这里将通过单因素对照试验验证这一模型的可靠性。试验选择的工艺参数组合如表10所示，其中层厚0.15 mm、挤出宽0.4 mm均为常用工艺参数。喷嘴温度为210 ℃，打印速度为40 mm/s。

表10　验证试验选取的工艺参数组合

Table 10　Process parameter combinations selected for validation tests

各工艺参数组合打印出的试样的侧表面粗糙度的测量值和代入预测模型中得到各组表面粗糙度的理论预测值如表11所示。

表11　验证试验测量结果

Table 11　Measurement results of verification tests

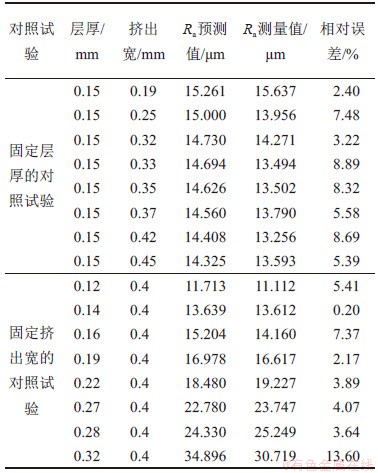
从表11可知：预测模型预测出的侧表面粗糙度与实际测量结果较接近，2组试验的粗糙度平均相对误差分别为6.25%和5.04%，都在10%以内。因此，这一预测模型能够有效地预测成形角为90°，不同层厚和挤出宽组合下对应的制件表面粗糙度。

4  结论

1) 喷嘴温度、打印速度对表面粗糙度的影响相对较小，层厚和挤出宽组合对制件表面粗糙度的影响相对较大。当挤出宽和层厚的比值大于1且小于6时，层厚越大，制件的表面粗糙度显著增大；挤出宽对制件表面粗糙度的影响相对较小。但当挤出宽和层厚的比值小于1或者挤出宽和层厚的比值为6时，制件的表面形貌会出现塌陷等异常现象，导致表面粗糙度过高。

2) 基于对试样表面轮廓形成过程的分析，建立了根据工艺参数预测制件表面粗糙度的预测模型。在2组验证试验中，这一模型的粗糙度预测值与实际测量值的平均相对误差都在10%以内。该模型可以有效预测90°成形角下制件的侧表面粗糙度，并为进一步研究不同成形角下，制件的表面形貌和表面粗糙度与工艺参数的关系提供参考。

参考文献：

[1] KANG Jianfeng, WANG Ling, YANG Chuncheng, et al. Custom design and biomechanical analysis of 3D-printed PEEK rib prostheses[J]. Biomechanics and Modeling in Mechanobiology, 2018, 17(4): 1083-1092.

[2] KUMAR R, SINGH R, AHUJA I P S. Investigations of mechanical, thermal and morphological properties of FDM fabricated parts for friction welding applications[J]. Measurement, 2018, 120: 11-20.

[3] 肖建华, 高延峰, 陈思维, 等. 基于塑料微挤出成型的熔融沉积成型技术表面粗糙度研究进展[J]. 高分子材料科学与工程, 2017, 33(4): 160-167.

XIAO Jianhua, GAO Yanfeng, CHEN Siwei, et al. Research progress on surface roughness of fused deposition modeling technology based on plastic micro-extrusion molding[J]. Polymer Materials Science and Engineering, 2017, 33(4): 160-167.

[4] SINGH R, SINGH S, SINGH I P, et al. Investigation for surface finish improvement of FDM parts by vapor smoothing process[J]. Composites Part B: Engineering, 2017, 111: 228-234.

[5] PANDEY P M, VENKATA REDDY N, DHANDE S G. Improvement of surface finish by staircase machining in fused deposition modeling[J]. Journal of Materials Processing Technology, 2003, 132(1/2/3): 323-331.

[6] LIAN K, LING Z G. Post-exposure heat treatment to reduce surface roughness of PMMA surfaces formed by radiation lithography: US, 6387578[P]. 2002-05-14.

[7] CAMPBELL R I, MARTORELLI M, LEE H S. Surface roughness visualisation for rapid prototyping models[J]. Computer-Aided Design, 2002, 34(10): 717-725.

[8] AHN D K, KWON S M, LEE S H. Expression for surface roughness distribution of FDM processed parts[C]// 2008 International Conference on Smart Manufacturing Application. Goyang-si, South Korea: IEEE, 2008: 490-493.

[9] PANDEY P M, THRIMURTHULU K, REDDY N V. Optimal part deposition orientation in FDM by using a multicriteria genetic algorithm[J]. International Journal of Production Research, 2004, 42(19): 4069-4089.

[10] BYUN H S, LEE K H. Determination of optimal build direction in rapid prototyping with variable slicing[J]. The International Journal of Advanced Manufacturing Technology, 2006, 28(3/4): 307-313.

[11] WANG Peng, ZOU Bin, DING Shouling. Modeling of surface roughness based on heat transfer considering diffusion among deposition filaments for FDM 3D printing heat-resistant resin[J]. Applied Thermal Engineering, 2019, 161: 114064.

[12] 赵庆红, 郭俊卿, 陈拂晓, 等. FDM工艺缝隙模型及消除方法研究[J]. 大连理工大学学报, 2018, 58(1): 38-42.

ZHAO Qinghong, GUO Junqing, CHEN Fuxiao, et al. Study on FDM process gap model and elimination method[J]. Journal of Dalian University of Technology, 2018, 58(1): 38-42.

[13] WANG Peng, ZOU Bin, XIAO Hongchuan, et al. Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK[J]. Journal of Materials Processing Technology, 2019, 271: 62-74.

[14] AHN D K, LEE S H. Improving the surface roughness of SL parts using a coating and grinding process[J]. International journal of precision engineering and manufacturing, 2007, 8(3): 14-19.

[15] 张欣, 田勇, 刘佳丽, 等. 测量表面粗糙度和测量结果不确定度的研究[J]. 天津科技, 2012, 39(2): 76-77.

ZHANG Xin, TIAN Yong, LIU Jiali, et al. Study on the measurement of surface roughness and uncertainty of measurement results [J]. Tianjin Science and Technology, 2012, 39(2): 76-77.

[16] ANANDA M M A, WEERAHANDI S. Two-way ANOVA with unequal cell frequencies and unequal variances[J]. Statistica Sinica, 1997: 631-646.

[17] GENG Peng, ZHAO Ji, WU Wenzheng, et al. Effects of extrusion speed and printing speed on the 3D printing stability of extruded PEEK filament[J]. Journal of Manufacturing Processes, 2019, 37: 266-273.

[18] 王天明, 金烨, 习俊通. FDM工艺过程中丝材的粘结机理与热学分析[J]. 上海交通大学学报, 2006, 40(7): 1230-1233, 1238.

WANG Tianming, JIN Ye, XI Juntong. The adhesive mechanism and thermal analysis of fibers in the FDM process[J]. Journal of Shanghai Jiao Tong University, 2006, 40(7): 1230-1233, 1238.

[19] 孟祥德, 张俊红, 李立顺, 等. 基于回归分析的车用柴油机声品质预测技术[J]. 内燃机学报, 2011, 29(6): 534-537.

MENG Xiangde, ZHANG Junhong, LI Lishun, et al. Acoustic quality prediction of automotive diesel engines based on regression analysis[J]. Journal of Internal Combustion Engine, 2011, 29(6): 534-537.

(编辑  杨幼平)

收稿日期： 2019 -12 -04; 修回日期： 202 0-03 -17

基金项目(Foundation item)：国家重点研发计划项目(2017YFB1103000)；江苏省重点研发计划项目(BE2015165) (Project(2017YFB1103000) supported by the National Key R&D Program of China; Project(BE2015165) supported by the Provincial Key R&D Program of Jiangsu Province)

通信作者：廖文和，博士，教授，从事增材制造、数字化设计与制造研究；E-mail:cnwho@njust.edu.cn