多负载IPT系统效率分析与控制
孙跃,吕潇,唐春森,王智慧,李玉鹏
(重庆大学 自动化学院,重庆,400030)
摘要:针对感应电能传输(inductive power transfer, IPT)系统多负载条件下能量传输效率问题研究频率与效率的关系,并从系统能量流动的角度解释效率特性。为了验证最大传输效率结论的正确性,采用双工作模式切换的电流调节方法和离散准滑模控制策略来维持原边谐振电流(激磁电流)的恒定。基于系统能量平衡函数关系,建立关于激磁电流峰值包络的系统离散变结构模型,构建具有重置积分环节的切换函数来改善系统的稳态响应。实验结果表明,当工作频率偏离副边固有谐振频率时,系统效率最大,合理的积分增益可以使系统具有较好的控制性能,对于负载大范围变化具有较强的鲁棒性,如当负载完全拿开时,控制器经过时长约为5 ms的调节,激磁电流最终稳定在参考值,表现出较好的抗扰动性,且系统效率均保持90%以上。
关键词:感应电能传输系统;多负载;效率;能量函数;离散准滑模控制
中图分类号:TM133 文献标志码:A 文章编号:1672-7207(2013)07-2793-08
Control and efficiency analysis of IPT system with multiple loads
SUN Yue, L Xiao, TANG Chunsen, WANG Zhihui, LI Yupeng
Xiao, TANG Chunsen, WANG Zhihui, LI Yupeng
(College of Automation, Chongqing University, Chongqing 400030, China)
Abstract: Focusing on the efficiency problem of inductive power transfer (IPT) system with multiple loads, the methodology of the power-flow analysis was carried out to analyze the relationship between efficiency and frequency. In order to validate the conclusion and keep the stability and high efficiency of power transmission, the primary resonant current (exciting current) was regulated by switching between energy injection mode and free resonance mode, and a discrete-time quasi sliding mode control strategy was proposed. The variable structure model about the envelope of exciting current was constructed with energy equilibrium relations. Furthermore, a switching function was established with reset integral units to improve the steady state response. The results show that in the condition of multiple loads, the maximum efficiency can be achieved when operate frequency shifts away from the secondary inherent resonant frequency. The appropriate integrator gain can give the system good robustness when load changes in large scale. As the pick-ups are fetched away from the system completely, the exciting current returns to the reference value within 5 ms. Besides, the efficiency keeps a high level being above 90%.
Key words: inductive power transfer (IPT) system; multiple loads; efficiency; energy function; discrete-time quasi sliding mode control
感应电能传输(inductive power transfer,IPT)技术作为一种新型供电技术,借助于高频磁场构建供电侧与负载侧之间的能量通道,实现电能的非接触传输,克服了传统有线传输方式在恶劣环境下的弊端。故受到国内外专家的广泛关注和重视[1-8]。当原副边谐振频率一致时,IPT系统效率最大[2-3],但随着人们应用需求的增加,一对多的工作模式的应用越来越广泛,即1个供电侧对应多个负载设备,此时则有多个拾取回路。与传统一对一传输模式不同,一对多模式存在多个原副边能量通道。另外,该模式下负载变化及投切的随机性增加,导致系统原边形成动态阻抗变化,从而影响系统的工作频率和磁场稳定,进而大大降低传输功率和效率。针对这一问题,文献[4]采用增加π型谐振网络来提高多负载条件下系统高效运行的稳定性。该方法仅从频率的角度来考虑系统稳定性,另外,额外增加的π网络也会使系统的效率降低。文献[5]提出一种解耦控制策略, 在能量拾取侧中增加一个Boost 电路,但该方法是轻载条件下一种被动控制的方法,在负载动态变化和投切时,原边系统稳定性仍会受到影响。文献[6]提出一种于智能分段算法的移相控制策略,该方法通过调节开关管脉冲移相角实现恒流控制保证系统传输的稳定,但较大范围的移相角调节会造成谐振波形出现畸变导致功率传输能力显著下降,且该控制器的设计过于依赖经验。文献[7]提出基于反射阻抗辨识的恒流控制策略,通过辨识动态反射阻抗来实现恒流的目的。但该方法需要额外增加DC/DC变换器来实现恒流,效率低。文献[8]提出一种能量注入和自由振荡2种工作模式来实现激磁电流的调节,但该文并未给出相应的控制策略。滑模变结构控制作为一种特殊的非线性控制策略,由于无需在线辨识而具有很强的鲁棒性,且易于实现[9],目前还尚未应用于IPT系统。为实现多负载条件下IPT系统的高效运行,本文作者分析了效率与频率的关系,并从能量流动的角度阐释多负载条件下的效率特性。基于恒流假设,采用双工作模式切换的电流调节方法和离散准滑模控制策略解决恒流控制问题,根据能量平衡关系建立了系统的离散动态变结构模型,并在离散准滑模控制器中加入重置积分环节保证系统的稳态性能。利用matlab仿真确定积分增益,搭建实验系统进行实验验证。
1 多负载IPT系统效率特性
多负载IPT系统的原理图如图1所示。由S1~S4 4个开关管构成全桥逆变网络,谐振线圈Lp和谐振电容Cp构成原边谐振网络。拾取线圈Li(i=1, 2, …, n)和补偿电容Ci(i=1, 2, …, n)构成n个副边拾取网络,Ri和RLi(i=1, 2, …, n)分别是副边线圈的等效内阻和负载电阻,M为线圈之间的互感。
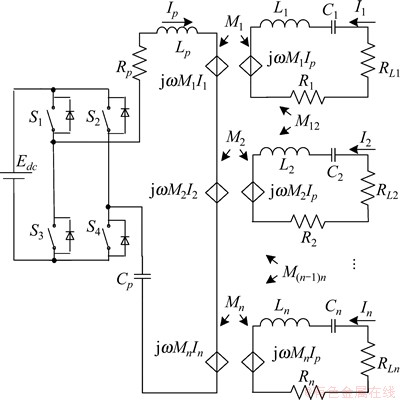
图1 多负载IPT系统原理图
Fig.1 Schematic diagram of IPT system with multiple loads
通常对于IPT系统负载侧拾取机构的设计应满足
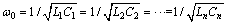 (1)
(1)
其中:ω0为副边固有谐振频率,rad/s。
根据文献[10]的效率分析,可得多负载IPT系统的效率η表达式为

 (2)
(2)
其中:I1, I2, …, In为副边拾取网络的电流;Ip为原边谐振电流(激磁电流),其满足关系
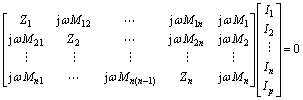 (3)
(3)
其中: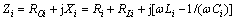 (i=1, 2, …, n);
(i=1, 2, …, n);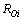 为拾取回路阻抗的实部,
为拾取回路阻抗的实部,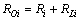 ;Xi为拾取回路阻抗的虚部,
;Xi为拾取回路阻抗的虚部,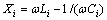 。
。
在2个负载的情况下,根据式(2)和(3)可得效率为
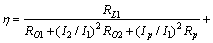
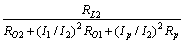 (4)
(4)
其中,
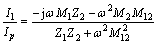
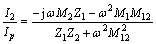 (5)
(5)
系统参数如表1所示。系统在单负载和多负载情况下的效率随工作频率变化的曲线如图2所示。
表1 系统参数
Table 1 Parameters of systems
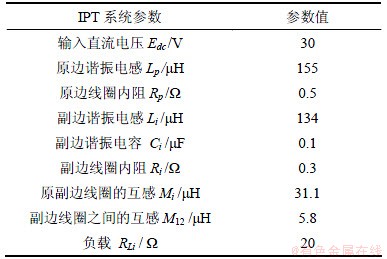

图2 效率随工作频率变化曲线
Fig.2 Variations of efficiency with operating frequency
由图2可知,在单负载时,系统工作在副边固有谐振频率时效率最高。而对于多负载,当系统工作频率偏离副边固有谐振频率时,效率达到最大。为分析这一现象,首先假设激磁电流Ip保持恒定,该电流的恒定首先保证能量传输的稳定性,在频率和互感一定的前提下,Ip的恒定直接体现出拾取电压的恒定。其次,空载时保证系统的安全和高效,尤其在多负载条件下,负载投切的随机性大,当拾取线圈完全移开(M=0)时,原边谐振网络阻抗接近于0,如果不加任何控制,此时的激磁电流将很大,影响系统的稳定性,大电流的存在也大大降低了效率。此处设Ip为恒定值k,则可根据互感得到系统各能量通道的复功率为
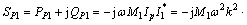
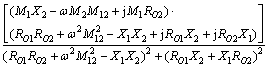 (6)
(6)

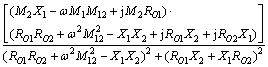 (7)
(7)
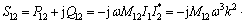
 (8)
(8)
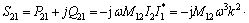
 (9)
(9)
对于负载支路1,其复功率为
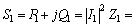
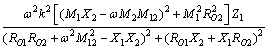 (10)
(10)
对于负载支路2,其复功率为
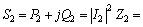
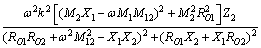 (11)
(11)
经计算,SP1+S21=S1,SP2+S12=S2,满足有功能量和无功能量的能量守恒。
当系统工作频率为ω0时,有
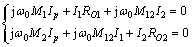 (12)
(12)
可得
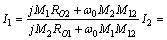
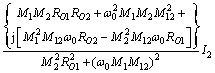 (13)
(13)
由于IPT属于松耦合系统,互感M一般都为微亨级,故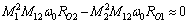 ,则式(13)可写成
,则式(13)可写成
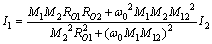 (14)
(14)
由式(8)和(14)可知,系统在固有谐振频率ω0下工作,S12只有虚部,有功部分为0。欲使多负载IPT系统得到最大传输效率,必须保证所有能量通道的畅通,故在设计原边谐振参数的时候,适当的使原边等效阻抗零相角频率偏离系统副边的固有谐振频率,保证在软开关工作条件下使系统效率最大。
2 离散系统准滑模变结构控制
基于以上分析可知,为保证系统能量传输的稳定与高效,须保持激磁电流Ip恒定。为提高系统效率,在不额外增加电能变换环节的条件下采用脉冲控制方式来调节激磁电流,即工作在双模式下,能量注入和自由谐振2种状态。
2.1 基于能量函数的动态离散变结构模型
对于高阶非线性系统,传统的建模方法复杂,从能量平衡的角度建立系统的变结构模型。对于图1所示的多负载IPT系统,考虑多个副边的反射阻抗后可得到以下等效模型,如图3所示,其输入为方波电压源uac,其幅值为Edc。
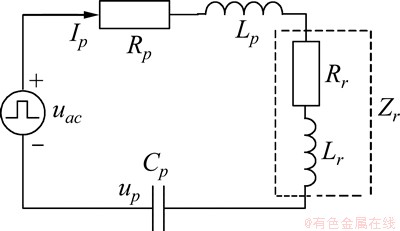
图3 原边谐振网络等效模型
Fig.3 Equivalent model of primary resonant network
反射阻抗Zr通过互感模型计算,可将其分成有功Rr和无功Lr 2个部分,即
 (15)
(15)
则可得系统储存能量函数[7]为
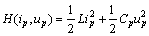 (16)
(16)
供给函数为
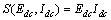 (17)
(17)
耗散函数为
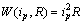 (18)
(18)
其中:R=Rp+Rr,L=Lp+Lr。
当系统在能量注入模式下工作,开关管S1~S4互补导通切换,切换总是在激磁电流的过零点进行,实现实时软开关状态,此时输入源向谐振网络注入能量,当激磁电流达到峰值Ipm时,此时谐振电容电压为0 V,由能量平衡关系有
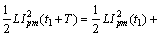
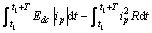 (19)
(19)
在自由谐振状态工作时,开关管S1和S2关闭,阻止能量注入,能量在谐振网络内自由流动,此时有
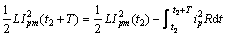 (20)
(20)
由式(19)和(20)可得关于激磁电流峰值Ipm的离散变结构模型:
 (21)
(21)
其中: 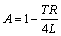 ,
, ,
,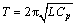 。
。
控制量
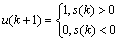 (22)
(22)
u=0表示系统工作在自由谐振状态,u=1表示系统工作在能量注入状态。系统的离散周期等于系统谐振周期T。由控制量u可知,激磁电流的峰值Ipm最大为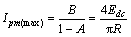 ,最小值为
,最小值为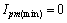 。
。
2.2 离散准滑模控制器设计
2.2.1 离散滑模面的选取
由于不增加额外的DC/DC变换器,系统只工作在能量注入和自由谐振2种模态下,故属于一种受限控制,控制量只有0和1这2个离散变量。对于该系统,滑模变结构控制不能产生理想的滑动模态,即常表现出稳态误差不为0,只能产生准滑模运动,即在某一邻域内做滑动运动。故在传统滑模切换函数的基础上增加额外的积分环节,以改善系统的稳态误差。取具有积分环节的切换函数来代替传统的滑模面函数,即
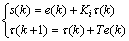 (23)
(23)
其中:Ki为积分增益;e=Iref -Ipm为电流误差。
在IPT系统中,电路参数L,Cp和R已定,则系统的响应完全由Ki决定。从系统稳定性、快速响应性和负载变化的不敏感性等方面考虑,可以用较大的增益Ki来快速补偿偏移量。积分增益Ki设计的恰当,能有效消除基频偏移量,得到稳定的激磁电流。
2.2.2 积分增益Ki的确定
积分增益Ki的选择应满足可达条件:
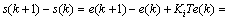
 (24)
(24)
即可得最大积分增益为
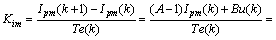
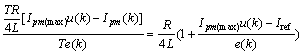 (25)
(25)
由于u(k)的取值为0和1,故当Iref=Ipm(max)或者Iref=0时,得到积分增益Ki的上限值,即取值范围为
0<Ki<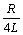 (26)
(26)
2.2.3 误差带 的确定
的确定
当电流误差大于准滑模运动的误差带时,此时积分环节需要复位。因此,为了得到较小的超调量,需要确定误差带的值。根据图4所示控制量与电流的关系,确定系统可能产生的最大电流误差。假设t0时刻,e=0。由图4可知,最大电流误差为
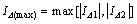 (27)
(27)
其中: ;
;
 。
。
由以上分析可得系统的误差带为
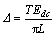 (28)
(28)

图4 控制输入与电流最大误差关系
Fig.4 Illustrations of current maximum error and control input
2.3 稳定性分析
滑模控制的3个基本问题为滑动模态的存在性、可达性和稳定性。要保证实现滑模控制,必须使切换面具有可到达性[11-13]。考虑控制量u(k),当输出电流小于参考电流时,即s(k)>0,则u(k+1)为1,系统处于能量注入状态,使导轨电流上升有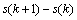 <0;当大于参考值时,u(k+1)的值为0,系统切换为自由谐振状态,导轨电流必然小于参考值,满足连续系统的可达性条件
<0;当大于参考值时,u(k+1)的值为0,系统切换为自由谐振状态,导轨电流必然小于参考值,满足连续系统的可达性条件
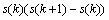 <0 (29)
<0 (29)
但是上述的可达性条件不充分,因为它们不能排除渐近稳定,从而不能保证有限时间到达,故要保证滑动模态的存在性和可达性,还需要判断系统是否满足李亚普诺夫稳定性条件[14]。
取李亚普诺夫函数为
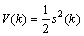 (30)
(30)
已知
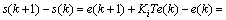
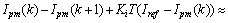
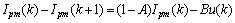 (31)
(31)
当s(k)<0,u=0,则显然有s(k+1)-s(k)>0;当s(k)>0,u=1,则显然有s(k+1)-s(k)<0,即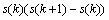 <0。
<0。
同样有

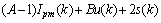 (32)
(32)
当s(k)<0,u=0,则显然有s(k+1)+s(k)<0;当s(k)>0,u=1,则显然有s(k+1)+s(k)>0,即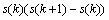 >0。
>0。
满足李亚普诺夫稳定性条件
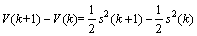 <0 (33)
<0 (33)
则同时满足存在性和可达性条件。
系统的控制框图如图5所示,控制系统通过高速AD芯片TLC5510检测激磁电流的峰值,并保存1个谐振周期,并与参考信号比较并产生误差信号,与误差的积分结果一起构成切换函数,决定下一个运行状态。当电流误差大于Δ时,积分环节复位。
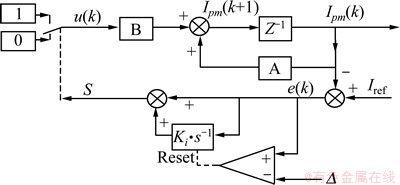
图5 具有重置积分环节的离散准滑模控制结构图
Fig.5 Structure diagram of discrete-time quasi sliding mode controller with reset intergrator
3 仿真及实验验证
为确定控制器的相关参数,首先进行matlab仿真[15],参数如表1所示,根据图2的分析结果,可计算原边电容Cp的取值为0.079 μF。计算出积分增益的取值范围为0<Ki<4 000。令激磁电流峰值的参考值为Iref=10 A。当Ki =0时,即切换函数不带积分环节,为传统滑模切换面,得到的激磁电流峰值响应和切换面动态轨迹如图6(a)所示。当Ki =50时,系统控制效果如图6(b)所示。当Ki =500时,如图6(c)所示。
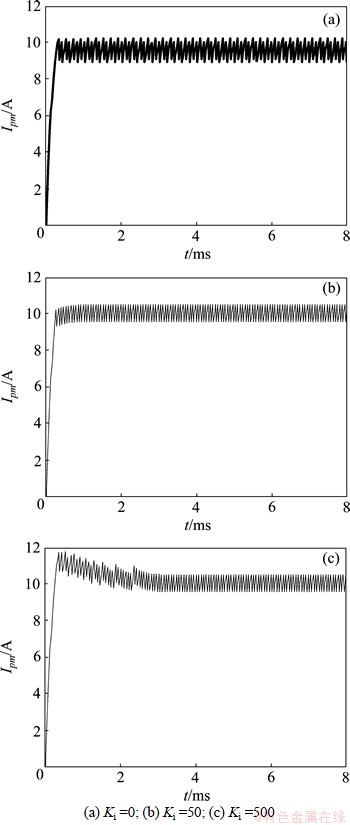
图6 不同积分增益下激磁电流峰值响应曲线
Fig.6 Response curves of exciting current of controller with different integrator gain
由图6(a)可知,当滑模面采用传统切换函数时,系统表现出较大的稳态误差,不能达到理想的滑模面。由图6(b)和图6(c)可以看出,具有积分环节的切换函数,系统能在某一领域内做准滑模运动,所得到的激磁电流的峰值也能在(10±0.5) A范围内做均匀运动,使得电流的均方根值稳定,但是积分增益取值过大,将导致系统超调量大。故此处积分增益选取Ki =50。
其次搭建实验系统,验证控制效果。实验系统的开关管采用IRF460,驱动采用IR2103,控制器采用高速32位 DSP(TMS320F2812),检测到激磁电流过零信号时就切换开关状态,保证系统的实时软开关状态。图7所示为2个负载同时工作时的稳态波形。可以看出系统在能量注入和自由谐振2种模式的切换之下,激磁电流的峰值稳定在10 A。
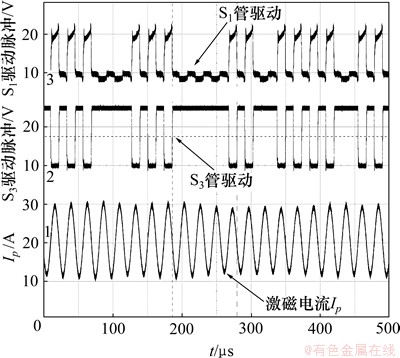
图7 多负载条件下系统稳态波形
Fig.7 Steady state waveforms of system with multiple loads
验证了控制策略的有效性后,在恒流的基础上改变无感电容Cp,以达到改变原边工作频率的目的,取Cp的值分别为0.094,0.087,0.083,0.079和0.068 μF,测得系统效率随频率的关系如图8所示。
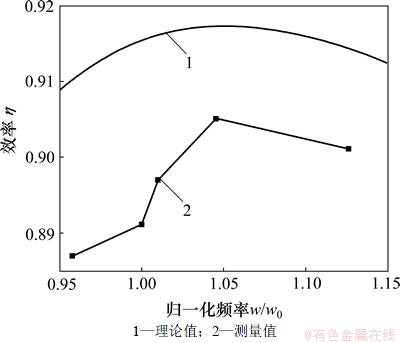
图8 效率随频率变化的曲线
Fig.8 Curves of efficiency varying with frequency
由于实际开关损耗的存在,实际测得的系统效率均略低于理论值。但是从测试结果可以看出,当频率偏离副边固有谐振频率点时效率最大,证明多负载条件下的效率分析正确。
系统在负载变化和拾取线圈完全拿开时激磁电流的实验波形如图9所示。从图9(a)可以看出,在负载从20Ω向10Ω跃变时,通过控制作用,激磁电流经过约20ms(包括手动切换电阻的时间,约15ms)的调整,使系统的激磁电流的稳态峰值稳定在10A,满足控制要求。由于系统激磁电流的恒定,使得系统在10Ω负载稳态运行时,测得效率为91.2%。当拾取线圈突然完全拿开时,从图9(b)可以看出,经过1A左右的超调后进入稳态,激磁电流在控制器的作用下重新回到参考值。
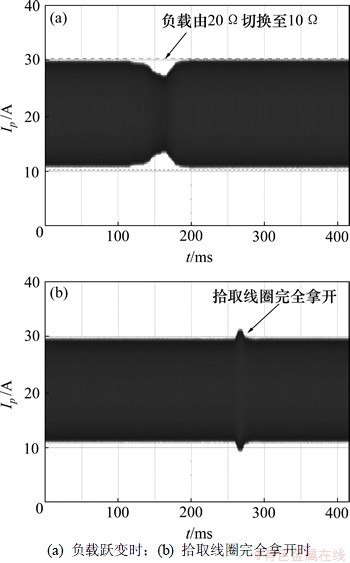
图9 负载扰动下激磁电流实验波形
Fig.9 Waveform of exciting current with load disturbance
4 结论
(1) 针对多负载IPT系统,当工作频率偏离副边固有谐振频率时,系统效率最高,并从系统各部分能量流动情况解释了系统的效率特性。
(2) 针对系统高效稳定传输问题,采用了双工作模式切换的调节手段和离散准滑模控制策略来使激磁电流稳恒。从能量平衡关系建立了系统的离散变结构模型,在传统滑模面函数的基础之上加入积分环节。
(3) 改进后的离散准滑模控制器性能明显比基于传统切换函数的滑模控制器的更优,且对于负载大范围扰动,具有较好的动态响应性能和较高的稳态性能,从而提高了系统的效率和传输稳定性。
参考文献:
[1] 苏玉刚, 唐春森, 孙跃, 等. 非接触供电系统多负载自适应技术[J]. 电工技术学报, 2009(1): 153-157.
SU Yugang, TANG Chunsen, SUN Yue, et al. Load adaptive technology of contactless power transfer system[J]. Transactions of China Electrotechnical Society, 2009(1): 153-157.
[2] 夏晨阳. 感应耦合电能传输系统能效特性的分析与优化研究[D]. 重庆: 重庆大学自动化学院, 2009: 34-37.
XIA Chenyang. Research on analysis and optimization for transmission power and efficiency of inductively coupled power transfer system[D]. Chongqing: Chongqing University. College of Automation, 2009: 34-37.
[3] Wang C S, Covic G A, Stielau O H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 148-157.
[4] 王智慧, 韩信, 苏玉刚. 基于π型补偿网络的多负载CPT系统稳定性仿真分析[J]. 计算机应用研究, 2011, 28(6): 2130-2136.
WANG Zhihui, HAN Xin, SU Yugang. Stability simulation analysis of multi-load CPT system based on π-type compensation network[J]. Application Research of Computers, 2011, 28(6): 2130-2136.
[5] 杨民生, 王耀南, 欧阳红林. 新型无接触电能传输系统多负载解耦控制研究[J]. 湖南大学学报, 2007, 34(10): 53-56.
YANG Minsheng, WANG Yaonan, OUYANG Honglin. Research on the decoupling control of contactless power transfer system with multiple Loads[J]. Journal of Hunan University, 2007, 34(10): 53-56.
[6] 孙跃, 陈国东, 戴欣, 等. 非接触电能传输系统恒流控制策略[J]. 重庆大学学报, 2008, 31(7): 766-769.
SUN Yue, CHEN Guodong, DAI Xin, et al. A constant current control method for contactless power transmission systems[J]. Journal of Chongqing University, 2008, 31(7): 766-769.
[7] 戴欣, 孙跃, 苏玉刚, 等. 感应电能传输系统参数辨识与恒流控制[J]. 重庆大学学报, 2011, 34(6): 98-104.
DAI Xin, SUN Yue, SU Yugang, et al. Study on constant current control of inductive power transfer with parameter identification[J]. Journal of Chongqing University, 2011, 34(6): 98-104.
[8] Li H L, Hu A P, Covic G A. FPGA controlled high frequency resonant converter for contactless power transfer[C]// 39th IEEE Power Electronics Specialists Conference. Piscataway: IEEE, 2008: 3642-3647.
[9] 王丰尧. 滑模变结构控制[M]. 北京: 机械工业出版, 1998: 1-20.
WANG Fengyao. The sliding mode variable structure control[M]. Beijing: China Machine Press 1998: 1-20.
[10] 孙跃, 夏晨阳,戴欣. 感应耦合电能传输系统互感耦合参数的分析与优化[J]. 中国电机工程学报, 2010, 30(33): 44-50.
SUN Yue, XIA Chenyang, DAI Xin. Analysis and optimization of mutual inductance for inductively coupled power transfer system[J]. Proceedings of the CSEE, 2010, 30(33): 44-50.
[11] 许飞, 马皓, 何湘宁. 基于离散变速趋近率控制的电流源逆变器[J]. 中国电机工程学报, 2007, 27(33): 98-102.
XU Fei, MA Hao, HE Xiangning. A discrete-time variable rate reaching law controlled current-source inverter[J]. Proceedings of the CSEE, 2007, 27(33): 98-102.
[12] Ramos R, Biel D, Fossas E. A fixed-frequency quasi-sliding control algorithm: application to power inverters design by means of FPGA implementation[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 344-355.
[13] Mam G K, Dae S L, Myang J Y. A new state feedback control of resonant converters[J]. IEEE Transactions on Industrial Electronic, 1991, 38(3): 173-179.
[14] GAO W B, WANG Y F, Homaifa A. Discrete-time variable structure control systems[J]. IEEE Transactions on Industrial Electronic, 1995, 42(2): 117-122.
[15] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005: 65-108.
LIU Jinkun. Matlab simulation for sliding mode control[M]. Beijing: Tsinghua University Press, 2005: 65-108.
(编辑 赵俊)
收稿日期:2012-07-16;修回日期:2012-10-08
基金项目:国家自然科学基金资助项目(51207173,51277192);教育部博士点基金资助项目(20090191110021)
通信作者:吕潇(1987-),男,江西贵溪人,博士研究生,从事感应电能传输技术的能效分析与控制研究;电话:13637972543;E-mail: lvxiao87@126.com