
Flow behavior and microstructure evolution of
TB8 alloy during hot deformation process
DUAN Yuan-pei(段园培), LI Ping(李 萍), XUE Ke-min(薛克敏),
ZHANG Qing(张 青), WANG Xiao-xi(王小溪)
School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China
Received 15 July 2007; accepted 10 September 2007
Abstract: Hot compression tests of metastable β titanium alloy TB8 were carried out using a Gleeble-1500 thermal simulation testing machine in the temperature range of 750-1 100 ℃, at constant strain rate from 0.01 s-1 to 1 s-1 and with height direction reduction of 60%. Flow stress behavior and microstructure evolution during hot compression of TB8 alloy were investigated. The hyperbolic-sine-type constitutive model of TB8 alloy was obtained to provide basic data for determining reasonable forming process. The results indicate that hot deformation behavior of TB8 alloy is highly sensitive to the temperature and strain rate. An analysis of the flow stress dependence on strain rate and temperature gives a stress exponent of n≈3.416 19 and a deformation activation energy of Q≈227.074 4 kJ/mol. According to the deformation microstructure, no dynamic recrystallization happens below β-phase transus temperature and as a result dynamic recovery is the predominant softening mechanism. On the other hand, the main softening mechanism is characterized as dynamic recrystallization at a slow strain rate above β-phase transus temperature.
Key words: TB8 titanium alloy; hot compressive deformation; flow stress; activation energy; microstructure
1 Introduction
Owing to their high specific strength, excellent fracture toughness, good creep and corrosion resistance and extensive ductility, titanium and titanium alloys constitute an important class of metals with many commercial applications in the defense, aerospace, biomedical, and sporting goods industries[1-4]. However, it is widely understood that titanium alloys are difficult-to-form materials and their mechanical properties are very sensitive to the processing parameters and the characteristics of the microstructure. Therefore, careful process control and profound knowledge of the influence of processing on flow behavior and microstructure are of significant importance for the manufacturing of titanium alloy products of good performance.
TB8 alloy is a metastable beta titanium alloy similar to American titanium alloy β-21S, which not only offers the high specific strength and good cold formability, but has been specially designed for improved oxidation resistance, elevated temperature strength, creep resistance and thermal stability[5]. Due to its excellent mechanical properties, TB8 alloy is ranked among the most important advanced materials for a variety of technological applications. In previous scientific literatures, most researches were focused on the cold formability of TB8 alloy, whereas no systematic investigation on the hot deformation behavior has been reported[6-9]. In fact, due to the high cost and working complexity of titanium alloys, experimental testing of material plays a central role for process simulation and optimization. Consequently, in this study the deformation behavior of TB8 alloy was investigated by isothermal hot compression tests.
The main objectives of the present work are: 1) to characterize the flow stress behavior of TB8 alloy under different hot working conditions and analyze the influence of processing parameters on the deformation behavior; 2) to develop a constitutive equation for the flow stress dependence on strain rate and temperature in the considered extended range; 3) to further understand the characteristics of microstructure evolution during hot compression. 2 Experimental
The chemical composition of TB8 alloy used in this investigation is specified in mass fraction in Table 1. The initial microstructure is characterized by almost equiaxed beta phase,with a very small amount of alpha phase on the beta-phase grain boundaries. The beta-phase transus temperature reported for this material is approximately 815 ℃[7]. Cylindrical specimens for the compression tests were machined to 8 mm in diameter and 15 mm in height utilizing electro-discharge machine. In order to decrease the friction and maintain uniform deformation, thin tantalum sheets were placed between the compression specimen and the die.
Table 1 Chemical composition of TB8 titanium alloy (mass fraction, %)

Isothermal hot compression tests were performed on a Gleeble-1500 thermal simulation testing machine in the temperature range of 750-1 100 ℃, at constant strain rates of 0.01, 0.1 and 1 s-1, respectively (shown schema- tically in Fig.1). The maximum height reduction of all the specimens was 60%. The specimens were heated to 1 200 ℃ at 10 ℃/s and homogenized for 300 s to eliminate thermal gradients, then cooled at 5 ℃/s to the deformation temperature, and deformed at the selected constant temperature. The as-deformed specimens were immediately water quenched to room temperature. The load—stroke curves obtained from the compression tests are converted into true stress—strain curves by standard equations. After hot deformation, the specimens were cut symmetrically into two parts parallel to the compression axis. Central regions of the specimens where the specimens had the largest deformation were chosen as the investigation area of interest. After adequate grinding,

Fig.1 Schematic diagram of hot compression test
polishing and etching of the cutting surface, frozen microstructures were observed using conventional optical microscopy(OM).
3 Results and discussion
3.1 True stress—true strain curves
Typical true stress—true strain curves obtained at various temperatures and strain rates are presented in Fig.2, where Figs.2(a), (b) and (c) correspond to strain rates of 0.01, 0.1 and 1 s-1, respectively. As seen in Fig.2, flow stress behavior of TB8 alloy is sensitively dependent on the strain rate and temperature. In general, the flow stress diminishes with the rise in temperature and decrease in strain rate.

Fig.2 Experimental true stress—true strain curves of TB8 alloy at different strain rates and temperatures: (a) 0.01 s-1; (b) 0.1 s-1; (c) 1 s-1
As illustrated in Fig.2, there is a significant difference in the overall shapes of true stress—true strain curves observed for deformation in the two phase α+β region as compared to the single phase β region. At the temperatures below β-phase transus, the true stress—true strain curves show an initial sharp yield drop and then reach a steady-state stress condition at strain rate of 0.01 and 0.1 or decrease gradually at the strain rate of 1 s-1. On the other hand, when TB8 alloy is deformed in β single-phase region, true stress reaches a steady state or increases a little as deformation proceeds without showing a yield drop.
The occurrence of “initial sharp peak” phenomenon can be rationalized to the existence of a little amount of alpha phase. It is concluded that alpha phase that acts as hard particles plays an important role in dislocation pinning. Therefore, the true stress increases abruptly due to a fast generation of dislocations in early period of deformation. However, when the stress becomes large enough, dislocation starts to slip from the pinning sites. Consequently, the true stress decreases sharply. Another explanation for “initial sharp peak” is reported to be the phenomenon of discontinuous yielding produced by the interaction between the solutes and mobile dislocations [8]. The observation of an abrupt decrease in the flow stress during initial deformation has been reported for a range of materials with a body-centered-cubic crystal structure[10-11].
The effect of temperature on the flow stress behavior for TB8 at various strain rates was examined in great detail by plotting the stresses at 0.3 strain(ε0.3) and 0.6 strain(ε0.6) as a function of deformation temperature, as shown in Fig.3. The magnitude of stress drop varies with the increase of temperature in different temperature regions. As shown in Fig.3, flow stress at strains of 0.3 and 0.6 steeply falls at 750-1 000 ℃, especially at high strain rate of 1 s-1. When the temperature increases over 1 000 ℃, the decrease of the flow stress becomes slow.
3.2 Constitutive modeling
Deformation of the specimens in isothermal hot compression tests is inhomogeneous due to the friction. Some researchers attempt to develop correction methods to eliminate the influence of friction[12-14]. A simple method only by measuring the maximum barreling radius and height of cylinder after deformation was adopted in order to reflect the deformation behavior of the material exactly. In this study, the constitutive equation is established based on the corrected flow curves.

Fig 3 Variation of flow stress with temperature at different strains: (a) ε=0.3; (b) ε=0.6
High temperature deformation is a process of thermal activation. Numerous investigations have been performed to characterize the material deformation behavior. In 1944, Zener and Hollomon found that the stress—strain relation of steel depended on deformation temperature and strain rate. They proposed that a material flow stress model can be expressed as a function of strain, strain rate and temperature, and the relationship of temperature and strain rate can be also denoted by a parameter Z:
σ=σ(Z, ε) (1)
 (2)
(2)
where σ is the flow stress;  is the strain rate; Q is the average apparent activation energy of deformation; R is the ideal gas constant (R=8.314 J/(mol K)); T is the deformation temperature; Z is Zener-Hollomon parameter, the physical meaning of which is the so-called temperature compensated strain rate parameter.
is the strain rate; Q is the average apparent activation energy of deformation; R is the ideal gas constant (R=8.314 J/(mol K)); T is the deformation temperature; Z is Zener-Hollomon parameter, the physical meaning of which is the so-called temperature compensated strain rate parameter.
Up to now, three expressions of constitutive equations as the following have been widely reported in literatures to model the material flow behavior:
 (3)
(3)
 (4)
(4)
 (5)
(5)
where A1, A2, A, n1, n, β and α(=n/β) are material constants. The power law, Eqn.(3), and the exponential law, Eqn.(4), are suitable for a low stress and a high stress, respectively. Eqn.(5) that is in the hyperbolic sine law proposed by Sellars and Tegart was generally used to describe the flow stress and deformation activation behavior over a wide range of temperatures and strain rates. Therefore, a constitutive equation for TB8 alloy was proposed by employing hyperbolic-sine-type equation. A numerical curve-fitting method was used to yield values of the kinetic parameters.
By taking natural logarithm, Eqn.(5) can be written as follows:
 (6)
(6)
So the hot deformation activation energy Q(J/mol) that is an important physical parameter serving as indicator of deformation difficulty degree in plasticity deformation theory can be calculated by the following equation:
 (7)
(7)
The first term on the right-hand side of Eqn.(7) ?ln[sinh(ασ)]/?(1/T) refers to the slope of ln[sinh(ασ)] versus the reciprocal of temperature 1/T at different strain rates, and the second term refers to the slope of
refers to the slope of  versus ln[sinh(ασ)] at different deformation temperatures.
versus ln[sinh(ασ)] at different deformation temperatures.
By linear regression of the relations of  —σ and
—σ and  —lnσ at different temperatures, an optimum value α is determined as 8.112×10-3 MPa-1. Fig.4(a) shows the the relation between
—lnσ at different temperatures, an optimum value α is determined as 8.112×10-3 MPa-1. Fig.4(a) shows the the relation between  and ln[sinh(ασ)], and Fig.4(b) shows the relation between ln[sinh(ασ)] and 1/T. The regression coefficients of several groups of parallel and straight lines are all greater than 0.98. The hot deformation activation energy Q of TB8 alloy is determined through substituting the slopes of Fig.4(a) and Fig.4(b) into Eqn.(7), and the calculated value is obtained to be about 227.074 4×103 kJ/mol.
and ln[sinh(ασ)], and Fig.4(b) shows the relation between ln[sinh(ασ)] and 1/T. The regression coefficients of several groups of parallel and straight lines are all greater than 0.98. The hot deformation activation energy Q of TB8 alloy is determined through substituting the slopes of Fig.4(a) and Fig.4(b) into Eqn.(7), and the calculated value is obtained to be about 227.074 4×103 kJ/mol.
Substitution of Eqn.(5) into Eqn.(2) yields
 (8)
(8)
Take the natural logarithm of each side, then
lnZ=lnA+nln[sinh(ασ)] (9)
Substitution of Q and strain rates at different temperatures into Eqn.(2), the values of lnZ of TB8 alloy on different conditions are obtained. Based on the peak stresses, the relation between lnZ and ln[sinh(ασ)] is plotted in Fig.5 through linear regression. As shown in Fig.5, the slope corresponding to the value of stress exponent n in Eqn.(9) can be obtained as 3.416 19, and the intercept corresponding to lnA as 21.130 83. The regression coefficient reaches 0.98. That is to say, the results above give better approximation, demonstrating that the flow stress for the TB8 titanium alloy can be represented by a hyperbolic-sine-type equation expressed as follows:

Fig.4 Variation of flow stress with process parameters

Fig.5 Variation of  with peak stresses
with peak stresses
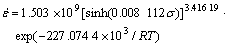 (10)
(10)
3.3 Microstructure observation
Deformation is actually the process of competition between strain hardening and dynamic softening that take place and compete with each other at the same time. Dynamic softening can be caused by deformation heating and also by microstructural instabilities, such as dynamic recovery(DRV), dynamic recrystallization(DRX), and texture formation. As two critical softening mechanisms, both DRX and DRV are of vital importance in determining the hot deformation behavior of alloys to a large extend. So in order to further understand the characteristics of microstructure evolution and give an insight into the hot deformation behavior of TB8 alloy, frozen microstructures obtained by the hot compression tests were investigated.
Typical optical microstructures of TB8 alloy after hot compression are shown in Fig.6. The effects of high temperature on the evolution of the microstructures can be seen clearly from these optical micrographs. In Fig.6(a), almost all of the grains are obviously elongated in the perpendicular direction of compression axis. The boundaries of elongated grains are nearly straight and no recrystallization grain is observed. However, while the temperature is higher, elongated thin grains with serrations developed on the grain boundaries are observed in Figs.6(b) and (d), where DRX grains can be
easily distinguished. As shown in Fig.6(b), fine DRX grains nucleate almost exclusively at grain boundaries and only partial DRX takes place. There is still a large quantity of elongated grains in the deformed microstructures. As temperature increases to 1 000 ℃, more DRX grains are generated and as a result recrystallization volume fraction is increased (Fig.6(d)). It is convinced that no DRX phenomenon is observed below β-phase transus in the experimental range of strain rate.
Meanwhile, strain rate also has remarkable effect on the microstructure of hot deformation. The flow softening seems more pronounced at low strain rates, indicating that microstructural instabilities play an important role in the flow softening. It is evident from Figs.6(b) and (c) that the softening mechanism changes as strain rate increases. DRX occurs at a low strain rate, as shown in Fig.6(b), whereas no recrystallization grain is observed at a higher strain rate in Fig.6(c). At high strain rates, the accumulated energy increases, as dislocations have not enough time to consume or continually generate. When the strain rate is relatively low, DRX grain has more time to nucleate and grow. DRX is prone to occur probably because dislocation glide/climb process provokes elongated and thin recrystallization grains[15]. More new grains generate on the grain boundaries and dislocation that usually act as the preferential sites for heterogeneous nucleation. The results indicate that DRX occurs during hot compression deformation and the degree of DRX is dependent sensi-tively on deformation temperature and strain rate. Both increasing the temperature at a given strain rate and decreasing the strain rate at a given temperature seem to promote more homogeneous microstructure.

Fig.6 Optical microstructures of deformed TB8 alloy at different temperatures and strain rates: (a) t=750 ℃,  =0.01 s-1; (b) t=900 ℃,
=0.01 s-1; (b) t=900 ℃,  =0.01 s-1; (c) t= 900 ℃,
=0.01 s-1; (c) t= 900 ℃,  = 1 s-1; (d) t=1 000 ℃,
= 1 s-1; (d) t=1 000 ℃,  =0.01 s-1
=0.01 s-1
Specifically, during the process of hot deformation, the variation of flow stress to some extent reflects the evolution of microstructure of the material. In the present case, the influence of temperature and strain rate on the flow stress that increases with increasing strain rate and decreasing temperature is also in accordance with the microstructural evolution.
4 Conclusions
1) The flow stress behavior of TB8 alloy is temperature- and strain rate-sensitive. An increase of strain rate intensifies the flow stress and an increase in temperature significantly decreases the flow stress. The decrease of stress differs with the increasing temperature in different temperature regions.
2) A constitutive equation for TB8 alloy is formulated by employing a hyperbolic-sine type equation to describe the temperature and strain rate dependence of the flow stress. Stress exponent and the deformation activation energy are determined to be about 3.416 19 and 227.074 4 kJ/mol, respectively.
3) Deformation temperature and strain rate also cause tremendous changes in the microstructural evolution. It is concluded that the softening mechanism is dominated by DRV below β-phase transus, whereas above β-phase transus at a low strain rate, the main softening mechanism is characterized as DRX.
References
[1] FROES F H, ALLEN P G, NIINOMI M. Non-aerospace implications of titanium—An overview [C]// FROES F H, ALLEN P G, NIINOMI M, eds. Proc of Symposium on Non-Aerospace Applications of Titanium. Warrendale, PA: TMS, 1998: 3-18.
[2] WANJARA P, JAHAZI M, MONAJATI H, YUE J P. Hot working behavior of near-α alloy IMI834 [J]. Mater Sci Eng A, 2005, 396(1/2): 50-60.
[3] EVANS W J. Optimizing mechanical properties in alpha+beta titanium alloys [J]. Mater Sci Eng A, 1998, 243(1/2): 89-96.
[4] LI Miao-quan, PAN Hong-si, LIN Ying-ying, LUO Jiao. High temperature deformation behavior of near alpha Ti-5.6Al-4.8Sn- 2.0Zr alloy [J]. J of Mater Process Technol, 2007, 183: 71-76.
[5] BANIA P J. Beta titanium alloys and their role in the titanium industry [C]// EYLON D, BOYER R R, KOSS D A. Beta Titanium Alloy in the 1990’s. Warrendale, PA: TMS, 1993: 3-14.
[6] YU Dong-mei. The Application Study of the new type Titanium TB8 [J]. Aircraft Design, 2002(2): 57-65. (in Chinese)
[7] ZHU Zhi-shou, WANG Qing-ru. Cold forming processes and applications of TB8 Titanium sheet [J]. Acta Metallurgica Sinica, 2002, 38(suppl 9): 414-416. (in Chinese)
[8] YE Wen-jun, TUO Xiang-ming, WANG Shi-hong. Hot compressive behavior of β-21S titanium alloy [J]. Chinese Journal of Rare Metals, 2002, 26(1): 23-27. (in Chinese)
[9] TAL-GUTELMACHER E, ELIEZER D, BOELLINGHAUS T H. Investigation of hydrogen-deformation interactions in β-21S titanium alloy using thermal desorption spectroscopy [J]. Journal of Alloys and Compounds, 2007, 440: 204-209.
[10] COURTNEY T H. Mechanical behaviour of materials [M]. New York: McGraw-Hill, 2000.
[11] BAO Ru-qiang, HUANG Xu, HUANG Li-jun, CAO Chun-xiao. Investigation on hot deformation behavior of Ti-10V-2Fe-3Al alloy [J]. Material Engineering, 2003, (12): 3-6. (in Chinese)
[12] EBRAHIMI R, NAJAFIZADEH A. A new method for evaluation of friction in bulk metal forming [J]. J of Mater Process Technol, 2004, 152(20): 136-143.
[13] LUO Zi-jian, YANG Qi, JI Wan-hua. New method to establish constitutive relationship considering effect of deformation heating [J].The Chinese Journal of Nonferrous Metals, 2000, 10(6): 804-808. (in Chinese)
[14] ZHANG Wei-hong, ZHANG Shi-hong. Correction of hot compression test data and constitutive equation of NiTi alloy [J]. Acta Metallurgica Sinica, 2006, 42 (10): 1036-1040. (in Chinese)
[15] WANG X, JAHAZI M, YUEA S. Substructure of high temperature compressed titanium alloy IMI 834 [J]. Mater Sci Eng A, 2006, 434(1/2): 188-193.
(Edited by YANG Bing)
Foundation item: Project(50405020) supported by the National Natural Science Foundation of China
Corresponding author: XUE Ke-min; Tel: +86-551-2904758; E-mail: xuekm0721@sina.com