Delamination analysis of woven fabrication laminates usingcohesive zone model
来源期刊:中南大学学报(英文版)2016年第1期
论文作者:Mohsen Moslemi MohammadrezaKhoshravan azar
文章页码:27 - 38
Key words:cohesive zone model; delamination; cohesive strength; finite element prediction
Abstract: A new test method was proposed to evaluate the cohesive strength of composite laminates. Cohesive strength and the critical strain energy for Mode-II interlamiar fracture of E-glass/epoxy woven fabrication were determined from the single lap joint (SLJ) and end notch flexure (ENF) test, respectively. In order to verify their adequacy, a cohesive zone model simulation based on interface finite elements was performed. A closed form solution for determination of the penalty stiffness parameter was proposed. Modified form of Park-Paulino-Roesler traction-separation law was provided and conducted altogether with trapezoidal and bilinear mixed-mode damage models to simulate damage using Abaqus cohesive elements. It was observed that accurate damage prediction and numerical convergence were obtained using the proposed penalty stiffness. Comparison between three damage models reveals that good simulation of fracture process zone and delamination prediction were obtained using the modified PPR model as damage model. Cohesive zone length as a material property was determined.To ensure the sufficient dissipation of energy, it was recommended that at least 4 elements should span cohesive zone length.
J. Cent. South Univ. (2016) 23: 27-38
DOI: 10.1007/s11771-016-3045-9
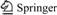
Mohsen Moslemi, Mohammadreza Khoshravan azar
Department of Mechanical Engineering, University of Tabriz, 5166614766, Tabriz, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: A new test method was proposed to evaluate the cohesive strength of composite laminates. Cohesive strength and the critical strain energy for Mode-II interlamiar fracture of E-glass/epoxy woven fabrication were determined from the single lap joint (SLJ) and end notch flexure (ENF) test, respectively. In order to verify their adequacy, a cohesive zone model simulation based on interface finite elements was performed. A closed form solution for determination of the penalty stiffness parameter was proposed. Modified form of Park-Paulino-Roesler traction-separation law was provided and conducted altogether with trapezoidal and bilinear mixed-mode damage models to simulate damage using Abaqus cohesive elements. It was observed that accurate damage prediction and numerical convergence were obtained using the proposed penalty stiffness. Comparison between three damage models reveals that good simulation of fracture process zone and delamination prediction were obtained using the modified PPR model as damage model. Cohesive zone length as a material property was determined. To ensure the sufficient dissipation of energy, it was recommended that at least 4 elements should span cohesive zone length.
Key words: cohesive zone model; delamination; cohesive strength; finite element prediction
1 Introduction
Fiber reinforced composite materials are susceptible to delamination due to out of-plane and shear loads, so reduction in structural integrity and service lifetime occur. Delaminations in laminated composite materials usually initiate from discontinuities, such as matrix cracks and free edges, or manufacturing faults, such as embedded defects. Therefore, it is important to analyze the progressive growth of delamination in order to predict the performance of a composite structure and improve reliable and safe designs. One of the most frequently modes of delamination in composite layered materials is mode-II interface cracking due to the loss of cohesion between layers of material. The delamination resistance of polymer–matrix composites has been extensively investigated in the framework of fracture mechanics [1].In order to model crack propagation, it was assumed that the delamination propagates when the available strain energy release rate is greater than or equal to a critical value, which is considered a mechanical parameter of the interface. Techniques, such as the virtual crack closure (VCC) [2],the J-integral [3], the virtual crack extension [4], and extended finite element [5],are some of the most prevalent procedures used to predict damage growth. These techniques are used to compute the distribution and components of the strain energy release rate. However, there are some difficulties when these techniques are performed using finite element codes. The computation of fracture parameters, such as stress intensity factors or energy release rates, requires nodal variable and geometrical information from the nodes ahead and behind the crack tip. These calculations can be performed with some effort for a stationary crack, but when progressive crack propagation is involved, such calculation can be extremely difficult. Another method to the numerical modeling of the delamination growth can be developed within the framework of damage mechanics. Models formulated according to damage mechanics are based on the concept of the cohesive crack model which considers a zone of vanishing thickness ahead of the crack front in order to describe more realistically the fracture nature without the use of stress singularity.The origin of the cohesive zone model goes back to Dugdale [6] who demonstrated the concept that stresses in the material are confined by the yield stress and that a thin plastic zone is generated in front of the crack tip. Barenblatt [7] proposed a cohesive zone concept to study the fracture nature of brittle materials and to introduce a separation mechanism at the atomic scale in order to describe the real separation of materials, and to remove stress singularity at the crack tip. Hillerborg et al [8] suggested a model similar to the Barenblatt model. Their model allowed for existing cracks to grow and also allowed for the initiation of new cracks. For practical applications the model became considerable when numerical methods such as the finite element method, were applicable to fracture problems. Needleman [9] was the first who related the cohesive zone model with finite element (FE) analysis. Xu and Needleman [10] developed the cohesive finite element method and successfully applied it to simulating dynamic fracture problems. Recently, NGUYEN et al [11] developed isogeometric cohesive elements for two- and three-dimensional delaminations requiring minimal user intervention to simulate delamination in composite structures. Vandellos et al [12] proposed a new framework for the development in an implicit finite element code of cohesive zone models adapted to the description of the mixed-mode delamination. To date, cohesive zone model has been used to model fracture for different variety of materials, such as metals, polymers, concrete, ceramics, functionally graded materials, fiber reinforced materials [13-16] and its range of applications will be continued to expand. In order to simulate the fiber bridging effect on multidirectional laminates, ZhaO et al [17] proposed a cohesive zone model in which fracture toughness function that reflects the variation of fiber bridging tractions was used. Morais [18-19] developed a cohesive zone model for mode I and mixed-mode I-II delamination in composite beams that was an extension of a beam on elastic foundation analysis. Khoshravan and moslemi [20] developed a cohesive zone model to fracture simulation of composite laminates under pure mode III loading. An important issue in conjunction with the use of cohesive zone model is the specification of the traction-separation law. In particular, the related fracture parameters, such as cohesive strength and fracture toughness, as well as the shape of the traction-separation law, must be determined. In the case of traction-separation law, there are some models that can be used. For example, the traction- separation based on exponential form [10], the trapezoidal form [21] and the bilinear form [13, 22] are traction-separation laws that widely adopted. Recently, Liu and Islam [23] proposed an anisotropic nonlinear cohesive model for mixed-mode delamination using a damaged exponential traction-displacement jump relationship. Since there are no available standardized tests and existence of some difficulties corresponding to the direct measurement of the theses parameters, in most cases these parameter are determined by comparison of a measured fracture property with numerical predictions based on an idealized cohesive zone model [22, 24-25]. However, cohesive strength and fracture toughness are found to have higher importance as comparised to the specific traction-separation shape chosen for the cohesive model [26]. Turon et al [27] proposed a methodology to estimate the constitutive parameters for the finite element simulation of progressive delamination using bilinear cohesive zone model. According to their methodology, the cohesive strength is in proportion to the length of the cohesive zone and this parameter should be modified with respect to the cohesive zone length that suggests as the cohesive strength decreases, the length of the cohesive zone should be artificially lengthened to ensure that it spans enough elements of a given size. In order to overcome this deficiency, recently Alvarez et al [28] proposed two-dimensional linear and quadratic cohesive elements to simulate crack initiation and propagation. These elements have a modified topology that allows a user-defined number of integration points to enable the use of coarser meshes, resulting in shorter simulation time.
The objective of this work is to provide a suitable methodology for fracture characterization of delamination under pure mode II loading. Simple structure test is proposed to compute interlaminar tangential cohesive strength of composite laminates. The values for critical mode-II strain energy release rate (GIIC) and mode-II tangential cohesive strength (τIIC) were computed at room temperature. Modified form of Park-Paulino-Roesler (PPR) [29] traction separation law was provided and conducted altogether with trapezoidal and bilinear mixed-mode damage model to simulate the crack initiation and propagation using the experimentally obtained cohesive parameters. The numerical methods were validated by experimental test and a guideline methodology was proposed for selection of mode II penalty stiffness, cohesive zone length and mesh refinement to obtain successful prediction of delamination onset and propagation.
2 Cohesive zone model approach
Cohesive zone model based on interface finite elements is applied to simulating damage onset and propagation. Cohesive zone model relates tractions to separation at an interface where a crack may initiate. Crack initiation is related to the cohesive strength, i.e., the maximum traction on the traction separation law. When the area under the traction–separation law reaches the fracture toughness, the traction is declined to zero and new crack surfaces are generated. The objective is to replace the usual solid elements of the cohesive layer. By assigning an appropriate traction separation model to the interface, the stress singularity is eliminated. The elastic deformation in the bulk material is governed by bulk material behavior while the cohesive behavior is governed by separate traction separation model.
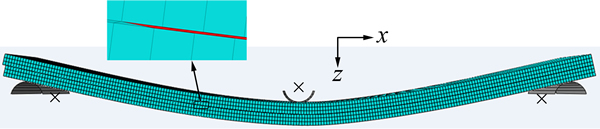
In this work, in order to simulate Mode-II fracture of E-glass/epoxy woven composite laminate using cohesive elements, three types of traction separation law including mixed-mode triangular traction-separation response, trapezoidal softening law and modified PPR model which is potential-based model, were conducted and compared with experimental results. The objective is to determine an appropriate methodology to predict interlaminar crack growth in composite structures. Figure 1 shows three types of traction-separation laws that relate stresses (s) and relative displacements (δ) of cohesive elements. The subscript m referred to mixed mode and subscript c and u referred to critical and ultimate (failure) values respectively and i=I, II, III referred to pure modes of fracture. The area under the curves represents the corresponding critical strain energy release rate. Fracture simulations of material using cohesive elements require substantial experience for determining the mesh requirements and the measurement of parameter that characterizes the traction-separation law. In order to determine the mixed-mode traction-separation law, the properties required to be defined are the three critical strain energy release rate (Gic), the penalty stiffness (Ki) and the cohesive strengths (sic).
In the present work, the Mode-III cohesive parameters were assumed to be equal to those of Mode-II, so the shear strengths in the two orthogonal directions, τIIC and τIIIC, and also critical strain energies, GIIC and GIIIC, are identical. In the case of simulation mode-II fracture, prediction of delamination onset and growth is more sensitive to the parameters τIIC and GIIC than other interfacial properties. So, in the present study the end notch flexure (ENF) test and the single lap joint (SLJ) test were carried out for determining GIIC and τIIC, respectively. Other fracture parameters were determined by calibration of cohesive parameters. In other words, numerical results are fitted with experimental results according to the methodology described in Refs. [14, 22, 24-25].
2.1 penalty stiffness of cohesive elements
As shown in Fig. 1, the initial response of the cohesive elements at each damage model is based on linear elastic fracture mechanics (LEFM) and is assumed to be linear until a crack initiation criterion is satisfied. The penalty stiffness, Ki, of each traction-separation response law that relates traction to separation of cohesive elements before crack onset, is defined as
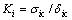 (1)
(1)
where i=I, II, III is fracture modes; sic and δic are the cohesive strength and critical separation of pure modes of fracture, respectively. In the present work, the penalty stiffnesses for all modes of fracture are considered to be the same, i.e. KI=KII=KIII=K. Several methodologies have been proposed to determine the penalty stiffness of cohesive elements. In the case of Mode-I loading, several guidelines have been proposed for determining the penalty stiffness of the cohesive elements [27, 30-31]. In the present work, in order to determine the penalty stiffness for the case of Mode-II loading, it is considered that the effective elastic properties of the whole composite depend on the properties of both the cohesive layer and the bulk constitutive relation of the plies. The influence of compliance of the cohesive layer on the bulk properties of a laminate is shown in the 1D model illustrated in Fig. 2. The equilibrium condition requires
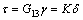 (2)
(2)
where τ refers to the traction on the surface; γ=2δ1/t is the shear strain; t represents the thickness of a bulk sublaminate; K is the interface stiffness that relates the resulting tractions at the interface to the transverse displacement δ; G13 is the shear modulus of the bulk material. The effective shear strain of the laminate is as follows:

Fig. 1 Traction-separation laws of cohesive elements:

Fig. 2 Effect of cohesive layer on deformation:
 (3)
(3)
Since the equilibrium condition requires τ=Geff×γeff, the equivalent shear modulus Geff can be expressed as a function of the shear modulus of the material, the mesh size, and the interface stiffness. Using Eqs.(2)-(3), the effective shear modulus can be expressed as
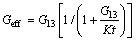 (4)
(4)
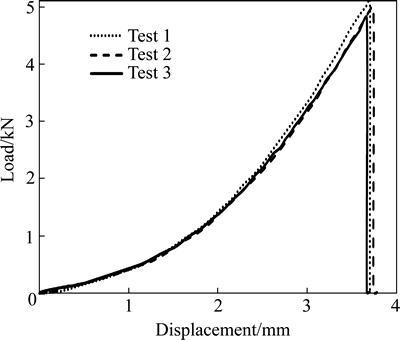
The effective elastic properties of the material will not be influenced by the cohesive layer while G13< where χ is a coefficient much larger than 1 (χ>>1). The magnitude of the penalty stiffness must be high enough to avoid interpenetration of the crack surfaces and to avoid artificial compliance from being defined into the model by the cohesive elements. However, a more than enough value can lead to numerical problems. In this work, it is found that for values of χ greater than 25, the loss of stiffness between sublaminates due to the presence of the cohesive layer was vanished. So, this value is considered sufficiently accurate for most problems. 2.2 Crack initiation criterion In order to simulate delamination using cohesive element, there are four well-known crack initiation criteria including: maximum stress, quadratic stress, maximum strain and quadratic strain criterion. In this analysis, the quadratic stress criterion that is expressed in Eq. (6), was used [27]. Under mixed-mode loading, an interaction between modes must be taken into account. This criterion model, readily takes into account the interaction of the traction components in the prediction of damage onset. Moreover, due to high sensivity of failure initiation to the strain and displacement, a stress based criterion give an accurate failure prediction as compared to other models, such as strain based or displacement based criterion. The quadratic stress criterion is defined as where x, y and z are referred to Cartesian coordinate as shown in Fig. 3. The macaulay bracket, < >, states that the compressive stress does not contribute to crack onset. Whenever the damage initiation criterion of Eq. (6) for the cohesive element is satisfied, the stiffness of the element is declined according to the corresponding constitutive law that was used. Fig. 3 Finite element model of ENF specimen during crack propagation 2.3 Damage evolution criterion After damage initiation, the softening procedure occurrs. This procedure is governed by the corresponding traction separation law as bellow. 2.3.1 Bilinear traction-separation law As shown in Fig. 1(a), in the mixed-mode constitutive law, smc and δmc represent the cohesive strength and critical separation (separation at which crack initiates) respectively. Moreover, δmu refers to separation at which failure occurs. The softening relation of cohesive elements that are governed by bilinear constitutive law can be expressed as where d is variable that relates damage condition, which has the magnitude d=0 when the interface is undamaged, and the magnitude d=1 when the interface is completely fractured. In numerical analysis of damage evolution there are two crack evolution criteria including: energy and displacement based. In the analyses presented herein, energy-based Benzeggagh and Kenane (BK) damage evolution criterion was used as [32] where κ is refereed to the BK material parameter; GShear= GII+GIII and GT=GI+GII+GIII. 2.3.2 Trapezoidal traction-separation law Trapezoidal constitutive law accurately regenerates the behavior of thin adhesive layers in mode I [33] and mode II [34] and adhesive repairs [35]. In the current work, this type of constitutive behavior was conducted for numerical prediction of delamination growth as shown in Fig. 1(b). Considering the pure-mode model, after δ1i (the first inflexion point, which leads to the plateau part of the constitutive law) the material softens progressively or, in other words, withstands damage. This is simulated by the energy being released in a cohesive zone behind the crack front. This region, named as fracture process zone (FPZ), is where the material withstands softening damage by different ways such as microscopic cracks and extensive plasticity. Numerically, the softening process is performed by a damage parameter whose values vary from zero (undamaged) to unity (completely damaged) as the material fractures. In total, the softening relationship can be written as where I is the identity matrix; D is a diagonal matrix containing, at the position corresponding to mode i(i=I, II), the damage parameter. Using the proposed damage initiation criterion (Eq. (6)) and the power law damage evolution criterion with unit power, it is possible to establish the equivalent mixed-mode displacements (δ1m, δ2m and δmu) and to establish the damage parameter in the plateau region as And in the stress softening part of the traction-separation law (after δ2m), there is All parameters in Eqs. (11) and (12) are depicted in Fig. 1(b). The damage parameter is introduced in Eq. (9), thus simulating damage propagation. A more detailed description of the trapezoidal law model is presented in Ref. [35]. This type of damage was applied to numerical model using tabular capability which relates the damage parameter dm as tabular function of relative displacement (δm). 2.3.3 PPR traction-separation law In this model, the traction force in the interface is obtained by differentiating a potential function with respect to the interface separation. Figure 1(c) shows the typical modified PPR traction-separation law of cohesive zone modeling. Park et al [29] proposed this potential based model for mixed mode fracture. This law can be used for wide variety of ductile and brittle fracture. Since it behaves nonlinearly prior to damage, it is required to develop a user defined element in ABAQUS for this model. In this work, same as other mentioned constitutive laws, linear elastic response was assumed before damage initiation (δ<δc). So, this modified version of PPR model allows for a straightforward implementation of the model in the commercial finite element code ABAQUS using tabular capability. After damage initiation, the softening relationship in this model can be expressed as [29] where δ is tangential displacement; F, n, β and δu are PPR parameters that can be determined by satisfying all boundary condition including: where G is total strain energy release rate. By applying the above mentioned boundary conditions it can be expressed as where And δu can be determined by In numerical simulation same as trapezoidal damage model, the corresponding damage variable can be defined using Eq. (9). After generating the damage variable at all the displacements, the modified PPR model can be directly implemented in ABAQUS using the tabular capability same as trapezoidal model. 3 Finite element modeling of cohesive zone Three-dimensional finite element models are developed in ABAQUS to model the delamination onset and growth using three different constitutive laws. The ENF model was composed of two layers of eight-nodded solid elements, C3D8R (adherent layers), that were connected with a layer of zero thickness eight-node cohesive element, COH3D8 (cohesive layer). Adherent layers connected to cohesive layer by surface to surface tie constraints. Figure 3 illustrates the deformed shape of the ENF specimen during crack propagation. Boundary conditions included fixing the supporting cylinders in the x, y and z directions and restraining the loading cylinder in the z direction. The lowest nodes at the specimen mid-section were restrained in the x direction. The FEM model of the ENF specimen has a uniform mesh in a damage propagation zone ahead of the crack tip. In order to predict an accurate propagation of delamination, it is necessary to have an adequate fine finite element discretization of the cohesive zone length to achieve a good estimation of the interlaminar stress fields. When the cohesive zone is discretized by too few numbers of elements, the distribution of tractions ahead of the crack tip is not represented accurately. So, in order to achieve successful FEM results, it is necessary to have a minimum number of elements in the cohesive zone length. The number of cohesive elements in the cohesive zone is: where le is the length of the cohesive elements in direction of crack propagation and lcz is the cohesive zone length. There are several guidelines for the minimum number of element in cohesive zone length. However, the minimum number of required cohesive elements in cohesive zone length is not well established. 4 Experimental procedures 4.1 Specimens and materials 4.1.1 ENF specimen Figure 4(a) shows the geometry and dimensions of the ENF specimens. In the process of specimen’s fabrication, first, E-glass/epoxy composite plate with the thickness of 2h=4.2 mm was prepared. The E-glass fibers were impregnated with a ML506 epoxy resin and HA11 hardener. The laminates were fabricated by the hand lay-up technique and the pre-crack length was produced by positioning a 13 μm thick Teflon insert at the mid-plane of the plate. In order to achieve plates with desired fiber volume fraction, special pressure tool was applied in order to squeeze out excess resin. Then, the plate was left at room temperature for 24 h to become dry. After that, the plate was trimmed by a water jet machine along the longitudinal direction in order to obtain narrow specimens with the desired dimension and initial crack length. After trimming, the nominal length (l) and the nominal width (b) of the ENF specimen were 100 and 25 mm, respectively. The initial crack length (a) was 35 mm. Fiber volume fractions, Vf, was measured using the resin burn-off method [36]. Table 1 lists the mechanical property of E-glass/epoxy woven fabrication with Vf=49% that was used in this work. 4.1.2 SLJ specimen No standard SLJ specimen is currently available for composite materials. The current specimen is believed to yield an appropriate value for τIIc. The objective of the SLJ test is to determine the Mode-II cohesive strength (τIIC) as an essential parameter in description of traction law of cohesive elements. Materials and the manufacture procedure of SLJ specimen are the same as those of ENF specimen. For SLJ specimen production, first a platewith 20 layers woven laminate [0/90]20 was fabricated. During fabrication and after the 10th layer a 13 μm thick Teflon was inserted at the both side of the plate so that a 10 mm length at middle of plate was released. This length is overlap or cohesive length of SLJ specimen. After that the plate was trimmed to 195 mm×25 mm composite specimens so that cohesive area located at the middle of the specimens. In each side of specimen, one of the delaminated sublaminate was trimmed so that an SLJ specimen as shown in Fig. 5(a) was obtained. The geometry of the SLJ specimen after trimming is shown schematically in this figure. The nominal length (l) of the SLJ specimen is 195 mm and the nominal width (b) is 25 mm. Overlap length (l2) and nominal thickness (2h) are 10 mm and 3.3 mm, respectively. In order to place the specimen in test machine fixture, two additional tabs with 50 mm length were prepared. Fig. 4 ENF specimen geometry (a) and typical ENF test (b) Table 1 mechanical property of ENF specimen 4.2 Mode-II fracture toughness GIIc All of the experiments were completed on a ZWICK electro-mechanical loading frame at room ambient temperature. Figure 4(b) shows a typical ENF test. The precision of displacement recording was 1 μm. ENF tests were carried out by displacement control at the crosshead speed of 1 mm/min. Three specimens with a=35 mm crack length were tested. A load-displacement response was recorded for each specimen during the test. In this work, the crack length was monitored by bonding to the specimen’s edge a strip of paper with the graduations printed on it and by taking photos during the experiments with 5 s intervals using a 10 mega pixel digital camera. The experimental magnitudes of P-δ-a as a function of time were determined. The time of each P-δ data point was computed using the applied displacement and the corresponding loading rate. The time for each value of crack length is the one at which the corresponding photo was taken. These experimental results were then used to verify the adequacy of the three-dimensional finite element scheme utilized to obtain GIIc. In order to calculate the mode-II critical strain energy release rate, there are many commonly used data reduction methods including compliance calibration method (CCM) that is based on the Irwin-Kies principle, direct beam theory (DBT) and the corrected beam theory. In the present work, corrected beam theory proposed by Moura et al [21] was used. Only one specimen is sufficient to obtain the resistance curve of the specimen (r-curve) which is the main advantage of this method. According to this theory, mode-II critical strain energy release rate can be computed as where P and a are load and crack length, respectively; B and L are specimen width and half of the span length, respectively; E11 is axial modulus; h is the half thickness of ENF specimen; △1 is the crack length correction to account for shear deformation and is given by [21] where where E33 and G13 are through-the-thickness and shear modulus, respectively. 4.3 Tangential cohesive strength τIIC The tangential cohesive strength (τIIC) is the most important parameter in the traction-separation law for prediction of critical Mode-II strain energy release rate. In the current work, this parameter was determined using SLJ test. In this process, three SLJ failure tests were completed. Figure 5(b) shows a typical SLJ test. In order to prevent slippage during the test, specimen was accurately balanced, and also specimen surface and additional tab surfaces were roughened. All of the tests were carried out by displacement control at the crosshead speed of 0.5 mm/min until fracture. Figure 6 shows the scanning electron microscopic (SEM) image of a typical cohesive area after test. Decohesion between fiber and matrix is dominant failure mode as it was observed in the gage portion. So, it is obvious that bulk matrix behaves differently as thin cohesive layer due to constraint effects induced by the adhesion between fiber and matrix. As a result, bulk properties should not be used and the tangential cohesive strength should be determined by an SLJ test method. For data reduction, all specimens were assumed to have failed instantly. Figure 7 shows the load-displacement response of three tested SLJ specimens. The measured load is initially negligible, corresponding to clearance of fixture. The test was preceded until a maximum load is achieved and followed by a sudden load drop, indicating specimen failure. Fig. 5 SLJ specimen geometry (a) and typical SLJ test (b) Fig. 6 Scanning electron microscopic (SEM) image of SLJ cohesive area The specimen failure is assumed at this maximum load. The critical stress values (τIIC) were computed using Eq.(12): Fig. 7 Load-displacement response of SLJ specimens where Pmax is the maximum load in which failure occurs and Acoh is the cohesive area of the SLJ specimen. The mean value of the maximum loads which are illustrated in Fig. 7 was considered Pmax. 5 Results and discussion Using Eq. (12) for data reduction and substitution this value for Pmax, the tangential cohesive strength of material, is computed as 19.86 MPa. Table 2 lists the cohesive properties of E-glass/epoxy woven composite laminate. FEM models of each specimen were performed using ply elastic properties of adherent layers that are given in table 1 and the interfacial properties are listed in Table 2. Table 2 interfacial property of E-glass/epoxy 5.1 cohesive zone length estimation The length of the cohesive zone lcz is introduced as the distance between the crack tip and the point where the maximum cohesive traction is achieved. The length of the cohesive zone at the initiation of crack growth is independent of applied load and crack length. This means cohesive zone length at the crack initiation is a material property. There are several models in the literature that estimated the length of the cohesive zone [6-8, 37-38]. All of the models for estimation of the cohesive zone length have similar forms as mentioned in Eq. (22) [8]. where GIIC is the critical strain energy release rate; sIIC is the cohesive strength; R is a parameter that depends on each cohesive zone model. For instance, in Irwin’s model [39] carried out with R=0.31 or in Dugdale [6] and Barenblatt [7] models, the value for R is considered 0.4. In the current work, in order to calculate the distribution of tractions in cohesive layer of model and the corresponding cohesive zone length, a very refined mesh using cohesive element size of 0.25 mm was used in the modeling of an ENF specimen. The distribution of tractions ahead of the crack tip at the delamination onset of ENF specimen is illustrated in Fig. 8. At crack initiation point, traction on crack tip vanished as it expected from the cohesive zone model theory. According to this analysis, the cohesive zone length of material is calculated as 4.45 mm as shown in Fig. 8. Using the material property listed in Tables 1 and 2, the parameter R in Eq. (22) is computed as 0.07. Cohesive zone length is a material property that has a high order of importance regarding to reach a successful prediction of delamination onset. This parameter previously introduced as a function of cohesive strength [27]. So, using the tangential cohesive strength value that is obtained using SLJ test, this parameter as a material property is characterized. Fig. 8 Distribution of traction ahead of crack front 5.2 Effect of penalty stiffness on damage prediction The cohesive zone length was discretized using cohesive element size of 0.5 mm and different values of the penalty stiffness in order to investigate the effect of the stiffness on the predicted load-displacement response of composite material. The results of the simulations are illustrated in Fig. 9. As shown in this figure, the load–displacement response curves achieved from simulations with applying penalty stiffness greater than 109 N/m3 are approximately identical. Moreover, smaller values of the penalty stiffness have a strong effect on the predicted load–displacement responses since a stiff connection between the two sublaminates is not established. Fig. 9 Effect of penalty stiffness on load-displacement response However, the number of iterations needed for the solution when using penalty stiffness 109 N/m3 is smaller than that of iterations needed in a range of the interface stiffness between 1011 and 1014 N/m3. For values of the penalty stiffness greater than 1014 N/m3, poor convergence was resulted. The stiffness obtained from Eq. (5) with χ=25 is 27.14×1012 N/m3, which is ideal value for good prediction and convergence procedure. 5.3 Effect of mesh refinement on damage prediction Several ENF specimens were simulated with different sizes of cohesive element in cohesive zone length using the material properties listed in Tables 1 and 2 and interfacial stiffness of K=27.14×1012 N/m3. The predicted load-displacement responses obtained using ENF models are compared with the experimental result in Fig. 10. In this analysis cohesive element sizes (in direction of crack propagation) range from 0.25 mm to 2 mm. Fig. 10 Experimental and cohesive zone model predictions of delamination with various element lengths (le) in direction of crack growth The results illustrate that for all mesh sizes converge solution is obtained but it is necessary to apply a mesh size, le, less than 1 mm to accurate prediction of delamination initiation. The analyses using coarser meshes significantly overpredict the strength of the ENF specimen and the response does not follow the experimental results. Cohesive zone length, lcz, for the material described in tables 1 and 2 is 4.45 mm as previously obtained from Eq. (22). Therefore, according to Eq. (17), for a mesh size smaller than 1 mm, more than four elements would span the cohesive zone length, which is enough for an accurate prediction of the fracture onset. There are several guidelines for a minimum required element in cohesive zone length. For example, MO 5.4 Comparison between traction separation laws To verify the adequacy of the three traction separation laws used to measure GIIC, a numerical study was also conducted. The objective is to determine how the used models reproduce the crack initiation and propagation. The load-displacement response of modified PPR traction separation law is depicted in Fig. 11. In the current study, the value of shape parameter β varies from 1 to 4. The value of penalty stiffness, K, for all numerical damage prediction was set to K=27.14×1012 N/m3. As shown in this figure, increasing the value of shape parameter β increases the rate at which material loses its stiffness once damage initiated. Fig. 11 Load-displacement responses of modified PPR model compared with experimental results In other words, increasing the parameter β decreases the fracture process zone effect ahead of crack tip. In the case of β=1 and 2.3, there is a gradual fall in the load and the material does not completely fracture. In the case of β=3 and 4, a sudden drop in the load-displacement response is achieved, which means that a large number of cohesive elements failed at the same time. As the β further increases, the drop becomes steeper. It is obvious that changing the value of β changes the place of pick point in load-displacement response. In this work, a value of β=2.3 was chosen as an optimum value for numerical prediction of damage propagation. Figure 12 shows load-displacement response of ENF specimen calculated using three different constitutive laws and compared with experimental result. As shown in this figure, the modified PPR model was found adequate to reproduce the experimentally observed behavior of the composite specimen. Trapezoidal and modified PPR models reproduced approximate smooth crack initiation and propagation while bilinear model depicted sudden damage propagation. This means that trapezoidal and modified PPR models accounted for fracture process zone created ahead of crack tip. On the other hand, a complete R-curve was determined using experimental and numerical P-δ data. To calculate the experimental R-curve, the numerical values of P-δ-a parameters were recorded during crack propagation and were used to obtain the critical fracture energies versus crack length. Figure 13 shows the results of one case compared with numerical results for the same specimen used in Fig. 12. The bilinear model underestimated the critical fracture energy which can be explained by the non-negligible amount of energy being dissipated in the FPZ that is not accounted for in this model. The initial part of the R-curves does not correspond to crack propagation, but to FPZ development. So, the difference between trapezoidal and modified PPR models with experimental R-curve is lower than that of bilinear model. Fig. 12 Load-displacement responses of three different damage models compared with experimental results Fig. 13 Numerical and experimental R-curves Accurate prediction was achieved with modified PPR model. 6 conclusions 1) Mode II interfacial delamination of E-glass/ epoxy composite laminates is characterized using a proposed cohesive zone model. For this purpose, a simple structural SLJ test has been proposed to compute the Mode-II cohesive strength, τIIC, as a cohesive parameter. The corresponding critical fracture energy (GIIC) is measured by ENF tests, using corrected beam theory as data reduction scheme. A modified version of PPR damage model is proposed to reproduce damage onset and growth and compared with mixed-mode triangular and trapezoidal constitutive relationship between stress (s) and relative displacements (δ) of cohesive element. A closed-form solution based on mechanical consideration of composite material for estimating of penalty stiffness required for the constitutive response of a cohesive finite element is presented. In order to numerical prediction of damage initiation and propagation, 3-D finite element analysis with cohesive element of ABAQUS is conducted. 2) It is verified that the proposed penalty stiffness conducted good damage prediction and also convergence procedure. The results of 3-D finite element analysis with experimentally obtained cohesive parameters (τIIC, GIIC) enclosed that accurate delamination prediction is achieved using the modified PPR model and this model is considered an accurate model for delamination characterization of woven E-glass/epoxy composite laminate. It is concluded that trapezoidal and modified PPR models accounted for fracture process zone created ahead of crack tip as compared to bilinear model. Cohesive zone length as a material property is determined. 3) SEM image of SLJ cohesive area after test enclosed that decohesion between fiber and matrix is dominant failure mode. To ensure the sufficient dissipation of energy, finite element analysis with different discretization of cohesive zone length is conducted and shown that the predicted responses are obtained using the cohesive element correlate well with the experimental solutions when at least 4 elements span cohesive zone length. Acknowledgment This work has been funded by University of Tabriz and authors would like to thank the University of Tabriz for the grant. References [1] Brunner A, Blackman B, Davies P. A status report on delamination resistance testing of polymer-matrix composites [J]. Engineering Fracture Mechanics, 2008, 75: 2779-2794. [2] Liu P, Yang Y. Finite element analysis of the competition between crack deflection and penetration of fiber-reinforced composites using virtual crack closure technique [J]. Applied Composite Materials, 2014, 21: 759-771. [3] Judt P O, Ricoeur A, Linek G. Crack path prediction in rolled aluminum plates with fracture toughness orthotropy and experimental validation [J]. Engineering Fracture Mechanics, 2015, 138: 33-48. [4] Davis B, Wawrzynek P, Hwang C, Ingraffea A. Decomposition of 3-D mixed-mode energy release rates using the virtual crack extension method [J]. Engineering Fracture Mechanics, 2014, 131: 382-405. [5] Qian Z D, Hu J. Fracture properties of epoxy asphalt mixture based on extended finite element method [J]. Journal of Central South University, 2012, 19: 3335-3341. [6] Dugdale D. Yielding of steel sheets containing slits [J]. Journal of the Mechanics and Physics of Solids 1960, 8: 100-104. [7] Barenblatt G. The mathematical theory of equilibrium cracks in brittle fracture [J]. Advances in applied mechanics, 1962, 7: 55-129. [8] Hillerborg A, Modéer M, Petersson P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J]. Cement and concrete research, 1976, 6: 773-781. [9] Needleman A. An analysis of decohesion along an imperfect interface [J]. International Journal of Fracture, 1990, 42: 21-40. [10] Xu X P, Needleman A. Numerical simulations of fast crack growth in brittle solids [J]. Journal of the Mechanics and Physics of Solids, 1994, 42: 1397-1434. [11] Nguyen V P, Kerfriden P, Bordas S. Two-and three-dimensional isogeometric cohesive elements for composite delamination analysis [J]. Composites Part B: Engineering, 2014, 60: 193-212. [12] Vandellos T, Huchette C, Carrère N. Proposition of a framework for the development of a cohesive zone model adapted to carbon-fiber reinforced plastic laminated composites [J]. Composite Structures, 2013, 105: 199-206. [13] Zhang Z J, Paulino G H. Cohesive zone modeling of dynamic failure in homogeneous and functionally graded materials [J]. International Journal of Plasticity, 2005, 21: 1195-1254. [14] Song S H, Paulino G H, Buttlar W G. Simulation of crack propagation in asphalt concrete using an intrinsic cohesive zone model [J]. Journal of Engineering Mechanics, 2006, 132: 1215-1223. [15] Park K, Paulino G H, Roesler J R. Determination of the kink point in the bilinear softening model for concrete [J]. Engineering Fracture Mechanics, 2008, 75: 3806-3818. [16] de Morais A, Pereira A, de Moura M. Mode III interlaminar fracture of carbon/epoxy laminates using the six-point edge crack torsion (6ECT) [J]. Composites Part A: Applied Science and Manufacturing, 2011, 42: 1793-1799. [17] Zhao L, Gong Y, Zhang J, Chen Y, Fei B. Simulation of delamination growth in multidirectional laminates under mode I and mixed mode I/II loadings using cohesive elements [J]. Composite Structures, 2014, 116: 509-522. [18] de Morais A. Mode I cohesive zone model for delamination in composite beams [J]. Engineering Fracture Mechanics, 2013, 109: 236-245. [19] de Morais A. Cohesive zone beam modelling of mixed-mode I–II delamination [J]. Composites Part A: Applied Science and Manufacturing, 2014, 64: 124-131. [20] Khoshravan M R, Moslemi M. Investigation on mode III interlaminar fracture of glass/epoxy laminates using a modified split cantilever beam test [J]. Engineering Fracture Mechanics, 2014, 127: 267-279. [21] de Moura M, Campilho R, [22] Liljedahl C, Crocombe A, Wahab M A, Ashcroft I. Damage modelling of adhesively bonded joints [J]. International journal of fracture, 2006, 141: 147-161. [23] Liu P, Islam M. A nonlinear cohesive model for mixed-mode delamination of composite laminates [J]. Composite Structures, 2013, 106: 47-56. [24] Blackman B, Hadavinia H, Kinloch A, Williams J. The use of a cohesive zone model to study the fracture of fibre composites and adhesively-bonded joints [J]. International journal of fracture, 2003, 119: 25-46. [25] Song S H, Paulino G H, Buttlar W G. A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material [J]. Engineering Fracture Mechanics, 2006, 73: 2829-2848. [26] Kafkalidis M, Thouless M D, Yang Q, Ward S. Deformation and fracture of adhesive layers constrained by plastically-deforming adherends [J]. Journal of adhesion science and technology, 2000, 14: 1593-1607. [27] Turon A, Davila C G, Camanho P P, Costa J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models [J]. Engineering Fracture Mechanics, 2007, 74: 1665-1682. [28] Alvarez D, Blackman B, Guild F, Kinloch A. Mode I fracture in adhesively-bonded joints: A mesh-size independent modelling approach using cohesive elements [J]. Engineering Fracture Mechanics, 2014, 115: 73-95. [29] Park K, Paulino G H, Roesler J R. A unified potential-based cohesive model of mixed-mode fracture [J]. Journal of the Mechanics and Physics of Solids, 2009, 57: 891-908. [30] Zou Z, Reid S, Li S, Soden P. Modelling interlaminar and intralaminar damage in filament-wound pipes under quasi-static indentation [J]. Journal of Composite Materials, 2002, 36: 477-499. [31] Camanho P P, Davila C, de Moura M. Numerical simulation of mixed-mode progressive delamination in composite materials [J]. Journal of Composite Materials, 2003, 37: 1415-1438. [32] Benzeggagh M, Kenane M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus [J]. Composites Science and Technology, 1996, 56: 439-449. [33] Andersson T, Stigh U. The stress–elongation relation for an adhesive layer loaded in peel using equilibrium of energetic forces [J]. International Journal of Solids and Structures, 2004, 41: 413-434. [34] Leffler K, Alfredsson K, Stigh U. Shear behaviour of adhesive layers [J]. International Journal of Solids and Structures, 2007, 44: 530-545. [35] Campilho R, de Moura M, Domingues J. Using a cohesive damage model to predict the tensile behaviour of CFRP single-strap repairs [J]. International Journal of Solids and Structures, 2008, 45: 1497-1512. [36] Carlsson L, Adams D F, Pipes R B. Experimental characterization of advanced composite materials [M]. United States: CRC press, 2002. [37] Hui C Y, Jagota A, Bennison S, Londono J. Crack blunting and the strength of soft elastic solids [J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2003, 459: 1489-1516. [38] Falk M L, Needleman A, Rice J R. A critical evaluation of cohesive zone models of dynamic fracture [J]. Le Journal de Physique IV, 2001, 11: Pr5-43-Pr5-50. [39] Irwin G. Plastic zone near a crack and fracture toughness [C]// Proceedings of the Seventh Sagamore Ordance Materials Conference. New York: Syracuse University, 1960, IV: 63-78. [40] MO [41] Dávila C G, Camanho P P, de Moura M F. Mixed-mode decohesion elements for analyses of progressive delamination [J]. Proceedings of the 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Seattle: NASA, 2001. (Edited by YANG Hua) Received date: 2015-03-02; Accepted date: 2015-06-04 Corresponding author: Mohsen Moslemi, PhD Candidate; Tel: +98-4113392484; Fax: +98-4113354153; E-mail: m.moslemi@tabrizu.ac.ir (5)
(5) (6)
(6)
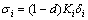 (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12)
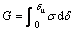 (13)
(13)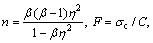
 (14)
(14) (15)
(15) (16)
(16) (17)
(17)

 (18)
(18) (19)
(19)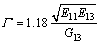 (20)
(20)

 (21)
(21)
 (22)
(22)


 S and Belytschko [40] proposed using more than 10 elements and Falk et al [38] suggested between 2 and 5 elements in their work. In the work of Dávila et al [41], the minimum required element length to predict the delamination in a double cantilever beam (DCB) model was 1 mm. According to the results of this work, it is recommended using more than 4 elements in cohesive zone of simulated ENF specimen. The difference between predictions from using a coarse mesh in the modeling of delamination in an ENF specimen is due to the magnitude of tractions ahead of the crack tip.
S and Belytschko [40] proposed using more than 10 elements and Falk et al [38] suggested between 2 and 5 elements in their work. In the work of Dávila et al [41], the minimum required element length to predict the delamination in a double cantilever beam (DCB) model was 1 mm. According to the results of this work, it is recommended using more than 4 elements in cohesive zone of simulated ENF specimen. The difference between predictions from using a coarse mesh in the modeling of delamination in an ENF specimen is due to the magnitude of tractions ahead of the crack tip.


 J. Pure mode II fracture characterization of composite bonded joints [J]. International Journal of Solids and Structures, 2009, 46: 1589-1595.
J. Pure mode II fracture characterization of composite bonded joints [J]. International Journal of Solids and Structures, 2009, 46: 1589-1595. S N, Belytschko T. Extended finite element method for cohesive crack growth [J]. Engineering Fracture Mechanics, 2002, 69: 813-833.
S N, Belytschko T. Extended finite element method for cohesive crack growth [J]. Engineering Fracture Mechanics, 2002, 69: 813-833.

