DOI: 10.11817/j.issn.1672-7207.2017.11.025
优化的灰色离散Verhulst模型在基坑沉降预测中的应用
张闯,彭振斌,彭文祥
(中南大学 地球科学与信息物理学院,湖南 长沙,410083)
摘要:基于传统的灰色Verhulst模型在基坑沉降预测中精度较低的问题,提出优化的灰色离散Verhulst模型。在基坑沉降监测中,由于有新的监测沉降值不断补充到原始数据序列中,各种因素会带来新的扰动,原来的模型精度降低,为避免由此产生的误差,用新陈代谢方法建立优化灰色离散Verhulst一维、二维新陈代谢模型。将传统Verhulst模型、优化的灰色离散Verhulst模型及优化灰色离散Verhulst一维、二维新陈代谢模型进行比较。研究结果表明:该模型通过采用离散化思维对原数据序列进行倒数变换,从连续形式向离散形式变化,减小了传统Verhulst模型建模过程中从微分方程到差分方程带来的误差;采用新陈代谢方法的优化灰色离散Verhulst模型精度更高,可选用该模型对基坑进行沉降预测。
关键词:沉降预测;优化的灰色离散Verhulst模型;新陈代谢方法;预测精度
中图分类号:TU432 文献标志码:A 文章编号:1672-7207(2017)11-3030-07
Application of optimized grey discrete Verhulst model in settlement prediction of foundation pit
ZHANG Chuang, PENG Zhenbing, PENG Wenxiang
(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Abstract: Considering the low accuracy of the traditional grey Verhulst model in the foundation pit settlement prediction, the optimized discrete grey Verhulst model was put forward. In the settlement monitoring of foundation pit, the new monitoring settlement data was constantly added to the original data sequence, and all kinds of factors would bring new disturbance, so the original model accuracy was reduced. In order to avoid the resulting errors, the metabolic method was used to establish the optimization of one-dimensional and two-dimensional metabolic model of grey discrete Verhulst model. The traditional Verhulst model, the optimization of the discrete grey Verhulst model and the optimization of one- dimensional and two-dimensional metabolic model of grey discrete Verhulst model were compared. The results show that the proposed model is based on the reciprocal transformation of the original data sequence by using discrete thinking, and the change from continuous form to discrete form reduces the error from the differential equation to the difference equation in the modeling process of the traditional Verhulst model. The optimized grey discrete Verhulst model based on the metabolic method has higher accuracy, and the model can be used to predict the settlement of the foundation pit.
Key words: settlement prediction; optimized discrete grey Verhulst model; metabolism method; prediction precision
基坑沉降预测是工程监测中非常重要的内容。在施工过程中,通过监测可以及时发现问题,从而采取补救措施,减少事故的发生。但有些基坑沉降监测周期太长,因此,进行沉降预测很有必要。现在使用较多的方法有灰色关联支持向量机、人工神经网络法、双曲线法、Asaoka法、遗传算法、灰色理论GM(1,1)和Verhulst法等[1-10]。土力学理论已证实,当符合线性加载条件时,基坑全过程沉降与时间的关系呈饱和状态呈“S”形曲线[11],灰色Verhulst模型表现出的规律也呈“S”形变化,因此,基坑沉降经常用灰色Verhulst模型预测。但灰色Verhulst模型预测精度较低,对此人们提出优化的灰色离散Verhulst模型。在建立离散灰色模型过程中,首先对原始数据进行倒数变换,然后进行预测、模拟。参数估计都是利用离散方程,没有使用离散模型与连续模型之间的近似代替方程,因而降低了误差,模型的精度大幅度提高[12]。基坑沉降监测时间长,会有新的监测沉降值不断补充到原始数据序列中,各种因素带来新的扰动,原来的模型会渐渐老化,精度降低,因此,模型需要不断优化更新[13]。通常用新陈代谢方法建立优化灰色离散Verhulst模型的一维、二维新陈代谢模型,以进一步提高模型的精度和稳定性。
1 优化模型
在建模之前,检验所用的数据序列是否可以用来建模,一般用数据序列级比来检验。
定义1[14]设
 ;k=2, 3, …, n (1)
;k=2, 3, …, n (1)
为X序列的级比。因为Verhulst模型是GM(1,1)的幂模型,而GM(1,1)模型要求级比 满足覆盖
满足覆盖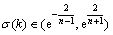 的序列,不管是原始的还是倒数变换后的,都能够作为GM(1,1)建模的序列,因此,Verhulst模型的级比也遵循此原则。
的序列,不管是原始的还是倒数变换后的,都能够作为GM(1,1)建模的序列,因此,Verhulst模型的级比也遵循此原则。
1.1 传统灰色Verhulst模型
定义2[12, 15]:设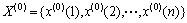 为原始非负数据序列,
为原始非负数据序列, 的一阶累加生成序列为
的一阶累加生成序列为 ,
, 的紧邻均值生成序列为
的紧邻均值生成序列为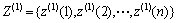 ,则称
,则称
 (2)
(2)
为灰色Verhulst模型。其中: ,k=1, 2, …, n;
,k=1, 2, …, n; ,k=2, 3, …, n。
,k=2, 3, …, n。
根据式(2)利用最小二乘法,估计出参数a和b,得
 (3)
(3)
其中: ;
;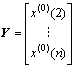 。
。
定义3[12, 15]:将
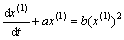 (4)
(4)
称作灰色Verhulst模型白化方程。
定理1[12, 15]:设B,Y和 ,如上所述,
,如上所述, ,灰色Verhulst模型白化方程
,灰色Verhulst模型白化方程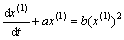 的解也称为时间响应函数,即
的解也称为时间响应函数,即
 ;k=1, 2, …, n-1 (5)
;k=1, 2, …, n-1 (5)
Verhulst模型的已知数据序列应是等时间段的,原始数据序列很多时候都是不等距的,因此,利用spline三次样条插值[16-17]、Hermite插值[18]等方法对原始数据进行等距处理。
1.2 优化的灰色离散Verhulst模型
定义4:设有非负数据序列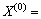
 ,
, 为
为 的一阶累加生成序列,记为
的一阶累加生成序列,记为 。式中,
。式中,
 ,
, 为
为 的倒数序列,即有
的倒数序列,即有 (k=1, 2, …, n),则称
(k=1, 2, …, n),则称
 (6)
(6)
为优化的离散Verhulst模型。
优化的灰色离散Verhulst模型中的待估参数为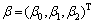 ,采用最小二乘法对式(6)进行计算可得
,采用最小二乘法对式(6)进行计算可得
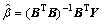 (7)
(7)
式中: ;
; 。
。
定理2 若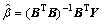 ,且初始条件为
,且初始条件为 ,则优化的灰色离散Verhulst模型解为
,则优化的灰色离散Verhulst模型解为

 ;
;
k=1, 2, …, n-1 (8)
定理3 若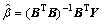 ,且初始条件为
,且初始条件为 ,则优化的灰色离散Verhulst模型解为
,则优化的灰色离散Verhulst模型解为

 (9)
(9)
其中:k=1, 2, …, n-1。
1.3 优化的灰色离散Verhulst新陈代谢模型
在监测过程中,会有新的监测数据被补充。随着施工的进行,也会有扰动或驱动因素进入系统,影响系统的发展,从而使系统发展到远离时间原点,旧数据将失去意义,因此,要将新数据补充到系统中且同时除去旧数据,建模序列才会体现出系统现在的特征。新陈代谢建模方法[12]为:将预测得到的1个新数据加到现有数据序列之后,同时除去第1个已有的数据,使数据序列等维,建立优化的灰色离散Verhulst模型预测下一个值。将新预测值补充到数据序列后,再去掉上一数据序列中的第1个数据,直到完成预测目标为止。本文结合新陈代谢的方法,建立优化的灰色离散Verhulst一维、二维新陈代谢模型,以举例说明优化的灰色离散Verhulst新陈代谢模型可以很好地反映基坑沉降的趋势与变化,以及该新陈代谢方法能提高模型的稳定性和预测精度。
1.4 预测值的精度检验[12-13]
设e(i)为原始数据列 和预测数据列
和预测数据列 的残差,即
的残差,即 ,则可用下列指标对预测值进行精度检验。
,则可用下列指标对预测值进行精度检验。
1) 相对误差α:
 (10)
(10)
2) 均方差比值C:
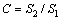 (11)
(11)
式中:S1为原始数据的均方差;S2为残差的均方差。
3) 绝对关联度 :
:

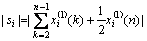
 (12)
(12)
 (13)
(13)
4) 小误差概率P:
 (14)
(14)
式中: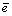 为残差均值。模型精度等级见表1。
为残差均值。模型精度等级见表1。
表1 模型精度等级
Table 1 Grads model precision

2 应用实例
广东省深圳市深房御府东区基坑支护工程位于深圳市光明新区,北靠牛山,东临光侨路,西南侧为观光路;场地高差较大,四周已新建市政道路。该地块开发建设为7 栋高层,均为16 层,剪力墙结构,设2层地下室,局部3层地下室;联排别墅均为3 层,框架结构,设1层地下室。基础埋深8~10 m。该基坑开挖深度较深,在基坑、桩基础及地下室施工过程中必须进行监测,从而保证基坑的安全和稳定,达到信息化施工、及早发现问题和处理问题的目的。本基坑共有33 个沉降监测点,点号为W1~W33。选取2个监测点W32和W33的原始数据序列建立传统Verhulst模型、优化的灰色离散Verhulst模型及优化的灰色离散Verhulst一维、二维新陈代谢模型,对基坑进行沉降预测。每个月为1个监测周期,共选9个周期的累计沉降数据。前7个数据用来建立模型,后2个数据用来与预测值对比。
由式(1)得监测点W32和W33级比,见表2。本文取前7个数据序列建模,即n=7,则级比覆盖 ,由表2中监测点W32和W33级比可知都在级比覆盖范围之内,故监测点W32和W33原始数据序列可以用来建模。
,由表2中监测点W32和W33级比可知都在级比覆盖范围之内,故监测点W32和W33原始数据序列可以用来建模。
表2 监测点累计沉降和级比
Table 2 Cumulative settlement of monitoring points and class ratio

选取表2中监测点W32前7个实测值进行预测建模。
1) 求出传统灰色Verhulst模型参数a=-0.435 660,b=-0.033 442,代入式(5)得
 ;
;
k=1, 2, …, 8 (15)
2) 求出优化的灰色离散Verhulst模型参数为 ,
, ,
, ,代入式(8)得
,代入式(8)得

 ;
;
k=1, 2, …, 8 (16)
3) 建立优化的灰色离散Verhulst一维新陈代谢模型[19],去除第1个监测数据,使用第2~8期监测数据作为原始时间序列得模型参数为 ,
, ,
, ,代入式(8)得
,代入式(8)得

 ;
;
k=1, 2, …, 8 (17)
4) 建立优化的灰色离散Verhulst二维新陈代谢模型[19]。同理使用第3~9期监测数据作为原始时间序列得模型参数为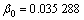 ,
, ,
, ,代入式(8)得
,代入式(8)得

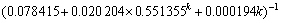 ;
;
k=1, 2, …, 8 (18)
求出4个模型的拟合值及预测值见表3。同理取表2中监测点W33前7个实测值进行预测建模。
1) 求出传统灰色Verhulst模型为
 ;
;
k=1, 2, …, 8 (19)
2) 求出优化的灰色离散Verhulst模型为

 ;
;
k=1, 2, …, 8 (20)
3) 求出优化的灰色离散Verhulst一维新陈代谢模型为

 ;
;
k=1, 2, …, 8 (21)
4) 求出优化的灰色离散Verhulst二维新陈代谢模型为

 ;
;
k=1, 2, …, 8 (22)
求出4个模型的拟合值及预测值见表4。
用式(10)~(14)检验4种模型的拟合程度和预测效果,检验结果见表5。
由表3和表4可知优化的灰色离散Verhulst模型的拟合值比传统的灰色Verhulst模型的拟合值更接近实测值,而用新陈代谢方法建立的优化的灰色离散Verhulst模型的拟合值更进一步接近实测值,且随着新陈代谢维数的增加,预测值也更接近实测值,预测精度更高。从表5可知监测点W32的传统灰色Verhulst模型平均相对误差为1.205 2,优化的灰色离散Verhulst模型平均相对误差只有0.600 1,为传统灰色Verhulst模型平均相对误差的1/2;优化的灰色离散Verhulst一维新陈代谢模型平均相对误差只有0.493 3,为传统灰色Verhulst模型平均相对误差的1/3;优化的灰色离散Verhulst二维新陈代谢模型平均相对误差只有0.483 6,为传统灰色Verhulst模型平均相对误差的1/3,而且可知优化的灰色离散Verhulst二维新陈代谢模型平均相对误差比优化的灰色离散Verhulst一维新陈代谢模型平均相对误差小。监测点W33的传统灰色Verhulst模型平均相对误差为2.379 3,优化的灰色离散Verhulst模型平均相对误差只有0.401 4,仅为传统灰色Verhulst模型平均相对误差的1/6;优化的灰色离散Verhulst一维新陈代谢模型平均相对误差只有0.329 4,仅为传统灰色Verhulst模型平均相对误差的1/7;优化的灰色离散Verhulst二维新陈代谢模型平均相对误差只有0.329 3,仅为传统灰色Verhulst模型平均相对误差的1/7,而且优化的灰色离散Verhulst二维新陈代谢模型平均相对误差比优化的灰色离散Verhulst一维新陈代谢模型的平均相对误差小。由表5还可知优化模型的均方差比值都比传统Verhulst模型的均方差比值小,这说明优化模型预测精度高。由表1得到优化模型的精度等级为1级。从上面的分析得出优化模型比传统模型具备更高的可靠性和预测精度,由新陈代谢方法建立的优化模型有更好的模拟预测效果。
表3 点W32不同模型沉降拟合预测值和相对误差
Table 3 Fitted and predictive settlements and relative errors of different models for point W32

表4 点W33不同模型沉降拟合预测值和相对误差
Table 4 Fitted and predictive settlements and relative errors of different models for point W33

表5 不同模型的沉降精度检验
Table 5 Prediction and analysis settlements of different models

3 结论
1) 优化的灰色离散Verhulst模型是由变换倒数生成的序列建立的,将适用范围扩展到近似“S”型数据序列,而且能有效地减小由微分方程到差分方程建模过程中所带来的误差。
2) 采用新陈代谢方法建立模型,将新的监测数据补充到数据序列中同时去掉老数据,从而使模型参数不断更新优化,模型的稳定性和预测精度有很大提高。
3) 优化的灰色离散Verhulst模型和优化的灰色离散Verhulst一维、二维新陈代谢模型与传统灰色Verhulst模型相比,优化模型具备较好的实用性和可靠性,且新陈代谢方法建立的优化模型精度更高。
4) 优化模型具有预测精度高、预测误差波动小等特点,且拟合值与实测值非常接近,所以,优化模型具备更好的适用性。
参考文献:
[1] 谭鹏, 曹平. 基于灰色关联支持向量机的地表沉降预测[J]. 中南大学学报(自然科学版), 2012, 43(2): 632-637.
TAN Peng, CAO Ping. Predicting surface settlement of tunnel using grey relational-support vector machine[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 632-637.
[2] 李长冬, 唐辉明, 胡斌, 等. 小波分析和RBF神经网络在地基沉降预测中的应用研究[J]. 岩土力学, 2008, 29(7): 1917-1922.
LI Changdong, TANG Huiming, HU Bin, et al. Research on application of wavelet analysis and RBF neural network to prediction of foundation settlement[J]. Rock and Soil Mechanics, 2008, 29(7): 1917-1922.
[3] 何良德, 姜晔. 双曲型曲线模型在路基沉降预测中的应用[J]. 河海大学学报(自然科学版), 2009, 37(2): 200-205.
HE Liangde, JIANG Ye. Application of hyperbolic curves to prediction of embankment settlements[J]. Journal of Hohai University (Natural Sciences), 2009, 37(2): 200-205.
[4] ASAOKA A. Observational procedure of settlement prediction[J]. Soils and Foundations, 1978, 18(4): 87-101.
[5] 夏江, 严平, 庄一舟, 等. 基于遗传算法的软土地基沉降预测[J]. 岩土力学, 2004, 25(7): 1131-1135.
XIA Jiang, YAN Ping, ZHUANG Yizhou, et al. Predictions of soft ground settlements based on genetic algorithm[J]. Rock and Soil Mechanics, 2004, 25(7): 1131-1135.
[6] 吴大志, 李夕兵, 蒋卫东. 灰色理论在高路堤沉降预测中的应用[J]. 中南工业大学学报(自然科学版), 2002, 33(3): 230-233.
WU Dazhi, LI Xibing, JIANG Weidong. Application of grey theory to the settlement prediction for high fills[J]. Journal of Central South University of Technology (Natural Science), 2002, 33(3): 230-233.
[7] 崔广强, 林从谋, 耿鹏. 爆炸挤淤筑堤沉降的Verhulst预测[J]. 岩土力学, 2009, 30(9): 2770-2774.
CUI Guangqiang, LIN Congmou, GENG Peng. Verhulst prediction model and its application to embankment settlement with explosive compaction method[J]. Rock and Soil Mechanics, 2009, 30(9): 2770-2774.
[8] 张庆伟, 肖建清. GM(1,1)与Verhulst模型在地基沉降预测中的适用性比较[J]. 沈阳工业大学学报, 2014, 36(6): 716-720.
ZHANG Qingwei, XIAO Jianqing. Comparison in applicability of GM(1,1) and Verhulst models in prediction of foundation settlement[J]. Journal of Shenyang University of Technology, 2014, 36(6): 716-720.
[9] 杨英华. 土力学[M]. 北京: 地质出版社, 1986: 65-107.
YANG Yinghua. Soil mechanics[M]. Beijing: Geology Press, 1986: 65-107.
[10] 顾晓鲁. 地基与基础[M]. 北京: 中国建筑工业出版社, 1993: 189-191.
GU Xiaolu. Ground and foundations[M]. Beijing: China Architecture and Building Press, 1993: 189-191.
[11] 刘子彤, 梅国雄, 宰金珉, 等. 沉降-时间曲线呈“S”形的证明: 从一维固结理论角度[J]. 南京工业大学学报, 2003, 25(5): 1-3.
LIU Zitong, MEI Guoxiong, ZAI Jinmin, et al. Proof of s-t curve appearing “S” shape based on one-dimensional consolidation[J]. Journal of Nanjing University of Technology, 2003, 25(5): 1-3.
[12] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 5版. 北京: 科学出版社, 2010: 176-179.
LIU Sifeng, DANG Yaoguo, FANG Zhigeng, et al. Grey information theory and practical application[M]. 5th ed. Beijing: Science Press, 2010: 176-179.
[13] 刘寒冰, 向一鸣, 阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用[J]. 岩土力学, 2013, 34(1): 173-181.
LIU Hanbing, XIANG Yiming, RUAN Youxing. A multivariable grey model based on background value optimization and its application to subgrade settlement prediction[J]. Rock and Soil Mechanics, 2013, 34(1): 173-181.
[14] 邓聚龙. 灰色预测与灰决策[M]. 武汉: 华中科技大学出版社, 2002: 111-112.
DENG Julong. Grey forecasting and grey decision making[M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 111-112.
[15] LIU S F, LIN Y. Grey systems theory and application[M]. Berlin: Springcr-Vcrlag, 2011: 169-190.
[16] 常方强, 涂帆, 贾永刚. Verhulst模型在预测软基路堤沉降中的应用[J]. 岩石力学与工程学报, 2007, 26(1): 3122-3126.
CHANG Fangqiang, TU Fan, JIA Yonggang. Application of Verhulst model to prediction of roadbed settlement on soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 3122-3126.
[17] 吴剑, 张迎春. 软基路堤最终沉降量的灰色预测[J]. 西部探矿工程, 2003, 15(7): 30-33.
WU Jian, ZHANG Yingchun. Gray forecast of final settlement of soft ground[J]. West-China Exploration Engineering, 2003, 15(7): 30-33.
[18] 廖延周, 王浩宇. 基于Verhulst模型的长短桩复合地基沉降预测[J]. 交通科技, 2013, 258(3): 69-71.
LIAO Yanzhou, WANG Haoyu. Settlement prediction of long short pile composite foundation based on Verhulst model[J]. Transportation Science & Technology, 2013, 258(3): 69-71.
[19] 曾贤敏, 黄腾, 李桂华, 等. 新陈代谢GM(1,1)模型在大坝边坡沉降监测中的应用[J]. 测绘工程, 2015, 24(8): 53-56.
ZENG Xianmin, HUANG Teng, LI Guihua, et al. Application of metabolic GM(1,1) model in forecast of the dam slope’s settlement[J]. Engineering of Surveying and Mapping, 2015, 24(8): 53-56.
(编辑 陈灿华)
收稿日期:2016-10-12;修回日期:2016-12-26
基金项目(Foundation item):国家自然科学基金资助项目(50878212);中南大学中央高校基本科研业务费专项资金资助项目(2016zzts435) (Project(50878212) supported by the National Natural Science Foundation of China; Project(2016zzts435) supported by the Fundamental Research Funds for the Central Universities of Central South University)
通信作者:张闯,博士研究生,从事基坑沉降和滑坡预测研究;E-mail: 980191776@qq.com