J. Cent. South Univ. Technol. (2007)06-0870-07
DOI: 10.1007/s11771-007-0165-2
Improved response surface method and its application in stability reliability degree analysis of tunnel surrounding rock
SU Yong-hua(苏永华), ZHANG Peng(张 鹏), ZHAO Ming-hua(赵明华)
(Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China)
Abstract: An approach of limit state equation for surrounding rock was put forward based on deformation criterion.A method of symmetrical sampling of basic random variables adopted by classical response surface method was mended, and peak value and deflection degree of basic random variables distribution curve were took into account in the mended sampling method. A calculation way of probability moment, based on mended Rosenbluth method, suitable for non-explicit performance function was put forward. The first, second, third and fourth order moments of functional function value were calculated by mended Rosenbluth method through the first, second, third and fourth order moments of basic random variable. A probability density the function(PDF) of functional function was deduced through its first, second, third and fourth moments, the PDF in the new method took the place of the method of quadratic polynomial to approximate real functional function and reliability probability was calculated through integral by the PDF for random variable of functional function value in the new method. The result shows that the improved response surface method can adapt to various statistic distribution types of basic random variables, its calculation process is legible and need not iterative circulation. In addition, a stability probability of surrounding rock for a tunnel was calculated by the improved method, whose workload is only 30% of classical method and its accuracy is comparative.
Key words: response surface method; Rosenbluth method; statistic moment; entropy density function; quadratic polynomial
1 Introduction
An information design and construction method for underground rock mass structure take the modern rock mechanics theory as a foundation, and take the mutual effect of the adjoining rock and the lining structure of sap as the starting point. This method takes the uncertainty of the each stratum physics mechanical characters and the response to excavation as a premise. It emphasizes to reduce the adjoining rock pressure and fully exert the bearing capacity itself. Under the instruction of this theory, the basic routine of the design and the construction mainly considers the adjoining rock category of the underground structure, burying depth of tunnel and so on. It draws the stratum characteristic curve based on the massive measured data, and takes the biggest permission deformation of the adjoining rock (generally arch subsidence) as lining design rule. Not only is deformation of adjoining rock decided by initial pressure, but also it relates to physics mechanical properties of surrounding rock mass as well as stratum of adjacent surrounding rock of the tunnel. Therefore, deformation of surrounding rock of the tunnel is the function of the initial stress and physical mechanic parameters of the adjoining rock. Because of the complexity of rock mass medium and randomness of the physical mechanic parameters, deformation of surrounding rock of sap is also a random variable. Based on the mutual mechanism adjoining rock of underground structure and supports, and considering the uncertainty of physical mechanic parameters of the rock mass and the correlation factors, in this paper a response surface method was studied for stability reliability analysis of the underground rock mass tunnel according to the New Austrian Tunneling Method design and construction way.
2 Establishment method of limit state equation based on deformation
2.1 Mutual action of surrounding rock and supporting structures
The theoretical basis of surrounding rock of modern supports method for the underground engineering is the mutual action of the surrounding rock and the supporting structures. As shown in Fig.1, curve 1 is the function of the surrounding rock pressure with sap peripheral displacement. It is divided into two stages. The curve between points A and B is at the deformation pressure stage, the surrounding rock pressure gradually reduces with the displacement releasing of the peripheral layer for sap. After point B, the surrounding rock looses, the pressure increases. From the chart, when the peripheral displacement of sap achieves its limited allowable displacement umax, the pressure of the adjoining rock is the smallest. So the support resisting force that the lining needs to provide should be most reasonable at this point. Curves 2 and 3 are the supporting structure characteristic curves, and the shape of the characteristic curve is related to its rigidity. The two curves express the force starts to exert when the initial displacement of the sap of peripheral surrounding rock reaches u01 and u02, respectively, the coordination deformation between the supporting structure and the adjoining rock reaches ur01 and ur02, respectively. When the released displacement of the surrounding rock just reaches umax, the ideal supporting state is achieved[1-3].
Supposing that the elasticity module of the rock mass is E, cohesive force is c, angle of internal friction is φ, and side press coefficient λ=1 in initial stress field, and the rock mass is the ideal elastoplasticity rock one, then there is a analytic function relationship between displacement u of peripheral rock-mass of sap and the surrounding rock pressure p. u could be expressed as function of the stress field and the rock mass physical mechanics parameters as follows.
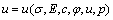 (1)
(1)
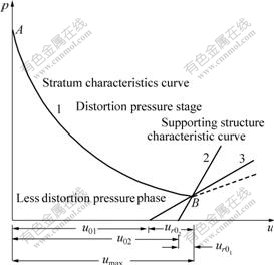
Fig.1 Scheme of ideal supporting state
1-Stratum pressure variation curve; 2,3-Pressure variation curves of support structure with rigidity K and support structure with rigidity coefficient K′ respectively, K′>K
Under usual condition, the initial stress field is heterogeneous stress one, the geometry shape of the sap is not generally a circle, the analytic relationship between u and p does not exist. So it is unable to determine analytical formula of umax theoretically. Therefore, in order to achieve the ideal supporting state, determination of umax is a key issue under all kinds of conditions.
2.2 Determination of umax
So far, a lot of researchers, both the domestic and the overseas, put forward the range of allowable value for umax based on massive monitor and measurement data of practical engineering. The allowable value range relates to burying depth of sap, category of surrounding rock, characteristic of physical and mechanical and cross section size of sap.
Tables 1-3 are allowable ranges of umax, which are proposed by the researchers in France, Russia and the Chinese Railroad Tunnel Design and the Construction Department, respectively[2]. Moreover, scholars in Japan also give the similar control rule[2].
Table 1 Allowable values of subsidence of vault(France)
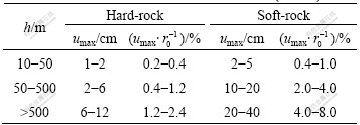
Table 2 Allowable values of displacement for surrounding rock of tunnel (Russia)
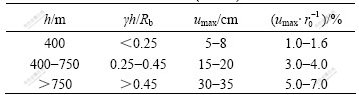
Table 3 Allowable values of displacement of surrounding rock about railway tunnel (China) (cm)
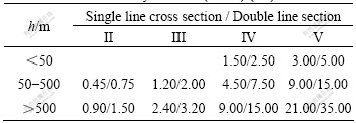
In Tables 1-3, r0 is the most dimension of cross-section for tunnel, h is the depth buried, γ is the unit gravity of rock-mass and Rb is the uniaxial resistance strength of rock-mass under saturated state and Roman numerals “II, III, IV, V” stand for category of surrounding rock of tunnel.
These allowable values of umax determined by actual measurement data are used as guidance for the design and construction of tunnel. For example,it is usually used as a foundation to design bearing capacity and rigidity of ling, and to put apart a deformation value for supporting structure.
2.3 Establishment of limit state equation
After umax is determined, we can establish the structure performance function based on the criterion of displacement. According to Eqn.(1) and umax, an equation of performance function for tunnel structure may be obtained as follows:
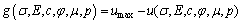 (2)
(2)
The basic random variable of structure can be expressed as a stochastic vector, X=(X1, X2, …, Xn). correspondingly, the limit state equation may be expressed as:
G(X)-umax-u(X)=0 (3)
3 Solution for response surface method of limit state equation
3.1 Solution process by classical method
Eqn.(3) is often solved by response surface method. Generally speaking, quadratic polynomial with no crossing terms is adopted to approximate response surface function. Assuming that a structure has n random variables x1, x2, …, xn, these random variables obey normal distribution. The form of quadratic polynomial term is usually expressed as follows[3-6]:
 (4)
(4)
where a, bi and di (i=1, 2, …, n) are the undetermined coefficients,and the total accounts are 2n+1.
The process of confirming undetermined coefficients and analyzing reliability is as follows.
1) Assume iterative point 
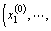
 , generally, taking the average values at the first time.
, generally, taking the average values at the first time.
2) Functional function values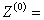

 and z(i)=
and z(i)=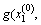
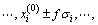
 are computed by finite element numerical simulation test and (2n+1) values will be acquired(coefficient f equals 3 at first time,then it equals 1,σi is mean-square deviation of xi);
are computed by finite element numerical simulation test and (2n+1) values will be acquired(coefficient f equals 3 at first time,then it equals 1,σi is mean-square deviation of xi);
3) Coefficient a, bi, di(i=1, 2,…, n) are confirmed through solving the equation group and an approximate quadratic polynomial term of the functional function is determined.
4) Checking point method JC rule is used to solve checking point x*(K) and reliability index β(K), where superscript K represents the Kth step iterative calculation.
5) Judge the constringency of reliability index β according to the following inequality:
|β(K)-β(K+1)|<ε (5)
If the above inequality is unsatisfied, namely the calculation result does not constringe, a new expansion point can be got through insert method by the following function:
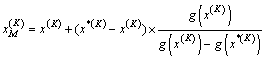 (6)
(6)
Then return to step 2) and take the next iteration, until Eqn.(5) is satisfied. At last, the reliability index can be calculated in the standard normal space.
3.2 Deficiencies of classical response surface method
Some deficiencies in classical response surface method were found from above-mentioned solving process for limit state equation.
1) Quadratic polynomial expression is used to approximate practical functional function of very complicated structure. The error range of failure probability between quadratic polynomial expression and real limit state equation cannot be estimated accurately.
2) After reliability index is calculated, a supposition that reliability index obeys normal distribution is required.
3) The method is only suitable for some functional functions whose basic variables obey normal distribution. If the basic variable is non-normal, it needs to be normalized.
4) Samples of basic random variables are gathered symmetrically and equably on both sides of mean values point or expansion point before finite element simulation experiment. The sampling method does not consider characteristic of distribution curve of basic random variables.
Aiming at the problems mentioned-above, basic random variables are sampled according to Rosenbluth method[7] at first, then sample storehouse of the functional function value is gained through finite element simulation test; an improved Rosenbluth method is adopted to calculate the statistic moment of the functional function[8]. Probability density function is confirmed by statistic moment of the functional function. A reliability degree is obtained through integral finally.
4 Improvement for classical response surface method
4.1 Estimate point of statistic moment
For convenience, basic random parameters of surrounding rock are expressed by vector, X=(X1, X2, …, Xn), mean value and variance of the random variable are μxi, σXi, respectively, the kth central moments (k=2, 3) are expressed respectively for 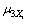 and
and  The coefficient of variation which reflects discrete degree of every random variable is marked as
The coefficient of variation which reflects discrete degree of every random variable is marked as 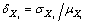 , the lean coefficient which reflects decline degree of the density function curves is marked as
, the lean coefficient which reflects decline degree of the density function curves is marked as 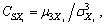 the Kurtosis coefficient which reflects the sharp or evenness degree of the densities functions curve is marked as
the Kurtosis coefficient which reflects the sharp or evenness degree of the densities functions curve is marked as  .
.
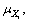
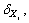
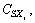
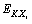 are called statistical parameters of the former four order moment. They can portray the probability characteristic of the random variables perfectly[11-12].
are called statistical parameters of the former four order moment. They can portray the probability characteristic of the random variables perfectly[11-12].
Assuming that universal formula of functional function is Z=g(X)=g(X1, X2, …, Xn), its individual order origin point moment mk=E(zk) of functional function value Z=g(X) can be calculated through point estimation method put forward by ROSENBLUETH[7]. Formula of calculation is as follows:
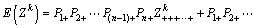

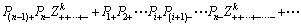
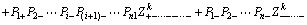 (7)
(7)
According to above formula, if the number of random variable is n, there are 2n functional function Z that need to be calculated. Then the value of corresponding functional function and the skewness coefficient Pi+ and Pi- can be calculated by the following formulae based on ROSENBLUETH point estimation method.
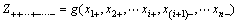 (8)
(8)
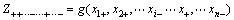 (9)
(9)
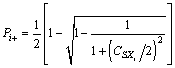 (10)
(10)
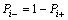 (11)
(11)
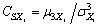 is skewness coefficient of the random variable Xi,sample point xi± of the basic random variable is confirmed by the following equations:
is skewness coefficient of the random variable Xi,sample point xi± of the basic random variable is confirmed by the following equations:
 (12)
(12)
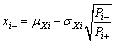 (13)
(13)
4.2 Improved moment point estimation method for response surface
From Eqns.(7)-(10), we can see that moment mk=E(Zk) only relate to the first, second and third moments, but entire description of shape for curve of probability density function needs their information of forth order moment. TONG[8] studied the influence of parameter 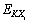 of the forth order statistical moment, and proposed the following calculation formulae improved for origin point moment mk:
of the forth order statistical moment, and proposed the following calculation formulae improved for origin point moment mk:
m1=E(Z) (14)
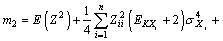
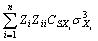 (15)
(15)
 (16)
(16)
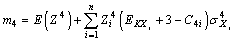 (17)
(17)
where C4i calculated can be calculated by the following equation:
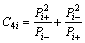
and E(Zk) is calculated by Eqn.(4), 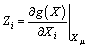 and
and mean that the first order and second order partial derivative values of functional function versus Xi at mean value point Xu of the basic random variable.
mean that the first order and second order partial derivative values of functional function versus Xi at mean value point Xu of the basic random variable.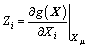 and
and 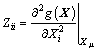 may be calculated through limited difference method[13-20].
may be calculated through limited difference method[13-20].
4.3 Entropy density function
After the first, second, third and forth order origin point moments of functional function are confirmed, the corresponding centre point moment can be calculated according to Eqn.(18)
 (18)
(18)
Then we can get the statistic moment parameters of the functional function Z from the first to forth order moment, namely μZ, δZ, CSZ and EKZ. Functional function Z is turned into a standardization random variable (mean value is 0, the standard deviation is 1)[9] by the following formula:
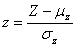 (19)
(19)
According to the greatest entropy principle, the probability density function of the random variable Z is[9-10]
 (20)
(20)
Undetermined parameter λi(i=0-4) is confirmed through solving the simultaneous equations groups shown as follows:
 i=0-4 (21)
i=0-4 (21)
where
ρ0=1, ρ1=0, ρ2=1, ρ3=CSZ, ρ4=EKZ+3.
After confirming probability density of functional function Z, we calculate the reliability Ps according to the following formula[10]:
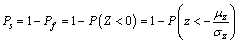
 (22)
(22)
4.4 Computational step
Operation procedure for the above-mentioned response surface method of reliability degree analysis for underground structure surrounding rock based on deformation criteria is summarized as follows.
1) Confirming stochastic varibles in limit state Eqn.(3), according to conditions of surrounding rock and their parameters variance size.
2) Analyzing the concrete shape of distribution curve of basic random variables of structure and calculating the former four order statistical moments  ,
,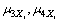 of the random variables and the corresponding statistical parameters
of the random variables and the corresponding statistical parameters 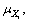
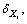
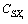 and
and 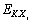 .
.
3) Calculating Pi+, Pi- and C4i by their corresponding skewness coefficient and the Kurtosis coefficient of the random variable, then drawing samples of random variable and constructing a sample group with 2n samples through permutation and combination.
4) Getting 2n value of performance function, 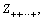
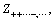
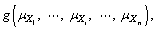
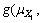
 and
and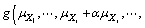
 through finite element numerical simulation calculation and E(Zk).
through finite element numerical simulation calculation and E(Zk).
5) Calculating the former four order origin moments m1, m2, m3, m4 and changing them into μZ, σZ, μ3Z and μ4Z, standardizing the random variable of functional function value and calculating the former four order statistical moment parameter μZ, δZ, CSZ and EKZ of functional function Z.
6) Getting λ0, λ1, λ2, λ3 and λ4 through solving simultaneous equations groups, at the same time, confirming probability density function f(Z) of random variable of functional function Z.
7) Calculating stability reliability probability PS of the structure through integral.
5 Engineering analysis
5.1 General situation for engineering
One highway tunnel in Xiangxi district is a single lane of two-way. Its transect profile is arch with meandering wall, cross-section area is 11.5 m×10.0 m (width×height), its depth is 365 m. The exposed strata of the tunnel site are mainly Quaternary, Devonian and Silurian system. The thickness, the physical and mechanical parameters are shown in Table 4. The lithology of every stratum is shown as follows.
1) Quaternary system. It is mainly composed of planting soil and its thickness about 2 m.
2) Devonian system. It is composed of siltstone, sandy shale and thin shale. The joint fissure of the vertical or oblique bedding in rock mass is medium -developed or better-developed. The thickness is 94 m, Poisson ratio is 0.39.
3) Silurian system. It consists of soft rock. The joint fissure in rock mass is developed or developed relatively well. This stratum is great in thickness with the Poisson ratio of 0.31.
From Table 4, it can be seen that some variation coefficients of physical and mechanical parameters, including Poisson ratio, friction angle and density of Silurian system rock are less than 0.05. In order to simplify the calculation and consider the main factors, they will be regarded as certain parameters in the following analysis. Therefore, the main random parameters are the rock density γ1 of the Devonian system, the deformation modulus E1, E2 and the cohesion C1, C2 of the Devonian system and Silurian system. For the sake of convenience, these five random parameters γ1, E1, E2, C1, C2 are expressed as form of a random vector X= (g 1, E1, E2, C1, C2= (X1, X2, X3, X4, X5). According to statistical analysis, rock deformation modulus obeys the normal distribution; rock cohesive force obeys the lognormal distribution, the rock weight g1 of the Devonian system obeys Extreme I distribution.
Supporting design of the tunnel is composite lining structure, according to construction principles of the New Austrian Tunneling method, deformation value of tunnel vault is not larger than 15 cm.
Stability limit state equation for above-mentioned surrounding rock can be expressed as follows according to deformation criterion:
g(X)=umax-u(X)= umax-u(X1, X2, X3, X4, X5)=15-u(g 1, E1, E2, C1, C2)=0
5.2 Computational results and comparison
The former four order statistical moments of functional function Z are μZ=2.210 4,σZ=0.853 7, μ3=-0.478 2,μ4=0.996 52, which are gained according to the above-mentioned steps from 1) to 6). The corresponding statistical moment parameters of μZ, δZ, CSZ and EKZ, are 2.210 4, 0.492 8, -0.976 5 and 0.543 1, respectively. The undetermined coefficient λ0-λ4 of the corresponding density function can be determined by the discrete numerical method[9-10]. They are λ0=0.986 35, λ1=-0.728 28, λ2=0.293 40, λ3=0.199 80, λ4=0.095 63. Through the integral of probability density function, structural failure probability is  .
.
Table 4 Rock-mass mechanical parameters of surrounding rock of tunnel

In order to analyze the precision of improved method, we simultaneously adopt the direct Monte Carlo law and classical response surface method to study the reliability respectively. The calculation result of the classical respond surface method is  .
.
Iterative calculation of 7 circulations was carried out when calculation result achieved constringency. 12 times of simulation calculation of finite element method were carried out before calculation result achieved constringency in a circulation. 84 times of simulation calculation of finite element method were finished in total to calculate failure probability of surrounding rock of tunnel.
When adopting the Monte Carlo method to simulate, 112 000 times simulation calculations were carried out before convergence. Failure probability of surrounding rock for tunnel is  .
.
The result Pf obtained through Monte Carlo law is regarded as an accurate solution. The relative error, absolute error and calculation times of simulation through classical method and improved method respectively are shown in Table 5.
Table 5 Comparison among results by different calculation ways
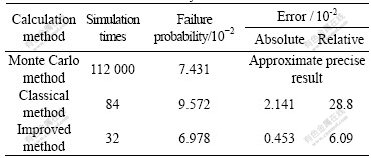
From Table 5, it is found that calculation workload of the improved method is about 30% of the classical method, yet its computation precision of that is advanced slightly and the improved method does not need iterative calculation.
6 Conclusions
1) An approach established for limit state equation for surrounding rock is put forward based on deformation criterion.
2) Based on relationship between statistical moment parameter and shape of curve for PDF, an amended calculation method of sample is put forward.
3) Improved point estimation calculation method of the first, second, third and fourth order statistical moments for unknown structure performance function is proposed through combining calculation way of partial differential coefficient by difference with finite element method.
4) A fitting way of most entropy probability density function of limit state equation is deduced by first to fourth order moments and then a new response surface method that calculates failure probability by integral through most entropy probability density function is worked out. Analysis process of failure probability is concision and does not need iterative calculation in the new way.
5) A stability reliability degree of a tunnel structure under serviceability limit state is analyzed by the new way. This shows that calculation workload is less and its accuracy is higher than classical response surface method.
References
[1] SU Yong-hua, JIANG De-song, ZHAO Ming-hua. Estimation of stability reliability degree of tunnel structure in soft and loose rock mass[J]. Journal of Hunan University, 2006, 33(2): 10-14. (in Chinese)
[2] LI Zhi-ye, ZENG Yan-hua. Design Principle and Ways for Underground Structure[M]. Chengdu: South-West Traffic University Press, 2005: 304-310. (in Chinese)
[3] BUCHER C G, BOUGUND U. A fast and efficient response surface approach for structural reliability problem[J]. Structural Safety, 1990, 34(1): 57-66.
[4] SCH?ELLER G I. On efficient computational scheme to calculate structural failure probability[J]. Probability Engineering Mechanics, 1989, 4(1): 10-18.
[5] LIU Y W, MOSES F. A sequential response surface methods and its application in the reliability analysis of aircraft structural system[J]. Structural Safety, 1994, 16(1/2): 39-46.
[6] FARAVELLI L A. Response surface approach for reliability analysis[J]. Journal of Engineering Mechanics, 1989, 115(12): 2763-2781.
[7] ROSENBLUETH E. Point estimate for probability moment[C]// Proc Nat Acad Sci, USA, 1975, 72: 3812-3814.
[8] TONG Xiao-li. Improved Rosenbluth method and its application in structure stability reliability degree analysis[J]. Journal of Dalian Science and Technology of University, 1997, 37(3): 316-321. (in Chinese)
[9] ZHAO Guo-fan. Engineering Structural Reliability Theory and Its Application[M]. Dalian: Dalian Technology University Press, 1996: 145-148. (in Chinese)
[10] ZHAO Wen-gui. Fourth order moment analysis method for structure stability reliability degree[J]. Journal of Dalian Science and Technology of University, 1992, 32(4): 455-459. (in Chinese)
[11] SU Yong-hua, HE Man-chao, GAO Qian. Applying of Rosenblueth method in evaluating stability reliability of anchor-shotcrete net support system for soft-fracture surrounding rock[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 373-379. (in Chinese)
[12] SU Yong-hua, HE Man-chao. Simplified calculation approach of response surface method reliability index by point estimation of probability moment[J]. Engineering Mechanics, 2007, 24(7): 11-15. (in Chinese)
[13] ZHANG Xiao-qing, KANG Hai-gui, WANG Fu-ming. A new method for reliability problem without explicit performance function[J]. Journal of Dalian University of Technology, 2003, 43(5): 650- 654. (in Chinese)
[14] SU Yong-hua, ZHAO Ming-hua, ZHANG Yue-ying, et al. On analysis of reliability of slope stability based on Spencer model by the method of difference[J]. Journal of Rock Mechanics and Engineering, 2006, 25(S1): 2750-2756. (in Chinese)
[15] SU Yong-hua, ZHAO Ming-hua. Application of response surface method in stability reliability degree analysis for slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1417-1425. (in Chinese)
[16] HAN Bin, WU Ai-xiang, DENG Jian, et al. Backfill technical analysis based on reliability theory in the underhand drift cut and filling stoping[J]. Journal of Central South University: Science and Technology, 2006, 37(3): 583-587. (in Chinese)
[17] HE Yue-gang, LI Zhi-wei, YANG Xiao-li. Hazard development mechanism and deformation estimation of water solution mining area[J]. Journal of Central South University of Technology, 2006, 13(6): 738-742.
[18] XIE Xue-bin, PAN Chang-ling, CAO Ping, et al. An optimization method of stope structure parameter for rock burst tendency mine[J]. Journal of Central South University: Natural Science, 1999, 30(2): 121-125. (in Chinese)
[19] DENG Jian, BIAN Li, LI Xi-bing, et.al. Analysis of factors and countermeasures of mining subsidence in Kaiyang phosphorus mine[J]. Journal of Central South University of Technology, 2006, 13(6): 733-737.
[20] TU Wen-ge, LIN Li-chuan. Analysis on fuzzy reliability of structure[J]. Journal of Central South University of Technology: Natural Science, 2000, 31(4): 371-375. (in Chinese)
(Edited by YANG Hua)
Foundation item: Project(50378036) supported by the National Natural Science Foundation of China; Project (200503) supported by the Foundation of Communications Department of Hunan Province, China
Received date: 2007-04-02; Accepted date: 2007-06-18
Corresponding author: SU Yong-hua, Professor, PhD; Tel: +86-731-8812659; E-mail: syh5327@hnu.cn