Effects of temperature on MWCNTs/PDMS composites based flexible strain sensors
来源期刊:中南大学学报(英文版)2020年第11期
论文作者:何虎 郭登机 潘旭东
文章页码:3202 - 3212
Key words:flexible strain sensors; conductive polymer composites; temperature; multi-walled carbon nanotubes (MWCNTs)
Abstract: Conductive polymer composites (CPCs) are widely used in the flexible strain sensors due to their simple fabrication process and controllable sensing properties. However, temperature has a significance impact on the strain sensing performance of CPCs. In this paper, the strain sensing characteristics of MWCNTs/PDMS composites under temperature loading were systematically studied. It was found that the sensitivity decreased with the increase of temperature and the phenomenon of shoulder peak also decreased. Based on the theory of polymer mechanics, it was found that temperature could affect the conductive network by changing the motion degree of PDMS molecular chain, resulting in the change of sensing characteristics. Finally, a mathematical model of the resistance against loading condition (strain and temperature), associated with the force-electrical equivalent relationship of composites, was established to discuss the experimental results as well as the sensing mechanism. The results presented in this paper was believed helpful for the further application of strain sensors in different temperature conditions.
Cite this article as: GUO Deng-ji, PAN Xu-dong, HE Hu. Effects of temperature on MWCNTs/PDMS composites based flexible strain sensors [J]. Journal of Central South University, 2020, 27(11): 3202-3212. DOI: https://doi.org/10.1007/s11771-020-4540-6.

J. Cent. South Univ. (2020) 27: 3202-3212
DOI: https://doi.org/10.1007/s11771-020-4540-6
GUO Deng-ji(郭登机), PAN Xu-dong(潘旭东), HE Hu(何虎)
State Key Laboratory of High Performance Complex Manufacturing, School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Conductive polymer composites (CPCs) are widely used in the flexible strain sensors due to their simple fabrication process and controllable sensing properties. However, temperature has a significance impact on the strain sensing performance of CPCs. In this paper, the strain sensing characteristics of MWCNTs/PDMS composites under temperature loading were systematically studied. It was found that the sensitivity decreased with the increase of temperature and the phenomenon of shoulder peak also decreased. Based on the theory of polymer mechanics, it was found that temperature could affect the conductive network by changing the motion degree of PDMS molecular chain, resulting in the change of sensing characteristics. Finally, a mathematical model of the resistance against loading condition (strain and temperature), associated with the force-electrical equivalent relationship of composites, was established to discuss the experimental results as well as the sensing mechanism. The results presented in this paper was believed helpful for the further application of strain sensors in different temperature conditions.
Key words: flexible strain sensors; conductive polymer composites; temperature; multi-walled carbon nanotubes (MWCNTs)
Cite this article as: GUO Deng-ji, PAN Xu-dong, HE Hu. Effects of temperature on MWCNTs/PDMS composites based flexible strain sensors [J]. Journal of Central South University, 2020, 27(11): 3202-3212. DOI: https://doi.org/10.1007/s11771-020-4540-6.
1 Introduction
With the further development of electronic information industry, intelligent medicine is gradually entering the daily life of the public [1]. Flexible sensors are widely used as an important tool for doctors to collect patients’ health status. Among them, flexible strain sensor has been widely used for its ability to detect the joint movement, muscle movement, respiratory rate, pulse, blood pressure and many other physiological indicators [2-9]. Conductive polymer composites (CPCs) are widely used in the study of flexible strain sensors due to their advantages of simple manufacturing process, diverse material selection, strong mechanical and electrical controllability and low cost. In practical application, flexible strain sensors need to face complex loading conditions (e.g., strain rate and temperature). The strain sensor is used to detect the change of strain, so it is required to maintain the stability of electrical response under complex loading conditions.
The sensing performance of strain rates on flexible strain sensors based on CPCs has attracted large amount attention recently. It was found that the strain rates can improve the sensitivity of the composites and the hysteresis in the dynamic cyclic test, which depends on the impact of the strain rates on the destruction and reconstruction of the conductive network and the viscoelasticity of the polymer [2, 10, 11]. However, the influence of temperature on the sensing performance of strain sensors based on CPCs has yet been specifically investigated, even if many researchers have studied the influence of temperature on the electrical performance of CPCs [12-14]. WANG et al [14] found that the resistance of MWCNTs/epoxy resin composites increased at the early stage and then decreased with the increase of temperature, and the change trend of temperature-resistance curve of composites was closely related to the state of polymer. In particular, when the temperature reached the glass phase transition point of the polymer, the temperature has little effect on the resistance. However, as the temperature changes, the resistance of polymers has positive temperature coefficient at the high elastic state stage, while a negative temperature coefficient presents at the viscous flow state. ZHAO et al [13] prepared the conductive filler/PA6/UHMWPE composite material, and verified that the type of conductive filler would change the degree of influence of temperature on the resistance. Additionally, the graphene/PA6/UHMWPE composites exhibit repeatable resistance changes under the temperature cyclic loading test. In summary, temperature has significant effect on the conductivity of CPCs. However, the effect of temperature on the strain sensing performance of CPCs has still required further investigation. The flexible strain sensor will face different temperature environments in the practical application, and the research on the influence of temperature on the strain sensing performance of CPCs is helpful to promote the application of strain sensors based on CPCS under complex temperature environment. In addition, the study of the mechanism of temperature on the strain sensing performance of CPCs can provide a theoretical basis for the application of strain sensors based on CPCs under complex temperature conditions.
In this paper, the effect of temperature on the sensing performance of flexible strain sensor based on multi-walled carbon nanotubes (MWCNTs)/ polydimethylsiloxane (PDMS) composites, especially the sensitivity and sensing performance under stretching/releasing cycles, was systematically investigated. Based on the theory of polymer viscoelastic mechanics, the influence mechanism of temperature on the performance of composites was discussed. Furthermore, a mathematical model associated with the force- electric equivalence of composites was established to analyze the sensing behavior of presented CPCs based strain sensors.
2 Materials and methods
PDMS (Sylgard 184 Silicone Elastomer) was applied for the matrix of prepared sensors [15]. Multi-walled carbon nanotube (TNM8, 30-80 nm in diameter, less than 10 μm in length, the purity as 98 wt% and the density as 2.1 g/cm3) was purchased from Chengdu Organic Chemical Co. Ltd. n-hexane was purchased from Aladdin Co. Ltd. Note that all these materials are applied in the experiments as ordered.
Figure 1(a) describes the schematic process of the preparation of MWCNTs/PDMS composites. Firstly, MWCNTs are added into n-hexane and dispersed by ultra-sonication for 30 min. Then, the PDMS base is added into the dispersion solution. The MWCNTs are uniformly dispersed in the PDMS base by magnetic stirring and ultrasonic dispersion. In the following, the curing agent is mixed into the prepared solution according to the mass ratio 10:1 of PDMS base to curing agent. The mixture is stored in a Petri dish at room temperature for 10 h to fully evaporate the n-hexane. The MWCNTs/PDMS composites films are finally obtained after curing at 100 °C for 2 h. The test samples with the appropriate size (35 mm×5 mm× 0.5 mm) were prepared. Note that n-hexane is used to disperse carbon nanotubes in the high viscosity PDMS base in this experiment.
The presented work focuses on the influence of temperature on the strain sensing characteristics of the MWCNTs/PDMS composites, and the MWCNTs/PDMS composites with the content of MWCNTs as 5 wt% is employed to ensure the stability of the electrical properties of the composites (Figure 1(b)). The liquid nitrogen embrittlement and gold spraying were applied to obtain the cross section of samples. As shown in Figure 1(c), MWCNTs are evenly dispersed in PDMS matrix without apparent agglomeration. A flexible test system consisting of a micro force fatigue testing machine and a high-precision LCR bridge is deployed to obtain electromechanical signals under desired loading conditions.
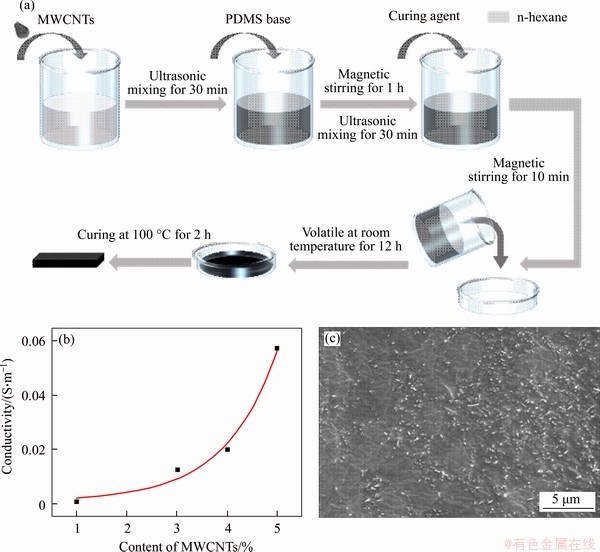
Figure 1 (a) Schematic of fabrication process MWCNTs/PDMS composites; (b) Conductivity of MWCNTs/PDMS composites with different content of MWCNTs; (c) SEM characterization of MWCNTs/PDMS composites (5 wt% MWCNTs)
3 Results and discussion
3.1 Effects of temperature on sensitivity of MWCNTs/PDMS composites
The sensitivity of the MWCNTs/PDMS composites depends on the variation of the tunneling distance between the carbon nanotubes and the variation of the number of conducting pathways in the conductive network within the unit strain [16]. The relative resistance change (△R/R0) of MWCNTs/PDMS composites increases with the decrease of temperature, which indicates that the sensitivity of the composites increases with the decrease of temperature (Figure 2(a)). The results show that the variation of the tunneling distance and the number of conductive pathways increases with the decrease of the temperature. As shown in SEM, MWCNTs are coated with PDMS. When the composites bear external strain, the external force drives the PDMS molecular chain movement, and the molecular chain movement drives the spatial position of the carbon nanotubes to change, thus affecting the tunneling distance and the number of conductive pathways. Therefore, the movement of PDMS molecular chain can reflect the change of the conductive network, and the stress can reflect the movement of PDMS molecular chain. However, there is no significant difference in the stress of the composites under different temperatures (Figure 2(b)). The temperature range selected in this paper was relatively narrow, resulting in insignificant stress differences. Besides, the sampling frequency of the LCR meter was relatively low.
The stress relaxation in viscoelastic mechanics was introduced to further analyze the deformation degree of PDMS molecular chain. The deformation of cross-linked polymer is composed of high elastic deformation and instantaneous elastic deformation. Stress relaxation refers to the phenomenon of stress attenuation with the increase of relaxation time when the strain remains unchanged [17]. As shown in Figure 3(a), the stress and resistance of MWCNTs/PDMS composites decay with time in the stress relaxation stage. In the stress relaxation stage, the chain segment of PDMS extends continuously with the increase of the relaxation time, resulting in the transformation of all the instantaneous elastic deformation into high elastic deformation. In this process, energy loss is generated due to the need to overcome the friction between the chain segments. Therefore, the degree of stress attenuation can reflect the weight of the instantaneous elastic deformation and high elastic deformation of PDMS molecular chain in the tensile stage. In other words, the greater the degree of stress attenuation, the lower the weight of the high elastic deformation of PDMS molecular chain in the tensile stage, and the higher the weight of the instantaneous elastic deformation. Meanwhile, the △R/R0 attenuation in the stress relaxation stage implicates that the resistance would decrease in the transition from the instantaneous elastic deformation to high elastic deformation. The results indicate that the increase of resistance caused by the instantaneous elastic deformation is greater than that caused by the high elastic deformation. In addition, the molecular chain deformation during the stress relaxation stage leads to the reduction of the tunneling distance and tunneling resistance [18].
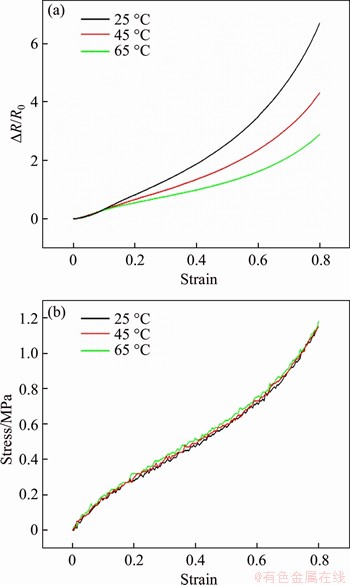
Figure 2 △R/R0 (a) and stress (b) of MWCNTs/PDMS composites at different temperature during stretching stage (ε=0.8, ν=0.3 mm/s)
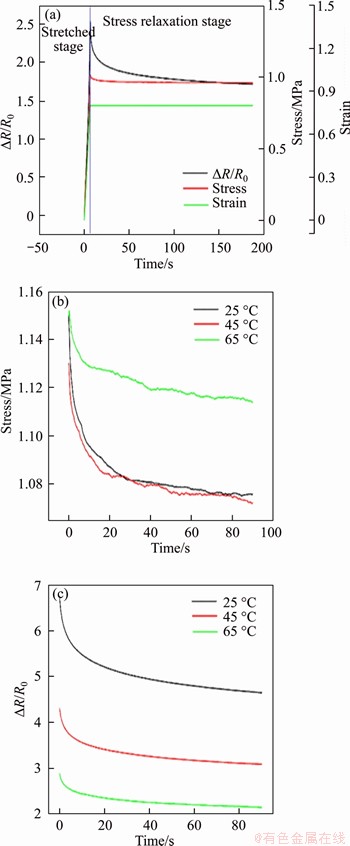
Figure 3 (a) Change of △R/R0, stress and strain during stretched stage and stress relaxation stage, with 25 °C for temperature, 1.5 mm/s for strain rate and 0.8 for the maximum strain; stress (b) and △R/R0 (c) of MWCNTs/PDMS composites at different temperature during stress relaxation stage (ε=0.8, ν=0.3 mm/s)
As shown in Figures 3(b) and (c), the attenuation degree of stress and resistance decreases with the increase of temperature at the stress relaxation stage. The results show that the weight of the instantaneous elastic deformation during tensile stage decreases at high temperature, and thus, the weight of the high elastic deformation becomes more significant under the fixed total deformation. In general, the friction between the chain segments is attenuated and the degree of high elastic deformation is then improved at high temperate [19]. Furthermore, the resistance change induced by instantaneous elastic deformation is more significant than that induced by high elastic deformation. Therefore, the resistance change of the conductive polymer composites at higher temperature slows down and the sensitivity would decrease accordingly.
3.2 Effects of temperature on hysteresis of MWCNTs/PDMS composites
As shown in Figure 4(a), the △R/R0 of MWCNTs/PDMS composites exhibits good stability and repeatability at different temperatures. In addition, the shoulder peak of the composites gradually increases with the decrease of temperature (Figures 4(a) and (b)), but the stress has no obvious difference at different temperature (Figure 4(c)). The phenomenon of shoulder peak refers the non-monotonic changes in resistance to strain and the occurrence of multiple peaks [2, 20].
In order to further analyze the effect of temperature on the shoulder peak, the concept of mechanical loss △W is introduced. △W can reflect the mechanical loss of composites in stretching/ releasing cycle and some studies have demonstrated that the greater the mechanical loss, the more significant the shoulder peak phenomenon [21-23]. The value of mechanical loss △W can be calculated by the stress-strain curve of the composites and the calculation formula is as follows:
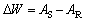 (1)
(1)
where AS and AR are respectively the area enclosed by the tensile curve and the recovery curve and the x-axis in the stress-strain curve. Figure 5(a) shows a schematic diagram of the calculation of mechanical loss △W. △W can explain the hysteresis between the deformation and stress of the composites and reflect the hysteresis of the molecular chain movement of the PDMS in the composites. As shown in Figure 5(b), the mechanical loss of MWCNTs/PDMS composites in the first cycle decreases with the increase of temperature and the phenomenon of shoulder peak also decreases. The mechanical loss △W of composites is due to the energy loss caused by the need to overcome the friction between the chain segments of PDMS molecular chain. When the temperature is increased, the friction between the segments of the molecular chain of PDMS is reduced, resulting in the reduction of the mechanical loss △W of the composites. Therefore, when the composites are in the recovery stage, the recovery speed of the chain segment of PDMS molecular chain will be improved in the high temperature environment, making the recovery degree of the molecular chain closer to the initial state. At the same time, the conductive network of MWCNTs in the composites also recovers gradually under the drive of chain segment motion. The tunneling distance between the MWCNTs is further reduced and the number of effective conductive pathways is further increased, so that the resistance of composites recovers closer to the original value at high temperature. Therefore, with the increase of the ambient temperature, the phenomenon of shoulder peak of the composites in the first cycle also decreases.
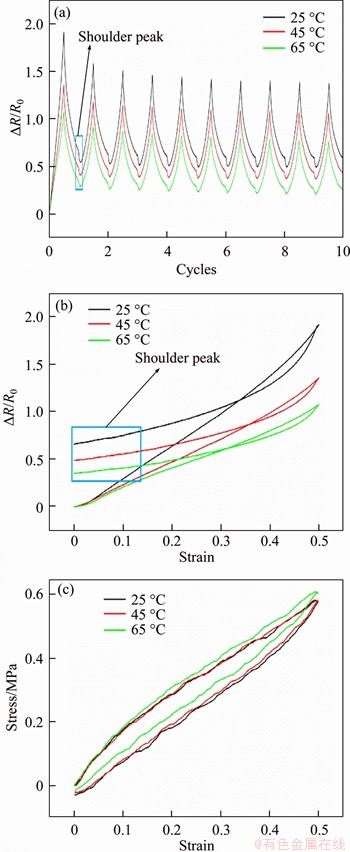
Figure 4 (a) △R/R0 of composites at different temperature during stretching/releasing cycles (ε=0.5);(b) △R/R0 of strain sensor at different temperature during the first cycle; (c) Stress of composites at different temperature during the first cycle

Figure 5 (a) Schematic of calculation of △W; (b) △W of different temperature at the first cycle
3.3 Force-electric equivalence model and sensing mechanism
According to the aforementioned experimental results, the change tendency of △R/R0 and stress of MWCNTs/PDMS composites during the stretching stage and stress relaxation stage is similar. When the composites are at the low strain interval, the PDMS molecular chain extends gradually and the stress increases slowly. Meanwhile, as the molecular chain motion drives the conductive network, the tunneling distance slowly increases and the number of conductive paths slowly decreases. When the composites enter the high- strain interval from the low-strain interval, the stress starts to increase rapidly because the molecular chain has been deformed to a certain extent, so more forces are needed for deformation. At the same time, the increasing tunneling distance makes the tunneling resistance increase sharply and the number of conductive paths decrease rapidly. In addition, the stress and resistance changes of the composites are similar in the stress relaxation stage. Both stress and resistance decrease with the increase of relaxation time and the rate of change decreases with the increase of relaxation time. The above results show that the responses of stress and resistance to strain are similar. In addition, many studies have shown the consistency between the stress change and the resistance change of composites [18].
As PDMS is a cross-linked polymer, it is suitable for the standard linear solid model. As shown in Figure 6, the standard linear solid model consists of springs and dashpot. “0” denotes zero stress of component in the model. ε1 and ε2 represent the shape variable of the instantaneous elastic deformation and the high elastic deformation, respectively. G and G' represent the elastic modulus of the spring element. η represents the viscosity coefficient of the dash pot. GR and G′R represent the coefficients of resistance change due to high elastic deformation and instantaneous elastic deformation, respectively, which are analogical to G and G'. ηR is the coefficient of the hysteresis effect on the resistance, which is analogical to η. The deformation of composites is composed of two parts. The first part is the instantaneous elastic deformation caused by the change of bond length and bond angle of the molecule. This deformation ε1 is completed instantaneously and is simulated by a hard spring with a modulus of G. The second part is the high elastic deformation caused by the stretching and curling of the chain segment. This deformation ε2 changes with the change of time and temperature, and it can be simulated by a soft spring of modulus G' (G'
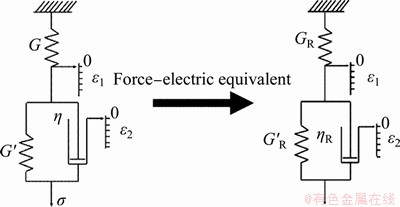
Figure 6 Standard linear solid model and force-electric equivalent model
According to the force-electric equivalent model of the composites, the calculation of the resistance of the composites consists of two parts. The resistance of the first part is the increase of the resistance caused by the hard spring deformation. This part is related to the strain range and can be calculated by the tunneling effect and the percolation theory. The second part of the resistance is caused by the parallel model deformation of the spring and the dash pot, which is related to time and temperature. Therefore, the resistance of composites can be decomposed into two stages with the change of strain (Figure 7(a)). The first stage is that the resistance of composites increases with the increase of strain only under the effect of strain, and the whole process ignores the influence of time and temperature. The second stage is the resistance relaxation of composites on the basis of the first stage under the influence of time and temperature. Finally, the resistance of the composites at a certain strain, rate and temperature is obtained.
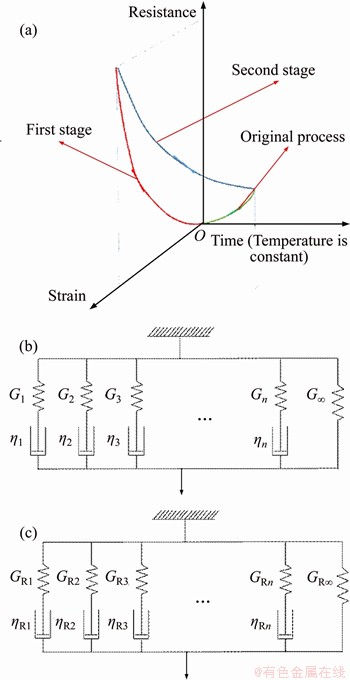
Figure 7 (a) Schematic diagram of resistance variation in two stages; (b) Generalized model of viscoelasticity;(c) Equivalent electrical model
According to the theory of tunneling effect and percolation theory, the calculation formula of real-time resistance Rε and initial resistance R0 of CPCs are as follows [16]:
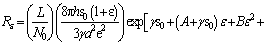
 (2)
(2)
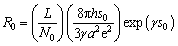 (3)
(3)
where Rε WERon at different temperature.
eis the resistance of real-time strain; ε is the strain of composites; L is the number of particles forming one conducting path; N0 is the number of initial conducting paths; h is Plank’s constant; a2 is the effective cross-sectional area; e is the electron charge; s0 is the shortest distance between adjacent conductive particles;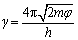 (m is the electron mass; φ is the height of the potential barrier between the adjacent particles) Rε
(m is the electron mass; φ is the height of the potential barrier between the adjacent particles) Rε represents the change of resistance in the first stage and the mathematical model’s variable is only the strain ε.
represents the change of resistance in the first stage and the mathematical model’s variable is only the strain ε.
Based on the force-electric equivalent model discussed above, the generalized viscoelastic model is applied to the calculation of resistance relaxation. As shown in Figure 7(b), the generalized model form of viscoelastic mechanics consists of multiple Maxwell models in parallel with a spring element. Therefore, based on the above discussion of force-electric equivalence, the electrical model of composites can be expressed in the same form (Figure 7(c)). Gi represents the elastic modulus of the spring element. ηi represents the viscosity coefficient of the dash pot. GRi
represents the elastic modulus of the spring element. ηi represents the viscosity coefficient of the dash pot. GRi represents the coefficient of resistance increase against elastic deformation for the i-th Maxwell unit model, which is analogical to Gi. ηRi is the coefficient of the hysteresis effect on the resistance for the i-th Maxwell unit model, which is analogical to ηi. At present, studies have shown that three parallel Maxwell equations can well represent the stress relaxation process of composites [24]. The stress calculation equation of composites is as follows:
represents the coefficient of resistance increase against elastic deformation for the i-th Maxwell unit model, which is analogical to Gi. ηRi is the coefficient of the hysteresis effect on the resistance for the i-th Maxwell unit model, which is analogical to ηi. At present, studies have shown that three parallel Maxwell equations can well represent the stress relaxation process of composites [24]. The stress calculation equation of composites is as follows:
 (4)
(4)
where σ(t) is the real-time stress; t is the action time during the stage of stress relaxation; Gi is the elastic modulus of springs in different Maxwell models; τi is the relaxation time of different Maxwell models; G∞ is the elastic modulus of the spring in parallel with the Maxwell models. The initial stress σ0=ε(G1+G2+G3+G∞) in the stress relaxation stage is substituted into Eq. (4).
 (5)
(5)
Based on the stress relaxation formula, the resistance relaxation is expressed as follows:
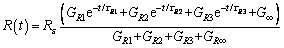 (6)
(6)
where R(t) represents the resistance at time t in the stress relaxation stage; R is the resistance at time t=0. The empirical equation of Williams-Landel- Ferry (WLF) can well represent the relationship between temperature and relaxation time, and its expression is as follows [17, 25]:
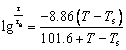 (7)
(7)
where Ts is the reference temperature; T is the real-time temperature; τs and τ are the relaxation time at specified temperature Ts and T, respectively. The time t can be calculated as t=εL0/v, where L0 is the initial length of the composites and v is the strain rate. Substitute Eq. (7) into Eq. (6):
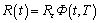
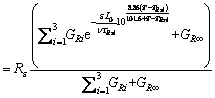 (8)
(8)
where Φ(t, T) is the second stage of the resistance relaxation function. Substitute Eqs. (3) and (8) into Eq. (6):
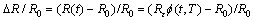

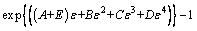 (9)
(9)
where E=γs0.
As shown in Figure 8(a), experimental results with different temperatures were fitted according to Eq. (9), and the fitting results were highly consistent with the experimental results. The Φ(t, T) of the second stage decreases with the increase of temperature (Figure 8(b)), which indicates that the temperature will affect the variation of the high elastic deformation and affect the resistance change. The variation of high elastic deformation increases with the increase of temperature, resulting in the relaxation of resistance in the second stage.
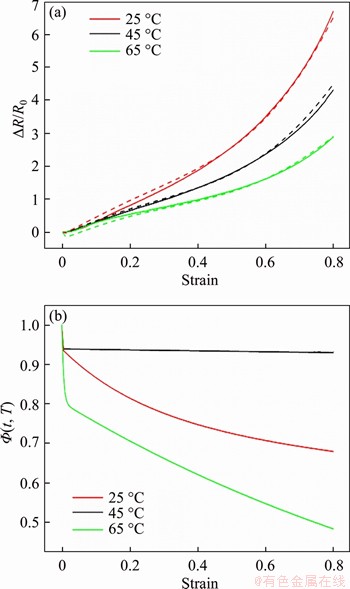
Figure 8 (a) Experimental results and fitting results of resistance at different temperatures (solid line represents experimental results and dashed line represents fitting results); (b) Relaxation function Φ(t, T) changes with strain at different temperatures
4 Conclusions
In this paper, the effect of temperature on the sensing performance (sensitivity and hysteresis) of the flexible strain sensor based on MWCNTs/ PDMS composites is studied. The sensitivity of composites decreases with the increase of temperature, and the phenomenon of shoulder peak decreases with the increase of temperature, which all depend on the effect of temperature on the polymer molecular chain motion. At high temperature, the friction force to be overcome by the chain movement will be weakened, resulting in the increase of the high- elastic deformation ratio of PDMS molecular chain. As the damage degree of high elastic deformation to the conductive network is less than that of the instantaneous elastic deformation, the resistance variation of the composites is weakened. In addition, the increase of temperature will reduce the mechanical losses in cyclic testing and slow down the hysteresis degree between molecular chain deformation and external strain, resulting in the increase of the recovery degree of the conductive network and the decrease of the phenomenon of shoulder peak. Combined with the force-electric equivalent relationship of the composites based on the standard linear solid model, a mathematical model of the resistance of MWCNTs/PDMS composites against loading condition (strain and temperature) was established to discuss the experimental results as well as the sensing mechanism. The value of the relaxation function Φ(t, T) in the mathematical model decreases with the increase of temperature, which proves that the temperature affects the resistance change of the composites by affecting the shape variable of the high-elastic deformation. The research in this paper is believed to facilitate the application of flexible strain sensors based on conductive polymer composites in complex temperature environments.
Contributors
The overarching research goals were developed by HE Hu, GUO Deng-ji and PAN Xu-dong. GUO Deng-ji and PAN Xu-dong prepared the test samples. GUO Deng-ji was responsible for the sample testing. The initial draft of the manuscript was written by HE Hu and GUO Deng-ji. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
HE Hu, GUO Deng-ji and PAN Xu-dong declare that they have no conflict of interest.
References
[1] KIM J H, HWANG J Y, HWANG H R, KIM H S, LEE J H, SEO J W, SHIN U S, LEE S H. Simple and cost-effective method of highly conductive and elastic carbon nanotube/polydimethylsiloxane composite for wearable electronics [J]. Scientific Reports, 2018, 8(1): 1375. DOI: 10.1038/s41598-017-18209-w.
[2] LIU Hu, LI Qian-ming, ZHANG Shuai-di, YIN Rui, LIU Xian-hu, HE Yu-xin, DAI Kun, SHAN Chong-xin, GUO Jiang, LIU Chun-tai, SHEN Chang-yu, WANG Xiao-jing, WANG Ning, WANG Zi-cheng, WEI Ren-bo, GUO Zhan-hu. Electrically conductive polymer composites for smart flexible strain sensors: A critical review [J]. Journal of Materials Chemistry C, 2018, 6: 12121-12141. DOI: 10.1039/c8tc04079f.
[3] BINGGER P, ZENS M, WOIAS P. Highly flexible capacitive strain gauge for continuous long-term blood pressure monitoring [J]. Biomedical Microdevices, 2012, 14(3): 573-581. DOI: 10.1007/s10544-012-9636-9.
[4] LEE J, LIM M, YOON J, KIM M S, CHOI B, KIM D M, KIM D H, PARK I, CHOI S J. Transparent, flexible strain sensor based on a solution-processed carbon nanotube network [J]. ACS Applied Materials & Interfaces, 2017, 9(31): 26279-26285. DOI: 10.1021/acsami.7b03184.
[5] WANG Yan, WANG Li, YANG Ting-ting, LI Xiao, ZANG Xiao-bei, ZHU Miao, WANG Kun-lin, WU De-hai, ZHU Hong-wei. Wearable and highly sensitive graphene strain sensors for human motion monitoring [J]. Advanced Functional Materials, 2014, 24(29): 4666-4670. DOI: 10.1002/adfm.201400379.
[6] YAO Shan-shan, ZHU Yong. Wearable multifunctional sensors using printed stretchable conductors made of silver nanowires [J]. Nanoscale, 2014, 6(4): 2345-2352. DOI: 10.1039/c3nr05496a.
[7] CHEN Jian-wen, YU Qun-li, CUI Xi-hua, DONG Meng-yao, ZHANG Jiao-xia, WANG Chao, FAN Jin-cheng, ZHU Yu-tian, GUO Zhan-hu. An overview of stretchable strain sensors from conductive polymer nanocomposites [J]. Journal of Materials Chemistry C, 2019, 7(38): 11710-11730. DOI: 10.1039/c9tc03655e.
[8] ZHENG Yan-jun, LI Yi-long, DAI Kun, WANG Yan, ZHENG Guo-qiang, LIU Chun-tai, SHEN Chang-yu. A highly stretchable and stable strain sensor based on hybrid carbon nanofillers/polydimethylsiloxane conductive composites for large human motions monitoring [J]. Composites Science and Technology, 2018, 156: 276-286. DOI: 10.1016/j.compscitech.2018.01.019.
[9] WANG Ya-long, HAO Ji, HUANG Zhen-qi, ZHENG Guo-qiang, DAI Kun, LIU Chun-tai, SHEN Chang-yu. Flexible electrically resistive-type strain sensors based on reduced graphene oxide-decorated electrospun polymer fibrous mats for human motion monitoring [J]. Carbon, 2018, 126: 360-371. DOI: 10.1016/j.carbon.2017.10.034.
[10] LIU Chao-xuan, CHOI J W. Analyzing resistance response of embedded PDMS and carbon nanotubes composite under tensile strain [J]. Microelectronic Engineering, 2014, 117: 1-7. DOI: 10.1016/j.mee.2013.11.013.
[11] YANG Heng, YAO Xue-feng, ZHENG Zhong, GONG Ling-hui, YUAN Li, YUAN Ya-nan, LIU Ying-hua. Highly sensitive and stretchable graphene-silicone rubber composites for strain sensing [J]. Composites Science and Technology, 2018, 167: 371-378. DOI: 10.1016/ j.compscitech.2018.08.022.
[12] RYBAK A, BOITEUX G, MELIS F, SEYTRE G. Conductive polymer composites based on metallic nanofiller as smart materials for current limiting devices [J]. Composites Science and Technology, 2010, 70(2): 410-416. DOI: 10.1016/j.compscitech.2009.11.019.
[13] ZHAO Shuai-guo, LOU Dan-dan, ZHAN Peng-fei, LI Guo-jie, DAI Kun, GUO Jiang, ZHENG Guo-qiang, LIU Chun-tai, SHEN Chang-yu, GUO Zhan-hu. Heating-induced negative temperature coefficient effect in conductive graphene/polymer ternary nanocomposites with a segregated and double-percolated structure [J]. Journal of Materials Chemistry C, 2017, 5(32): 8233-8242. DOI: 10.1039/ c7tc02472j.
[14] WANG Wen-long, WANG Chao, YUE Xia, ZHANG Chun- liang, ZHOU Chao, WU Wen-qiang, ZHU Hou-yao. Raman spectroscopy and resistance-temperature studies of functionalized multiwalled carbon nanotubes/epoxy resin composite film [J]. Microelectronic Engineering, 2019, 214: 50-54. DOI: 10.1016/j.mee.2019.04.029.
[15] ZHOU Xin, ZHU Li, FAN Li, DENG Hua, FU Qiang. Fabrication of highly stretchable, washable, wearable, water-repellent strain sensors with multi-stimuli sensing ability [J]. ACS Applied Materials & Interfaces, 2018, 10(37): 31655-31663. DOI: 10.1021/acsami.8b11766.
[16] ZHENG Yan-jun, LI Yi-long, LI Ze-yu, WANG Ya-long, DAI Kun, ZHENG Guo-qiang, LIU Chun-tai, SHEN Chang-yu. The effect of filler dimensionality on the electromechanical performance of polydimethylsiloxane based conductive nanocomposites for flexible strain sensors [J]. Composites Science and Technology, 2017, 139: 64-73. DOI: 10.1016/j.compscitech.2016.12.014.
[17] RIANDE E, DIAZ-CALLEJA R, PROLONGO M, MASEGOSA R, SALOM C. Polymer viscoelasticity: Stress and strain in practice [M]. CRC Press, 1999. DOI: 10.1201/9781482293241.
[18] WANG Lu-heng, HAN Yan-yan. Compressive relaxation of the stress and resistance for carbon nanotube filled silicone rubber composite [J]. Composites Part A: Applied Science and Manufacturing, 2013, 47: 63-71. DOI: 10.1016/ j.compositesa.2012.11.018.
[19] ANGELL C. Why C1=16–17 in the WLF equation is physical—and the fragility of polymers [J]. Polymer, 1997, 38(26): 6261-6266. DOI: 10.1016/s0032-3861(97)00201-2.
[20] YANG Heng, YAO Xue-feng, YUAN Li, GONG Lin-hui, LIU Ying-hua. Strain-sensitive electrical conductivity of carbon nanotube-graphene-filled rubber composites under cyclic loading [J]. Nanoscale, 2019, 11(2): 578-586. DOI: 10.1039/c8nr07737a.
[21] WANG Ning, XU Zhuo-yan, ZHAN Peng-fei, DAI Kun, ZHENG Guo-qiang, LIU Chun-tai, SHEN Chang-yu. A tunable strain sensor based on a carbon nanotubes/ electrospun polyamide 6 conductive nanofibrous network embedded into poly (vinyl alcohol) with self-diagnosis capabilities [J]. Journal of Materials Chemistry C, 2017, 5(18): 4408-4418. DOI: 10.1039/c7tc01123g.
[22] YILGOR I, EYNUR T, BILGIN S, YILGOR E, WILKES G L. Influence of soft segment molecular weight on the mechanical hysteresis and set behavior of silicone-urea copolymers with low hard segment contents [J]. Polymer, 2011, 52(2): 266-274. DOI: 10.1016/j.polymer.2010.11.040.
[23] LOZANO-PEREZ C, CAUICH-RODRIGUEZ J V, AVILES F. Influence of rigid segment and carbon nanotube concentration on the cyclic piezoresistive and hysteretic behavior of multiwall carbon nanotube/segmented polyurethane composites [J]. Composites Science and Technology, 2016, 128: 25-32. DOI: 10.1016/j.compscitech. 2016.03.010.
[24] WANG Lu-heng, MA Fang-fang, SHI Qian-shu, LIU Huang- hai, WANG Xue-ting. Study on compressive resistance creep and recovery of flexible pressure sensitive material based on carbon black filled silicone rubber composite [J]. Sensors and Actuators A: Physical, 2011, 165(2): 207-215. DOI: 10.1016/j.sna.2010.10.023.
[25] LJUBIC D, STAMENOVIC M, SMITHSON C, NUJKIC M, MEDO B, PUTIC S. Time: Temperature superposition principle: Application of WLF equation in polymer analysis and composites [J]. Zastita Materijala, 2014, 55(4): 395-400. DOI: 10.5937/ZasMat1404395L.
(Edited by ZHENG Yu-tong)
中文导读
温度对基于MWCNTs/PDMS复合材料的柔性应变传感器的影响
摘要:导电聚合物复合材料由于其制造工艺简单和传感性能可控性强的优势而被广泛应用于柔性应变传感器的制造。然而,温度会对导电聚合物复合材料的应变传感性能产生巨大的影响。本文研究了MWCNTs/PDMS复合材料在不同温度加载条件下的应变传感性能。结果表明,应变传感器的灵敏度会随着温度的升高而提高,而且肩峰现象也会随之减弱。根据聚合物力学理论,温度能够通过改变PDMS分子链的运动程度来影响复合材料的导电网络,且最终导致复合材料的传感性能变化。最后,结合复合材料的力电等效关系,建立了复合材料在不同加载条件(应变和温度)下的电阻变化的数学模型,并对实验结果和传感机理进行了讨论。研究结果可为应变传感器在不同温度条件下的进一步应用提供参考。
关键词:柔性应变传感器;导电聚合物复合材料;温度;多壁碳纳米管
Foundation item: Project(ZZYJKT2019-05) supported by State Key Laboratory of High Performance Complex Manufacturing, China; Project(51605497) supported by the National Natural Science Foundation of China; Project(2020CX05) supported by Innovation-Driven Project of Central South University, China
Received date: 2020-03-19; Accepted date: 2020-05-25
Corresponding author: HE Hu, PhD, Associate Professor; Tel: +86-18670327639; E-mail: hehu.mech@csu.edu.cn; ORCID: https://orcid. org/0000-0002-4199-027X

