J. Cent. South Univ. (2017) 24: 2914-2923
DOI: https://doi.org/10.1007/s11771-017-3705-4
Role of equal-strain assumption in unit-cell theory for consolidation with vertical drains
LEI Guo-hui(雷国辉)1, XU Li-dan(徐梨丹)1, ZHENG Qiang(郑强)1, NG Charles Wang Wai(吴宏伟)1, 2
1. Key Laboratory of Geomechanics and Embankment Engineering of the Ministry of Education,Geotechnical Research Institute, Hohai University, Nanjing 210098, China;
2. Department of Civil and Environmental Engineering, The Hong Kong University of Science and Technology, Hong Kong 999007, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: In the development of unit-cell theory for the analytical analysis of consolidation with vertical drains, the equal-strain assumption is often made with the intention of modelling consolidation under uniform settlement conditions. In contrast, the free-strain assumption for modelling consolidation under uniform load conditions is seldom employed, mainly because of the complexities involved in the analysis. This study derives a rigorous analytical solution to the generalised governing equations of free-strain consolidation with a vertical drain subjected to an instantaneous load. Calculated results from the newly proposed solution are compared with those from three available solutions derived based on the equal-strain assumption. Surprisingly good agreement is obtained in terms of excess pore-water pressure, degree of consolidation, and settlement. Horizontal profiles of settlement were not uniform before the end of consolidation. This indicates that the uniform settlement condition is not actually reproduced by the analytical solutions derived based on the equal-strain assumption. The equal-strain assumption is a sufficient but not necessary condition for deriving an analytical solution to unit-cell consolidation theory. The assumption plays no role in modelling consolidation under uniform settlement conditions but simplifies the analytical analysis of free-strain consolidation and results in an approximate solution of high accuracy for consolidation under uniform load conditions. Moreover, drain resistance and smear effects not only retard the consolidation rate, but also importantly shape the vertical and horizontal profiles of excess pore-water pressure, respectively.
Key words: consolidation; ground improvement; pore pressures; settlement; vertical drain
1 Introduction
For preliminary design purposes, analytical solutions for consolidation of soft ground with vertical drains under preloading are conventionally derived from the consolidation models of a unit cell of soil around a single vertical drain. Various unit-cell consolidation theories have been proposed since the pioneering work of BARRON [1]. Free-strain and equal-strain assumptions were made with the intention of modelling consolidation under uniform load (flexible foundation) and uniform settlement (rigid foundation) conditions, respectively [1]. A large number of solutions were derived for equal-strain consolidation based on various considerations [1–18]. However, owing to the difficulties involved in the analysis, only a very limited number of solutions were obtained for simplified governing equations of free-strain consolidation, which are listed in Table 1 [1, 19–28]. It can be seen that drain resistance and smear effect were ignored in Refs. [1, 19, 22, 23, 25, 26] and Refs. [19, 20, 25], respectively. Vertical flow and compressibility of smeared soil were ignored in Refs. [1, 22–24]. In addition, the vertical hydraulic conductivity of soil was assumed to be the same as the horizontal hydraulic conductivity in Refs. [20, 21].
Table 1 A list of simplified governing equations of free-strain consolidation whose analytical solutions are available

This study derives an analytical solution to the generalized governing equations of free-strain consolidation under an instantaneous step load. Simultaneous radial and vertical flow conditions, as well as the combined effects of drain resistance and smear, are fully taken into account. For simplicity, the mechanical and hydraulic properties of soil and drain are assumed to be uniform and constant. The excess pore-water pressures, settlements and degrees of consolidation calculated using the newly proposed free-strain solution are compared with those calculated using three available equal-strain solutions (HANSBO [18]; ZENG and XIE [17]; LEI et al [4]). Based on these comparisons, the calculation accuracies of the equal-strain solutions are calibrated, and the role of the equal-strain assumption in unit-cell consolidation theory is assessed. This helps to understand the applicability of the equal-strain solutions to the modelling of consolidation under uniform settlement (rigid foundation) conditions.
2 Description of free-strain consolidation problem
Figure 1 shows a unit-cell model for the free-strain consolidation of undisturbed and smeared soils with a vertical drain. The soils are subjected to a step increase in total stress under instantaneous loading. The governing equations of the free-strain consolidation of undisturbed and smeared soils assuming constant material properties [1, 29] are given in full by

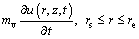 (1)
(1)

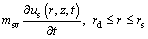 (2)
(2)
where r and z are the radial and vertical coordinates, respectively; t is the time; rd, rs and re are the radii of the vertical drain, the smear zone and the effective influence zone of the vertical drain, respectively; u and us are the excess pore-water pressures of undisturbed soil and smeared soil, respectively; kh, kv and mv are the horizontal and vertical hydraulic conductivities and volume compressibility of the undisturbed soil,respectively; ksh, ksv and msv are the horizontal and vertical hydraulic conductivities and volume compressibility of the smeared soil, respectively; and γw is the unit weight of water.
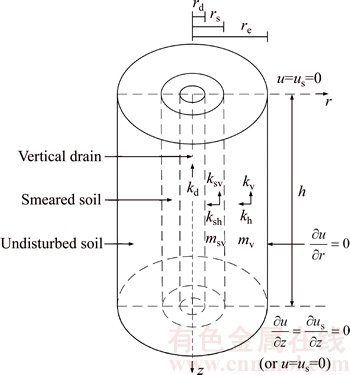
Fig. 1 A unit-cell consolidation model
According to the continuity of the excess pore-water pressure and the flow rate at the interface between the vertical drain and the smeared soil, the drain resistance can be expressed as [1, 18]
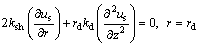 (3)
(3)
where kd is the hydraulic conductivity of the vertical drain.
The continuity of the excess pore-water pressure and the flow rate at the interface between the smeared soil and the undisturbed soil can be described by
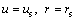 (4)
(4)
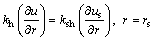 (5)
(5)
The hydraulic boundary conditions can be expressed as follows:
For the pervious top:
 (6)
(6)
For the pervious bottom:
 (7)
(7)
For the impervious bottom:
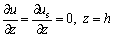 (8)
(8)
For the impervious vertical boundary:
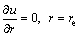 (9)
(9)
where h is the depth of the vertical drain.
The initial condition is given by
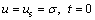 (10)
(10)
where σ is the increase in vertical total stress of soil due to an instantaneous load.
The ten equations above describe the unit-cell free- strain consolidation problem to be solved.
3 Derivation procedures
3.1 Consolidation of undisturbed soil
By introducing the Fourier sine series, the excess pore-water pressure of undisturbed soil can be expressed in fulfillment of Eqs. (6) to (8) describing the top and bottom drainage boundary conditions as follows:
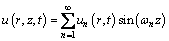 (11)
(11)
where un is the corresponding Fourier coefficient; and ωn is dependent on an indicator parameter (D) of the drainage boundary, as given by
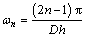 (12)
(12)
where D=1 for pervious top and bottom boundaries; D=2 for pervious top and impervious bottom boundaries.
Substituting Eq. (11) into the governing Eq. (1) yields
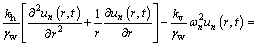
 (13)
(13)
By using the method of separation of variables, the following equation can be written:
 (14)
(14)
where A and B are functions of radial coordinate and time, respectively. Substituting Eq. (14) into Eq. (13) gives

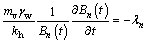 (15)
(15)
where λn is the separation constant, which can be written as
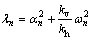 (16)
(16)
where αn is a constant to be determined. Substituting Eq. (16) into Eq. (15) gives
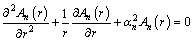 (17)
(17)
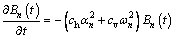 (18)
(18)
where cv=kv/(mvγw) and ch=kh/(mvγw) are the coefficients of the vertical and horizontal consolidation of undisturbed soil, respectively. The solutions to Eqs. (17) and (18) are
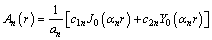 (19)
(19)
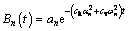 (20)
(20)
where J0 and Y0 are the Bessel functions of the first and second kind of zero order, respectively; an, c1n and c2n are the constants of integration to be determined.
Based on Eqs. (14), (19) and (20), Eq. (11) can be rewritten as
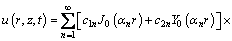
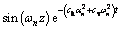 (21)
(21)
3.2 Consolidation of smeared soil
Again by introducing the Fourier sine series, the excess pore-water pressure of smeared soil can be expressed in fulfillment of Eqs. (6) to (8) describing the top and bottom drainage boundary conditions as follows:
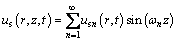 (22)
(22)
where usn is the corresponding Fourier coefficient.
By using the method of separation of variables, the following equation can be written:
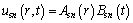 (23)
(23)
Following the same derivation procedures as above for the consolidation of undisturbed soil, the following solutions to Eq. (23) for the consolidation of smeared soil can be obtained:
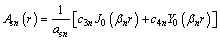 (24)
(24)
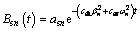 (25)
(25)
where asn, c3n, c4n and βn are constants to be determined; and csh=ksh/(msvγw) and csv=ksv/(msvγw) are the coefficients of consolidation of smeared soil in the horizontal and vertical directions, respectively.
Based on Eqs. (23) to (25), Eq. (22) can be rewritten as
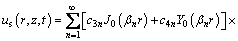
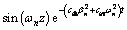 (26)
(26)
In the following sections, the constants of integration in Eqs. (21) and (26) are determined according to the initial and boundary conditions, together with the equations of drain resistance and interface drainage.
3.3 Drainage conditions on vertical boundary
Substituting Eq. (21) into Eq. (9) yields
 (27)
(27)
where J1 and Y1 are the Bessel functions of the first and second kind of order one, respectively.
3.4 Interface continuity
Substituting Eqs. (21) and (26) into Eqs. (4) and (5) yields
 (28)
(28)
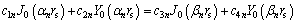 (29)
(29)
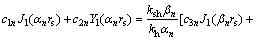
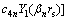 (30)
(30)
Substituting Eq. (27) into Eqs. (29) and (30) gives
 (31)
(31)
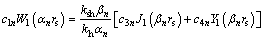 (32)
(32)
where
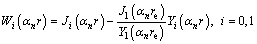 (33)
(33)
From Eqs. (31) and (32), the following can be derived:
 (34)
(34)
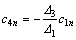 (35)
(35)
where
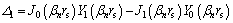 (36)
(36)
 (37)
(37)
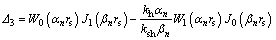 (38)
(38)
3.5 Drain resistance
Substituting Eq. (26) into Eq. (3) yields

 (39)
(39)
Substituting Eqs. (34) and (35) into Eq. (39) gives
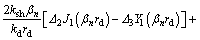
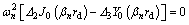 (40)
(40)
Since the number of eigenvalues of the Bessel functions in Eq. (40) is infinite for ωn, the eigenvalue βn should be rewritten as βmn. Similarly, it can be seen from Eq. (28) that αn should be rewritten as αmn. The values of βmn and αmn are the positive roots of simultaneous Eqs. (28) and (40), which can be solved using the exhaustive trial-and-error method. Therefore, based on Eqs. (27) and (33), Eq. (21) can be rewritten as
 (41)
(41)
where Cmn are series of constants to be determined from the initial conditions. Similarly, based on Eqs. (28), (34) and (35), Eq. (26) can be rewritten as
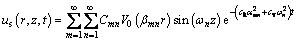 (42)
(42)
where
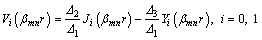 (43)
(43)
3.6 Initial conditions
Substituting Eqs. (41) and (42) into Eq. (10) gives
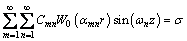 (44)
(44)
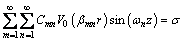 (45)
(45)
After multiplying both sides of Eqs. (44) and (45) by sin(ωkz) and integrating from 0 to h, Eqs. (46) and (47) can be obtained with the aid of the orthogonal relationship between triangular functions sin(ωkz) and sin(ωnz).
 (46)
(46)
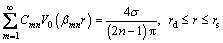 (47)
(47)
To solve Cmn, the same derivation procedures as those used by YOSHIKUNI and NAKANODO [20] and ONOUE [21] are adopted. After multiplying both sides of Eq. (46) by (kh/ksh)rW0(αknr) followed by integration from rs to re, and multiplying both sides of Eq. (47) by (ch/csh)rV0(βknr) followed by integration from rd to rs,Eq. (48) can be obtained by adding the two integrated equations together.
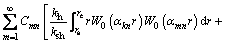
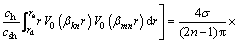
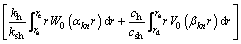 (48)
(48)
It can be proved that by Eqs. (28), (31)–(35), (40) and (43), the result of the bracketed terms for k≠m on the left-hand side of Eq. (48) is zero. Thus, the constant, Cmn, can be derived as given by
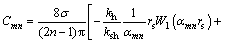

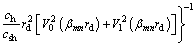 (49)
(49)
3.7 Free-strain solution
Based on the above derivations, analytical solutions are obtained for calculating the excess pore-water pressure at any arbitrary point in the undisturbed soil and the smeared soil, as given by Eqs. (41) and (42).
As usual, the overall average degree of consolidation is defined as follows:
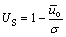 (50)
(50)
where  is the overall average excess pore-water pressure, which can be derived as
is the overall average excess pore-water pressure, which can be derived as
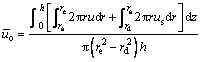

 (51)
(51)
where W1(αmnr) and V1(βmnr) are linear combinations of the Bessel functions of the first and second kind of order one, as given by Eqs. (33) and (43), respectively.
The ground surface settlements in the undisturbed soil and the smeared soil can be derived as
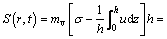
 (52)
(52)
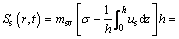
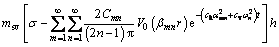 (53)
(53)
For ease of use of the proposed solution, a simple Fortran program has been developed. The results are obtained through double-precision arithmetic calculation.
4 Free-strain versus equal-strain solutions
In order to investigate the role of the equal-strain assumption in unit-cell consolidation theory, calculated results from the proposed free-strain solution are compared with those from three available equal-strain solutions, i.e., the well-known radial consolidation solution derived by HANSBO [18], an amended version of HANSBO’s radial consolidation solution by ZENG and XIE [17], and the most recently published solution for radial and vertical consolidation derived by LEI et al [4]. In the present study, HANSBO’s solution [18], as well as that of ZENG and XIE [17], is combined with the one-dimensional consolidation solution [29] by using the well-known CARRILLO [30] method to obtain the results for radial and vertical consolidation. The difference between the solution proposed in this study and the solution of LEI et al [4] stems from the vertical strain terms on the right-hand side of the governing equations of consolidation only. Instead of the governing Eqs. (1) and (2), LEI et al [4] adopted a depth-dependent radial average excess pore-water pressure to describe the terms of vertical strain, according to the equal-strain assumption. Although their solution was derived under multi-ramp loading conditions, it can also be used to analyse the consolidation under instantaneous loading by simply letting the duration of ramp loading be close to zero. For comparison purposes, a set of calculation parameters shown in Table 2 are adopted from LEI et al [4] for modelling consolidation with both drain resistance and smear effects. Two additional consolidation cases are also studied. One is consolidation with smear effects but without drain resistance, which is modelled by letting kd=1 m/s. The other is consolidation without drain resistance and smear effects, which is modelled by letting kd=1 m/s, ksh=kh, ksv=kv and msv=mv. By using the free-strain solution proposed in this study and the equal-strain solutions of HANSBO [18], ZENG and XIE [17] and LEI et al [4], the excess pore-water pressure, settlement and degree of consolidation can be obtained.
Table 2 Calculation parameters

Figures 2 and 3 show the isochrones of normalised excess pore-water pressure (u/σ or us/σ) at a radial distance of r/re=0.5 from the centre-line of the vertical drain and at a depth of z/h=0.5, respectively (see the coordinate system defined in Fig. 1). It can be seen that the excess pore-water pressures dissipate with elapsed time. The slopes of the isochrone curves in Figs. 2 and 3 represent the hydraulic gradients in the vertical and radial directions, respectively. Relatively higher hydraulic gradients are found closer to the pervious top boundary and the vertical drain as expected.
It can be seen from Fig. 2(a) and Fig. 2(b) that for consolidation without drain resistance (where the vertical drain becomes a pervious boundary), the excess pore- water pressures at depths greater than approximately 0.2h are generally uniformly distributed with depth. This is as expected as the radial consolidation is dominant. For consolidation with drain resistance (see Fig. 2(c)), however, the excess pore-water pressures are not uniformly distributed with depth, because of combined radial and vertical consolidation. The drain resistance evidently has a significant influence on the vertical profiles of excess pore-water pressure. As shown in Fig. 2(c), the excess pore-water pressures at t=50 and 100 d obtained from HANSBO’s solution [18] are noticeably different from those obtained from the other solutions. This is attributed to the fact that the strain rate terms in the governing equations of consolidation were implicitly assumed to be depth-independent (see HANSBO’s derivation [18] from Eqs. (11) and (12)), which is not the case for consolidation with drain resistance as explained by XIE and ZENG [31].

Fig. 2 Vertical profiles of isochrones of excess pore-water pressure at a radial distance of r/re=0.5 from centre-line of vertical drain:
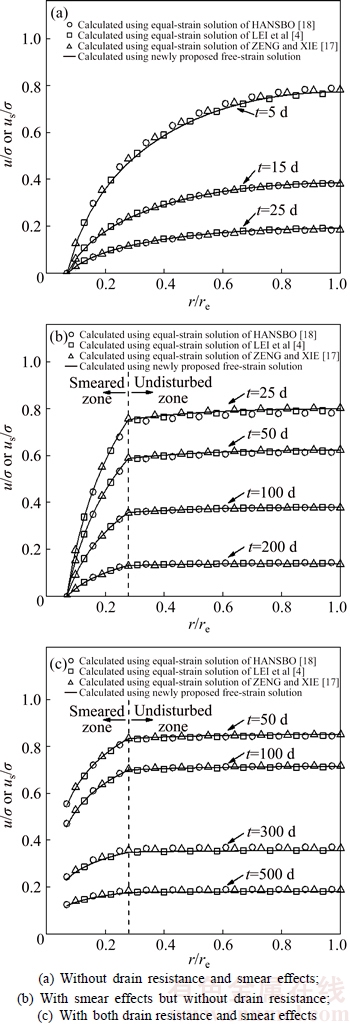
Fig. 3 Horizontal profiles of isochrones of excess pore-water pressure at a depth of z/h=0.5:
Figure 3(a) shows that for consolidation without smear effects, the distribution curves of excess pore- water pressure in the radial direction have a parabolic shape. For consolidation with smear effects as shown in Figs. 3(b) and (c), the excess pore-water pressure in the undisturbed soil is nearly uniformly distributed in the radial direction, while that in the smeared soil decreases relatively sharply as the distance from the vertical drain is reduced. This is because consolidation in the undisturbed soil is significantly retarded by the smear effects. Obviously, the smear effects have a significant influence on the horizontal profiles of excess pore-water pressure.
Figure 4 shows the calculated ground surface settlements derived from depth-averaged excess pore-water pressures. As expected, the settlements have similar horizontal profiles to the excess pore-water pressures (see Fig. 3). Before the end of consolidation (that is, t=∞), the settlements calculated using the equal- strain solutions are actually not uniformly distributed in the radial direction, especially for the case of consolidation without drain resistance and smear effects (see Fig. 4(a)). Figure 5 shows the calculated degrees of consolidation. Clearly, both the drain resistance and smear effects considerably retard the consolidation rates, resulting in changes in the vertical and horizontal profiles of excess pore-water pressure (as illustrated in Figs. 2 and 3).
A comparison of the calculated results from the three available equal-strain solutions with those from the newly proposed free-strain solution shown in Figs. 2 to 5 reveals that excellent agreement is obtained in terms of excess pore-water pressure, settlement and degree of consolidation. Particularly, the results obtained from the equal-strain solution Proposed by LEI et al [4] are basically identical to those obtained from the proposed free-strain solution. A possible mathematical explanation to this surprisingly interesting phenomenon is given in the next section, though it is beyond the scope of this study.
5 A possible explanation
For simplicity, radial consolidation without smear effects is considered. The governing equation of free-strain radial consolidation is given in a compact form by
 (54)
(54)
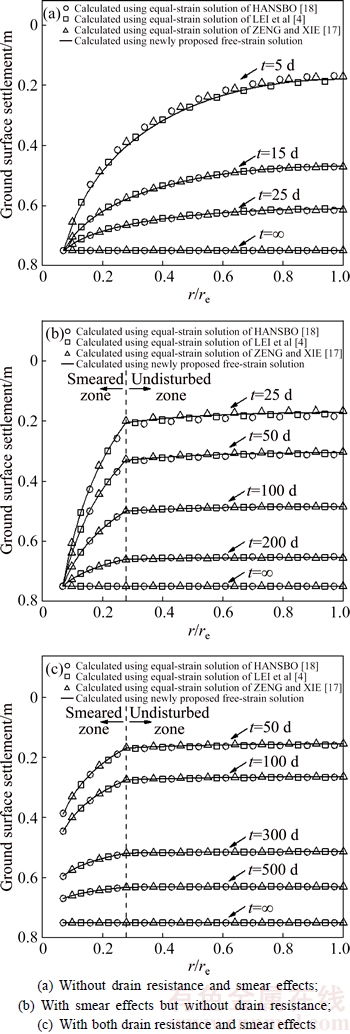
Fig. 4 Horizontal profiles of settlement:
After multiplying both sides of Eq. (54) by r and integrating from rd to re, Eq. (55) can be obtained with the consideration of the boundary conditions described by Eq. (9).
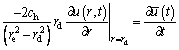 (55)
(55)

Fig. 5 Degrees of consolidation as function of time
where 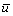 is the radial average excess pore-water pressure as given by
is the radial average excess pore-water pressure as given by
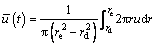 (56)
(56)
The governing equation of equal-strain radial consolidation is given by
 (57)
(57)
After multiplying both sides of Eq. (57) by r and integrating from rd to re, Eq. (55) can also be obtained. Obviously, the integrated forms of the governing equations of free-strain and equal-strain radial consolidation are the same. This may be the reason for the excellent agreement between the free-strain and equal-strain solutions, given that radial consolidation is dominant.
6 Conclusions
1) Before the end of consolidation, the uniform settlement conditions are in fact not reproduced by those unit-cell theories derived based on the equal-strain assumption.
2) The equal-strain assumption plays no role in modelling consolidation under uniform settlement conditions but simplifies the analytical analysis of free-strain consolidation and results in an approximate solution of high accuracy for consolidation under uniform load conditions.
3) The equal-strain assumption is a sufficient but not necessary condition for deriving an analytical solution to unit-cell consolidation theory. To avoid conceptual confusion, an average-strain assumption is preferred to the equal-strain assumption from a terminology perspective.
4) Apart from retarding the consolidation, drain resistance and smear effects importantly shape the vertical and horizontal profiles of excess pore-water pressure, respectively.
References
[1] BARRON R A. Consolidation of fine-grained soils by drain wells [J]. Transactions, ASCE, 1948, 113: 718–754.
[2] FU Cui-wei, LEI Guo-hui. A general solution for vertical-drain consolidation with impeded drainage boundaries [J]. Journal of Central South University, 2016, 23(4): 934–943.
[3] LEI Guo-hui, FU Cui-wei, NG Charles Wang Wai. Vertical-drain consolidation using stone columns: an analytical solution with an impeded drainage boundary under multi-ramp loading [J]. Geotextiles and Geomembranes, 2016, 44(1): 122–131.
[4] LEI Guo-hui, ZHENG Qiang, NG Charles Wang Wai, CHIU Abraham Chung Fai, XU Bo. An analytical solution for consolidation with vertical drains under multi-ramp loading [J]. Géotechnique, 2015, 65(7): 531–547.
[5] RUJIKIATKAMJORN C, INDRARATNA B. Analytical solution for radial consolidation considering soil structure characteristics [J]. Canadian Geotechnical Journal, 2015, 52(7): 947–960.
[6] LIU Jia-cai, LEI Guo-hui, ZHENG Ming-xin. General solutions for consolidation of multilayered soil with a vertical drain system [J]. Geotextiles and Geomembranes, 2014, 42(3): 267–276.
[7] KIANFAR K, INDRARATNA B, RUJIKIATKAMJORN C. Radial consolidation model incorporating the effects of vacuum preloading and non-Darcian flow [J]. Géotechnique, 2013, 63(12): 1060–1073.
[8] WALKER R, INDRARATNA B, RUJIKIATKAMJORN C. Vertical drain consolidation with non-Darcian flow and void-ratio-dependent compressibility and permeability [J]. Géotechnique, 2012, 62(11): 985–997.
[9] INDRARATNA B, RUJIKIATKAMJORN C, AMERATUNGA J, Boyle P. Performance and prediction of vacuum combined surcharge consolidation at Port of Brisbane [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2011, 137(11): 1009–1018.
[10] WALKER R, INDRARATNA B. Consolidation analysis of a stratified soil with vertical and horizontal drainage using the spectral method [J]. Géotechnique, 2009, 59(5): 439–449.
[11] CONTE E, TRONCONE A. Radial consolidation with vertical drains and general time-dependent loading [J]. Canadian Geotechnical Journal, 2009, 46(1): 25–36.
[12] INDRARATNA B, ALJORANY A, RUJIKIATKAMJORN C. Analytical and numerical modeling of consolidation by vertical drain beneath a circular embankment [J]. International Journal of Geomechanics, ASCE, 2008, 8(3): 199–206.
[13] WALKER R, INDRARATNA B. Vertical drain consolidation with overlapping smear zones [J]. Géotechnique, 2007, 57(5): 463–467.
[14] LEO C J. Equal strain consolidation by vertical drains [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(3): 316–327.
[15] HANSBO S. Consolidation equation valid for both Darcian and non- Darcian flow [J]. Géotechnique, 2001, 51(1): 51–54.
[16] CHAI J C, MIURA N, SAKAJO S. A theoretical study on smear effect around vertical drain [C]// Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering. Hamburg: Balkema, Rotterdam, 1997, 3: 1581–1584.
[17] ZENG Guo-xi, XIE Kang-he. New development of the vertical drain theories [C]// Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering [M]. London: CRC Press. 1989, 2: 1435–1438.
[18] HANSBO S. Consolidation of fine-grained soils by prefabricated drains [C]// Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering. Rotterdam: A.A Balkema, 1981, 3: 677–682.
[19] HORNE M R. The consolidation of a stratified soil with vertical and horizontal drainage [J]. International Journal of Mechanical Sciences, 1964, 6(2): 187–197.
[20] YOSHIKUNI H, NAKANODO H. Consolidation of soils by vertical drain wells with finite permeability [J]. Soils and Foundations, 1974, 14(2): 35–46.
[21] ONOUE A. Consolidation by vertical drains taking well resistance and smear into consideration [J]. Soils and Foundations, 1988, 28(4): 165–174.
[22] ZHAO Wei-bing. Theoretical solution to symmetrical consolidation of saturated clays with generalized Voigt model [J]. Journal of Hohai University, 1988, 16(5): 47–56. (in Chinese)
[23] ZHAO Wei-bing. Consolidation theory and its application of saturated soil with generalized Voigt model [D]. Nanjing: Hohai University, 1987. (in Chinese)
[24] WANG Rui-chun, XIE Kang-he. Analytical solutions for viscoelastic consolidation by vertical drains under time-dependent loading [J]. China Civil Engineering Journal, 2001, 34(6): 93–99. (in Chinese)
[25] ZHU G, YIN J H. Consolidation of soil with vertical and horizontal drainage under ramp load [J]. Géotechnique, 2001, 51(4): 361–367.
[26] ZHU G, YIN J H. Consolidation analysis of soil with vertical and horizontal drainage under ramp loading considering smear effects [J]. Geotextiles and Geomembranes, 2004, 22(1, 2): 63–74.
[27] NOGAMI T, LI M. Consolidation of clay with a system of vertical and horizontal drains [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2003, 129(9): 838–848.
[28] INDRARATNA B, GENG X, RUJIKIATKAMJORN C. Nonlinear analysis for a single vertical drain including the effects of preloading considering the compressibility and permeability of the soil [C]// FRATTA D O, PUPPALA A J, MUHUNTHAN B. Proceedings of GeoFlorida 2010: ASCE Conference on Advances in Analysis, Modeling and Design. Reston: American Society of Civil Engineers, Geotechnical Special Publication No.199, 2010: 147–156.
[29] TERZAGHI K. Theoretical soil mechanics [M]. New York: John Wiley & Sons, Inc., 1943.
[30] CARRILLO N. Simple two- and three-dimensional cases in the theory of consolidation of soils [J]. Journal of Mathematics and Physics, 1942, 21(1): 1–5.
[31] XIE Kang-he, ZENG Guo-xi. Consolidation theories for drain wells under equal strain condition [J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 3–17. (in Chinese)
(Edited by HE Yun-bin)
Cite this article as: LEI Guo-hui, XU Li-dan, ZHENG Qiang, NG Charles Wang Wai. Role of equal-strain assumption in unit-cell theory for consolidation with vertical drains [J]. Journal of Central South University, 2017, 24(12): 2914–2923. DOI:https://doi.org/10.1007/s11771-017-3705-4.
Foundation item: Projects(51278171, 51578213, 41530637) supported by the National Natural Science Foundation of China; Project(B13024) supported by the “111” Project, China; Projects(2015B06014, 2017B20614) supported by the Fundamental Research Funds for the Central Universities of China
Received date: 2016-03-03; Accepted date: 2016-05-04
Corresponding author: LEI Guo-hui, Professor, PhD; Tel: +86–13851922201; E-mail: leiguohui@hhu.edu.cn