
DOI: 10.11817/j.issn.1672-7207.2021.05.010
套筒式力臂补偿器对短棒料V型槽尖端起裂的影响
杨宁1,张立军1,张军伟1,郭伟健1,赵升吨2,王智伟3,田玉臣4
(1. 中国石油大学(华东) 机电工程学院,山东 青岛,266580;
2. 西安交通大学 机械工程学院,陕西 西安,710049;
3. 山东科技大学 机械电子工程学院,山东 青岛,266590;
4. 玫德艾瓦兹(济南)金属制品有限公司,山东 济南,250403)
摘要:针对短棒料在低应力下料中加载力臂过短的难题,提出一种套筒式力臂补偿方法。采用扩展有限元法(XFEM)研究套筒式力臂补偿器参数对短棒料V型槽尖端起裂力、起裂位置、起裂角和起裂前最大Mises应力的影响,并提出短棒料下料断面的起裂质量评价方法。研究结果表明:当增长力臂L4≤20 mm时,V型槽尖端所需起裂力随L4增大而逐渐减小,且起裂角在10°左右变化;当L4≥20 mm时,起裂力的变化稳中有降,变化幅度较小,但起裂角逐渐增大。套筒厚度H对V型槽应力集中效应的影响明显,当H≤4 mm时,V型槽尖端Mises应力随H增大逐渐增大;当H≥4 mm时,Mises应力随H增大逐渐减小。夹持力臂L3对V型槽应力集中效应的影响不明显。直径为13~18 mm、长度为20~25 mm的短棒料的套筒式力臂补偿器的合理参数为L3=18 mm,L4=20 mm,H=4 mm。这种补偿器有利于短棒料V型槽的尖端起裂,起裂衔接系数高,起裂偏距小,且起裂角明显减小。
关键词:短棒料下料;套筒式力臂补偿器;裂纹起裂;V型槽
中图分类号:TK83 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2021)05-1482-11
Influence of sleeve-type force arm compensator on crack initiation at V-shaped notch tip of short bar
YANG Ning1, ZHANG Lijun1, ZHANG Junwei1, GUO Weijian1, ZHAO Shengdun2, WANG Zhiwei3, TIAN Yuchen4
(1. College of Mechanical and Electronic Engineering, China University of Petroleum, Qingdao 266580, China;
2. School of Mechanical Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
3. College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao 266590, China;
4. Meide Ayvaz (Jinan) Metal Products Co. Ltd., Jinan 250403, China)
Abstract: Aiming at the problem that the loading force arm of short bar is too short in the low-stress cropping, a method of sleeve-type force arm compensation was proposed. The effects of sleeve-type force arm compensator parameters on the cracking force, cracking position, cracking angle and maximum Mises stress of V-shaped notch tip of short bar before cracking were studied by using XFEM method. An evaluation method of section cracking quality of short bars was proposed. The results show that when the increased force arm L4 is ≤20 mm, the required cracking force at tip of V-shaped notch gradually decreases with the increase of L4, and the cracking angle changes about 10°. After L4≥20 mm, the cracking force decreases in a small range, but the cracking angle gradually increases. The thickness H has a significant effect on the stress concentration of V-shaped notch. When H is ≤4 mm, the Mises stress at tip of V-shaped notch gradually increases with the increase of H; when H is ≥4 mm, the Mises stress gradually decreases. The effect of clamping arm L3 on the stress concentration of V-shaped notch is not obvious. The reasonable parameters of the sleeve-type force arm compensator for short bars with a diameter of 13-18 mm and length of 20-25 mm are as follows: L3 =18 mm, L4 =20 mm and H =4 mm. The compensator is beneficial to crack initiation at the tip of V-shaped notch of short bars, the cracking cohesion coefficient is high, the cracking deviation distance is small, and the cracking angle is obviously reduced.
Key words: short bar cropping; sleeve-type force arm compensator; crack initiation; V-shaped notch
金属棒料切断分离的下料工序应用量大面广,通常是装备制造业、汽车工业、石油化工等行业中常用机械零部件制造的第一道工序,下料质量直接影响零件的制造精度和生产成本[1]。传统的金属棒料下料方法主要是剪切下料、切割下料、车削下料等,其中,剪切下料的棒料几何精度较差,对剪切模具损耗较高;切割下料对材料的浪费较为严重,噪声污染大,很难满足绿色、节能的现代制造业要求。低应力下料技术是在棒料表面预制1圈V型槽,加载后利用V型槽的应力集中效应使其底部产生裂纹,通过控制施加在棒料上的载荷使裂纹可控扩展,获得断面平整度高的棒料[2]。这种下料技术能耗低、节约原材料,日渐受到重视,国内外学者们对棒料V型槽尖端初始裂纹萌生和裂纹扩展进行了大量的研究工作,如化春键等[3]采用有限元法对V型槽几何参数进行了研究,确立了合适的V型槽参数;赵升吨等[4]提出了热应力预制裂纹的方法,为棒料V型槽底部初始裂纹的产生创造了条件;ARUN[5]采用有限元法,结合断裂力学和Rousselier损伤模型模拟了不锈钢件的裂纹萌生和扩展形态,分析了机械载荷和残余应力对钢料的延性断裂行为的影响;KIM等[6-7]研究了缺口形状、偏心度和倾角对聚乙烯棒材裂纹疲劳寿命的影响。
现有的低应力下料机能动态调节棒料的夹持与加载位置[8],对于长度较短的棒料,依靠下料机本身去调整加载力和加载力臂进而达到V型槽尖端起裂所需的载荷理论上是可以实现的。但是过高的加载力存在如下问题:一是可能导致下料机本身的某些关键零部件在高压作用下较快的疲劳失效;二是过高的加载力使棒料起裂后,加大了起裂力平稳过渡到裂纹扩展所需外力的控制难度[9-10],致使裂纹起裂质量差,下料断面粗糙。而对于长度过短的棒料,因下料形位尺寸限制,这种局限性进一步凸显。因此,本文作者提出一种添加套筒式力臂补偿器的方法进行低应力可控加载下料,采用扩展有限元法(XFEM)在未预加裂纹的情况下模拟添加套筒式力臂补偿器的短棒料V型槽尖端起裂过程,研究不同参数的套筒式力臂补偿器对短棒料V型槽尖端起裂时的起裂力、起裂角等参数的影响,并提出一种新型棒料起裂质量评价方法,为短棒料的精密下料技术奠定基础。
1 多缸可控加载下料系统的工作原理
多缸可控加载下料系统主要由伺服开槽机、棒料进给系统以及多气缸径向可控加载下料机3部分组成。首先,采用伺服开槽机按照制造要求在棒料表面的特定位置预制环状V型槽,使棒料表面应力集中;然后,通过棒料进给系统把带环状V型槽的棒料送入多气缸径向可控加载下料机中夹持位置;最后,通过PLC有规律地控制下料机气缸,使加载锤头依次对带套筒式力臂补偿器的棒料施加大小和频率变化的径向载荷,这样棒料V型槽底部产生微裂纹,并且随着载荷的施加沿径向往棒料轴心扩展,到达棒料的临界点便会发生瞬时断裂,完成棒料的下料[11]。多缸可控加载下料工作原理如图1所示,其中,F为加载力,N;D为棒料直径,mm;L为单节棒料长度,mm;Leqv为等效棒料长度,mm;L3为夹持力臂,mm;L4为增长力臂,mm;H为套筒式力臂补偿器壁厚,mm;Φ为V型槽张角,(°);d为V型槽深度,mm;ρ为V型槽底角半径,mm。V型槽局部区域用G表示。可见,多缸可控加载下料方法是充分利用逆向思维,在较低外加载力所产生的拉应力和剪切应力的耦合作用下,优先考虑工程实际中最为常见、最为危险和最容易产生脆断的近似I型裂纹失效形式[12]。
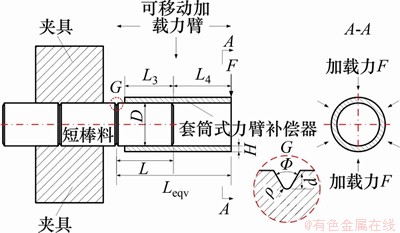
图1 多缸可控加载下料基本原理
Fig. 1 Basic principle of multi-cylinder controllable cropping
2 短棒料-套筒式力臂补偿器模型起裂原理与分析
V型槽处应力及裂纹示意图如图2所示。在裂纹的萌生阶段,理想的裂纹起裂应该在等效模型V型槽尖端最低点M点垂直起裂,但由于棒料的受载方式不是纯弯曲而是横力弯曲,即裂纹断裂形式为I型裂纹为主导的I-II型的复合裂纹形式,因此,外载荷除了会在棒料V型槽底部以弯矩的形式产生正应力外,还会在M截面产生切应力,如图2(a)所示,在正应力和切应力的共同作用下,最大主应力出现在V型槽底部靠右的位置,裂纹便在此处萌生,即图2(b)中N点。由于裂纹尖端应力场的复杂性,裂纹在V型槽底部是同时沿着周向和径向扩展。为了便于研究,将三维裂纹投影至平面,如图2(c)所示,C1为裂纹沿径向扩展的平面投影,C2为裂纹沿周向扩展的平面投影,O1为V型槽的中心线,O2为经过裂纹起裂位置的中心线,α为裂纹的起裂角,即C1和O2之间的夹角,β为C2和O2之间的夹角。
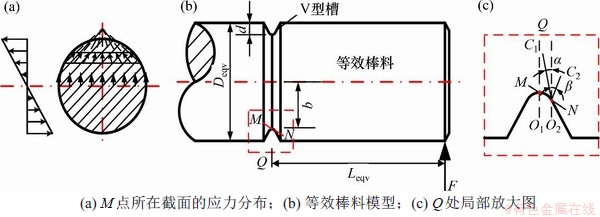
图2 V型槽处应力及裂纹示意图
Fig. 2 Model diagram of stress and crack at V-shaped notch tip
对普通加载条件下短棒料的V型槽尖端复杂的应力应变场和位移场进行分析,由位移法可得棒料V型槽尖端的应力场为[13]:
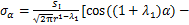
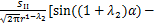
 (1)
(1)

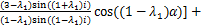

 (2)
(2)



 (3)
(3)
式中: 和
和 分别为极坐标(r,α)下的正应力分量,MPa;
分别为极坐标(r,α)下的正应力分量,MPa;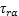 为剪应力,MPa;
为剪应力,MPa;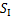 和
和 分别为I型和II型切口强度因子,MPa·mm1/2;
分别为I型和II型切口强度因子,MPa·mm1/2; 和
和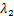 为第一、二本征值;i为本征值参数;r为初始裂纹的径向长度,mm。
为第一、二本征值;i为本征值参数;r为初始裂纹的径向长度,mm。
可以看出, ,
, 和
和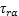 的场函数由切口强度因子
的场函数由切口强度因子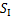 和
和 决定,经节点外推[14],并令最大主应力状态下的V型槽尖端剪应力
决定,经节点外推[14],并令最大主应力状态下的V型槽尖端剪应力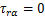 ,得到
,得到


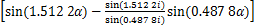 (4)
(4)
V型槽尖端应力强度因子主要取决于切口强度因子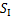 和
和 ,基于本模型中I-II型复合裂纹的加载形式,V型槽尖端应力强度因子
,基于本模型中I-II型复合裂纹的加载形式,V型槽尖端应力强度因子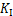 和
和 可表示为:
可表示为:

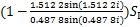 (5)
(5)
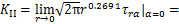
 (6)
(6)
由式(4)~(6)可知,应力强度因子亦与起裂角α有关,且研究和试验证明短棒料普通加载下料方式(即Leqv=L)下塑性材料的起裂角为13.8°[14]。由断裂力学可知,当下料模型的应力强度因子变程[15] 达到棒料的裂纹扩展门槛值△Kth时,才发生起裂过程,即:
达到棒料的裂纹扩展门槛值△Kth时,才发生起裂过程,即:

 (7)
(7)
式中: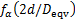 为修正系数;Deqv为模型中棒料的等效直径,mm;b为断面所在处的棒料半径,mm。
为修正系数;Deqv为模型中棒料的等效直径,mm;b为断面所在处的棒料半径,mm。
由式(7)可知:应力强度因子变程△K与模型的等效棒料参数有关,故起裂角及起裂过程亦受模型中等效棒料参数(即套筒式力臂补偿器力臂、厚度等)影响。而由于I-II型复合裂纹下料方式中I型、II型应力强度因子的权重不易确定,很难从理论上直接量化这些等效棒料参数对起裂过程的影响,因此有必要进一步分析该套筒式力臂补偿器对起裂效果的影响,并对其参数进行确定。
3 套筒式力臂补偿器参数对短棒料起裂效果的影响
裂纹仿真方法主要有有限元法(FEM)、无网格法、边界有限元法和扩展有限元法(XFEM)等,其中基于ABAQUS的扩展有限元方法(XFEM)不需要对网格进行特殊处理就能对裂纹萌生过程进行模拟,而且模拟任意的裂纹扩展路径,且与解无关[16],故本文采用基于ABAQUS软件的扩展有限元法[17],并以最大主应力准则判定短棒料-套筒式力臂补偿器模型的起裂过程。材料断裂指标f表达式为
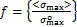 (8)
(8)
式中: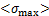 为V型槽尖端处的最大主应力,MPa;
为V型槽尖端处的最大主应力,MPa;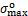 为最大许用应力,MPa。
为最大许用应力,MPa。
当f达到1且满足一定误差ftol[18]时,即满足
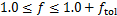 (9)
(9)
模型起裂,初始微裂纹产生,初始微裂纹的起裂方向为垂直于最大主应力方向。
基于上述起裂原理与分析,重点讨论套筒式力臂补偿器参数(夹持力臂L3、增长力臂L4和厚度H)对短棒料V型槽尖端起裂的影响,特别是对V型槽尖端起裂前最大Mises应力、起裂加载力、起裂位置和起裂角等参量的影响,以此来确定用于实际短棒料最佳的套筒式力臂补偿器参数。
3.1 夹持力臂L3对棒料V型槽尖端应力集中效应的影响
通常下料过程中棒料的几何参数[19]取为D=15 mm,ρ=0.2 mm,Φ=60°,d=1 mm。实际下料中套筒式力臂补偿器与短棒料之间无轴向位移和相对转动,因此,分析时把套筒式力臂补偿器与短棒料按照一体化处理并保持过渡配合。然后对棒料的左端面全约束,代替夹持装置的固定作用,同时,使用静态加载方式在右侧施加竖直向下的加载力。本文选取的短棒料长L为20 mm。
为保证较高的计算精度和减少计算时间,对于模型底部的网格加密,确定最小的网格尺寸为0.1 mm,而其他部分的网格尺寸适当增加,建立如图3所示的分析模型,节点数量为291 422,网格数量为173 310。套筒式力臂补偿器和棒料均取45号钢,弹性模量为2.10×105 MPa,泊松比为0.3,材料强度极限为639 MPa。
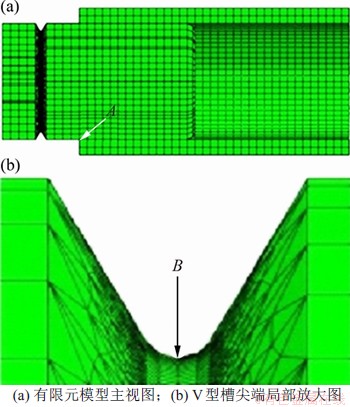
图3 带套筒式力臂补偿器的力学仿真模型示意图
Fig. 3 Schematic diagram of simulation model with sleeve force arm compensator
为了验证夹持力臂L3对棒料V型槽尖端起裂的影响程度且保证端面质量,仿真时首先采用单一变量法,在套筒式力臂补偿器上施加恒定载荷F=500 N,增长力臂L4为15 mm,厚度H=2 mm不变,对模型接触处A点的Mises应力σa和V型槽尖端B点的轴向拉应力σb进行分析,得到的结果如图4所示。
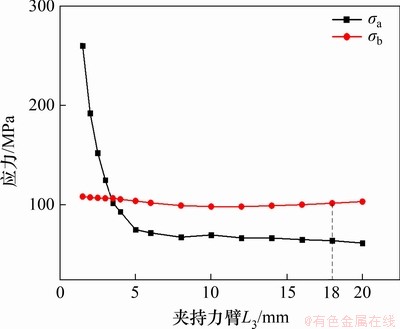
图4 σa和σb与夹持力臂L3的关系
Fig. 4 Relationship between σa and σb and L3
从图4可以看出:在F,L4,H恒定的情况下,当夹持力臂L3≤5 mm时,σa随着L3的增大急剧减小,应力变化率高达70.1%;当L3≥5 mm时,σa的变化趋于平缓,其应力变化率最小仅为1.02%。而随着L3的变化,σb无明显波动趋势,总体变化率最大仅为9.26%,故L3对V型槽尖端应力的影响可以忽略。在L3较大的情况下,接触点A处应力较小,套筒式力臂补偿器不会对棒料表面造成损伤,因此L3越大越好。但在实际下料中,当L3超过棒料的节长时(此处为20 mm),套筒式力臂补偿器极可能在棒料V型槽尖端起裂后与下一段棒料发生碰撞,如图5所示。为此,在保证L3对V型槽尖端及与套筒式力臂补偿器接触位置的应力影响最小的情况下,需在套筒式力臂补偿器与V型槽之间留出一定的安全距离。在设计多种直径的套筒式力臂补偿器时,安全距离为2 mm,此处夹持力臂L3长度宜取18 mm。
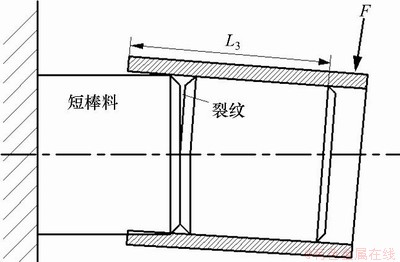
图5 套筒式力臂补偿器与棒料间的碰撞
Fig. 5 Collision between sleeve force arm compensator and bar
3.2 增长力臂L4对棒料的起裂力和挠度的影响
确定夹持力臂L3为18 mm,补偿器的厚度H为2 mm,此时,增长力臂L4成为影响棒料V型槽尖端应力场的主要因素,要使棒料在最佳的加载力下起裂,并且得到最为稳定的起裂质量,必须确定L4。
由材料力学可知,当L4较大时,较小的加载力F也能在V型槽尖端处产生较大的应力,因此,适当加大L4,保证裂纹在Ⅰ型裂纹形式的扩展[20],有利于实现低应力、低能耗的下料。加载后,根据式(9)给出的起裂判据,当加载到V型槽尖端出现一个长约0.2 mm,深约0.1 mm的裂纹片段时,认为是起裂阶段,这与文献[21]中规定的初始裂纹尺寸一致。ABAQUS中采用线性加载的方式,故由分析步时间与加载力乘积就可求出裂纹的起裂临界加载力,得到的结果如图6所示。
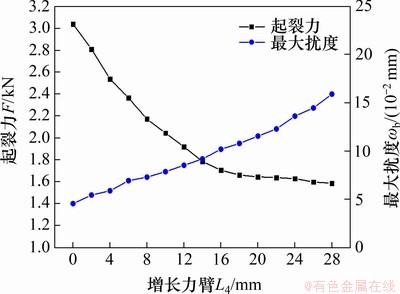
图6 起裂力和等效棒料右端面最大挠度与L4的关系
Fig. 6 Relationship between cracking force F and bar deflection  of right end of equivalent bar and L4
of right end of equivalent bar and L4
从图6可以看出:在L3和厚度H恒定的情况下,增长力臂L4与F负相关,起裂力变化率达到42.3%,但L4到达20 mm后,起裂力的变化趋势趋于平缓;当L4=28 mm时,起裂力为1 586.8 N,起裂力变化率仅为3.56%。可见:补偿器对短棒料V型槽底部的起裂有明显促进作用。
然而,套筒式力臂补偿器长度L4的增加也会使等效棒料右端面对应的挠度增大,棒料-套筒式力臂补偿器模型受力挠度示意图如图7所示。由公式
 (10)
(10)
式中:M为力矩。通过连续积分法可得到棒料理论挠度 的曲线方程为
的曲线方程为
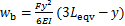 (11)
(11)
式中:E为材料的弹性模量,MPa;I为转动惯量,kg·m2。
当y=Leqv时,棒料理论最大挠度方程为
 (12)
(12)
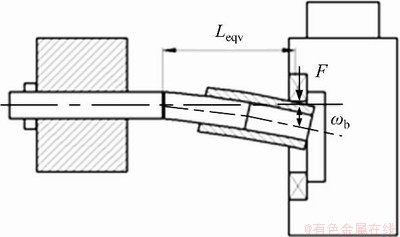
图7 棒料-套筒式力臂补偿器模型受力挠度示意图
Fig. 7 Schematic diagram of deflection of bar-sleeve force arm compensator model
在低应力下料中,为了让初始裂纹尽快生成并获得更好的断面质量,首先在裂纹萌生前给套筒式力臂补偿器上施加高频率、大载荷,当初始裂纹萌生以后,为了减小断面瞬断区面积,外载荷应该有规律地减小直至棒料失稳断裂[10]。在同一套筒式力臂补偿器下,V型槽起裂加载力最大,此时等效棒料右端面对应的挠度也最大,如图7所示。而由式(12)可知,V型槽尖端起裂前等效棒料右端面对应的挠度ωb不仅与F有关,还与Leqv有关,当Leqv较大时,短棒料便可在较小的加载力下起裂,但等效棒料右端面对应的挠度也可能较大,这会导致套筒式力臂补偿器与加载锤头之间的接触面积减小,加载锤头会对其表面造成损伤,如图7所示;下一节棒料过度弯曲,导致棒料与夹持装置下边缘过度接触,对棒料表面和夹持装置造成损伤或者使第二节棒料断裂。因此,L4的增加不但使起裂力减小,而且使等效棒料右端面挠度变大,故还应综合其他判断标准来确定合适的L4。
3.3 L4对棒料V型槽尖端起裂位置及起裂角的影响
棒料的断面质量直接影响到后续加工的效率和成本,而下料的断面质量主要取决于裂纹的起裂位置和起裂方向,因此对裂纹的萌生阶段进行研究是十分必要的。而前期相关仿真和试验结果显示,采取旋转弯曲型加载方式,棒料起裂位置均位于接近V型槽底角半径的1/2处[18]。因此,本文通过控制在初始裂纹深度一定的条件下,分析不同L4下V型槽尖端初始裂纹起裂角的变化。图8所示为初始裂纹的形态。在ABAQUS中,因为加载力的变化是从0开始线性加载至设定值的,所以裂纹就会在分析步的增量步中逐步扩展,这样就可以通过控制增量步来控制裂纹扩展的深度和长度。不同L4棒料V型槽尖端起裂角的仿真结果如图9所示。
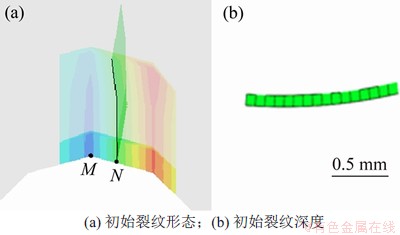
图8 ABAQUS仿真模型中萌生的裂纹
Fig. 8 Crack initiated in simulation model of ABAQUS
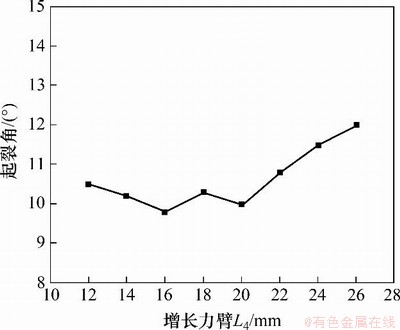
图9 V型槽尖端处起裂角与L4的关系
Fig. 9 Relationship between cracking angle and L4
由图9可知:在L3和厚度H恒定情况下,增大L4对裂纹起裂角有较为明显的影响。当L4≤20 mm时,棒料V型槽底部起裂角变化较为平缓,一直都在10°左右;当L4≥20 mm时,起裂角呈增大趋势;当L4=26 mm时,起裂角增大到12°。因为起裂角会严重影响到棒料的起裂质量和平整度,而起裂角又与棒料的直径D(13≤D≤18 mm)有关[18]。将仿真数据进行数据拟合,得到L4和起裂角α之间的关系为
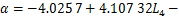
 (13)
(13)
由式(13)求出的起裂角α与仿真数据的最大相对误差为3.21%,说明式(13)的表征关系可以用于工程实际。由于目前低应力下料机的工作特点,起裂角无法完全减小到0°,但起裂角在一定范围内应该越小越好。综合考虑L4对起裂力、起裂角和棒料挠度的影响,当起裂角小于10°时,起裂力较大,对减小能耗不利;当起裂角大于10°时,对应的L4较大,等效棒料端面的挠度较大,加载锤头易对套筒式力臂补偿器表面造成损伤。当起裂角选取为10°时,对应的L4=20 mm,F=1 645.4 N,ωb=0.115 6 mm,此时,棒料V型槽所需起裂力较小,且加载锤头不会对套筒式力臂补偿器表面造成损伤。
3.4 厚度H对棒料V型槽应力集中效应的影响
夹持力臂L3和增长力臂L4确定后,套筒式力臂补偿器厚度H成为影响棒料V型槽尖端起裂的主要因素。在ABAQUS中,当L3=18 mm,L4=20 mm时,建立不同厚度的套筒式力臂补偿器的三维有限元模型,结果如图10所示。从图10可以看出:在同一加载力且L3和L4恒定情况下,H≤4 mm时,V型槽尖端的临界Mises应力随H逐渐增大,相对应力增大了40.2%;而H≥4 mm时,V型槽底部应力呈减小趋势,相比最大应力减小了24.1%。当H=4 mm时,V型槽处最大Mises应力为605.4 MPa,小于45号钢的强度极限639 MPa,符合低应力下料要求。因此,确定L3和L4后,H=4 mm时,V型槽尖端处Mises应力最大,此时最有利于裂纹起裂。
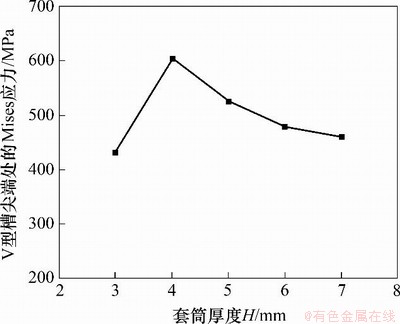
图10 V型槽尖端处Mises应力与厚度H的关系
Fig. 10 Relationship between Mises stress at the tip of V-shaped notch and H
4 试验验证与讨论
4.1 试验平台及条件
多气缸径向可控加载下料机如图11所示,该下料机由机身、多缸体机构、加载锤头、套筒式力臂补偿器、排气孔、套筒支架、夹具等组成。为了提质增效,下料过程中需不断增大平均应力比、不断减小加载频率[22-23]。故以工业上常用的长度为20~25 mm、直径为15 mm的4种不同材质的短棒料为试样,控制伺服电机按照线性递增的位移-时间曲线来驱动锤头的加载位移;同时,采用变频器根据线性递减的频率-时间曲线调节锤头的加载频率,实现下料中对平均应力比和载荷频率的要求。
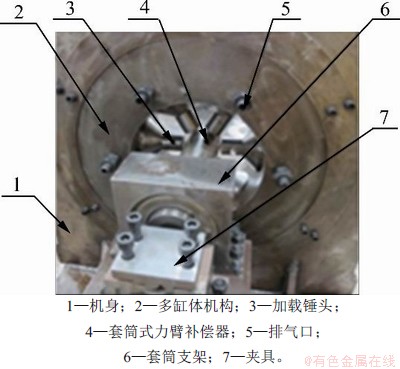
图11 多气缸径向可控加载下料机试验装置
Fig. 11 Experimental device of multi-cylinder radial controllable cropping machine
4.2 下料断面起裂质量评价方法
低应力下料中,棒料断面质量综合评价方法中的断面凸起高度和凹陷深度可以很好地对下料断面进行整体评判[24],但是对于起裂效果及起裂质量不能进行准确而有效的判断,故针对本文新型多缸可控加载下料试验结果和综合评价方法中的指标导向,提出一种适用于短棒料低应力下料断面的起裂质量评价方法,并用以评价套筒式力臂补偿器及其参数对短棒料V型槽尖端起裂的稳定可靠性。多缸加载下料所得断面如图12所示,其表现出明显的起裂区X、裂纹扩展区Y和瞬断区Z。为有效判定断面的起裂质量,提出3个起裂阶段特征评价指标:起裂衔接系数e/h、起裂偏距l和起裂角α,如图13所示,其中e表示起裂区迹线(起裂区与扩展区的衔接线)到棒料轴心的最短距离,mm;h为起裂区不平度(起裂区与裂纹扩展区衔接处凹陷的最大值),mm。起裂衔接系数e/h表征起裂与裂纹扩展的衔接程度,反映裂纹从起裂阶段过渡到扩展阶段的稳定性,故起裂衔接系数越大,起裂越稳定可靠;而起裂偏距l反映起裂位置与理想起裂位置的偏离程度,根据生产质量的实际要求,l越小越好;起裂角α表示裂纹沿径向扩展平面的角度,直接决定裂纹的扩展路径和起裂区的平整度,因此,起裂质量亦与起裂角负相关。

图12 多缸加载下料棒料
Fig. 12 Drawing of bar of multi-cylinder loading cropping
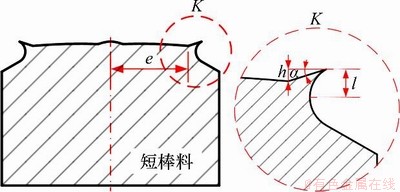
图13 棒料的起裂特征评价指标示意图
Fig. 13 Schematic diagram of evaluation index of bar’s crack initiation characteristics
4.3 下料试验结果分析与讨论
为进一步证实上述获取的套筒式力臂补偿器参数的合理性,对长度为20~25mm,直径为15 mm的4种不同材质的短棒料,添加夹持力臂L3=18 mm、增长力臂L4=20 mm、厚度H=4 mm的套筒式力臂补偿器,进行气动式多缸可控加载低应力下料试验。试验所得棒料断面照片如图14所示。不同材质短棒料断面的起裂质量的特征评价指标如表1所示。可见:根据起裂判据,试验结果与仿真模型得到的起裂值较为吻合,实现了对短棒料-套筒式力臂补偿器模型的低应力稳定可靠起裂。
表1 不同材质短棒料断面的起裂质量的特征评价指标
Table 1 Characteristic evaluation indexes of cracking quality of sections of different short bars


图14 不同材质的棒料的下料断面
Fig. 14 Cropping sections of bars with different materials
由图14可见:4种材质的短棒料V型槽的起裂位置相对稳定,起裂区断面平整度较高,没有明显的凹凸和毛刺痕迹。从V型槽尖端到中心瞬断区可以看出,裂纹有明显的沿周向疲劳扩展的痕迹,这表明起裂区与裂纹扩展区衔接性高,起裂衔接系数e/h近30,最终均呈现出稳定的裂纹扩展断面。从试验结果还可看出:裂纹的起裂位置不是从V型槽最尖端开始,而是从尖端靠右起裂偏距约0.1 mm的位置开始,45号钢试验断面的起裂角仅为10.3°,相比于短棒料普通加载下料方式下塑性材料的起裂角13.8°有明显降低,这说明套筒式力臂补偿器有利于短棒料V型槽尖端裂纹起裂,且研究得到的补偿器参数也是合适的。进一步多次下料试验结果显示,上述套筒式力臂补偿器参数对直径为13~18 mm的金属棒料下料也是适用的。
5 结论
1) 提出一种专用于短棒料的套筒式力臂补偿下料方法,研发了气动式多缸可控加载下料系统,它主要由伺服开槽机、棒料进给系统和多气缸径向可控加载下料机等组成,具有实现对短棒料低应力可控加载并能补偿棒料挠度的特点。
2) 套筒式力臂补偿器参数中,夹持力臂L3对棒料V型槽的应力集中效果影响不大,考虑到生产实际和套筒式力臂补偿器与棒料接触处的应力影响,夹持力臂L3越长越好,对于本文中的短棒料,夹持力臂L3选为18 mm。套筒式力臂补偿器厚度H对棒料V型槽应力集中有较为明显的影响,在现有参数下,厚度为4 mm时,棒料V型槽尖端应力集中现象最明显,最有利于裂纹起裂。
3) 增长力臂L4对棒料V型槽尖端起裂有影响明显。当L4≤20 mm时,起裂力F与增长力臂L4负相关,而起裂角α在10°左右变化;当L4≥20 mm时,起裂力变化趋于平缓,而L4对起裂角α有较大的影响,起裂角α从10°开始逐渐增大。综合考虑增长力臂L4和棒料直径D对V型槽尖端起裂角的影响,提出针对直径在13~18 mm范围内的短棒料的套筒式力臂补偿器的增长力臂L4与起裂角α之间的计算公式,给出L4的衡量标准;L4取20 mm时,套筒式力臂补偿器最有利于V型槽尖端起裂。
4) 采用具有合理参数的套筒式力臂补偿器后,45号钢短棒料下料试验断面的起裂角仅为10.3°,相比于同类材料的短棒料普通加载下料方式下的起裂角13.8°有明显降低,这说明套筒式力臂补偿器有利于短棒料V型槽尖端裂纹起裂。本文确定的套筒式力臂补偿器参数对直径为13~18 mm、长度为20~25 mm的金属棒料也适用。
参考文献:
[1] 顾海澄, 何家文. 节约金属材料手册[M]. 北京: 机械工业出版社, 1995: 12-60.
GU Haicheng, HE Jiawen. Manual for saving metal materials[M]. Beijing: China Machine Press, 1995: 12-60.
[2] 马广英, 郎福元, 龚俊. 裂纹技术在应力下料中的研究与应用[J]. 甘肃科学学报, 2003, 15(3): 86-90.
MA Guangying, LANG Fuyuan, GONG Jun. The investigation and application of crack technique in stress bar severing[J]. Journal of Gansu Sciences, 2003, 15(3): 86-90.
[3] 化春键, 赵升吨, 宋涛, 等. V型槽几何参数对裂纹萌生的影响规律[J]. 西安交通大学学报, 2004, 38(9): 947-950.
HUA Chunjian, ZHAO Shengdun, SONG Tao, et al. Influence of the geometric parameters of the V shaped groove on initialization of ideal crack in precision cropping[J]. Journal of Xi'an Jiaotong University, 2004, 38(9): 947-950.
[4] 赵升吨, 张立军, 柳伟, 等. 棒料热应力预制V型槽尖端理想裂纹的可行性研究[J]. 塑性工程学报, 2006, 13(5): 51-57.
ZHAO Shengdun, ZHANG Lijun, LIU Wei, et al. Feasibility investigation of ideal fracture caused by thermal stress[J]. Journal of Plasticity Engineering, 2006, 13(5): 51-57.
[5] ARUN S. Finite element modelling of fracture and damage in austenitic stainless steel in nuclear power plant[D]. Manchester: UK University, 2015: 20-30.
[6] KIM I, ZHAO Yongjian, CHOI B H, et al. Numerical analysis of asymmetric fatigue crack growth behaviors of circular notched bar specimen resulting from various geometric misalignments[J]. Engineering Fracture Mechanics, 2013, 108: 50-64.
[7] ZHAO Yongjian, KIM I, CHOI B H, et al. Variation of the fatigue lifetime with the initial notch geometry of circular notched bar specimens[J]. International Journal of Fracture, 2011, 167(1): 127-134.
[8] 张立军, 金永山, 张军伟, 等. 液压补偿型低应力精密断料教学实验平台开发[J]. 实验技术与管理, 2020, 37(1): 91-96.
ZHANG Lijun, JIN Yongshan, ZHANG Junwei, et al. Development of hydraulic compensation type low-stress precision material cutting teaching test platform[J]. Experimental Technology and Management, 2020, 37(1): 91-96.
[9] ZHANG Lijun, CHEN Xianfeng, WANG Hanxiang, et al. Research on critical loading force in precision cropping system based on hydraulic compensation[J]. International Journal of Mechanical Sciences, 2018, 142/143: 44-50.
[10] ZHANG Lijun, ZHANG Depei, WANG Hanxiang, et al. Research on variable frequency-loading curve in precision cropping system with high-speed and centrifugal action[J]. The International Journal of Advanced Manufacturing Technology, 2018, 97(5/6/7/8): 2969-2978.
[11] 唐勇. 多气缸径向冲击可控精密下料新工艺及其低周疲劳裂纹扩展规律的研究[D]. 西安: 西安交通大学, 2010: 15-30.
TANG Yong. Research on a new precision cropping process with controlled radial impact of multiple cylinders and the law of low-cycle fatigue crack propagation[D]. Xi'an: Xi'an Jiaotong University, 2010: 15-30.
[12] 杜瑞妍. 金属棒材疲劳断裂研究与应用[D]. 郑州: 郑州大学, 2008: 18-28.
DU Ruiyan. Research and application of metal bar fatigue fracture[D]. Zhengzhou: Zhengzhou University, 2008: 18-28.
[13] 匡震邦. 裂纹端部场[M]. 西安: 西安交通大学出版社, 2002: 40-60.
Kuang Zhenbang. Crack tip field[M]. Xi'an: Xi'an Jiaotong University Press, 2002: 40-60.
[14] 王振伟, 田野, 陈丰, 等. V形切口尖端裂纹起裂方向的主应力判别准则及其验证[J]. 中国机械工程, 2014, 25(6): 794-799.
WANG Zhenwei, TIAN Ye, CHEN Feng, et al. Principle stress rule for crack propagation direction of V notch crack tip and its application[J]. China Mechanical Engineering, 2014, 25(6): 794-799.
[15] 张立军, 赵永瑞, 相恒富, 等. 下料时初始激振频率的选择方法[J]. 机械强度, 2009, 31(3): 365-368.
ZHANG Lijun, ZHAO Yongrui, XIANG Hengfu, et al. Selection of initial excited frequency in precision cropping[J]. Journal of Mechanical Strength, 2009, 31(3): 365-368.
[16] ABAQUS/Standard. ABAQUS analysis user's manual[M]. RI: ABAQUS Inc, 2014: 36-50.
[17] 张立军, 张军伟, 金永山, 等. 偏心切口对棒料裂纹起裂和扩展的影响[J]. 中南大学学报(自然科学版), 2020, 51(5): 1245-1254.
ZHANG Lijun, ZHANG Junwei, JIN Yongshan, et al. Influence of eccentric incision on crack initiation and propagation of metal bars[J]. Journal of Central South University(Science and Technology), 2020, 51(5): 1245-1254.
[18] 陈先锋, 张立军, 张德培, 等. 基于XFEM的加载参数对棒料V型槽尖端起裂影响规律[J]. 塑性工程学报, 2018, 25(4): 254-261.
CHEN Xianfeng, ZHANG Lijun, ZHANG Depei, et al. Influence rule of loading parameters on crack initiation at the tip of V-shaped notch of bars based on XFEM[J]. Journal of Plasticity Engineering, 2018, 25(4): 254-261.
[19] 张立军, 赵升吨, 雷净. 棒料几何参数对其预制表面V型槽槽底应力集中系数的影响规律[J]. 塑性工程学报, 2007, 14(1): 66-71.
ZHANG Lijun, ZHAO Shengdun, LEI Jing. Influence of the geometric parameters of slotted bar on stress concentration factor at prefabricated V-shaped groove bottom of the bar surface[J]. Journal of Plasticity Engineering, 2007, 14(1): 66-71.
[20] ZHANG L J, ZHAO S D, LEI J, et al. Investigation on the bar clamping position of a new type of precision cropping system with variable frequency vibration[J]. International Journal of Machine Tools and Manufacture, 2007, 47(7/8): 1125-1131.
[21] 郑修麟. 金属疲劳的定量理论[M]. 西安: 西北工业大学出版社, 1994: 22-50.
ZHENG Xiulin. Quantitative theory of metal fatigue[M]. Xi'an: Northwestern Polytechnical University Press, 1994: 22-50.
[22] ZHANG L J, ZHAO S D, HUA C J, et al. Investigation on a new type of low-stress cropping system with variable frequency vibration[J]. The International Journal of Advanced Manufacturing Technology, 2008, 36(3/4): 288-295.
[23] WANG Zhenwei, ZHAO Shengdun, YU Yating. Study on the dynamic characteristics of the low-stress vibration cropping machine[J]. Journal of Materials Processing Technology, 2007, 190(1/2/3): 89-95.
[24] 唐勇, 赵升吨, 王振伟. 金属棒料精密下料新工艺及实验研究[J]. 中国机械工程, 2010, 21(3): 359-363.
TANG Yong, ZHAO Shengdun, WANG Zhenwei. Experimental study on new precision cropping process for metal bars[J]. China Mechanical Engineering, 2010, 21(3): 359-363.
(编辑 赵俊)
收稿日期: 2020 -05 -27; 修回日期: 2020 -08 -18
基金项目(Foundation item):国家自然科学基金资助项目(51575532) (Project(51575532) supported by the National Natural Science Foundation of China)
通信作者:张立军,博士,教授,博士生导师,从事可再生能源技术和绿色装备制造研究;E-mail:zlj-2@163.com
引用格式: 杨宁, 张立军, 张军伟, 等. 套筒式力臂补偿器对短棒料V型槽尖端起裂的影响[J]. 中南大学学报(自然科学版), 2021, 52(5): 1482-1492.
Citation: YANG Ning, ZHANG Lijun, ZHANG Junwei, et al. Influence of sleeve-type force arm compensator on crack initiation at V-shaped notch tip of short bar[J]. Journal of Central South University(Science and Technology), 2021, 52(5): 1482-1492.