J. Cent. South Univ. (2020) 27: 674-697

DOI: https://doi.org/10.1007/s11771-020-4323-0

Effects of microstructural heterogeneity on fatigue properties of cast aluminum alloys

JIAO Yi-nan(焦忆楠)^{1, 2}, ZHANG Yi-fan(张依凡)^{2, 3}, MA Shi-qing(马世卿)^{1, 2},

SANG De-li(桑德利)^{1, 2, 4}, ZHANG Yang(张洋)^{1, 2}, ZHAO Jin-jin(赵晋津)^{1, 2, 3, 4},

WU Sheng-chuan(吴圣川)⁵, LIU Yong-qiang(刘永强)^{2, 3}, YANG Shao-pu(杨绍普)^{2, 3}

1. School of Materials Science and Engineering, Hebei Key Laboratory for Mechanics of Intelligent Materials and Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;

2. State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;

3. School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;

4. State Key Laboratory of Metastable Materials Science and Technology, Yanshan University,Qinhuangdao 066004, China;

5. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: Cast Al alloys are widely employed for engine components, structural parts, gear box, chassis, etc. and subjected to mechanical cyclic load during operation. The accurate fatigue life prediction of these alloys is essential for normal operation as fatigue cracks initiated during operation induce the lubrication oil leak and serious safety hazard. Microstructural heterogeneity, including shrinkage/gaspores and secondary phase particles, is the most detrimental factor that affects fatigue life of cast Al alloys. The approximate fatigue life cycles could be estimated based on the size distribution and locations of shrinkage pores/defects. The relationship between crack population and stress was reported by statistical distributions and the cumulative probability for cast Al alloys fail at a certain stress could be predicted by combination of Paris law and pore size distribution. Pore depth was found to dominate the stress field around the pore on the surface and the maximum stress increases sharply when the pore intercepted with the surface at its top. The microstructure of cast Al alloys usually is composed of primary Al dendrites, eutectic silicon, Fe-rich particles and other intermetallic particles are dependent upon alloy composition and heat treatment. The coalescence of microcracks initiated from the fractured secondary phases was clearly found and can accelerate the initiation and propagation of the fatigue cracks. A link between defect features and the fatigue strength needs to be established through a good understanding of the fatigue damage mechanisms associated with the microstructural features under specific loading conditions. This paper reviews the influences of shrinkage/gaspores and secondary phase particles, formed during casting process, on the fatigue life of Al-Si-Mg cast Al alloys.

Key words: cast aluminum alloys; fatigue; microstructural heterogeneous; shrinkage/gas pore; secondary phase particles

Cite this article as: JIAO Yi-nan, ZHANG Yi-fan, MA Shi-qing, SANG De-li, ZHANG Yang, ZHAO Jin-jin, WU Sheng-chuan, LIU Yong-qiang, YANG Shao-pu. Effects of microstructural heterogeneity on fatigue properties of cast aluminum alloys [J]. Journal of Central South University, 2020, 27(3): 674-697. DOI: https://doi.org/10.1007/s11771- 020-4323-0.

1 Introduction

Due to the increasing concern over greenhouse gases and global warming, there is a scream demand to reliable, sustainable and affordable energy and energy saving techniques [1, 2]. One effective method to decrease energy cost is lowering the total weight of delivery vehicles [3-9]. The cast Al alloys are widely used in automotive industries [3, 4], aircrafts [5, 6, 8], aerospaces [6, 9] and high speed railways [7] due to their good integrated properties including relative good strength, low density and excellent conductivity. They are employed for engine components [3-5, 8], structural parts [4, 5, 9], gear boxes [4, 7], chassis [10], etc. They are normally subjected to mechanical cyclic loads and may potentially initiate cracks due to mechanical fatigue. Efforts have been conducted to avoid fatigue crack initiation including appropriate design methodologies. Majority of these designs are based on appropriate fatigue criteria that are carried out by fatigue tests. The fatigue test specimens, on the other hand, usually have quite different size from the size of the fatigue critical zones found on the real manufactured components [10].

The fatigue strength of cast Al alloys is profoundly affected by different types of microstructural heterogeneities such as micro- shrinkage/gas defects/pores, gas porosity and eutectic phases introduced during manufacturing processes. Despite the efforts taken to understand the influence of these microstructural heterogeneities on the high cycle fatigue (HCF) behavior of these alloys [11, 12], the development of design methodologies taking the effects of defects on the fatigue life prediction of structures into consideration is still under progress [10, 13, 14]. Besides, manufacturers also need a standard to ensure targeted level of reliability of their components. In the case of shrinkage pores, manufacturers set up control procedures via X-ray inspection for defects inspection and reject all those who have unacceptable risk of failure [10, 15]. The classification procedures for casting pores characterization are given in Ref. [16]. The presence of defects, however, is not able to be directly related to the capacity of a component or a structure to fulfill the requirements of the technical specifications [10]. A link between defect features and the fatigue strength needs to be established through a good understanding of the fatigue damage mechanisms associated with the microstructural features under specific loading conditions.

This paper reviews the link between features of the microstructural porosity and its influences on fatigue of cast Al alloys.

2 Fatigue behavior of metallic materials

2.1 Fatigue failure processes

Fatigue damage is caused by the simultaneous action of cyclic stress, tensile stress and plastic strain [17]. Fatigue cracks will not be initiated and propagate if any one of these factors is absence. The fatigue failure process normally could be divided into five stages [17]: 1) cyclic plastic deformation prior to fatigue crack initiation; 2) initiation of microcrack; 3) propagation or coalescence of microcracks to form one or more microcracks (stage I of crack growth); 4) propagation of macrocracks (stage II of crack growth); 5) final failure. When metallic materials subjected to cyclic deformation, their matrix will be hardened/softened as a result of dislocation movement [18]. Large amount of plastic strain will be accumulated at surface as a result of dislocation saturation. Strain localization at surface will finally induce crack initiation to release strain energy and the fatigue crack is therefore initiated [18]. Three approaches have been conducted to predict fatigue life of metallic materials [17]: 1) the stress-based (S-N curve) approach; 2) the strain-based approach;3) the fracture mechanics approach.

2.2 Stress-based approach (S-N curve)

A typical S-N curve of metallic materials is shown in Figure 1(a). Around 1900, BASQUIN [19] showed that the S_a-lgN_f plots could be linearized with log coordinates and established the exponential law of fatigue, where S_a is the stress amplitude and N_f is cycles to failure. Estimation of S-N curves is illustrated in Figure 1(b): N_e is specified, 10⁶ cycles for steels for instance, above which the S-N curve is horizontal; fatigue limit stress of unnotched material, σ_er, could be expressed as:

σ_er=mσ_u                                                   (1)

where m is the reduction facture applied to the ultimate tensile strength; σ_u is the ultimate tensile strength.

Similarly, the fatigue limit stress, S_er, for notched material could be estimated by:

                             (2)

where k_f is fatigue notch factor. The second point, at N_f=10³, could be expressed as [20, 21]:

σ_er=m′S_ar                                                   (3)

and

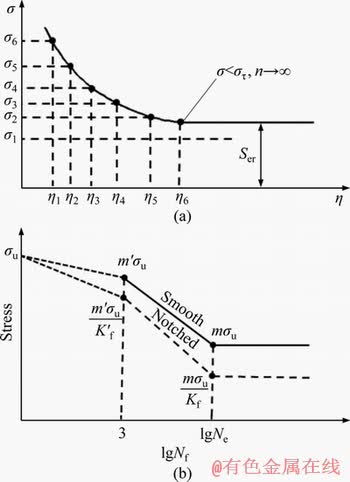
Figure 1 (a) Typical S-N curve of metallic materials;(b) Estimation of S-N curves for smooth and notched materials (redrawn from [22])

                              (4)

for unnotched σ_er and notched S_er materials, respectively. The m′ is dependent upon testing method such as bending, torsion and axial loading. It is assumed that S-N curve passes through the ultimate tensile strength, σ_u, for lives shorter than 10³ cycles [17].

2.3 Strain-based approach

Basquin’s equation later was modified by COFFIN [23] and MANSON [24] who reported that plastic strain-life data could also be linearized with log-log coordinates. And they elucidated that the total strain amplitude ε_a,t could be divided into elastic ε_a,e and plastic ε_a,p components [25]:

       (5)

where σ′_f is fatigue-strength coefficient; b is fatigue-strength exponent (Basquin exponent); ε′_f is fatigue-ductility; c is fatigue-ductility exponent (approximately equals fracture ductility ε_f for many metals [24]; for ductile metals, ε_f≈1; for strong metals, ε_f≈0.5 [24]). Eq. (1) could be linearized by log-log coordinates [25]:

                         (6)

where Y=lgε_a,_e and X=lg(2N_f).

Similarly, RAMBERG et al [26] proposed that the stresses and strains in materials subjected to constant amplitude cyclic loading could be expressed as:

                (7)

where σ_a is stress amplitude; E is elastic modulus; K′ and n′ are constant dependent upon materials. Again, Eq. (7) also could be linearized through logarithms of the equation:

                              (8)

obtaining:

                           (9)

where Y=lgσ_a and X=lgε_a,p.

Manson-Coffin-Basquin curve is frequently used to predict fatigue lifetime of metallic materials [27] due to its higher efficiency [28]. The Ramberg- Osgood curve was applied in cases that plastic strain amplitude is acquired using stable hysteresis loop [29, 30]. More recently, NIESLONY et al [28] proposed a 3D projections method to accommodate compatibility conditions and combined the two equations together.

2.4 Fracture mechanics approach

Fracture mechanics focuses on the propagation of cracks in materials. In fracture mechanics, PARIS [31] derived relationships for the stage II of crack growth (propagation of macrocrack) with cycles N in terms of stress intensity factor K:

                          (10)

where a is the crack length and m is ranging from 3 to 5 for metals. Small-crack (cracks less than 2 mm) analyses were frequently used to calculate the total fatigue life (S-N) behavior of Al alloys [32]. Linear-elastic fracture mechanics (LEFM) and non-linear fracture mechanics were employed to explain the fatigue cracking behaviors of cast Al alloys. LEFM assumes that material is isotropic and linear elastic, and the stress field near the crack tip is calculated based on elasticity theory. Cracks will grow when the stresses near the crack tip exceed the material fracture toughness. Non-linear fracture mechanics, on the other hand, is used for cases that materials are not perfectly elastic and undergo a certain extent of plastic deformation at the crack tip. Based on LEFM, Al alloys under cyclic loading exhibited strong small-crack effects [33, 34]: small fatigue cracks in some materials grow faster at low stress intensity factor regime than predicted from large crack data using LEFM as illustrated in Figure 2. △K_th is the threshold stress intensity factor below which cracks will not grow. This phenomenon has been attributed to lack of prior plastic deformation to develop closurewhen small cracks initiated at inclusion particles, voids, or weak grains [32]. Consequently, the crack- opening stress behavior has to go through a transient behavior to reach steady-state conditions. At high stress levels, however, the LEFM procedures are invalid due to larger plastic-zone sizes compared with crack sizes [35, 36]. Non- linear fracture mechanics concepts such as J integral [36] and crack closure model [37, 38] have been applied to explain the small-crack effects. TING et al [39] pointed that the total fatigue life (N_T) is the sum of the crack nucleation life (N_n) and the total propagation life (N_f, includes both short-crack and long-crack propagation):

N_T=N_n+N_f                                               (11)

The N_n, in the long-life regime, could be predicted using Basquin-Morrow relation and stress concentration factor (K_t) [40]:

                    (12)

where S_a is applied stress amplitude; σ_m is mean stress; σ′_f is fatigue strength coefficient for smooth specimen. And N_f could be estimated by integrating the Paris power law from a specified nucleated crack length to the final crack length at failure [39]:

 (13)

where x* is spatial extent of notch stress field; x_f is the final crack length at failure; C and m are constants for the relationship of da/dN versus △K; U(x) is the effective stress intensity ratio for cracks emanating from notches. Besides notched specimens, the model proposed by TING et al [39] also could be applied for as-cast Al alloys.

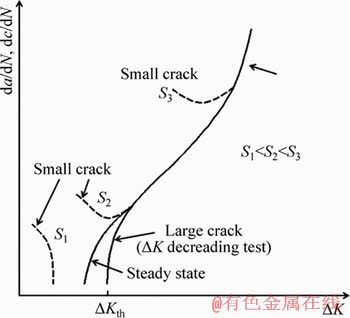
Figure 2 Typical fatigue crack growth rates for large cracks and small cracks at various stress intensity factors [32]

2.5 Low-cycle fatigue

It should be noted that the fatigue life prediction referred above is focusing on high-cycle fatigue (require more than 10⁴ cycles to failure) in which materials are subjected to small stresses (below yield stress, YS) and fracture mechanics are normally explained by LEFM. When the stress is high enough to initiate plastic deformation, the components usually undergo a relatively small number of cycles to failure. And the fracture mechanics of low-cycle fatigue (LCF) should be explained by non-linear fracture mechanics as it noted above. The fatigue life could be expressed by Coffin-Manson relation [23, 41]:

                         (14)

where △ε_p/2 is the plastic strain amplitude; ε′_f is fatigue ductility coefficient; 2N is the number of reversals to failure; C is fatigue ductility exponent (ranging from -0.7 to -0.5 for metals in time independent fatigue).

To sum up, large amount of efforts has been conducted to predict fatigue life of metallic materials [42-49]. The proposed methodology includes stress-based models [42-44], strain-based models [45, 46], strain energy-based models [47, 48]. Recently, KAMAL et al [49] made a detailed review in advances in fatigue life modeling. Considering the fact that fatigue behaviors of cast Al alloy are generally HCF due to their relatively low strength compared with steels. The following sections are focusing on the influences of microstructural heterogeneity on the HCF life of cast Al alloys.

3 Casting defects in Al alloys

Casting defects in Al alloys mainly include shrinkage defects (pores), gas porosity, pouring metal defects and metallurgical defects [50, 51]. Shrinkage pores occur when standard feed metal is not enough to compensate for shrinkage during the solidification of metals. Gas porosity is the formation of bubbles within the casting after it has cooled due to the gas dissolved in liquid materials. For cast Al alloys, hydrogen is the only gas that dissolves in large quantity and may result in hydrogen gas porosity [52]. Pouring metal defects include misruns, cold shuts and inclusions. Metallurgical defects include hot tears and hot spots [51]. Among all four casting defects referred, shrinkage/gaspores are the most detrimental to fatigue properties of cast Al alloy and difficult to be avoided. The following sections are focusing on effects of shrinkage pores on the fatigue properties of cast Al alloys.

3.1 Effects of shrinkage/gas pores

It has been recognized that the fatigue lives of cast Al alloys containing casting defects could be one or two order of magnitude lower than defects free Al alloys [53, 54]. Shrinkage/gaspores, as it referred above, among all the possible casting defects, are the most detrimental to fatigue properties of cast Al alloys [53, 55]. For metallic materials that contain crack-like defect with an initial length a_i, the crack length increases to value a at a given number of stress cycles, N. Assuming the stress acting on it is S, then the stress intensity factor, K at length a is 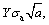where Y is correction factor depending upon the location and the shape of the crack. As it referred above, cast Al alloys components are usually subjected to low- stress cycle loadings in which fatigue life is normally predicted by Paris’ law. The fatigue crack growth rate in the power-law or steady-state stage could be expressed as [56]:

                   (15)

where C and n are Paris constants. For Al alloys, n equals approximately 4 [57]. After manipulation and integration, the Paris equation could be expressed as [58]:

                     (16)

where N₀ is the number of cycles to initiate a fatigue crack; B is a constant and A_i is the area of the failure-initiating defect lying on the fracture surface. The fraction of the crack initiation stage in the total fatigue life is dependent upon stress ranges and porosity level in cast Al alloy [58]. Considering the fact that cracks could be observed to grow from defects shortly after the first stress cycle [59], N₀ could be taken as zero in Al castings [58]. The validity of Eq. (2) is confirmed by WANG et al [57] who investigated serious data in literatures on cast Al-Si alloys. They plotted A_i vs. N_f and found that the slope of lgA_i vs. lgN_f is approximately -0.5, suggesting that N_f is related tofor cast Al-Si alloys. Similarly, MURAKAMI et al [60, 61] used as modeling parameter to estimate fatigue limit of surface and internal defects in steels.

3.2 Characterization of casting pores in cast Al alloys

Characterization of cast pores based on the metallography methodology was proposed by MURAKAMI [61]. The process is based on optical microscopic observations of polished samples. Several observations need to be conducted on each sample using a constant inspection area S₀ as shown in Figure 3(a), where area_max,i is the largest defect size.

The critical defect characterization based on the analysis of fatigue surfaces after the fatigue tests was illustrated by OSMOND et al [10]. This method measures the size of casting pores at the origin of fatigue failure as shown in Figure 3(b). Only the defect at the origin of the principal crack will be considered if there are multiple cracks on fatigue failure surface. This is because cracks preferentially initiated at the surface and sur-surface defects which will be reviewed in detail later. The comparison of these two characterization methodologies will be discussed later.

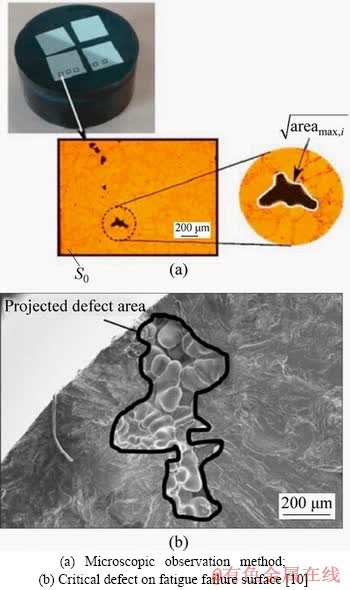
Figure 3 Illustration of casting pores characterization methodologies:

3.3 Size distribution of casting pores in cast Al alloys

The largest defects (upper tail of the defect size distribution) received large amount of attentions as they were believed to be responsible for crack-initiation as suggested by MURAKAMI et al [60]. GNEDENKO [62] defined three types of limiting extreme value distributions: Gumbel distribution, Fréchet distribution and Weibull distribution. The distribution of largest/smallest values is dependent on the distribution from which the sample is taken [62]. The general extreme value (GEV) distribution was introduced by JENKINSON [63] to incorporate all three types distributions proposed by GNEDENKO [62]. The validity of GEV distribution was confirmed by TIRYAKIOGLU [64]. TIRYAKIOGLU [64] fitted GEV distribution to 17 datasets from literature including four Al-casting and three Mg-casting alloys. The results indicated that 16 of the datasets followed the Gumbel distribution and one followed the Fréchet distribution. SHI et al [65, 66] proposed generalized Pareto distribution (GP) method to characterize the size of the largest inclusions in steels. However, to the author’s knowledge, GP distribution still is not applied to fatigue- initiating defect sizes in cast Al alloys so far.

ZHANG et al [55] measured the pore size of A713 sand cast Al alloy and fitted pore size distribution curve with Weibull, Gumbel and general extreme value. They reported that the GEV distribution function gives rise to a better fitting as shown in Figure 4. The GEV distribution fitted well with results in Ref. [55] for A713 cast Al alloy except for the small diameter regions (i.e., <5 μm). They attributed this phenomenon to experimental error in counting small pores: eutectic phase particles and grain boundaries, etc., could be regarded as small pores by computer. OSMOND et al [10] fitted pore distribution of two cast Al alloys, namely, AlSi₇Cu_0.5Mg_0.3 (alloy A) and AlSi₇Mg_0.3(alloy B), and found that the pore size distribution follows Gumbel distribution as shown in Figure 5. It should be noted that the defect sizes measured using critical defect at fatigue surface proposed by OSMOND et al [10] are much larger than those obtained by metallography methodology which was proposed by MURAKAMI [61]. OSMOND et al [10] attributed this phenomenon to the difference between observation zones. For instance, defect size distribution measured using Murakami’s methodology is dependent upon the inspection area S₀ while their methodology is related to the critical loaded volume of the tested specimen.

Figure 4 (a) Cumulative pore size distribution plot of A713 Al alloy; (b) Pore size distribution in A713 Al alloy [55]

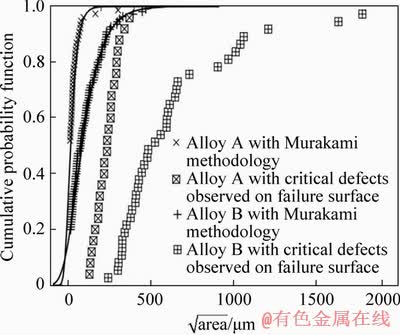
Figure 5 Defect size distribution for AlSi₇Cu_0.5Mg_0.3 (alloy A) and AlSi₇Mg_0.3 (alloy B)

The distribution of size of fatigue-initiating defects and their cumulative probability functions were summarized by TIRYAKIOGLU [58] as shown in Table 1. Probability plot was employed for the size of fatigue-initiating defects to evaluate whether they follow the log-normal [67], GEV [64] and Weibull distribution [68, 69]. However, TIRYAKIOGLU [58] pointed out that using probability plot is subjective and insufficient to test the hypothesis that the data come from the particular distribution. And he strongly recommended that probability plots should be always argued by goodness-of-fit tests. Consequently, TIRYAKIOGLU [58] evaluated the goodness-of-fit of the distributions listed in Table 1 using data in Ref. [71]. The empirical distribution function (EDF) statistics were applied to measuring the difference between the fitted distribution and the experimental data. There are two types of EDF statistics as described by STEPHENS [72]: supremum which measures the maximum discrepancy between the fit and data, and quadratic which measures the discrepancy for all data. One quadratic test, namely Anderson-Darling goodness- of-fit test statistic, was selected by TIRYAKIOGLU [58] as it is sensitive to the tails of the distribution and was proved to be superior to a majority of other goodness-of-fit tests for a variety of distributions. The tested statistic A² was expressed as [58]:

               (17)

where P(x_i) is the cumulative probability for each data point calculated with the estimated distribution parameters. The lower the value of A², the higher the confidence that data follow the distribution being tested. Based on the goodness-of-fitting tests for the seven distributions referred in Table 1, the Gumbel and GEV distributions were suggested to be adopted to represent the size variability of critical defects in Al-Si alloy castings [58]. And the results of goodness-of-fit tests should be present to confirm that the distribution of choice is appropriate [58].

Table 1 Distribution of fatigue-initiating defects’size and cumulative probability functions [58]

3.4 Effect of distribution selection on fatigue life estimations

It should be noted that the selection of correct distribution has profound influences on the estimation of fatigue life. TIRYAKIOGLU [58] compared correct distribution (Gumbel distribution which has the lowest value of A²) and the worst fit (Fréchet distribution which has the highest value of A²) using data in Ref. [71]. The inverse functions of Gumbel and Fréchet distributions of equivalent defect diameter d_eq could be expressed as [58]:

                  (18)

                    (19)

The cumulative probability of fatigue life when d_eq follows the Gumbel and Fréchet distribution could be expressed as [58]:

 (20)

 (21)

The probability function versus fatigue life was plotted in Figure 6. Gumbel distribution provides excellent fit to the experimental data except for the two tails. The Fréchet distribution, on the other hand, overestimated fatigue life for intermediate to high probabilities as shown in Figure 7. Selection of wrong distribution for the defect size could underestimate the design fatigue life as high as 38% [58]. This is why TIRYAKIOGLU [58] reiterated the significance of showing the results of goodness-of-fit tests to prove the validity of distribution fits. To the author’s knowledge, unfortunately, there is still no researcher presenting goodness-of-fit test results so far.

Figure 6 Probability density functions (P) vs. fatigue life time (N_f) [58]

Figure 7 Maximum stress concentration and pore surface diameter vs. pore position

3.5 Prediction of maximum pore size

Extrapolation of fatigue critical defect size from the 2D metallography analysis, namely normalized method, was introduced by MURAKAMI [61] and formalized in the ASTM standards [73]. This method is based on the concept of a return period (T):

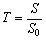                                (22)

where S is the area of interest and S₀ is the inspection area (150 mm²). Thus, the distribution function for the presence of the largest defect on surface of size S could be expressed as:

                     (23)

And the largest defect size within surface S could be expressed as:

                      (24)

where μ and β are the Gumbel distribution parameters acquired by fitting pore size distribution probability curve; y_T is the reduced variable, which could be expressed as:

                   (25)

The definition of defect size may vary depending on the type of defects. The inclusions in steels, for instance, the square root of the defect area at a cross-section of a specimen, will be applied [61]. Considering the fact that the casting pores are 3-dimentaional, MURAKAMI [61] proposes extension of the 2D model to 3D by assuming that the inspection volume V₀ is equal to the product of the inspection area S₀ multiplied by the average largest pore size on S₀. The return period T is consequently expressed as:

                                (26)

The biggest problem for the normalized methodology is that: 1) the extrapolation from a large area/volume to a smaller area/volume is not possible (T<1); 2) it is impossible to link the largest defect extrapolation to a specific probability of occurrence (T=1) [74]. It is therefore suggested the return period in Eq. (26) should be defined as [75, 76]:

                             (27)

An alternative methodology was proposed by MAKKONEN et al [74] based on the quantile functions: the P-quantile size here was defined as the defect size X_p which is not exceeded in the area with the probability of P. Thus, the appropriate P could be chosen freely. In engineering work, P=0.5, i.e. the median, in which is usually interesting, is frequently used. Other quantile such as the mean, and the mode may also be used if the probability P is consistent with the design philosophy of the final product in question [74]. When the P-quantile size was defined as the defect size X_p was not exceeded in the area with the probability of P. The probability of non-exceedance in n (n=A/A₀>1) could be expressed as [74]:

                           (28)

where P is the non-exceedance probability in one sample. The size correction factor X_P/X_P,0 could be expressed as:

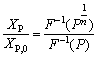                         (29)

where F is cumulative distribution function. Any distributions of defects referred above could be considered using methodologieies in Refs. [74, 77].

Using the above method considering the 3D defects in cast Al alloys, the distribution function of largest defect size distribution in a volume V could be expressed as [10]:

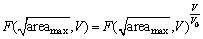          (30)

The largest defect size distribution relative to the volume V, for the case of Gumbel distribution, could be expressed as [10]:

 (31)

3.6 Fatigue weak link density

Despite the size of defects distribution of Al alloys as reviewed by TIRYAKIOGLU [58], not all pores promote cracks during fatigue tests [55, 78]. ZHANG et al [55] reported that the total number of fatigue cracks generated on the surface of an A713 Al alloy was a Weibull distribution whereas the pore size distribution of as casted material follows GEV distribution. The number of cracks could be estimated by [55]:

           (32)

where N₀ is the number of cracks in the surface area of 10 mm×6 mm at the stress level close to 100% yield strength σ_y; k is a constant; m is Weibull modulus; and σ₀ is the fatigue limit. Similarly, ZHAI [79] reported that the distribution of weak link of high strength AA8090 Al alloy also follows Weibull distribution.

Assuming that all cracks were initiated at fatigue weak link, the fatigue weak link density in one alloy could be expressed by crack density as shown in Figure 8 [55]. It should be noted that the number of weak links is underestimated by this way due to crack coalescence and crack shielding effects [55]. Thus, the number of weak links indicated by crack density is useful in illustration while sufficient sampling will be required to insure the accuracy of the results [55].

Figure 8 Strength distribution of fatigue weak links in A713 Al alloy [55]

3.7 Strength distribution of fatigue weak links

ZHANG et al [55] plotted the strength distribution of fatigue weak links of A713 Al alloy by derivative of the Weibull function obtained by fitting the crack population-stress curve:

 (33)

where n is the number of fatigue weak links that have a fatigue fracture strength σ; and C is a scaling constant that could be determined by:

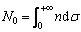                           (34)

The strength distribution of fatigue weak links in A713 Al alloy is shown in Figure 8. As it depicted in Figure 8, the strength of weak links in the A713 Al alloy reaches its highest value at about 65% σ_y. The crack initiation process tends to slow down at higher stress levels due to shielding effect [55]. The number of weak links is therefore decreased with increasing stress at high stress level region. The huge differences between strength distribution of fatigue weak links (as shown in Figure 8) and pore size distribution (as shown in Figure 4(b)) for A713 Al alloy suggest that the size distribution function of the pores is not able to be directly used to evaluate the fatigue crack initiation behaviors even though fatigue cracks were predominantly initiated from pores [55]. This suggests that the tendency for a pore to initiate cracks is not only dependent on its size, but also dependent on its location [78, 80].

3.8 Effect of pore position on stress concentration

As it referred above, although it was reported that surface porosity of Al alloys has significant influences on cracking initiation during fatigue [55, 81], not all pores promote cracks during fatigue tests. ZHANG et al [55], for instance, claimed that only 1.4% casting pores induced initiation of fatigue cracks during fatigue tests of A713 Al alloy. Besides, these cracks are even not necessarily initiated at the larger pores [74, 81-83]. ZHAI et al [81] investigated crack growth of short fatigue cracks in Al-Li 8090 alloy and reported that the short crack growth is controlled by the twist and tilt angles in the alloy. These results suggest that fatigue crack in Al-Li 8090 alloy is dependent upon crystallographic orientation instead of size of defects/pores. Fatigue cracks tend to initiate at coarse particles in cases of wrought Al alloys, which contains hard, brittle secondary phases. BOZEK et al [84], for instance, reported that the fracture of Al₇Cu₂Fe particles is the primary crack initiation sites of AA7075-T651 Al alloy during fatigue tests. Only about 4% of these particles on the surface induced cracking initiation in AA7075-T651 Al alloy [84]. Moreover, PANG et al [85] pointed out that fatigue cracks actually tended to be initiated at pores which were just buried beneath the surface.

All those results referred above are contrary to traditional theories in which fatigue cracks were believed to be initiated at the largest casting defect/pore. It was believed that largest pores tend to have the highest stress concentration around them and cracks are consequently initiated at locations that have higher stress. Therefore, the larger the casting pores are, the shorter the fatigue life of cast Al alloys will be. This is true for macro pores (above 200 μm in diameter) as increased pore size inducing decreased cross-sectional areas that undertake the loadings [78]. However, this theory is incapable in explaining experimental results as reported by ZHANG et al [55] due to decreased pore size (pore size below 200 μm in diameter). FAN et al [86] attributed this phenomenon to varied shear stress due to variation of relative position of surface pores. They examined the effects of particle size, spacing, aspect ratio as well as the effects of pore size, spacing, distance of a pore from surface, local curvature and clustering in cast A365 Al-Si alloys using finite element analyses method [86], and found that the maximum range of plastic shear strain is the highest when the spacing between particles along the loading direction is on the order of the pore size [86]. Pore aspect ratio effects are less significant than the spacing effects [86]. A modified Manson-Coffin law was used to predict the time needed for fatigue crack initiation using the plastic shear strain range. And the effects of distance between the free surface and the pore on the maximum range of plastic shear strain and the cycles for crack incubation are shown in Figure 9. It is clear that the plastic shear strain range decreases and the number of cycles needed to initiate fatigue crack increases when the pore moves away from the place near the free surface to the inside of the material. When the distance from the free surface to pore increases to about the same order of the pore’s largest dimension, the decrease of plastic shear strain range and increase of cycles needed to initiate fatigue cracks terminated. Constraint effects of the materials on plastic deformation are more pronounced for internal pores than those close to the free surface. Similarly, GAO et al [87] analyzed the stress and strain fields around the pores in A356-T6 Al alloy using finite element method. They demonstrated that the high stress/strain concentration is induced by pores that are both large and near the free surface of the specimen [87]. In a later work, LI et al [88] characterized the interaction between fatigue crack evolution and porosity in A356-T6 alloys using both X-ray microtomography and finite-element analysis. They concluded that the formation and propagation of fatigue cracks are dominated by the highest local stress-strain concentration which is caused by the pores adjacent to the free surface and the crack tip respectively [88]. The work done by LI et al [88] was focusing on large pores with a mean diameter of 236 μm. The effects of pores smaller than 200 μm in diameter were discussed by XU et al [78, 80]. They investigated the stress field around surface pores using finite element model and reported that the pore size only affects the size of stress concentration region whereas the magnitude of the maximal stress concentration ratio around a pore only dependent upon the relative depth of the pore is. They believed that the stress concentration ratio reaches its maximal value when the pore is tangent with surface and decreases sharply when the pore diverges from the tangency position as shown in Figure 7 [80]: the maximum stress concentration factor increases sharply at D/r=1 (where D is the distance between the pore center and the alloy free surface, and r is the pore radius). The maximum stress concentration factor was 2 or less when half or less than half of the pore was in the alloy (D/r≤0), indicating that only pores located between D/r=0 and 2 may cause initiation of fatigue crack in the alloy. The diameter of the pore on the alloy free surface was also plotted as a function of D/r, and the results suggest that the pore size on free surface varies with pore depth. The surface pores that have a high stress concentration factor usually do not have a large size on the surface. The stress concentration could be released through plastic deformation inducing decreased K_t value in elastic-plastic model. The modeling results by XU et al [78, 80] explained why fatigue cracks were often initiated from those pores that intercepted the free surface at the top halves or were completely buried beneath the surface within one radius in depth.

Figure 9 Effect of distance between pore and free surface on:(R_ε=-1, D_max/ D_min=2, D_max=40 μm, α′=0.5464, C′=0.0622) [86]

SERRANO-MUNOZ et al [83] further confirmed results in Refs. [78, 80] using X-ray synchrotron tomography to monitor the in-situ fatigue tests. A comparison of pore size evolution of internal pore vs. surface pore was illustrated in Figure 10. It is clear that the surface crack growth rates are significantly higher than those located internally. Many researchers’ results [83, 89-96] indicated that the internal cracks were assumed to propagate in a vacuum like environment and grow with a rate about one order of magnitude lower than surface cracks (ambient air environments). HENAFF et al [89] have proven that very low partial pressure of water vapour (10^-3 Pa) could increase the growth rates of a stage II fatigue crack propagation (propagation of macro-cracks) in a high-strength low-alloyed steel by a factor of four. They attributed the phenomena to the adsorption of water vapor molecules on fresh crack surfaces [89]: adsorbed water vapor molecules induce enhanced plasticity of the cyclically strained material at the crack tip. The crack propagation rates are therefore increased. Similarly, GASQUERES et al [90] reported decreased crack growth rate of 2024A Al alloy at 223 K. They attributed this to transition of stage II propagation (propagation of macro-cracks) mode at room temperature to stage I like mode at 223 K: the water vapor molecules (about 40 ppm) in atmospheric environment could be adsorbed by the newly created fatigue surfaces and may promote the activation of two or more slip systems and hence inhibit the crystallographic propagation as shown in Figure 11. It is clear that fracture surface morphology in ambient air tends to have smooth surface whereas the fracture surface tends to have highly crystallographic with large facets morphology in low temperature and low partial pressure of water vapor environments. In a later work, RICHARD et al [93] also showed that the slip morphology controls the crack growth rate of Al-Cu-Li alloys. A similar mechanism was observed in Al-Cu-Mg alloys that the fatigue tests were conducted in cold dry air in which the exposure to water vapor is restricted [93]. SERRANO-MUNOZ et al [95] investigated the effects of casting defects/pores on the fatigue behavior of A356-T6 cast Al alloy. They found that the fatigue life was increased, compared with that performed in ambient air, when the fatigue tests are conduct in vacuum for artificial defects located at free surface. The internal defects, on the other hand, exhibited similar number of cycles in vacuum.

Figure 10 Evolution of square root of projected surface of cracks against number of cycles to failure for pore 1 (surface pore) and pore 3 (internal pore) [83]

Figure 11 SEM observations on fracture surface after fatigue crack growth rate tests at 223 K in air:

Although the exact environmental conditions of internal cracks are still not well understood by researchers, there is no doubt that the behaviors of internal cracks are dependent upon the intrinsic properties of material themselves. There are evidences that internal crack nucleation in IMI 834 Ti alloy is induced by the microstructure itself through facet formation rather than defects [94]. It was therefore proposed that the extent of vacuum in internal cracks is even higher than that produced at the pumped free surface [83].

Based on the results reviewed above, it is reasonable to conclude that the presence of internal defects in cast components could be tolerated as long as the size of casting pores could be redistricted. Fatigue cracks are easier to be initiated at surface voids/defects, and propagate faster as a result of atmospheric moisture. People just need to focus on the surface defects or defects just buried beneath the free surface when predicting the fatigue life of cast Al alloys.

4 Microstructural heterogeneity in cast Al alloys

Cast Al alloys are mostly 300-series, such as Ai-Si-Cu and Al-Si-Mg [97]. The principal alloying element in these alloys is Si, which enhances fluidity of liquid Al [97]. Besides 300-series alloys, the 200-series (Al-Cu) alloys are also a significant family of cast Al alloys. However, they exhibit poor fluidity, tightness and corrosion resistance compared with 300-series alloys and are prone to cracking [98]. Alloying elements such as Cu, Zn, Mg, were intentionally added for purpose of precipitation hardening. In addition to these beneficial effects, these alloying, accompanied with other alloying elements such as Fe, Sr, etc., have profound influences on the microstructures of cast Al alloy and potentially affect their fatigue properties. For the sake of simplicity, the following sections are focusing on the microstructural heterogeneity in cast Al alloys that affects fatigue life.

4.1 Dendritic feature in cast Al alloys

The dendrite arm spacing (DAS) has a strong effect on both the strain hardening and fracture behavior of Al-Si-Mg casting alloys [99-102]. The ductility of cast Al alloys reaches its lowest value at intermediate DAS value, and the fracture mode tends to be transgranular for the larger DAS and intergranular for the finer DAS [100]. Despite the primary dendritic features, there also exists fine size dendrite arm spacing in cast Al-Si-Mg alloys known as secondary dendrite arming spacing (SDAS), which is strongly dependent upon alloy composition and heat treatment [101, 103]. The measurement of SDAS could be achieved using SEM micrographs with an accurate scale bar [11, 54, 104-107]. A line parallel to the primary growth direction needs to be drawn and the SDAS could be measured by averaging the distance between adjacent side branches on the longitudinal section of a primary dendrite as shown in Figure 12. The SDAS of A356/357 alloys could also be estimated using the empirical equation [107]:

                      (35)

where R=dT/dt is the mean cooling rate of the primary Al dendrite cells during solidification.

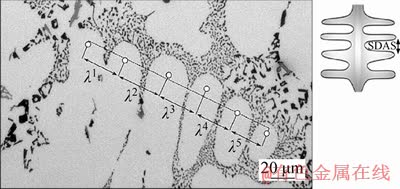
Figure 12 Measurement of SDAS [11]

4.2 Effects of SDAS on fatigue properties of cast Al alloys

The influence of SDAS on fatigue properties of cast Al alloys has been understood in terms of dispersion hardening [104]. Local yielding of materials, due to inhomogeneous deformation, occurs when alloys are subjected to external stress/strain. And slipping/slip bands formation in matrix arises as a result of local yielding. Dislocations will interact with dendrite cells, grain boundaries and eutectic particles as deformation proceeds induce dispersion hardening in the materials [101, 108, 109]. The presence of constituents in the alloy that blocks dislocation movement or interacts with dislocation will increase the local internal stress and local damages. The primary influences of SDAS on fatigue properties of cast Al alloys is that their existence resulted in decreased mean free path for dislocation movement as shown in Figure 11. The dendrite cells, in coarse microstructures (large SDAS value), as well as the eutectic particles clustered along the cells/grain boundaries isolated dendrites as individuals. Dislocations will be blocked at thick eutectic walls resulting in dislocation pile-up along the cell/grain boundaries. The deformation strain induced by dislocation pile-up will increase continuously until being released by crack initiation or fracture of eutectic particles. BOILEAU et al [110] have demonstrated that finer microstructure is beneficial for the fatigue resistance of cast A319 Al alloy. This could be attributed to distribution of eutectic particles: eutectic particles are less concentrated on dendrite cell boundaries in fine microstructures (small SDAS values) [104]. Dislocation can move across dendrite cell boundaries easily where there are fewer eutectic particles to block them. The interactions between dislocations and eutectic particles are consequently less significant in fine microstructures (small SDAS values). The image stress induced by dislocations due to their interaction with eutectic particles in a coarse microstructure could be expressed as [101, 108, 109]:

                (36)

where λ=SDAS; L is the average slip distance; μ_m is the shear modulus of Al matrix; ε is the local relaxed strain; b is the Burgers vector; C, C₁ and C₂ are constants. As shown in Eq.(36), the image stress is contributed by geometrically necessary dislocations (C₂/λ) and statistically stored dislocations (C₁/L) [104]. The statistically stored dislocations are accumulated during uniform deformation (matrix hardening). For cast Al alloys, C≈1.25 and C₁/L≈0.05 μm^-1 [109]. The geometrically necessary dislocations are dislocations required to avoid overlaps and voids around particles in SDAS cell or grain boundaries. The image stress induced by dislocations as a function of SDAS is illustrated in Figure 13. Around pores (purple), the Fe-rich (green) and Al₂Cu (yellow) particles form a dense 3D network.

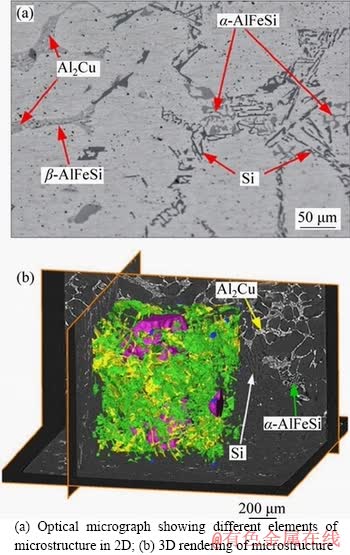
Figure 13 Microstructure of cast AlSi₇Cu₃Mg [106]:

The Si particles were deliberately omitted in the 3D rendering for the sake of clarity. Image stress is dominated by dislocations interacting with cell boundaries in coarse microstructure (large SDAS). Increased SDAS increases slip distance (λ) of dislocation resulting in decreased work hardening rate and image stress. In fine microstructures (small SDAS), on the other hand, the interaction between dislocations and grain boundaries dominates the hardening rate. The work hardening rate decreases with decreasing SDAS as dislocations can slip longer distances in fine structures. Consequently, the image stress reaches its maximum value at intermediate SDAS value where interaction changes from dislocations with grain boundaries to dislocations with cell boundaries as shown in Figure 14 [104]. It should be noted that the critical value of SDAS applied to define coarse or fine grain size is dependent upon alloy composition, cooling conditions and heat treatments [104]. As all these parameters are related to size and distributions of eutectic particles in cast Al alloys. And it should, affect dislocation blockage during deformation.

Figure 14 Image stress induced by dislocations with SDAS [104]

4.3 Secondary particles in cast Al alloys

As it referred above, cooling process of cast Al alloys usually accompanied with formation of microstructural heterogeneities, except for micro- shrinkage voids/defects and gas porosity, secondary phase particle is another microstructural heterogeneity that has a significant influence on the fatigue properties of cast Al alloys [11, 54, 100, 101, 106, 108, 111-113]. The microstructure of cast Al alloys usually is composed of primary Al dendrites, eutectic silicon, Fe-rich particles and other intermetallic particles (such as Al₂Cu, Al₉FeMg₃Si₅, etc.) dependent upon alloy composition [100, 101, 108, 111, 112, 114, 115]. It has long been known that fatigue crack path could be altered when the cracks tip interacted with interdendritic boundaries, particle/matrix interface and fractured particles [86, 116]. For convenience purpose, all phases, such as eutectic Si, Fe-rich particles and other intermetallic particles, except for Al dendrites are termed as secondary phase particles in this paper. The microstructure of AlSi₇Cu₃Mg Al alloy cast using the lost foam casting (LFC) process is shown in Figure 12. The 3D microstructure of this material consists of a complex network of relatively coarse phases. The volume fraction of dendrites and eutectic particles is determined by alloy composition [101, 108, 111, 114, 115], whereas the size and distribution of the dendrites and eutectic particles are dominated by solidification conditions and eutectic modification [54, 101, 111-113, 115]. Besides, the matrix and eutectic structure can also be affected by the heat treatment [108, 110]. For a given alloy, consequently, the size, volume and morphology of microstructural constituents are functions of chemistry, solidification conditions and heat treatments [54, 100, 108, 110-112, 114, 115].

4.4 Stress/strain inhomogeneous induced by secondary phase particles

The presence of these secondary particles induces stress/strain inhomogeneous when the bulk material is subjected to external stress/strain [117]. During the deformation of multi-phase alloys, the soft phases tend to accommodate higher strain whereas the hard phases tend to accommodate higher stress [118, 119]. Small cavities or microcracks may be initiated depending on the mechanical properties of bulk matrix and secondary phase particles [120]: decohesion of matrix and secondary phase particles occurs if either the normal stress at the interface exceeds the critical fracture stress or the strain energy stored during plastic deformation exceeds the energy of the new surfaces formed by cavitation. The former is termed as critical stress criteria whereas the later is termed as energy criteria [120]. The stress criteria require that the secondary particles have a certain degree of strength that is not cracked in response to external stress/strain and the energy criteria should always be satisfied [120]. In cases in which stress criteria are not able to be satisfied, microcracks inside secondary phase particles will be initiated as a result of deformation [121, 122]. The stress/strain partitioning theories could perfectly explain why secondary particles oriented with the long axis perpendicular to the main loading direction tend to experience interface decohesion whereas tend to break into several fragments when they oriented parallel to the loading directions as indicated by LASSANCE et al [123]. The secondary phase particles inside cast Al alloy are generally hard and brittle with very limited ductility and could easily be fractured due to straining. Besides, strain localization as a result of dislocation movement induces fatigue crack initiation at sample surface as referred above. Secondary phase particles have been reported effectively block transmission of slip plane across the phase/matrix interface [121, 122, 124]. The resulting localized stress accumulation caused by blocking may be sufficiently high to cause preferential cracking of the blocking particle, depending upon the hardness and size of the particle among other factors [122, 124]. The strain partitioning around hard coarse-scale, opposed to fine-scale, precipitates tend to be more uniform [125]. As the bonding strength between coarse hard secondary phase particles and the matrix in cast Al alloys is typically strong enough to avoid decohesion of particle/matrix interface, but brittle enough to preferential crack during plastic deformation [121, 122] as the local stress exceeds the fracture stress. This is why initiation of particle/matrix interface cavities and microcracks interior particles is dependent upon not only particle size, but also angle between particle orientation and. loading direction.

4.5 Effect of eutectic structure

Despite the defects/voids induced shrinkage during solidification process of cast Al alloy, internal defects/voids can also be introduced through the fracture of eutectic particles [99, 100, 111, 112, 114, 115, 123, 126]. The internal stress developed on the eutectic particles could be expressed as [104]:

                   (37)

where μ_p is the shear modulus of eutectic silicon particles; f_uc is the volume fraction of uncracked eutectic particles and α is the aspect ratio of eutectic particles. p_c is the probability of fracture of a particle of size d and aspect ratio α. And p_c is governed by Weibull statistics through [104]:

               (38)

where d₀, σ₀ are the characteristic particle size and stress at which the probability of particle cracking is 63%; m is the Weibull modulus. It was even reported that fatigue cracks tend to initiate from secondary phase particles rather than defects for semi-solid cast Al alloys [126]. This suggests that the stress developed on the secondary phase particles may be higher than that generated around shrinkage pores. Besides, shrinkage pores are frequently observed accompanied with brittle intermetallic phases [116, 127]. Interaction between shrinkage pores and secondary phase particles enhances detrimental effects induced individually. Large and elongated eutectic particles tend to crack during early stages of plastic deformation resulting in large amount of microcracks in the microstructure [99, 100, 111, 112, 114, 115]. These microcracks continue to accumulate and grow as deformation proceeds. A fatigue crack is initiated when the size of microcracks exceeds a critical value. The fatigue life of cast Al alloys is consequently decreased due to the presence of microcracks as shown in Figure 15. It should be noted that the microcracks initiated due to fracture of secondary phase particles are normally microscale and/or sub-micron scale and their initiation is difficult to be captured using traditional material characterization techniques such as SEM and standard light microscopy. A novel technique namely synchrotron radiation X-ray microtomography gives rise to chances observing sub-micron spatial resolution of microcracks. The imaging of failure in structural materials by synchrotron radiation X-ray microtomography was recently reviewed by WU et al [15, 128, 129]. Results in Refs. [99-101, 104, 108, 111, 112, 114, 115] were later confirmed by DEZECOT et al [106] who investigated fatigue properties of cast AlSi₇Cu₃Mg alloys at 250 °C using synchrotron in-situ X-ray tomography and reported that coarse eutectic particles form a quasi-continuous network. Cracks tend to be initiated at stress/strain concentrations and high triaxiality pores and propagate through the 3D network of cracked eutectic particles. Similar to shrinkage voids inducing fatigue cracking, eutectic particles do not have identical tendency to crack when subjected to external stress/strain. CACERES et al [108] investigated tensile properties of Al-7Si-0.4Mg cast Al alloy and reported that 3%-10% of the eutectic particles were cracked in the uniform region of samples deformed to fracture. This value increased to about 15%-20% at areas close to the fracture surface. Interestingly, the cracking of eutectic particles can be described in terms of Weibull statistics as well [108]. The Weibull modulus for the Si particles was reported to vary between 1.2 and 3.9 with the average of about 3 [108].

Figure 15 Micrographs of fatigue specimen [104]:

4.6 Effect of alloying elements

Efforts have been conducted to elucidate the effect of alloying elements on the fatigue properties of cast Al alloys [54, 104, 108, 111, 112, 114, 115, 130], all of which could be explained by variation of microstructure induced by alloying elements.

Si is the primary alloying element in cast Al alloys due to its ability to improve the castability and mechanical properties of Al alloys [131]. However, high Si content in cast Al alloys induces decreased fatigue crack growth resistance [132]. This was attributed to enlarged eutectic Si areas as shown in Figure 16. Fatigue cracks propagate by material separation on certain slip systems until dislocation obstacles (such as grain boundary) which causes an orientation change reached in alloys with low eutectic Si. In alloys with high amount of Si, however, crack tips encounter with Si particles and propagation along the microcracks induced by fracture of Si particles as referred above. As a result, the detrimental effect of Si on the fatigue life of cast Al alloys is more pronounced than other particles due to its higher content [99, 101, 108, 111, 112, 114, 115]. In cast A356 Al alloy, in particularly, cracking of Si particles dominated the accumulation of damage whereas cracking of Fe-rich particles (will be discussed later) is less important [115].

Figure 16 Alloy microstructures after heat treatment:

Due to the detrimental effects of Si contents on the fatigue properties of cast Al alloys, microstructural modifications such as solution treatment and Sr additives were employed to improve the microstructure of cast Al alloys [131]. Both methodologies promote fragmentation/ spheroidization of eutectic Si particles [100, 114, 115, 131]. Despite the beneficial effects of Sr additions, DASGUPTA et al [133] pointed out that over-modification of A356 Al alloy with Sr is a major parameter for porosity formation. ARGO et al [134], however, believed that Sr could redistribute the global volume of porosity from coarse localized shrinkage into relatively uniformly distributed microporosity with significantly decreased pore diameters. Similarly, LEE et al [135] found that Sr depresses the eutectic temperature, inducing decreased time for pore growth. However, MOUSTAFA et al [136] showed reduced initial growth rate of pores due to Sr addition. They consequently concluded that additional Sr gives no significant net effect on the final pore size.

Mg is added to Al-7Si cast Al alloys to induce age hardening through precipitation of Mg-Si particles such as Mg₂Si, Mg₅Si₆ [137]. Mg content, however, is also known to be detrimental to fatigue life due to its ability to promoting eutectic particle size of Fe-rich phase [103, 114]. Besides, increased Mg content also induces increased Si particle area length and flakes in unmodified Al-Si-Mg alloys [107, 131]. Increased eutectic particle size results in more particle fracture and, non-surprisingly, shorter fatigue lives. However, Mg does not affect the transformation of eutectic Si particles during solution treatment [131]. In other words, about 0.4% Mg does not affect the fragmentation and spheroidization processes of cast Al-7Si alloys. MOUSTAFA et al [136] even reported that the partial refinement of the eutectic Si particles in the presence of 0.4% Mg when alloy was cooled at 0.8 °C/s. On the other hand, in Sr-modified alloys, the eutectic Si particle size is virtually independent of cooling rate [114]. However, JOENOES et al [138] believed that additional Mg induces increased Si particle size due to the formation of the Sr rich intermetallic phase (Mg₂SrAl₄Si₃). The modification effects are therefore alleviated due to the decreased amount of Sr.

The presence of Fe in cast Al alloy should be avoided if possible. Higher Fe content in cast Al alloys induces increased amount and size of plate-like Fe-rich phases, particularly at large SDAS values [104, 111]. The Fe intermetallic particles may exist as α-Al₁₅(MnFe)₃Si, β-Al₅Fe-Si, π-Al₉FeMg₃Si₅, etc. dependent upon alloy composition and heat treatment. Fe-rich intermetallic phases observed in low Mg alloys are almost exclusively small β-Fe phase [114] whereas large π-Fe phase, along with a small amount of β-Fe phases, is dominant in the high Mg alloys [139]. The influence of β-Fe phase on the mechanical properties of cast Al alloys is trivial compared with eutectic Si particles due to their fine size and small populations [114]. The cracking π-Fe phase, on the other hand, accounts for the majority of damage at low and intermediate strains in cast A357 Al alloys [115]. At large strain regime, damage by cracking of eutectic Si particles becomes comparable to of π-Fe phase [115]. Be has been added to reduce the amount of π-Fe phase that formed in high Mg alloys [140]. And this is why A357 is regarded as a higher grade alloy compared with A356.

Cu was occasionally added for precipitation hardening (Al₂Cu, Al₅Mg₈Si₆Cu₂, Al₅Mg₈Cu₂₆,etc.). Despite enhanced hardness, increased Cu content induces reduced ductility and changes the morphology of the Cu-containing phases [141, 142]. The morphology of Al₂Cu phase could be either eutectic-like [136] or block-like [143]. Tensile properties of cast Al alloys could be enhanced by increasing cooling rate (as indicated by dendrite arm spacing DAS) which increases the amount of Cu in solid solution [136]. Empirical equations have been proposed to determine the approximate hardness of cast Al alloys as a function of Cu, Mg, Si, solution treatment and ageing [144, 145]. Similar to Mg effects as referred above, Cu also was believed to increase the area and length of Si particles by forming Al-Cu-Sr compounds [136].

As it reviewed above, effects of alloying element on the mechanical properties of cast Al alloys could be associated with microstructural variation. Alerted morphology of eutectic Si particles and π-Fe phase changed tendency of these particles to fracture in response to external stress/strain. Fracture of secondary phase particle induces significant amount microcracks [99, 100, 111, 112, 114, 115]. These microcracks continue to accumulate and grow as deformation proceeds. A fatigue crack is initiated when the size of microcracks exceeds a critical value. The fatigue lives of cast Al alloys are therefore decreased. The growth/coalescence of microcracks/microvoids takes place by classical dislocation plasticity mechanism and highly dependent upon stress triaxiality [123]. At small stress triaxiality, the voids grow faster in the direction of the maximum stress whereas rounded voids tend to keep their shape at larger stress triaxiality [146-148].

In summary, the presence of intermetallic precipitates, eutectic Si particles and π-Fe phase in specific, induce significant amount of microcracks/ microvoids when bulk materials are subjected to external stress/strain. The coalescence of these microcracks/microvoids accelerated fatigue crack initiation of cast Al alloys. Their fatigue lives are consequently decreased.

5 Summary

Effects of microstructural heterogeneity on the fatigue properties of cast Al alloys were reviewed. Shrinkage voids/defects and secondary phase particles are the two most detrimental factors to affect fatigue life of cast Al alloys. The large shrinkage voids/defects (above 200 μm in diameter) formed during solidification process induce decreased cross-sectional area. The stress is therefore transferred to areas without casting voids/defects inducing increased stress concentration around large voids/defects. The largest pores tend to have the highest stress concentration around them and crack is consequently initiated at the locations where have higher stress. As a result, the larger casting pores are, the shorter the fatigue life of cast Al alloys will be. The small shrinkage voids, on the other hand, tend to have the highest stress concentration when these microvoids are tangent with surface and decrease sharply when the pore diverges from the tangency position. In other words, stress concentration ratio around microvoids is dependent upon their relative position instead of size. There totally are 7 mathematical distributions which were proposed to express the distribution of casting pores/voids in Al alloys. Gumbel distribution and GEV distributions were reported to provide the best fitting. Goodness of fitting of distribution data was suggested to ensure a more accurate fatigue life prediction. Besides fatigue crack initiation, surface fatigue cracks were observed to propagate much faster than internal cracks. This was attributed to atmospheric moisture. The internal cracks, on the other, propagate in a similar manner of vacuum cracks. Consequently, surface voids/defects could receive more concern when predicting fatigue life of cast Al alloys.

The secondary phase particles, such as Si and Fe-rich particles, nucleated during the solidification normally possess mechanical properties that very different from α-Al matrix. Due to their mechanical properties, secondary phase particles introduce significant un-uniformly distributed stress/strain partitioning in response to deformation. Due to their brittle nature, secondary phase particles are prone to fracture when subjected to external stress/strain. The fracture of secondary phases induces large number of microcracks/microvoids around dendrite cells. For fine grain size secondary particles which are difficult to be ruptured by deformation, micro-cavities may be initiated at particle/matrix interface. The coalescence of these microcracks/microvoids induces decreased fatigue crack initiation time and the fatigue life of cast Al alloy is therefore shortened. Efforts (including heat treatment, additives, etc.) should be taken to avoid formation of coarse secondary phase particles or promoting rounded particles instead of plate-like particles.

References

[1] CHU S, MAJUMDAR A. Opportunities and challenges for a sustainable energy future [J]. Nature, 2012, 488(7411): 294-303.

[2] ZINKLE S J, WAS G S. Materials challenges in nuclear energy [J]. Acta Mater, 2013, 61(3): 735-758.

[3] BERANGER M, FIARD J M, AMMAR K, CAILLETAUD G. A new fatigue model including thermal ageing for low copper aluminum-silicon alloys [J]. Procedia Engineering, 2018, 213: 720-729.

[4] PRASAD S V, ASTHANA R. Aluminum metal-matrix composites for automotive applications: Tribological considerations [J]. Tribology Letters, 2004,17(3): 445-453.

[5] IMMARIGEON J, ZHAO L, WALLACE W J. Lightweight materials for aircraft applications [J]. Materials Characterization, 1995, 35(1): 41-67.

[6] RIOJA R J. Fabrication methods to manufacture isotropic Al-Li alloys and products for space and aerospace applications [J]. Materials Science & Engineering A, 1998, 257(1): 100-107.

[7] SONSINO C M. Structural durability of cast aluminium gearbox housings of underground railway vehicles under variable amplitude loading [J]. International Journal of Fatigue, 2005, 27(8): 944-953.

[8] DIXON B, MOLENT L, BARTER S. A study of fatigue variability in aluminium alloy 7050-T7451 [J]. International Journal of Fatigue, 2016, 92: 130-146.

[9] OZDES H, TIRAKIOGLU M. On the relationship between structural quality index and fatigue life distributions in aluminum aerospace castings [J]. Metals, 2016, 6(4): 81-91.

[10] OSMOND P, LE V D, VIET-DUC, MOREL F, BELLETT D, SAINTIER N. Effect of porosity on the fatigue strength of cast aluminium alloys: From the specimen to the structure [J]. Procedia Engineering, 2018 , 213: 630-643.

[11] HOURIA M I, NADOT Y, FATHALLAH R, ROY M, MAIJER D M. Influence of casting defect and SDAS on the multiaxial fatigue behaviour of A356-T6 alloy including mean stress effect [J]. International Journal of Fatigue, 2015, 80: 90-102.

[12] LE V D, MOREL F, BELLETT D, SAINTIER N, OSMOND P. Multiaxial high cycle fatigue damage mechanisms associated with the different microstructural heterogeneities of cast aluminium alloys [J]. Materials Science & Engineering A, 2016, 649(1): 426-440.

[13] KOUTIRI I, BELLETT D, MOREL F, PESSARD E. A probabilistic model for the high cycle fatigue behaviour of cast aluminium alloys subject to complex loads [J]. International Journal of Fatigue, 2013, 47: 137-147.

[14] ROTELLA A, NADOT Y, AUGUSTIN R, PIELLARD M, L'HERITIER S. Defect size map for cast A357-T6 component under multiaxial fatigue loading using the defect stress gradient (DSG) criterion [J]. Engineering Fracture Mechanics, 2016, 174: 227-242.

[15] WU Sheng-chuan, XIAO Ti-qiao, WITHERS P J. The imaging of failure in structural materials by synchrotron radiation X-ray microtomography [J]. Engineering Fracture Mechanics, 2017, 182: 127-156.

[16] ASTM, E155-15. Standard reference radiographs for inspection of aluminum and magnesium castings[M]. West Conshohocken, PA: ASTM International, 2015.

[17] LAMPMAN S R. ASM handbook: Volume 19, fatigue and fracture [M]. Park, Ohio: Materials, ASM International, 1996.

[18] MUGHRABI H. Dislocations and properties of real materials [M]. London: The Institute of Metals, 1985: 244.

[19] BASQUIN O. The exponential law of endurance tests [C]// Proc Am Soc Test Mater. 1910: 625-630.

[20] SHIGLEY J E, MISCHKE C R. Mechanical engineering design [M]. Singapore: McGraw-Hill, 1989.

[21] JUVINALL R C, MARSHEK K M. Fundamentals of machine component design [M]. New Jersey, US: Wiley, 1991.

[22] DOWLING N E. Mechanical behavior of materials: engineering methods for deformation, fracture, and fatigue [M]. New Jersey: Prentice Hall, 2012.

[23] COFFIN L F. A study of the effects of cyclic thermal stresses on a ductile metal [J]. Transactions of the American Society of Mechanical Engineers, 1954, 76: 931-950.

[24] MANSON S S. Fatigue: A complex subject—Some simple approximations [J]. Experimental Mechanics, 1965, 5: 193-226.

[25] MITCHELL M. Fundamentals of modern fatigue analysis for design [C]// Fratigue and Fracture. Ohio: ASM internationd, 1996: 227-249.

[26] RAMBERG W, OSGOOD W R. Description of stress-strain curves by three parameters [R]. Washington, DC: NACA, 1943.

[27] BAUMEL A, SEEGER T, BOLLER C, Materials data for cyclic loading: Supplement 1 [R]. Dutch: Elsevier Science Ltd, 1990.

[28] NIESLONY A, DSOKI C E, KAUFMANN H, KRUG P. New method for evaluation of the Manson-Coffin-Basquin and Ramberg-Osgood equations with respect to compatibility [J]. Materialwissenschaft und Werkstofftechnik, 2008, 30(10, 11): 1967-1977.

[29] RICHARD C, RICE M. SAE fatigue design handbook [M]. Warrendale (PA): SAE Publication, 1988.

[30] SKELTON R, MAIER H, CHRIST H J. The bauschinger effect, masing model and the Ramberg-Osgood relation for cyclic deformation in metals [J]. Materials Science and Engineering A,1997, 238(2): 377-390.

[31] PARIS P C. A rational analytic theory of fatigue [J]. The Trend in Engineering, 1961, 13: 9.

[32] NEWMAN J C. Review of modelling small-crack behavior and fatigue-life predictions for aluminum alloys [J]. Fatigue & Fracture of Engineering Materials & Structures, 1994, 17(4): 429-439.

[33] NEWMAN J C, EDWARDS P. Short-crack growth behaviour in an aluminum alloy—An AGARD cooperative test programme[M]. France: Advisory Group for Aerospace Research and Development Neuilly-Sur-Seine, 1988.

[34] EDWARDS P, NEWMAN J C. Short-crack growth behaviour in various aircraft materials [R]. Washington, DC: NACA, 1990.

[35] PEARSON S. Initiation of fatigue cracks in commercial aluminium alloys and the subsequent propagation of very short cracks [J]. Engineering Fracture Mechanics, 1975, 7(2): 235-247.

[36] HADDAD M H E, DOWLING N E, TOPPER T H, SMITH K N. Jintegral applications for short fatigue cracks at notches [J]. International Journal of Fracture, 1980, 16(1): 15-30.

[37] HIRONOBU N, KEN-ICHI T. Significance of initiation, propagation and closure of microcracks in high cycle fatigue of ductile metals [J]. Engineering Fracture Mechanics, 1981, 15(3, 4): 445-456.

[38] NEWMAN J C. A nonlinear fracture mechanics approach to the growth of small cracks [R]. Virgina: NASA Langley Research Center, 1983.

[39] TING J C, LAWRENCE F V. Modeling the long‐life fatigue behavior of a cast aluminum alloy [J]. Fatigue & Fracture of Engineering Materials & Structures, 1993, 16(6): 631-647.

[40] PARK S K, LAWRENCE F V. A long-life regime probability-based fatigue design method for weldments [R]. Illinois: University of Illinois at Urbana-Champaign, 1988.

[41] MANSON S S. Behavior of materials under conditions of thermal stress, national advisory committee for aeronautics [R]. NACA TN-2933, 1954.

[42] DANG-VAN K. Macro-micro approach in high-cycle multiaxial fatigue [C]// Advances in Multiaxial Fatigue. ASTM International, 1993: 120-130.

[43] SINES G. Behavior of metals under complex static and alternating stresses [J]. Metal Fatigue, 1959, 1: 145-169.

[44] CHARKALUK E, CONSTANTINESCU A, MAITOURNAM H, VAN K D. Revisiting the Dang Van criterion [J]. Procedia Engineering, 2009, 1(1): 143-146.

[45] BROWN M, MILLER K. Two decades of progress in the assessment of multiaxial low-cycle fatigue life [C]// Low-cycle Fatigue and Life Prediction. ASTM International, 1982.

[46] WANG C H, BROWN M W. A path-independent parameter for fatigue under proportional and non-proportional loading [J]. Fatigue & Fracture of Engineering Materials & Structures, 1993, 16(12): 1285-1297.

[47] LIU K. A method based on virtual strain-energy parameters for multiaxial fatigue life prediction [C]// Advances in Multiaxial Fatigue. ASTM International, 1993: 67-84.

[48] GLINKA G, WANG G. A. Plumtree, mean stress effects in multiaxial fatigue [J]. Fatigue & Fracture of Engineering Materials & Structures, 1995, 18: 755-764.

[49] KAMAL M, RAHMAN M M. Advances in fatigue life modeling: A review [J]. Renewable & Sustainable Energy Reviews, 2018, 82(1): 940-949.

[50] LAMPAN S. Casting design and performance [M]. Materials Park, Ohio: ASM International, 2009: 165.

[51] RAO P N. Manufacturing technology [M]. New York: Tata McGraw- Hill Education, 2013.

[52] PRILLHOFER B, BOTTCHER H, ANTREKOWITSCH H. Development and practical performance characteristics of a new impeller for metal treatment in casting/holding furnaces [C]// Light Metals, TMS Annual Meeting, 2009: 749-754.

[53] AMMAR H R, SAMUEL A M, SAMUEL F H. Effect of casting imperfections on the fatigue life of 319-F and A356-T6 Al–Si casting alloys [J]. Materials Science and Engineering A, 2008, 473(1): 65-75.

[54] WANG Q G, APELIAN D, LADOS D A. Fatigue behavior of A356-T6 aluminum cast alloys. Part I. Effect of casting defects [J]. Journal of Light Metals, 2001, 1(1): 73-84.

[55] ZHANG Yuan-bing, XU Jian-hui, ZHAI Tong-guang. Distributions of pore size and fatigue weak link strength in an A713 sand cast aluminum alloy [J]. Materials Science and Engineering A, 2010, 527(16, 17): 3639-3644.

[56] PARIS P, ERDOGAN F J. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528-539.

[57] WANG Q G, CREPEAU P N, DAVIDSON C J, GRIFFITHS J R. Oxide films, pores and the fatigue lives of cast aluminum alloys [J]. Metallurgical and Materials Transactions B, 2006, 37(6): 887-895.

[58] TIRYAKIOGLU M. Statistical distributions for the size of fatigue-initiating defects in Al–7%Si–0.3%Mg alloy castings: A comparative study [J]. Materials Science and Engineering A, 2008, 497(1): 119-125.

[59] BARTER S, MOLENT L, GOLDSMITH N, JONES R. An experimental evaluation of fatigue crack growth [J]. Engineering Failure Analysis, 2005, 12(1): 99-128.

[60] MURAKAMI Y, ENDO M. Effects of defects, inclusions and inhomogeneities on fatigue strength [J]. International Journal of Fatigue, 1994, 16(3): 163-182.

[61] MURAKAMI Y. Metal fatigue: Effects of small defects and nonmetallic inclusions [M]. Dutch: Elsevier, 2002.

[62] GNEDENKO B. Sur la distribution limite du terme maximum d'une serie aleatoire [J]. Annals of Mathematics, 1943, 44(3): 423-453.

[63] JENKINSON A F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements [J]. Quarterly Journal of the Royal Meteorological Society, 1955, 81(348): 158-171.

[64] TIRYAKIOGLU M. On the size distribution of fracture-initiating defects in Al- and Mg-alloy castings [J]. Materials Science and Engineering A, 2008, 467(1, 2): 174-177.

[65] SHI G, ATKINSON H V, SELLARS C M, ANDERSON C W. Application of the generalized pareto distribution to the estimation of the size of the maximum inclusion in clean steels [J]. Acta Materialia, 1999, 47(5): 1455-1468.

[66] ATKINSON H V, SHI G. Characterization of inclusions in clean steels: A review including the statistics of extremes methods [J]. Progress in Materials Science, 2003, 48(5): 457-520.

[67] MAYER H, PAPAKYRIACOU M, ZETTL B, STANZL- TSCHEGG S. Influence of porosity on the fatigue limit of die cast magnesium and aluminium alloys [J]. International Journal of Fatigue, 2003, 25(3): 245-256.

[68] NAYHUMWA C, GREEN N R, CAMPBELL J. Influence of casting technique and hot isostatic pressing on the fatigue of an Al-7Si-Mg alloy [J]. Metallurgical and Materials Transactions A, 2001, 32(2): 349-358.

[69] WANG Q, JONES P, OSBORNE M. The effects of applied pressure during solidification on the microstructure and mechanical properties of lost foam A356 castings [J]. Advances in Aluminum Casting Technology II, 2002, 10: 75-84.

[70] PRZYSTUPA M A, BUCCI R J, MAGNUSEN P E, HINKLE A J. Microstructure based fatigue life predictions for thick plate 7050-T7451 airframe alloys [J]. International Journal of Fatigue, 1997, 19(93): 285-288.

[71] YI J Z, GAO Y X, LEE P D, FLOWER H M, LINDLEY T C. Scatter in fatigue life due to effects of porosity in cast A356-T6 aluminum-silicon alloys [J]. Metallurgical and Materials Transactions A, 2003, 34(9): 1879-1890.

[72] STEPHENS M A. Tests based on EDF statistics[M]// Goodness-of-Fit Techniques. New York: Marcel Dekker, 1986.

[73] ASTM, E2283-08(2014). Standard practice for extreme value analysis of nonmetallic inclusions in steel and other microstructural features [S]. West Conshohocken, PA: ASTM International, 2014.

[74] MAKKONEN L, RABB R. TIKANMAKI M. Size effect in fatigue based on the extreme value distribution of defects [J]. Materials Science and Engineering A, 2014, 594: 68-71.

[75] MAKKONEN L. Problems in the extreme value analysis [J]. Structural Safety, 2008, 30(5): 405-419.

[76] MAKKONEN M. Predicting the total fatigue life in metals [J]. International Journal of Fatigue, 2009, 31(7): 1163-1175.

[77] WALLIN K. Statistical aspects of fatigue life and endurance limit [J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 33(6): 333-344.

[78] XU Zhi-qiang, ZHANG Xin-liang, WANG Wei, ZHAI Tong-guang. Effect of pore position in depth on stress concentration around pore on sample surface [J]. Journal of Yansan University, 2012, 36(4): 293-297. (in Chinese)

[79] ZHAI T. Strength distribution of fatigue crack initiation sites in an Al-Li alloy [J]. Metallurgical and Materials Transactions A, 2006, 37(10): 3139-3147.

[80] XU Zhi-qiang, WEN Wei, ZHAI Tong-guang. Effects of pore position in depth on stress/strain concentration and fatigue crack initiation [J]. Metallurgical and Materials Transactions A, 2012, 43: 2763-2770.

[81] ZHAI T, WILKINSON A J, MARTIN J W. A crystallographic mechanism for fatigue crack propagation through grain boundaries [J]. Acta Materialia, 2000, 48(20): 4917-4927.

[82] WANG L, DANIEWICZ S R, HORSTEMEYER M F, SINTAY S, ROLLETT A D. Three-dimensional finite element analysis using crystal plasticity for a parameter study of microstructurally small fatigue crack growth in a AA7075 aluminum alloy [J]. International Journal of Fatigue, 2009, 31(4): 651-658.

[83] SERRANO-MUNOZ I, BUFFIERE J Y, MOKSO R, VERDU C, NADOT Y. Location, location & size: Defects close to surfaces dominate fatigue crack initiation [J]. Scientific Reports, 2017, 7: 45239.

[84] BOZEK J E, HOCHHALTER J D, VEILLEUX M G, LIU M, HEBER G, SINTAY S D, ROLLETT A D, LITTLEWOOD D J, MANIATTY A M, WEILAND H, CHRIST R J, PAYNE J, WELSH G, HARLOW D G, WAWRZYNEK P A, INGRAFFEA A R. A geometric approach to modeling microstructurally small fatigue crack formation: I. Probabilistic simulation of constituent particle cracking in AA 7075-T651 [J]. Modelling and Simulation in Materials Science and Engineering, 2008, 16(6): 065007.

[85] PANG H T, REED P A S. Fatigue crack initiation and short crack growth in nickel-base turbine disc alloys—The effects of microstructure and operating parameters [J]. International Journal of Fatigue, 2003, 25: 1089-1099.

[86] FAN J, MCDOWELL D L, HORSTEMEYER M F, GALL K. Cyclic plasticity at pores and inclusions in cast Al–Si alloys [J]. Engineering Fracture Mechanics, 2003, 70: 1281-1302.

[87] GAO Y X, YI J Z, LEE P D, LINDLEY T. The effect of porosity on the fatigue life of cast aluminium‐silicon alloys [J]. Fatigue & Fracture of Engineering Materials & Structures, 2004, 27: 559-570.

[88] LI P, LEE P D, MAIJER D M, LINDLEY T C. Quantification of the interaction within defect populations on fatigue behavior in an aluminum alloy [J]. Acta Materialia, 2009, 57: 3539-3548.

[89] HENAFF G, MARCHAL K, PETIT J. On fatigue crack propagation enhancement by a gaseous atmosphere: Experimental and theoretical aspects [J]. Acta Metallurgicaurgica et Materialia, 1995, 43: 2931-2942.

[90] GASQUERES C, SARRAZIN-BAUDOUX C, PETIT J, DUMONT D. Fatigue crack propagation in an aluminium alloy at 223 K [J]. Scripta Materialia, 2005, 53: 1333-1337.

[91] PETIT J, SARRAZIN-BAUDOUX C. Some critical aspects of low rate fatigue crack propagation in metallic materials, An overview on the influence of the atmosphere environment on ultra-high-cycle fatigue and ultra-slow fatigue crack propagation [J]. International Journal of Fatigue, 2006, 28: 1471-1478.

[92] PETIT J, SARRAZIN-BAUDOUX C. Some critical aspects of low rate fatigue crack propagation in metallic materials [J]. International Journal of Fatigue, 2010, 32(6): 962-970.

[93] RICHARD S C, GASQUERES SARRAZIN-BAUDOUX C, PETIT J. Coupled influence of microstructure and atmosphere environment on fatigue crack path in new generation Al alloys [J]. Engineering Fracture Mechanics, 2010,77(11): 1941-1952.

[94] CHAPMAN T P, KAREH K M, KNOP M, CONNOLLEY T, LEE P D, AZEEM M A, RUGG D, LINDLEY D, DYE D. Characterisation of short fatigue cracks in titanium alloy IMI 834 using X-ray microtomography [J]. Acta Materialia, 2015, 99: 49-62.

[95] SERRANO-MUNOZ I, BUFFIERE J Y, VERDU C, GAILLARD Y, MU P, NADOT Y. Influence of surface and internal casting defects on the fatigue behaviour of A357-T6 cast aluminium alloy [J]. International Journal of Fatigue, 2016, 82: 361-370.

[96] BILLAUDEAU T, NADOT Y. Support for an environmental effect on fatigue mechanisms in the long life regime [J]. International Journal of Fatigue, 2004, 26: 839-847.

[97] MALLICK P K. 2-advanced materials for automotive applications: An overview [M]. Cambridge, UK: Woodhead Pubishing, 2012.

[98] KAUFMAN J G. Understanding wrought and cast aluminum alloy designations [R]. NASA, 2013.

[99] WANG Q G, CACERES C H. On the strain hardening behaviour of Al-Si-Mg casting alloys [J]. Materials Science and Engineering A, 1997, 234-236: 106-109.

[100] CACERES C H, DAVIDSON C J, GRIFFITHS J R. The deformation and fracture behaviour of an Al-Si-Mg casting alloy [J]. Materials Science and Engineering A, 1995, 197: 171-179.

[101] CACERES C H, GRIFFITHS J R, REINER P. The influence of microstructure on the Bauschinger effect in an Al-Si-Mg casting alloy [J]. Acta Materialia,1996, 44: 15-23.

[102] JIAO Yi-nan, ZHANG Yi-fan, MA Shi-qing, SANG De-li, ZHANG Yang, ZHAO Jin-jin, LIU Yong-qiang, YANG Shao-pu. Role of secondary phase particles in fatigue behavior of high-speed railway gearbox material [J]. International Journal of Fatigue, 2020, 131: 105336.

[103] WANG Q G, DAVIDSON C J. Solidification and precipitation behaviour of Al-Si-Mg casting alloys [J]. Journal of Materials Science, 2001, 36: 739-750.

[104] WANG Q G, APELIAN D, LADOS D A. Fatigue behavior of A356/357 aluminum cast alloys. Part II-Effect of microstructural constituents [J]. Journal of Light Metals, 2001, 1: 85-97.

[105] ODANOVIC Z, DURDEVIC M, PAVLOVIC J K, ARSIC M, KATAVIC B. Some applications of the image analysis in the metal material science [J]. Acta Physica Polonica A, 2012, 121: 111-113.

[106] DEZECOT S, BUFFIERE J Y, KOSTER A, MAUREL V, SZMYTKA F, CHARKALUK E, DAHDAH N, El BARTALI A, LIMODIN N, WITZ N. In situ 3D characterization of high temperature fatigue damage mechanisms in a cast aluminum alloy using synchrotron X-ray tomography [J]. Scripta Materialia, 2016, 113: 254-258.

[107] WANG Q G, CARLOS H, CACERES C H. Mg effects on the eutectic structure and tensile properties of Al-Si-Mg alloys [J]. Materials Science Forum, 1997, 242: 159-164.

[108] CACERES C H, GRIFFITHS J R. Damage by the cracking of silicon particles in an Al-7Si-0.4Mg casting alloy [J]. Acta Materialia, 1996, 44(1): 25-33.

[109] BROWN L M. Back-stresses, image stresses, and work- hardening [J]. Acta Materialia, 1973, 21: 879-885.

[110] BOILEAU J M, ALLISON J E. The effect of solidification time and heat treatment on the fatigue properties of a cast 319 aluminum alloy [J]. Metallurgical and Materials Transactions A, 2003, 34(9): 1807-1820.

[111] WANG Q, CACERES C, GRIFFITHS J. Cracking of Fe-rich intermetallics and eutectic Si particles in an Al-7Si-0.7 Mg casting alloy [J]. Transactions of the American Foundrymen’s Society, 1998, 106: 131-136.

[112] WANG Q G, CACERES C H. The fracture mode in Al–Si–Mg casting alloys [J]. Materials Science and Engineering A,1998, 214(1, 2): 72-82.

[113] NADOT Y, IBEN HOURIA M I, FATHALAH R, MAIJER D. Through process modelling applied to the fatigue resistance of cast aluminum [J]. Procedia Engineering, 2018, 213: 296-302.

[114] CACERES C H, DAVIDSON C J, GRIFFITHS J R, WANG Q G. The effect of Mg on the microstructure and mechanical behavior of Al-Si-Mg casting alloys [J]. Metallurgical and Materials Transactions A,1999, 30(10): 2611-2618.

[115] WANG Q G, CACERES C H, GRIFFITHS J R. Damage by eutectic particle cracking in aluminum casting alloys A356/357 [J]. Metallurgical and Materials Transactions A, 2003, 34(12): 2901-2912.

[116] CHAN K S, JONES P, WANG Q. Fatigue crack growth and fracture paths in sand cast B319 and A356 aluminum alloys [J]. Materials Science and Engineering A, 2003, 341: 18-34.

[117] DYE D, STONE H J, REED R C. Intergranular and interphase microstresses [J]. Current opinion in Solid State and Materials Science, 2001, 5(1): 31-37.

[118] CHO K, GURLAND J. The law of mixtures applied to the plastic deformation of two-phase alloys of coarse microstructures [J]. Metallurgical Transactions A, 1988, 19(8): 2027-2040.

[119] BYUN T S, KIM I S. Stress and strain partition in elastic and plastic deformation of two phase alloys [J]. Journal of Materials Science,1991, 26: 3917-3925.

[120] ARGON A, IM J, SAFOGLU R. Cavity formation from inclusions in ductile fracture [J]. Metallurgical and Materials Transactions A,1975, 6(4): 825-837.

[121] GELL M, WORTHINGTON P J. The plastic deformation and fracture of Iron-3% Silicon in the temperature range 295 K– 473 K [J]. Acta Materialia,1996, 14: 1265-1271.

[122] BARNBY J T. The initiation of ductile failure by fractured carbides in an austenitic stainless steel [J]. Acta Metallurgica, 1967,15: 903-909.

[123] LASSANCE D, FABREGUE D, DELANNAY F, PARDOEN T. Micromechanics of room and high temperature fracture in 6xxx Al alloys [J]. Progress in Materials Science, 2007, 52(1): 62-129.

[124] JIAO Y, ZHENG W, KISH J R. Stress corrosion cracking susceptibility of thermally-aged Type 310S stainless steels in supercritical water [J]. Corrosion Science, 2018, 135: 1-11.

[125] LEE J, EARMME Y, AARONSON H, RUSSELL K. Plastic relaxation of the transformation strain energy of a misfitting spherical precipitate: Ideal plastic behavior [J]. Metallurgical and Materials Transactions A, 1980,11(11): 1837-1847.

[126] BROCHU M, VERREMAN Y, AJERSCH F, BUCHER L. Fatigue behavior of semi-solid cast aluminum: A critical review [J]. Solid State Phenomena, 2008, 141: 725-730.

[127] CHAN K S. Roles of microstructure in fatigue crack initiation [J]. International Journal of Fatigue, 2010, 32(9): 1428-1447.

[128] WU S C, HU Y, DUAN H, YU C, JIAO H. On the fatigue performance of laser hybrid welded high Zn 7000 alloys for next generation railway components [J]. International Journal of Fatigue, 2016, 91: 1-10.

[129] WU S C, YU C, YU P S, BUFFIERE J, HELFEN L, FU Y. Corner fatigue cracking behavior of hybrid laser AA7020 welds by synchrotron X-ray computed microtomography [J]. Materials Science and Engineering A, 2016, 651: 604-614.

[130] LIU Y L, KANG S B, KIM H W. The complex microstructures in an as-cast Al–Mg–Si alloy [J]. Mater Lett, 1999, 41(6): 267-272.

[131] MOUSTAFA M A, SAMUEL F H, DOTY H W. Effect of solution heat treatment and additives on the microstructure of Al-Si (A413.1) automotive alloys [J]. Journal of Materials Science, 2003, 38(22): 4507-4522.

[132] LADOS D A, APELIAN D. Fatigue crack growth characteristics in cast Al–Si–Mg alloys: Part I. Effect of processing conditions and microstructure [J]. Materials Science and Engineering A, 2004, 385: 200-211.

[133] DASGUPTA R, BROWN C, MAREK S. Analysis of overmodified 356 aluminum alloy [J]. AFS Trans, 1988, 96: 297-310.

[134] ARGO D, GRUZLESKI J. Porosity in modified aluminum alloy castings [J]. AFS Transactions, 1988, 96: 65-74.

[135] LEE P D, SRIDHAR S. Direct observation of the effect of strontium on porosity formation during the solidification of aluminium-silicon alloys [J]. International Journal of Cast Metals Research, 2000, 13(4): 185-198.

[136] MOUSTAFA M A, SAMUEL F H, DOTY H W, VALTIERRA S. Effect of Mg and Cu additions on the microstructural characteristics and tensile properties of Sr-modified Al-Si eutectic alloys [J]. International Journal of Cast Metals Research, 2002, 14(4): 235-253.

[137] ZANDBERGEN H, ANDERSEN S, JANSEN J. Structure determination of Mg₅Si₆ particles in Al by dynamic electron diffraction studies [J]. Science, 1997, 227: 1221-1225.

[138] JOENOES A, GRUZLESKI J. Magnesium effects on the microstructure of unmodified and modified Al-Si alloys [J]. Cast Metals, 1991, 4: 62-71.

[139] SIMENSEN C J, ROLFSEN T L. Production of π-AlMgSiFe crystals [J]. Zeitschrift für Metallkunde, 1997, 88: 142-146.

[140] TAN Y H, LEE S L, LIN Y L. Effects of Be and Fe additions on the microstructure and mechanical properties of A357.0 alloys [J]. Metallurgical and Materials Transactions A, 1995, 26: 1195-1205.

[141] SAMUEL F, SAMUEL A, DOTY H. Factors controlling the type and morphology of Cu-Containing phases in 319 Al alloy (96-30) [J]. Transactions of the American Foundrymen’s Society, 1996, 104: 893-902.

[142] MIAO W, LAUGHLIN D. Effects of Cu content and preaging on precipitation characteristics in aluminum alloy 6022 [J]. Metallurgical and Materials Transactions A, 2000, 31: 361-371.

[143] SHIH T S, SHIH F S. Effects of silicon, magnesium and strontium content on the qualities of Al-Si-Mg alloys [J]. Journal of Cast Metals Research, 1998, 10: 273-282.

[144] SINGH R, GANGULY R, DHINDAW B. Application of statistical design of experiments for quantitatively studying the strengthening characteristics of cast Al-Si-Cu-Mg alloys [J]. British Foundryman, 1984, 77: 436-440.

[145] TASH M, SAMUEL F, MUCCIARDI F, DOTY H, VALTIERRA S. Experimental correlation between metallurgical parameters and hardness in heat-treated 319 alloys: A quantitative study using factorial analysis [J]. Transactions of the American Foundry Society, 2006, 114: 71-84.

[146] BUDIANSKY B, HUTCHINSON J, SLUTSKY S. Mechanics of solids [M]. Oxford, UK: Pergamon Press, 1982.

[147] PARDOEN T, HUTCHINSON J. An extended model for void growth and coalescence [J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 2467-2512.

[148] GOGOGANU M, LEBLOND J B, DEVAUX J. Approximate models for ductile metals containing non-spherical voids—Case of axisymmetric prolate ellipsoidal cavities [J]. Journal of the Mechanics and Physics of Solids, 1993, 41: 1723-1754.

(Edited by ZHENG Yu-tong)

中文导读

铸造铝合金中的组织异质性对其疲劳性能的影响

摘要：铸造铝合金材料被广泛应用于发动机部件、结构材料、齿轮箱、底盘等部件，在使用过程中承受交变应力。准确预测铸铝材料的使用寿命对于部件的安全运转极为重要，因疲劳裂纹而导致的漏油等事故可能产生极为危险的后果。铸铝材料的使用寿命可以通过其铸造缩/气孔的尺寸分布或者尺寸最大的缩/气孔的直径结合裂纹扩展速率公式进行预测。缩孔的深度及相对位置对于应力集中具有重要影响。通常情况下，铸造铝合金的组织主要包括铝基体、共晶硅、富铁相及其他一些第二相颗粒。因这些第二相颗粒开裂而产生的微裂纹会导致铸铝材料疲劳寿命的降低。因此，如何通过显微组织合理预测铸铝材料的疲劳寿命对于铸铝材料的使用极为重要。本文回顾了以往研究中铸造缩/气孔和第二相颗粒等组织缺陷对Al-Si-Mg铸造铝合金疲劳寿命的影响。

关键词：铸造铝合金；疲劳；组织异质性；缩/气孔；第二相颗粒

JIAO Yi-nan and ZHANG Yi-fan contributed equally to this work

Foundation item: Projects(11790282, U1534204, 11572267, 51804202, 51705344) supported by the National Natural Science Foundation of China; Project(E2019210292) supported by the Natural Science Foundation of Hebei Province, China; Project(A2019210204) supported by the National Natural Science Foundation for Distinguished Young Scholars, China; Project(KQTD20170810160424889) supported by the Shenzhen Peacock Team Program, China; Project(2019DB013) supported by the Key Research Project of Southern Xinjiang, China; Project(C201821) supported by the High Level Talent Support Project in Hebei, China; Project supported by the Youth Top-notch Talents Supporting Plan of Hebei Province, China; Project(MCMS-E-0519G04) supported by the State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, China; Project(201919) supported by the Open Fund of State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, China

Received date: 2019-06-12; Accepted date: 2020-01-03

Corresponding author: ZHAO Jin-jin, PhD, Professor; Tel: +86-311-87936084; E-mail: jinjinzhao2012@163.com; ORCID: 0000-0003- 1620-3040; WU Sheng-chuan, PhD, Professor; Tel: +86-28-87602402; E-mail: wusc@swjtu.edu.cn; ORCID: 0000-0002-7437-2021; LIU Yong-qiang, PhD, Professor; Tel: +86-311-87936742; E-mail: liuyq@stdu.edu.cn; ORCID: 0000-0001-7114-0797; YANG Shao-pu, PhD, Professor; Tel: +86-311-87935519; E-mail: yangsp@stdu.edu.cn; ORCID: 0000-0002-3888-4169