基于改进型粒子群优化的节点自定位算法
刘志坤1，刘忠1，唐小明2
(1. 海军工程大学 电子工程学院，湖北 武汉，430033；
2. 海军航空工程学院 信息融合技术研究所，山东 烟台，264001)
摘要：为了提高测距误差影响下无线传感器网络节点自定位精度，提出一种基于距离的节点自定位新算法。对混沌搜索与粒子群优化进行算法融合，给出一种改进型粒子群优化算法，将其应用于节点自定位。新算法利用未知节点与信标节点之间的距离信息，通过改进型粒子群优化算法获取未知节点的位置。仿真结果表明，改进型粒子群优化算法对两种标准测试函数的搜索结果优于一般的粒子群优化算法。在测距误差和信标节点数量相同的条件下，相对于最小二乘估计法，新算法在各个测距误差级上的定位精度更高，其定位误差随测距误差增大而上升的趋势更缓慢。新算法具有更好的鲁棒性，适用于测距误差较大、信标节点数量较少的情况。
关键词：无线传感器网络；粒子群算法；混沌；节点自定位
中图分类号：TP393 文献标志码：A 文章编号：1672-7207(2012)04-1371-06
Node self-localization algorithm based on modified particle swarm optimization
LIU Zhi-kun1, LIU Zhong1, TANG Xiao-ming2
(1. College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China;
2. Research Institute of Information Fusion, Naval Aeronautical Engineering Institute, Yantai 264001, China)
Abstract: In order to improve the node self-localization precision in wireless sensor networks despite ranging error, a new range-based node self-localization algorithm was proposed. A modified particle swarm optimization that combines chaotic and particle swarm optimization was studied and used in the field of node self-localization. The new algorithm uses range information between unknown node and anchor node and gets the node location through the modified particle swarm optimization. The simulation results show that the modified particle swarm optimization algorithm is better than the original in terms of searching results of two standard test functions. When ranging error and anchor node number are the same, the new algorithm, compared with the least square method, has higher localization precision at each ranging error level. As the ranging error increases, the localization error grows more slowly. It enjoys better robustness and is suitable for the situation of big ranging error and few anchor nodes.
Key words: wireless sensor networks; particle swarm optimization; chaos; node self-localization
节点自定位技术是无线传感器网络的关键技术之一，这是因为在无线传感器网络的应用中，各个传感器所获取的数据必须与位置信息相结合，只有在确定节点位置信息后，才能进一步指导节点的行为，灵活地调整路由，节约能耗，提高网络的性能。虽然通过搭载GPS(全球定位系统)是获取节点地理位置信息最便捷的途径，但是对于一个节点众多的无线传感器网络而言，如果给每个节点都配备GPS将造成惊人的成本，显然是不现实的。此外，GPS的使用会受限于遮挡条件，在很多环境下无法使用(例如水下)，因此必须寻求其他的解决途径。根据定位机制的不同，目前的节点自定位方法可分为2类[1-2]：基于距离(Range-based)的方法和距离无关(Range-free)的方法。相对于距离无关的方法，基于距离的方法能够获得更高的定位精度。这类算法通过接收信号强度(RSSI)[3]、不同信号的到达时间差(TDOA)[4]、到达角度(AOA)[5]或是到达时间(TOA)[6]等方法测得节点间距离，根据距离信息进行定位。常用的方法有：三边定位法、改进bounding box法、三角定位法和最小二乘估计法等。然而，这几种方法受测距误差的影响较大，最小二乘估计法虽然一定程度上降低了这种影响，但是定位精度高。而在实际环境中，受外在条件的影响，测距误差非但难以避免，有时甚至较大。这种情况下，以上的几种方法就显得无能为力。为了克服测距误差对定位精度的影响，近年来很多学者做了大量的工作。文献[7]提出了一种基于粒子群的节点自定位算法，一定程度上提高了定位精度。但是由于粒子群优化算法(PSO)自身存在进化后期易陷入局部极小点、易早熟收敛的缺陷，使得该方法对定位精度提高有限。针对这些缺陷，本文作者对传统的PSO算法进行了改进：将混沌搜索引入PSO并将其应用于节点自定位领域，利用混沌搜索具有的规律性、随机性和遍历性，改善算法的性能，从而提高节点的定位精度。
1 改进型粒子群优化算法
粒子群优化算法是一种基于种群搜索策略的全局优化算法[8-9]，它的优势在于构造简单、易于实现、搜索速度快，因此在科研和工程领域得到了广泛应用。
PSO算法的具体搜索过程是：在空间中初始化一群随机粒子，每个粒子代表解空间内的一个随机解，粒子在搜索空间内飞行，根据其自身经验和整个群体的经验动态调整自己的速度，通过迭代找到最优解，在每一次迭代中，粒子通过跟踪2个“极值”来更新自己：一个是粒子本身所能找到的最优解，称为个体极值；另一个极值是整个种群目前找到的最优解，称为全局极值。在找到这2个最优值后，每个粒子根据式(1)和(2)来更新自己的速度和位置[9]，当算法执行到预先设定的最大迭代次数或者粒子群当前搜索到的最优解位置满足预定最小适应度阈值时，停止迭代计算，输出当前的全局最优解。
(1)
(2)
其中，vk为粒子的速度向量；xk为当前粒子的位置；
为粒子本身所找到的最优解的位置；
为整个种群目前找到的最优解的位置；vk+1为vk，
和
矢量和；惯性权重c0一般取介于(0，1)之间的随机数，用于保持粒子的运动惯性，使其具有扩展搜索空间的能力，当它取较大值时，有利于跳出局部极小值，当它取较小值时，有利于算法收敛。加速常数c1，c2取(0，2)之间的随机数，分别为将每个粒子推向pbest和gbest位置的统计加速项的权重。加速权重较小时，允许粒子在被拉回来之前可以在目标区域外徘徊，值较高时则导致粒子突然冲向或超过目标区域。c0，c1，c2在取值范围内随机选定后，在算法执行过程中作为常数出现，不再改变以免造成结果的不稳定，导致无法进行相应的评估比较。
粒子群算法在搜索过程中利用式(1)和(2)更新自己的速度和位置，其本质是利用本身信息、个体极值信息和全局极值3个信息，来指导粒子下一步迭代位置。这实际上是一个正反馈过程，当其本身信息和个体极值信息占优势时，该算法很容易陷入局部最优 解[10-11]。在传感器网络中信标节点数量较少，搜索区间较大的情况下，应用该算法进行节点自定位，这一问题就更加凸现，将限制定位精度的提高。
根据最优化理论领域的NFL(No free lunch theorem)定理[12]，没有一种算法对任何问题的解都是最优的。因此，需要分析不同算法的特点，针对某一实际问题，融合不同算法的各自优势，构造出适应该问题的新算法。基于这一思路本文对PSO算法进行改进。
混沌是存在于非线性系统中的一种貌似随机的运动形式，是确定性系统内在随机性的表现，它具有随机性，遍历性和规律性3个特点[13]。混沌的这些特征，十分有利于PSO的优化和改进：随机性有利于算法获得大范围搜索能力，遍历性使得最终解有能力逼近最优解，规律性可以保证算法使用固定的迭代方程，从而便于编程计算。改进后的算法思路是：首先初始化种群，设定种群数量n、迭代次数M、惯性权重c0、加速常数c1和c2等。而后计算每个粒子的适应度，选出个体极值和全局极值，利用式(1)和(2)开始迭代寻优过程。此迭代过程与之前的不同之处在于：当运算到预先设定的次数后，启动混沌搜索，对历史最优解gbest施加混沌扰动，获得最优解gbest′，计算其适应值s′并与历史最优解s的适应值进行比较，如果s′＜s(即加入混沌扰动后的最优解优于历史最优解)，则选取gbest′作为新的全局最优解继续迭代计算。
以往的研究通常使用logistic映射产生混沌扰动，但是根据文献[14]的结论，Tent映射的遍历均匀性优于logistic映射，可以获得更高的搜索寻优效率，因此本文采用Tent映射作为混沌扰动产生器，它的表达式如下[15]：
(3)
产生混沌点列的过程如下：
(1) 设粒子的n维位置向量为xi=(xi1，xi2，…，xin)，根据(4)把xi的每一维xik，k=1，…，n，映射到[0，1]区间上得到向量yi=(yi1，yi2，…，yin)；
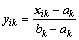(4)
其中，bk和ak分别是第k维变量xik的上界和下界。
(2) yi中的每一维yik根据式(3)进行变异，产生混沌序列
；
(3) 由式(5)将混沌序列中的点映射回原空间，得到xi经过Tent映射后的混沌点列：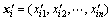
。
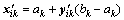(5)
2 节点自定位算法
本文提出的节点自定位算法的特点在于充分考虑到了传统PSO存在的早熟收敛缺陷，对粒子群优化计算出新位置进行混沌扰动，适当扩展了粒子的搜索范围，使解有能力跳出局部极值区间。由于PSO算法一般是在迭代后期陷入局部最优，如果从算法一开始就加入混沌搜索，缺乏必要性而且会增加算法的复杂度和计算量，因此可根据实际经验在PSO迭代后期对粒子的最优解加入混沌扰动。应用在节点自定位时体现为以相对较少的锚节点数目，在更大的布设范围内，获取更高的定位精度。其中，混沌扰动按照上节的描述产生。以三维空间节点自定位为例，新定位方法的具体实现步骤如下：
(1) 在三维空间内初始化一定数量的粒子群，设定粒子数为n，随机产生n个初始位置和n个初始速度；
(2) 计算每个粒子的适应值，选择适应值最小的粒子作为全局极值gbest，选择各个粒子的初始位置作为个体极值pbest。适应值的计算公式如下：
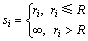(6)
其中，ri是未知节点到第i个信标节点的距离；R是信标节点的覆盖半径，距离信息可以通过接收信号强度(RSSI)、到达时间差(TDOA)、到达角度(AOA)或是到达时间(TOA)等方法测得，因此在本文属已知量。如果未知节点不在信标节点的覆盖半径内，适应值就取一个设定好的极大值，使之在迭代计算中被淘汰；
(3) 迭代进行到预先设定的次数时，启动混沌搜索，设此时的历史最优解对应的坐标向量xik=(xik1，xik2，xik3)，根据式(3)和(4)，式(5)产生新的坐标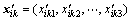
，xik+1=xik+vik+1，
vk+1，计算这2个位置的适应值s和s′。若s′＜s，则取
；
(4) 分别将，代入式(1)和(2)中，输出粒子新的位置，转到(2)；
(5) 当迭代次数达到设定值后，退出循环，输出全局极值对应的坐标。
此算法的特点在于在普通PSO的基础上，通过引入混沌理论增强了算法的全局搜索能力，避免过早收敛陷入局部极值点，应用在节点自定位时有助于提高定位精度。
3 试验及结果分析
为了检测新算法的定位性能，本文对其进行了仿真试验。在试验中，首先将改进型粒子群优化算法与普通粒子群优化算法进行比较，以验证前者相对普通算法的性能改善，而后将本文提出的节点自定位算法与目前节点自定位领域广泛使用的最小二乘估计法进行定位精度比较。
3.1 改进型PSO与PSO的性能比较
试验中采用2个典型的优化测试函数来比较2种算法的性能。其中，Rastrigrin函数是一种病态多峰函数，具有广阔的搜索空间，大量的局部极小点，可以有针对性地检验新算法的改进。Rosebrock函数则是一个病态单峰函数，该函数为优化算法提供的搜索信息较少，使算法难以找到全局极小点，可以用来检测新算法的执行效率。
(1) Rastrigrin函数
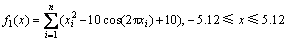
(2) Rosebrock函数
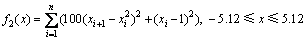
2个函数理论上的全局最优解都是0，试验中取50个粒子，设惯性权重c0取为0.729 8，加速常数c1和c2取为1.496 2，最大速度为5，迭代次数设为1 000次。为减小误差，对每个函数的测试独立运行30次取平均值。表1所示为采用PSO和改进型PSO分别对2个函数求解的结果。
从仿真结果可以看出：随着搜索维数的增加，2个函数求得的最优解距离真实最优解的误差越来越大，这是由于维数越高，其搜索难度越大。改进型PSO的平均搜索结果在各个维数级上明显优于PSO算法，这验证了迭代过程后期的混沌扰动提高了算法的全局搜索能力。测试结果说明：改进型PSO算法有效地提高了搜索精度。
3.2 改进型PSO定位算法与最小二乘估计法比较
在验证了改进型PSO算法相对普通PSO算法性能提高后，将其应用在节点自定位领域，将新定位算法与被广泛采用的最小二乘估计法进行比较。试验场景设置为一个100 m×100 m×100 m的三维空间，网络规模为200个节点，信标节点随机布放在此区间，节点的通信半径设为60 m，惯性权重c0取为0.729 8，加速常数c1和c2取为1.496 2，最大速度为5。试验结果的优劣用平均定位误差来评估，平均定位误差定义为：
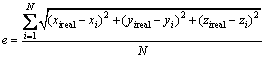(5)
其中：N为参与定位统计的未知节点数量，(xireal，yireal，zireal)为第i个未知节点的真实位置，(xi，yi，zi)为第i个节点的测量位置。
(1) 不同测距误差情况下基于改进型PSO的定位算法与最小二乘估计法比较。
在实际应用中，测量节点间的距离信息不可能做到严格准确，现有的测距方法一般都会伴随一定的误差。因此有必要测试测距误差对定位算法的影响。试验中误差依次取真实距离的5%，10%，15%，20%，25%，30%，信标节点数取30。试验结果如图1所示。
从图1可以看出，在各个测距误差级上，新算法的定位误差均低于最小二乘估计法，特别是在测距误差增加到5%以上时，新算法的优势更为明显，其定位误差随测距误差增大的上升趋势也明显较低。当测距误差在30%以内时，新算法的最大定位误差为7.935 1 m，而最小二乘估计法最大误差高达30.926 5 m，在测距误差不超过15%的情况下，新算法的定位误差在1 m左右，具有很高的精度。说明利用改进型PSO的高效全局搜索能力，提高了节点自定位算法的鲁棒性，在受到测距误差影响时，获得了相对较好的定位精度。
(2) 不同信标节点数量情况下基于改进型PSO的定位算法与最小二乘估计法比较。
信标节点的数量是一个评价无线传感器网络性能的重要指标，信标节点过多会增加系统成本、功耗，过少会降低定位精度，在信标节点数量一定的情况下，不同算法的定位精度也会不同。试验中信标节点的数量依次为10，20，30，40，50，60个，测距误差均取10%。试验结果见表2。
仿真结果表明：在信标节点数量相同时，新算法的平均定位误差远低于最小二乘估计法。信标节点数量为10和20时，平均定位误差相对较大，从信标节点数量为30开始，平均定位误差急剧下降，之后误差虽然仍会随着信标节点的数量增加而降低，但是降幅趋于平缓。分析原因认为是粒子群算法对初始值位置依赖性较大，如果信标节点太少，获得的初始信息量也少，搜索难度增大，势必造成误差增加，但即使在信标节点数量较少时，新算法的定位精度也远远高于最小二乘估计法的定位精度，例如，在信标节点数目为10时，新定位算法的平均定位误差为1.740 7 m，而最小二乘估计法的平均定位误差为31.927 8 m。说明新定位算法比最小二乘估计法更适合信标节点比较少的情况。而随着信标节点的数目不断增加，到达一定数量后，由于搜索空间范围不变，此时信标节点数量的再增加就难以明显地提升定位精度，因此定位精度趋于稳定。
总之，随着测距误差的增大，2种算法的平均定位误差也逐渐增大，在测距误差相同的情况下，新算法的定位误差比最小二乘估计法要小，其增长趋势更缓慢；随着信标节点数量的增加，2种算法的平均定位误差逐渐减小，在信标节点数量和测距误差相同的情况下，新算法的平均定位误差比最小二乘估计法的要低。此外，如果增加新算法的迭代次数，能进一步提高定位精度，但是这将带来更大的数据处理量，实际网络搭建中必须权衡处理。在同等条件下，新的定位算法较之传统方法极大地提高了对未知节点的定位精度，性能更为优越，能更好地应对测距误差较大、信标节点不多的客观条件限制。
表1 2种算法的测试结果
Table 1 Test results of two algorithms
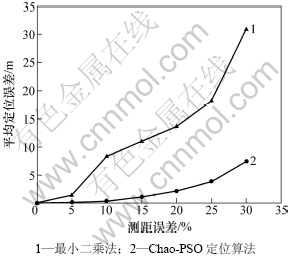
图1 不同测距误差时2种算法的定位误差
Fig.1 Localization error of two algorithms in different ranging error
表2 不同信标节点数量时2种算法的平均定位误差
Table 2 Average localization error of two algorithms in different anchor nodes number
4 结论
(1) 针对传统PSO算法搜索后期易陷入局部极值的缺陷，将混沌搜索引入其中，利用混沌自身的随机性，遍历性和规律性等特点，提高了PSO算法的全局搜索能力，对Rastrigrin函数和Rosebrock函数的测试结果表明改进后的PSO性能得到了提高。
(2) 将改进型PSO算法运用在无线传感器网络节点自定位领域，提出了一种基于距离的节点自定位算法，该算法较好地克服了测距误差大和信标节点数目少等因素对定位造成的负面影响，相比原有的最小二乘估计法大幅提高了定位精度，在无线传感器网络实际应用中具有一定的价值。
参考文献：
[1] Girod L, Bychovskiy V, Elson J, et al. Locating tiny sensors in time and space: a case study[C]//Proceedings of IEEE International Conference on Computer Design: VLSI in Computers and Processors. New York: IEEE Press, 2002: 214-219.
[2] He T, Huang C D, Blum B M, et al. Range-free localization schemes in large scale sensor networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking. New York: ACM Press, 2003: 81-95.
[3] 鲍喜荣, 张立立, 张石. 基于RSSI的多维定标迭代定位算法[J]. 东北大学学报, 2009, 30(12): 1694-1697.
BAO Xi-rong, ZHANG Li-li, ZHANG Shi. The research of multi-dimensional scaling iterations localization algorithm based on RSSI[J]. Journal of Northeastern University： Natural Science, 2009, 30(12): 1694-1697.
[4] 孟令军, 王建亮, 潘峰. 基于TDOA定位机制的无线传感器节点设计[J]. 传感器与微系统, 2009, 28(6):101-103.
MENG Ling-jun, WANG Jian-liang, PAN Feng. Design of wireless sensor networks node based on TDOA localization mechanism[J]. Transducer and Microsystem Technologies, 2009, 28(6): 101-103.
[5] Niculescu D, Nath B. Ad Hoc positioning system using AOA[C]//Proceedings of IEEE INFOCOM. San Francisco: IEEE Service Center, 2003: 1734-1743.
[6] 焦磊, 邢建平, 张军, 等. 一种非视距环境下具有鲁棒特性TOA无线传感网络定位算法[J]. 传感技术学报, 2007, 20(7): 1625-1629.
JIAO Lei, XING Jian-ping, ZHANG Jun, et al. A new NLOS TOA-based wireless sensor network localization algorithm with robust character[J]. Chinese Journal of Sensors and Actuators, 2007, 20(7): 1625-1629.
[7] 周书旺, 王英龙, 郭强, 等. 基于微粒群算法的无线传感器网络节点定位方法[J]. 山东大学学报: 理学版, 2009, 44(9): 52-55.
ZHOU Shu-wang, WANG Ying-long, GUO Qiang, et al. Particle swarm optimization-based wireless sensor network nodes localization method[J]. Journal of Shandong University: Natural Science, 2009, 44(9): 52-55.
[8] Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks IV. Piscataway: IEEE Press, 1995: 1941-1948.
[9] Eberhart R, Kennedy J. A new optimizer using particle swarm optimization theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science. Nagoya: IEEE Press, 1995: 39-43.
[10] Barskar S, Suganthan P N. A novel concurrent particle swarm optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation. Portland: IEEE Press, 2004: 792-796.
[11] 吕振肃, 侯志荣. 自适应变异的粒子群优化算法[J]. 电子学报, 2004, 32(3): 416-420.
L? Zhen-su, HOU Zhi-rong. Particle swarm optimization with adaptive mutation[J]. Acta Electronica Sinica, 2004, 32(3): 416-420.
[12] Wolpert D H, Macready W G. No free lunch theorems for optimization[J]. IEEE Trans on Evolutionary Computation, 1997, 1(1): 67-82.
[13] 李兵, 蒋慰孙. 混沌优化方法及其应用[J]. 控制理论与应用, 1997, 14(4): 613-615.
LI Bing, JIANG Wei-sun. Chaos optimization method and its application[J]. Control Theory and Applications, 1997, 14(4): 613-615.
[14] 单良, 强浩, 李军, 等 基于Tent影射的混沌优化算法[J]. 控制与决策, 2005, 20(2): 179-182.
SHAN Liang, QIANG Hao, LI Jun, et al. Chaotic optimization algorithm based on Tent map[J]. Control and Decision, 2005, 20(2): 179-182.
[15] 程志刚, 张立庆, 李小林, 等. 基于Tent映射的混沌混合粒子群优化算法[J]. 系统工程与电子技术, 2007, 29(1):103-106.
CHENG Zhi-gang, ZHANG Li-qing, LI Xiao-lin, et al. Chaotic hybrid particle swarm optimization algorithm based on Tent map[J]. Systems Engineering and Electronics, 2007, 29(1): 103-106.
(编辑 赵俊)
收稿日期：2011-06-15；修回日期：2011-09-27
基金项目：国家自然科学基金资助项目(60972160)；国防预研基金资助项目
通信作者：刘志坤(1984-)，男，山东寿光人，博士，从事无线传感器网络研究；电话：13477093865；E-mail：bill1302lzk@sina.com
