J. Cent. South Univ. (2019) 26: 711-718

DOI: https://doi.org/10.1007/s11771-019-4041-7

Numerical study of flocculation settling and thickening of whole-tailings in deep cone thickener using CFD approach

WU Ai-xiang(吴爱祥)^{1, 2}, RUAN Zhu-en(阮竹恩)^{1, 2}, LI Cui-ping(李翠平)^{1, 2},WANG Shao-yong(王少勇)², WANG Yong(王勇)², WANG Jian-dong(王建栋)¹

1. School of Civil & Resources Engineering, University of Science & Technology Beijing,Beijing 100083, China;

2. Key Laboratory of High-Efficient Mining and Safety of Metal Mines of the Ministry of Education, University of Science & Technology Beijing, Beijing 100083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: Deep cone thickener (DCT) is the key equipment in cemented paste backfill (CPB), so it is essential to study the flocculation settling and thickening characteristics of the whole-tailings in DCT. Coupled with population balance model (PBM), computational fluid dynamics (CFD) was used to study the characteristics, namely particle size distribution (PSD) and underflow concentration in DCT. Based on actual production, the effects of rake rotational speed, feed rate and tailings slurry concentration were simulated and analyzed in a certain range. The PSD varied with rake rational speed, feed rate and tailings slurry concentration almost in the same trend, but the influence of feed rate was less than that of rake rational speed and tailings slurry concentration. The underflow concentration increased at first and then declined with rake rational speed and feed rate, but it rose and fell with the tailings slurry concentration. Finally, the optimal key parameters on the flocculation settling and thickening of the whole-tailings in DCT were obtained: rake rotational speed of 17 r/min, feed rate of 3.25 m³/h and tailings slurry concentration of 20%, giving the reference values to the industrial production in Baishitamu Copper Mine.

Key words: deep cone thickener; flocculation settling; thickening; whole-tailings; computational fluid dynamics

Cite this article as: WU Ai-xiang, RUAN Zhu-en, LI Cui-ping, WANG Shao-yong, WANG Yong, WANG Jian-dong. Numerical study of flocculation settling and thickening of whole-tailings in deep cone thickener using CFD approach [J]. Journal of Central South University, 2019, 26(3): 711–718. DOI: https://doi.org/10.1007/s11771-019-4041-7.

1 Introduction

For the advantages of safety, green, economy and efficiency, whole-tailings cemented paste backfill (CPB) technology has been widely accepted and applied all over the world [1, 2]. CPB represents the development direction of mine filling technology, and is known as the new green mining technology in the 21st Century [3]. The whole-tailings with ultrafine particles are difficult to be separated from water, that is to say, it is not easy to thicken the whole-tailings slurry to paste [4]. Nowadays, deep cone thickener (DCT) has been developed for the whole-tailings thickening and flocculant is used for the whole-tailings flocculation settling. It is necessary to study the flocculation settling and thickening performance of whole- tailings particles in DCT [5]. The particle size of whole-tailings floc changes with many parameters and has great influence on the underflow concentration. Accordingly, the effect of key parameters on the particle size distribution (PSD) and the underflow concentration were investigated in this paper.

Recent years, many researches have conducted experimental and simulational studies on the effect of parameters on the flocculation settling and thickening characteristics of tailings. BANISI et al [6] studied the effect of tailings slurry concentration on the underflow concentration and overflow concentration. Using settling curve, USHER et al [7] studied the influence of slurry concentration on settling velocity and underflow concentration. WU et al [8] and JIAO et al [9] considered tailings slurry concentration, flocculant solution concentration, flocculant unit consumption as the important influence factors of whole-tailings flocculation sedimentation. Similarly, the same conclusion was drawn by other researchers [4, 10] and they considered tailings slurry concentration as the most important parameter. In addition, CIFTCI et al [11] investigated the effects of pulp density and polymer on the flocculation of coal tailings.

At the same time, the feed rate also affects the flocculation settling and thickening of tailings. OWEN et al [12] and NGUYEN et al [13] studied the effect of inlet feed rate and feed direction on the performance of industrial thickener using computational fluid dynamics (CFD) and then designed a new thickener feedwell. Using pilot- scale test, TAO et al [14] investigated the effects of key operating parameters on waste clay thickening performance and the influence of feed rate, sand addition rate, bed depth and flocculant dosage were analyzed deeply. GHESHLAGHI et al [15, 16] coupled CFD with population balance models (PBM) to investigate the effect of feed flow rate and inlet slurry concentration on the performance of thickener. ZHOU et al [17] established 3D CFD model to analyze the flow regions of feedwell on an industrial scale and studied the effect of inlet feed rate on the performance of feedwell. They obtained an optimum feed inlet rate depending on the feedwell design finally. RAHIMI et al [18] carried out dynamic simulation on the thickener at coal washing plant and investigated the effect of feed flow rate variations on underflow concentration and bed height using the phenomenological model in thickener.

Thickener rakes are key parts to improve the underflow concentration in DCT. Many studies were conducted on the rake torque and the design of rake. HUANG et al [19] performed a numerical simulation to predict the influence of impeller size and agitating speed on the performance of rake in an agitating tank using CFD approach. UTALO et al [20] also used CFD to simulate the flow patterns around the rakes and proved the validity of the CFD model in scaling up to full-scale units. KAHANE et al [21] and LI et al [22] studied the variation of rake torque and analyzed the reasons for the pressure rake of DCT based on dynamic settlement test and rheological parameters measurement. RUDMAN et al [23, 24] considered the yield stress of the suspension and the rake rotational speed are the major factors in determining rake torque and they can be taken into consideration to modify and improve rake design and operation. Nevertheless, only few studies of the effect of rakes on the underflow concentration have been published. DU et al [25] investigated the effect of rake on floccule macroscopically, and put forward the existence of drainage channel due to rake stirring. WU et al [26, 27] conducted experiments to investigate the influence of rake rod number and rake rod arrangement on the tailings thickening performance.

Throughout the existing research results, slurry concentration (C₀), feed rate (FR) and rake rotational speed (N) are the key parameters on the flocculation settling and thickening characteristics of the whole-tailings in DCT. In addition, the results imply that the CFD is a simple and effective approach to study the flocculation settling and thickening.

At the same time, it is the ultimate goal of a DCT to obtain higher and stable underflow concentration, which is the key of CPB. Apart from the parameters mentioned above, the PSD of tailings in the inlet of DCT also affects the underflow concentration [28]. And the spatial- temporal changes of PSD always appear in DCT [5].

Therefore, CFD approach was used to simulate and study the flocculation settling and thickening characteristics, i.e. PSD of the whole-tailings and underflow concentration in DCT. The effect of tailings slurry concentration (C₀), feed rate (FR), rake rotational speed (N) will be analyzed deeply to provide technological support for industrial production.

2 Materials and methods

2.1 Basic properties of whole-tailings

The whole-tailings were sampled from Baishitamu Copper Mine in Xinjiang province, China. Using laser particle size analyzer, the PSD curve of whole-tailings was obtained as shown in Figure 1. The density of whole-tailings was 2750 kg/m³, the content of fine particles (smaller than 20 μm) was 29.8%, and the average diameter was 58.3 μm. The coefficient of uniformity(C_u) and coefficient of curvature(C_c) are used to indicate the gradation of sands. Only when C_u ≥ 6 and 1c<3, can a sand be classified as well gradated and compacted [29]. They can be calculated using the equations mentioned in Ref. [30]. The C_u and C_c are 18.36 and 1.62, respectively, indicating that the whole-tailings is well gradated and has a good continuity of PSD. The Ciba1# flocculant was added into the whole-tailings slurry. The flocculant unit consumption and flocculant solution concentration were 28.35 g/t and 0.15%, respectively.

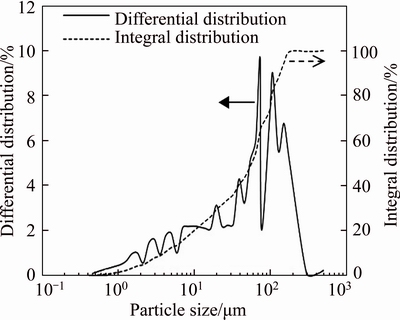
Figure 1 PSD curve of whole-tailings

2.2 DCT model

On the basis of similitude principle, a DCT model was established by Gambit, the preprocessor software of CFD [5]. As shown in Figure 2, the diameter and height of the DCT are 1.1 and 1.6 m, respectively. The model was discretized to 1026376 cells with good grid independence.

2.3 Computational methods

The mixture model in CFD was adopted to describe the flow in DCT. With the heat transfer during the flocculation settling and thickening being neglected, the realizable k-ε turbulence model was applied as the turbulence closure model. Being effective and ideal for describing the PSD of discrete phase, PBM was used to deal with the influence of whole-tailings floc’ aggregation and breakage on PSD in DCT.

Figure 2 Geometric structure and domain mesh of DCT

In terms of length number density function n (L; x, t), the Reynolds-averaged form of PBM expression can be defined. Where x and t are spatial coordinate vector and time, respectively. To simplify the expression, the PBM was defined as [31, 32]:

                  (1)

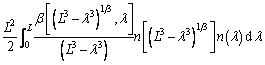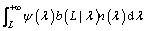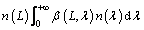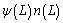where n(L) is a length number density function; u represents the average velocity vector; G(L) represents the linear growth rate; and represent the birth rates due to aggregation and breakage, respectively; and represent the death rates due to aggregation and breakage accordingly;and ψ(λ) are the aggregation kernel and breakage kernel, respectively; b(L|λ) is the distribution function of fragmentation.

Being ideal for the computationally demand of CFD codes [33], the quadrature method of moments, proposed by MCGRAW [34], was adopted to deal with aggregation and breakage. LUO aggregation model [35] was used to study the aggregation mechanism of whole-tailings while GHADIRI breakage model [36, 37] was used to study the breakage of whole-tailings floc.

LUO aggregation model was defined by the frequency of collision and probability that the collision results in aggregation. It was written as the rate of particle length as a result of binary collisions of particles with length of L_i and L_j:

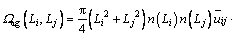
     (2)

where and are the frequency of collision and probability that the collision results in aggregation, respectively; ρ₁ is the density of water and ρ₂ is the density of whole-tailings; c₁ is a constant; 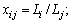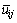is the characteristic velocity of collision of two particles with length of L_i and L_j and number density of n(L_i) and n(L_j), it was defined as:

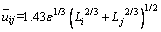                 (3)

where ε is the water eddy dissipation.

The Weber number was defined as:

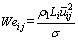                            (4)

where σ is the surface tension.

GHADIRI breakage model was defined by the breakage frequency and the distribution function of fragmentation as follows.

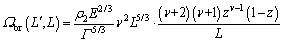 (5)

where the original particle has a length of L and the daughter particle has a length of L′. 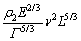and are the breakage frequency and the distribution function of fragmentation [38],respectively; E represents the elastic modulus of the granule; Γ represents the interface energy; v is the impact velocity of particle. According to the self-similar formulation [32], z represents the similarity which is the ratio of daughter-to-original (parent) particle parent size,

Reynolds averaged Navier–Stokes equations were solved to obtain the 3-D flow filed. A no-slip wall boundary and a standard wall function were adopted to define the solid wall in DCT. The semi-implicit method for pressure-linked equations consistent was used to deal with the coupling of velocity and pressure. The pressure staggered option was adopted as the pressure interpolation scheme. The momentum equation and realizable k–ε equations were discretized with the second order upwind scheme. The volume fraction equation and PBM were discretized with the quadratic upwind interpolation and the first order upwind scheme, respectively.

3 Results and discussion

3.1 Effect of rake rotational speed

As the impact on the floccule structure and drainage channel [25], rakes would affect the flocculation settling and thickening characteristics of the whole-tailings. According to the actual production process (rake rotational speed of 18 r/min, feed rate of 2.85 m³/h and tailings slurry concentration of 20% by mass) in Baishitamu copper mine, the simulations were conducted under the rake rotational speed of 16–19 r/min.

The PSD in DCT is shown in Figure 3. Although the curve of PSD changes in the same trend with different rake rotational speeds, the number density of particles, especially that of the diameter of 1000–1500 μm, under the rake rotational speed of 17 or 18 r/min, is much larger than others. It indicates that these speeds are better for the flocculation of whole-tailings in DCT. If the rake rotational speed is too slow, the whole-tailings particles are not likely to aggregate to floc. While if the speed is too high, the whole-tailings floc will be broken by the shear of the rake.

Figure 3 PSD in DCT:

From Figure 4, it can be seen that the underflow concentration also changes with the rake rotational speed under the feed rate of 2.45–3.65 m³/h and tailings slurry concentration of 20%, and it increases at first and then declines with rotational speed. No matter what the feed rate is, the concentration always peaks to the top point at the rake rotational speed of 17 r/min, illustrating that this speed may be the optimal speed within the limit of 16 to 19 r/min. This is because the drainage channel under this speed is the best for dewatering of whole-tailings. And the whole-tailings slurry is thickened deeply as a result.

3.2 Effect of feed rate

Then the effects of feed rate under the rake rotational speed of 17 r/min and tailings slurry concentration of 20% by mass were investigated.

Figure 4 Underflow concentration under different rake rotational speeds (N)

The PSD in DCT under different feed rates is shown in Figure 5. The curve of PSD changes a little with feed rate, but the number density of particles under the feed rate of 3.25 m³/h is larger than others to some degree. The feed rate has little effect on the flocculation of whole-tailings in DCT but effects the underflow concentration obviously. As shown in Figure 6, the underflow concentration increases at first and then declines with the feed rate, and it almost reaches to the peak under the feed rate of 3.25 m³/h. However, it downed to the bottom under the rake rotational speed of 16 r/min and feed rate of 3.25 m³/h, indicating that this condition was most disadvantageous to flocculation settling and thickening of whole-tailings. Accordingly, it can be concluded that the rate of 3.25 m³/h is the best for this DCT in Baishitamu copper mine.

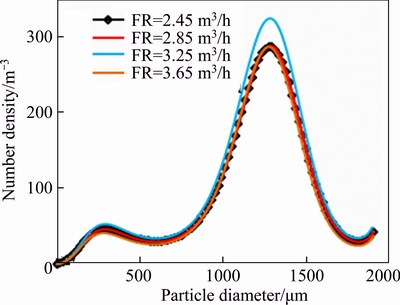
Figure 5 PSD in DCT under different feed rates (FR)

Figure 6 Underflow concentration under different feed rates (FR)

3.3 Effect of tailings slurry concentration

Finally, the effect of the most important parameter, tailings slurry concentration, was investigated under the rake rotational speed of 17 r/min and feed rate of 3.25 m³/h.

The PSD in DCT under different tailings slurry concentration is shown in Figure 7. The curve of PSD varies with the tailings slurry concentration apparently and the number density of particles under the concentration of 20% by mass almost is the largest. While the bimodal phenomenon of PSD under concentration of 18% by mass is the most obvious. It means that the flocculation is the best under the concentration of 20% by mass. As shown in Figure 8, the tailings slurry concentration also affects the underflow concentration apparently. The underflow concentration rises and falls with the tailings slurry concentration. The maximum underflow concentration, 64.35% by mass, was obtained under the concentration of 20%. Accordingly, the tailings slurry concentration of 20%, which is in agreement with the actual production, is optimal for this DCT.

Figure 7 PSD in DCT under tailings slurry concentration (C₀)

Figure 8 Underflow concentration under different tailings slurry concentration (C₀)

4 Conclusions

Flocculation settling and thickening characteristics of whole-tailings in DCT are studied using CFD approach. The effect of rake rational speed, feed rate and tailings slurry concentration on PSD in DCT and underflow concentration is discussed, respectively. Based on the simulation and discussions, the following conclusions can be drawn.

1) The PSD varies with rake rational speed, feed rate and tailings slurry concentration almost in the same trend, the particle size mainly distributes in 1000–1500 μm. The influence of feed rate is the least but that of tailings slurry concentration is the largest.

2) The underflow concentration increases at first and then declines with rake rational speed and feed rate in a certain range. However, it rises and falls with the tailings slurry concentration drastically. The maximum underflow concentration is 64.35% by mass under the concentration of 20%.

3) The optimal key parameters on the flocculation settling and thickening of the whole-tailings in DCT are rake rotational speed of 17 r/min, feed rate of 3.25 m³/h and tailings slurry concentration of 20%. The relative parameters in Baishitamu Copper Mine could be adjusted properly.

References

[1] CAO Shuai, SONG Wei-dong. Effect of filling interval time on the mechanical strength and ultrasonic properties of cemented coarse tailing backfill [J]. International Journal of Mineral Processing, 2017, 166: 62-68. DOI: 10.1016/ j.minpro.2017.07.005.

[2] WU Ai-xiang, CHENG Hai-yong, YANG Ying, ZHANG Lian-fu. Development and challenge of paste technology in China [C]// 20th International Seminar on Paste and Thickened Tailings (Paste 2017). Beijing, China: Paste, 2017: 2–11. DOI: https://papers.acg.uwa.edu.au/p/1752_01_Wu/.

[3] WU Ai-xiang, WANG Yong, WANG Hong-jiang. Status and prospects of the paste backfill technology [J]. Metal Mine, 2016, 45(7): 1–9. DOI: 10.3969/j.issn.1001-1250.2016. 07.001. (in Chinese)

[4] ZHANG Qin-li, ZHOU Deng-hui, WANG Xin-min, ZHAO Jian-wen. Experimental study on flocculating sedimentation of ultra-fine unclassified tailings [J]. Journal of Guangxi University: Nat Sci Ed, 2013, 38(2): 451–455. DOI: 10.13624/j.cnki.issn.1001-7445.2013.02.004 .(in Chinese)

[5] RUAN Zhu-en, LI Cui-ping, SHI Cong. Numerical simulation of flocculation and settling behavior of whole- tailings particles in deep-cone thickener [J]. Journal of Central South University, 2016, 23(3): 740–749. DOI: 10.1007/s11771-016-3119-8.

[6] BANISI S, YAHYAEI M. Feed dilution-based design of a thickener for refuse slurry of a coal preparation plant [J]. International Journal of Coal Preparation & Utilization, 2008, 28(4): 201–223. DOI: 10.1080/19392690802391189

[7] USHER S P, SPEHAR R, SCALES P J. Theoretical analysis of aggregate densification: Impact on thickener performance [J]. Chemical Engineering Journal, 2009, 151(1): 202–208. DOI: 10.1016/j.cej.2009.02.027.

[8] WU Ai-xiang, ZHOU Jing, YIN Sheng-hua, WANG Lei-ming. Influence factors on flocculation sedimentation of unclassified tailings [J]. The Chinese Journal of Nonferrous Metals, 2016, 26(2): 439–446. DOI: 10.19476/j.ysxb.1004. 0609.2016.02.023. (in Chinese)

[9] JIAO Hua-zhe, WU Ai-xiang, WANG Hong-jiang, LIU Xiao-hui, YANG Sheng-kai, XIAO Yun-tian. Experiment study on the flocculation settlement characteristic of unclassified tailings [J]. Journal of University of Science & Technology Beijing, 2011, 33(12): 1437–1441. DOI: 10.13374/j.issn1001-053x.2011.12.005. (in Chinese)

[10] YANG Chao, GUO Li-jie, XU Wen-yuan, LI Xin, XUE Shan-shan. Experimental study on the rule of flocculation sedimentation of filling tailings [J]. Gold, 2014, 35(6): 39–42. DOI: 10.11792/hj20140610. (in Chinese)

[11] CIFTCI H, ISIK S. Settling characteristics of coal preparation plant fine tailings using anionic polymers [J]. Korean Journal of Chemical Engineering, 2017: 1–7. DOI: 10.1007/s11814-017-0123-0.

[12] OWEN A T, NGUYEN T V, FAWELL P D. The effect of flocculant solution transport and addition conditions on feedwell performance in gravity thickeners [J]. International Journal of Mineral Processing, 2009, 93(2): 115–127. DOI: 10.1016/j.minpro.2009.07.001.

[13] NGUYEN T V, FARROW J B, SMITH J, FAWELL P D. Design and development of a novel thickener feedwell using computational fluid dynamics [J]. Journal-South African Institute of Mining and Metallurgy, 2012, 112(112): 939–948. DOI: http://www.saimm.co.za/Journal/v112n11p939.pdf.

[14] TAO D, PAREKH B K, ZHAO Yue-ming, ZHANG P. Pilot-scale demonstration of deep Cone^TM paste thickening process for phosphatic Clay/Sand disposal [J]. Separation Science & Technology, 2010, 45(10): 1418–1425. DOI: 10.1080/01496391003652783.

[15] GHESHLAGHI M E, GOHARRIZI A S, SHAHRIVAR A A. Simulation of a semi-industrial pilot plant thickener using CFD approach [J]. International Journal of Mining Science and Technology, 2013, 23(1): 63–68. DOI: 10.1016/j.ijmst. 2013.01.010.

[16] GHESHLAGHI M E, GOHARRIZI A S, SHAHRIVAR A A, ABDOLLAHI H. Modeling industrial thickener using computational fluid dynamics (CFD), a case study: Tailing thickener in the Sarcheshmeh copper mine [J]. International Journal of Mining Science and Technology, 2013, 23(6): 885–892. DOI: 10.1016/j.ijmst.2013.11.002.

[17] ZHOU Tian, LI Mao, LI Qiu-long, LEI Bo, ZHOU Qian, ZHOU Jie-ming. Numerical simulation of flow regions in red mud separation thickener’s feedwell by analysis of residence-time distribution [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(4): 1117–1124. DOI: 10.1016/S1003-6326(14)63170-8.

[18] RAHIMI M, ABDOLLAHZADEH A A, REZAI B. Dynamic simulation of tailing thickener at the Tabas coal washing plant using the phenomenological model [J]. International Journal of Mineral Processing, 2016, 154: 35–40. DOI: 10.1016/j.minpro.2016.07.003

[19] HUANG Gen, LIU Jiong-tian, WANG Li-jun, SONG Zhi-hao. Flow field simulation of agitating tank and fine coal conditioning [J]. International Journal of Mineral Processing, 2016, 148: 116–123. DOI: http://dx.doi.org/10.1016/j.minpro. 2016.01.020.

[20] UTALO I D, PATERSON D A, RUDMAN M. Flow visualisation and computational prediction in thickener rake models [J]. Minerals Engineering, 2003, 16(2): 93–102. DOI: 10.1016/S0892-6875(02)00256-X.

[21] KAHANE R B, NGUYEN T, SCHWARZ M P. CFD modelling of thickeners at Worsley Alumina Pty Ltd [J]. Applied Mathematical Modelling, 2002, 26(2): 281–296. DOI: 10.1016/s0307-904x(01)00061-0.

[22] LI Hui, WANG Hong-jiang, WU Ai-xiang, JIAO Hua-zhe, LIU Xiao-hui. Pressure rake analysis of deep cone thickeners based on tailings’ settlement and rheological characteristics [J]. Journal of University of Science & Technology Beijing, 2013, 35(12): 1553–1558. DOI: 10.13374/j.issn1001-053x. 2013.12.007. (in Chinese)

[23] RUDMAN M, SIMIC K, PATERSON D A, STRODE P, BRENT A, UTALO I D. Raking in gravity thickeners [J]. International Journal of Mineral Processing, 2008, 86(1): 114–130. DOI: 10.1016/j.minpro.2007.12.002.

[24] RUDMAN M, PATERSON D A, SIMIC K. Efficiency of raking in gravity thickeners [J]. International Journal of Mineral Processing, 2010, 95(1): 30–39. DOI: 10.1016/ j.minpro.2010.03.007.

[25] DU Jian-hua, PUSHKAROVA R A, SMART R S C. A cryo-SEM study of aggregate and floc structure changes during clay settling and raking processes [J]. International Journal of Mineral Processing, 2009, 93(1): 66–72. DOI: 10.1016/j.minpro.2009.06.004.

[26] WU Ai-xiang, WANG Yong, WANG Hong-jiang. Effect of rake rod number and arrangement on tailings thickening performance [J]. Journal of Central South University, 2014, 45(1): 244–248. DOI: http://www.zndxzk.com.cn/down/ 2014/01_zkb/34-p0244-123425.pdf. (in Chinese)

[27] WU Ai-xiang, JIAO Hua-zhe, WANG Hong-jiang, YANG Sheng-kai, YAO Gao-hui, LIU Xiao-hui. Mechanical model of scraper rake torque in deep-cone thickener [J]. Journal of Central South University, 2012, 43(4): 1469–1474. DOI: http://www.zndxzk.com.cn/down/upfile/soft/20120419/43-p1469-110030.pdf. (in Chinese)

[28] WEI Lu-bin, SUN Ming-yang. Numerical studies of the influence of particles’ size distribution characteristics on the gravity separation performance of liquid-solid fluidized bed separator [J]. International Journal of Mineral Processing, 2016, 157: 111–119. DOI: 10.1016/j.minpro.2016.10.004.

[29] AJAMU S O, IGE J A. Influence of coarse aggregate type and mixing method on properties of concrete made from natural aggregates in Ogbomoso Oyo state Nigeria [J]. International Journal of Engineering and Technology, 2015, 5(7): 426–433. DOI: http://www.iet-journals.org/archive/ 2015/july_vol_5_no_7/272614314 46178.pdf.

[30] WU Ai-xiang, RUAN Zhu-en, WANG Yi-ming, YIN Sheng-hua, WANG Shao-yong, WANG Yong, WANG Jian-dong. CFD simulation of long-distance pipeline transportation properties of whole-tailings paste with high sliming [J]. Journal of Central South University, 2018, 25(1): 141–150. DOI: 10.1007/s11771-018-3724-9.

[31] RANDOLPH A D, LARSON M A. Theory of particulate processes (2nd ed) [M]. San Diego, CA: Academic Press, 1988: 41–63.

[32] RAMKRISHNA D. Population balance: Theory and application to particulate systems in engineering [M]. New York: Academic Press, 2000: 7–45.

[33] YUAN C, LAURENT F, FOX R O. An extended quadrature method of moments for population balance equations [J]. Journal of Aerosol Science, 2012, 51(51): 1–23. DOI: 10.1016/j.jaerosci.2012.04.003.

[34] McGRAW R. Description of aerosol dynamics by the quadrature method of moments [J]. Aerosol Science & Technology, 1997, 27(2): 255–265. DOI: 10.1080/ 02786829708965471.

[35] LUO H, SVENDSEN H F. Theoretical model for drop and bubble breakup in turbulent dispersions [J]. Aiche Journal, 1996, 42(5): 766–776. DOI: 10.1002/aic.690420505.

[36] GHADIRI M, ZHANG Z. Impact attrition of particulate solids. Part 1: A theoretical model of chipping [J]. Chemical Engineering Science, 2002, 57(17): 3659–3669. DOI: 10.1016/S0009-2509(02)00240-3.

[37] MORENO-ATANASIO R, GHADIRI M. Mechanistic analysis and computer simulation of impact breakage of agglomerates: Effect of surface energy [J]. Chemical Engineering Science, 2006, 61(8): 2476–2481. DOI: 10.1016/j.ces.2005.11.019.

[38] VIGIL R D, ZIFF R M. On the stability of coagulation–fragmentation population balances [J]. Journal of Colloid & Interface Science, 1989, 133(1): 257–264. DOI: 10.1016/0021-9797(89)90300-7.

(Edited by FANG Jing-hua)

中文导读

深锥浓密机内全尾砂絮凝沉降与浓密的CFD模拟

摘要：深锥浓密机是膏体充填的关键设备，研究其内部全尾砂絮凝沉降与浓密特性很有必要。本文将CFD和群体平衡模型（PBM）进行耦合，用以研究深锥浓密机内的颗粒粒径分布（PSD）及其底流浓度。基于生产实际，研究了耙架转速、进料流量、进料料浆浓度对PSD和底流浓度的影响。PSD随着耙架转速、进料流量、进料料浆浓度的变化趋势几乎一致，但是进料流量的影响最小。底流浓度随着耙架转速和进料流量先上升后减小，但是随着进料料浆浓度不断波动。最终，获得了最佳耙架转速、进料流量、进料料浆浓度分别为17 r/min、3.25 m³/h、20%，从而为拜什塔木铜矿的实际生产提供指导。

关键词：深锥浓密机；絮凝沉降；浓密；全尾砂；计算流体动力学

Foundation item: Project(2016YFC0600709) supported by the National Key R & D Program of China; Projects(51574013, 51774039) supported by the National Natural Science Foundation of China; Project(FRF-TP-17-024A1) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2018-03-11; Accepted date: 2018-05-05

Corresponding author: RUAN Zhu-en, PhD Candidate; Tel: +86-10-62334680; E-mail: ziyuan0902rze@163.com; ORCID: 0000-0002- 1553-2208; LI Cui-ping, PhD, Professor; Tel: +86-10-62334756; E-mail: cpli@ustb.edu.cn; ORCID: 0000- 0002-8046-8695