Variational analysis of mid-span deflection of gantry cranes
来源期刊:中南大学学报(英文版)2017年第11期
论文作者:张大鹏 程文明 王彬
文章页码:2705 - 2716
Key words:gantry crane; deflection; structural stiffness; variational analysis
Abstract: In practical application, it is very important to master the influence of structure parameters on the mid-span deflection quantificationally. For large-span and heavy-duty gantry cranes, the influence of the rigid leg and the soft leg on mid-span deflection has not been considered in the past. In the paper, the mathematical model is established for universal large-span and heavy-duty gantry cranes. The analytical solution for the mid-span deflection of gantry-frame structure girder is derived and obtained based on the variation principle by considering the coupling effect of the bending moments of girder and legs, the axial force and the secondary bending moments. The relation between the load and the deflection on the mid-span of the gantry-frame structure girder is known. Then, the experimental model is designed according to dimensional analysis method. And experiments were performed on the WEW-600B type testing machine. Hackling experimental data, the regular of the load and deflection on the girder mid-span is obtained, namely, the deformation of the gantry-frame structure resists the external load to do work. The validity of the nonlinear analytical solution of the girder deflection is verified. Experimental results show that the analytical solution of the gantry-frame structure deflection has much higher calculation accuracy than previous calculation method. This work provides a theoretical basis for the design and inspection of gantry-frame structures.
Cite this article as: ZHANG Da-peng, CHENG Wen-ming, WANG Bin. Variational analysis of mid-span deflection of gantry cranes [J]. Journal of Central South University, 2017, 24(11): 2705–2716. DOI: https://doi.org/10.1007/s11771- 017-3683-6.
J. Cent. South Univ. (2017) 24: 2705-2716
DOI: https://doi.org/10.1007/s11771-017-3683-6

ZHANG Da-peng(张大鹏)1, 2, CHENG Wen-ming(程文明)2, WANG Bin(王彬)3
1. School of Mechanical and Electronic Engineering, Mianyang Teachers’ College, Mianyang 621000, China;
2. Research Institute of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. Brunel University, London, UK
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: In practical application, it is very important to master the influence of structure parameters on the mid-span deflection quantificationally. For large-span and heavy-duty gantry cranes, the influence of the rigid leg and the soft leg on mid-span deflection has not been considered in the past. In the paper, the mathematical model is established for universal large-span and heavy-duty gantry cranes. The analytical solution for the mid-span deflection of gantry-frame structure girder is derived and obtained based on the variation principle by considering the coupling effect of the bending moments of girder and legs, the axial force and the secondary bending moments. The relation between the load and the deflection on the mid-span of the gantry-frame structure girder is known. Then, the experimental model is designed according to dimensional analysis method. And experiments were performed on the WEW-600B type testing machine. Hackling experimental data, the regular of the load and deflection on the girder mid-span is obtained, namely, the deformation of the gantry-frame structure resists the external load to do work. The validity of the nonlinear analytical solution of the girder deflection is verified. Experimental results show that the analytical solution of the gantry-frame structure deflection has much higher calculation accuracy than previous calculation method. This work provides a theoretical basis for the design and inspection of gantry-frame structures.
Key words: gantry crane; deflection; structural stiffness; variational analysis
1 Introduction
Cranes are used widely in the railways, ports, electricity and other business sectors, which can make the transportation of the heavy goods more secure and efficient. As crane was regarded as safety critical equipment [1], there were strict rules and regulations governing the design, manufacturing, installation and operation of such machines. When inspecting cranes for safety reasons, the deflection value of the crane girder under the rated load was one of the important safety indicators to assess the state of metal structures. The recorded deflection must not exceed the critical value specified in the relevant national or international regulations/standards. For heavy-duty cranes, the rated load required for acceptance tests could be enormous, for instance, reaching thousands of tons. To obtain, transport and apply such a large dead weight was expensive and difficult. For example, when inspecting the crane of Tibet Jinhe Hydropower station for detecting deflection in installing, the inspection could be carried out on condition that they specially bought more than 60 t of steel as weights. Because the supporting legs were involved in deformation, the deflection analysis formula of gantry crane was more general. Therefore, to predict the deflection of gantry cranes, it was very important to qualify the influence of structure parameters on the gantry crane mid-span deflection. It had a great significance to analyze the relationship between load and deflection.
Extended work has been carried out on the crane strength and stiffness by researchers. ABBAS et al [2, 3] and SAUSE et al [4] studied the bending strength and stiffness of corrugated web I-girders, without considering the influence of the rigid legs on the calculation results. CHENG et al [5] studied the coupling relations between the cross-sectional parameters and the stiffness of girders and cantilever beams, but the interactions between the supporting legs and the main beam were not analyzed. YAO and YE [6] provided an analytical solution for bending-compression column with different tension- compression modulus, which provided a helpful reference for the calculation of girder. HOLST et al [7, 8] analyzed deflections of the main girder using a bi-variate polynomial model. They concluded that the deflection depends mainly on the loading and the applied position; Combining with experimental data, HOLST et al managed to derive the useful deflection curve of the portal frames without considering the horizontal displacement and the effect of the moment of inertia of legs when they were different. L et al [9] estimated the girder deflection by using the three-point deviation method (GECS) in experiments. As the local points were used for mutual reference, there were some limitations to detect the deformation of the whole portal frame structure. PINCA et al [10] analyzed the stress–strain relationship in the structure using finite element method. The effect of the structural parameters was discussed, but without considering the influence of the loading history, fatigue, and manufacturing process. LEE and PARK [11] measured girder deflections using the terrestrial laser scanning technology (TLS). Combining finite element analysis, they proposed an automatic calculation for the girder stresses. However, the method was dependent on the degree of discretion, which depends on the boundary and loading conditions, beam span and deformation. CASTILLO et al [12] analyzed the sensitivity of the structure parameters by the objective function, and the method was confined to bridge cranes. RI et al [13] studied the method of large structural deflection measurement. Though the measurement accuracy was high, the method depends on experience to select measurement spacing, order, grating and the judgment on the noise influence, thus poor practicability. YAN et al [14] investigated the relationship between the parameters of support structure and the variation of the maximum deflection and compressive stress, and analyzed the importance of the parameters.
et al [9] estimated the girder deflection by using the three-point deviation method (GECS) in experiments. As the local points were used for mutual reference, there were some limitations to detect the deformation of the whole portal frame structure. PINCA et al [10] analyzed the stress–strain relationship in the structure using finite element method. The effect of the structural parameters was discussed, but without considering the influence of the loading history, fatigue, and manufacturing process. LEE and PARK [11] measured girder deflections using the terrestrial laser scanning technology (TLS). Combining finite element analysis, they proposed an automatic calculation for the girder stresses. However, the method was dependent on the degree of discretion, which depends on the boundary and loading conditions, beam span and deformation. CASTILLO et al [12] analyzed the sensitivity of the structure parameters by the objective function, and the method was confined to bridge cranes. RI et al [13] studied the method of large structural deflection measurement. Though the measurement accuracy was high, the method depends on experience to select measurement spacing, order, grating and the judgment on the noise influence, thus poor practicability. YAN et al [14] investigated the relationship between the parameters of support structure and the variation of the maximum deflection and compressive stress, and analyzed the importance of the parameters.
There were two traditional formulas to calculate the gantry crane deflection. One was calculated according to the calculation formula of the deflection for simply supported beam (SSB) and the calculation result was on the high side. The other one was the calculation formula of the gantry crane deflection considering the effect of the legs only and the calculation result was on the low side. The relationship between the load and the deflection was linear according to the previous calculation methods, which was not in conformity with the actual situation.
For large-span and heavy-duty gantry cranes, the effect of rigid-soft legs to mid-span deflection was not considered in the past. Here the mathematical model was established about universal large-span and heavy-duty gantry cranes. In order to improve the accuracy of calculation, considering the girder bending, leg bending and axial force and the secondary bending moment coupling action, the calculation formula derivation of gantry girder deflection could be carried out based on the variational principle. Then the relationship between the structure stiffness and load was analyzed by the experiment data qualitatively and quantitatively, and the result provided a useful reference for the design and inspection of portal structure.
2 Analysis of girder deflection
The gantry-frame plane was composed of a girder and two supporting legs for a universal gantry crane, as schematically shown in Fig. 1. Due to the long span of the girder beam CD, deformation occurred primarily in the gantry-frame plane with the girder beam deflecting under the loading weight. The deflection was analyzed and calculated on the gantry-frame plane only. The gantry-frame structure could be simplified into three components: girder CD as the main beam ①, the left leg AC as a beam ②, and the right leg BD as a beam ③. The joints of the beam and the two legs were assumed to maintain rectangular throughout deformation, yielding in different profiles of deformation of the two legs. To derive the governing equation of elastic deformation of the gantry-frame, let the span of the beam (CD) be l, the length of the legs (AC and BD) be h. F is a concentrated load applied at the mid-span position K on the girder. Ii (i=1, 2, 3) is the moment of inertia of the girder and two legs. The N2 and N3 are the axial force of the legs, respectively. Assume that the gantry-frame structure had a horizontal displacement uK and a vertical deflection vK at K; M2 and M3 are the bending moments at C and D; uA and uB are the deflection functions of leg ② and ③, respectively. According to the basic equation of elastic structure mechanics, the deflection equation of leg ② is:
 (1)
(1)
or
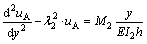 (2)
(2)
where  and E was elastic modulus of the leg material.
and E was elastic modulus of the leg material.
The solution of Eq. (2) could be obtained as
 (3)
(3)

Fig. 1 Calculating gantry-frame structure diagram
where sh was the hyperbolic sine function.
Similarly, for leg (3) we had:
 (4)
(4)
where
The rotation angles θC, θD at the joints C and D could be obtained as
 y=h(5)
y=h(5)
 y=h(6)
y=h(6)
where ch was the hyperbolic cosine function.
Assuming vC as the deflection flexural function of the girder section C-K, we had:
 (7)
(7)
Integration of Eq. (7) led to
 (8)
(8)
To satisfy the compatibility condition at joints C and D, rotation angles θ2 & θ3 of the main girder at the join points should be equal to –θC & θD, respectively. There were
 (9)
(9)
and
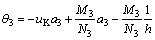 (10)
(10)
where 

At x=0, 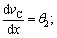 Therefore;
Therefore; 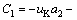
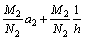 .
.
Integrating Eq. (8) yielded:
 (11)
(11)
At x=0, vC(x)=0; Thus, C2=0 and

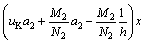 (12)
(12)
Similarly, for segment K-D, we could get vD as the deflection flexural function of K-D:

At x=l, vD(x)=0 and 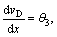 solving the equation, we had:
solving the equation, we had:

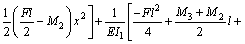

 (13)
(13)
When K is at the mid-point of the girder, i.e. x=l/2,
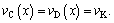 Thus,
Thus,
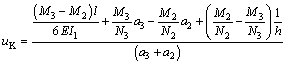 (14)
(14)
 (15)
(15)

 (16)
(16)
The total energy of the gantry-frame ∏ should be equal to the sum of the strain energy U in the beam and legs, and the work done by the external loading H. This gave

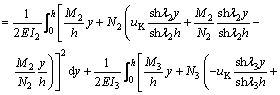
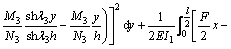

 (17)
(17)
where П is a variational function for which differentiation could be taken to obtain the stationary points for its minima under the condition that the boundary condition Eqs. (14), (15) and (16) needed to be satisfied. Here we introduced a Lagrange multiplier ζ, and changed the conditional variational problem into unconditional variational problem. We got a new functional equation. Let the first order variational equation of the new functional equation be 0. We had:


 (18)
(18)
Rearranging Eq. (18), we had:


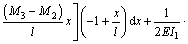



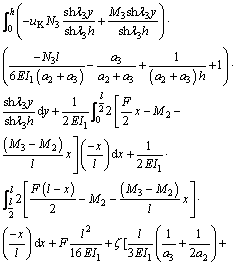
 (19)
(19)
which led to:
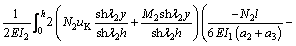

 (20)
(20)


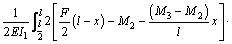

 (21)
(21)

 (22)
(22)
Under small deformation, we had N2=N3=F/2. Solution of the simultaneous Eqs. (20), (21) and (22) gave:
 (23)
(23)
 (24)
(24)
 (25)
(25)
where

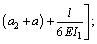


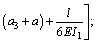
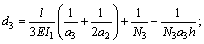

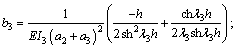
 .
.
Equation (23) was the analytical solution of the vertical deflection of a gantry-frame structure based on the above theoretical assumptions, and Eq. (24) of the bending moment of points C and D in Fig. 1, and Eq. (25) of the horizontal displacement. In addition to the vertical deflection (vK), the horizontal displacement (uK) was also caused by the load. At the right-hand side of Eq. (23), the first term was the deflection of a simply supported beam; the second one was the deflection that was caused by the action of legs bending and the secondary bending moment. It could be seen from Eq. (23) that, the deflection value vK was not only dependent on the mid-span load (F), but also was closely related to the span (l), height of legs (h), inertia moment of girder (I1), inertia moment of legs (I2 and I3). The deflection and the load in Eq. (23) had a nonlinear relationship instead of the linear relationship in the original calculating methods. Eq. (26) was the equation calculating the deflection value for simply supported beam (SSB) and Eq. (27) was the previous equation calculating the deflection value for the gantry-frame structure. The meaning of symbols in the equations was the same as above.
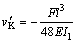 (26)
(26)
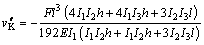 (27)
(27)
Because coordinate axis y is upward, the calculated deflection value is the opposite value of the measured deflection, i.e. negative value. The deflection value vK' calculated according to Eq. (26) and the deflection value vK" calculated according to Eq. (27), were listed in Table 1.
Table 1 Theoretical calculation deflection value of girder mid-span point step by step loading

The deflection value vK and its nonlinear increment (dK) calculated according to Eq. (23) were also listed in Table 1. The relationship between dK and loads was shown in Fig. 2(b). The values of vK in Table 1 showed that the structure stiffness increased along with the increasing of load which caused deformation of gantry- frame structure. Therefore, when the load was applied to the mid-span, the deformation of the gantry-frame structure would resist external load to do work. The structure stiffness increased as a result of the gantry- frame structure deformation (for the load position). It could be known that, under the same load, the deflection was the maximum if it was calculated according to Eq. (26), the deflection was the minimum if it was calculated according to Eq. (27), and, the deflection was the medial if it was calculated according to Eq. (23). Because of considering the effect of axial force of legs and the secondary bending moment, the deflection value calculated according to Eq. (23) was more close to the actual deflection. Next, the experiments were performed to compare the experimental results with the theoretical calculation results.

Fig. 2 Relationship between deflection increment dK and loads:
3 Experiment
Dimensional analysis could be used to design a scaled model [15], to adjust system parameters proportionally. Dimensional analysis determined the relations among the physical variables based on dimensionally homogeneous principles and Buckingham Π theorem [16]. Suppose that in a physical process, there were n physical quantities, i.e. s1, s2, …, sn. If k basic physical quantities were independent, then there were (n–k) dimensionless groups (similarity criteria) [16], denoted by π1, π2, …, πn-k. Hence, a physical equation f(s1, s2, …, sn)=0 describing the physical process could be expressed by a similarity criterion equation g(π1, π2, …, πn-k)=0. For the gantry-frame structure, let l, vK, F, E, σ, ε, EI, W and T be the girder span, deflection, concentrated force, elastic modulus, stress, strain, bending rigidity, bending modulus and time, respectively. The corresponding similarity coefficients of the prototype were denoted by SL, SvK, SF, SE, Sσ, Sε, SEI, SW, ST, respectively. The dimensional matrix is shown in Table 2 with stress[σ], length[L] and time [T] as the basic dimensions.
Table 2 Analysis matrix of dimensions

When solving the dimensional matrix, there were l=SvK, SvK=SF Sl3 SEI–1, SF=SσSl2=Sσ SWSl–1, SE=1, Sσ=1, Sε=1, SEI=SσSl4, SW=SFSl2Sσ–1. Considering the size effect of the model, let Sσ=1, Sl=100, ST=1. Based on the similarity theory, the rest of the similarity coefficients were obtained as follows: SvK=100, SF=146, SE=1, Sε=1, SEI=1.4648×106, SW=14650. In accordance to the calculated similarity coefficients, a test specimen was manufactured using the same material. The specimen’s span, leg height, inertia moment of girder, bending modulus and inertia moment of collateral legs were as follows: l=350 mm, h=220 mm, I1=43691 mm4, W1= 2730.69 mm3, I2=24533 mm4 and I3=8693 mm4.
The experiment was run in a microcomputer- controlled hydraulic universal testing machine, with model number WEW-600B. The specimen was placed on the machine, loaded at the mid-span of the girders, as shown in Fig. 3.
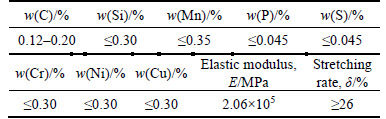
It was a gantry-frame structure made up from steel Q235. Mass fraction of Q235 material chemical Composition and mechanical properties were shown in Table 3. The girder bottom surfaces and the leg sides were polished to eliminate the influence of knife tool traces. The model was placed on the test machine, loaded at the mid-span of the girders. Simultaneously, the horizontal displacement uK were measured by a grating ruler and the precision of the one was 1 μm. The laboratory temperature was 25 °C. The loading rate was 0.01 kN/s, and the discharge rate was 0.03 kN/s.
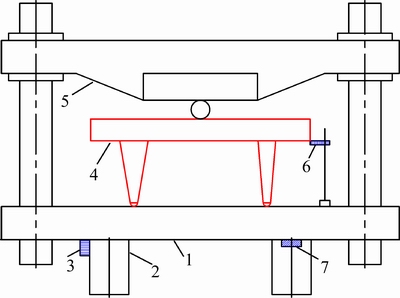
Fig. 3 Gantry-frame structure experiment diagram (1—Stage; 2—Oil cylinders; 3—Displacement sensor; 4—Test specimen; 5—Beam; 6—Raster rule; 7—Pressure sensor)
Table 3 Mass fraction of Q235 material chemical composition and mechanical properties
The experiments were conducted under four different working conditions:
Condition 1:The simple supported beam,of which the span and the moment of inertia were same to these of the gantry-frame structure loaded in the experiment.The result was shown in Fig.4(a).
Condition 2:It was statically determinate working condition, in which the loading was performed with no constraint to the feet of gantry-frame structure.The experimental result was shown in Fig.4(b).
Condition 3:It was statically indeterminate working condition which was realized by simulating that the feet of gantry-frame structure had no slipping through setting constraint to the feet of gantry-frame structure. The result was shown in Fig.4(c).
Condition 4:In the experiment, there was a space between the feet and the constraint points of the gantry-frame, and the space was 0.28 mm. The space between the crane traveling wheels with the flanges and the cross section of rail was simulated based on the value of 0.28 mm. The result was shown in Fig.4(d).
In order to reduce errors, the deflection should be measured under the steady state of structure. Therefore, loading and unloading under above four working conditions should be performed many times. Figure 4(e) shows the three-dimensional diagram of cyclic loading for condition 4.
4 Analysis and discussions
4.1 Comparison between theoretical calculation deflections and measured deflections
In Figs. 4(a)–(d), the intersected area of loading curve and unloading curve meant the structural dissipation energy. With the increasing of loading cycles, the loading curve moved to the right, as shown in Figs. 4(b)–(d), and the structural dissipation energy tended to be stable. In condition 3, the system did not do work externally or did work little. In conditions 2 and 4, the system did work externally, and the work of condition 2 was larger than that of condition 4 because the feet had 0.62 mm slippage in condition 2 and the feet was restricted when the slippage reached 0.28 mm in condition 4. When the external work done by the gantry- frame structure was concerned, the work for condition 2 was the maximum, the work for condition 4 took second place and the work for condition 3 was the minimum. The experimental deflection under different conditions and loads was listed in Table 4. The experimental data showed that the deflection in condition 3 was the smallest, the deflections in conditions 4 and 2 increased one after another.
When the loads were 2, 3, 4 and 5 kN, respectively, the deflections calculated according to Eq. (26), Eq. (27) and Eq. (23), and the measured deflection in test were shown in Fig. 5. As can be seen in Fig. 5, the deflection (–vK') calculated according to Eq. (26) is larger than the measured deflection in experiment; the deflection (–vK") calculated according to Eq. (27) is smaller than that the measured deflection in experiment. The slope of the deflection line calculated according to Eq. (26) is small, and the slope of the deflection line calculated according to Eq. (27) is large. With the increase of load, the difference between the deflections calculated according to Eq. (26) and Eq. (27) and the measured deflection gradually becomes large, and the difference between the deflection (–vK) calculated according to Eq. (23) and the measured deflection gradually becomes small.
The calculation accuracy of Eq. (23) improved by a large extent compared to that of pre-existing deflection equations. For examples, when the load was 5 kN, the measured deflection of the gantry-frame structure was 0.409 mm, the deflections calculated according to Eq. (26), Eq. (27) and Eq. (23) were 0.4962, 0.3398 and 0.3877 mm, respectively. The relative error of the calculated value equals (the calculated value–the measured value)/the measured value, and then absolute value was used. Thus, the relative error of the calculated deflection value according to Eq. (26) is 21.32%, and that according to Eq. (27) is 16.92%, and that according to Eq. (23) is 5.21%. Because Eq. (23) did not consider the influence of girder shearing strength and axial compression of legs, the deflection was on the low side. The influence of girder shearing strength and axial compression of legs on the calculated value was 1.2%–2.4% usually [17].
Because of the various forms of gantry crane, the stress values at the girder mid-span point under the rated load were uncertain, and its stress value was usually 60–140 MPa. The stress value at the girder mid-span point meant the surface stress value of the bottom board at the girder mid-span point. Under different loads, the stress value at the mid-span point of bridge girder; σb, and the stress value at the mid-span point of gantry girder; σg, were listed in Table 5. In order to simulate the deflection under the rated load, the stresses of the mid-span point were compared when the stress of the mid-span point was 140 MPa. The values of the stress in Table 5 showed that σg was about 140 MPa when the load was 5 kN. Therefore, when the load was 5 kN, the comparison was carried out.

Fig. 4 Relationship between load and deflection:
Table 4 Experimental deflection of mid-span point for hierarchical load

Table 5 Stress values at girder mid-span point under different loads
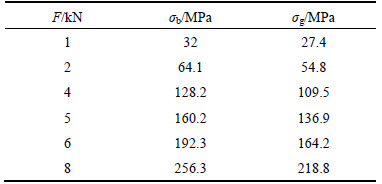

Fig. 5 Theoretical calculation deflections and measured deflection under different loads diagram
4.2 Discussions
The measured deflection line was not a straight line in Fig. 5. The structure with “strong beam and weak column” was established to suit the working characteristics of gantry crane. If the span was large, for the legs on the two sides, one leg would be designed to be rigid leg and the other one would be designed to be flexible usually. As the inertia moments were different for the legs on both sides, the actual deformation would be out of sync inevitably and the storage of elastic strain energies would be different, too. Due to the limit of structure, the distribution of stress in the structure was not uniform. At the beginning of loading, the leg deformation was small, and the bending strain energy mainly was stored in the girder. With the increase of load, the stress was distributed to the legs gradually, and tended to be more uniform. In initial loading phase, the structure deformation was not uniform, and the deflection curve fluctuated. The coordination of subsystems improved with the increasing load, which made the structure stable. When the stress of girder mid-span point reached 140 MPa in the experiments, the elastic deformation of the structure tended to stable, until plastic deformation occurred.
The yielding indication did not appear at top of the deflection curve in Fig. 4, which showed that the structure was in elastic range. If the potential energy was deemed as the generalized force and the increase rate of elastic deformation energy was deemed as the generalized flow, the entropy production tended small [18, 19]. The increasing process of structure deflection could be deemed as the reducing process of entropy production, namely it was also the increasing process of structure deformation energy. The loading process and the stiffness change of structure in the experiment were shown in Fig. 6, where, curves 11, 21, 31 and 41 are the loading curves of conditions 1, 2, 3 and 4, respectively, and curves 12, 22, 32 and 42 are the stiffness change curves of conditions 1, 2, 3 and 4 when loading. At the beginning of loading, the stiffness of gantry-frame structure was large, and then it decreased, increased, decreased, and increased successively, and stabilized after the load reached 4.5 kN.
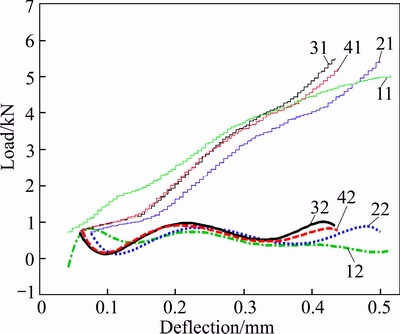
Fig. 6 Load–deflection curve and stiffness variation
After the gantry-frame structure was loaded at the mid-span point, it not only produced vertical deflection vK but also generated the horizontal displacement uK. The relationship between the deflection and the horizontal displacement was shown in Fig. 7 and it was nonlinear. In Fig. 7, curves 23, 33 and 43 denoted the relationship between the deflection and the horizontal displacement of girder for conditions 2, 3 and 4, respectively. The horizontal displacement uK of condition 2 was small, and the deflection was larger because the gantry-frame structure feet were not constrained in this condition and the structure slipped and the energy were dissipated. Whereas, the gantry-frame structure feets were constrained in conditions 3 and 4, the structure had a horizontal displacement, the energy was stored and the distribution of elastic strain energy tended to be uniform. Therefore, the horizontal displacement uK was larger, and the deflection was smaller. The relationship among the deflection, the horizontal displacement and the load in conditions 3 and 4 was shown in Fig. 8, and it was nonlinear too.

Fig. 7 Relationship between horizontal displacement uK and girder deflection

Fig. 8 Relationship among deflection, horizontal displacement and load:(1–Three-dimensional curve of deflection, horizontal displacement and load; 2, 3, 4–Projection of curve 1 onto deflection-horizontal displacement plane, deflection-load plane and horizontal displacement-load plane)
The structure stiffness of condition 3 was larger at the beginning of loading. At this time, the stiffness was the embodiment of local contact stiffness. In the experiment, the cylinder was in contact with the elastic half-space and the contact stiffness c should be:
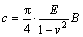 (28)
(28)
where c is contact stiffness; v is Poisson ratio, and it is 0.3 for metal material; B is contact width.
Therefore, the initial stiffness was larger. With the continuing of loading, the main girder bended and the structural stiffness decreased. At that time, the inertial moment of the girder dominated the stiffness change. The amplitude of deflection increasing was large in this phase, whereas the horizontal displacement uK increased slowly. With the continuing of loading, when the load was between 1.5 kN and 3.5 kN, the increasing of horizontal displacement and deflection tended to be linear, which increased synchronously. The increment of horizontal displacement became larger at this phase. The difference between the bending moment of point C, M2, and the bending moment of point D, M3, in Fig. 1 diminished due to the structure displacement at x axial direction. e.g., when the load was 5 kN, M2=62994 N·mm, M3=64597 N·mm. This process of structure displacement was the redistribution process of structure elastic strain energy. The redistribution was proportional to the reciprocal of subsystem stiffness in the series system. The redistribution was proportional to the subsystem stiffness in the parallel system, minimizing the total potential energy of the system. After the loading reached 4.5 kN, the cooperativity of each subsystem increased, the structure and the change of structure stiffness tended to be stable until the plastic deformation appeared. At the moment, the whole structure stiffness was presented.
The fluctuation of curve 43 in condition 4 was slightly larger than that of curve 33 in condition 3 in Fig. 7. The structure stiffness was large at the beginning of loading and it was the local contact stiffness still. For condition 4, the loading continued and when the load was 1.3–1.8 kN, the girder bended and the structural stiffness decreased. At the moment, the gantry-frame structure feet slipped until the 0.28 mm space disappeared and the feet were constrained. The added deflection was larger than that of condition 3 in this phase, but, comparing to condition 3, the horizontal displacement increased slowly. The load increased continually; the deflection and horizontal displacement increased steadily. After the load was added to 4.5 kN, curve 43 was similar to curve 33 in Fig. 7. That means that the structure entered into a stable stage and the structure stiffness became stable until plastic deformation occurred.
Condition 4 coincides with the actual situation most. The distance between the flanges of crane travelling wheel was larger by dozens of millimeters than that width of the rail head, as shown in Fig. 9.
The dead weight of gantry-frame structure caused static friction force to be created between the travelling wheel and the rail; therefore, the initial state was a statically indeterminate condition. When the load increased to a certain value, the feet began to slide and the system did work externally. When the space between the flanges and the flanks of the rail disappeared due to slippage, the feet of gantry-frame structure were restricted by the flanks of the rail again, and the structure turned back into a statically indeterminate condition once again. Whether the gantry crane was in statically indeterminate working condition when it run, depended on whether the static friction force was greater than the horizontal component force. Namely:
 (29)
(29)
where n is ratio of dead weight of gantry crane to rated lifting weight; μ is static friction factor between the wheel/and rail.
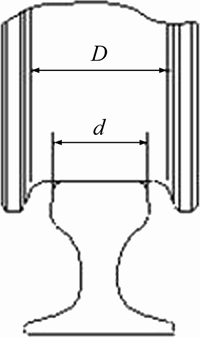
Fig. 9 Contact diagram of crane travelling wheel and rail head (D—Width between flanges of crane travelling wheel; d—Width of rail head)
Parameter n depended on the structure of gantry crane, lifting height, span and working level, and so on, and n was 2–7 usually; μ depended on the wheel/rail material, the working environment and so on, e.g. whether the rail had oil pollution, whether the working condition was outdoor working rainy condition. Therefore, its value range was wider relatively, 0.1–0.33 usually. On both sides of gantry crane, if the legs were different, the positive pressure would be different and the static friction force should be different also. With loading, the feet on one side would first slide definitely, and after the flange on the side contacted with the rail, the feet on the other side began to slide, until the feet on both sides were restricted and the working condition became statically indeterminate condition. Of course, maybe it was alternative slippage and after one flank contradicted the rail, the other one flank contradicted the rail through slippage. At the same time, the deflection–load curve was also affected by the initial position of gantry crane, so the deflection would be bound to have uncertain fluctuations.
The practical work condition of gantry crane was more complex than condition 4. The key was to ascertain the sliding process, the slippage and the friction force of the gantry-frame structure feet before they were restricted by measuring. To sum up, the calculation could be performed by two steps: step 1, calculating the deflection before the gantry-structure feet were restricted by addition of the deflection calculated according to Eq. (23) and the deflection caused by feet sliding resulting in decreasing of potential energy; step 2, calculating the deflection after the gantry-structure feet were restricted according to Eq.(23).
The deflection of a gantry crane was measured in a forest farm. The measured deflections of each point within girder span step by step loading [20] were shown in Fig. 10(a) and the relationship between the load and the measured deflection at the girder mid-span point was shown in Fig. 10(b). Actually, when the crane lifted the rated load, the stress of girder was generally within 110 MPa. The actual results also showed that the stiffness of gantry-frame structure was large at beginning, and decreased, increased, then decreased successively. That was consistent with the change rule of experimental data before the inflection point. The experimental results reflect the deformation regular of the gantry-frame structure well, and verify the correctness of theoretical analysis. For this gantry crane, the deflection value calculated by the pre-existing equation was 15.67 mm [20], the measured value was 13.90 mm [20], and the calculation error was 12.73%. If Eq. (23) was applied, the calculation error would be reduced.
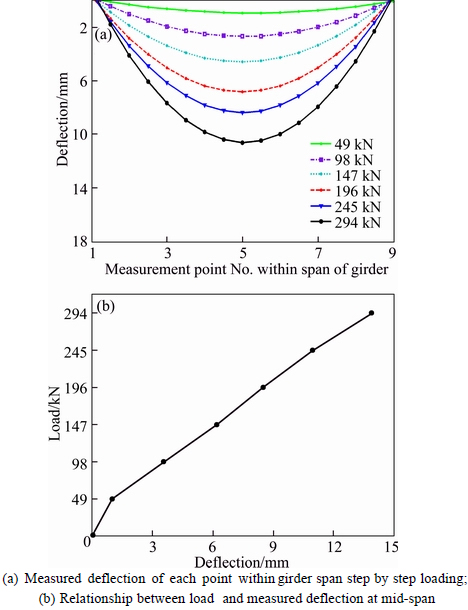
Fig. 10 Relationship between load and measured deflection for a gantry crane:
5 Conclusions
1) The calculation precision for the nonlinear analytical solution of the girder deflection, i.e. Eq. (23), improves by about 12% comparing to pre-existing equations.
2) The deformation of the gantry-frame structure resists the external load to do work when loading is performed in mid-span. Namely, the gantry-frame structure deformation results in increasing of structure stiffness.
3) In conclusion, the relationship between load and deflection at mid-span point of gantry-frame girder is nonlinear. Load–deflection curve will present a turning point when the load reaches a certain value for the gantry-frame structure. Results show that the nonlinear analytical solution for the min-span deflection has great significance to analyze the relationship between various structural parameters and deflection, which provides theoretical basis and reference for the design and test of gantry-frame structure. Next, the change of the shearing force of girder shall be taken into account.
Conflict of Interests
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
References
[1] Decree No. 4, 2013 of the president of the people's republic of China. Law on safety of special equipment of the people’s republic of China [S]. Beijing: China Legal Publishing House, 2013. (in Chinese)
[2] ABBAS H H, SAUSE R, DRIVER R G. Behavior of corrugated web I-girders under in-plane loads [J]. Journal of Engineering Mechanics, 2006, 132(8): 806–814.
[3] ABBAS H H, SAUSE R, DRIVER R G. Analysis of flange transverse bending of corrugated web I-girders under in-plane loads [J]. Journal of Structural Engineering, 2007, 133(3): 347–355.
[4] SAUSE R, ABBAS H H, DRIVER R G, ANAMI K, FISHER J W. Fatigue life of girders with trapezoidal corrugated webs [J]. Journal of Structural Engineering, ASCE, 2006, 132(7): 1070–1078.
[5] CHENG Wen-ming, WANG Jin-nuo, DENG Bin. The coupling relation between structural parameters and dynamic indexes of gantry crane [J]. Journal of Southwest Jiaotong University, 2002, 37(6): 651–654. (in Chinese)
[6] YAO Wen-juan, YE Zhi-ming. Analytical solution of bending- compression column using different tension-compression modulus [J]. Applied Mathematics and Mechanics, 2004, 25(9): 901–909.
[7] HOLST C, BURGHOF M, KUHLMANN H. Modeling the beam deflection of a gantry crane under load [J]. Journal of Surveying Engineering, ASCE, 2014, 140: 52–59.
[8] HOLST C, ELING C, KUHLMANN H. Automatic optimization of height network configurations for detection of surface deformations [J]. J Appl Geod, 2013, 7(2): 103–113.
[9] L C, LIU W, ZHAN Y, ZHAO H. Experimental estimating deflection of a simple beam bridge model using grating eddy current sensors [J]. Sensors, 2012, 12(8): 9987–10000.
C, LIU W, ZHAN Y, ZHAO H. Experimental estimating deflection of a simple beam bridge model using grating eddy current sensors [J]. Sensors, 2012, 12(8): 9987–10000.
[10] PINCA C B, TIRIAN G O, JOSAN A, CHETE G. Quantitative and qualitative study on the state of stresses and strains of the strength structure of a crane bridge [J]. WSEAS Trans Appl Theor Mech, 2010, 5(4): 231–241.
[11] LEE H M, PARK H S. Gage-free stress estimation of a beamlike structure based on terrestrial laser scanning [J]. Comput Aided Civ Infr Eng, 2011, 26(8): 647–658.
[12] CASTILLO E,  R, CASTILLO C. Sensitivity analysis in optimization and reliability problems [J]. Reliab Eng Syst Saf, 2008, 93(12): 1788–1800.
R, CASTILLO C. Sensitivity analysis in optimization and reliability problems [J]. Reliab Eng Syst Saf, 2008, 93(12): 1788–1800.
[13] RI S, MURAMATSU T, SAKA M. Accuracy of the sampling moire method and its application to deflection measurements of large-scale structures [J]. Exp Mech, 2012, 52(4): 331–340.
[14] YAN Hong, ZHANG Ji-xiong, LI Lin-yue. Stability assessment of rock surrounding an I-beam supported retreating roadway [J]. Journal of Central South University, 2015, 22: 3598–3607.
[15] TAN Qing-ming. Dimensional analysis [M]. Hefei: China Science and Technology University Press, 2005. (in Chinese)
[16] BHASKAX X, NIGAM A. Qualitative physics using dimensional analysis [J]. Artif Intell, 1990, 45(1, 2): 73–111.
[17] WANG Jin-nuo, YU Lan-feng. Cranes metal structure [M]. Beijing: China Railway Press, 2001. (in Chinese)
[18] GLANSDORFF P, PRIGOGINE I, HILL R N. Thermodynamics theory of structure, stability and fluctuations [J]. New York: Interscience Pub, 1971: 30–72.
[19] NICOLIS G. Self-organization in nonequilibrium system, from dissipative structure to order through fluctuations [M]. New York: Interscience Pub, 1977: 40–60.
[20] ZOU Yun-sheng, WU Xue-wen, LIU Jin-hao. Methods on measuring the static stiffness of gantry crane girder [J]. Forest Lumbering Science, 1992(1): 38–42. (in Chinese)
(Edited by YANG Hua)
Cite this article as: ZHANG Da-peng, CHENG Wen-ming, WANG Bin. Variational analysis of mid-span deflection of gantry cranes [J]. Journal of Central South University, 2017, 24(11): 2705–2716. DOI: https://doi.org/10.1007/s11771- 017-3683-6.
Foundation item: Project(51175442) supported by the National Natural Science Foundation of China; Project(QD2012A09) supported by Teachers’ College Research Project, China; Project(14ZA0263) supported by Research Project of Sichuan Provincial Department of Education, China
Received date: 2015-12-20; Accepted date: 2017-10-20
Corresponding author: ZHANG Da-peng, Associate Professor, PhD; Tel: +86–18048907001; E-mail: zdp51368@163.com

