Article ID: 1003-6326(2005)02-0344-05
Model of magnetostrictive actuator
LI Lin(李 琳), ZHANG Yuan-yuan(张媛媛)
(School of Jet Propulsion, Beijing University of Aeronautics and Astronautics, Beijing 100083, China)
Abstract: The hysteresis of the magnetostrictive actuator was studied. A mathematical model of the hysteresis loop was obtained on the basis of experiment. This model depends on the frequency and the amplitude of the alternating current inputted to the magnetostrictive actuator. Based on the model, the effect of hysteresis on dynamic output of the magnetostrictive actuator was investigated. Then how to consider hysteresis and establish a dynamic model of a magnetostrictive actuator system is discussed when a practical system was designed and applied.
Key words: magnetostrictive actuator; hysteresis loop; dynamic feature CLC number: V214.3+
Document code: A
1 INTRODUCTION
The magnetostrictive actuator is a kind of actuator which is powered by the magnetostrictive material pod. Under the external magnetic field the phenomena of elongating or shortening with the shape will occur. In contrast with other smart materials the magnetostrictive pod has quite a lot of merits such as greater deformation, higher power, bigger energy density and faster velocity of response. All these features make the magnetostrictive actuator be the basic intelligent component of the high accuracy linear motor and the Stewart Platform which are broadly used in active vibration control. In the former paper[1] the authors have gained the hysteresis loop and illustrated the dynamic feature. In this paper, according to this important feature, the numerical fitting coefficients of our mathematical model are quantitatively analyzed. Though many researchers go deep into the investigation of this problem, for example, ZHU and GU[2] did some researches in the actuators feature of the vibration amplitude and the frequency by means of experiments; and TAN and Baras[3] proposed a hysteresis model by the feature of Preisach operator. Here the least square method is used to fit the experimental curve and get a very approximative fitting result.
In this paper the authors pay attention to do research on the question of the pre-pressed magnetostrictive actuators vibration response of a real application. The material used is a certain magnetostrictive Tb0.3Dy0.7Fe1.98, which is usually called Terfenol-D[4]. A set of experiments are designed and the results can well illustrate the system model we have established. According to the experiment, a dynamic model of the system with a magnetostrictive actuator has been established. Using this model, the vibration response of the single current exciter can be gained. This achievement provides a basement for further solution and control of the vibration of the smart structure which is composed of such kind of actuators[5].
2 DYNAMIC FEATURE OF PRE-PRESSED MAGNETOSTRICTIVE ACTUATOR
2.1 Structure and working principle
The structure of the pre-pressed magnetostrictive actuator is shown in Fig.1[6-8]. The spring is always in the pressed state in order to ensure the contact situation between the output pod and the magnetostrictive pod. The permanent magnet provides a bias magnet field in order to make the material work in a linear area, and the electro-magnetic loop is used to provide the magnetic field to make the magnetostrictive pod work. The loop will be imported with alternating current and provide a changing magnetic field to make the pod move. Since the vibration amplitude of the pod is in the range of micron, the actuator actualizes the micro-amplitude vibration.
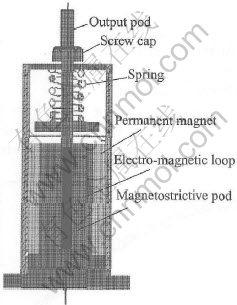
Fig.1 Structure of actuator
2.2 Linear modeling of hysteresis loop
Former results[1] show that the nonlinear terms in the fitting semi-analytical expression have little effect on the output results, so after being proved by the experiments, we predigest the fitting model into a linear one, which can be written as[9]
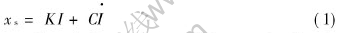
where K and C are the coefficient to be fitted, and I and [AKI·] are the current and its differential inputted to the actuator. The transformation of the hysteresis loop has no relation to the amplitude according to the fitting coefficient as shown in Fig.2 but it is related to the frequency. From Eqn.(1) we can see that the slope of the hysteresis loop is determined mainly by K and the outline mainly by C. For any loop a set of K and C can be obtained. The change of K and C with frequency f is drawn in Figs.3 and 4. By using the least square method we have obtained the fitting formula of the coefficient K and C as
K=0.000008f3-0.000002f2-
0.136812f+4.43221(2)
Cf=0.000006f3-0.000988f2+
0.041681f-0.005216(3)
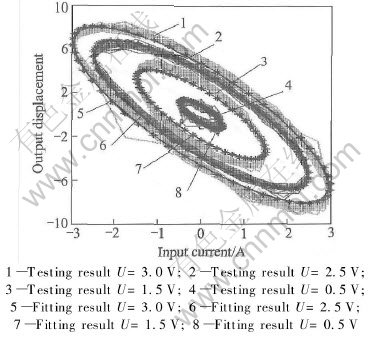
Fig.2 Experimental and fitting curves at 60Hz
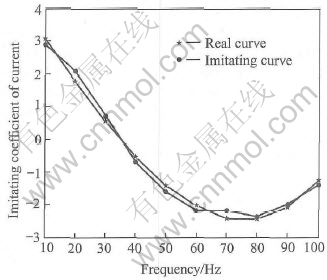
Fig.3 Fit result of K
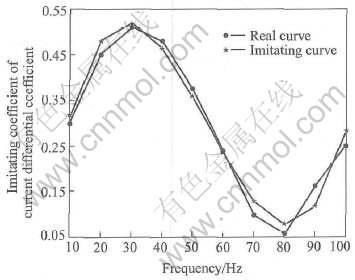
Fig.4 Fit result of C
In Fig.5 we give out the comparisons between the fitted and the experimental curves with different f.
2.3 Frequency-response feature of actuator
Using the former complex fitting results of xs, if we give an input current I=Asin(2πft) to the actuator, then we can get xs which has the frequency components of f, 2f, 4f because of the nonlinear terms. Taking the input current of U=2.5V, f=60Hz as an example by comparing the experimental and fitted results, we get different frequency curves of xs, which are shown in Fig.5. The above figures show that the results of the theoretical fit are basically matched with the experimental results in the question of the amplitudes, the cycles and the transformation trends. The fitted curves of the no-loading system show that the major component of the frequency is just the excitation frequency, but for the existence of the high exponential term in the fitted polynomial, there are high frequency components in the curve. The model can reflect the system dynamic feature factually and it is pivotal for vibration control. However, as we see, the amplitudes of the components are far less than the major part, so in some cases the nonlinear terms can be ignored to predigest the model. If a linear fitting model is given as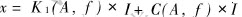 
, the following frequency-response results in Fig.6 can be obtained. Figs.6(a) and (b) show the theory and the experiment results and Fig.6(c) shows the result of the predigested linear model. Fig.6(d) shows the comparison of the input current and output displacement of the linear and nonlinear models.
3 ESTABLISHED MODEL
3.1 Modeling of actuator
Considering the working principle of a magnetostrictive actuator, we have tried to build a dynamic model of it, by the gained magnetostrictive pods hysteresis loop[10, 11]. As has been analyzed in part 2, the relationship between the spring and the pod is shunt-wound since they have the same connection point. When the control current is input, the pod will generate elongating and shortening. Under such circumstance, the pod tends to be a super-elastic body, whose deformation can be described as xs. Then if no current is input, the pod is comparatively rigid, whose stiffness can be written as k=EA/l, where E, A, l are the elastic modulus, the sectional area and the length of the pod, respectively. In view of the above course, we can predigest the actuator model as shown in Fig.7, where Dc is a mark to illustrate the differ ent working situations, it is a gangway when current is input, otherwise it is broken[12].
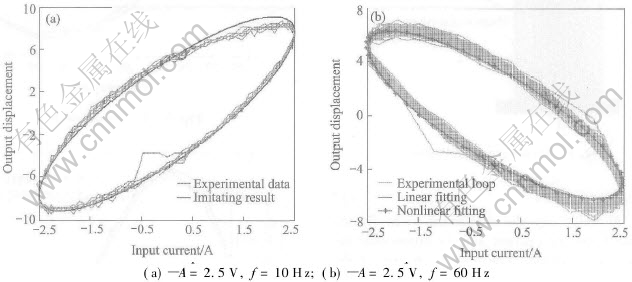
Fig.5 Comparison between fitted and experimental curves
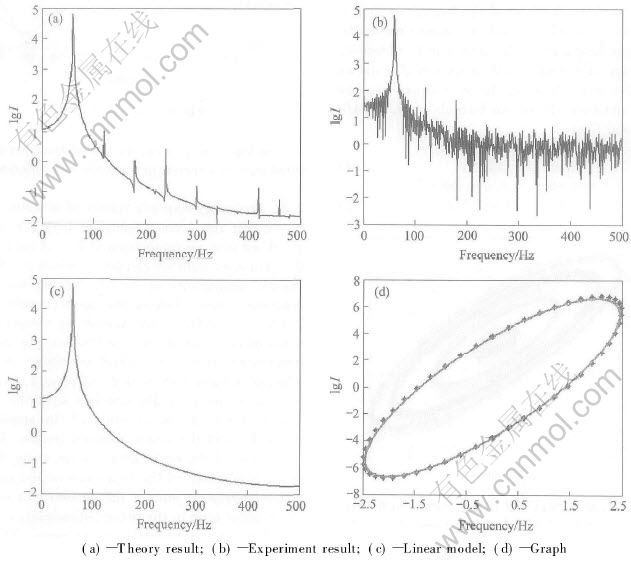
Fig.6 Frequencies-response curves of A=2.5V, f=60Hz
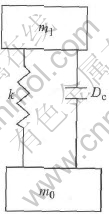
Fig.7 Actuators dynamic model
3.2 Modeling of system
To testify the rationality of the actuators model, a two-freedom-degree experimental system was designed[13]. A thin aluminum board was made and used to bolster the actuator with an extra mass on the top of it. The board is connected with the ground through four elastic braces. In view of the inner structure of the actuator we prestige the dynamic model as shown in Fig.8. The theory and experimental response values can be achieved as shown in Fig.9. In the established system,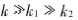
. When we input a control current I=Asin(2πft) to the actuator, dynamic equation of the system should be written as
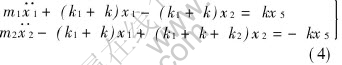
where xs is the output of the magnetostrictive pod when a control current is given, which has been described as in the fitting mathematical model, x1 and x2 are the displacement of the two mass in that two-freedom degree system respectively.
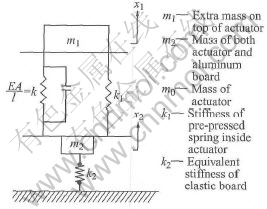
Fig.8 System dynamic model
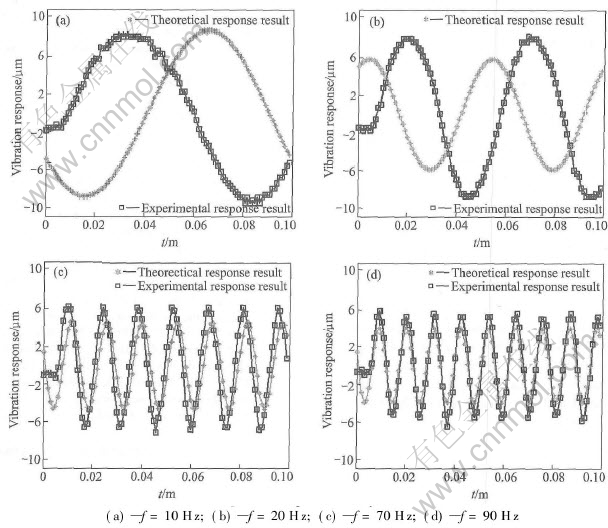
Fig.9 Response of system
According to the parameters of the system, vibration response is solved.
The experimental results indicate that the vibration response value is becoming smaller and smaller with the increase of the exciting frequency. From the calculation results we can conclude that the theoretical calculation is correct and the dynamic model of the system is acceptable, the amplitude is decreasing with the frequency and the absolute value of the extra mass displacement can match the experimental results in the range of error. At the same time the frequency of the theoretical response is the same as that of the experiment result. As the initial condition has not been considered, the phase factor should be out of investigation. We can draw a conclusion that the above model can describe the system well and may be used in further research[14].
4 CONCLUSIONS
Using the method mentioned, the problem of dynamic responses of an actuator, excited by single current input, which has an obvious characteristic of hysteresis, is solved. Through the established mathematical model in this paper, the theoretical response value of the two-degree-freedom dynamic model is gained. The theoretical and experimental results have been shown in the above figures and we can see through the comparison the that theoretical results reflect the experimental value perfectly from the point of view of the amplitudes, the cycles or the frequencies and the changing trend with the frequency. Only under the single current input exciter, the linear model is substantial to solve the vibration responses and fit well with the experimental data. The significant aim of this paper is to make the actuator apply to a practical system and build a theorectical analysis basement for further vibration control[16].
REFERENCES
[1]ZHANG Yuan-yuan, LI Lin. Research of the characteristic of magnetostriictive actuator [A]. Proceedings of the Smart Material [C]. Australia: Society of Optical Engineering, 2004. 16-20.
[2]ZHU Jin-cai, GU Zhong-quan. Nanjing University of Aeronautics & Astronautics of China—Modeling of the magnetostrictive material actuator and analysis of its dynamic feature [J]. Journal of Nanjing University of Aeronautics & Astronautics, 1998, 30(4): 34-37.
[3]TAN Xiao-bo, Baras J S. Modeling and control of a magnetostrictive actuator [A]. Proceeding of the 41st IEEE Conference on Decision and Control [C]. University of Maryland, 2002, 26: 101-112.
[4]TAO Bao-qi. Smart Material Structure [M]. Beijing: National Defence Industry Press, 1997. 110.
[5]DING Wen-xiao. Main reasearch field of vibration control [J]. Dynamic Development, 1994, 24(2): 173-180.
[6]Geng Z J, Haynes L S. Six degree-of freedom active vibration control using the stewart platform [J]. IEEET-CST, 1994, 2(1): 45-53.
[7]WANG Bao-feng. Actie Vibration Control of the Magnetostrictive Material Platform [D]. Beijing: Beijing University of Aeronautics & Astronautics, 2003.
[8]LI Chao. Vibration Control of the Two-freedom-degree System using Magnetostrictive Actuator [D]. Beijing: Beijing University of Aeronautics & Astronautics, 2002.
[9]WANG Ling. Modeling and imitation of the magnetostrictive actuator control system [J]. Journal of Hebei Industrial University, 2002, 31: 1-4.
[10]McInroy J E. Dynamic modeling of flexure jointed hexapods for control purposes [A]. Proceedings of the 1999 IEEE [C]. 2001, 9(1): 5-16.
[11]Chua L O. Modeling and design of flexure jointed Stewart platforms for control purposes [J]. IEEE/ASME Transactions on Mechanics, 2002, 7(1): 95-99.
[12]Chen H J. Approaches to matched basis function repetitive control [J]. Advances in the Astronautical Sciences, 2001, 109: 931-950.
[13]Dong T. Six-axis vibration isolation system using soft actuators and multiple sensors [J]. Journal of Spacecrafts and Rockets, 2002, 39(2): 206-212.
[14]Hiroaki F. Development spatial parallel manipulators with six degree of freedom [J]. JSME International Journal, Series 3: Vibration, Control, Engineering, Engineering for Industry, 1991, 34(3): 382-387.
[15]Kim N I, Lee C W. Precise fault-tolerant pointing using a Stewart platform [J]. IEEE/ASME Transactions on Mechanics, 1999, 4(1): 91-95.
[16]Darby A P, Pellegrino S. Modeling and control of a flexible structure incorporating inertial slip-stick actuators [J]. Journal of Guidance, Control and Dynamics, 1999, 22(1): 36-42.
Foundation item: Project(90205012) supported by the National Natural Science Foundation of China; Project(K1200060301) supported by the National Basic Defence Research Program of China Received date: 2004-11-20; Accepted date: 2005-01-18
Correspondence: LI Lin, Professor, PhD; Tel: +86-10-82317435; E-mail: flytofar@vip.sina.com
(Edited by LONG Huai-zhong)
