J. Cent. South Univ. (2016) 23: 201-208
DOI: 10.1007/s11771-016-3063-7
Characteristics of unsteady flow in porous media while considering threshold pressure gradient with Green’s function
CAO Ren-yi(曹仁义)1, CHEN Ling(陈岭)1, Y. Zee Ma2, LIU Xue-ying(刘雪莹)1, YU Bai-hui(于柏慧)1
1. College of Petroleum Engineering, China University of Petroleum, Beijing 102249, China;
2. Schlumberger Company, #400 Greenwood Village, Colorado 80111, USA
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The flow behavior in porous media with threshold pressure gradient (TPG) is more complex than Darcy flow and the equations of motion, and outer boundary and inner boundary with TPG are also different from Darcy flow for unsteady flow of a producing well in a reservoir. An analytic method to solve this kind of problem is in a need of reestablishment. The classical method of Green’s function and Newman product principle in a new way are used to solve the unsteady state flow problems of various shapes of well and reservoir while considering the TPG. Four Green’s functions of point, line, band and circle while considering the TPG are achieved. Then, two well models of vertical well and horizontal well are built and simultaneously the function to calculate the moving boundary of each well model is provided. The results show that when considering TPG the pressure field is much different, which has a sudden pressure change, with a moving boundary in it. And the moving boundary of each well model increases with time but slows down rapidly, especially when the TGP is large.
Key words: non-Darcy flow; Green’s function; moving boundary; threshold pressure gradient (TPG)
1 Introduction
Vertical and horizontal wells are commonly used to produce fluids to surface from subsurface formations. The fluid flow from subsurface formations to a well is generally believed to follow the Darcy’s law. During natural depletion, the flow is unstable due to the elastic release of fluids and rock. For the radial flow that follows the Darcy’s law in natural depletion, a governing equation with two boundary condition and one initial condition can describe this kind of flow [1].
A number of experiments have recently proved that fluid flow in low permeability porous media{Aifen, 2008 #3;Chengyuan, 2002 #4;Fei, 2006 #1;Quanlin, 2011 #5} or high viscous fluids in porous media is not Darcy flow [2–5], and the fluids will not flow until pressure gradient is higher than the value of threshold pressure gradient (TPG). The existence of TPG will bring a change to the mathematical description of this non-Darcy flow and to its mathematical description [6–7]. In the description of this non-Darcy flow, there is a critical parameter R(t) called the non-Darcy moving boundary, which is a self-formed outer boundary. As the pressure and flowing of fluid out of the moving boundary are not influenced by the well production, the solution of R(t) in the outer boundary condition is the key to solve this non-Darcy problem.
In order to calculate the moving boundary, HAO et al [8] and CHENG et al [9] developed approximation methods, but these methods only deal with a vertical well problem when the moving boundary is a circle. LU [10] attempted to solve a horizontal well problem, while assuming the moving boundary as an ellipse as a precondition. However, the shape of the moving boundary is difficult to depict, especially when the well type is more complex than a vertical well. A method that determines the shape of the moving boundary without assumption before calculating the pressure propagation is needed.
Green’s function is a good way to calculate unsteady state flow in porous media. Once a proper Green’s function is found, the solution to the flow problem in any initial condition and boundary condition could be obtained [11–13]. It can also solve the unsteady flow problems with a source or sink in this condition. The Green’s function that has a source is also called source function. With the Newman product principle, some simple Green’s functions or source functions could be combined to form more complex sources or boundaries of actual reservoirs [14]. However, a proper Green’s function to calculate unsteady state flow with TPG is lacking.
In this work, the source functions of point, line, band and circle while considering the TPG are built, and Green’s function and source function are employed to describe the unsteady state flow problems with TPG. After studies on a number of cases using vertical and horizontal wells, a method is proposed to deal with the complex well types without any assumption on moving boundary shape. This method enables calculation of the moving boundary with TPG, determination of the largest drainage area by the lowest well density and optimizing well space [15], which is a much different and convenient method compared with the physical experiment method [16] and the numerical simulation method [17–18].
2 Green’s function with TPG
2.1 Assumptions
The following assumptions are made:
1) The reservoir is heterogeneous with an infinite boundary.
2) The single fluid in the reservoir is slightly compressible and isothermal.
3) The development method of reservoir is natural depletion above the bubble point.
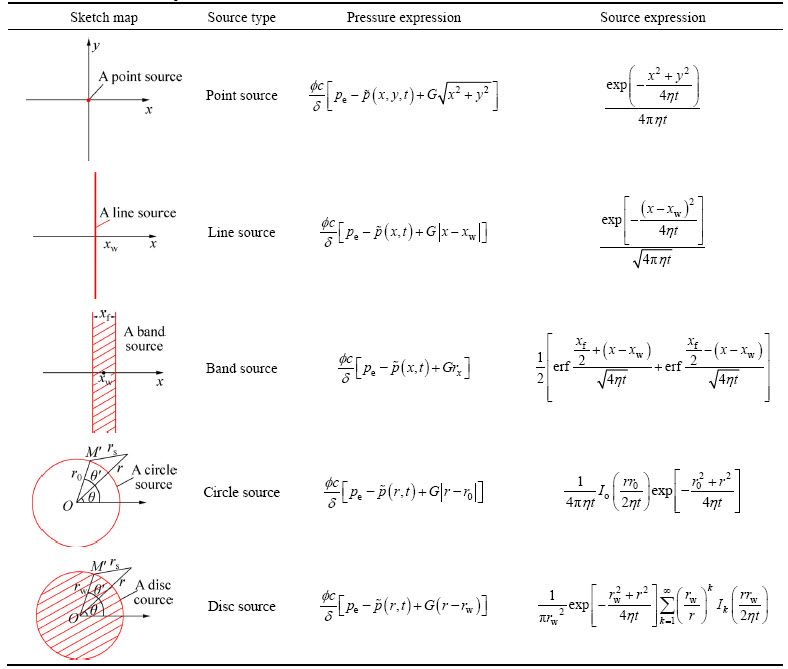
2.2 Point Green’s function with TPG
The governing equation for compressible fluid flow in elastic porous media with TPG in polar coordinates can be expressed as
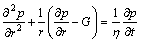 (1)
(1)
The inner and outer boundary conditions are expressed, respectively, as
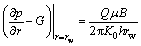 (2)
(2)
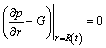 (3)
(3)
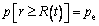 (4)
(4)
And the initial condition is
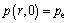 (5)
(5)
Set φ=p–G(r–rw) for variable substitution, and set ξ=r2/ηt for Boltzmann transformation. If this production well is taken as a point, the wellbore radius rw tends to be zero, and the governing equation can be solved as
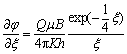 (6)
(6)
When t=0, there is φ=pe and ξ=∞. At time t, there is φ=p–Gr and ξ=r2/(ηt). Integration within the interval [0, t] results in
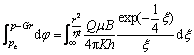 (7)
(7)
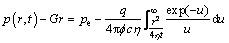 (8)
(8)
If q is an instantaneous quantity as an instantaneous source, Eq. (8) becomes
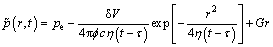 (9)
(9)
where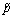 is the pressure caused by an instantaneous stimulation that occurs at time τ, and δV is the volume of the stimulation.
is the pressure caused by an instantaneous stimulation that occurs at time τ, and δV is the volume of the stimulation.
Equation (9) is the solution to the pressure change in the infinity reservoir caused by an instantaneous source when TPG exists. The point source function is described as
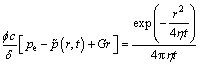 (10)
(10)
The left side of Eq. (10) shows a characteristic of non-Darcy seepage with TPG and its right side has the same form with the point source function following the Darcy’s law [1].
A point source in a two-dimensional infinite plane is shown in Fig. 1, and it is expressed as
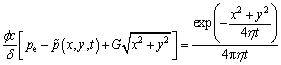 (11)
(11)
Fig. 1 Sketch map of a point source
2.3 Line Green’s function with TPG
By line integration of Eq. (11) in the interval [–∞, +∞], the line source is obtained, as shown in Fig. 2. Its function is described as
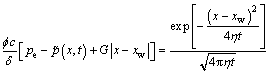 (12)
(12)
Fig. 2 Sketch map of a line source
2.4 Band Green’s function with TPG
By taking xw as the middle point and integration of Eq. (12) in the interval [–xf/2, xf/2], a band source (Fig. 3) is obtained. Its function is expressed as
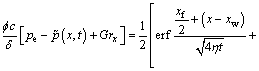
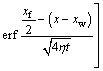 (13)
(13)
In Eq. (13), when 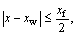 set rx=0, and when
set rx=0, and when 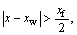 set
set 
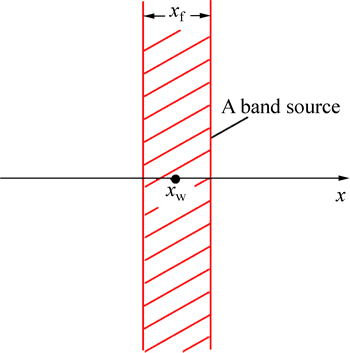
Fig. 3 Sketch map of a band source
2.5 Circle Green’s function with TPG
A circle source is shown in Fig. 4, and its function is described as
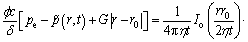
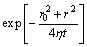 (14)
(14)
where Io is an integration of Bessel function, which is described as
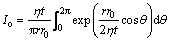 (15)
(15)
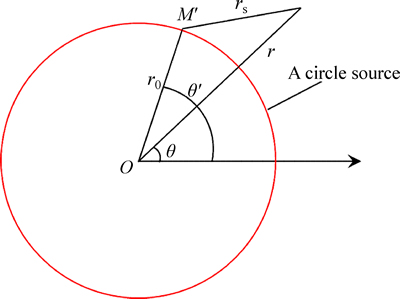
Fig. 4 Sketch map of a circle source
2.6 Disc Green’s function with TPG
By integrating the variable r0 in the circle source, Eq. (14), from 0 to rw, we can obtain the disc source in an infinite plane (Fig. 5), and its function is expressed as
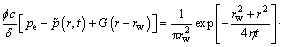
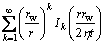 (16)
(16)
In Eq. (16), we focus on the area where r≥rw.
These source functions are summarized in Table 1.
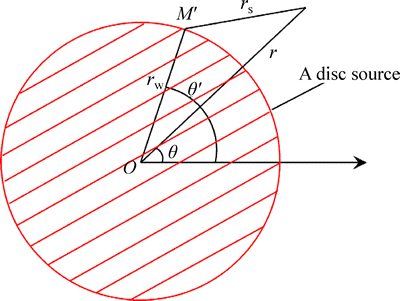
Fig. 5 Sketch map of a disc source
Table 1 Source functions of point, line, band, circle and disc with TPG
3 Case studies and discussion
With the four source functions discussed above, the Newman product principle can be used to establish the formulations that describe the flow of different well configurations, outer boundary types and interference of multiple wells. Using vertical and horizontal wells, how to use source function and Newman product to solve the unsteady flow problem with TPG in porous media is discussed.
3.1 Vertical well model
Since the dynamic change of a vertical producing well in an infinite reservoir can be described by a point source in an infinite plane, source function can be taken as the basis for a vertical well model.
If the well produces at a constant flow rate, the pressure function is
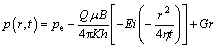 (17)
(17)
where 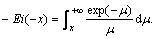
Combining Eq. (17) and boundary condition, Eq. (4), leads to the following formula for moving boundary at the constant flow rate:
 (18)
(18)
When the well produces at shifty flow rates, the pressure function can be obtained by using the pressure composition principle at every dispersed time point:
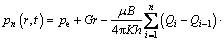
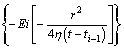 (19)
(19)
If the bottom hole pressure is to be controlled at a constant value of Pwf, the flow rate Qi at any dispersed time point is solved as
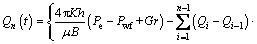
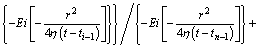
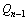 (20)
(20)
Combining Eq. (19) and boundary condition, Eq. (4), the formula for moving boundary at a series of shifty flow rates can be described as
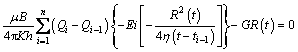 (21)
(21)
By using the functions generated above and the parameters given in Table 2, the typical pressure field is obtained, as shown in Fig. 6.
Table 2 Calculation parameters

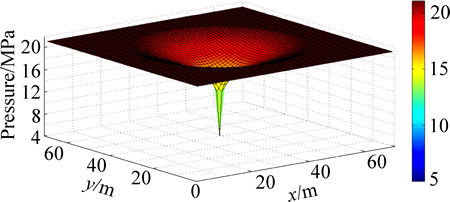
Fig. 6 Typical pressure field of a vertical well
The moving boundary of a vertical well is clearly shown as a sudden pressure change in the shape of a circle (Fig. 6). The pressure sections crossing a vertical well with different TPGs (Fig. 7) show that the lower the TPG is, the farther the pressure propagates at an unique time (200 d for example). Because of the TPG, the pressure drops less at the same location and at the same time.
Figure 8 shows the moving boundary as a function of time for several TPGs. The higher the TPG is, the more slowly the pressure propagates. The higher TPG leads to a smaller moving distance of the moving boundary and a smaller drainage area.
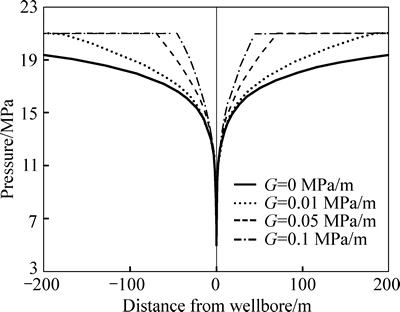
Fig. 7 Pressure section crossing well with different TPGs
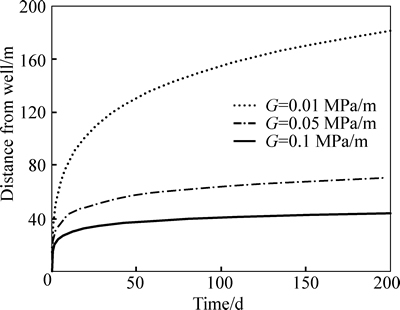
Fig. 8 Moving features of moving boundary with different TPGs
3.2 Horizontal well model
By using the Newman product of a line source function and a band source function, a line source with a length of xf can be obtained. In a two-dimensional plane, it is a horizontal well model.
When the well produces at a constant flow rate, the pressure function is
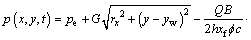
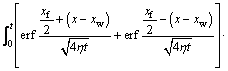
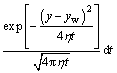 (22)
(22)
When 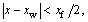 set rx=0, and when
set rx=0, and when 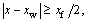 set
set 
Following the same approach as solving the vertical well’s problem, the moving boundary formula for a horizontal well can be obtained as
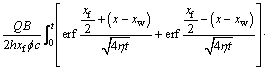
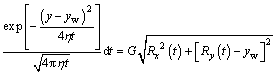 (23)
(23)
Unlike the moving boundary of a vertical well, which has the same value in any direction in the two-dimensional plane, description of the moving boundary of a horizontal well needs a known correlation between Rx and Ry.
If the well produces at a constant bottom hole pressure, the pressure function can be generated in the same way as the vertical well model:
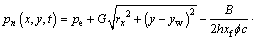
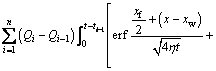
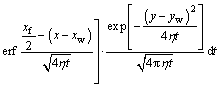 (24)
(24)
The flow rate Qi at any dispersed time point is expressed as
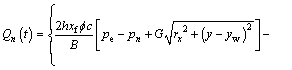
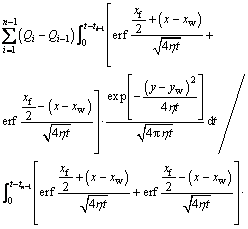
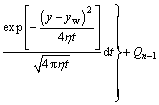 (25)
(25)
And the expression of the moving boundary is
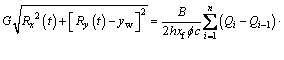
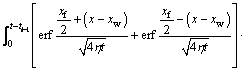
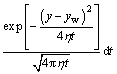 (26)
(26)
Using the functions above and parameters in Table 2, the typical pressure field of a horizontal well is obtained (Fig. 9).
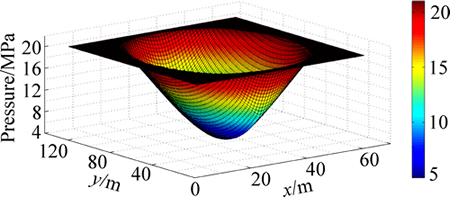
Fig. 9 Typical pressure field of a horizontal well
The moving boundary of a horizontal well is clearly shown as a sudden pressure change in Fig. 9. The pressure sections in the two directions of the well, i.e. perpendicular to well and along well, with different TPGs are shown in Figs. 10 and 11. Similar to the vertical well case, the lower the TPG is, the farther the pressure propagates at a unique time (200 d for example). Because of the TPG, the pressure drops less at the same location and at the same time.
The moving boundaries of a horizontal well as a function of time for different TPGs in two directions are shown in Figs. 12 and 13. The higher the TPG is, the more slowly the pressure propagates. The higher TPG leads to a smaller moving distance of the movingboundary and a smaller drainage area. Moreover, it can also be seen that the pressure perpendicular to the well propagates faster than that along the well.
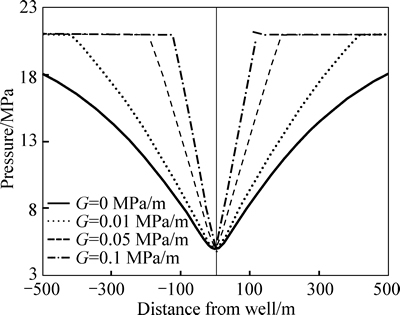
Fig. 10 Pressure section perpendicular to well
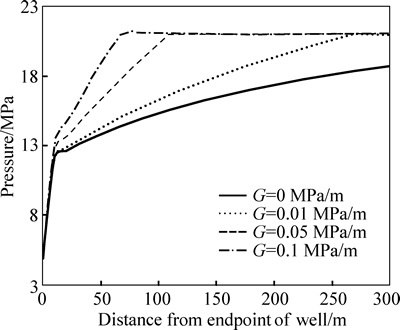
Fig. 11 Pressure section along well
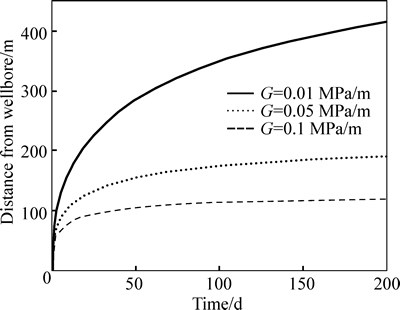
Fig. 12 Moving boundary perpendicular to well as a function of time for 3 different TPGs
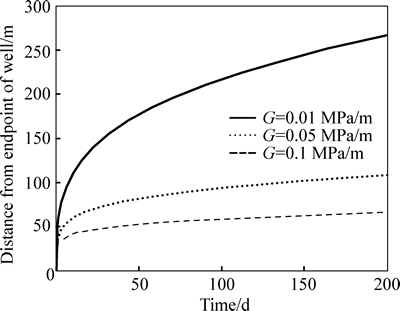
Fig. 13 Moving boundary along well as a function of time for 3 different TPGs
Using the above workflow, a multi-fractured horizontal well model can be achieved by taking every fracture as a finite line source [19], an explosive fracturing well model can take a disc source as its basis [20], and a multi-well interference problem can also be solved.
4 Conclusions
Four basic source functions with TPG are proposed to describe the non-Darcy flow problems with a point source, a line source, a band source, and a circle source and any combination of these four sources. The principle of Newman product is introduced to solve the non-Darcy problems of complex well types and complex boundary conditions, and applied to case studies. From these studies, it is concluded that a moving outer boundary exists for flow in porous media with TPG. Under a constant bottom hole pressure, with increasing TPG, the pressure propagates more slowly and drainage area is smaller. With this method, the guidance for well space optimization and drainage area evaluation while considering TPG during depletion of a field is provided.
Nomenclatures
p
Pressure
pe
Initial pressure of reservoir
pi
Pressure at time-step i
r
Radius
rw
Radius of wellbore
rx
Absolute distance from a band source
r0
Radius of a circle source
η
Pressure diffusivity coefficient
t
Time
ti
Time at beginning of time-step i
Q
Rate of flow
Qi
Rate of flow at time-step i
μ
Viscosity
B
Volume factor
K
Permeability
h
Thickness
G
Threshold pressure gradient
R
Distance of moving boundary from well
f
Porosity
c
Total compressibility
x
x coordinate in a Cartesian coordinate system
y
y coordinate in a Cartesian coordinate system
xw
x location of source in a Cartesian coordinate system
yw
y location of source in a Cartesian coordinate system
xf
Width of a band source
References
[1] CHENG Lin-song. Advanced mechanics of porous media flow [M]. Beijing: Petroleum Industry Press, 2011: 7–20. (in Chinese)
[2] LEI Qun, WEI Xiong, YUAN Jiang-ru, GAO Shu-sheng, WU Yu-shu. Behavior of flow through low-permeability reservoirs [C]// 2008 SPE Europec/EAGE Annual Conference and Exhibition. Rome, Italy, 2008: 113144.
[3] ZENG Bao-quan, CHENG Lin-song, HAO Fei. Experiment and mechanism analysis on threshold pressure gradient with different fluids [C]// 34th Annual SPE International Conference and Exhibition. Tinapa-Calabar, Nigeria, 2010: 140678.
[4] BLASINGAME T A. The characteristic flow behavior of low-permeability reservoir systems [C]// 2008 Unconventional Reservoirs Conference. Keystone, Colorado, USA, 2008: 114168.
[5] THOMAS L K, KATZ D L, TEK M R. Threshold pressure phenomena in porous media [J]. Society of Petroleum Engineers Journal, 1968, 8(2): 174–184.
[6] WU Yu-shu, PRUESS K, WITHERSPOON P A. Flow and displacement of Bingham non-Newtonian fluids in porous media [J]. SPE Reservoir Engineers, 1992, 7(3): 369–376.
[7] LIU X, CIVAN F, EVANS R D. Correlation of the non-darcy flow coefficient [J]. Journal of Canadian Petroleum Technology, 1995, 34(10): 50–54.
[8] HAO Fei, CHENG Lin-song, LI Chun-lan. Unsteady seepage model for low-permeability reservoir with threshold pressure gradient [J]. Oil Drilling and Production Technology, 2006, 28(5): 58–60. (in Chinese)
[9] CHENG Shi-qing, ZHANG Sheng-zong, HUANG Yan-zhang. An internal solution of free-boundary problem of non-darcy flow behavior [J]. Mechanics in Engineering, 2002, 24(3): 15–17. (in Chinese)
[10] LU Jing. Pressure behavior of a hydraulic fractured well in tight gas formation with threshold pressure gradient [C]// SPE Middle East Unconventional Gas Conference and Exhibition. Abu Dhabi, UAE, 2002: 152158.
[11] GRINGARTEN A C, RAMEY H J. The use of source and Green’s functions in solving unsteady-flow problems in reservoirs [J]. Society of Petroleum Engineers Journal, 1973, 13(5): 285–296.
[12] ADEWOLE E S. Compilation of instantaneous source functions for varying architecture of a layered reservoir with mixed boundaries and horizontal well completions [C]// Nigeria Annual International Conference and Exhibition. Lagos, Nigeria, 2013: 167599.
[13] ADEWOLE E S. Compilation of instantaneous source functions for varying architecture of a layered reservoir with mixed boundaries and horizontal and vertical well completions [C]// Nigeria Annual International Conference and Exhibition. Lagos, Nigeria, 2013: 167545.
[14] CHEN H Y, POSTON S W, RAGHAVAN R. An application of the product solution principle for instantaneous source and Green’s functions [J]. SPE Formation Evaluation, 1991, 6(2): 161–168.
[15] ZHU Wei-yao, LIU Jin-zi, SONG Hong-qing. Calculation of effective startup degree of non-Darcy flow in low or ultra-low permeability reservoirs [J]. Acta Petrolei Sinica, 2010, 31(3): 452–457. (in Chinese)
[16] XIAO Qian-hua, WEI Guo-qi, YANG Zheng-ming, XU Xuan, TIAN Wen-bo, ZHANG Ya-pu. Experimental evaluation on well pattern adaptability of ultra-low permeability reservoir using sandstone flat model [J]. Journal of Central South University, 2014, 21: 2334-2340.
[17] YU Rong-ze, BIAN Ya-nan, ZHOU Shu, WANG Kai-jun, L Qi, CHEN Zhao-hui. Nonlinear flow numerical simulation of low-permeability reservoir [J]. Journal of Central South University, 2012, 19: 1980-1987.
Qi, CHEN Zhao-hui. Nonlinear flow numerical simulation of low-permeability reservoir [J]. Journal of Central South University, 2012, 19: 1980-1987.
[18] XU Jian-chun, JIANG Rui-zhong, XIE Li-sha, WANG Rui-heng, SHAN Li-jun, LI Lin-kai. Non-darcy flow numerical simulation for low-permeability reservoirs [C]// EAGE Annual Conference & Exhibition incorporating SPE Europec. Copenhagen, Denmark, 2012: 154890.
[19] ZHANG Feng, YANG Dao-yong. Effects of non-darcy flow and penetrating ratio on performance of horizontal wells with multiple fractures [C]// SPE Unconventional Resources Conference Canada. Calgary, Alberta, Canada, 2013: 167218.
[20] GRADY D E, KIPP M E, SMITH C S. Explosive fracture studies on oil shale [J]. Society of Petroleum Engineers Journal, 1980, 20(5): 349–356.
(Edited by YANG Bing)
Foundation item: Project(51304220) supported by the National Natural Science Foundation of China; Project(3144033) supported by the Beijing Natural Science Foundation, China; Project(20130007120014) supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China
Received date: 2014-12-02; Accepted date: 2015-04-10
Corresponding author: CAO Ren-yi, PhD; Tel: +86–10–89733218; E-mail: caorenyi@126.com