
Numerical simulation for thermal flow filling process of casting
CHEN Ye(陈 晔)1, ZHAO Yu-hong(赵宇宏)2, HOU Hua(侯 华)1
1. College of Materials Science and Engineering, North University of China, Taiyuan 030051, China;
2. College of Materials Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China
Received 20 April 2006; accepted 30 June 2006
Abstract: The solution algorithm (SOLA) method was used to solve the velocity and pressure field of the thermal flow filling process, and the volume of fluid (VOF) method for the free surface problem. Since the “donor-acceptor” rule often results in the free interface vague, the explicit difference method was adopted, and a method describing the free surface state at 0<F<1 was proposed to deal with this problem. In order to raise the computation efficiency, such algorithms were investigated and invalidated as: 1) internal and external area separation simplification algorithm; 2) the reducing necessary search area method. With the improved algorithms, the filling processes of the valve cover castings with gravity cast and an up cylinder block casting with low-pressure cast were simulated, the simulation results are believable and the computation efficiency is greatly improved. The SOLA-VOF model and its difference method for thermal fluid flow filling process were introduced.
Key words: thermal flow; numerical simulation; filling process; free surface; computation efficiency
1 Introduction
Cast filling process refers to pouring molten metal into the gating system, which consists of fluid flow and heat transfer processes and is companied by the heat loss and solidification. Unreasonable filling process may result in considerable defects. So it is critical to deign suitable gating system and optimized filling technology. Today, numerical simulation technology presents an effective approach to these problems [1-4].
In filling algorithm, the iterative times often extends to several thousands even millions, hence the computation efficiency is considerably low, so it is important to develop more efficient and precise arithmetic. In addition, casting filling experiments are usually difficult to carry out and simulation results are often unsatisfied.
2 Solution algorithm method for velocity and pressure field
Mass conservation and momentum conservation are represented by the continuum equation (Eqn.(1)) and N-S equation (Eqn.(2)) respectively as follows:
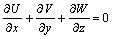 (1)
(1)

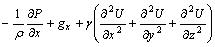 (2)
(2)
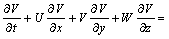
 (3)
(3)

 (4)
(4)
where U, V and W are the velocity components of x, y and z coordinates, ρ is the fluid density; p is the pressure; gx, gy and gz are the gravity accelerate velocities of x, y and z orientations; γ is the momentum viscosity. The weighting factor α was used to control the discrete format with α=0 representing the central difference format and α=1 representing the upper hand difference format. Here, Eqn.(1) is discrete by the central format and Eqn.(2) is discrete by the upper hand format. The interleaving mesh was used to discrete the velocity and pressure for many advantages[5-10].
3 Coupling filling and temperature calculation
According to the energy conservation equation:
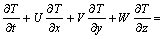
 (5)
(5)
or
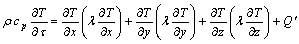 (6)
(6)
where ρ is the density, T is the temperature, τ is the time, λ is the coefficient of thermal conductivity, cp is the specific heat capacity, 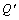 is the thermal source, σt is the Purante coefficient, and is generally within 0.9-1.0, μt is the dynamic viscosity of turbulent flow:
is the thermal source, σt is the Purante coefficient, and is generally within 0.9-1.0, μt is the dynamic viscosity of turbulent flow:
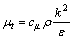 (7)
(7)
where k is the energy of turbulence, ε is the dissipation rate of turbulence.
The explicit difference format was adopted to solve the above equations, and the computational time can be greatly reduced compared to the implicit difference method.
Based on the double equations model k—e equations proposed by Launder and Spalding, k and ε can be obtained.
The law of power function was used to judge the way of heat exchange and the power function A(|P|) is given by
 (8)
(8)
where p=UL/α represents the Beketoria number, U is the fluid flow velocity, m/s; L is the distance, m; α is the thermal conductive coefficient, m2/s. Beketoria number can measure the action degree of flow and heat conduction.
When fluid flows very fast, p is large, A(|p|) approaches 0, which indicates that flow heat transfer takes the main effect, thermal conduction is lost comparatively; when the speed of fluid is small, p is very small, A(|p|) approaches 1, now thermal conduction plays an important role, flow heat transfer is more few, this is consistent with actual condition.
It is also necessary to calculate the temperature field of some cooling mediums such as casting mould, mould core and others.
4 Improved VOF method for interface vague phenomenon during free surface calculation
The volume equation is shown as
 (9)
(9)
where F is the ratio of flow volume within one cell to volume of one cell (0≤F≤1), when F=0, the cell is empty; when F=1, the cell is full of fluid; and when 0<F<1, there is some liquid in the cell, and the free surface exists.
The Donor-Acceptor method was adopted in VOF model to assure that the free boundary definition will not be damaged. Fluid flows out of the donor cells and into the acceptor cells. When a plane passing through a cell, its orientation can be obtained by solving the normal vector representing the free surface in VOF method, and then the location of free surface can be determined according to F of the adjacent cells.
Since the “Donor-Acceptor” method was originally adopted in 1-D or 2-D simulations, in 3-D case, fluid could flow into or out of the six faces of a mesh unit simultaneously, so there will appear some “false” diffusions, and this method could bring some errors, even could result in interface vague phenomenon. There are plenty of free surface units (0 <F<1) between the full unit (F=1) and empty unit (F=0) along a certain direction, the more this kind of free surface units, the more serious the interface vague phenomenon.
With implicit method, in an arbitrary time step, there would be no empty units due to the false diffusion, which can result in serious interface vague. Otherwise, with the explicit method, it is left empty since the free surface carries only one unit forward in every time step, so interface vague is not very serious. In order to get more actual free surfaces, the explicit method should be adopted and the free surface of 0<F<1 should be described.
5 Increase of calculation efficiency
Usually, it takes most time to solve the pressure and velocity field in filling process calculation. Some methods have been explored to improve the calculation efficiency with decreasing iteration frequency and quickening convergence speed. And now there are such methods as the conjugate gradient method, pre-treatment conjugate gradient method, dynamic relaxation factor method, etc. The mixture model was also proposed to simplify the physical model and reduce calculation.
The internal and external area separation simplifi- cation algorithm and the reducing search area method were adopted in this study.
5.1 Internal and external area separation simplification algorithm
The liquid metal filling area was divided into two parts: the internal unit and free surface unit. At every time step dt, the free surface units move continuously forward, and form new free surfaces units to form new internal and external areas as shown in Fig.1.

Fig.1 Chart of internal and external zone separation
With this scheme, the velocity and pressure contained in a unit will not change again after the unit becomes an internal unit. All changes occur in the free surface units and their nearest units. The iteration calculation of speed and pressure was carried out in this area. As shown in Fig.1, the iteration calculation at t+dt was carried out only in 1-10 units. So the grid number of participating in the iteration decreases greatly to raise calculation efficiency. Yet the absence of pressure and speed in the internal units could affect the calculation precision and flow state.
5.2 Reduction of necessary search area
During filling process calculation, it is necessary to calculate the coupling pressure, velocity and temperature fields for those grid units filled with liquid metal. So it is important to search the corresponding needed units. The circulating algorithm is usually adopted to search the needed units during all the units of the entire casting and mould one by one and the efficiency is very low, because the mould is not all filled with liquid during most calculating time, full-course searching entire cast and casting mould will result in great time waste.
By this method, the search region can be reduced to raise calculation speed and the calculation precision can be maintained. The specific procedures are as follows.
1) A 3-D array is arranged to stock the grid units of liquid metal at the most forward position, compared to find their biggest values im, jm, km, and the minimum values in, jn, kn in the three directions.
2) Comparing the above six values with the coordinates of the inlet, the new biggest values im, jm, km, and minimum values in, jn, kn can be obtained in the three directions.
3) Then, judge the six values whether or not the maximum or minimum value of the entire x, y, and z coordinates. If all not, then im, jm, km, in, jn and kn are the search ranges at the next time step. If one of the six values is the maximum or minimum value, for example, in is the minimum value in x direction, which indicates that liquid metal has already flowed to the mould, and in the following search scope in is always the minimum value along x direction. Other five values are also such. Then, release the memory used in stocking the fluid grid unit of forward position immediately.
4) After stocking the new grid location of the metal surface forward position of liquid state, repeat the above steps again.
6 Simulation for filling process of castings
6.1 Filling process of valve covers casting
The sand gravity casting with the “one type and much castings” was adopted and the filling order during each one casting influences its casting property.
The distribution of castings in the mould and the corresponding grid partition system are shown in Fig.2. Cast material is ZG (casting steel) 25, outline over all dimensions is 75 mm×82 mm×8 mm, mass is 158 g; mesh size is 3.5 mm×3.5 mm×3.5 mm, the total unit number is 1 928 090, the total filling time is 10 s.

Fig.2 3D-solid(a) and meshing system(b) of valve covers
The algorithms of improving calculation efficiency proposed in this study were adopted, the calculation was carried out on the computer with main frequency 2.8 G and 512 M, and the needed time is 983 min. Yet in the same case, it would take 1 808 min with the unimproved algorithm. So, the computation efficiency can be greatly increased. The simulation results for filling process are shown in Fig.3.

Fig.3 Simulated thermal filling process of valve covers
Initially, the liquid metal filled the bottom quickly, and then filled stability gradually, which is consistent with the experimental investigation in factories. At the same time, the changed temperature can be obtained and observed by the temperature bar.
6.2 Filling process of up-cylinder block casting
The low-pressure cast technology with sand mould was adopted, so the castings quality strongly depends on the filling state. The solid diagram and grid partition system are shown in Fig.4. The cast material is AlSi7Mg, outline over all dimensions is 983 mm×677 mm×540 mm, the mass is 117.4 kg, the dimension of mesh is 5 mm×5 mm×5 mm, the total unit number is 2 570 388, and the total filling time is 19 s.
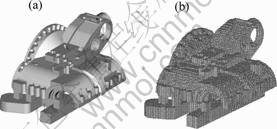
Fig.4 Solid(a) and mesh system(b) of up-cylinder block
The algorithm of improving the calculation efficiency proposed in this study was also adopted, the calculation was carried out on the computer with main frequency 2.8 G and memory 512 M, the needed time is 1 456 min. Yet in the same case, it would take 2 832 min with the unimproved algorithm. So, the computation efficiency has been greatly improved. The simulation results for filling process are shown in Fig.5.

Fig.5 Simulated filling process of up cylinder block
It can be seen from Fig.5 that the filling process is stable, which is consistent with the experimental investigation in factories. The changed temperature can also be observed by the temperature bar.
7 Conclusions
1) Combined with the SOLA-VOF model and the energy conservation equation, the numerical simulation for thermal fluid flow filling process was carried out.
2) Since the “Donor-Acceptor” rule often results in the free interface vague, the explicit difference method was adopted, and a method describing the free surface state at 0<F<1 was proposed to deal with this problem.
3) In order to raise the computation efficiency, such algorithms as internal and external area separation simplification algorithm and the reducing necessary search area method were investigated and invalidated.
4) With the improved algorithms, the filling processes of the valve cover castings with gravity cast were simulated, the simulation results are believable and the computation efficiency is greatly improved.
References
[1] JU D Y, NISHIDA M, HANABUSA T. Simulation of the thermo-mechanical behavior and residual stresses in the spray coating process[J]. Journal of Materials Processing Technology, 1999, 92-93: 243-250.
[2] HOU H, XU H, CHENG J. The Computer design system of the casting drawing and casting card[J]. Journal of North China Institute of Technology, 1999, 12(4): 230-233.
[3] HOU H, JU D Y, ZHAO Y H, CHENG J. Numerical simulation for dendrite growth of binary alloy with phase-field method[J]. J Mater Sci Technology, 2004, 20(12): 45-48.
[4] HOU H, ZHAO Y H, CHU Z, XU H. Numerical simulation of 3-D displacement fields of steel casting during solidification process[J]. Foundry Technology, 2002(3): 145-149. (in Chinese)
[5] TAO W Q. Numerical Heat Transfers Science [M]. Xi’an: Xi’an Jiaotong University Press, 1988.
[6] YOU B K. Temperature Measurement and Instrument: Couple and Thermal Resistance [M]. Beijing: The Document Press of Science and Technology, 1990.
[7] BEN-JACOB E, GOLENFELD N, LANGER J S. Boundary-layer model of pattern formation in solidification[J]. Phys Rev A, 1984, 29: 330-340.
[8] ZHAO Y H, HOU H, JU D Y. Atomic-scale computer simulation of mixture precipitation mechanism for Ni75AlxV25-x alloy[J]. Material Science Forum, 2005, (475-479): 3115-3118.
[9] BEN-JACOB E, GOLENFELD N, KOTLIAR B G. Pattern selection in dendritic solidification[J]. Phys Rev Lett, 1984, 53: 2110-2113.
[10] ZHAO Y H, CHEN Z, WANG Y X. Atomic-scale computer simulation for early precipitation process of Ni75Al10V15 alloy[J]. Progress in Natural Science, 2004, 14(3): 241-246
(Edited by CHEN Wei-ping)
Corresponding author: ZHAO Yu-hong; Tel: +86-351-8608320; E-mail: oneleafwater@yahoo.com.cn