DOI: 10.11817/j.ysxb.1004.0609.2021-39742
基于结构参数的超细尾砂充填料浆双变量流变模型及应用
付自国1, 2, 3,李 化1, 2, 3,邓建辉1, 2, 3,乔登攀4,王佳信4
(1. 四川大学 水力学与山区河流开发保护国家重点实验室,成都 610065;
2. 四川大学 水利水电学院,成都 610065;
3. 四川大学 深地科学与工程教育部重点实验室,成都 610065;
4. 昆明理工大学 国土资源工程学院,昆明 650093)
摘 要:超细尾砂已成为金属矿山充填处理的最大宗固体废料,流变模型是刻画超细尾砂料浆流动特性及确定管输参数的主要依据。基于超细颗粒絮凝结构形成机制,引入结构参数来描述超细尾砂料浆剪切响应过程。采用旋转黏度计对某矿山质量分数72%、74%、76%和水泥添加量240、260 kg/m3的超细尾砂充填料浆进行24组不同剪切强度下的流变测试。结果表明:在恒定剪切速率下,料浆剪切应力随着剪切时间延长而逐渐减小,最后趋于稳定;任意剪切时间下,剪切应力与剪切速率(>20 s-1)的关系近似满足Bingham模型,且Bingham回归参数具有明显的时变性。这些宏观规律的原因可归结于浆体结构参数的变化。基于此,构建了关于浆体剪切强度和剪切时间的双变量流变模型,模型中7个参数均具有物理含义。通过试验数据对模型进行了验证,拟合得到试验配比下的超细尾砂料浆流变参数,最大屈服应力和最大塑性黏度范围分别为120~220 Pa和1.7~7.2 Pa·s,可为启动压力计算提供参考;极限屈服应力和极限塑性黏度范围分别为20~120 Pa和0.5~3.2 Pa·s,可为浆体稳态流动阻力计算提供参考。另外,介绍了新流变模型的适用条件及应用方法,并与现有流变模型进行了对比讨论。
关键词:充填料浆;超细尾砂;絮凝结构;触变性;流变参数;流变模型
文章编号:1004-0609(2021)-06-1672-14 中图分类号:TD853;X751 文献标志码:A
引文格式:付自国, 李 化, 邓建辉, 等. 基于结构参数的超细尾砂充填料浆双变量流变模型及应用[J]. 中国有色金属学报, 2021, 31(6): 1672-1685. DOI: 10.11817/j.ysxb.1004.0609.2021-39742
FU Zi-guo, LI Hua, DENG Jian-hui, et al. Bivariate rheological model of ultrafine tailings backfill slurry based on structural parameter and its applications[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(6): 1672-1685. DOI: 10.11817/j.ysxb.1004.0609.2021-39742
深地面临“三高一扰动”的复杂环境,使得深井开采理论成为学界的研究热点[1]。而充填采矿作为绿色开采理念[2-3]的一大创新,具有以下特点:1) 能够再造井下人工回采环境[4];2) 改善岩体受力状 态;3) 吸收和隔绝地热[5];4) 提高“三率”指标[6];5) 减缓地表尾矿库库容压力、无害化处理固体废料、节约征地。这些优点使得充填采矿逐渐成为深部资源开采的首选方案。为降低充填成本,矿山就地取材,使得尾砂成为充填材料的主要来源[7-8]。近年来,随着选矿技术的进步,尾砂颗粒越来越细。由于尾砂充填料浆中含有大量超细颗粒,其流变特性,特别是管输的稳定性和采场的流动性越趋复杂。以往的流变模型对其刻画存在局限性,而流变模型的选取直接影响流变参数的确定,进而影响充填系统输送参数设计的准确性[9-10]。因此,建立超细尾砂充填料浆更为合理的流变模型显得尤为重要。
超细尾砂充填料浆作为一种高固含、多细粒、多相、多尺度混合材料,表现出明显的非牛顿流体特性[11]。以往,Bingham模型和Herschel-Bulkley模型对其流变特性定量描述最为广泛[12-13]。学者普遍注意到,这两个模型只对充填料浆某一剪切强度范围内的流变数据拟合较好,但不能从机理上解释料浆的某些流变行为,例如触变性[14]。张修香等[15]采用旋转黏度计对高浓度料浆进行了测试,发现应用H-B模型拟合得到的黏度普遍偏大,严重失真,基于此,提出了对试验数据具有较高拟合度的流变新模型,然而其模型中的一个参数没有具体的物理意义。胡华等[16]从理论角度分析了似膏体的黏、弹及塑性力学性质,建立了其广义黏弹塑性流变本构方程;该模型考虑较为全面,但模型过于复杂,难以推广。蔡嗣经等[17]通过R/S浆式流变仪对尾砂料浆进行测试,并借用Papanastasiou流变模型验证了尾砂料浆是一种黏塑性流体。另外,在浆体流变学范畴内,IMRAN等[18]在研究泥石流的流变特性时发现:在高剪切速率下,流动表现为低黏度的Bingham流体特性;在低剪切速率下,流动表现为高黏度的牛顿流体特性,基于此,提出了双线性流变模型。TREGGER等[19]研究了黏土对水泥浆体流变性质的影响,基于Bingham 模型,提出了含一个临界剪切速率的修正模型。此外,KLEIN等[20]提出了一个屈服塑性模型,能够准确反映膏体在不同剪切速率范围内的流变规律。
随着充填料浆中超细颗粒含量的增多和充填浓度的提高,相关学者研究发现,浆体在受剪切时的流变上行曲线与下行曲线并不重合,即具有一定的触变性。TOORMAN[21]首次引入无量纲结构参数描述了黏性泥沙的触变行为。吴爱祥等[22]借助扫描电镜技术观测了膏体微观结构在恒定剪切作用下的变化规律,并基于图形处理和分形理论,建立了结构参数的时间演化模型。杨柳华等[23]研究发现了全尾砂料浆的触变性受超细颗粒成分、灰砂比和固相质量分数的影响,加深了对料浆流变性质的认识。李帅等[24]建立了考虑时变性的H-B修正模型,为超细全尾砂料浆长距离自流管输的阻力计算提供依据。刘晓辉[25]基于浆体微观结构,引入Morre 结构动力学模型,建立了描述膏体触变-屈服流变模型。该模型首次将浆体结构的概念引入到充填料浆,是矿山充填料浆流变模型研究的一大进步;但模型的6个参数确定需要建立非线性多元方程组优化求解,每组参数的确定需要多组试验曲线,且不同配比的浆体达到动态平衡的条件难以统一。
鉴于此,本文在以上研究成果基础上,探讨了超细尾砂料浆微观絮凝结构的形成机制,采用试验研究与理论分析相结合的方法,提出采用结构参数的方法来表征浆体在外部剪切作用下微观结构的演化规律。基于实验结论,对Binghan流变模型进行修正,构建含7个参数的双变量流变模型,验证了该模型具有较高的可靠度,并详细介绍了模型的适用条件和应用方法。该模型丰富了浆体流变学的研究内容,为矿山充填料浆输送提供理论基础。
1 料浆微观结构与结构参数
1.1 料浆絮凝结构形成机制
超细尾砂充填料浆中的超细颗粒粒径一般在20 μm 以下,多属于黏土或粉体颗粒。这些颗粒比表面积较大,在浆体中极易发生“自絮凝”作用而形成具有一定抗剪强度的微观结构[26]。
超细尾砂在选矿厂经过药剂的浮选作用,其中含有或多或少的电解质。一般尾砂中的超细颗粒表面总是带有负电荷,处于不稳定状态,它会吸附浆体中的阳离子,在颗粒周围形成双电层,如图1所示。在颗粒表面电场作用下,双电层的外层阳离子会吸附周围的极性水分子,使水分子有序紧密地排列起来,以致完全失去了自由活动的能力,这部分水失去了各向传压特性,其分子受颗粒的吸引力极大,称为黏结水。由于静电引力场的作用,距离颗粒较远的水分子也会被吸引,排列在黏结水的外层,由于静电引力场强度较低,这些水分子的活动能力稍强,称为黏滞水。将黏结水和其所含的离子组成双电层的内层,或称吸附层;将黏滞水和其所含的离子组成双电层的外层,或叫扩散层。由于黏结水与黏滞水失去或部分失去了自由活动的能力,统称为束缚水或吸附水膜。水膜厚度与颗粒的矿物成分、周围水体的化学性质、离子种类、浓度等有关,一般为0.1 μm的数量级。由于束缚水的单向传压性质,大大地提高了颗粒之间的亲和能力,为絮凝创造了必要的条件[27]。
物料在配制成料浆的过程中,受到持续的剪切搅拌作用,引起分散介质的碰撞、接触,使得带有吸附水膜的颗粒形成公共吸附水膜,而将它们连结起来,形成颗粒黏结,称此过程为絮凝。另外,料浆浓度越大,颗粒平均距离越小,单位时间内颗粒自由无碰撞距离就越小,碰撞的概率也就越大,即随着充填料浆浓度的提高,絮凝作用越强烈。但存在一个极限体积浓度,当固体颗粒含量越过这个极限浓度后,对絮凝的影响并不明显。
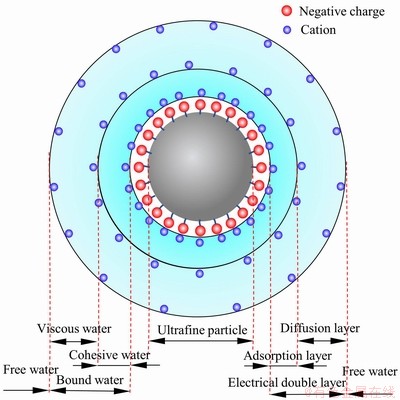
图1 尾砂超细颗粒扩散双电层模型
Fig. 1 Electrical double layer model of ultrafine tailings
颗粒在絮凝作用下会连接成具有复杂内部结构的絮团,相对于单颗粒而言,絮团个体尺寸变大,相对密度变小,导致絮团的整体特性将取代单一尾砂颗粒特性。絮团结构的存在改变了料浆的黏性,使得浆体成为具有屈服应力的非牛顿流体。随着絮凝作用的发育,絮团个数不断增加,出现絮团与絮团连接成片,片状絮团结片形成一种松散的网状结构,大的絮团缓慢沉积、压缩密实,最终达到稳定状态(见图2)。BERKER等[28]通过扫描电镜观测到了尾砂浆体絮凝网状的发育过程。
1.2 浆体结构动力学方程
料浆絮凝结构不会无终点发育,在静置状态下,结构随着时间的延长而增强,但存在一个极限值;在剪切作用下,结构随着剪切作用的增强而变弱,即图2所示的尾砂颗粒絮凝结构发育过程是一个可逆的过程。浆体在流动过程中,其内部结构的变化存在破坏和修复两个过程。当结构完全发育时,只要对浆体施加某一剪切作用,絮凝网状结构将会被拉断、裂降,大结构分解成小结构,甚至单一的颗粒。但同时,当外部剪切作用减弱时,随着时间的持续,由于颗粒之间的表面力作用,被破坏的结构会自动搭接、重组和恢复,最终达到结构的破坏和修复的动态平衡状态。
Morre结构动力学模型认为[25],流变参数均为结构参数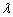 的函数,并认为
的函数,并认为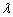 是关于剪切时间t和剪切速率
是关于剪切时间t和剪切速率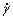 的函数,即
的函数,即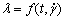 ,且满足:
,且满足:
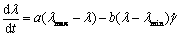 (1)
(1)
式中: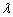 为结构参数,其取值范围为[0,1];当结构完全发育时,
为结构参数,其取值范围为[0,1];当结构完全发育时,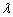 取1;当结构完全破坏时,
取1;当结构完全破坏时,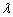 取0,即
取0,即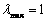 ,
, ;t为剪切时间,s;
;t为剪切时间,s;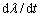 为料浆结构参数的变化速率;a,b分别为结构建立速率常数和结构破坏速率常数,与料浆的物料性质及浓度有关。
为料浆结构参数的变化速率;a,b分别为结构建立速率常数和结构破坏速率常数,与料浆的物料性质及浓度有关。
式(1)的边界条件为
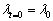 ,
,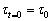 (2)
(2)
式中: 为料浆的初始结构参数;
为料浆的初始结构参数;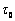 为初始剪切应力,即为最大剪切应力,Pa。
为初始剪切应力,即为最大剪切应力,Pa。
当式(1)右侧为负值时,表明结构破坏速率大于重建速率,即结构正在被剪切破坏;反之,结构正在恢复。当剪切时间趋于无穷时,结构的破坏速率与重建速率相当,物料达到动态平衡状态,即结构参数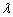 不再改变,它将趋于一个稳定值,则有:
不再改变,它将趋于一个稳定值,则有:
 (3)
(3)
联立式(1)和式(3)可得:
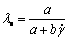 (4)
(4)
式中: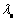 为平衡结构参数。
为平衡结构参数。
注意到式(1)为一阶非齐次线性常微分方程,代入边界条件,解方程得到结构参数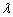 的表达式:
的表达式:
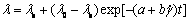 (5)
(5)
式(5)描述了料浆结构随剪切速率和时间的变化关系。浆体在恒定剪切速率下,结构参数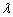 随着剪切时间的增加而逐渐减小,并最终趋于平衡。
随着剪切时间的增加而逐渐减小,并最终趋于平衡。

图2 尾砂颗粒絮凝结构发育过程示意图
Fig. 2 Schematic diagram of development process of flocculation structure of tailings
2 双变量流变模型的构建
2.1 试验材料与方案
超细尾砂选自大红山铜矿立式砂仓进砂管(见图3(a))。经室内实验测定,尾砂密度为2.82 t/m3,平均粒径为76.12 μm,其中粒径小于74 μm的含量达80%以上,粒径小于20 μm的含量达到40%。胶凝材料为C42.5普通硅酸盐水泥。充填物料级配曲线如图4所示。实验用水为城市自来水。将尾砂烘干后,按照实验浓度和水泥添加量混合搅拌成均质料浆。其中,质量浓度为73%、水泥添加量为240 kg/m3的料浆为观测组。验证组为由质量浓度分别为72%、74%、76%和水泥添加量分别为240、260 kg/m3构成的两因素三水平全面实验,共6组。流变测试仪器为美国Brookfield公司生产的DVⅡ+Pro数字型黏度计(见图3(b))。该装置外接电脑,通过编制流变控制程序,对浆体分别施加20、40、80、100 s-1 4个恒定剪切应变率(对照组增加一个60 s-1剪切速率),剪切持续时间设定为800 s(对照组为900 s)。
2.2 试验结果与分析
观测组在不同剪切速率下剪切应力随时间变化曲线如图5所示。由图5可以看出:1) 在任意恒定剪切速率下,料浆所受剪应力随着剪切时间的增加表现为,先急速减小,再缓慢减小,最后趋于稳定,即不随时间而变化。与学者观测到的“剪切变稀”现象一致[23-25]。这是因为在剪切作用下,料浆结构发生破坏,且破坏速率大于重建速率,最后达到破坏和恢复的动态平衡。此过程中料浆结构参数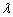 由初始值逐渐较小,最后趋于一个极限值。2) 同一配比超细尾砂料浆,在不同恒定剪切速率条件下,其初始剪切应力(最大剪切应力)和平衡剪切应力(最小剪切应力)均不同,且加载的剪切速率越大,其对应的初始剪切应力和平衡剪切应力越大。这说明了超细尾砂料浆的剪切应力是剪切速率的正相关函数,相关因子即为料浆的黏度。3) 料浆初始剪切应力和平衡剪切应力可对应于充填管输设计中的启动压力和稳态剪切压力,由于管输过程一般为恒定速率剪切作用,因此这个指标具有重要的工程参考价值。4) 剪切时间大约在200 s时,料浆开始进入动态平衡过程中,经过一定时间的震荡,即大约在800 s时,剪切应力基本不再随时间而变化。
由初始值逐渐较小,最后趋于一个极限值。2) 同一配比超细尾砂料浆,在不同恒定剪切速率条件下,其初始剪切应力(最大剪切应力)和平衡剪切应力(最小剪切应力)均不同,且加载的剪切速率越大,其对应的初始剪切应力和平衡剪切应力越大。这说明了超细尾砂料浆的剪切应力是剪切速率的正相关函数,相关因子即为料浆的黏度。3) 料浆初始剪切应力和平衡剪切应力可对应于充填管输设计中的启动压力和稳态剪切压力,由于管输过程一般为恒定速率剪切作用,因此这个指标具有重要的工程参考价值。4) 剪切时间大约在200 s时,料浆开始进入动态平衡过程中,经过一定时间的震荡,即大约在800 s时,剪切应力基本不再随时间而变化。

图3 试验材料取样点与试验仪器
Fig. 3 Test material sampling point and test instrument

图4 充填骨料颗粒粒径分布
Fig. 4 Particle size distribution of filling aggregates
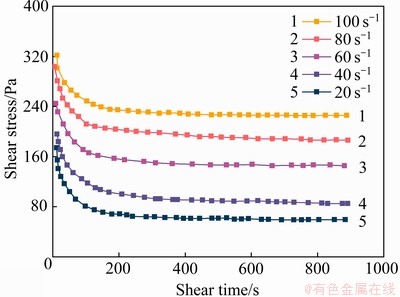
图5 观测组在不同剪切速率下剪切应力随时间变化曲线
Fig. 5 Changing curves of shear stress with time under different shear rates for observation group
2.3 流变模型的建立
将不同剪切速率加载下,料浆任意时刻所受的剪切应力统计结果见表1。由表1可知,料浆在流动的任意时刻,剪切应力与剪切速率呈现较好的线性关系,即满足Bingham流变模型,其表达式为
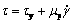 (6)
(6)
式中: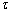 为剪切速率,Pa;
为剪切速率,Pa;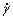 为剪切速率,s-1;
为剪切速率,s-1;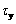 为料浆的屈服应力,Pa;
为料浆的屈服应力,Pa;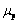 为浆体的塑性黏度,Pa·s。拟合曲线如图6所示。每一时刻拟合得到的屈服应力和塑性黏度见表1,相关系数都在0.95以上。这说明,料浆在流动的任意时刻的流变关系均满足Bingham模型,但屈服应力和塑性黏度都随时间变化,具有明显的时变性。出现上述现象的根本原因在于料浆结构参数的改变。
为浆体的塑性黏度,Pa·s。拟合曲线如图6所示。每一时刻拟合得到的屈服应力和塑性黏度见表1,相关系数都在0.95以上。这说明,料浆在流动的任意时刻的流变关系均满足Bingham模型,但屈服应力和塑性黏度都随时间变化,具有明显的时变性。出现上述现象的根本原因在于料浆结构参数的改变。
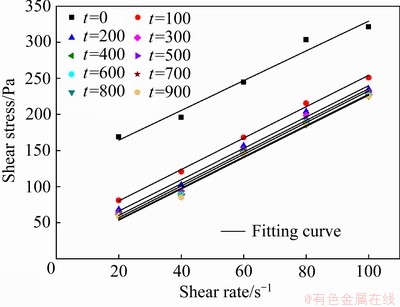
图6 不同时刻剪切应力与剪切速率的宾汉姆模型拟合曲线
Fig. 6 Bingham model fitting curves of shear stress and shear rate at different time
对流变参数的时变性规律进行考察(见图7)。 剪切初期,屈服应力和塑性黏度都存在一个最大值,随着剪切时间的持续,料浆结构持续发生变化,屈服应力和塑性黏度逐渐减小,最后趋于一个极限值,即流变参数为时间的函数。由前面分析可知,随着剪切时间的延长,料浆的结构参数不断发生变化,反映了料浆宏观流变参数的变化。故可以将流变参数的时变性归结于结构参数的函数,提出如下表达式:
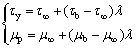 (7)
(7)
式中: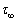 、
、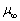 分别为料浆在某一剪切速率下结构达到动态平衡时的屈服应力和塑性黏度,即为一个极限值;
分别为料浆在某一剪切速率下结构达到动态平衡时的屈服应力和塑性黏度,即为一个极限值; 、
、 分别为料浆剪切初期所具有的最大屈服应力和最大塑性黏度。
分别为料浆剪切初期所具有的最大屈服应力和最大塑性黏度。
将式(7)代入式(6),并结合式(5),化简得到料浆关于剪切时间和剪切速率的双变量流变模型。式(8)含有7个参数,均具有一定的物理意义,可以从多方面刻画特定料浆所对应的流变特性。同时,7个参数对实际充填管输设计具有一定的指导价值,且可以通过后文介绍的拟合方法唯一确定。

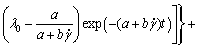
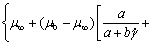
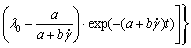 (8)
(8)
表1 不同剪切速率任意时刻的剪切应力及拟合关系
Table 1 Shear stress and fitting relation at any time and at different shear rates
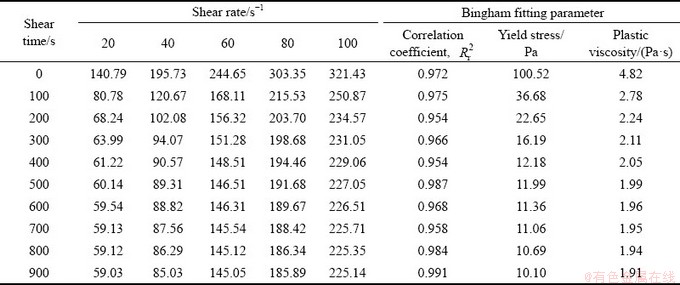

图7 尾砂料浆宾汉姆流变参数随时间的变化关系
Fig. 7 Variation of Bingham rheological parameters with time
2.4 模型拟合结果及分析
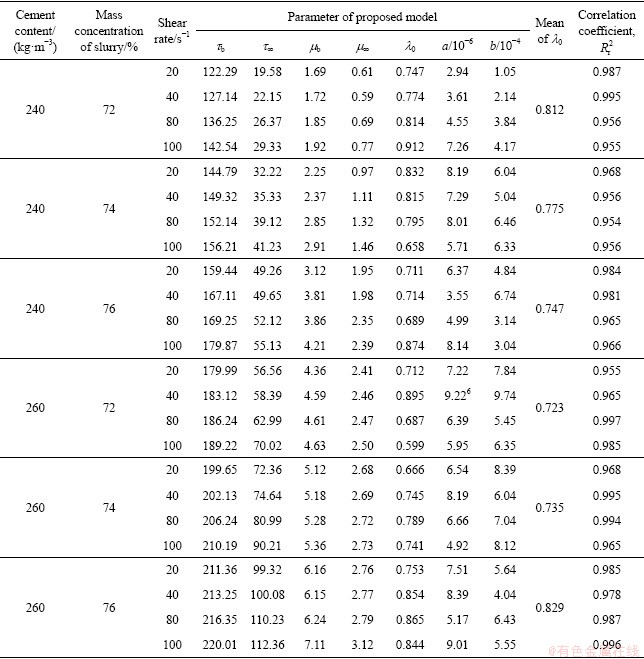
为了验证建立的流变模型的准确性,采用ORIGIN软件自定义函数,对验证组的试验数据进行拟合,试验数据及拟合结果如图8所示,各个配比料浆的模型参数拟合值见表2。从图8和表2可以看出,式(8)对试验数据拟合较好,相关性系数都在0.95以上,且拟合得到的流变参数较为合理。由此说明,建立的模型对超细尾砂充填料浆关于剪切时间和剪切速率的流变特性具有较好的刻画,可以作为料浆流变特性的理论参考公式。
由表2可得如下结论,并对其进行分析如下:
1) 料浆初始屈服应力 在120~220 Pa之间,初始塑性黏度
在120~220 Pa之间,初始塑性黏度 在1.7~7.2 Pa·s之间,均较大。这是因为在剪切初期料浆的结构破坏程度较小,结构参数
在1.7~7.2 Pa·s之间,均较大。这是因为在剪切初期料浆的结构破坏程度较小,结构参数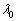 较大。
较大。 和
和 可作为料浆管输启动或停泵再启动压力设计参考值。
可作为料浆管输启动或停泵再启动压力设计参考值。
2) 随着剪切的持续,料浆进入稳定流动状态,其流变参数趋于一个稳定值。这是料浆结构破坏与重组达到一个动态平衡的结果。极限屈服应力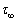 在20~120 Pa范围内,极限塑性黏度
在20~120 Pa范围内,极限塑性黏度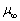 在0.5~3.2 Pa·s范围内。
在0.5~3.2 Pa·s范围内。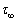 和
和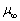 相对于初始状态的值均较小,表示料浆稳定流动时流变参数,而料浆在管道输送时处于持续剪切过程中,因此可作为浆体稳态流动阻力计算参数。
相对于初始状态的值均较小,表示料浆稳定流动时流变参数,而料浆在管道输送时处于持续剪切过程中,因此可作为浆体稳态流动阻力计算参数。
3) 在相同加载条件下,料浆浓度越高,水泥添加量越多,其初始结构参数值越大,初始屈服应力、塑性黏度和极限屈服应力、塑性黏度均越大。这是因为升高料浆浓度缩小了固体颗粒之间的距离,料浆中的超细颗粒越容易相互结合,形成大的絮团结构,从而使得浆体结构参数变大。水泥添加量越大,一方面增加了浆体中的超细颗粒含量,另一方面水泥与水发生水化反应消耗了部分水,相当于提高了料浆浓度,从而提高了料浆的结构参数。该配比下的超细尾砂料浆,结构参数平均值在0.7左右,可作为高浓度充填料浆判据。
4) 不同恒定剪切速率加载下,同一配比料浆流变参数是变化的,其初始流变参数和动态平衡时的流变参数均不同。屈服应力相差不超过21 Pa,塑性黏度相差不超过1.1 Pa·s。产生这一差距的原因主要是料浆结构对不同强度的剪切作用的动力响应程度不同。按照常识,对于同一配比的料浆,其初始结构参数应该相同,但根据新流变模型的回归结果显示,且初始结构参数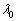 并不相同,但相差也不大。在不同的剪切速率作用下,料浆结构变化程度不同,导致浆体动力响应过程不同,说明料浆的结构参数在一定范围内是剪切强度的函数。
并不相同,但相差也不大。在不同的剪切速率作用下,料浆结构变化程度不同,导致浆体动力响应过程不同,说明料浆的结构参数在一定范围内是剪切强度的函数。
由以上结论及分析可知,料浆流变参数不仅受物料性质、质量浓度和水泥添加量的影响,同时还受到剪切强度及时间的影响。这给料浆流变参数的测定带来了困难。
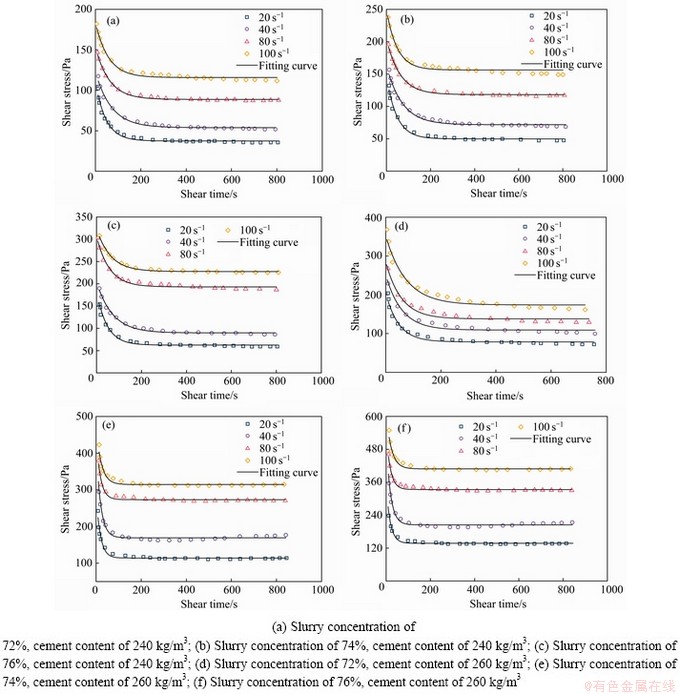
图8 模型对不同配比料浆流变数据的拟合曲线
Fig. 8 Fitting curves of proposed model on rheological data of slurry with different proportions
表2 不同配比料浆在不同剪切速率加载下的模型参数求解结果
Table 2 Solution parameters of different proportions of slurry under different shear rates
鉴于此,若要使得新流变模型得到广泛应用,必须提出一种流变参数的测定方法。其具体操作如下:将某一配比的充填料浆在某一恒定剪切速率下持续作用一段时间,使得料浆的剪切应力趋于一个稳定值,即料浆的内部结构的破坏速率和重建速率达到动态平衡,结构参数保持恒定,此状态下获得料浆的剪切应力随时间变化曲线,然后采用新流变模型对其进行回归,得到模型参数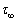 和
和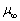 ,即可作为料浆实际计算中的屈服应力和塑性黏度,其一般流程如图9所示。需要注意的是,在这一流变参数测定方法中应该提前确定两个值,一个是剪切速率的选取,一个是剪切时间的选择。
,即可作为料浆实际计算中的屈服应力和塑性黏度,其一般流程如图9所示。需要注意的是,在这一流变参数测定方法中应该提前确定两个值,一个是剪切速率的选取,一个是剪切时间的选择。
由以上分析可以看出,不同剪切速率作用下获得的流变参数略有差异,为了精确获得料浆在流动过程中的流变参数,必须知道料浆在流动过程中受到的剪切速率大小,然后在这一剪切速率下进行流变测试试验。实际上,对于料浆在管道中流动而言,其剪切速率可按照水力学公式计算如下:
 (9)
(9)
式中: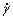 为料浆在流动过程中所受剪切速率,Pa·s;v为料浆的输送流速,根据矿山充填经验,一般取1~2 m/s;D为输送管道管径,矿山充填管道管径一般为100~200 mm。
为料浆在流动过程中所受剪切速率,Pa·s;v为料浆的输送流速,根据矿山充填经验,一般取1~2 m/s;D为输送管道管径,矿山充填管道管径一般为100~200 mm。
对于剪切时间的选择涉及到料浆结构破坏与重建的动态平衡条件。充填料浆由于物料性质、水泥添加量、固体体积浓度和超细组分的含量不同,使得浆体触变性强弱存在较大差异,直接决定了料浆发生应力松弛现象的时间。为了使料浆在流变测试过程中结构都达到动态平衡状态,恒定剪切速率加载时间应尽可能的延长,但时间过程也会影响测试效果,因为料浆长时间静置,浆体中粗颗粒会发生沉降、水砂分离等现象。根据前面试验可知,料浆在恒定剪切速率持续作用800 s左右后剪切应力关于剪切时间几乎是一条水平线。因此,可将800 s作为流变参数测定的剪切时间。
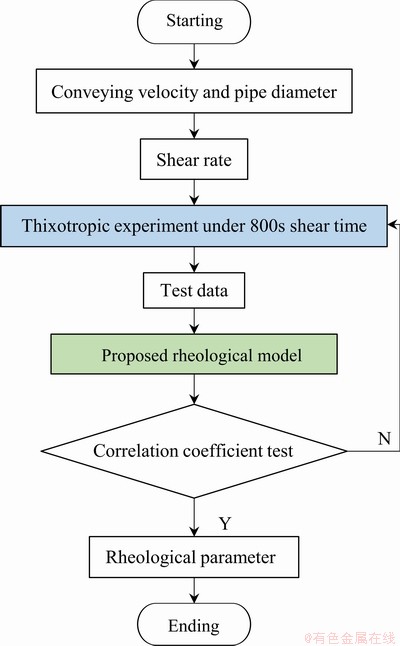
图9 基于新流变模型的料浆流变参数确定的一般流程
Fig. 9 Flow chart for solving rheological parameters based on proposed rheological model
3 新流变模型的应用
新流变模型含有2个变量和7个参数,主要有以下几个方面的应用。
1) 对流变参数的预测。由于模型中含有最大屈服应力和最小屈服应力,最大塑性黏度和最小塑性黏度,在某一恒定剪切速率下对料浆进行流变测试,即可得到剪切应力随时间的关系曲线,然后,用新模型对曲线进行拟合,即可得到这些流变参数值。屈服应力和塑性黏度的最大值可以作为料浆在管道输送开始或停输再启动的屈服应力参考值,而其最小值可以作为料浆在稳定流动过程中的参考值,代入阻力公式,计算出压力损失,对料浆输送进行有效指导。
2) 计算料浆任意状态下的剪切应力。模型是剪切速率和时间的函数,即可对料浆应力松弛和触变性进行客观描述。首先在室内配制一定配比的料浆进行流变测试,根据模型方程对试验数据进行拟合,得到该配比料浆的流变方程。然后根据流变方程即可计算出该配比料浆在任意状态下的剪切应力,如知道料浆在管道的流动速度,代入水力学公式即可换算出剪切速率,则可计算料浆在流动的任意时刻的剪切应力。以水泥量240 kg/m3,质量浓度为72%的料浆流变模型为例,如图10所示。
3) 反演出料浆的触变曲线。料浆在进行触变性测试时,一般设置剪切速率从零线性增大,然后线性下降至零,如式(10)所示:
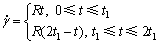 (10)
(10)
式中:R为剪切速率变化率,s-2;t为剪切时间,s;t1为剪切速率上升时间,s。新流变模型可以不用对料浆进行这一测试过程而直接反演出触变曲线。例如,剪切速率按每秒2 s-1线性增加,上升时间为500,然后按同样的速率线性降低至零。以水泥添加量为240 kg/m3、质量浓度为72%的料浆为例,将式(10)代入式(8),得到料浆触变上行曲线方程和触变下行曲线方程,如式(11)所示:
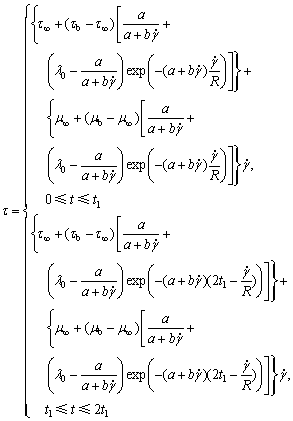 (11)
(11)
将表2中料浆的模型参数代入式(11),反演出该配比料浆的触变曲线,如图11所示。由图11可知,在高剪切速率下(>20 s-1),触变环是封闭的;而在低剪切速率下(<20 s-1),剪切上行曲线与下行曲线相互颠倒,由此说明模型对料浆在高剪切速率下的触变行为具有较好的描述,而实际的料浆输送也处于高速率流场下,因此提出的模型具有一定的现实指导意义。

图10 某一配比料浆的双变量流变模型
Fig. 10 Bivariate rheological model of slurry with 72% mass concentration and 240 kg/m3 cement content
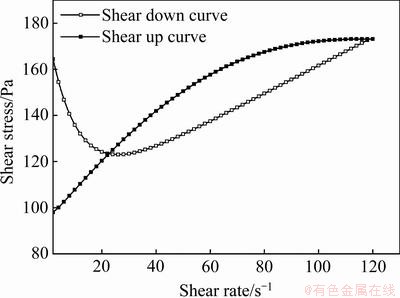
图11 某一配比料浆的模型反演触变曲线
Fig. 11 Thixotropic curve of model inversion
4 讨论
本文在实验的基础上假设超细尾砂料浆的流变本构模型为时变性Bingham流体,而充填料浆在外部剪切作用下要经历蠕变、屈服和流动阶段。图12所示为尾砂料浆流速曲线。由图12可以看出,在低剪切速率下,料浆处于伪塑性变形阶段;在高剪切速率下,料浆进入稳定流动阶段,即Bingham流动。建立的双变量流变模型对料浆稳定流动(高剪切速率下)描述较好,因此,有必要继续研究充填料浆固液转化的整个阶段的特征解析描述方法和定量评价模型。
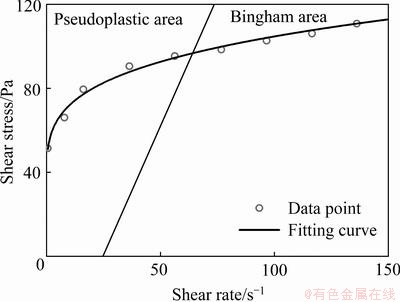
图12 尾砂料浆流变曲线
Fig. 12 General rheological curve of tailings slurry
考虑料浆屈服应力和黏度具有时变性,基于图7的数据变化趋势,提出了流变参数时变性的修正方程(式(7)为结构参数的线性表示),而这个表达式的形式并不唯一,导致得到的流变模型并不唯一。因此,需要研究流变参数关于结构参数时变性的最优数学表达式。
本文通过理论分析,提出一个描述料浆微观结构的指标,进而建立了剪切应力关于剪切速率和剪切时间的函数,即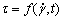 。现有的试验设备只能研究较高剪切速率(>20 s-1)下的流变规律,导致建立的流变模型无法准确地反演出低剪切速率下的触变曲线(见图11)。而低剪切速率下的流变试验数据更能有利于揭示浆体从固态向液态转化的起动机制,更有利于揭示微观结构决定屈服应力的本质。因此,开发适用于充填料浆低剪切速率下流变特性的精密测量仪器和方法,进而确定浆体的本构方程,对矿山充填理论与技术的发展有着重要意义。
。现有的试验设备只能研究较高剪切速率(>20 s-1)下的流变规律,导致建立的流变模型无法准确地反演出低剪切速率下的触变曲线(见图11)。而低剪切速率下的流变试验数据更能有利于揭示浆体从固态向液态转化的起动机制,更有利于揭示微观结构决定屈服应力的本质。因此,开发适用于充填料浆低剪切速率下流变特性的精密测量仪器和方法,进而确定浆体的本构方程,对矿山充填理论与技术的发展有着重要意义。
文献[24]和[25]都是基于结构参数建立考虑时变性的流变模型,但对于结构动力学方程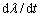 =
= ,两者都没有给出合理的边界条件,即认为料浆存在平衡结构而没有考虑不同配比料浆的初始结构参数不同。
,两者都没有给出合理的边界条件,即认为料浆存在平衡结构而没有考虑不同配比料浆的初始结构参数不同。
文献[24]基于H-B模型对流变参数进行时变性修正,而没有设计试验对修正关系式验证,其中认为屈服应力与结构参数成正比列关系,这与图7(a)中的数据变化关系不一致。
对于大流量充填矿山,料浆与管道的相对流速较大,即浆体处于高剪切速率下,稳定流动时浆体表现为Bingham流体特性,而文献[24]却对H-B模型进行修正,还有待商榷。
文献[24]和[25]均需要构建方程组对模型参数进行求解。文献[25]基于Bingham流体的时变模型含有6个参数,需要设计5个不同恒定剪切速率下的应力松弛试验,通过数据建立5元非线性方程组对参数进行优化求解,求解过程需要反复迭代。在求解之前,需要通过观察流变曲线,确定初始屈服应力、平衡塑性黏度和平衡剪切应力的值,观察确定的值存在误差,使得模型参数求解结果存在差异。而本文建立的流变模型直接对某一剪切速率下的曲线进行拟合,拟合参数均具有一定的物理意义,且参数求解简单,不需要多组试验曲线。另外,文献[24]的试验曲线中不同剪切速率下的初始屈服应力不同,而模型求解结果中的参数(屈服应力)却只有一个值。
5 结论
1) 超细尾砂充填料浆表现出应力松弛和触变性等复杂流变行为的根本原因在于微观结构的变化。
2) 剪切应力不仅与剪切速率有关,还是剪切时间的函数,且料浆在外部剪切作用下表现出剪切变稀的现象;在高剪切速率下,料浆流动的任意时刻表现出Bingham流体特性,且流变参数具有明显的时变性。理论分析得出,出现这些性质的根本原因在于浆体结构的动态变化。在试验的基础上,建立了基于结构参数的Bingham时变性流变模型。
3) 验证了提出的双变量流变模型对试验数据拟合程度较高,且模型的参数均具有一定的物理意义。拟合得到试验配比下的超细尾砂料浆流变参数,最大屈服应力和最大塑性黏度范围分别为120~ 220 Pa和1.7~7.2 Pa·s,极限屈服应力和极限塑性黏度范围分别为20~120 Pa和0.5~3.2 Pa·s。
REFERENCES
[1] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803-2813.
HE Man-chao, XIE He-ping, PENG Su-ping, et al. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics & Engineering, 2005, 24(16): 2803-2813.
[2] 钱鸣高, 许家林, 王家臣. 再论煤炭的科学开采[J]. 煤炭学报, 2018, 43(1): 1-13.
QIAN Ming-gao, XU Jia-lin, WANG Jia-chen. Further on the sustainable mining of coal[J]. Journal of China Coal Society, 2018, 43(1):1-13.
[3] 缪协兴, 巨 峰, 黄艳利, 等. 充填采煤理论与技术的新进展及展望[J]. 中国矿业大学学报, 2015, 44(3): 391-399.
MIAO Xie-xing, JU Feng, HUANG Yan-li, et al. New development and prospect of backfilling mining theory and technology[J]. Journal of China University of Mining & Technology, 2015, 44(3): 391-399.
[4] 周科平, 朱和玲, 高 峰. 采矿环境再造地下人工结构稳定性综合方法研究与应用[J]. 岩石力学与工程学报, 2012, 31(7): 1429-1436.
ZHOU Ke-ping, ZHU He-ling, GAO Feng. Research on stability of reconstructed underground artificial structure in mining environment by comprehensive method and its application[J]. Chinese Journal of Rock Mechanics & Engineering, 2012, 31(7): 1429-1436.
[5] 李夕兵, 周 健, 王少锋, 等. 深部固体资源开采评述与探索[J]. 中国有色金属学报, 2017, 27(6): 1236-1262.
LI Xi-bing, ZHOU Jian, WANG Shao-feng, et al. Review and practice of deep mining for solid mineral resources[J]. Chinese Journal of Nonferrous Metals, 2017, 27(6): 1236-1262.
[6] 付自国, 乔登攀, 郭忠林, 等. 基于RSM-BBD的废石-风砂胶结体配合比与强度试验研究[J]. 煤炭学报, 2018, 43(3): 694-703.
FU Zi-guo, QIAO Deng-pan, GUO Zhong-lin, et al. Experimental research on mix proportioning and strength of cemented hydraulic fill with waste rock and eolian sand based on RSM-BBD[J]. Journal of China Coal Society, 2018, 43(3): 694-703.
[7] 饶运章, 邵亚建, 肖广哲, 等. 聚羧酸减水剂对超细全尾砂膏体性能的影响[J]. 中国有色金属学报, 2016, 26(12): 2647-2655.
RAO Yun-zhang, SHAO Ya-jian, XIAO Guang-zhe, eet al. Effect of polycarboxylate-based superplasticizer on performances of super fine tailings paste backfill[J]. Chinese Journal of Nonferrous Metals, 2016, 26(12): 2647-2655.
[8] 付自国, 乔登攀, 郭忠林, 等. 超细尾砂胶结充填体强度计算模型及应用[J]. 岩土力学, 2018, 39(9): 3147-3156.
FU Zi-guo, QIAO Deng-pan, GUO Zhong-lin, et al. A model for calculating strength of ultra-fine tailings cemented hydraulic fill and its application[J]. Rock and Soil Mechanics, 2018, 39(9): 3147-3156.
[9] 吴爱祥, 刘晓辉, 王洪江, 等. 结构流充填料浆管道输送阻力特性[J]. 中南大学学报(自然科学版), 2014, 45(12): 4325-4330.
WU Ai-xiang, LIU Xiao-hui, WANG Hong-jiang, et al. Resistance characteristics of structure fluid backfilling slurry in pipeline transport[J]. Journal of Central South University (Science and Technology), 2014, 45(12): 4325-4330.
[10] 张修香, 乔登攀. 粗骨料高浓度充填料浆的管道输送模拟及试验[J]. 中国有色金属学报, 2015, 25(1): 258-266.
ZHANG Xiu-xiang, QIAO Deng-pan. Simulation and experiment of pipeline transportation of high density filling slurry with coarse aggregates[J]. Chinese Journal of Nonferrous Metals, 2015, 25(1): 258-266.
[11] 吴爱祥, 李 红, 程海勇, 等. 全尾砂膏体流变学研究现状与展望(上): 概念、特性与模型[J]. 工程科学学报, 2020, 42(7): 803-813.
WU Ai-xiang, LI Hong, CHENG Hai-yong, et al. Status and prospects of researches on rheology of paste backfill using unclassified-tailings (Part 1): Concepts, characteristics and models[J]. Chinese Journal of Engineering, 2020, 42(7): 803-813.
[12] 杨志强, 高 谦, 王永前, 等. 金川全尾砂-棒磨砂混合充填料胶砂强度与料浆流变特性研究[J]. 岩石力学与工程学报, 2014, 33(S2): 3985-3991.
YANG Zhi-qiang, GAO Qian, WANG Yong-qian, et al. Research on filling body strength and rheological properties of mixed filling mortar with unclassified tailings and rod milling sand in Jinchuan mine[J]. Chinese Journal of Rock Mechanics & Engineering, 2014, 33(S2): 3985-3991.
[13] BELEM T, BENZAAZOUA M. Design and application of underground mine paste backfill technology[J]. Geotechnical & Geological Engineering, 2008, 26(2): 147-174.
[14] 张友志, 甘德清, 陈 勋, 等. 尾砂胶结充填料浆剪切触变实验及其基于量纲分析的触变性预测模型[J]. 中国有色金属学报, 2020, 30(4): 951-959.
ZHANG You-zhi, GAN De-qing, CHEN Xun, et al. Experiment of shear thixotropy of cemented tailings filling slurry and its prediction model based on dimensional analysis[J]. Chinese Journal of Nonferrous Metals, 2020, 30(4): 951-959.
[15] 张修香, 乔登攀. 废石-尾砂高浓度料浆的流变特性及屈服应力预测模型[J]. 安全与环境学报, 2015, 15(4): 278-283.
ZHANG Xiu-xiang, QIAO Deng-pan. Rheological property and yield stress forecasting model of high-density slurry with waste rock-tailings[J]. Journal of Safety & Environment, 2015, 15(4): 278-283.
[16] 胡 华, 孙恒虎, 黄玉诚, 等. 似膏体粘弹塑性流变模型与流变方程研究[J]. 中国矿业大学学报, 2003, 32(2): 119-122.
HU Hua, SUN Heng-hu, HUANG Yu-cheng, et al. Rheological model and equation of viscoelastic-plasticity of paste-like backfill pulp[J]. Journal of China University of Mining & Technology, 2003, 32(2): 119-122.
[17] 蔡嗣经, 黄 刚, 吴 迪, 等. 尾砂充填料浆流变性能模型与试验研究[J]. 东北大学学报(自然科学版), 2015, 36(6): 882-886.
CAI Si-jing, HUANG Gang, WU Di, et al. Experimental and modeling study on the rheological properties of tailings backfill[J]. Journal of Northeastern University(Natural Science), 2015, 36(6): 882-886.
[18] JEONG S W, LOCAT J, LEROUEIL S, et al. Rheological properties of fine-grained sediment: The roles of texture and mineralogy[J]. Canadian Geotechnical Journal, 2010, 47(10): 1085-1100.
[19] TREGGER N A, PAKULA M E, SHAH S P. Influence of clays on the rheology of cement pastes[J]. Cement & Concrete Research, 2010, 40(3): 384-391.
[20] KLEIN B. A physical model for yield plastic fluids[J]. Particulate Science & Technology, 2009, 27(1): 1-15.
[21] TOORMAN E A. Modelling the thixotropic behaviour of dense cohesive sediment suspensions[J]. Rheologica Acta, 1997, 36(1): 56-65.
[22] 吴爱祥, 刘晓辉, 王洪江, 等. 恒定剪切作用下全尾膏体微观结构演化特征[J]. 工程科学学报, 2015, 37(2): 145-149.
WU Ai-xiang, LIU Xiao-hui, WANG Hong-jiang, et al. Microstructural evolution characteristics of an unclassified tailing paste in constant shearing[J]. Chinese Journal of Engineering, 2015, 37(2): 145-149.
[23] 杨柳华, 王洪江, 吴爱祥, 等. 全尾砂膏体搅拌剪切过程的触变性[J]. 工程科学学报, 2016, 38(10): 1343-1349.
YANG Liu-hua, WANG Hong-jiang, WU Ai-xiang, et al. Thixotropy of unclassified pastes in the process of stirring and shearing[J]. Chinese Journal of Engineering, 2016, 38(10): 1343-1349.
[24] 李 帅, 王新民, 张钦礼, 等. 超细全尾砂似膏体长距离自流输送的时变特性[J]. 东北大学学报(自然科学版), 2016, 37(7): 1045-1049.
LI Shuai, WANG Xin-min, ZHANG Qin-li, et al. Time-varying characteristic of paste-like super-fine unclassified tailings in long self-flowing transportation[J]. Journal of Northeastern University(Natural Science), 2016, 37(7): 1045-1049.
[25] 刘晓辉. 膏体流变行为及其管流阻力特性研究[D]. 北京: 北京科技大学, 2015.
LIU Xiao-hui. Study on rheological behavior and pipe flow resistance of paste backfill[D]. Beijing: University of Science and Technology Beijing, 2015.
[26] 王党伟, 吉祖稳, 邓安军, 等. 絮凝对三峡水库泥沙沉降的影响[J]. 水利学报, 2016, 47(11): 1389-1396.
WANG Dang-wei, JI Zu-wen, DENG An-jun, et al. Regularity for sediment floc deposition in the Three Gorges Reservoir[J]. Journal of Hydraulic Engineering, 2016, 47(11): 1389-1396.
[27] 李文杰, 杨胜发, 胡 江, 等. 三峡库区细颗粒泥沙絮凝的试验研究[J]. 应用基础与工程科学学报, 2015, 23(5): 851-860.
LI Wen-jie, YANG Sheng-fa, HU Jiang, et al. Experimental study on the fine sediment flocculation in the Three Gorges Reservoir[J]. Journal of Basic Science and Engineering, 2015, 23(5): 851-860.
[28] BERKER A, ARSDALE W E V. Phenomenological models of viscoplastic, thixotropic, and granular materials[J]. Rheologica Acta, 1992, 31(2): 119-138.
Bivariate rheological model of ultrafine tailings backfill slurry based on structural parameter and its applications
FU Zi-guo1, 2, 3, LI Hua1, 2, 3, DENG Jian-hui1, 2, 3, QIAO Deng-pan4, WANG Jia-xin4
(1. College of Water Resources and Hydropower, Sichuan University, Chengdu 610065, China;
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China;
3. Key Laboratory of Deep Earth Science and Engineering, Ministry of China, Sichuan University, Chengdu 610065, China;
4. Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093, China)
Abstract: Ultrafine tailings have become the largest solid waste in metal mine filling treatment. The rheological model provides a theoretical foundation for capturing its flow characteristics and determining the pipeline transportation parameters. To describe the shear response process of ultrafine tailings slurry, firstly, the concept of the structural parameter in this paper was introduced based on the formation mechanism of ultrafine particle flocculation structure. Then, a rotary viscometer was used to conduct 24 groups of rheological tests on the ultrafine tailings slurry with mass fractions of 72%, 74% and 76% and cement contents of 240 and 260 kg/m3 under different shear strengths. The results show that under constant shear strength, the shear stress of the slurry gradually decreases with the increase of shear time, and ultimately tends to be stable; under any shear time, the shear stress and shear rate (>20 s-1) approximately satisfy the Bingham model, and the Bingham regression parameters are obviously time-varying. The reason for these macroscopic laws can be attributed to the change of the slurry structural parameters. According to these evidences, a bivariate rheological model of the ultrafine tailings slurry with respect to shear strength and shear time was proposed, in which seven parameters have certain physical meanings. The proposed model was verified by the experimental data, and the rheological parameters of the ultrafine tailings slurry with the given mix are obtained by the best fitting. The maximum yield stress and maximum plastic viscosity range from 120 Pa to 220 Pa and from 1.7 Pa·s to 7.2 Pa·s, respectively, which can provide a reference for the calculation of the starting pressure; the range of the limit yield stress and plastic viscosity are from 20 Pa to 120 Pa and from 0.5 Pa·s to 3.2 Pa·s, respectively, which can give a reference for the calculation of the steady-state flow resistance of the slurry. Lastly, the applicable conditions and methods of the proposed rheological model are discussed, and also compared with the existing rheological model. The research results can provide theoretical and experimental basis for mine filling design.
Key words: filling slurry; ultrafine tailings; flocculation structure; thixotropy; rheological parameter; rheological model
Foundation item: Projects(U19A2098, 41772322) supported by the National Natural Science Foundation of China; Project(2016YFC0600702) supported by the National Key Research and Development Program of China
Received date: 2020-07-27; Accepted date: 2021-03-12
Corresponding author: LI Hua; Tel: +86-15882201391; E-mail: huali@scu.edu.cn
(编辑 龙怀中)
基金项目:国家自然科学基金资助项目(U19A2098,41772322);国家重点研发计划资助项目(2016YFC0600702)
收稿日期:2020-07-27;修订日期:2021-03-12
通信作者:李 化,博士;电话:15882201391;E-mail:huali@scu.edu.cn