文章编号：1004-0609(2014)04-1028-08

Pd基Heusler合金Pd₂CrGa和Pd₂FeGa的第一性原理研究

刘国平^{1, 2}，米传同^{1, 2}，钱  帅^{1, 2}，余新泉^{1, 2}，赵  昆^{1, 2}，于  金^{1, 2}

(1. 东南大学 材料科学与工程学院，南京 211189；

2. 东南大学 江苏省先进金属材料高技术研究重点实验室，南京 211189)

摘  要：运用基因遗传算法的晶格结构预测技术预测Pd基Heusler合金Pd₂MnSn、Pd₂CrGa和Pd₂FeGa的结构；采用基于密度泛函理论(DFT)的投影缀加波(PAW)方法研究Pd₂CrGa和Pd₂FeGa的四方变形、磁性、态密度、弹性常数和声子谱线，最后通过Helmholtz自由能的计算预测了Pd₂CrGa和Pd₂FeGa的相变温度。结构预测显示：极限条件0 K时，Pd₂MnSn以L2₁立方结构稳定存在，而Pd₂CrGa和Pd₂FeGa均以四方结构稳定存在。四方变形中，Pd₂CrGa、Pd₂FeGa在c/a＜1.0和c/a＞1.0处均有一个能量的局域最小值，分别对应一个稳定的结构。Pd₂CrGa、Pd₂FeGa在两种状态下均表现为铁磁性，Cr原子和Fe原子是总磁矩的主要贡献者。弹性常数计算结果显示：Pd₂CrGa和Pd₂FeGa仅在四方结构时才满足稳定性判据。c/a≈1.24处的四方结构Pd₂CrGa转变为立方结构的相变温度在350 K左右，c/a≈1.30处的四方结构Pd₂FeGa转变为立方结构的相变温度在130 K左右。

关键词：Heusler合金；结构预测；四方变形；声子

中图分类号：O482.54        　   　     文献标志码：A

First-principles study on Pd-based Heusler alloy Pd₂CrGa and Pd₂FeGa

LIU Guo-ping^{1, 2}, MI Chuan-tong^{1, 2}, QIAN Shuai^{1, 2}, YU Xin-quan^{1, 2}, ZHAO Kun^{1, 2}, YU Jin^{1, 2}

(1. School of Materials Science and Engineering, Southeast University, Nanjing 211189, China;

2. Jiangsu Key Laboratory of Advanced Metallic Materials, Southeast University, Nanjing 211189, China)

Abstract: Based on genetic algorithm, the structures of Pd-based Heusler alloy Pd₂MnSn, Pd₂CrGa and Pd₂FeGa were forecasted. The tetragonal distortion, magnetic, DOS elastic constants and phonon dispersion spectra of Pd₂CrGa and Pd₂FeGa were calculated by first-principles calculation based on DFT with projector augmented wave pseudopotential (PAW). At last, based on the result of Helmholtz free-energy, the phase transition temperatures of Pd₂CrGa and Pd₂FeGa were predicted. The crystal structure prediction shows that Pd₂MnSn is L2₁ cubic structure, but Pd₂CrGa and Pd₂FeGa are tetragonal structures at 0 K. The tetragonal distortion analysis show that there are local minimums total energy at c/a＜1.0 and c/a＞1.0, which correspond to stable martensitic phases. Pd₂MGa (M=Cr，Fe) are ferromagnetic in these two postures, and M (M=Cr，Fe) is the main magnetic contribution to its alloys, respectively. The elastic constants of Pd₂CrGa, Pd₂FeGa show that, cubic structure doesn’t satisfy stability conditions, but tetragonal structure satisfy the stability conditions at c/a≈1.24 and c/a≈1.30, respectively. Based on the results of Helmholtz free-energy, the phase transition temperatures of Pd₂CrGa and Pd₂FeGa tetragonal structure transferring to cubic structure are about 350 K and 130 K, respectively.

Key words: Heusler alloy; structure prediction; tetragonal distortion; phonon

磁性形状记忆合金(Magnetic shape memory alloy，MSMA)因其独特的磁性形状记忆效应^[1-2]，而成为备受关注的一种新型功能材料。MSMA兼有大恢复应变、大输出应力、高响应频率等优良性能，是一种理想的驱动与传感材料，有着广泛的应用前景^[3-4]。

Heusler合金是目前研究最多的一种MSMA材料，目前已经发现多种Heusler合金具有磁性形状记忆效应，如Ni基^[5-9]、Mn基^[10]、Cu基^[11]、Co基^[12-13]Heusler合金等；但Pd基Heusler合金的报道相对较少，Heusler合金结构预测和声子方面的研究也明显不足。Pd基Heusler合金与其他种类相比具有较高的超导临界温度，其研究也多集中在超导方面^[14-16]。因此，Pd基Heusler合金结构、四方变形、磁性、弹性常数和声子等方面的理论研究都具有重要的意义。

为验证计算方法的可靠性，本文作者前期对实验数据和计算数据都较丰富的Heusler合金Ni₂MnGa进行过较为全面的计算^[17]。在前期大量研究工作的基础上，本文作者运用基因遗传算法的晶格结构预测技术预测Pd基Heusler合金Pd₂MnSn、Pd₂CrGa和Pd₂FeGa的结构；采用基于密度泛函理论(DFT)的第一性原理方法研究Pd₂CrGa、Pd₂FeGa的四方变形、磁性、态密度、弹性常数和声子谱线。最后通过Helmholtz自由能的计算预测Pd₂CrGa、Pd₂FeGa的相变温度。较为系统地研究该合金的结构、磁性、弹性常数、声子、相变等规律，为今后的研究和开发工作提供理论依据。

1  模型与计算方法

Heusler合金为高度有序排列的三元金属间化合物，其晶格结构可以看作由4个互相贯通的FCC次晶格组成(见图1示)。A、B、C、D 4个位置分别被不同的原子占据可以形成两种不同的结构，分别对应Cu₂MnAl 型(空间群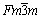)和Hg₂CuTi型(空间群)Heusler合金。

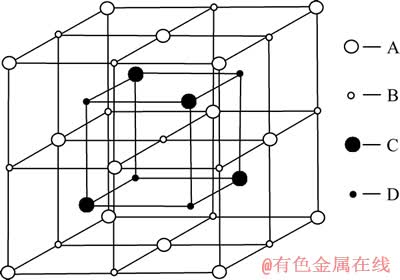
图1  Heusler合金的晶格结构

Fig. 1  Crystal structure of Heusler alloy

为了确定Pd₂CrGa、Pd₂FeGa的结构模型，本文作者首先采用基于基因遗传算法的USPEX软件包预测Pd₂CrGa、Pd₂FeGa的晶体结构。四方变形、磁性、态密度、弹性常数的计算是利用基于密度泛函理论(DFT, Density functional theory)的VASP软件包^[18-19]，采用经相对论校正的投影缀加波PAW(Projector augmented wave)方法^[20-21]，交换关联能采用广义梯度近似(GGA)，平面波截断能选取500 eV，K点网格采用12×12×12，计算过程均采用自旋极化的处理方式。进行立方结构声子计算时，建立了基于晶体学晶胞的2×2×2的超胞(128原子)；四方结构声子计算过程中，建立了基于物理学原胞3×3×3的超胞(108原子)，用VASP软件计算作用在胞内各个原子的力常数，然后用PHONOPY软件进行Pd₂CrGa、Pd₂FeGa声子的计算。

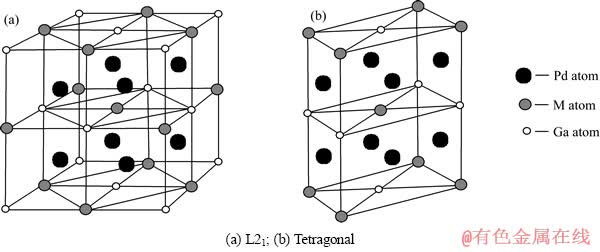
图2  Pd₂MGa(M=Cr, Fe)的晶格结构

Fig. 2  Crystal structure of Pd₂MGa(M=Cr, Fe)

结构预测显示，极限条件0 K时，Pd₂CrGa、Pd₂FeGa为四方结构(空间群I4/mmm)，如图2(b)所示，进而判定室温下，Pd₂CrGa、Pd₂FeGa为Cu₂MnAl 型L2₁结构(空间群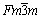)， 而非Hg₂CuTi型(空间群) Heusler合金。L2₁结构中，Pd原子的位置为(1/4, 1/4, 1/4)和(3/4, 3/4, 3/4)，M(M=Cr, Fe)和Ga原子则分别占据(0, 0, 0)和(1/2, 1/2, 1/2)位置，如图2(a)所示。

2  结果及分析

2.1  结构预测和四方变形

采用基于基因遗传算法软件包USPEX对Pd₂MnSn、Pd₂CrGa和Pd₂FeGa进行晶体结构预测，结果列于表1。结果显示，Pd₂MnSn以a=b=c=6.418 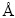的立方结构(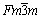)稳定存在，如图2(a)所示，该预测结果与实验值、理论计算值相符，表明可以采用此预测方法预测此类合金在极限条件0 K时的稳定结构。预测显示，Pd₂CrGa和Pd₂FeGa以四方结构(空间群I4/MMM)稳定存在，如图2(b)所示。

表1  Pd₂MnSn和Pd₂MGa(M=Cr, Fe)的晶格常数

Table 1  Lattice constants of Pd₂MnSn and Pd₂MGa(M=Cr, Fe)

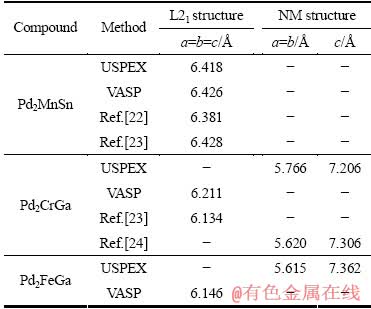
基于USPEX预测结果，本文作者建立Pd₂CrGa和Pd₂FeGa的L2₁结构模型，并采用自旋极化方式对Pd₂MnSn、Pd₂CrGa和Pd₂FeGa晶胞进行晶格优化。体积优化过程中，通过对一系列不同体积和能量的拟合，以确定立方结构的基态能量，进而获得立方结构的晶格常数，结果列于表1。

EBP’s方法^[25-27]是目前国内外研究Heusler合金常用的成熟方法。对优化后的Pd₂CrGa和Pd₂FeGa立方结构施加四方变形，变形过程中保持体积不变，变形曲线如图3所示。

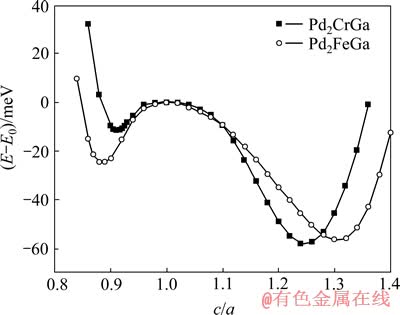
图3  Pd基Heusler合金Pd₂CrGa和Pd₂FeGa体积不变时总能差(相对于L2₁结构)与c/a的关系

Fig. 3  Total-energy difference (E-E₀) dependence of Pd₂CrGa and Pd₂FeGa on variation of c/a at constant volume (corresponding to L2₁ structure)

四方变形过程中，Pd₂CrGa、Pd₂FeGa在c/a＜1.0和c/a＞1.0处均出现总能的局域极小值，前者较浅，后者较深，这与Ni₂MnGa的四方变形曲线^{[9, 28]}极其相似。Pd₂CrGa、Pd₂FeGa在c/a>1.0时的四方结构马氏体相分别出现在c/a≈1.24和c/a≈1.30处，与前面USPEX预测的结果相吻合。Pd₂CrGa、Pd₂FeGa的这种性质预示着它在c/a＞1.0处会出现非调制(NM)四方结构的马氏体相，这种结构转变预示着Pd₂CrGa、Pd₂FeGa可能存在马氏体相变，具有较高的应用和开发价值。

2.2  磁性和态密度

表2  Pd₂CrGa、Pd₂FeGa的总磁矩和各原子的局域磁矩

Table 2 Total and local magnetic moments of Pd₂CrGa, Pd₂FeGa

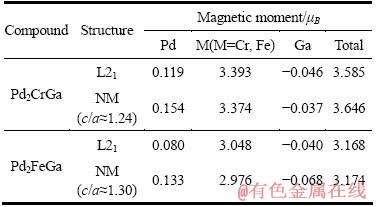
Pd₂CrGa、Pd₂FeGa的L2₁结构和NM四方结构的磁矩计算结果列于表2。从表2可知，无论是L2₁立方结构还是NM四方结构Pd₂CrGa、Pd₂FeGa均呈铁磁有序排列。L2₁结构中，Pd₂CrGa、Pd₂FeGa单胞总磁矩分别为3.585 μ_B、3.168 μ_B；NM四方结构中，Pd₂CrGa、Pd₂FeGa单胞总磁矩分别为3.646 μ_B、3.174 μ_B。在两种状态下， M(M=Cr, Fe)原子均是Pd₂MGa总磁矩的主要来源，Pd原子对磁矩的贡献较小，而Ga原子对总磁矩的贡献可以忽略。

Pd₂CrGa、Pd₂FeGa的L2₁结构和NM四方结构的态密度如图4所示。从图4中可以看出，Pd₂CrGa、Pd₂FeGa在两种状态下均表现出很强的自旋极化，而且在费米面附近尤为明显。M(M=Cr, Fe)原子的态密度差异是Pd₂MGa(M=Cr, Fe)总态密度差异的主要来源，而Pd原子、Ga原子的自旋向上和自旋向下态密度的对称性较高，对总磁矩的贡献有限。所以，M(M=Cr, Fe)原子是Pd₂CrGa、Pd₂FeGa磁性的主要贡献者。

2.3 弹性常数和体积模量

国内外利用第一性原理计算弹性常数最常用的方法有两种：应力应变法和能量法。本文作者采用能量法计算了Pd₂CrGa、Pd₂FeGa在L2₁结构和NM四方结构两种状态下的弹性常数和体积模量。L2₁结构属于立方晶系存在3个独立的弹性常数C₁₁、C₁₂和C₄₄。 NM四方结构包含6个独立的弹性常数C₁₁、C₁₂、C₁₃、C₃₃、C₄₄和C₆₆。

立方结构的计算采用的是文献[29]中介绍的变形矩阵，NM四方结构采用的是文献[28]中介绍的变形矩阵。体积模量是材料对于表面压强产生变形程度的度量，立方结构体积模量(B)可由式(1)给出：

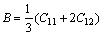                            (1)

四方结构的体积模量可由式(2)得到：

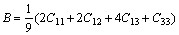                (2)

计算结果列于表3。

从表3的结果可以看出，Pd₂CrGa、Pd₂FeGa的立方结构不符合立方晶体的稳定性判据^[3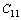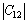0]：

＞,＞0, 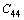＞0             (3)

但NM四方结构的弹性常数满足四方相稳定判据^[31]：

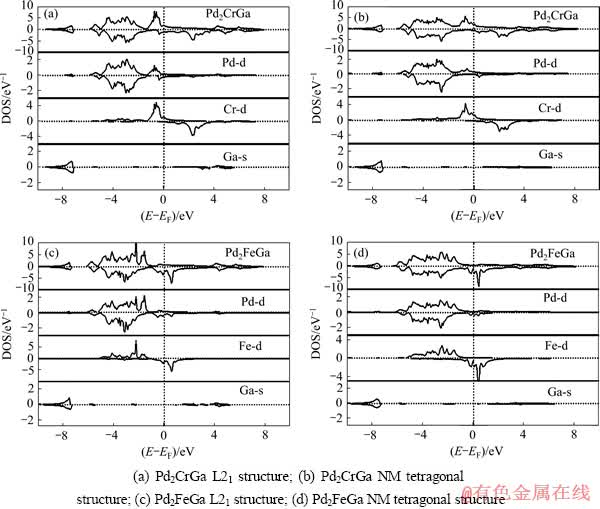
图4  Pd₂CrGa和Pd₂FeGa的态密度

Fig. 4  Calculated spin-projected DOS plots for Pd₂CrGa and Pd₂FeGa

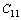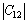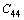＞,＞0,＞0, 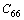＞0      (4)

通过对Pd₂CrGa、Pd₂FeGa立方结构和四方结构弹性常数的计算发现，四方结构比立方结构更加稳定，这与图4所示的能量曲线及结构预测结果相吻合。

2.4  声子谱和相变计算

声子谱线对研究材料的动力学特性是非常重要的，材料的许多物理特性都依赖于声子特性，例如比热、热膨胀、自由能、热传导、电子声子耦合等。声子谱线在不同条件下的变化情况是反映物质结构稳定性的有效方法，经常被用作结构稳定性的判定依据^[32-34]，如果计算得到的声子谱线存在虚频，则说明该结构是不稳定相。利用第一性原理计算来研究相变是一个常用的方法^[35-36]，通过计算赫姆霍兹自由能可以了解晶体的相变温度。本文作者采用第一性原理计算的方法计算Pd₂CrGa、Pd₂FeGa在两种状态下的声子谱线，其结果如图5和6所示。

表3  Pd₂CrGa、Pd₂FeGa的立方结构和四方结构的弹性常数

Table 3  Calculated bulk modulus and elastic constant for Pd₂CrGa, Pd₂FeGa

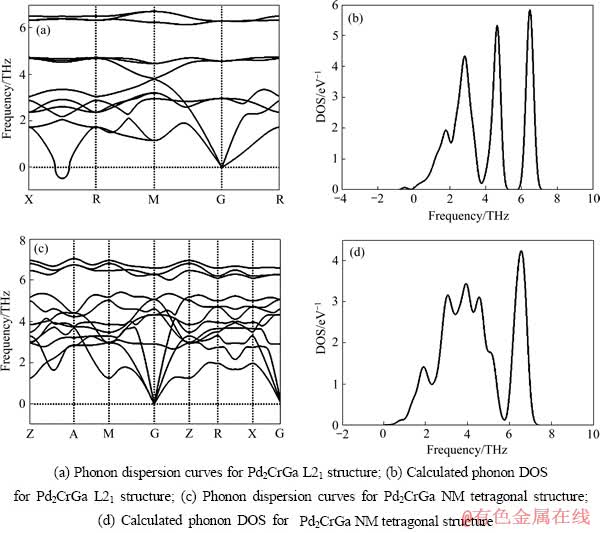
图5  Pd₂CrGa的声子色散曲线

Fig. 5  Phonon dispersion curves of Pd₂CrGa

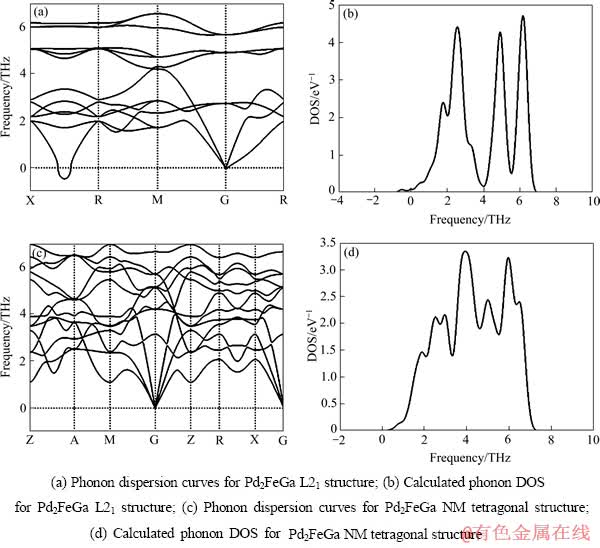
图6  Pd₂FeGa 的声子色散曲线

Fig. 6  Phonon dispersion curves of Pd₂FeGa

Pd₂CrGa、Pd₂FeGa的声子谱共有12条分支，每条分支对应一个振动模式，其中低频率的3支对应声学声子，高频率的9支对应光学声子。Pd₂CrGa、Pd₂FeGa立方结构的声子谱中，横向声学支的频率在X—R方向存在虚频，也就是说出现了具有负能量的声子。这就意味着该结构是不稳定的，易于在外界扰动下向另一种较稳定的结构转化。

Pd₂CrGa、Pd₂FeGa立方结构的声子谱中，在G－R方向声学支发生简并，而四方结构的声学支是非简并的。通过声子态密度可以看出，立方结构声子态密度的峰值较高、宽度较大，这些都说明立方结构时晶体内振动模式的频率较强，振动频率的范围也较多。多种振动频率的相互作用会使得原有的相互平衡的振动格局失去平衡；当平衡的振动格局被打破时便发生结构相变。

利用第一性原理计算Helmholtz自由能，进而研究晶体的相变温度是一种常用的方法。Helmholtz自由能分为3部分：0 K时的总能、振动自由能和激发电子自由能，表达式如式(5)所示：

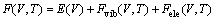           (5)

式中：E(V)是0 K时的总能；F_ele(V,T)是激发电子自由能；F_vib(V,T)是晶体振动自由能，其表达式如式(6)所示：

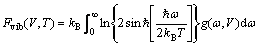   (6)

式中：k_B为玻尔兹曼常数；ω为声子频率；为频率和体积V对应的声子态密度。

激发电子自由能可以由式(7)得到：

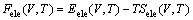              (7)

式中：E_ele(V,T)为激发电子能量，S_ele(V,T)为激发电子熵，分别如式(8)和(9)所示：

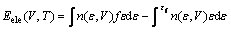        (8)

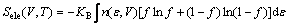(9)

式中：n(ε,V)为电子态密度；f为Fermi-Dirac分布。

本文作者通过计算得到Pd₂CrGa、Pd₂FeGa的Helmholtz自由能和温度的关系曲线，结果分别如图7和8所示。

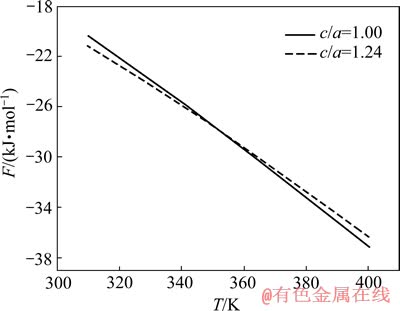
图7  Pd₂CrGa的Helmholtz自由能和温度的关系曲线

Fig. 7  Helmholtz free energy of Pd₂CrGa as function of temperature

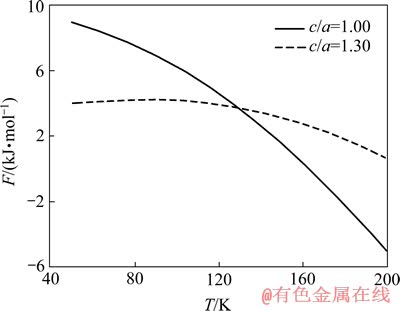
图8  Pd₂FeGa的Helmholtz自由能和温度的关系曲线

Fig. 8  Helmholtz free energy of Pd₂FeGa as function of temperature

从图7和8可知，c/a=1.0的立方结构Pd₂CrGa转变为c/a≈1.24的四方结构的相变温度在350 K左右，而c/a=1.0的立方结构的Pd₂FeGa转变为c/a≈1.30的四方结构的相变温度在130 K左右。在相变温度以下，Pd₂CrGa、Pd₂FeGa均是四方结构Helmholtz自由能更低，说明四方结构更加稳定，这也与前面结构预测、四方变形、弹性常数、声子谱线的计算结果相吻合。

3  结论

1) 利用基因遗传算法预测Pd基Heusler合金Pd₂MnSn、Pd₂CrGa和Pd₂FeGa的结构。Pd₂MnSn以L2₁立方结构(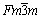)稳定存在，Pd₂CrGa、Pd₂FeGa以NM四方结构(I4/MMM)稳定存在。Pd₂MGa(M=Cr，Fe)的能量曲线与Ni₂MnGa的能量曲线类似，在c/a＞1.0处对应一个稳定的马氏体相，与预测结果吻合。

2) 利用基于DFT的第一性原理VASP软件包研究了Pd₂CrGa、Pd₂FeGa的四方变形、磁性、态密度、弹性常数和声子谱线的特性。Pd₂MGa(M=Cr, Fe)在两种状态下都表现为铁磁性，M(M=Cr, Fe)原子3d电子的自旋是Pd₂MGa(M=Cr, Fe)磁性的主要来源。结构预测、弹性常数和声子的计算结果均显示四方结构更加稳定。

3) 通过计算Helmholtz自由能和温度的关系预测Pd₂CrGa、Pd₂FeGa的相变温度分别在350 K和130 K左右。

REFERENCES

[1] ULLAKKO K, HUANG J K, KOKORIN V V, O’HANDLEY R C. Magnetically controlled shape memory effect in Ni₂MnGa intermetallics[J]. Scripta Materialia, 1997, 36(10): 1133-1138.

[2] ULLAKKO K. Magnetically controlled shape memory alloys: A new class of actuator materials[J]. Journal of Materials Engineering and Performance, 1996, 5(3): 405-409.

[3] CLAEYSSEN F, LHERMET N, LELETTY R, BOUCHILLOUX P. Actuators, transducers and motors based on giant magnetostrictive materials[J]. Journal of Alloys and Compounds, 1997, 258(1/2): 61-73.

[4] POPULOH S, AGUIRRE M H, BRUNKO O C, GALAZKA K, LU Y, WEIDENKAFF A. High figure of merit in (Ti,Zr,Hf)NiSn half-Heusler alloys[J]. Scripta Materialia, 2012, 66(12): 1073-1076.

[5] ULLAKKO K,HUANG J K, KANTNER C, O’ HANDLEY R C, KOKORIN V V. Large magnetic-field-induced strains in Ni₂MnGa single crystals[J]. Applied Physics Letters, 1996, 69(13): 1966-1968.

[6] LIU Z H, ZHANG M, CUI Y T, ZHOU Y Q, WANG W H, WU G H, ZHANG X X, XIAO G. Martensitic transformation and shape memory effect in ferromagnetic Heusler alloy Ni₂FeGa[J]. Applied Physics Letters, 2003, 82(3): 424-426.

[7] FUJITA A, FUKAMICHI K, GEJIMA F, KAINUNM R, ISSHIDA K. Magnetic properties and large magnetic-field- induced strains in off-stoichiometric Ni-Mn-Al Heusler alloys[J]. Applied Physics Letters, 2000, 77(19): 3054-3056.

[8] SUTOU Y, LMANO Y, KOEDA N, OMORI T, KAINUM R, ISHIDA K, OIKAWA K. Magnetic and martensitic transformations of NiMnX(X=In,Sn,Sb) ferromagnetic shape memory alloys[J]. Applied Physics Letters, 2004, 85(19): 4358-4360.

[9] 吴玉蓉, 胡望宇, 赵栋梁. Heusler合金Ni₂MnGa磁性微观机理的第一性原理[J]. 中国有色金属学报, 2005, 15(11): 1843-1847.

WU Yu-rong, HU Wang-yu, ZHAO Dong-liang. First-principles of magnetic microcosmic mechanism for Ni₂MnGa Heusler alloy[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(11): 1843-1847.

[10] LIU G D, DAI X F, YU S Y, ZHU Z Y, CHEN J L, WU G H. Physical and electronic structure and magnetism of Mn₂NiGa: Experiment and density-functional theory calculations[J]. Physical Review B, 2006, 74(5): 054435.

[11] 刘传歆, 郑玉红, 李崇剑, 龙 毅, 万发荣. Cu-Al-Mn合金的低温形状记忆效应与晶体结构的关系[J]. 中国有色金属学报, 2008, 18(7): 1254-1260.

LIU Chuan-xin, ZHENG Yu-hong, LI Chong-jian, LONG Yi, WAN Fa-rong. Relationship between shape memory effect at low temperature and microstructure of Cu-Al-Mn alloy[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(7): 1254-1260.

[12] WUTTIG M, LI J, CRACIUNESEU C. A new ferromagnetic shape memory alloy system[J]. Scripta Materialia, 2001, 44(10): 2393-2397.

[13] OIKAWA K, WULFF L, IIJIMA T, GEJIMA F, OHMORI T, FUJITA A, FUKAMICHI K, KAINUMA R, LSHIDA K. Promising ferromagnetic Ni-Co-Al shape memory alloy system[J]. Applied Physics Letters, 2001, 79(20): 3290-3292.

[14] KIERSTEAD H A, DUNLAP B D, MALIK S K, UMARJI A M, SHENOY G K. Coexistence of ordered magnetism and superconductivity in Pd₂YbSn[J]. Physical Review B, 1985, 32(1): 135-138.

[15] SHELTON R N, HAUSERMANN-BERG L S, JOHNSON M J, KLAVINS P, YANG H D. Coexistence of superconductivity and long-range magnetic order in ErPd₂Sn[J]. Physical Review B, 1986, 34(1): 199-202.

[16] DONNI A, FISCHER P, FAUTH F, CONVERT P, AOKI Y, SUGAWARA H, SATO H. Antiferromagnetic ordering in the cubic superconductor YbPd₂Sn[J]. Physica B, 1999, 259/261: 705-706.

[17] 刘国平. Pd基Heusler合金的第一性原理研究[D]. 南京: 东南大学, 2013.

LIU Guo-ping. First principles studies of Pd-based Heusler alloy[J]. Nanjing: Southeast University, 2013.

[18] HAFNER J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond[J]. Journal of Computational Chemistry, 2008, 29(13): 2044-2078.

[19] KRESSE G, FURTHMULLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16): 11169-11186.

[20] TORRENT M, JOLLET F, BOTTIN F. Implementation of the projector augmented-wave method in the ABINIT code: Application to the study of iron under pressure[J]. Computational Materials Science, 2008, 42(2): 337-351.

[21] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B, 1999, 59(3): 1758-1775.

[22] KANOMATAA T, ENDOA K, CHIEDAA Y, SUGAWARAA T, OBARAB K, SHISHIDOB T, MATSUBAYASHIC K, UWATOKOC Y, NISHIHARAD H, UMETSUB R Y, NAGASAKOE M, KAINUMAE R. Magnetic properties of Mn-rich Pd₂MnSn Heusler alloys[J]. Journal of Alloys and Compounds, 2010, 505(1): 29-33.

[23] GILLESSEN M. Made-to-measure products and substitute for analytics: About the quantum-chemical studies of some ternary intermetallic phase[D]. Aachen: Aachen University, 2009.

[24] GILLESSEN M, DRONSKOWSKI R. A combinatorial study of inverse Heusler alloys by first-principles computational methods[J]. Journal of Computational Chemistry, 2010, 31(3): 612-619.

[25] ALIPPI P, MARCUS P M, SCHEFFLER M. Strained tetragonal states and Bain paths in metals[J]. Physical Review Letters, 1997, 78(20): 3892-3895.

[26] MARCUS P M, ALIPPI P. Tetragonal states from epitaxial strain on metal films[J]. Physical Review B, 1998, 57(3): 1971-1975.

[27] 赵 昆, 张 坤, 王家佳, 于 金, 吴三械. Heusler合金Pd₂CrAl四方变形、磁性及弹性常数的第一性原理计算[J]. 物理学报, 2011, 60(12): 127101-1-6.

ZHAO Kun, ZHANG Kun, WANG Jia-jia, YU Jing, WU San-xie. A first principles study on tetragonal distortion, magnetic property and elastic constants of Pd₂CrAl Heusler alloy[J]. Acta Physica Sinica, 2011, 60(12): 127101-1-6.

[28] KART S O, ULUDOGAN M, KARAMAN I, CAGIN T. DFT studies on structure, mechanics and phase behavior of magnetic shape memory alloys: Ni(2)MnGa[J]. Physica Status Solidi A, 2008, 205(5): 1026-1035.

[29] RACHED H, RACHED D, KHENATA R, RESHAK ALI H, RABAH M. First-principles calculations of structural, elastic and electronic properties of Ni(2)MnZ (Z=Al, Ga and In) Heusler alloys[J]. Physica Status Solidi B, 2009, 246(7): 1580-1586.

[30] WALLACE D C. Thermodynamics of crystals[M]. New York: John Wiley & Sons, 1972: 39.

[31] JONA F, MARCUS P M. Structural properties of copper[J]. Physical Review B, 2001, 63(9): 094113-1-8.

[32] 原鹏飞, 祝文军, 徐济安, 刘绍军, 经福谦. BeO高压相变和声子谱的第一性原理计算[J]. 物理学报, 2010, 59(12): 8755-8761.

YUAN Peng-fei, ZHU Wen-jun, XU Ji-an, LIU Shao-jun, JING Fu-qian. High pressure phase transition and phonon-dispersion relations of BeO calculated by first-principles method[J]. Acta Physica Sinica, 2010, 59(12): 8755-8761.

[33] HAO Y J, ZHANG L, CHEN X R. Ab initio calculations of the thermodynamics and phase diagram of zirconium[J]. Physical Review B, 2008, 78(13): 134101-1-4

[34] MEI Z G, SHANG S L, WANG Y. Density-functional study of the thermodynamic properties and the pressure-temperature phase diagram of Ti [J]. Physical Review B, 2009, 80(10): 104116-1-9.

[35] WANG Y, LIU Z K, CHEN L Q. Thermodynamic properties of Al, Ni, NiAl, and Ni₃Al from first-principles calculations[J]. Acta Materialia, 2004, 52(9): 2665-2671.

[36] BERCEGEAY C, BERNARD S. First-principles equations of state and elastic properties of seven metals[J]. Physical Review B, 2005, 72(21): 21410-1-9.

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(21173041)

收稿日期：2013-01-20；修订日期：2014-02-28

通信作者：于  金，教授，博士；电话：025-82089129；E-mail: yujin@seu.edu.cn