J. Cent. South Univ. (2016) 23: 1556-1563

DOI: 10.1007/s11771-016-3208-8

Processing maps and hot working mechanisms of supercritical martensitic stainless steel

WANG Meng-han(王梦寒), WANG Rui(王瑞), MENG Lie(孟烈), WANG Gen-tian(王根田)

College of Material Science and Engineering, Chongqing University, Chongqing 400044, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: The hot working mechanism of 2Cr11Mo1VNbN steel was investigated by means of compression tests at temperatures of 900-1150 °C and strain rates of 0.005-5 s^-1. At strains of 0.2, 0.3, 0.5 and 0.7, the relationship among strain rate sensitivity, power dissipation efficiency and instability parameter under different conditions were studied. Power dissipation maps and instability maps at different strains were established. The optimal and the instable deformation regimes were established by the processing maps based on the dynamic material model. The processing maps were developed for the typical strains of 0.2, 0.3, 0.5 and 0.7, predicting the instability regions occurring at high strain rate more than 0.05 s^-1, which should be avoided during hot deformation. The optimized processing parameters for hot working of 2Cr11Mo1VNbN supercritical stainless steel were temperatures of 1080-1120 °C and strain rates of 0.005-0.01 s^-1.

Key words: martensitic stainless steel; processing map; strain-rate sensitivity; hot deformation

1 Introduction

With high strength, high toughness and good corrosion resistance, the martensitic stainless steels are widely used in vehicle structure, steam power plants, nuclear power equipment and so forth [1-4]. Based on the superior properties, these steels are suitable for a wide range of applications, such as steam generators, pressure vessels and aircraft engine. In the aircraft engine and steam turbine, turbine blade is a key component, which can affect the workability of equipment. Turbine blades often work in harsh environments, such as high temperature, high speed rotation, which require that the blades should have good characteristics to resist the bad work conditions. As an advance martensitic steel, 2Cr11Mo1VNbN steel shows an excellent property in extreme working environments.The turbine blade needs a good deformation process to get excellent properties for its complex shape and extreme working conditions [5].

It is well known that the investigation of hot deformation can provide a better selection of deformation parameters to improve the workability of the metal. During hot deformation process, the deformation parameters, such as strain rate, temperature and strain, are very important factors of getting good properties [6-8]. The material flow behavior during hot deformation is of complex, in which the work hardening and dynamic softening phenomena are affected by deformation parameters, such as temperature, strain and strain rate. Up to now, many researches have been done on the hot deformation behaviors and microstructure evolution of martensitic stainless steels [9-10]. The constitutive equation correlating the flow stress, strain, strain rate and temperature can be used to predict the flow stress during hot deformation [11-14]. In recent years, the Arrhenius equation has been widely used to establish the model of flow stress during hot deformation. Moreover, the constitutive model considering compensation strain is taken into account in many newly Arrhenius equations [15-16]. Processing maps, constructed by hot deformation test data, can be used to optimize deformation parameters, control microstructures and explain deformation mechanism and so forth [17-20]. Moreover, the instability in the hot deformation can also be predicted from the processing map, which will provide guidance for avoiding the deformation defects.

In this work, the effects of deformation temperature, strain rate and strain on the flow stress of 2Cr11Mo1VNbN steel were investigated by compression tests. The power dissipation parameter and instability parameter were analyzed to determine the stable and unstable regions for hot deformation. The processing maps based on the dynamic materials model (DMM) were developed to clarify the deformation mechanisms and optimize the hot working process. The optimum hot working conditions for 2Cr11Mo1VNbN steel are suggested.

2 Experimental procedures

Cylindrical specimens for compression tests (8 mm in diameter and 12 mm in height) were machined from the hot rolled sheet. Hot compression tests were conducted on a Gleeble-3500 thermo-mechanical simulator in the temperature range of 950-1150 °C with intervals of 50 °C and strain rate range of 0.005-5 s^-1. All the samples were heated to 1200 °C at heating rate of 10 °C/s and held for 3 min to obtain uniform microstructure. The specimens were cooled down to different temperatures at cooling rate of 20 °C/s and hold for 2 min. The specimens were compressed to total strain of 0.7 and then quenched in water within less than 5 s.

3 Results and discussion

3.1 Flow stress behavior

From the hot compression tests data, the true stress–true strain curves of 2Cr11Mo1VNbN measured at diverse strain rates and temperatures are shown in Fig. 1.

All the flow curves exhibit work hardening, peak flow stresses, flow softening and steady state. It is observed from Fig. 1 that the shapes of flow curves are dependent on the deformation temperature, the strain rate and the flow stress increase with increasing strain rate and stress decreases with increasing deformation temperature. The trends of the curves indicate the sensitivity of flow stress to the alteration of deformation temperature and strain rate. The phenomenon can be attributed to the high temperature and lower strain rates which can provide more time and energy for dislocation accumulation and annihilation, nucleation and growth of DRX. In hard working stage, the dislocations emerged and accumulated in matrix, which caused the increase of flow stress. The flow stress decreases according to the enhancement of dislocation movement and grain boundary diffusion and the occurrence of DRX at higher deformation temperatures [17-22]. In the steady state, the flow stress increases into a steady-state value, which is determined by the balance between the dislocation accumulation and the dislocation elimination.

Fig. 1 True stress-true strain curves of 2Cr11Mo1VNbN in strain range of 0.005-5 s^-1 at temperatures:

3.2 Strain rate sensitivity

Plot of ln σ versus 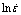is shown in Fig. 2, where the relationship can be fitted with cubic polynomial curves. As ln σ versus 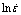obeys cubic polynomial relationship, the strain rate sensitivity parameters can be obtained by the instantaneous tangent vector at different positions of the curves. The strain rate sensitivity parameter (m) is an important factor in describing the hot deformation behavior in forming process. According to the Cottrell- Stokes law, m is considered an independent factor of the strain. DALLA TORRE et al [23] studied the relationship between m and strain, and found the relationship is complicated. In order to get a better understanding of the relationship of temperature, strain and strain rate, cubic fitting curves were established on the basis of ln σ value. The relationship among the m value, temperatures and strain rates at different strains is shown in Fig. 3. In Fig. 3, the m values are higher under the conditions of lower strain rates and higher temperature. The lower m value means microscopic defects to some extent; however, it is not the sufficient condition. The discrimination microscopic defects can be judged through the energy dissipation and instability criterion.

3.3 Characterization of processing map

In order to predict the deformation defects and identify the deformation mechanism, the approach of dynamic materials model is often used to construct the processing map. Actually, a processing map is plotted based on the power dissipation map which represents the response of material to the applied strain rate at a constant temperature. The flow stress-strain curve and the flow behavior of materials are strongly dependent on the strain rate and temperature. The total dissipated power P consists of two parts: G and J, and is described as follows [24]:

               (1)

where σ is the flow stress; is the strain rate. The first G content is defined as the main power dissipated in the deformation and second J represents the power dissipated in microstructures evolution. The flow stress data were used to calculate the strain rate sensitivity by using the following equation [25-27]:

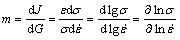                (2)

The general form of the flow behavior at constant strain and temperature can be expressed as

                                   (3)

where K and are constants; m is the strain rate sensitivity.

The dissipator co-content J can be described as follows:

                                (4)

For an ideal linear dissipater, the power dissipation efficiency occurring though microstructural changes is the maximum while m=1 and G=J. The efficiency of power dissipation η can be defined as [28]

                             (5)

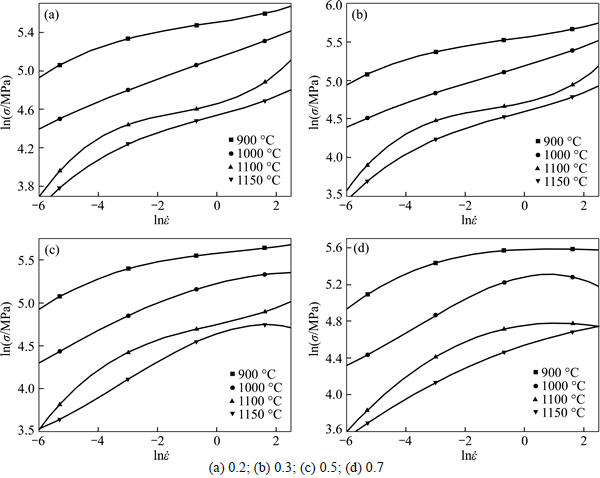
Fig. 2 Relationships between lnσ and at different temperatures and strain rates with strains:

Fig. 3 Relationship among m, temperatures and strain rates at strains:

The efficiency of power dissipation η is a dimensionless parameter to indicate the power dissipation by microstructure evolution, and the material deformed in the condition with high efficiency of power dissipation shows high workability. In order to display the power dissipation visually, the power dissipation graphs were established in Fig. 4. Figure 4 shows the power dissipation maps at strains of 0.2, 0.3, 0.5 and 0.7, and the iso-efficiency contours have been plotted. In the maps, the value on the line indicates the dissipation efficiency value of η in hot deformation. In maps, the values of power dissipation are associated with the microstructure evolution, such as recrystallization and recovery. At high value of power dissipation, materials have sufficient conditions for recrystallization and recovery. The regions with low values are considered to be unstable, which is at risk of defects. In Fig. 4(a), the map exhibits one region with high value range of 0.40-0.50 at temperature of 1050-1140 °C and stain rate of 0.005-0.02 s^-1. In Fig. 4(b), the map exhibits a region with high value range of 0.45-0.58, at temperatures of 1050-1140 °C and stain rates of 0.005-0.02 s^-1. In Fig. 4(c), the map exhibits a region with high value range of 0.40-0.54, at temperatures of 1020-1140 °C and stain rates of 0.005-0.02 s^-1. In Fig. 4(d), the map exhibits a region with high value range of 0.40-0.48, at temperatures of 1030-1125 °C and stain rates of 0.005- 0.025 s^-1. However, wedge cracks can also lead high η values in hot deformation. It can be conducted that the power dissipation map is inadequate to provide advice for deformation process. Thus, another parameter, which represents the instability, should be considered to determine the workability region for the material.

In order to identify whether these instabilities occur in the hot deformation, mathematically, another factor ξ can be used [29]:

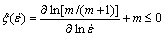                  (6)

where is the instability parameter. The flow in stabilities is predicted to occur when becomes negative.

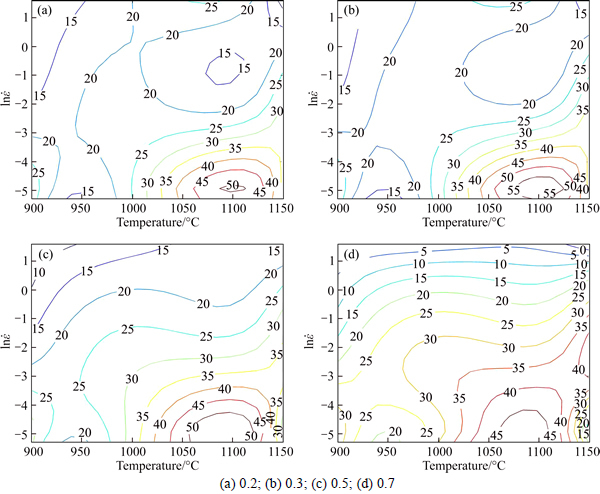
Fig. 4 Power dissipation maps of steel of different strains:

The instability map is superimposed on the dissipation map to obtain a processing map, which exhibits characteristics of different mechanisms. Figure 5 shows the contours of the instability maps for 2Cr11Mo1VNbN steel of different strains. In the unstable maps, the regions where <0 is viewed as unstable in material, while >0 is considered to be stable in the material [30-31]. The lower value the parameter ξ is, the higher risk of unstable flow behavior will be. In Fig. 5, the unstable regions often occur for the reason of microcracks, strain aging, localized plastic flow or adiabatic deformation bands [32]. In Fig. 5, the colored regions represent the unstable flow behavior of the material, and decreasing with the increasing of strain. In Fig. 5(a), the unstable flows occur in two regions: one is in temperature range of 1000-1150 °C and strain rate range of 0.013-0.6 s^-1; another is in temperature range of 900-1000 °C and strain rate range of 1-5 s^-1. In Fig. 5(b), the unstable regions occur in three regions: one is in temperature range of 1000-1150 °C and strain rate range of 0.015-0.6 s^-1; one is in temperature range of 900-1000 °C and strain rate range of 1-5 s^-1; another is in temperature range of 900-910 °C and strain rate range of 0.01-1.3 s^-1. In Figs. 5(c) and (d), the unstable regions occur in temperature range of 900-1000 °C and strain rate range of 0.15-5 s^-1 and temperature range of 1000-1150 °C and strain rate range of 0.04-5 s^-1.

The high efficiency of power dissipation indicates that the material dissipates more energy for the changes of structure, associated with the DRX which is thought to be a best choice for the hot deformation for it providing relatively stable flow stresses and low work hardening rate [26]. Therefore, the higher the power dissipation efficiency, the greater the m value, the more beneficial to the DRX process, grain refinement and improvement of hot workability of material. The value of ξ in instability map indicates the risk of defects which should be avoided during hot deformation process. The processing map, composed of instability map and power dissipation map, is designed and controlled to optimize hot workability and to produce desired microstructure [33-35].

The processing maps of 2Cr11Mo1VNbN supercritical steel at strains of 0.2, 0.3, 0.5 and 0.7 are shown in Fig. 6. In the figures, the contour numbers indicate the power dissipation efficiency in percent and the shaded regions correspond to the flow instability.

It can be seen in Fig. 6, the instability domains increase with the increasing strain. However, the variant of instability domain is not obvious at high strain than 0.5 (Figs. 6(c) and (d)). Figures 6(a) and (b) show that at the strains of 0.2 and 0.3, flow instability will occur in the domain in temperature range of 1020-1130 °C, strain rate range of 0.01-0.6 s^-1. Figures 6(c) and (d) show that flow instability will occur in the domain when the strain is higher than 0.36 s^{-1 in} the whole temperatures range. It can be seen in Fig. 6 that at the temperature of 1050-1120 °C and strain rates of 0.005-0.01 s^-1, the efficiency of power dissipation is higher than 45%.

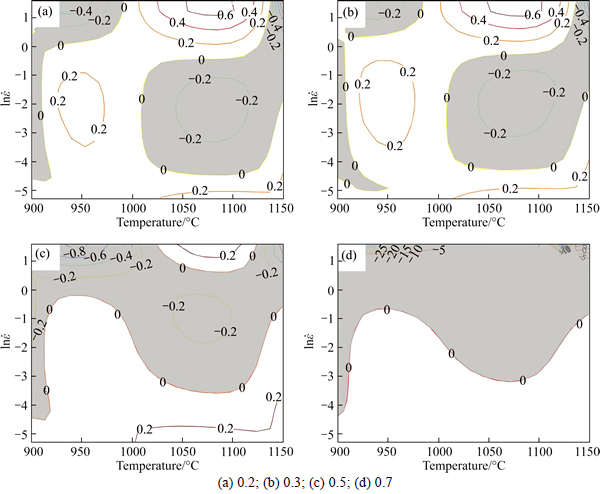
Fig. 5 Instability maps under different temperatures and strain rates at strains:

Fig. 6 Processing maps under different temperatures and strain rates at strains:

It can be seen from Figs. 6(a), (b), (c) and (d) that the shaded regions shrank according to the increase of strain. A maximum efficiency of about 58% occurring in the temperature range of 1080-1120 °C and strain rate range of 0.005-0.01 at strain of 0.3. The suitable regions for deformation process are not the shaded regions but with high efficiency, which can dissipate more power in the forming process.

4 Conclusions

1) The power dissipation efficiency is associated with the microstructure evolution. High value of power dissipation is considered to be dynamic recrystallization. The lower the unstable parameter is, the higher the risk of the unstable flow will be. The region with low values of ξ (ξ<0) is associated with microcracks, strain aging, localized plastic flow and so on.

2) The processing maps were established by considering power dissipation maps and instability maps. Based on the established processing maps of 2Cr11Mo1NbN stainless steel, the optimum domain with high values of power dissipation is in the temperature range of 1080-1120 °C and strain rate range of 0.005-0.01 s^-1 at strain of 0.3.

References

[1] MA X P, WANG L J, LIU C M, SUBRAMANIAN S V. Microstructure and properties of 13Cr5Ni1Mo0.025Nb0.09V0.06N super martensitic stainless steel [J]. Mater Sci Eng A, 2012, 539: 271-279.

[2] PECKER D, BERNSTEIN I M. Handbook of Stainless Steels [M]. New York: McGraw-Hill, 1977: 190.

[3] WEN Peng, CAI Zhi-peng, FENG Zhen-hua, WANG Gang. Microstructure and mechanical properties of hot wire laser clad layers for repairing precipitation hardening martensitic stainless steel [J]. Optics and Laser Technology, 2015, 75: 207-213.

[4] FAN Rui-cheng, GAO Ming, MA Ying-che, ZHA Xiao-dong, HAO Xiao-chao, LIU Kui. Effects of heat treatment and nitrogen on microstructure and mechanical properties of 1Cr12NiMo martensitic stainless steel [J]. J Mater Sci Technol, 2012, 28: 1059-1066.

[5] ISFAHANY A N, SAGHAFIAN H, BORHANI G. The effect of heat treatment on mechanical properties and corrosion behavior of AISI420 martensitic stainless steel [J]. Journal of Alloys and Compounds, 2011, 509: 3931-3936.

[6] SUN Chao-yang, LIU Geng, ZHANG Qing-dong, LI Rui, WANG Li-liang. Determination of hot deformation behavior and processing maps of IN 028 alloy using isothermal hot compression test [J]. Mater Sci Eng A, 2014, 595: 92-98.

[7] ZHONG T, RAO K P, PRASAD Y V R K, GUPTA M. Processing maps, microstructure evolution and deformation mechanisms of extruded AZ31-DMD during hot uniaxial compression [J]. Mater Sci Eng A, 2013, 559: 773-781.

[8] CHEN Liang, ZHAO Guo-qun, YU Jun-quan. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy [J]. Mater Des, 2015, 74: 25-35.

[9] REN Fa-cai, CHEN Jun, CHEN Fei. Constitutive modeling of hot deformation behavior of X20Cr13 martensitic stainless steel with strain effect [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 1407-1413.

[10] MOMENI A, DEHGHANI K. Characterization of hot deformation behavior of 410 martensitic stainless steel using constitutive equations and processing maps [J]. Mater Sci Eng A, 2010, 527: 5467-5473.

[11] ZHANG Peng, HUA Chao, ZHU Qiang, DING Chao-gang, QIN He-yong. Hot compression deformation and constitutive modeling of GH4698 alloy [J]. Mater Des, 2015, 65: 1153-1160.

[12] MIRZADEH H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions [J]. Mechanics of Materials, 2015, 85: 66-79.

[13] YIN F, HUA L, MAO H J, HAN X H. Constitutive modeling for flow behavior of GCr15 steel under hot compression experiments [J]. Mater Des, 2013, 43: 393-401.

[14] CHANGIZIAN P, ZAREI-HANZAKI A, ROOSTAEI ALI A. The high temperature flow behavior modeling of AZ81 magnesium alloy considering strain effects [J]. Mater Des, 2012, 39: 384-389.

[15] FAN Q C, JIANG X Q, ZHOU Z H, JI W, CAO H Q. Constitutive relationship and hot deformation behavior of Armco-type pure iron for a wide range of temperature [J]. Mater Des, 2015, 65: 193-203.

[16] GAN Chun-lei, ZHENG Kai-hong, QI Wen-jun, WANG Meng-jun. Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain [J]. Trans Nonferrous Met Soc China, 2014, 24: 3486-3491.

[17] LIU Gui-wu, HAN Ying, SHI Zhong-qi, SUN Jia-peng, ZOU De-ning, QIAO Guan-jun. Hot deformation and optimization of process parameters of an as-cast 6Mo superaustenitic stainless steel: A study with processing map [J]. Mater Des, 2014, 53: 662-672.

[18] MOMENI A, DEHGHANI K. Characterization of hot deformation behavior of 410 martensitic stainless steel using constitutive equations and processing maps [J]. Mater Sci Eng A, 2010, 527: 5467-5473.

[19] EZATPOUR H R, SAJJADI S A, HADDAD-SABZEVAR M, EBRAHIMI G R. Hot deformation and processing maps of K310 cold work tool steel [J]. Mater Sci Eng A, 2012, 550: 152-159.

[20] SAMANTARAY D, MANDAL S, KUMAR V, ALBERT S K, BHADURI A K, JAYAKUMAR T. Optimization of processing parameters based on high temperature flow behavior and microstructural evolution of a nitrogen enhanced 316L(N) stainless steel [J]. Mater Sci Eng A, 2012, 552: 236-244.

[21] WANG Ying, PAN Qing-lin, SONG Yan-fang, LI Chen, LI Zhi-feng. Hot deformation and processing maps of X-750 nickel-based superalloy [J]. Mater Des, 2013, 51: 154-160.

[22] LI Ju-qiang, LIU Juan, CUI Zhen-shan. Characterization of hot deformation behavior of extruded ZK60 magnesium alloy using 3D processing maps [J]. Mater Des, 2014, 56: 889-897.

[23] DALLA TORRE F H, PERELOMA E V, DAVIES C H J. Strain hardening behaviour and deformation kinetics of Cu deformed by equal channel angular extrusion from 1 to 16 passes [J]. Acta Materialia, 2006, 54: 1135-1146.

[24] RAO K P, PRASAD Y V R K, SURESH K. Hot working behavior and processing map of a γ-TiAl alloy synthesized by powder metallurgy [J]. Mater Des, 2011, 32: 4874-4881.

[25] ZHU Y C, ZENG W D, LIU J L, ZHAO Y Q, ZHOU Y G, YU H Q. Effect of processing parameters on the hot deformation behavior of as-cast TC21 titanium alloy [J]. Mater Des, 2012, 33: 264-272.

[26] ZHANG Hui, ZHANG Hong-gang, PENG Da-shu. Hot deformation behavior of KFC copper alloy during compression at elevated temperatures [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 562-566.

[27] NARAYANA MURTHY S V S, NAGESWARA RAO B, KASHYAP B P. Instability criteria for hot deformation of materials [J]. Int Mater Rev, 2000, 41: 15-26.

[28] LIN Yong-cheng, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Mater Des, 2011, 32: 1733-1759.

[29] PRASAD Y V R K, SASIDHARA S. Hot working guide: A compendium of processing maps [M]. Materials Park, Ohio: ASM International, 1997: 5-9.

[30] MOMENI A, DEHGHANI K. Characterization of hot deformation behavior of 410 martensitic stainless steel using constitutive equations and processing maps [J]. Mater Sci Eng A, 2010, 527: 5467–5473.

[31] GANESAN G, RAGHUKANDAN K, KARTHIKEYAN R, PAI B C. Development of processing map for 6061Al/15% SiCp through neural networks [J]. J Mater Pro Technol, 2005, 166: 423-429.

[32] WANG Meng-han, HUANG Long, CHEN Ming-liang, WANG Yan-li. Processing map and hot working mechanisms of Cu-Ag alloy in hot compression process [J]. Journal of Central South University, 2015, 22(3): 821-828.

[33] VENUGOPAL S, VENUGOPAL P, MANNAN S L. Optimization of cold and warm workability of commercially pure titanium using dynamic materials model (DMM) instability maps [J]. J Mater Process Technol, 2008, 202: 201-215.

[34] ZHANG Ming-jie, LI Fu-guo, WANG Shu-yun, LIU Chen-yi. Characterization of hot deformation behavior of a P/M nickel-base superalloy using processing map and activation energy [J]. Mater Sci Eng A, 2010, 527: 6771-6779.

[35] ZOU De-ning, HAN Ying, YAN Dong-na, WANG Duo, ZHANG Wei, FAN Guang-wei. Hot workability of 00Cr13Ni5Mo2 supermartensitic stainless steel [J]. Mater Des, 2011, 32: 4443-4448.

(Edited by YANG Hua)

Foundation item: Project(CDJZR14130006) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2015-04-30; Accepted date: 2015-09-11

Corresponding author: WANG Meng-han, PhD, Associate Professor; Tel: +86-13637957075; E-mail: cquwmh@163.com