Article ID: 1003-6326(2005)06-1373-07
Relationship between solids flux and froth features in batch flotation of sulphide ore
YANG Xiao-sheng(杨小生)1, Aldrich Chris2
(1. Institute of Mineral Engineering, Northeastern University, Shenyang 110004, China;
2. Department of Process Engineering, University of Stellenbosch,
Private Bag X1, Matieland 7602, South Africa)
Abstract: The froth features in the batch flotation of a sulphide ore were investigated by using the digital image parameters of the froth, the small number emphasis(Nsne), the average grey level(Dagl) and the instability number(Nins), under different conditions of impeller speeds and aeration rates. It is found that the value of Nsne is strongly dependent on the average bubble size of the froth and Dagl on the volume fraction of solid in the froth, and the froth features during the batch flotation are influenced by impeller speed and aeration rate. A kinetic model of the concentrate solid flux was developed which relates the flotation process to the image parameters, Nsne and Dagl of the froth and predictions are well consistent with the experimental data.
Key words: sulphide ores; batch flotation; small number emphasis; average grey level; instable number CLC
number: TD Document code: A
1 INTRODUCTION
The froth features in the sulphide ore flotation as an indication of the flotation process have been studied by Moolman et al[1-4] and Aldrich et al[5] by using digital image analysis and neural networks. In the study of Aldrich et al, the froth structures were represented by three features extracted from the digital images of the froth, viz, a statistical feature which is a rough indication of the average bubble size of the froth, a measure of the froth stability, as well as the average grey level of the froth, which is an indication of mineral loading on the bubble surface and the dependence of the grade and recovery on the froth features was discussed under different flotation conditions. But the correlations between the variables of the flotation and the froth features have not been established.
Hyotyniemi and Ylinen[6] pointed out the models tested on an image analysis of flotation froth to find features corresponding to the poisoning phenomenon in flotation cell. Niemi et al[7] presented dynamic models of pulps for industrial flotation cells and analyzed the results based on the recording of froth images in two plants. The time-averaged multiphase flow characteristics of air-sparged hydrocyclone flotation were studied by Das and Miller[8] and the criteria of flotation stability and the relationship between froth phase features and flotation response were established.
Flynn et al[9]and Woodburn et al[10]developed the kinetic models based on the flux of bubble surface overflowing the concentrate weir in a free flowing froth which describes the relationships between the froth structure and flotation performance of coal. According to Flynn and Woodburn each bubble in the froth is regarded as consisting of an aqueous shell containing only selectively attached hydrophobic solids and the interbubble lamella, having a thickness related to the froth condition, containing entrained material, the concentration of which can vary throughout a batch test. According to Hemmings[11] the froth lamella thickness can be measured directly by a conductance probe. Bradshow and OConnor[12] developed a method to measure bubble loading in a microflotation cell.
In addition, the effect of froth structure on the performance of froth flotation of coal was investigated by Banford and Woodburn[13] using image analysis. Neethling and Cilliers[14] studied the relationship between the flotation froth structure and the amount of entrained gangue that is collected to the concentrate. Aldrich and Feng[15] studied the effect of frothers on bubble size distributions in flotation pulp phase and surface froths. The study by Ata et al[16] suggested that the hydrophobic particles had a strong effect on the structure of the froth which in turn influences the drainage of hydrophilic particles in the froth.
In this paper, the influence of the impeller speed and aeration rate on the froth structures indicated by the three froth features, viz Nsne, Dagl and Nins, will be discussed for the batch flotation of a sulphide ore and the concepts of Flynn et al[9] and Woodburn et al[10] will be applied to develop the correlation between the solid flow rate and the froth features.
2 EXPERIMENTAL
2.1 Flotation
The test sample was a complex sulphide ore from a mine in South Africa, mainly consisting of oxides and metal sulphides. Mineralogical and elemental analyses were carried out on X-ray Fluorescence. The sulfur content is 2.13% (determined by Leco Sulfur Analyser). The sulphide minerals in the ore are complex, mainly the sulphides of Zn, Cu, and Pb, etc.
The sample was crushed to less than 4mm, and subsequently reduced in size in a dry rod mill with stainless steel milling media. The size distribution analyzed by a Malvern mastersizer is shown in Fig.1 and the density by a pycnometer is 2.78g/cm3.
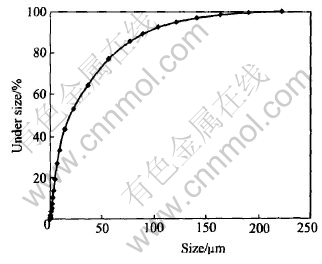
Fig.1 Curve of size distribution of sample
Preconditioning of the flotation pulp with 25% concentration was accomplished in a 5L laboratory-scale ultrasonic bath. The total preconditioning time is 10min, including activation for 5min with copper sulphate (50g/t) and subsequently for another 5min with sodium isobutyl xanthate(SIBX) (80g/t) as a collector and polypropylene glycol (100g/t) as a frother. Flotation experiments were conducted in an open top Leeds laboratory flotation cell with a capacity of 3L. Three impeller speeds of 1200, 1500 and 1800r/min, and three aeration rates of 2, 4 and 7L/min were used. The froth in the cell was controlled at a height of 25-30mm and was removed at 15-30s intervals with a scraper. Six samples were taken during each experimental run. The concentrates were weighed, dried and weighed for calculation of solid and water contents and analysis of sulfur with a Leco sulfur analyser.
2.2 Froth image analysis
The froth feature parameters were monitored with an industrial Baxall CD9312 videocamera with a 25mm lens with enlargement factor of 1∶1.14 and a window size of 75mm×95mm. The camera was mounted on a specially made bracket with an adjustable arm allowing lateral and vertical adjustment, which also prevented vibration from the flotation cell from influencing the image. The distance from the top of the cell to the lens was 485mm. The camera was connected to a VHS videorecorder and a television monitor. Digitization of the images and subsequent analysis of the data were done on a personal computer fitted with a frame grabber. Lighting was provided by a single 100W light bulb next to the camera[5].
The froth images were grabbed from the videotape at intervals of 30s after every scrape of the froth during flotation. The parameters of the average grey level(Dagl), the instability number(Nins), the small number emphasis(Nsne) and the average area(Aava) were gotten on-line.
Dagl was simply the arithmetic average of the grey levels of all the pixels in a digitised image. Nsne was a measure of the average bubble size of the froth. The characterization of the instability of the froth was based on the rate of bubble collapse in the froth. And the average area(Aava) was the statistic mean area of bubbles on the froth surface.
3 DISCUSSION
3.1 Froth image
The images of the top surface of the froth taken at specific time during flotation test at impeller speed of 1800r/min and aeration rate of 7L/min are shown in Fig.2, which shows that the bubble size in enlarged and the surface mineral loading becomes less as flotation time increases. The images at other impeller speeds and aeration rates are also gotten.
3.2 Small number emphasis Nsne
The inverse relationship between Nsne and average bubble size db under the experimental conditions is shown in Fig.3. That is, the average bubble size can be estimated by the linear regression as
db=aNsne+b(1)
The estimated values of coefficients a and b and R2 for different runs are summarized in Table 1.
Fig.4 shows the influence of aeration rates and impeller speeds on the value of Nsne, and du- ring flotation the value of Nsne decreases, or the
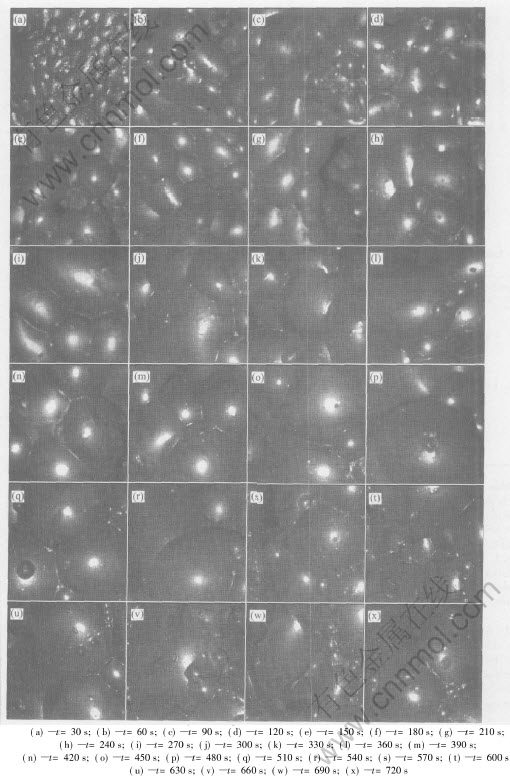
Fig.2 Images of top surface of froth at different time
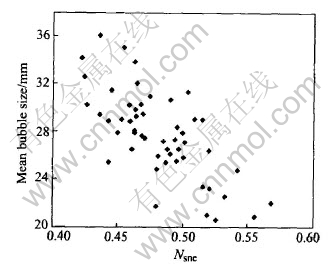
Fig.3 Relationship between Nsne and average bubble size
Table 1 Values of estimated coefficients in Eqn.(1) under experimental conditions
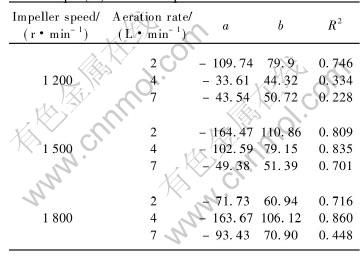

Fig.4 Influences of aeration rate and impeller speed on bubble size in froth during batch flotation at different impeller speeds
bubble size increases, with time increasing apparently at initial stage (t〈200s) and then the increase of the bubble size becomes relatively regardless of the aeration rate and impeller speed. This result is consistent with the observation shown in Fig.2. It is also evident that the mean bubble size is larger at higher aeration rate. But no evident influence of the impeller speed on the bubble size is found.
3.3 Average loading density of bubble surface
The loading density on the bubble surface of the froth, shown by the value of Dagl, is an important indication of flotation. As shown in Fig.5 the value of Dagl, or the loading density, initially increases and then decreases with increasing flotation time and the trend is more significant at higher impeller speed. That is at higher impeller speed the value of Dagl changes more evidently with increase of time. The influence of aeration rate on the loading density of the froth is not evident but at the impeller speed of 1200r/min the lower Dagl value is found at lower aeration rate.
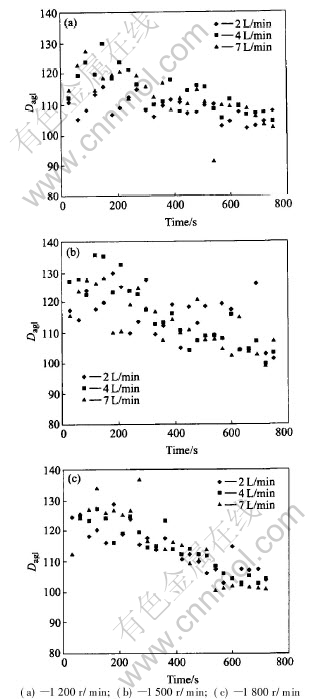
Fig.5 Influences of aeration rate and impeller speed on loading density of bubbles on top surface of froth during batch flotation at different impeller speeds
The mean volume fraction of solid on the bubble surface of the froth in concentrate stream can be calculated by
φs=Vs/(Vs+Vw)
=(Ms/ρs)/(Ms/ρs+Mw/ρw)(2)
where Vs and Vw are the volume of solid and water on the bubble surface in the froth, Ms and Mw the mass, and ρs and ρw the density of solid and water, respectively.
As shown in Fig.6 the loading density parameter Dagl can be related to φs as
φs=aDagl+b(3)
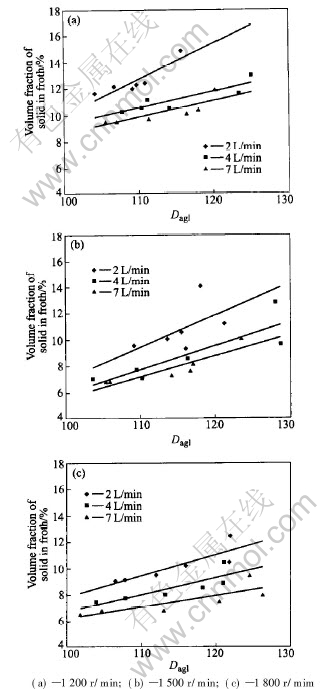
Fig.6 Relationships between Dagl and volume fraction of solid on bubble surface at different impeller speeds and aeration rates
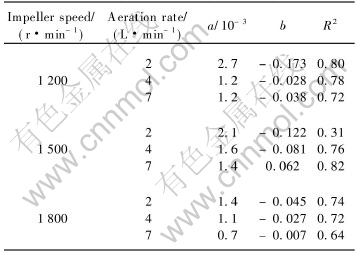
The values of the coefficients a, b and R2 under different conditions are listed in Table 2.
It is clearly seen from Table 2 that the loading density on the bubble surface and the volume fraction of solid are reasonably correlated by linear regressions. The values of coefficients a and b depend on the impeller speed and aeration rate. The slope (a) seems larger at lower impeller speed and aeration rate.
3.4 Stability of froth
The stability of the froth indicated by the
Table 2 Values of coefficients in relationships between Dagl and volume fraction of solid on bubble surface of froth
value of Nins at different impeller speeds and aeration rates is illustrated in Fig.7. It shows that most points distribute below the instability value of 0.02, or the froth is very stable during flotation. No accurate conclusion of the stability difference between the three aeration rates can be made. But it can be found that the instability value decreases for more points with the increase in impeller speed, or the froth is more stable for higher impeller speed.
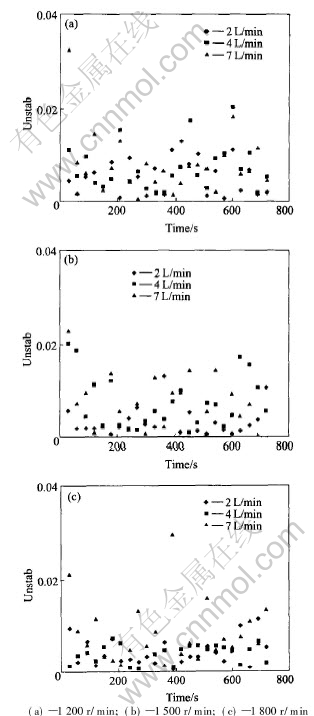
Fig.7 Influences of impeller speed and aeration rate on stability of froth at different impeller speeds
4 MODELLING OF SOLID FLUX BASED ON FROTH IMAGE
If the mean surface lamella thickness of the bubbles in the froth is δ, the mean volume fraction of solid on the bubble surface as φs, and the density of solid is ρs, the loading density of the froth can be expressed by
Γ=φsδρs(4)
According to Flynn et al(1987) the lamella thickness δ is related to the particle size, d90. So
Γ=φsd90ρs(5)
The flux of bubble surface in the overflowing froth is
Ψa=αQaSa(6)
where Qa is aeration rate, α is fraction of air supplied to cell which overflows in concentrate froth as unbroken bubbles and Sa specific surface of bubbles in overflowing froth, for spherical bubbles
Sa=6/db
So the solid flow rate of the concentrate can be expressed by
Φt=ΨaΓ=φsd90ρs(6αQa)/db(7)
Woodburn et al[7] assumed α=1.0 for coal flotation. The value of α can be estimated using experimental data.
By using the linear relationships between φs and Dagl, and between db and Nsne to substitute for φs and db respectively in Eqn.(6), the relationship between the solid flux and the image parameters can be obtained:
Φt=(aDagl+b)d90ρs(6αQa) /(a′Nsne+b′)(8)
The calculated data of flotation solid flux based on the froth image parameters Dagl and Nsne and the standard deviation report that the predictions are well consistent with the experimental data.
5 CONCLUSIONS
1) The froth images show the difference on bubble size and loading density on the bubble surface at different time for batch flotation tests. The small number emphasis Nsne is inverse linearly related to the average bubble size of the froth and the changes on the bubble size of the froth shown by the value of Nsne depend on flotation time and aeration rate. At initial stage (t〈200s) the bubbles of the froth are small and increase quickly and then keep stable on size with increasing time. At the fixed time the value of Nsne is lower, or the mean bubble size is larger, at higher aeration rate.
2) The significant linear relationships exist between the froth image parameter of loading density Dagl and the volume fraction of solid in the froth. The loading density of bubble surface is dependent on flotation time. At initial (t〈200s) the value of Dagl increases and then as time increases the value of Dagl goes down. At higher impeller speed the change of the loading density of bubble surface in the froth is more evident with increase in time.
3) No difference of froth stability on time is found but the higher impeller speed causes the froth to be more stable.
4) A model based on froth image parameters, Nsne and Dagl, is established to predict the solid flow rate along the concentrate stream and predictions are well consistent with experimental data. More research is needed to develop the relationships between froth image parameters and the grade and recovery of the valuable components for complex minerals flotation.
REFERENCES
[1]Moolman D W, Aldrich C, van Deventer J S J, et al. Digital image processing as a tool for on-line monitoring of froth in flotation plants [J]. Minerals Engineering, 1994, 7(9): 1149-1164.
[2]Moolman D W, Aldrich C, van Deventer J S J, et al. The classification of froth structures in a copper flotation plant by means of a neural net [J]. Int J Miner Process, 1995, 43: 193-208.
[3]Moolman D W, Aldrich C, van Deventer J S J. The interpretation of flotation froth surfaces by using digital image analysis neural networks [J]. Chemical Engineering Science, 1995, 50(22): 3501-3513.
[4]Moolman D W, Aldrich C, van Deventer J S J. The monitoring of froth surface on industrial flotation plants using connectionist image processing techniques [J]. Minerals Engineering, 1995, 8(1/2): 23-30.
[5]Aldrich C, Moolman D W, Bunkell S J, et al. Relationship between surface froth features and process conditions in the batch flotation of a sulphide ore [J]. Minerals Engineering, 1997, 10(11): 1207-1218.
[6]Hytyniemi H, Ylinen R. Modeling of visual flotation froth data [J]. Control Eng Practice, 2000, 8(3): 313-318.
[7]Niemi A J, Ylinen R, Hytyniemi H. On characterization of pulp and froth in cells of flotation plant [J]. Int J Miner Process, 1997, 51(1/4): 51-65.
[8]Das A, Miller J D. Swirl flow characteristics and froth phase features in air-sparged hydrocyclone flotation as revealed by X-ray CT analysis [J]. Int J Miner Process, 1996, 47(3/4): 251-274.
[9]Flynn S A, Woodburn E T. A froth ultra-fine model for the selective separation of coal from mineral in a dispersed air flotation cell [J]. Powder Technology, 1987, 49: 127-142.
[10]Woodburn E T, Austin L G, Stockton J B. A froth based flotation kinetic model [J]. Trans IChemE A, 1994, 72A: 211-226.
[11]Hemmings C E. On the significance of flotation froth liquid lamella thickness [J]. Trans Inst Min Metall C, 1981, 90: C96-C102.
[12]Bradshow D J, OConnor C T. Measurement of the sub-process of bubble loading in flotation [J]. Minerals Engineering, 1996, 9: 443-448.
[13]Banford A W, Aktas Z, Woodburn E T. Interpretation of the effect of froth structure on the performance of froth flotation using image analysis [J]. Powder Technology, 1998, 98: 61-73.
[14]Neethling S J, Cilliers J J. The entrainment of gangue into a flotation froth [J]. Int J Miner Process, 2002, 64: 2-3.
[15]Aldrich C, Feng D. The effect of frothers on bubble size distributions in flotation pulp phases and surface froths [J]. Minerals Engineering, 2000, 13: 10-11.
[16]Ata S, Ahmed N, Jameson G J. The effect of hydrophobicity on the drainage of gangue minerals in flotation froths [J]. Minerals Engineering, 2004, 17: 897-901.
(Edited by LONG Huai-zhong)
Foundation item: Project supported by the Postdoctoral Fellowship of South Africa
Received date: 2005-04-21; Accepted date: 2005-09-21
Correspondence: YANG Xiao-sheng, Professor, PhD; Tel: +86-24-83680162; E-mail: xsyang@mail.neu.edu.cn