基于Málek方程和过程热力学函数的Mn1.8Co0.1Mg0.1P2O7·2H2O热脱水动力学机理
来源期刊:中国有色金属学报(英文版)2018年第5期
论文作者:Chuchai SRONSRI
文章页码:1016 - 1026
关键词:非等温动力学;脱水;动力学机理;?esták-Berggren模型;热力学函数
Key words:non-isothermal kinetics; dehydration; kinetic mechanism; ?esták-Berggren model; thermodynamic function
摘 要:采用水热法合成Mn1.8Co0.1Mg0.1P2O7·2H2O,证实其热脱水产物为Mn1.8Co0.1Mg0.1P2O7。利用热重/微分热重/差热分析、傅里叶变换红外光谱、原子吸收分光光度、X射线衍射和扫描电镜等技术对样品进行表征。研究4种加热速率下空气气氛中(热脱水过程)的非等温动力学,发现其为单一的热脱水过程。用Kissinger-Akahira-Sunose方程迭代法计算出表观活化能Ea值,证实脱水过程是一个具有唯一动力学三因子的单步骤动力学过程。用Málek方程确定了热脱水过程的动力学模型f(a)和指前因子A,提出以?esták-Berggren模型作为脱水过程的机理函数。最佳拟合得出热脱水过程的的动力学三因子为Ea=79.97±6.51 kJ/mol,ln A=16.83,f(a)=a0.520(1-a)1.255。利用活化络合物理论并结合A值,计算活化过程的热力学函数。
Abstract: Mn1.8Co0.1Mg0.1P2O7·2H2O was synthesized via hydrothermal method and the thermal dehydration product was confirmed to be Mn1.8Co0.1Mg0.1P2O7. The thermogravimetry/differential thermogravimetry/differential thermal analysis, Fourier transform infrared, atomic absorption spectrophotometry, X-ray diffraction and scanning electron microscopy techniques were employed for sample characterization. Non-isothermal kinetics was studied under air atmosphere at four heating rates and the single thermal dehydration process was observed. Iterative Kissinger-Akahira-Sunose equation was used to calculate the apparent activation energy Eα values. Dehydration process was confirmed to be a single-step kinetic process with the unique kinetic triplets. Málek’s equations were used to determine the kinetic model f(α) and pre-exponential factor A. ?esták-Berggren model was suggested to be the mechanism function for the dehydration process. The best fit led to the kinetic triplets of Eα=(79.97±6.51) kJ/mol, ln A=16.83 and f(α)=α0.520(1-α)1.255 (α is the extent of conversion). The thermodynamic functions of activation were calculated using activated complex theory together with A value.
Trans. Nonferrous Met. Soc. China 28(2018) 1016-1026
Chuchai SRONSRI
Department of Chemistry, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
Received 27 March 2017; accepted 24 June 2017
Abstract: Mn1.8Co0.1Mg0.1P2O7·2H2O was synthesized via hydrothermal method and the thermal dehydration product was confirmed to be Mn1.8Co0.1Mg0.1P2O7. The thermogravimetry/differential thermogravimetry/differential thermal analysis, Fourier transform infrared, atomic absorption spectrophotometry, X-ray diffraction and scanning electron microscopy techniques were employed for sample characterization. Non-isothermal kinetics was studied under air atmosphere at four heating rates and the single thermal dehydration process was observed. Iterative Kissinger-Akahira-Sunose equation was used to calculate the apparent activation energy Eα values. Dehydration process was confirmed to be a single-step kinetic process with the unique kinetic triplets. Málek’s equations were used to determine the kinetic model f(α) and pre-exponential factor A. 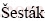 -Berggren model was suggested to be the mechanism function for the dehydration process. The best fit led to the kinetic triplets of Eα=(79.97±6.51) kJ/mol, ln A=16.83 and f(α)=α0.520(1-α)1.255 (α is the extent of conversion). The thermodynamic functions of activation were calculated using activated complex theory together with A value.
-Berggren model was suggested to be the mechanism function for the dehydration process. The best fit led to the kinetic triplets of Eα=(79.97±6.51) kJ/mol, ln A=16.83 and f(α)=α0.520(1-α)1.255 (α is the extent of conversion). The thermodynamic functions of activation were calculated using activated complex theory together with A value.
Key words: non-isothermal kinetics; dehydration; kinetic mechanism; 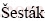 -Berggren model; thermodynamic function
-Berggren model; thermodynamic function
1 Introduction
Synthesis, structural, vibrational and thermal behavior studies of divalent-metal pyrophosphate hydrates M2P2O7·nH2O were reported in the literature such as the structure studies of Mg (n=1, 2, 3.5, 6) [1-3], Mn (n=2) [4] and Co (n=2) [5] compounds. The thermal properties were investigated for Ni (n=6, 8) compounds [6], whereas the vibrational spectroscopy of Ca (n=2) compound was studied [7]. The crystal structure, vibrational spectra and thermal decomposition of dipyrophosphate hydrates Zn4(P2O7)2·10H2O were reported [8]. In addition, the cobalt-pyrophosphates were reported to exist in four phases, namely α-Co2P2O7 at low temperature [9], β-Co2P2O7 at high temperature [10], γ-Co2P2O7 at high pressure [11] and the hydrate form Co2P2O7·2H2O [5]. Crystalline and amorphous anhydrous forms of M2P2O7 were used in many fields such as waste water purification systems, ferroelectrics and batteries [12-14]. These forms of M2P2O7 were interested in the catalytic activity such as the conversion of butane to maleic anhydride [15] and the oxidative decarboxylation [16]. Mn2P2O7 can be used as laser hosts, ion exchangers, catalysts, ionic conductors, reactants in ionic conditions, ceramic pigments, intercalation reactions and fertilizers [17-19]. Moreover, Mn2P2O7 showed the electrode property [20], but the property exhibited significant capacity fading upon cycling. However, the substitution by Co could overcome this disadvantage [21]. Cobalt can be a good doping candidate for Mn2P2O7 such as Mn2-xCoxP2O7. It has been reported that proper doping can perturb the crystalline growth process and the morphology [21]. Besides, the Co2-xMgxP2O7 was used as blue-violet ceramic pigments [22]. Mg is not only justified for its lower economical cost and less harmful to environment, but also for the high chemical and thermal stability [23,24]. Furthermore, the previous studies of M2-xMgxP2O7 system (M=Cr, Mn, Fe, Co, Ni and Cu) [24] reported that Mn-Mg crystallized with the thortveitite (β-Sc2Si2O7) structure (isostructure between β-Mg2P2O7 and Mn2P2O7).
Recently, the tertiary metal NH4Co0.8Zn0.1Mn0.1- PO4·H2O was reported about the synthesis and kinetic study [25]. The final thermal decomposition products of the above tri-metal phosphates as well as NH4MnPO4·H2O [26], NH4Mn0.5Mg0.5PO4·H2O [27] and NH4Co0.5Mg0.5PO4·H2O [27] compounds were confirmed to be metal pyrophosphates M2P2O7. They can be used as the precursors to synthesize the lithium single- or multi-metal phosphates (LiMPO4), which are used as the cathode materials in the Li-ion batteries. Metal doping is an effective approach to increase the electrochemical performance of LiMPO4. Most efforts have focused on the Mn-site doping [28-31]. In the previous studies, the multi-ions co-doping was carried out to improve the electrochemical performance of LiMnPO4 [28-31]. The hydrothermal method was used to synthesize various compounds, which is used to control the size and morphology with several other advantages [32].
Various mathematical models of the thermal decomposition kinetics were used to estimate the kinetic parameters, namely activation energy Eα, pre-exponential factor A and reaction mechanism f(α) [33,34]. The kinetic studies were carried out by simultaneous least-square analysis of the results from thermo- gravimetry/differential thermogravimetry/differential thermal analysis (TG/DTG/DTA) at different heating rates. The kinetic mechanism was achieved by Málek’s equations to confirm the correctness of the reaction model [35]. The relationship between kinetic parameters and thermodynamic functions using isoconversional model is also reported based on the thermal analysis techniques. Therefore, the motivation of this work is to synthesize, characterize as well as study the kinetics and thermodynamics of the new tertiary metals Co and Mg co-doped Mn2P2O7·2H2O as the Mn1.8Co0.1Mg0.1- P2O7·2H2O compound. This synthesized sample can be used as the precursor in the future to synthesize the cathode material of LiMn0.90Co0.05Mg0.05PO4 with the improved performance.
2 Method
Chemical reagents were purchased from Carlo Erba. The tertiary metal compound Mn1.8Co0.1Mg0.1P2O7·2H2O was synthesized via the low-temperature hydrothermal method using MnCl2·4H2 O, CoCl2·6H2 O, MgCl2·6H2 O and K4P2O7 separately dissolved in deionized (DI) water. In the typical synthesis, the mixture solution of 25 mL of 0.9 mol/L Mn2+, 25 mL of 0.05 mol/L Co2+ and 25 mL of 0.05 mol/L Mg2+ was added into 25 mL of 0.5 mol/L  solution with the mole ratio of total metals (Mn+Co+Mg) to pyrophosphate
solution with the mole ratio of total metals (Mn+Co+Mg) to pyrophosphate  of 2:1. This mixture was promptly transferred to a 100 mL Teflon-lined stainless steel autoclave and heated at 85 °C for 5 h. After the completion of hydrothermal reaction, the pink precipitates were obtained followed by filtering, washing with DI water and ethanol several times to remove ions possibly remaining in the final products. Then, the samples were dried in a desiccator for further investigation. The preparation of the title compound was carried out according to the following hydrothermal synthesis equation:
of 2:1. This mixture was promptly transferred to a 100 mL Teflon-lined stainless steel autoclave and heated at 85 °C for 5 h. After the completion of hydrothermal reaction, the pink precipitates were obtained followed by filtering, washing with DI water and ethanol several times to remove ions possibly remaining in the final products. Then, the samples were dried in a desiccator for further investigation. The preparation of the title compound was carried out according to the following hydrothermal synthesis equation:

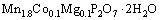 (1)
(1)
Water contents in the synthesized hydrate were determined by TG/DTG/DTA methods on a Pyris Diamond Perkin-Elmer. The Mn, Co and Mg contents were confirmed by atomic absorption spectrophotometry (AAS, Perkin Elmer, Analyst 100). Fourier transform infrared (FTIR) spectra were recorded in the wavenumber range of 4000-370 cm-1 using KBr pellet technique (KBr spectroscopy grade, Merck) on a Perkin Elmer spectrum GX FTIR/FT Raman spectrophotometer with 32 scans and the resolution of 4 cm-1. The crystal structures were determined by using X-ray powder diffraction (XRD) method and compared with the standard powder diffraction file (PDF) database of the International Center for Diffraction Data (ICDD). The 2θ angles were in the range of 5°-70° with 0.02° increment and 1 s/step scan speed using a D8 advanced powder diffractometer (Bruker AXS, Karlsruhe, Germany) with Cu Kα radiation. The lattice parameters and cell volumes can be obtained from a least square refinement of the XRD data with the aid of a computer program corrected for systematic experimental errors. The Scherrer equation, Eq. (2), can be used to calculate the crystallite size (D)
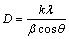 (2)
(2)
where λ is the wavelength of X-ray radiation (0.15406 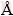 ), k is a constant taken as 0.89, θ is the diffraction angle and β is the full width at half maximum XRD intensity [36]. The morphologies were investigated by scanning electron microscopy (SEM) using LEO VP1450 SEM after gold coating technique. The thermal kinetic experiments were carried out using TG/DTG/ DTA at four heating rates of 5, 10, 15 and 20 °C/min over the temperature range of 90-150 °C in air with the air flow rate of 100 mL/min. The sample mass of about 8.5 mg was filled into an alumina pan without pressing and without a lid, and the TG/DTG/DTA curves were recorded by using α-Al2O3 as the reference material.
), k is a constant taken as 0.89, θ is the diffraction angle and β is the full width at half maximum XRD intensity [36]. The morphologies were investigated by scanning electron microscopy (SEM) using LEO VP1450 SEM after gold coating technique. The thermal kinetic experiments were carried out using TG/DTG/ DTA at four heating rates of 5, 10, 15 and 20 °C/min over the temperature range of 90-150 °C in air with the air flow rate of 100 mL/min. The sample mass of about 8.5 mg was filled into an alumina pan without pressing and without a lid, and the TG/DTG/DTA curves were recorded by using α-Al2O3 as the reference material.
3 Theoretical background
The isoconversional kinetic theory treatment of the solid state reaction of type A(solid)→B(solid) + C(gas) or ∑Ai(solid)→∑Bj(solid)+∑Ck(gas) [25-27,38] frequently expresses the reaction rate function of two variables (temperature T/K and extent of conversion α) by the following well-known equation [37-46]:
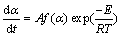 (3)
(3)
when A is the pre-exponential factor, R is the molar gas constant (8.314 J/(mol·K) and f(α) is the differential form of the mechanism function or conversion function. The α value from TG analysis is defined as the ratio of mass losses in the investigated process
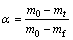 (4)
(4)
where mt is the mass of the sample at time t, m0 and mf are the masses of the sample at the beginning and the ending of mass loss in the TG curve, respectively.
Equation (3) can be modified based on a heating rate β=dT/dt [25] to be Eq. (5).
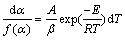 (5)
(5)
The solution of the left hand side of Eq. (5) represented by g(α), which is referred to as the integral form of the mechanism function:
 (6)
(6)
Function g(α) depends on the explicit expression of function f(α). Various scientists suggested different ways of solving Eq. (6). Thus, the kinetics of solid state reactions can be described by various equations depending on their assumptions and the mechanism involved.
3.1 Apparent Eα value determination
In the present work, the non-isothermal kinetic was studied using model-free or isoconversional method (such as KAS method). The apparent Eα value was evaluated by the iterative KAS method [47-49] according to the equation:
 (7)
(7)
where x=Eα/(RT) and π(x) is expressed by the eighth-order rational equation of  -Maqueda and Criado [50] approximation formula:
-Maqueda and Criado [50] approximation formula:

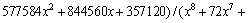

 (8)
(8)
The iterative procedure was performed in three following steps: 1) Assume π(x)=1 to estimate the initial value Eα,1. The isoconversional method stops the calculation at this step. 2) Using evaluated Eα,1 to calculate a new activation energy value or Eα,2 from the plot of ln [β/(π(x)T2)] vs 1/T. 3) Repeat step 2), replacing Eα,1 by Eα,2. When Eα,i-Eα,i-1 <0.1 kJ/mol, the last Eα,i value will be considered to be the reliable apparent Eα value of the reaction.
3.2 Mechanism function determination
The isoconversional (model-free) method can be applied without knowing the true reaction mechanism function, but this function must be invariant for all experimental heating rates. The invariance can be examined according to the procedure proposed by VYAZOVKIN et al [34] and  [35,51]. This procedure suggests that the mechanism function is proportional to two special functions y(α) and z(α), that can basically be obtained by a simple transformation of the TG data. In the present work, Málek equations were used to choose an appropriate kinetic model. According to Eq. (3), this equation can be rearranged to obtain Eq. (9) for further determination of the special function y(α) [34,35,38].
[35,51]. This procedure suggests that the mechanism function is proportional to two special functions y(α) and z(α), that can basically be obtained by a simple transformation of the TG data. In the present work, Málek equations were used to choose an appropriate kinetic model. According to Eq. (3), this equation can be rearranged to obtain Eq. (9) for further determination of the special function y(α) [34,35,38].
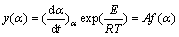 (9)
(9)
while the temperature integral 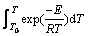 in Eq. (6) can be solved as follows [34]:
in Eq. (6) can be solved as follows [34]:
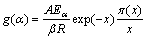 (10)
(10)
After that, multiply Eqs. (9) and (10), followed by some rearrangements. The z(α) function is introduced to formulate as
 (11)
(11)
As evidenced from Eqs. (9) and (11), it is necessary to know the Eα value in non-isothermal conditions. By plotting the y(α) and z(α) dependence, normalized with the values of 0-1. Therefore, the type of reaction model can be recognized by determining the maximal values including αp, αm and  observed from the plots between dα/dt, y(α) and z(α) functions vs α, respectively. The mathematical properties of the y(α) and z(α) functions for basic kinetic models are summarized in Table 1 [51].
observed from the plots between dα/dt, y(α) and z(α) functions vs α, respectively. The mathematical properties of the y(α) and z(α) functions for basic kinetic models are summarized in Table 1 [51].
4 Results and discussion
4.1 Characterization
Thermal analysis measurement of the synthesized hydrate compound, Mn1.8Co0.1Mg0.1P2O7·2H2O, was carried out at a heating rate of 10 °C/min. The typical TG/DTG/DTA curves recorded under flowing air atmosphere are shown in Fig. 1. The single decomposition step was observed over the experimentally temperature range of 90 and 150 °C according to the maximum temperature of DTG and endothermic DTA peaks at 120 and 121 °C, respectively. A single mass loss of the process is about 11.19% (theoretical value, 11.36%), which corresponds to the elimination of 2 mol crystallization water to form the anhydrous Mn1.8Co0.1Mg0.1P2O7. The non-isothermal TG/DTG/DTA curves of the title hydrate at four heating rates are shown in Fig. 2. According to the results from Figs. 1 and 2, the thermal dehydration process of the title hydrate can be suggested as follows.
Table 1 Summary of kinetic mechanism determinations [51]
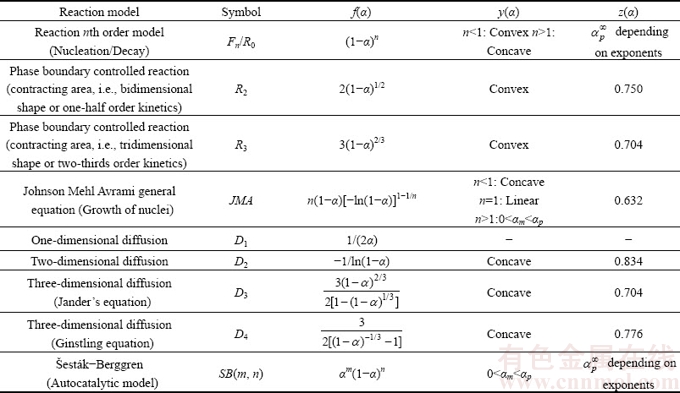
Fig. 1 Single thermal dehydration process of Mn1.8Co0.1Mg0.1- P2O7·2H2O obtained from TG/DTG/DTA techniques at heating rate of 10 °C/min
In the single thermal dehydration process (90-150 °C), there exists

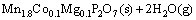 (12)
(12)
FTIR spectra of the synthesized hydrate Mn1.8Co0.1Mg0.1P2O7·2H2O and its thermal dehydration product Mn1.8Co0.1Mg0.1P2O7 are shown in Fig. 3. The broad bands in the region of 3600-3000 cm-1 are assigned to the O—H stretching vibrations of both asymmetric ν3B2(H2O) (higher energy) and symmetric ν1A1(H2O) (lower energy) modes, while the single band observed at 1650 cm-1 is assigned to H—O—H bending vibration of ν2A1(H2O) mode of water molecule. The FTIR spectra (Figs. 3(a) and (b)) of the hydrate and its anhydrous forms are interpreted according to the vibrating units of H2O molecule and  anion, respectively. The asymmetric νasym(PO2) and symmetric νsym(PO2) stretching vibrational modes of
anion, respectively. The asymmetric νasym(PO2) and symmetric νsym(PO2) stretching vibrational modes of  anion are observed in the regions of 1255-1140 and 1150-950 cm-1 [26,37,52], respectively. While the asymmetric νasym(P—O—P) and symmetric νsym(P—O—P) modes of P—O—P bridges are observed in the ranges of 1015-940 and 760-400 cm-1, respectively.
anion are observed in the regions of 1255-1140 and 1150-950 cm-1 [26,37,52], respectively. While the asymmetric νasym(P—O—P) and symmetric νsym(P—O—P) modes of P—O—P bridges are observed in the ranges of 1015-940 and 760-400 cm-1, respectively.
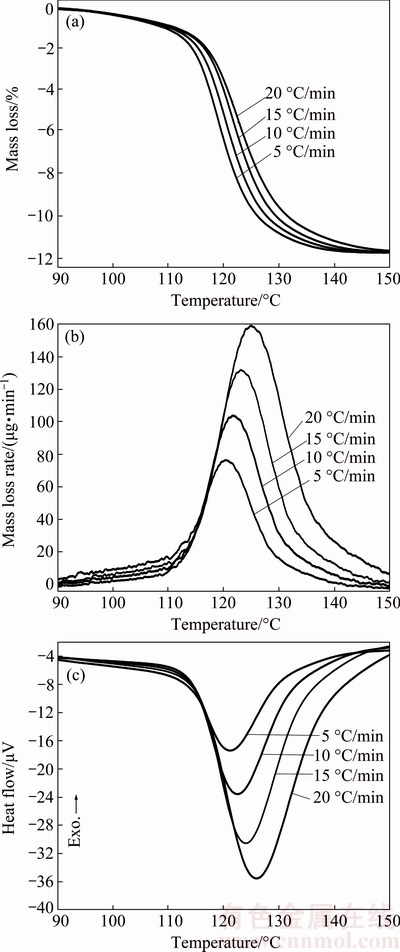
Fig. 2 TG (a), DTG (b) and DTA (c) curves of single thermal dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O at heating rates of 5, 10, 15 and 20 °C/min
XRD patterns of the synthesized hydrate and its thermal dehydration product are presented in Fig. 4. The very strong intensities and obviously smooth baselines of diffraction patterns of both hydrate and anhydrous compounds indicate the high crystallinity and excellent purity. All diffraction peaks in Fig. 4(a) are indexed as the monoclinic phase Mn1.8Co0.1Mg0.1P2O7·2H2O with the space group of P21/b (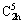 , No. 14) according to the PDF No. 71-0760 (standard Mn2P2O7·2H2O compound) with standard cell parameters a=6.461
, No. 14) according to the PDF No. 71-0760 (standard Mn2P2O7·2H2O compound) with standard cell parameters a=6.461 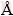 , b=14.320
, b=14.320 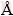 and c=7.570
and c=7.570 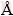 . The calculated cell parameters in this work are a=6.473
. The calculated cell parameters in this work are a=6.473 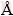 , b=14.342
, b=14.342 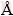 and c=7.558
and c=7.558 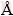 with α=γ=90°≠β. While the corresponding calculated cell volume and crystallite size are 701.65
with α=γ=90°≠β. While the corresponding calculated cell volume and crystallite size are 701.65 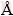 3 and 48.2 nm, respectively. On the other hand, a diffraction pattern in Fig. 4(b) observed after the completion of the thermal dehydration of the hydrate precursor is indexed as the well-crystalline phase Mn1.8Co0.1Mg0.1P2O7 according to the PDF No. 77-1243 (standard Mn2P2O7 compound), which crystallizes in the monoclinic system and the space group of C2/m (
3 and 48.2 nm, respectively. On the other hand, a diffraction pattern in Fig. 4(b) observed after the completion of the thermal dehydration of the hydrate precursor is indexed as the well-crystalline phase Mn1.8Co0.1Mg0.1P2O7 according to the PDF No. 77-1243 (standard Mn2P2O7 compound), which crystallizes in the monoclinic system and the space group of C2/m (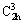 , No. 12). The standard cell parameters are a=6.633
, No. 12). The standard cell parameters are a=6.633 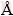 , b=8.584
, b=8.584 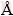 and c=4.646
and c=4.646 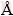 , compared with the calculated cell parameters in this work of a=6.649
, compared with the calculated cell parameters in this work of a=6.649 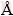 , b=8.598
, b=8.598 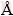 and c=4.635
and c=4.635 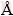 and α=γ=90°≠β. The corresponding cell volume and crystallite size are 264.97
and α=γ=90°≠β. The corresponding cell volume and crystallite size are 264.97 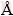 3 and 37.8 nm, respectively.
3 and 37.8 nm, respectively.
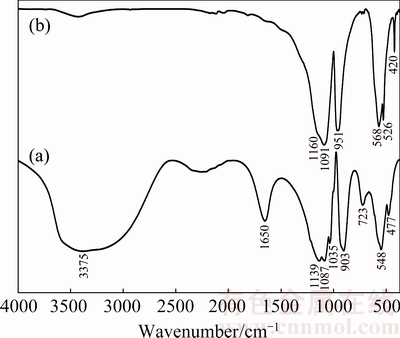
Fig. 3 FTIR spectra of Mn1.8Co0.1Mg0.1P2O7·2H2O (a) and its thermal dehydration product Mn1.8Co0.1Mg0.1P2O7 (b) by KBr pellet technique at room temperature in wavenumber range of 4000-370 cm-1

Fig. 4 XRD patterns of Mn1.8Co0.1Mg0.1P2O7·2H2O (a) compared with PDF No. 71-0760 (standard Mn2P2O7·2H2O compound) and its thermal dehydration product Mn1.8Co0.1Mg0.1P2O7 (b) compared with PDF No. 77-1243 (standard Mn2P2O7 compound)
SEM image of the synthesized hydrate in Fig. 5(a) illustrates the plate-like crystals having sizes of 4-6 mm in width and 7-8 mm in length together with smaller size irregular particles of 2-3 mm. While the final thermal dehydration product in Fig. 5(b) shows the irregular shape having sizes of 0.3-0.5 mm together with larger irregular particles with the sizes of 0.5-1 mm. The anhydrous product exhibiting significantly different morphologies is suggested to be due to the temperature effect upon dehydration process. The mole numbers of the divalent metals (Mn, Co, Mg) per chemical formula of both hydrate and anhydrous compounds were determined and confirmed by AAS method, while the mole number of the water in the hydrate was determined and confirmed from the mass loss in TG curve. The results confirmed that the formula of the synthesized hydrate is Mn1.8Co0.1Mg0.1P2O7·2H2O, while the final thermal dehydration product is Mn1.8Co0.1Mg0.1P2O7.

Fig. 5 SEM images after gold coating technique of Mn1.8Co0.1Mg0.1P2O7·2H2O (plate-like crystals) (a) and its thermal dehydration product Mn1.8Co0.1Mg0.1P2O7 (irregular shape) (b)
4.2 Kinetics, mechanism and thermodynamics
4.2.1 Apparent Eα value
Thermal analysis measurement of the synthesized hydrate, Mn1.8Co0.1Mg0.1P2O7·2H2O, was carried out under non-isothermal conditions. The TG/DTG/DTA results of the synthesized hydrate at four heating rates β of 5, 10, 15 and 20 °C/min over the experimentally temperature range of 90-150 °C are shown in Fig. 2. The peak temperatures of TG/DTG/DTA curves increase as the heating rate increases accompanied by shifting to a higher temperature. The isoconversional iterative KAS equation was used to evaluate the apparent Eα value with the reliable value. The Eα values of the single thermal dehydration process corresponding to different conversions α values ranging from 0.10 to 0.90 with a 0.02 increment are obtained. The variation of Eα and A values for α<0.10 and α>0.90 is not automatically a major concern, because those parameters can be affected greatly by possible minor errors in baseline determination [34]. In this work, the relations between the values of Eα and α of the dehydration process are shown in Fig. 6. If Eα values are roughly constant over the entire α range and if no shoulders are observed in the reaction process curve such as dα/dt vs T curve, it is likely that the process is dominated by a single step process and can be adequately described by a single-step kinetic model [34]. However, it is more common that the reaction parameters vary significantly with α. If the reaction process curve has multiple peaks and/or shoulders, the Eα and A values at appropriate levels of α can be used for the input to multi-step model fitting computations [34,53]. In addition, it can be also considered as the single-step kinetics, if the Eα values are independent of α values, by which the changes of the maximum Eα,max or minimum Eα,min values from the average one Eα,av must be less than 10% [34]. In this work, Eα values of the system tend to increase as α values increase (Fig. 6). The average apparent Eα,av value of the dehydration process was determined to be (79.97±6.51) kJ/mol with the corresponding average correlation coefficient (r2) of 0.9996 obtained from the iterative KAS equation plots ln [β/h(x)T2] vs 1/T). The TG/DTG/DTA curves in Fig. 2 exhibited neither multiple peaks nor shoulders and the relative errors between the maximum Eα,max or minimum Eα,min and the average Eα,av values displayed in Fig. 6 are 8.91% (Eα,max vs Eα,av) and 8.75% (Eα,min vs Eα,av), respectively, which are less than 10%. Therefore, the single thermal dehydration process of the studied hydrate was considered to be the single-step kinetic process and can be adequately described by the unique kinetic triplet (Eα, A and f(α)).

Fig. 6 Eα values for single thermal dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O with relative errors less than 10%
4.2.2 Kinetic mechanism and pre-exponential factor A

Fig. 7 Relation between α and T, dα/dt and T for single thermal dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O at heating rate of 5 °C/min
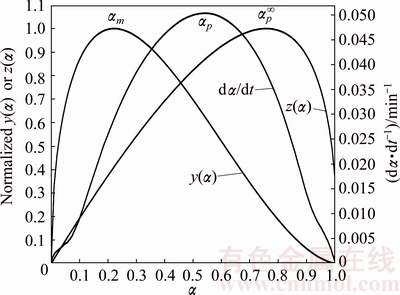
Fig. 8 dα/dt vs α, y(α) vs α and z(α) vs α plots for single thermal dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O at heating rate of 5 °C/min
Table 2 Values of αp, αm, 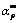 , n, m and ln A at four heating rates
, n, m and ln A at four heating rates

Reaction mechanism is the most important information to identify the physical meaning from the kinetic triplets of the thermal dehydration. According to the thermogravimetric experimental results and the average apparent Eα,av value obtained from the iterative isoconversional KAS equation in Eq. (7), the variations of α vs T and dα/dt vs T for the thermal dehydration of the synthesized hydrate Mn1.8Co0.1Mg0.1P2O7·2H2O can be determined and shown in Fig. 7. After that, the reaction rate dα/dt as well as the mentioned Málek equations (Eqs. (9) and (11)) will be used to generate the experimental plots between normalized y(α) vs α and normalized z(α) vs α. The variations of the normalized y(α) and z(α) functions on the conversion α are illustrated in Fig. 8. The shapes of the plots are practically unchanged with respect to heating rate β. For the calculation of the above functions (y(α) and z(α)), the average Eα,av value of 79.97 kJ/mol evaluated from iterative KAS method was used. Figure 8 illustrates the variations of dα/dt vs α, y(α) vs α and z(α) vs α at a heating rate of 5 °C/min. The results of the experimental plots for other three heating rates of 10, 15 and 20 °C/min do not exhibit significant variation. Subsequently, the determination of the most probable reaction mechanism function for the dehydration process is established. The reaction mechanism function to describe the experimental data was determined by the isoconversional Málek equations. The data in Table 2 extracted from Fig. 8 lead to the maximum peaks for the plots of dα/dt vs α, y(α) vs α and z(α) vs α and are denoted as αp, αm and  , respectively. The results are summarized in Table 2. The maximum values of the curves dα/dt vs α obtained from four different heating rates are observed in the α range of 0.541-0.543, whereas the maximum values in the cases of y(α) vs α and z(α) vs α are found in the α ranges of 0.217-0.221 and 0.758-0.761, respectively. That means 0<αm(0.219)< αp(0.542) and
, respectively. The results are summarized in Table 2. The maximum values of the curves dα/dt vs α obtained from four different heating rates are observed in the α range of 0.541-0.543, whereas the maximum values in the cases of y(α) vs α and z(α) vs α are found in the α ranges of 0.217-0.221 and 0.758-0.761, respectively. That means 0<αm(0.219)< αp(0.542) and  =0.760≠0.632 (see Table 1, JMA model for
=0.760≠0.632 (see Table 1, JMA model for  ). According to the decision standard of the Málek equations together with the consideration from Table 1, two-parameters in
). According to the decision standard of the Málek equations together with the consideration from Table 1, two-parameters in  -Berggren model (m, n) or SB (m, n) [35,51,54] can be used to fit the non-isothermal dehydration kinetic process of the studied system. The autocatalytic SB (m, n) model [54,55] in which f(α)=αm(1-α)n, where m and n represent the reaction orders or kinetic exponents, seems to be the most suitable for the dehydration process of the title synthesized hydrate. The mechanical reaction is autocatalytic chemical reaction when a concentration of product vs time plot exhibits an S-shaped profile [56]. According to the obtained result in this work, the reaction progress or extent of conversion α vs time t or temperature T shows the S-shaped curve (α vs T plot, Fig. 7). This type chemical reaction, the chemical rate increases as the materials react. The most important factor in predicting the effects is the temperature. It is clear that the temperature changes leads to the change of reaction rate [57]. If one of the reaction products is also a reactant, it behaves as a catalyst in the same or a coupled reaction. Common autocatalytic rate curve is like umbrella [57], which agrees with the autocatalytic curve of dα/dt vs T, as shown in Fig 7. The reaction rate increases with the increase of temperature in the autocatalytic curve until it reaches a maximum and then decreases [57]. By applying the SB (m, n) model, the simulation of TG curve using non-linear regression method leads to the kinetic parameters. The SB (m, n) model can be expressed by the following equation:
-Berggren model (m, n) or SB (m, n) [35,51,54] can be used to fit the non-isothermal dehydration kinetic process of the studied system. The autocatalytic SB (m, n) model [54,55] in which f(α)=αm(1-α)n, where m and n represent the reaction orders or kinetic exponents, seems to be the most suitable for the dehydration process of the title synthesized hydrate. The mechanical reaction is autocatalytic chemical reaction when a concentration of product vs time plot exhibits an S-shaped profile [56]. According to the obtained result in this work, the reaction progress or extent of conversion α vs time t or temperature T shows the S-shaped curve (α vs T plot, Fig. 7). This type chemical reaction, the chemical rate increases as the materials react. The most important factor in predicting the effects is the temperature. It is clear that the temperature changes leads to the change of reaction rate [57]. If one of the reaction products is also a reactant, it behaves as a catalyst in the same or a coupled reaction. Common autocatalytic rate curve is like umbrella [57], which agrees with the autocatalytic curve of dα/dt vs T, as shown in Fig 7. The reaction rate increases with the increase of temperature in the autocatalytic curve until it reaches a maximum and then decreases [57]. By applying the SB (m, n) model, the simulation of TG curve using non-linear regression method leads to the kinetic parameters. The SB (m, n) model can be expressed by the following equation:
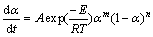 (13)
(13)
Equation (13) was obtained from the substitution according to f(α)=αm(1-α)n from the SB (m, n) model, into Eq. (3). By logarithmic transformation, Eq. (13) will be
 (14)
(14)
where m/n can be replaced by αm/(1-αm) [35]. Then, the special kinetic parameters, n, ln A and m can be obtained. For instance, the variations of the plots between  vs
vs 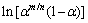 for 0.1≤α≤0.9 at a heating rate of 5 °C/min are shown in Fig. 9 with the corresponding correlation coefficient (r2) in the plots of 0.9998, 0.9997, 0.9997 and 0.9996 for the heating rates of 5, 10, 15 and 20 °C/min, respectively. The n and ln A values can be determined from the slope and intercept of the fitted lines, respectively. Then, m value can be obtained by multiplying n and αm/(1-αm). The results for other three heating rates (10, 15 and 20 °C/min) in the studied system are also presented in Table 2. According to the results from this method, the substitution of the calculated kinetic parameters in both kinetic triplets (Eα, A and f(α)) and special kinetic parameters (n and m) into Eq. (3) leads to an explicit rate equation for predicting the studied non-isothermal dehydration reaction as follows:
for 0.1≤α≤0.9 at a heating rate of 5 °C/min are shown in Fig. 9 with the corresponding correlation coefficient (r2) in the plots of 0.9998, 0.9997, 0.9997 and 0.9996 for the heating rates of 5, 10, 15 and 20 °C/min, respectively. The n and ln A values can be determined from the slope and intercept of the fitted lines, respectively. Then, m value can be obtained by multiplying n and αm/(1-αm). The results for other three heating rates (10, 15 and 20 °C/min) in the studied system are also presented in Table 2. According to the results from this method, the substitution of the calculated kinetic parameters in both kinetic triplets (Eα, A and f(α)) and special kinetic parameters (n and m) into Eq. (3) leads to an explicit rate equation for predicting the studied non-isothermal dehydration reaction as follows:
 (15)
(15)
The experimental and simulated curves between dα/dt vs T at four heating rates β are compared, as shown in Fig. 10. The initial condition for solving Eq. (15) was set at α=0.005 [39] and T=90 °C to cover the overall reaction of the thermal decomposition of studied system in this work. According to Fig. 10, Eq. (15) can appropriately describe the non-isothermal dehydration process of the synthesized hydrate Mn1.8Co0.1Mg0.1P2O7·2H2O.

Fig. 9 Plot of ln[(dα/dt)exp(E/(RT))] vs ln[αm/n(1-α)] for single dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O at heating rate of 5 °C/min

Fig. 10 Comparison between experimental and simulated curves (dα/dt vs T) for single dehydration process of Mn1.8Co0.1Mg0.1P2O7·2H2O at four heating rates of 5, 10, 15 and 20 °C/min
4.2.3 Thermodynamic functions
According to the transition state complex theory of Eyring [58], the entropy change of transition state complex or entropy of activation ΔSΘ is related to the pre-exponential factor or frequency factor A as follows [59]:
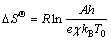 (16)
(16)
where e is the Neper number (2.7183), χ is the transition factor (=1 for the complete reaction), kB and h are the Boltzmann (1.3806×10-23 J/K) and Planck (6.6261× 10-34 J·s) constants, respectively, T0 is the peak temperature (393.60 K) from DTG curve at β=5 °C/min and R is the mole gas constant.
The enthalpy change or heat of activation ΔHΘ and Gibbs free energy change of activation or Gibbs free energy of activation ΔGΘ can be calculated according to Eqs. (17) and (18), respectively [60]:
ΔHΘ=Eα-RT (17)
ΔGΘ=ΔHΘ-TΔSΘ (18)
The calculated entropy of activation ΔSΘ for dehydration process is -115.61 J/(K·mol), while the corresponding enthalpy of activation ΔHΘ and the Gibbs free energy of activation ΔGΘ are 75.82 and 107.81 kJ/mol, respectively. The negative ΔSΘ value reveals that the activated state is less disordered compared with the initial state, which suggests a small number of degrees of freedom due to rotation and vibration. This may be interpreted as a “slow” stage [61]. The endothermic peak in DTA curve agrees well with the positive sign of ΔHΘ value. The positive ΔGΘ value confirms that the studied thermal dehydration reaction is a non-spontaneous process.
5 Conclusions
The single-step of the thermal dehydration process of monoclinic crystal system, Mn1.8Co0.1Mg0.1P2O7·2H2O, was observed and the final product was confirmed to be Mn1.8Co0.1Mg0.1P2O7. The kinetics of the non-isothermal dehydration process was accurately determined from a series of thermo-analytical experiments at four heating rates. The isoconversional kinetic study was carried out using the iterative KAS method and found that the calculated apparent Eα tends to increase as the α values increase. The average apparent Eα value as well as the absence of shoulder in the reaction process curve (dα/dt) indicates the single-step kinetic process and can be adequately described by the unique kinetic triplets (Eα, A and f(α)). The reaction model was suggested using two special functions from Málek’s equations. The shapes of y(α) and z(α) indicate that the autocatalytic  -Berggren model is the reaction model for describing the dehydration process. The related thermodynamic functions of the transition state complexes were calculated through the kinetic parameters and found to agree well with the thermal analysis data.
-Berggren model is the reaction model for describing the dehydration process. The related thermodynamic functions of the transition state complexes were calculated through the kinetic parameters and found to agree well with the thermal analysis data.
Acknowledgements
The author would like to thank the Department of Chemistry, Faculty of Science, Khon Kaen University, Thailand and also thank Dr. Chanaiporn Danvirutai for carefully reading the manuscript.
References
[1] OKA J, KAWAHARA A. The structure of synthetic dimagnesium diphosphate (V) dehydrate [J]. Acta Crystallographica: Section B, 1982, 38: 3-5.
[2] KONGSHAUG K O, FJELLVAG H, LILLERUD K P. Synthesis and crystal structure of the hydrated magnesium diphosphate Mg2P2O7·3.5H2O and its high temperature variant Mg2P2O7·H2O [J]. Solid State Sciences, 2000, 2: 205-214.
[3] SOUHASSOU M, LECOMTE C, BLESSING R H. Crystal chemistry of Mg2P2O7·nH2O, n=0, 2 and 6: Magnesium-oxygen coordination and pyrophosphate ligation and conformation [J]. Acta Crystallographica: Section B, 1992, 48: 370-376.
[4] SCHNEIDER S, COLLIN R L. Crystal structure of manganese pyrophosphate dihydrate Mn2P2O7·2H2O [J]. Inorganic Chemistry, 1973, 12: 2136-2139.
[5] EFFENBERGER H, PERTLIK F. Comparison of the crystal structures of Co2(X2O7)·2H2O, X=P and As [J]. Chemical Monthly, 1993, 124: 381-389.
[6] VOITENKO L V, ZHILYAK I D, KOPILEVICH V A. Hydrated cobalt (II) and nickel (II) ammine diphosphates isolated from aqueous solutions [J]. Russian Journal of Applied Chemistry, 2004, 77: 1409-1412.
[7] CORNILSEN B C. Solid state vibrational spectra of calcium pyrophosphate dehydrate [J]. Journal of Molecular Structure, 1984, 117: 1-9.
[8] ASSAAOUDI H, BUTLER I S, KOZINSKI J,  F. Crystal structure, vibrational spectra and thermal decomposition of a new tetrazinc(II) dipyrophosphate decahydrate, Zn4(P2O7)2·10H2O [J]. Journal of Chemical Crystallography, 2005, 35: 49-59.
F. Crystal structure, vibrational spectra and thermal decomposition of a new tetrazinc(II) dipyrophosphate decahydrate, Zn4(P2O7)2·10H2O [J]. Journal of Chemical Crystallography, 2005, 35: 49-59.
[9] KRISHNAMACHARI N, CALVO C. The crystal structure of cobalt diphosphate [J]. Acta Crystallographica: Section B, 1972, 28: 2883-2885.
[10] BELGHITTI A E, BOUKHARI A, HOLT E M. β-dicobalt pyrophosphate [J]. Acta Crystallographica: Section C, 1994, 50: 482-484.
[11] KOBASHI D, KOHARA S, YAMAKAWA J, KAWAHARA A. Structure of a synthetic dicobalt diphosphate: Co2P2O7 [J]. Acta Crystallographica: Section C, 1997, 53: 1523-1525.
[12] SUN X, WANG S, WANG Z, YE X, WEN T, HUANG F. Proton conductivity of CeP2O7 for intermediate temperature fuel cells [J]. Solid State Ionics, 2008, 179: 1138-1141.
[13] BIAN J, KIM D W, HONG K. Microwave dielectric properties of (Ca1-xZnx)2P2O7 [J]. Materials Letters, 2005, 59: 257-260.
[14] MASSON N C, de SOUZA E F, GALEMBECK F. Calcium and iron(III) polyphosphate gel formation and aging [J]. Colloids and Surfaces A, 1997, 121: 247-255.
[15] CHEN B, MUNSON E J. Investigation of the mechanism of n-butane oxidation on vanadium phosphorus oxide catalysts: Evidence from isotopic labeling studies [J]. Journal of the American Chemical Society, 2002, 124: 1638-1652.
[16] IKOTUN O F, MARINO N, KRUGER P E, JULVE M, DOYLE R P. Exploring the coordination chemistry of pyrophosphate: A ligand of diverse biological, magnetic and catalytic potential [J]. Coordination Chemistry Reviews, 2010, 254: 890-915.
[17] ONODA H, KOJIMA K, NARIAI H. Additional effects of rare earth elements on formation and properties of some transition metal pyrophosphates [J]. Journal of Alloys and Compounds, 2006, 408-412: 568-572.
[18] ONODA H, NARIAI H, MORIWAKI A, MAKI H, MOTOOKA I. Formation and catalytic characterization of various rare earth phosphates [J]. Journal of Materials Chemistry, 2002, 12: 1754-1760.
[19] WU W W, FAN Y J, WU X H, LIAO S, LI S S. Preparation via solid-state reaction at room temperature and characterization of layered nanocrystalline NH4MnPO4·H2O [J]. Journal of Physics and Chemistry of Solids, 2009, 70: 584-587.
[20] SHIQUAN W, XUEYA J, GUODONG D, ZAIPING G, JIYEON J, SEUNG-JOO K. Solvothermal synthesis of Mn2P2O7 and its application in lithium-ion battery [J]. Materials Letters, 2011, 65: 3265-3268.
[21] DHAOUADI H, TOUATI F. Synthesis and characterization of a series of cobalt-manganese pyrophosphate CoxMn2-xP2O7 (x=0, 0.25, 0.5, and 1) compounds [J]. Materials Letters, 2012, 82: 91-94.
[22] LLUSAR M, ZIELINSKA A, TENA M A, BADENES J A, MONRóS G. Blue-violet ceramic pigments based on Co and Mg·Co2-xMgxP2O7 diphosphates [J]. Journal of the European Ceramic Society, 2010, 30: 1887-1896.
[23] BOONCHOM B. Kinetic and thermodynamic studies of MgHPO4·3H2O by non-isothermal decomposition data [J]. Journal of Thermal Analysis and Calorimetry, 2009, 98: 863-871.
[24] MAASS K, GLAUM R, GRUEHN R. Contributions on crystal chemistry and thermal behaviour of anhydrous phosphates XXXI. (Mg1-xCrx)2P2O7, CaCrP2O7, SrCrP2O7 and BaCrP2O7—New diphosphates of divalent chromium [J]. Journal of Inorganic and General Chemistry, 2001, 627: 2081-2090.
[25] SRONSRI C, NOISONG P, DANVIRUTAI C. Isoconversional kinetic, mechanism and thermodynamic studies of the thermal decomposition of NH4Co0.8Zn0.1Mn0.1PO4·H2O [J]. Journal of Thermal Analysis and Calorimetry, 2015, 120: 1689-1701.
[26] SRONSRI C, NOISONG P, DANVIRUTAI C. Synthesis, non-isothermal kinetic and thermodynamic studies of the formation of LiMnPO4 from NH4MnPO4·H2O precursor [J]. Solid State Sciences, 2014, 32: 67-75.
[27] SRONSRI C, NOISONG P, DANVIRUTAI C. Synthesis and properties of LiMIIPO4 (MII = Mg, Mn0.5Mg0.5, Co0.5Mg0.5) affected by isodivalent doping and Li-sources [J]. Solid State Sciences, 2014, 36: 80-88.
[28] KIM J, SEO D H, KIM S W, PARK Y U, KANG K. Mn based olivine electrode material with high power and energy [J]. Chemical Communications, 2010, 46: 1305-1307.
[29] MINAKSHI M, KANDHASAMY S. Utilizing active multiple dopants (Co and Ni) in olivine LiMnPO4 [J]. Current Opinion in Solid State and Materials Science, 2012, 16: 163-167.
[30] YI H H, HU C L, FANG H H, YANG B, YAO Y H, MA W H, DAI Y N. Optimized electrochemical performance of LiMn0.9Fe0.1-xMgxPO4/ C for lithium ion batteries [J]. Electrochimica Acta, 2011, 56: 4052-4057.
[31] RAMAR V, BALAYA P. Enhancing the electrochemical kinetics of high voltage olivine LiMnPO4 by isovalent co-doping [J]. Physical Chemistry Chemical Physics, 2013, 15: 17240-17249.
[32] YOSHIMURA M, BYRAPPA K. Hydrothermal processing of materials: Past, present and future [J]. Journal of Materials Science, 2008, 43: 2085-2103.
[33] SHARP J H, BRINALEY G W, ACHAR B N N. Numerical data for some commonly used solid state reaction equations [J]. Journal of the American Ceramic Society, 1966, 49: 379-382.
[34] VYAZOVKIN S, BURNHAM A K, CRIADO J M,  -MAQUEDA L A, POPESCU C, SBIRRAZZUOLI N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520: 1-19.
-MAQUEDA L A, POPESCU C, SBIRRAZZUOLI N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520: 1-19.
[35]  J. The kinetic analysis of non-isothermal data [J]. Thermochimica Acta, 1992, 200: 257-269.
J. The kinetic analysis of non-isothermal data [J]. Thermochimica Acta, 1992, 200: 257-269.
[36] CULLITY B D. Elements of X-ray diffraction [M]. 2nd ed. Reading, MA: Addison-Wesley Publishing, 1978.
[37] DANVIRUTAI C, NOISONG P, YOUNGME S. Some thermodynamic functions and kinetics of thermal decomposition of NH4MnPO4·H2O in nitrogen atmosphere [J]. Journal of Thermal Analysis and Calorimetry, 2010, 100: 117-124.
[38] SRONSRI C, NOISONG P, DANVIRUTAI C. Solid state reaction mechanisms of the LiMnPO4 formation using special function and thermodynamic studies [J]. Industrial & Engineering Chemistry Research,2015, 54: 7083-7093.
[39] CAI J, ALIMUJIANG S. Kinetic analysis of wheat straw oxidative pyrolysis using thermogravimetric analysis: Statistical description and isoconversional kinetic analysis [J]. Industrial & Engineering Chemistry Research,2009, 48: 619-624.
[40] VYAZOVKIN S, CHRISSAFIS K, LORENZO M L D, KOGA N, PIJOLAT M, RODUIT B, SBIRRAZZUOLI N,  J J. ICTAC kinetics Committee recommendations for collecting experimental thermal analysis data for kinetic computations [J]. Thermochimica Acta, 2014, 590: 1-23.
J J. ICTAC kinetics Committee recommendations for collecting experimental thermal analysis data for kinetic computations [J]. Thermochimica Acta, 2014, 590: 1-23.
[41] El-THAHER N, MEKONNEN T, MUSSONE P, BRESSLER D, CHOI P. Nonisothermal DSC study of epoxy resins cured with hydrolyzed specified risk material [J]. Industrial & Engineering Chemistry Research,2013, 52: 8189-8199.
[42] LIU Y, GUO Q, CHENG Y, RYU H J. Reaction mechanism of coal chemical looping process for syngas production with CaSO4oxygen carrier in the CO2atmosphere [J]. Industrial & Engineering Chemistry Research,2012, 51: 10364-10373.
[43] KHACHANI M, HAMIDI A E, HALIM M, ARSALANE S. Non-isothermal kinetic and thermodynamic studies of the dehydroxylation process of synthetic calcium hydroxide Ca(OH)2 [J]. Journal of Materials and Environmental Science, 2014, 5: 615-624.
[44] FAN M, LI X, ZHANG J, CHENG J. Curing kinetics and shape-memory behavior of an intrinsically toughened epoxy resin system [J]. Journal of Thermal Analysis and Calorimetry, 2015, 119: 537-546.
[45] VLAEV L T, GEORGIEVA V G, GENIEVA S D. Products and kinetics of non-isothermal decomposition of vanadium (IV) oxide compounds [J]. Journal of Thermal Analysis and Calorimetry, 2007, 88: 805-812.
[46] TAGHIZADEH M T, YEGANEH N, REZAEI M. Kinetic analysis of the complex process of poly(vinyl alcohol) pyrolysis using a new coupled peak deconvolution method [J]. Journal of Thermal Analysis and Calorimetry, 2014, 118: 1733-1746.
[47] CHAI Q, CHEN Z, LIAO S, HE Y, LI Y, WU W, LI B. Preparation of LiZn0.9PO4:Mn0.1·H2O via a simple and novel method and its non-isothermal kinetics using iso-conversional calculation procedure [J]. Thermochimica Acta, 2012, 533: 74-80.
[48] GENIEVA S D, VLAEV L T, ATANASSOV A N. Study of the thermooxidative degradation kinetics of poly(tetrafluoroethene) using iso-conversional calculation procedure [J]. Journal of Thermal Analysis and Calorimetry, 2010, 99: 551-561.
[49] CHRISSAFIS K, PARASKEVOPOOLOS K M, PAPAGEORGIOU G Z, BIKIARIS D N. Thermal decomposition of poly(propylene sebacate) and poly(propylene azelate) biodegradable polyesters: Evaluation of mechanisms using TGA, FTIR and GS/MS [J]. Journal of Analytical and Applied Pyrolysis, 2011, 92: 123-130.
[50]  -MAQUEDA L A, CRIADO J M. The accuracy of Senum and Yang’s approximations to the Arrhenius integral [J]. Journal of Thermal Analysis and Calorimetry, 2000, 60: 909-915.
-MAQUEDA L A, CRIADO J M. The accuracy of Senum and Yang’s approximations to the Arrhenius integral [J]. Journal of Thermal Analysis and Calorimetry, 2000, 60: 909-915.
[51] 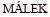 J. A computer program for kinetic analysis of non- isothermal thermoanalytical data [J]. Thermochimica Acta, 1989, 138: 337-346.
J. A computer program for kinetic analysis of non- isothermal thermoanalytical data [J]. Thermochimica Acta, 1989, 138: 337-346.
[52] HARCHARRAS M, ENNACIRI A, RULMONT A, GILBERT B. Vibrational spectra and structures of double diphosphates M2CdP2O7 (M = Li, Na, K, Rb, Cs) [J]. Spectrochimica Acta A, 1997, 53: 345-352.
[53] VLAEV L T, NIKOLOVA M M, GOSPODINOV G G. Non- isothermal kinetics of dehydration of some selenite hexahydrates [J]. Journal of Solid State Chemistry, 2004, 177: 2663-2669.
[54] 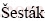 J, BERGGREN G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3: 1-12.
J, BERGGREN G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3: 1-12.
[55] SIMON P. Fourty years of the 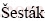 -Berggren equation [J]. Thermochimica Acta, 2011, 520: 156-157.
-Berggren equation [J]. Thermochimica Acta, 2011, 520: 156-157.
[56] MATA-PEREZ F, PEREZ-BENITO J F. The kinetic rate law for autocatalytic reactions [J]. Journal of Chemical Education, 1987, 64: 925-927.
[57] ROGERS R N. The chemistry of autocatalytic processes in the context of the shroud of Turin [M]. Oakland: University of California, 2002.
[58] ROONEY J J. Eyring transition-state theory and kinetics in catalysis [J]. Journal of Molecular Catalysis A: Chemical, 1995, 96: L1-L3.
[59] WU X H, WU W W, CUI X M, LIAO S. Selective self-assembly synthesis of MnV2O6·4H2O with controlled morphologies and study on its thermal decomposition [J]. Journal of Thermal Analysis and Calorimetry, 2012, 109: 163-169.
[60] WU X H, WU W W, CUI X M, LIAO S. Preparation of nanocrystalline BiFeO3 via a simple and novel method and its kinetics of crystallization [J]. Journal of Thermal Analysis and Calorimetry, 2012, 107: 625-632.
[61] SRONSRI C, NOISONG P, DANVIRUTAI C. Double function method for the confirmation of the reaction mechanism of LiCoPO4 nanoparticle formation, reliable activation energy, and related thermodynamic functions [J]. Reaction Kinetics, Mechanisms and Catalysis, 2017, 121: 555-577.
Chuchai SRONSRI
Department of Chemistry, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
摘 要:采用水热法合成Mn1.8Co0.1Mg0.1P2O7·2H2O,证实其热脱水产物为Mn1.8Co0.1Mg0.1P2O7。利用热重/微分热重/差热分析、傅里叶变换红外光谱、原子吸收分光光度、X射线衍射和扫描电镜等技术对样品进行表征。研究4种加热速率下空气气氛中(热脱水过程)的非等温动力学,发现其为单一的热脱水过程。用Kissinger-Akahira-Sunose方程迭代法计算出表观活化能Ea值,证实脱水过程是一个具有唯一动力学三因子的单步骤动力学过程。用Málek方程确定了热脱水过程的动力学模型f(a)和指前因子A,提出以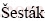 -Berggren模型作为脱水过程的机理函数。最佳拟合得出热脱水过程的的动力学三因子为Ea=79.97±6.51 kJ/mol,ln A=16.83,f(a)=a0.520(1-a)1.255。利用活化络合物理论并结合A值,计算活化过程的热力学函数。
-Berggren模型作为脱水过程的机理函数。最佳拟合得出热脱水过程的的动力学三因子为Ea=79.97±6.51 kJ/mol,ln A=16.83,f(a)=a0.520(1-a)1.255。利用活化络合物理论并结合A值,计算活化过程的热力学函数。
关键词:非等温动力学;脱水;动力学机理;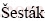 -Berggren模型;热力学函数
-Berggren模型;热力学函数
(Edited by Wei-ping CHEN)
Corresponding author: Chuchai SRONSRI; Tel: +66-88-3142630; E-mail: chuchai_sronsri@hotmail.com
DOI: 10.1016/S1003-6326(18)64739-9

