基于内聚力模型的高心墙堆石坝坝顶裂缝模拟及其成因分析

胡超，周伟，常晓林，马刚，郑华康

(武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉，430072)

摘要：将基于弹塑性断裂力学的内聚力模型引入有限元法，采用非线性界面单元，通过定义界面单元的法向和切向应力与张开和滑移变形之间的关系描述裂缝发生后的界面力学特性，模拟某高心墙堆石坝的坝顶裂缝。计算过程中考虑筑坝材料的流变和湿化变形。研究结果表明：基于内聚力模型的有限元法计算出的裂缝与实际情况比较吻合。采用该方法计算了蓄水期之后3年的坝顶裂缝，裂缝变化幅度微小，较为稳定，且并未深入心墙。在首次蓄水的过程中，上游堆石流变和湿化变形较大，上下游坝壳料沉降不均匀程度也较大，因此，坝体变形不协调导致坝顶出现纵向裂缝。

关键词：心墙堆石坝；内聚力模型；裂缝；裂缝成因

中图分类号：TV641；TV313           文献标志码：A         文章编号：1672-7207(2014)07-2303-08

Modeling of dam crest cracks of high core rockfill dam based on cohesive zone model and crack formation analysis

HU Chao, ZHOU Wei, CHANG Xiaolin, MA Gang, ZHENG Huakang

(State Key Laboratory of Water Resources and Hydropower Engineering Science,

Wuhan University, Wuhan 430072, China)

Abstract: The cohesive zone model based on elastoplastic fracture mechanics was introduced to the finite element model. Using nonlinear cohesive interface elements and defining the relationship between normal-tangential stresses and opening-slipping deformation of interface elements, interfacial mechanical characteristics of cracks were described. This method was employed to simulate crest cracks of a high core rockfill dam. Rheological and wetting deformation of the dam materials was taken into account in the calculation process. The results show that cracks calculated by this method are in satisfactory agreement with the actual situation. The dam crest cracks that develop three years after impounding are predicted. The cracks develop slightly and are relatively stable, without developing into the core wall. The rheological and wetting deformation of upstream rockfill are relatively large during the first impounding process and the degree of settlement non-uniformity between upstream and downstream dam materials is also large, and therefore uncoordinated deformation of the dam causes the longitudinal cracks in the crest region.

Key words: core rockfill dam; cohesive zone model; crack; cause of cracks

土石坝具有可就地取材、经济效益好、施工速度快、抗震性能好、对坝基工程地质条件要求较低等优点，因此应用前景广阔。但土石坝也不可避免地存在一些缺点，如较易产生裂缝。目前土石坝的仿真分析多采用常规有限元法，而对于裂缝、细观组构等的模拟还存在一定的难度。以离散元为基础的非连续介质模型在解决离散介质的破坏、倒塌、粉碎等问题上具有显著优点，但将实际工程如整个坝体离散为堆石颗粒集合体，在计算机处理能力很强的今天也是非常困难的。而另一方面，连续介质力学方法通过引入断裂力学模型或与非连续介质模型相结合，已能够预测裂纹的萌生与扩展^[1]。Tang等^[2]应用细观有限元网格离散岩石和混凝土，研究了岩石和混凝土材料的破裂、失稳过程。Owen等^[3]在有限元网格中嵌入裂缝模拟脆性材料的断裂，从而使最初的连续体逐渐转化为离散物质。潘鹏志等^[4]提出了细胞自动机模型，并开发了EPCA^3D软件模拟岩石破裂的基本过程。常晓林等^[5]引入界面单元，提出了实现岩体开裂扩展的连续-离散耦合分析方法。本文在有限元法中引入基于弹塑性断裂力学的内聚力模型(cohesive zone model)，以实现连续介质向非连续介质转化的力学模拟。内聚力模型的概念最早由Barenblatt^[6]提出，Dugdale^[7]在试验的基础上提出在裂纹尖端存在一个微小的塑性变形带状区域。在过去的几十年间，内聚力模型由于开裂计算研究的有效性越来越得到人们的重视，但已有的研究成果^[8-9]大多处于理论研究层面或者是对单个简单试件的开裂进行模拟。由于实际工程的复杂性，内聚力模型的工程应用少有涉及。为此，本文作者采用基于内聚力模型的有限元法，通过界面单元来表征位移场的非连续性，并在计算过程中考虑筑坝材料的流变和湿化变形，模拟某高心墙堆石坝的坝顶裂缝，计算出的裂缝与实际情况比较吻合。同时预测裂缝发展趋势，并对裂缝成因进行分析。

1  内聚力模型

内聚力模型可分别基于有限元、离散元和边界元等数值方法进行实现，该模型提出在裂纹尖端存在微小的内聚力区域，此区域内应力为开裂位移值的函数，即为张力位移关系^[10]。本文将内聚力模型引入有限元法，采用非线性界面单元，定义界面单元的法向和切向应力与张开和滑移变形之间的关系来描述裂缝发生后的界面力学特性，通过界面单元的起裂、扩展和失效，实现开裂扩展的数值模拟。内聚力模型具有如下显著优点：在开裂过程中应力为开裂位移的函数，从而避免了线弹性断裂力学中的裂纹尖端应力奇异性；基于弹塑性断裂力学，考察了裂纹尖端的塑性区，因此能解决裂纹尖端较大范围屈服的问题；不需要结构中包含预置的裂纹。

采用内聚力模型模拟开裂时，在裂缝可能发生和扩展的部位布置界面单元，界面单元与周围的实体单元相连。在加载的初始阶段，界面单元保持线性行为，随着加载的进行，界面单元的应力达到起裂准则，界面单元的刚度逐渐下降，承载能力降低，当刚度降低到0时，界面单元失效，新的裂缝面出现，如图1所示。

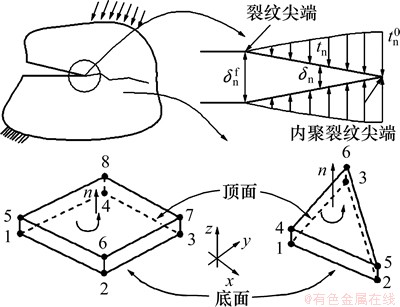
图1  内聚力模型与界面单元

Fig. 1  Schematic representation of cohesive zone model and cohesive interface element

不考虑界面法向和切向之间的相互作用，界面单元的应力状态达到破坏准则后出现损伤，采用标量损伤因子描述界面刚度的退化，界面应力与张开、滑移位移的关系为

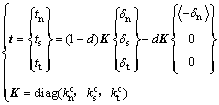     (1)

式中：t为界面应力向量；t_n，t_s和t_t分别为法向和2个切向的应力分量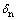；为法向张开位移量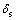；和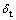为2个切向滑移量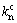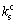；，和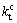分别为界面的法向和2个切向刚度，一般有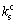=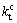；d为标量损伤因子；。

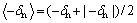采用带拉伸截断的Mohr-Coulomb准则作为界面的破坏准则。当界面单元的法向应力达到抗拉强度时发生拉伸破坏，当界面单元的切向应力超过抗剪强度则发生剪切破坏，计算过程中首先进行拉伸破坏判定。

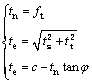               (2)

式中：f_t为界面法向抗拉强度；t_e为等效切向应力；c和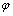分别为界面的黏聚力和内摩擦角。当界面完全开裂破坏后，在非挤压状态下其法向和切向刚度均降为零；在受挤压状态下，由于界面存在摩擦，即使发生宏观裂缝，界面具有一定的抗剪能力。

界面出现损伤后，采用Benzeggagh和Kenane^[11]提出的基于能量的复合损伤演化准则，界面单元的本构模型如图2所示。复合损伤演化准则为

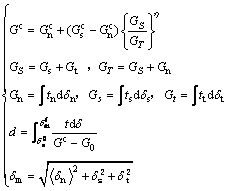      (3)

式中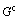：为复合断裂能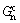；为Ⅰ型断裂能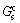；为Ⅱ型断裂能；G_n，G_s和G_t分别为法向和2个切向的应力分量在相应位移上所做的功；G₀为初始损伤时的弹性应变能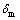；为表示法向张开和切向滑移的等效位移。

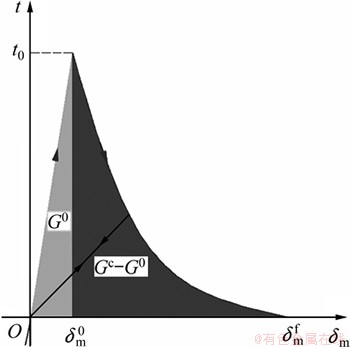
图2  界面单元的本构模型

Fig. 2  Constitutive response of cohesive interface element

材料整体的性能受界面单元的影响，界面单元的刚度等参数与实体单元材料参数的关系推导可参见文献[5]。

2  堆石体变形分析的本构模型

静力本构模型采用邓肯非线性E-μ模型。

流变模型采用沈珠江等^[12-13]建议的七参数模型。无论是体积流变还是轴向流变，流变曲线随时间基本都呈指数型衰减，符合Merchant模型描述的变形规律，流变变形可用下式表达：

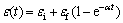            (4)

式中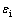：为瞬时变形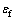；为随时间发展的最终流变量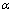；为流变随时间衰减的指数。

最终体积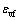流变、剪切流变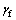与偏应力q、应力水平S₁的关系如下：

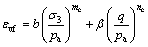           (5)

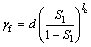                (6)

式中：b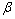，，m_c，n_c，d和l_c为模型参数。

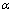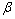式(4)~(6)及参数，b，，m_c，n_c，d和l_c完整地表达了堆石体的流变特性。

在心墙堆石坝的后期变形中，蓄水后的变形不可忽视。粗粒料浸水湿化产生变形，引起坝体应力应变状态发生变化。湿化模型采用南京水利科学研究院提出的堆石体浸水体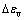应变和剪应变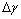的计算公式^[14]：

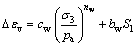           (7)

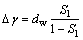               (8)

式中：c_w，n_w，b_w和d_w为模型参数；S₁为应力水平。

3  数值计算模型

3.1  计算模型及基本假定

本文计算模拟了某高心墙堆石坝的最大剖面，计算模型如图3所示。该心墙堆石坝最大坝高186 m，坝顶高程856 m，坝顶宽度14 m，上游坝坡1:2~1:2.25，下游坝坡1:1.8；心墙顶高程854 m，顶宽4 m，上、下游侧坡度均为1:0.25，底高程670 m。对该心墙堆石坝的不同部位分别采用不同的方式进行模拟：坝顶可能产生裂缝区域即852 m高程以上采用引入了内聚力模型的有限元法模拟，在这个区域内，遍历每个实体单元，重新定义单元的节点编号，在每一个实体单元与实体单元之间定义了无厚度的界面单元；而对坝体其他部位即852 m高程以下仍然采用常规有限元法模拟。为了更准确地模拟开裂行为，对坝顶的单元进行了加密。模型单元总数为7 517个，其中实体单元4 306个，界面单元3 211个，节点总数8 978个。材料分区如图4所示，图4中A和B点为大坝坝体变形监测测点中的某2个测点。

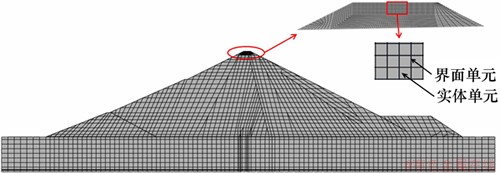
图3  心墙堆石坝二维计算网格图

Fig. 3  Two-dimensional element mesh of Pubugou core rockfill dam

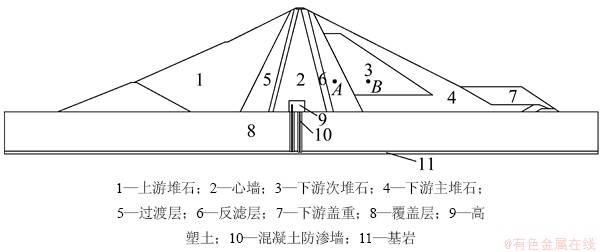
图4  材料分区图

Fig. 4  Schematic representation of material partition

在该模拟开裂过程的方法中，将岩土体视为胶凝颗粒材料，数值模拟时将其离散为实体单元和无厚度界面单元，实体单元对应于堆石体颗粒，无厚度界面单元对应于颗粒间的胶结层，实体单元只发生弹性变形，损伤和断裂发生于界面单元上。界面单元失效后从模型中删除，两侧实体单元的关系采用接触模拟。

3.2  材料参数

计算中考虑了筑坝材料的流变和湿化变形。为了更准确地模拟瀑布沟堆石坝的实际位移情况，本文利用实测位移资料，以对堆石坝变形较敏感的静力本构模型和流变模型参数为待反演参数，采用遗传算法和径向基函数神经网络进行参数反演，得到相应的E-μ参数、流变参数与湿化参数。由于参数较多，本文仅列出上游堆石的计算参数，如表1所示。坝顶界面单元计算参数见表2。

3.3  施工过程和蓄水过程

本文计算模拟了大坝施工填筑和蓄水过程。施工填筑过程按照施工顺序分析计算，二维模型共分13层进行加载。填筑完成后进行蓄水分析计算，完整模拟了大坝施工蓄水历时过程，并延续至大坝满蓄后3年。该心墙堆石坝填筑和蓄水过程如图5所示。

表1  上游堆石计算参数

Table 1  Mechanical parameters of upstream rockfill

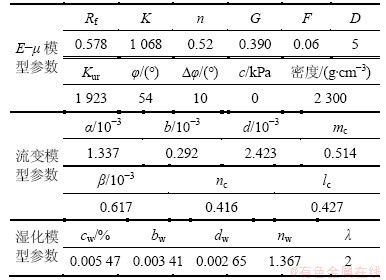
表2  界面单元计算力学参数

Table 2  Mechanical parameters of interface elements

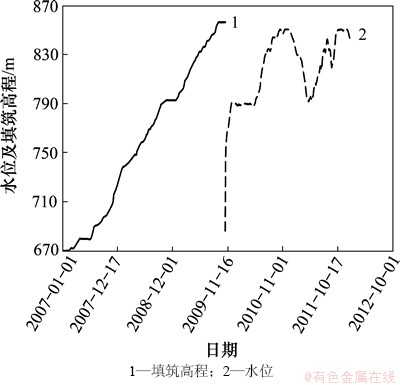
图5  大坝填筑过程和蓄水过程

Fig. 5  Filling and impounding process of dam

4  计算成果

本文中，竣工期是指大坝填筑完成的时刻，蓄水期是指大坝首次蓄水到正常蓄水位的时刻；铅直位移以竖直向上为正，水平位移以指向下游为正。

图6和图7所示为计算剖面基于参数反演的蓄水期(2010-10)考虑了流变效应和湿化效应的变形结果。计算的水平位移以及沉降与坝体已有变形监测资料规律一致，坝体最大沉降达3.319 m，出现在心墙中下部，占坝高的1.78%。

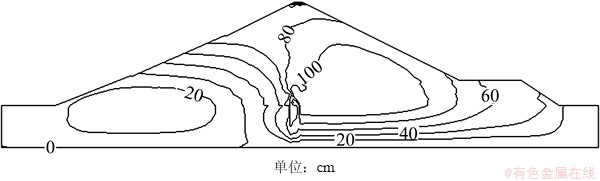
图6  蓄水期水平位移等值线

Fig. 6  Horizontal displacement contour during impounding period

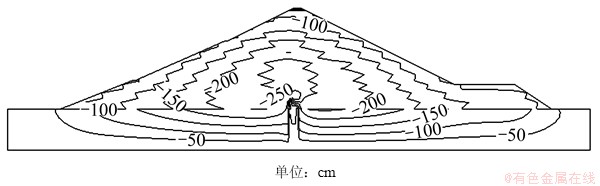
图7  蓄水期铅直位移等值线

Fig. 7  Vertical displacement contour during impounding period

提取测点坐标处(测点位置见图4)的计算沉降值与实测沉降值进行对比，如图8和图9所示。由图8和图9可知：计算的坝体测点位置处的沉降值和实测沉降值相比，两者变形规律一致，数值基本吻合。

图8  下游过渡层A测点实测值与计算值对比图

Fig. 8  Comparison chart of measured and calculated values (Measuring point A is at downstream transition layer)

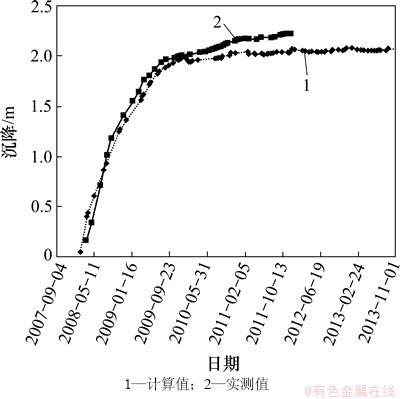
图9  下游次堆石区B测点实测值与计算值对比图

Fig. 9  Comparison chart of measured and calculated values (Measuring point B is at downstream secondary rockfill)

竣工期(图10)、首次蓄水至死水位时坝顶无裂缝。水位首次从死水位上升至正常蓄水位的过程中坝顶产生裂缝，这表明裂缝的产生与蓄水有密切的关联。采用引入内聚力模型的有限元法计算的蓄水期的裂缝如图11所示，裂缝最大深度为1.40 m，出现在坝轴线下游5.74 m，此外，坝轴线附近也有裂缝产生，但深度较小。图12所示为蓄水期的网格变形图(垂直位移扩大15倍)。该心墙堆石坝实际于2010-08发现坝顶裂缝，裂缝位于坝轴线下游5.5~6.0 m，基本平行于坝轴线，裂缝长约230 m，最大缝宽约5 cm，深度为1.0~2.5 m，此后在原裂缝的上游又发现新的裂缝。由图11可知：计算的坝顶裂缝与实际情况比较吻合。

采用引入内聚力模型的有限元法计算的蓄水期之后3年的坝顶裂缝如图13~15所示。2011-04，水位回落至死水位，坝顶裂缝有所发展，最大深度增大为1.6 m。2011-10，大坝第2次蓄水至正常蓄水位，坝顶裂缝有所愈合(对于曾经发生完全开裂破坏的界面，当法向受压时，界面两侧转为接触状态，相应法向和切向刚度均为非零值)，最大深度减小为1.4 m。大坝第3次满蓄(2012-10)、第4次满蓄(2013-10) 时，坝顶裂缝几乎不再发展，最大深度保持不变。

图10  竣工期坝顶无裂缝

Fig. 10  No cracks in dam crest region at time of completion

图11  蓄水期(2010-10)的坝顶裂缝图

Fig. 11  Distribution of cracks during impounding period (October 2010)

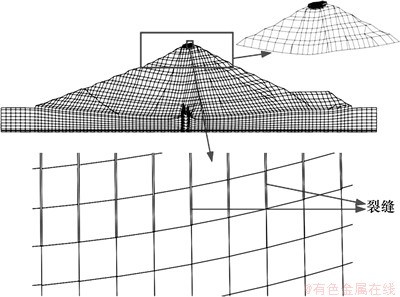
图12  蓄水期网格变形图(垂直位移扩大15倍)

Fig. 12  Mesh deformation during impounding period (Vertical displacement expands 15 times)

由图11和图13~15可知：裂缝为浅表层裂缝，深度范围处于心墙最大高程以上，且变化幅度微小，较稳定。

图13  2011-04水位回落至死水位时的坝顶裂缝图

Fig. 13  Distribution of cracks in dam crest region at death water level (April 2011)

图14  大坝第2次满蓄(2011-10)的坝顶裂缝图

Fig. 14  Distribution of cracks in dam crest region at normal water level for the second time (October 2011)

图15  大坝第4次满蓄(2013-10)的坝顶裂缝图

Fig. 15  Distribution of cracks in dam crest region at normal water level for the fourth time (October 2013)

5  裂缝成因分析

图16~19所示为坝体位移增量图。从图16可知：蓄水期与竣工期相比，上游堆石有较大的沉降增量，特别是坝顶上游侧和下游侧沉降增量差异较大。竣工期到蓄水期期间上游堆石产生的沉降增量最大值为0.572 m。坝体从第2次满蓄到第4次满蓄各自年沉降增量最大值分别为0.164，0.113和0.084 m，上游堆石的流变和湿化变形明显小于首次蓄水的流变和湿化变形，年沉降增量逐渐减小。

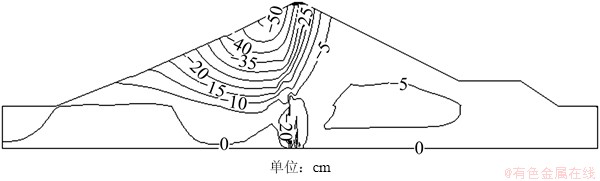
图16  竣工期到蓄水期铅直位移增量

Fig. 16  Vertical displacement increment from time of completion to impounding period

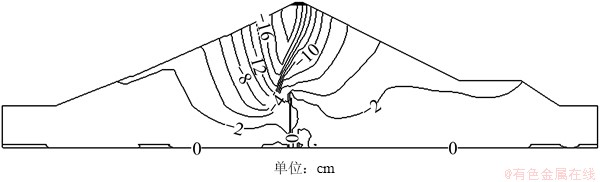
图17  蓄水期到第2次满蓄铅直位移增量

Fig. 17  Vertical displacement increment from the first to the second impounding period

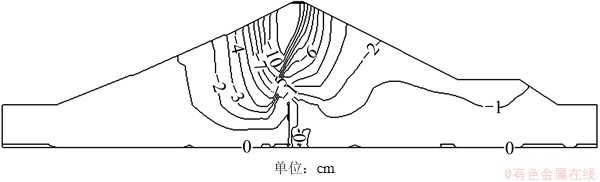
图18  第2次满蓄到第3次满蓄铅直位移增量

Fig. 18  Vertical displacement increment from the second to the third impounding period

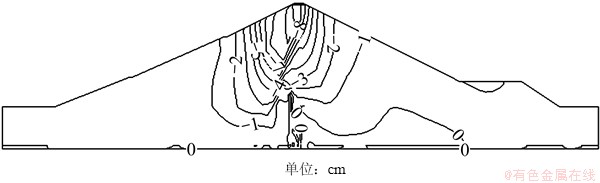
图19  第3次满蓄到第4次满蓄铅直位移增量

Fig.19  Vertical displacement increment from the third to the fourth impounding period

在坝顶区域852 m高程以上每隔2 m高程提取坝轴线处以及上下游分别距坝轴线4 m处的点(具体位置如图20所示)的沉降值，得到各高程不同时期的沉降增量如表3所示。

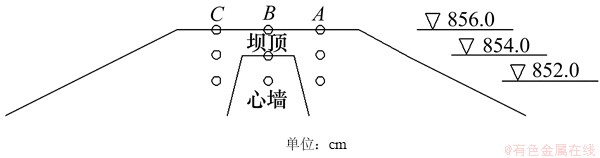
图20  坝顶区域提取沉降值的位置示意图

Fig. 20  Illustration of typical positions in dam crest region for settlement value extraction

表3  坝顶区域各高程不同时期的沉降增量

Table 3  Settlement increment at different elevations in dam crest region during different periods

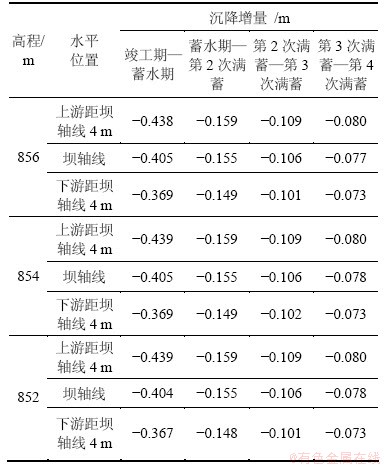
以坝顶高程856 m为例，不同时期上下游沉降增量如图21所示。由表3和图21可知：坝顶区域竣工期至蓄水期的沉降增量较大，并且上下游沉降增量不均匀程度也较大，而蓄水期之后坝顶的沉降增量逐年减小且上下游的沉降增量差别较小。

变形倾度能够反映坝体不均匀沉降变形的程度。采用变形倾度法判断土石坝产生裂缝的可能性，倾度计算公式为

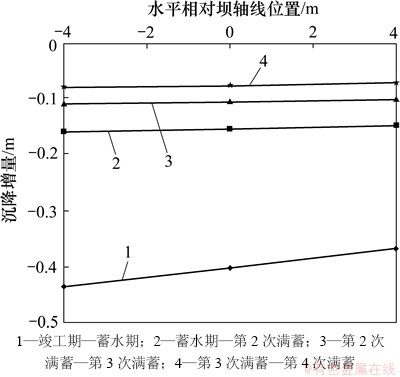
图21  坝顶不同时期上下游沉降增量图

Fig. 21  Settlement increment in dam crest during different periods

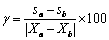            (9)

式中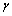：为a和b两点间的倾度(%)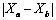；为a和b两点间的水平距离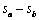；为两点自填筑之日起，至某一计算日期的累计沉降差。考虑坝顶开裂后对坝顶裂缝进行处理以及堆石体在水位上升产生不均匀沉降后的自我调整和自我修复，本文中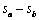取为1次满蓄水周期内的累计沉降差。

图22所示为坝顶变形倾度变化曲线图，其中图例“A-B”表示坝顶A点和B点(相对位置见图20)间的变形倾度，“B-C”类似。裂缝临界变形倾度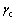一般通过对坝体土料土梁挠曲线试验来测定，该心墙堆石坝无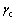的试验资料，根据工程类比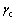，取为0.2%。由图22可知：竣工期至蓄水期坝顶变形倾度超过临界变形倾度，坝顶可能产生纵向裂缝，此计算结果与实际监测的裂缝相符；而2011-10以后，坝顶变形倾度趋于稳定且小于临界变形倾度。

图22  坝顶变形倾度变化曲线

Fig. 22  Crest deformation gradient curves

6  结论

(1) 将基于弹塑性断裂力学的内聚力模型引入有限元法，采用非线性界面单元，通过定义界面单元的法向和切向应力与张开和滑移变形之间的关系来描述裂缝发生后的界面力学特性，实现实际工程结构中开裂现象的模拟。

(2) 采用引入了内聚力模型的有限元法模拟某高心墙堆石坝的坝顶裂缝，并在计算过程中考虑了筑坝材料的流变和湿化变形，计算出的裂缝与实际情况比较吻合。采用该方法计算了蓄水期之后3年的坝顶裂缝，裂缝为浅表层裂缝，并未深入心墙，且变化幅度微小，较为稳定。

(3) 对心墙堆石坝坝顶裂缝成因的分析表明，在首次蓄水的过程中，上游堆石流变和湿化变形较大，上下游坝壳料沉降不均匀程度也较大，因此，坝体变形不协调导致坝顶出现纵向裂缝。

参考文献：

[1] Griffith A A. The phenomena of rupture and flow in solids[J]. Philosophical Transactions of the Royal Society of London, 1921, A221: 163-197.

[2] Tang C A, Kaiser P K. Numerical simulation of cumulative damage and seismic energy release in unstable failure of brittle rock. Part Ⅰ: Fundamentals[J]. International Journal of Rock Mechanics and Mining Science, 1998, 35(2): 113-121.

[3] Owen D R J, Feng Y T, de Souza Neto E A, et al. The modelling of multi-fracturing solids and particulate media[J]. International Journal for Numerical Methods in Engineering, 2004, 60(1): 317-339.

[4] 潘鹏志, 冯夏庭, 周辉. 脆性岩石破裂演化过程的三维细胞自动机模拟[J]. 岩土力学, 2009, 30(5): 1471-1476.

PAN Pengzhi, FENG Xiating, ZHOU Hui. Failure evolution processes of brittle rocks using 3D cellular automaton method[J]. Rock and Soil Mechanics, 2009, 30(5): 1471-1476.

[5] 常晓林, 胡超, 马刚, 等. 模拟岩体失效全过程的连续–非连续变形体离散元方法及应用[J]. 岩石力学与工程学报, 2011, 30(10): 2004-2011.

CHANG Xiaolin, HU Chao, MA Gang, et al. Continuous- discontinuous deformable discrete element method to simulate the whole failure process of rock masses and application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2004-2011.

[6] Barenblatt G I. The mathematical theory of equilibrium cracks in brittle fracture[J]. Advances in Applied Mechanics, 1962, 7: 55-129.

[7] Dugdale D. Yielding of steel sheets containing slits[J]. Journal of the Mechanics and Physics of Solids, 1960, 8(2): 100-104.

[8] Su X T, Yang Z J, Liu G H. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials: A 3D study[J]. International Journal of Solids and Structures, 2010, 47(17): 2336-2345.

[9] YANG Zhenjun, Xu X F. A heterogeneous cohesive model for quasi-brittle materials considering spatially varying random fracture properties[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(45): 4027-4039.

[10] 张军.界面应力及内聚力模型在界面力学的应用[M].郑州:郑州大学出版社,2011:1-96.

ZHANG Jun. The interface stress and cohesive zone model in the interface mechanics[M]. Zhengzhou: Zhengzhou University Press, 2011: 1-96.

[11] Benzeggagh M L, Kenane M. Measurement of mixed mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Composites Science and Technology, 1996, 56(4): 439-449.

[12] 沈珠江. 鲁布革心墙堆石坝变形的反馈分析[J]. 岩土工程学报, 1994, 16(3): 1-13.

SHEN Zhujiang. Back analysis of deformation of Lubuge earth core rockfill dam[J]. Chinese Journal of Rock Mechanics and Engineering, 1994, 16(3): 1-13.

[13] 李国英, 米占宽, 傅华, 等. 混凝土面板堆石坝堆石料流变特性试验研究[J]. 岩土力学, 2004, 25(11): 1712-1716.

LI Guoying, MI Zhankuan, FU hua, et al. Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam[J]. Rock and Soil Mechanics, 2004, 25(11): 1712-1716.

[14] 李国英, 王禄仕, 米占宽. 土质心墙堆石坝应力和变形研究[J]. 岩石力学与工程学报, 2004, 23(8): 1363-1369.

LI Guoying, WANG Lushi, MI Zhankuan. Research on stress-strain behaviour of soil core rockfill dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1363-1369.

(编辑  杨幼平)

收稿日期：2013-07-19；修回日期：2013-10-09

基金项目：国家自然科学基金资助项目(51379161)；中央高校基本科研业务费专项资金资助项目(2012206020207)

通信作者：周伟(1975-)，男，湖南岳阳人，教授，博士生导师，从事高坝结构数值仿真方面的教学与研究；电话：027-68773778；E-mail: zw_mxx@163.com