J. Cent. South Univ. (2017) 24: 2524-2531

DOI: https://doi.org/10.1007/s11771-017-3665-8

A novel LS-SVM control for unknown nonlinear systems with application to complex forging process

FAN Bin(范彬)^{1, 2}, LU Xin-jiang(陆新江)¹, HUANG Ming-hui(黄明辉)¹

1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. College of Mechanical and Electrical Engineering, Hunan City University, Yiyang 413002, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017

Abstract: A novel LS-SVM control method is proposed for general unknown nonlinear systems. A linear kernel LS-SVM model is firstly developed for input/output (I/O) approximation. The LS-SVM control law is then derived directly from this developed model without any approximation and assumption. It further proves that the control error is fully equal to the LS-SVM modeling error. This means that a desirable control performance can be achieved because the LS-SVM has been proven to have an outstanding modeling ability in the previous studies. Case studies finally demonstrate the effectiveness of the proposed LS-SVM control approach.

Key words: unknown system; inverse control; input/output approximation; LS-SVM control; linear kernel

1 Introduction

In industry, many systems are strongly nonlinear and unknown. A typical system is the complex forging process that is often time-varying, strongly nonlinear and has unknown dynamics and uncertainty since it consists of both microscale and macrosacle dynamics: complex time-varying microstructure process and complex macroscale motion of the forging process. Although many works have contributed to control of the forging process, such as PI control [1] and the iterative learning control [2], they cannot obtain the satisfactory control performance since these methods only aim at the simplified linear model and neglect the influence of uncertainty. In practice, modeling and control of this kind of systems are often challenging.

Generally, the use of the least squares support vector machine (LS-SVM) is an advisable means of producing a model and controller of this kind of systems using input/output data [3–5]. Since the LS-SVM is only to find the solutions of a set of linear equations instead of the computationally quadratic programming problem involved in the standard SVM, it is computationally more attractive than the standard support vector machines (SVM). This makes it have great successfully applications [6–9].

A great of studies are found in the LS-SVM modeling for unknown nonlinear systems. In modeling of the complex problem, many local LS-SVM models are trained to represent the local information according to the principle of “divide-and-conquer”, upon which the global model is obtained by integrating all sub-models [10, 11]. Some researchers also employed a series of different kernels to represent the local information in classification [12–14]. Usually, sampling errors, modeling errors, measurement errors and human errors generate uncertainty in the data [15, 16]. In order to handle uncertainty in the data, two kinds of approach are used in the LS-SVM. One is to obtain a robust estimation by reducing the effect of the noise to the LS-SVM model [17–19]. The other is to find the noisy characteristics underlying the training data and consider it in the LS-SVM modeling [10–23].

The LS-SVM control for nonlinear dynamic systems has also attracted much attention. In these studies, many authors used the LS-SVM to build the system model, upon which the controller was developed. WANG et al [24] presented a NN inverse controller derived from the online LS-SVM model. But this method can produce a more approximate error as using the NN to approximate the LS-SVM model in the controller design. YUAN and WANG [25] applied the LS-SVM model to design an approximate inverse controller. However, since the approximate inverse controller is developed on the linearization model derived from the LS-SVM model, it requires that variation of the control input should not be too large in order to limit the approximate error of the linearization model [26, 27]. The LS-SVM was also applied in the model predictive control [28]. All the abovementioned LS-SVM control methods are not directly applied the LS-SVM to design the controller due to the complexity of the nonlinear kernels used in these LS-SVM models. This causes certain approximations and assumptions in the controller development, which often leads to a poor control performance and limits application of these control methods. Alternatively, some studies employed the LS-SVM to model the control law, such as the N-stage optimal control [29, 30] and the inverse control law [31]. However, they require the fully known process model or the existence of the model inverse, as well as they are complex and the intensive computation. Thus, an effective LS-SVM control method is still necessary to develop for unknown nonlinear systems.

Unlike the previously mentioned approaches, a novel linear kernel LS-SVM control method is proposed without any approximation and assumption on the controller development via the LS-SVM model. First, a linear kernel LS-SVM model is developed for input/output (I/O) approximation. Then, the control law is directly derived from the LS-SVM model without any approximation and assumption, which may greatly improve the control ability. The stability and robustness of this developed controller is further proofed. Case studies finally demonstrate the effectiveness of the proposed LS-SVM control approach.

2 LS-SVM modeling for nonlinear systems

Nonlinear systems may be represented by the following state equation:

                       (1)

where x(k), u(k) and y(k) are the state, input and output of the systems, respectively; g and h are unknown nonlinear functions.

A general I/O representation of Eq. (1) may be described as follows [26, 27]:

                            (2)

where f is an unknown function and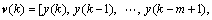

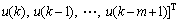
The LS-SVM has been widely used to model the I/O representation. Here, it is trained to represent the dynamic behavior of unknown systems (1), as shown in Fig. 1.

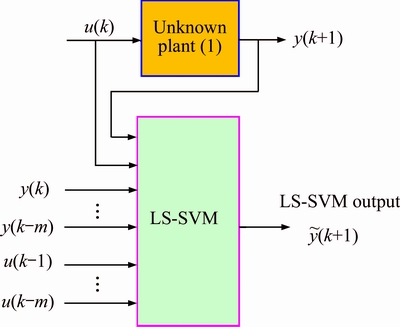
Fig. 1 LS-SVM model for I/O representation

Given the training set 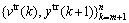from the original system (1), where v^tr(k) and y^tr(k+1) are training sample of v(k) and y(k+1) respectively and the superscript ‘tr’ represents training sample, the LS-SVM modeling problem is formulated as follows:

  (3)

where ε(k) is the modeling error; g is the regularization parameter; w and b are the model parameter vector; φ is the mapping to the high dimensional and potentially infinite dimensional feature space.

In order to solve this optimization problem, a Lagrangian function is constructed as

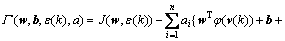
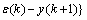                         (4)

where a_i (i=1, …, n) are the Lagrange multipliers. The conditions for the optimality of Eq. (4) are given by

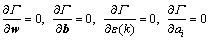            (5)

By solving Eq. (5), the parameters a_i and b are obtained as follows:

                    (6)

where 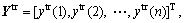I_n=[1 … 1]^T, a=[a₁ … a_n]^T, v^tr(j))=φ^T(v^tr(i))φ^T(v^tr(j)), K(·,·) is the positive definite kernel. The solution of Eq. (6) is below

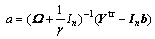
Thus, the LS-SVM model for estimation of the systems (1) becomes the following:

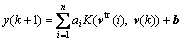                (7)

At the LS-SVM model (7), the kernel function is set beforehand and is deterministic when samples are given.

Thus, the system model (1) may be represented by

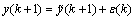                       (8)

As the statement of many previous studies [10–23, 30], the error ε(k) can be made arbitrarily small by increasing number of the support vector or selecting the suitable regularization parameter g. Thus, the LS-SVM model can approximate the original system well.

3 Novel LS-SVM control and stability proof

The chosen kernel function should be positive definite and satisfy the Mercer condition. Some typical choices are linear kernel, radial basis function kernel, polynomial kernel and multiplayer perceptron. The LS-SVM models under these nonlinear kernels are complex, which is difficultly used to directly design the controller. For this reason, they are usually linearized as used to design the controller [25]. This linearization usually produces certain approximations and assumptions in the controller development and, thus, causes a poor control performance. While the model under the linear kernel has a well linear structure, it is very suitable to design the controller. However, so far no study has been found on using the linear kernel LS-SVM model to design the controller. For this purpose, a linear kernel LS-SVM control method is proposed in this study.

Under the linear kernel, the LS-SVM model (7) may be rewritten as

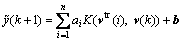
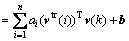                 (9)

since

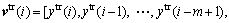
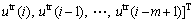
and

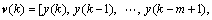
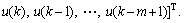
Equation (9) may be rewritten as follows:

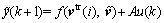                  (10)

here,

;

;

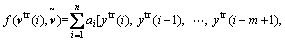
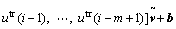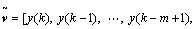
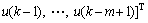Inserting Eq. (10) into Eq. (7), one has

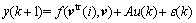             (11)

Since 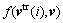is related to the past inputs and outputs, it is known at the present time. From the definition of the parameter A, it is clear that this parameter A is also known since it is decided by the training samples. In order to guarantee the system able to control, the parameter A must be not equal to zero. This may be avoided by adding or reducing the sample number or selecting the suitable regularization parameter g. From Eq. (11), it is clear that this linear kernel LS-SVM model has a well linear structure related to the control input. Thus, it is very suitably used to design the controller.

Based on the LS-SVM model (11), the LS-SVM control law can be derived straightforwardly as

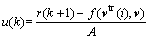                    (12)

where r(k) is the reference. Then, the control error e(k+1) is defined as

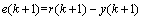
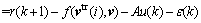       (13)

Theorem 1: Under the LS-SVM model (10), using the control law (12), the control error is fully equal to the modeling error and is uniformly ultimately bounded

(UUB) for all k and all 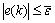and 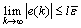with the parameter 0≤l≤1, where 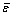is the upper bound of the modeling error.

Proof: inserting control law (12) into the error Eq. (13), one has

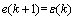                               (14)

From Eq. (14), it is clear that the control error is fully equal to the modeling error. This may limit the control error in a desirable bound. This is because the modeling error ε(k) can be made arbitrarily small by increasing the number of the support vector or selecting the suitable regularization parameter g in the LS-SVM modeling.

Moreover, according to the VC bound on the generalization error [30], one has

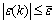                                  (15)

where 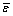is the upper bound of |ε(k)|, which can be estimated by the VC bound theory [30].

Thus, the control error is also limited by

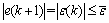                          (16)

Since the upper bound 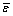of the modeling error is bounded, one concludes that, using the control law (12), the control error is UUB for all k and all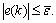

Furthermore, a Lyapunov function is chosen as 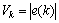. From Eq. (16), one has

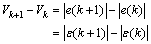
                         (17)

Since the parameter 0≤l≤1 and 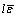is bounded, according to the lemma 13.1 in Ref. [32] and the theorem 1 in Ref. [26], the control error (13) is also UUB for all k and the ultimate bound is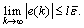

Since there is no approximation and assumption on the controller development via the LS-SVM model, it will greatly improve the control ability as compared to the common approximate inverse control methods whose controllers are developed on a linearization model derived from the LS-SVM model [25] or the NN model [26, 27]. It also proves that the control error is fully equal to the LS-SVM modeling error. This means that a desirable control performance can be achieved, because the LS-SVM has been proven to have an outstanding modeling ability in the previous studies. Of course, since this control method depends on the LS-SVM model, it is only suitable to the processes that can be modeled well by the LS-SVM.

The procedure of the proposed LS-SVM control approach is summarized in Fig. 2 with the following key points:

1) A linear kernel LS-SVM model is first developed to approximate the nonlinear systems.

2) On the basis of this developed model, the inverse control law is derived directly and its implementation for an unknown process is straightforward.

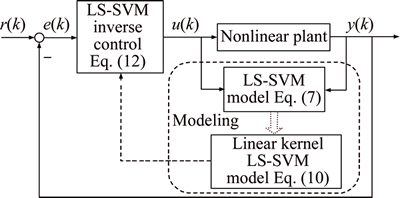
Fig. 2 A procedure for proposed modeling method

3) The stability and robustness of the developed LS-SVM controller are also proofed.

The proposed method has the following features:

1) The model developed has a well linear structure, which is easily used to design the controller. This avoids the linearization of the nonlinear model that is usually used in design of controllers, such as the NN controller [26, 27] and the LS-SVM controller [25].

2) The design of the controller is simple and effective due to without further training and simplification for the controller development.

3) The control ability is fully decided by the modeling ability. While the modeling error can be made arbitrarily small by increasing number of the support vector and selecting the suitable regularization parameter g, thus, the proposed LS-SVM method can achieve a desirable control performance.

4) It can easily be solved by the standard algorithms and the computational work is small.

4 Case studies

In this section, the proposed LS-SVM control method is evaluated on two simulation cases and one forging process case.

4.1 Example 1

An unknown nonlinear plant is described as

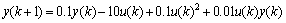(18)

The objective of the control is to make the plant (18) track the following reference signal:

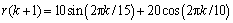       (19)

First, a thousand random input data in [–3, 3] are used to excite the system, upon which input/output data are employed to train the developed LS-SVM model (10) with the regularization parameter g equal to 5. This developed model is tested using the following signal:

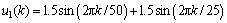        (20)

For this test signal, the output of the LS-SVM model (10) is very close to that of the system (18) with quite small approximate error as shown in Fig. 3.

Then, based on this developed model, the control law (12) is derived and used to real-time control the plant. The control input and the tracking performance are shown in Fig. 4. From this figure, the tracking error of the plant is quite small. Thus, the proposed method can effectively achieve the desirable tracking performance for this unknown nonlinear system.

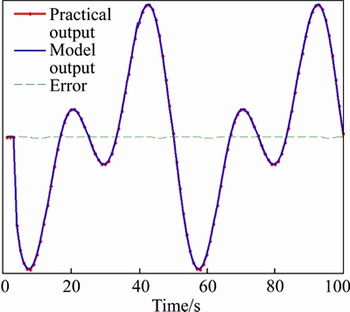
Fig. 3 Model test under input signal u1(k)

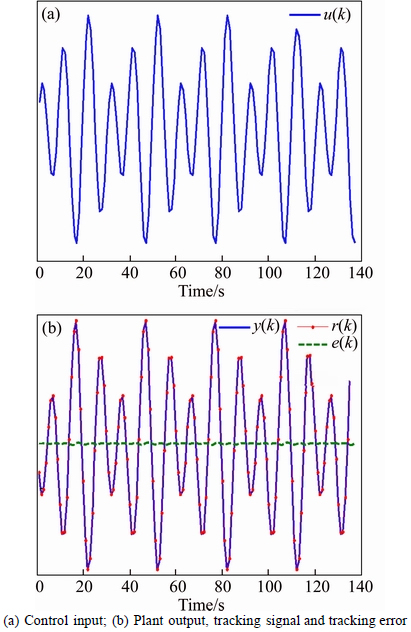
Fig. 4 Tracking performance of new LS-SVM control in Example 1:

Furthermore, the effectiveness of the proposed control method is verified in comparison with the existing LS-SVM control method [25] that applied the linearization model derived from the LS-SVM model to design the approximate inverse controller. The root mean square error (RSME) obtained by the proposed method and the existing LS-SVM control method are 3.41 and 40.7403 respectively, which shows that the proposed method has the better control performance than the existing one. This is because the proposed control law is derived directly from the LS-SVM model without any approximation and assumption, while the existing one does not. Moreover, the existing one requires that: 1) variation of the control input should not be too large in order to limit the approximate error of the linearization model [26, 27]; and 2) the derivation of the LS-SVM model related to u(k–1) must exist and cannot equal to zero in order to avoid the singular. All these limitations are not existence in the proposed method.

4.2 Example 2

Another unknown nonlinear system is described as

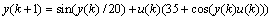 (21)

This system must be controlled to track the following reference signal:

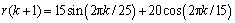       (22)

First, a thousand random input data in [–1.5, 1.5] are used to excite the system. These input/output data are used to train the developed LS-SVM model (10) with the regularization parameter g equal to 10. The following test signal is used to test the developed model.

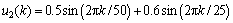       (23)

For this test signal, the output of the LS-SVM model (10) is very close to that of the system (22) with quite small approximate error as shown in Fig. 5.

Then, based on this developed model, the control law (12) is derived and used to real-time control the plant. The control input and the tracking performance are shown in Fig. 6. From this figure, the tracking error of the plant is quite small, which shows the effectiveness of the proposed method.

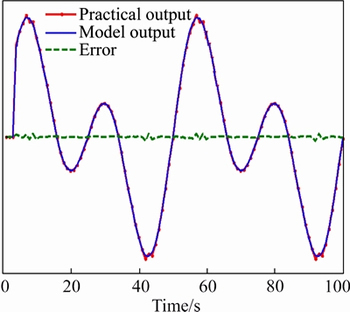
Fig. 5 Model test under input signal u₂(k)

Furthermore, the effectiveness of the proposed control method is verified in comparison with the existing LS-SVM control method [25]. The RSMEs obtained by the proposed method and the existing LS-SVM control method are 4.6769 and 23.9049 respectively, which also shows that the proposed method has better control performance than the existing one.

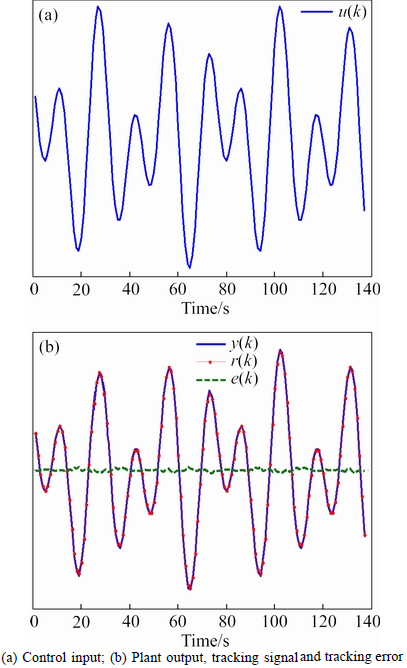
Fig. 6 Tracking performance of new LS-SVM control in Example 2:

4.3 Example 3

The control of a complex forging process is used to test this proposed method. Many industry productions must be shaped under forging. A typical forging process is shown in Fig. 7, where a metal forging (also called a work piece) is forged to form a desirable shape in the dies by the driving force from the work plate of the HPM. A high-quality forging usually requires the work plate to have a desirable velocity response [33, 34].

A typical forging process may be represented as

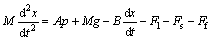          (24)

with

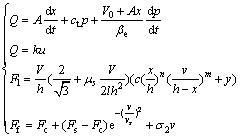
where M is the mass of both the work plate and all hydraulic cylinders of the hydraulic press machine respectively; x is the displacement of the work plate; B is the viscous damping coefficients; F_l is the deformation force of the long rectangular aluminum alloy work piece; F_s is the support force from the return cylinders; F_f is the friction, g is the acceleration of gravity; Q is the flow; k is the gain of the servo valve; u is the control input; p is the pressure; A is the area sum of all hydraulic cylinders; c_t is the leak coefficient; V₀ is the initial volume; β_e is the spring moment of medium; the height and length of the work piece are h, l respectively; V is the volume of the work piece; μ_s is the friction coefficient between the work piece and dies; c, n, m and y depend on the material and temperature of the work piece; F_c and F_s are the Coulomb and static friction values; v_s and σ₂ are the Stribeck velocity and the friction coefficient, respectively.

Obviously, this forging process is complex and strongly nonlinear. It is required to be controlled to track the following velocity trajectory.

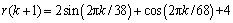       (25)

First, a thousand random input data in [–0.5, 0.5] are used to excite the system, upon which input/output data are used to train the developed LS-SVM model (10).

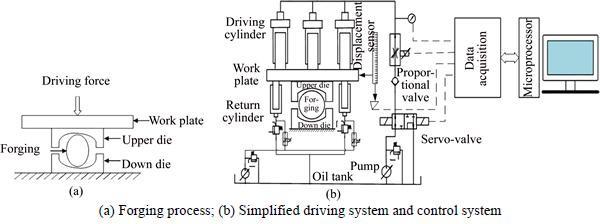
Fig. 7 Diagram of HPM:

The following test signal u(k)=u₃(k) is used to test the developed model.

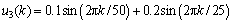       (26)

For this test signal, the output of the LS-SVM model (10) is very close to that of the system (24) with quite small approximate error as shown in Fig. 8.

Then, based on this developed model, the control law (12) is derived and used to real-time control this forging process. The control input and tracking performance are shown in Fig. 9, where y(k), r(k) and e(k) are the practical output, the reference output and the tracking error. From this figure, it is clear that the tracking error of the plant is quite small. This proves the effectiveness of the proposed method.

Fig. 8 Model test under input signal u₃(k)

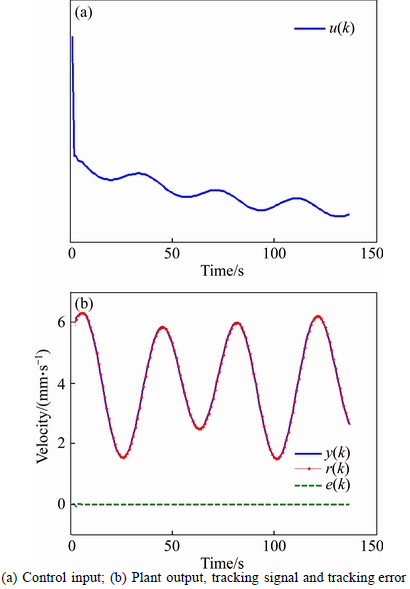
Fig. 9 Tracking performance of new LS-SVM control in Example 3:

Furthermore, the effectiveness of the proposed control method is verified in comparison with the existing LS-SVM control method [25]. The RSME obtained by the proposed method and the existing LS-SVM control method are 0.448 and 32.1888 respectively, which also shows that the proposed method is superior to the existing one.

5 Conclusions

1) The novel LS-SVM control method has a well linear structure, which avoids the linearization of the nonlinear model that is usually used in design of controllers.

2) Since the control law is directly derived from the LS-SVM model without any approximation and assumption, the control method developed may greatly improve the control ability.

3) A desirable control performance has been achieved due to the outstanding modeling ability of the LS-SVM. Extensive simulations demonstrate the superior performance of the proposed LS-SVM control as compared to the existing LS-SVM control method. Also, the similarity of the control error and the LS-SVM modeling error is proved.

4) The control algorithm developed here is simple and effective and may easily be added into the practical industry processes.

References

[1] CHO S J, LEE J C, JEON Y H, JEON J W. The development of a position conversion controller for hydraulic press systems [C]// Proc IEEE Int Conf Robot Biomimetics, 2009: 2019–2022.

[2] ZHOU Y C, LIU S J, LIU Z W, HUANG M H. Hydraulic position holding system of a huge water press based on iterative learning control [J]. Mechanical Science and Technology for Aerospace Engineering, 2008, 27(9): 1130–1133.

[3] GAO C, JIAN L, LUO S. Modeling of the thermal state change of blast furnace hearth with support vector machines [J]. IEEE Tran on Industrial Electronics, 2012, 59(2): 1134–1145.

[4] EBRAHIMI B M, JAVAN R M, FAIZ J, KHATAMI S V. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis [J]. IEEE Tran on Industrial Electronics, 2014, 61(4): 2041–2052.

[5] QI C K, LI H X, ZHANG X X, ZHAO X, LI SY, GAO F. Time/Space-separation-based SVM modeling for nonlinear distributed parameter processes [J]. Ind Eng Chem Res, 2011, 50: 332–341.

[6] HE K, LI X. A quantitative estimation technique for welding quality using local mean decomposition and support vector machine [J].Journal of Intelligent Manufacturing, 2016, 27(3): 525–533.

[7] KAO L J, LEE T S, LU C J. A multi-stage control chart pattern recognition scheme based on independent component analysis and support vector machine [J]. Journal of Intelligent Manufacturing, 2016, 27(3): 653–664.

[8] U, EKICI S. Support vector machines models for surface roughness prediction in CNC turning of AISI 304 austenitic stainless steel [J]. Journal of Intelligent Manufacturing,2012, 23(3): 639–650.

[9] BENKEDJOUH T, MEDJAHER K, ZERHOUNI N, RECHAK S. Health assessment and life prediction of cutting tools based on support vector regression [J]. Journal of Intelligent Manufacturing, 2015, 26(2): 213–223.

[10] ZHOU L, LAI K K, YU L. Least squares support vector machines ensemble models for credit scoring [J]. Expert Systems with Applications, 2010, 37(1): 127–133.

[11] KIM W, PARK J, YOO J, KIM H J, PARK C G. Target localization using ensemble support vector regression in wireless sensor networks [J].IEEE Transactions on Cybernetics, 2013, 43(4): 1189–1198.

[12] JIAN L, XIA Z, LIANG X, GAO C. Design of a multiple kernel learning algorithm for LS-SVM by convex programming [J]. Neural Networks, 2011, 24(5): 476–483.

[13] QI G J, TI Q, HUANG T. Locality-sensitive support vector machine by exploring local correlation and global regularization [C]// IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, USA: IEEE, 2011: 841–848.

[14] QIU S, LANE T. A framework for multiple kernel support vector regression and its applications to siRNA efficacy prediction [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2009, 6(2): 190–199.

[15] ZHANG G,LI H X, GAN M. Design a wind speed prediction model using probabilistic fuzzy system [J].IEEE Trans on Industrial Informatics, 2012, 8(4): 819–827.

[16] LIU Z,LI H X, ZHANG Y. A probabilistic wavelet system for stochastic and incomplete data-based modeling [J]. IEEE Trans Systems Man and Cybernetics Part B, 2008, 38(2): 310–319.

[17] SUYKENS J A, BRABANTER J, LUKAS L, VANDEWALLE J. Weighted least squares support vector machines: Robustness and sparse approximation [J]. Neurocomputing, 2002, 48: 85–105.

[18] VALYON J, HORVATH G. A robust LS-SVM regression [J]. International Journal of Computational Intelligence,2006, 3(3): 243–248.

[19] WEN W, HAO Z F, YANG X W. A heuristic weight-setting strategy and iteratively updating algorithm for weighted least-squares support vector regression [J]. Neurocomputing, 2008, 71(16–18): 3096–3103.

[20] WONG P K, XU Q, VONG C M, WONG H C. Rate-Dependent hysteresis modeling and control of a piezostage using online support vector machine and relevance vector machine [J]. IEEE Tran on Industrial Electronics, 2012, 59(4): 1988–2001.

[21] DE BRABANTER K, DE BRABANTER J, SUYKENS J A , de MOOR B. Approximate confidence and prediction intervals for least squares support vector regression [J]. IEEE Trans on Neural Networks,2011, 22(1): 110–120.

[22] LI H X, YANG J L, ZHANG G, FAN B. Probabilistic support vector machines for classification of noise affected data [J].Information Sciences, 2013, 221: 60–71.

[23] YANG J L, LI H X, YONG H. A probabilistic SVM based decision system for pain diagnosis [J]. Expert Systems with Applications, 2011, 38(8): 9346–9351.

[24] WANG Z, ZHANG Z, MAO J. Adaptive tracking control based on online LS-SVM identifier [J]. International Journal of Fuzzy Systems, 2012, 14(2): 330–336,

[25] YUAN X, WANG Y. LS-SVM modeling based inverse controller with uncertainty compensation [J]. Journal of Dynamic Systems Measurement and Control, 2007, 129: 845–850.

[26] DENG H, LI H X. A novel neural approximate inverse control for unknown nonlinear discrete dynamic systems [J]. IEEE Trans on Systems Man, and Cybernetics Part B: Cybernetics, 2005, 35(1): 115–123.

[27] LI H X, DENG H. An approximate internal model based neural control for unknown nonlinear discrete processes [J]. IEEE Trans on Neural Networks, 2006, 17(3): 659–670 .

[28] XI X C, POO A N, CHOU S K. Support vector regression model predictive control on a HVAC plant [J]. Control Engineering Practice, 2007, 15: 897–908.

[29] SUYKENS J A, VANDEWALLE J, MOOR B D. Optimal control by least squares support vector machines [J]. Neural Networks, 2001, 14(1): 23–25.

[30] SUYKENS J A, GESTEL T V, BRABANTER J D, MOOR B D, VANDEWALLE J. Least squares support vector machines [M]. Singapore: World Scientific, 2002: 236–251.

[31] WANG H, PI D, SUN Y. Online SVM regression algorithm based adaptive inverse control [J]. Neurocomputing, 2007, 7: 52–59 .

[32] SPOOER J T, MAGGIORE M, ORDONEZ R, PASSION K M. Stable adaptive control and estimation for nonlinear systems [M]. New York: Wiley, 2002: 69–76.

[33] LU X J, HUANG M H. A novel multi-level modeling method for complex forging processes on hydraulic press machines [J]. International Journal of Advanced Manufacturing Technology, 2015, 79(9): 1869–880.

[34] LU X J, HUANG M H. A simple online modeling approach for a time-varying forging process [J]. International Journal of Advanced Manufacturing Technology, 2014, 75: 1197–1205.

(Edited by HE Yun-bin)

Cite this article as: FAN Bin, LU Xin-jiang, HUANG Ming-hui. A novel LS-SVM control for unknown nonlinear systems with application to complex forging process [J]. Journal of Central South University, 2017, 24(11): 2524–2531. DOI:https://doi.org/10.1007/s11771-017-3665-8.

Foundation item: Project(51205420) supported by the National Natural Science Foundation of China; Project(NCET-13-0593) supported by the Program for New Century Excellent Talents in University, China; Project(14C0208) supported by the Research Foundation of Education Bureau of Hunan Province, China

Received date: 2015-12-03; Accepted date: 2016-02-23

Corresponding author: LU Xin-jiang, PhD, Professor; Tel: +86-13667336702; E-mail: luxj@csu.edu.cn