Article ID: 1003-6326(2005)05-1009-05
Solution for slab forging with bulge between two parallel platens by strain rate vector inner-product integration and series expansion
ZHAO De-wen(赵德文), WANG Lei(王 磊), LIU Xiang-hua(刘相华), WANG Guo-dong(王国栋)
(State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110004, China)
Abstract: A new linear integration was developed. First, effective strain rate for slab forging with bulge was expressed in terms of two-dimensional strain rate vector, and its inner-product was integrated term by term. Second, a summation process of term by term integrated results and a formula of the bulging were introduced, and an analytical solution of stress effective factor was obtained. It is proved that the expression of power by the above linear integration is the same as that of traditional immediate integration. Also, the solution was simplified by series expansion and compared by slab forging test with the others. It turns out that the calculated result of total forging pressure is basically in agreement with measured value in the actual press test.
Key words: slab forging; bulge; strain rate vector; inner-product; linear integration CLC number: TG301
Document code: A
1 INTRODUCTION
Slab forging with bulge between two parallel platens is shown in Fig.1. Friction over the surface decreases the velocity vx at the surface, and causes the center y=0 to move faster with a resultant bulge as shown in Fig.1(a). Therefore, this velocity gradient from the surface to the interior introduces a shear strain rate [AKε·D]xy.
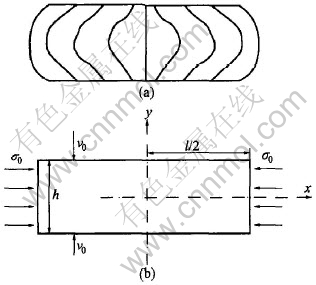
Fig.1 Slab forging with bulge between two parallel platens
It is the bulge that make the forging more difficult to be analytically solved[1]. However, numerical methods[2], including FEM[3] and UBEM[4] as well as numerical simulation[5] , have gradually come to their stage of maturity in recent years. In the present paper, the aim is to seek analytical solution by so-called inner-product of strain rate vector[6, 7], and then compare it with traditional immediate integration[8-10].
2 STRAIN RATE TENSOR FIELD
Assuming that vx varies exponentially with the y coordinate as shown in Fig.1(b), the velocity field becomes

The strain rate components are found when Cauchy equation is applied to the velocity field of Eqn.(1):

The detail deduction process of the above equations could be found in Refs.[8, 9]. Those strain rate components satisfy
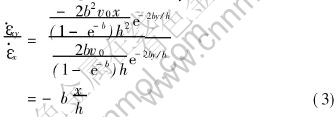
It must be pointed out that “-” should be added before vy in Eqn.(13.13c) of Ref.[8]. Then it would be the second formula[11] in Eqn.(1).
3 POWER OF DEFORMATION
3.1 Inner-product of strain rate vector for plastic power
The effective strain rate in the integrand of plastic power is expressed in inner-product of strain vector, the following is obtained:
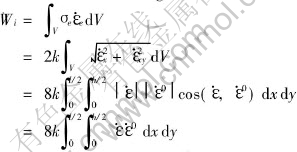
where  .
.
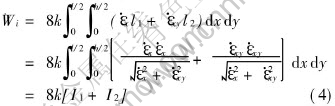
For Eqn.(4), term by term integration[6, 7] was used. And notice Eqn.(3), it follows that
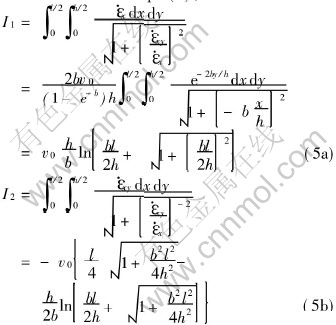
Substitution of Eqns.(5a) and 5(b) into Eqn.(4) leads to
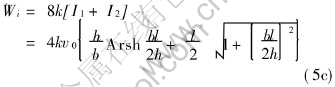
Eqn.(5c) is analytical solution for internal power of deformation, which is integrated term by term and summed according to strain vector inner-product. It should be noticed that there is an arc-hyperbolic sine in Eqn.(5c) and its the same as that of Avitzurs immediate integration[8, 9].
3.2 Friction losses and power to overcome resistance
Here constant friction (τf=mk) is assumed and the velocity discontinuity by Eqn.(1) is

Friction losses become
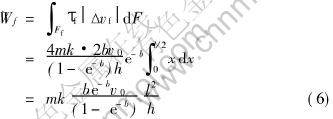
If external stress σ0 is applied at the free surfaces , then the power to overcome the resistance of this pressure is
, then the power to overcome the resistance of this pressure is

4 TOTAL POWER AND MINIMIZATION
4.1 Total power and series expansion
Substitution of Eqns.(5(c)), (6) and (7) into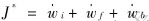 leads to
leads to
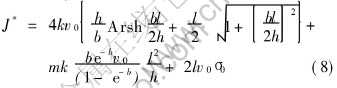
When
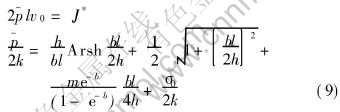
If no external pressure exists, then σ0=0.
The upper-bound analytic solution of slab forging is obtained by Eqn.(9).
Expanding Eqn.(9) into series:
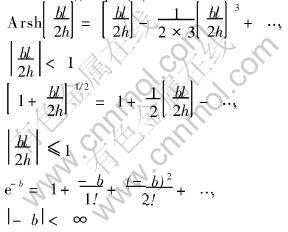
These expansions hold if  .
.
Omitting terms to the second power and higher:

Eqn.(10) is the simplified analytic solution by series expansion.
The arbitrary parameter b is to be so chosen that Eqn.(10) is minimized. Differentiation of Eqn.(10) and equating to zero leads to
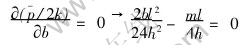
Therefore,

Substitution of Eqn.(11) into Eqn.(10) leads to the minimum upper-bound solution:
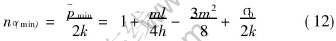
This is the minimum upper-bound solution of stress effective factor. σ0=0 means no external pressure.
Avitzurs approximate solution[8] for the same problem is
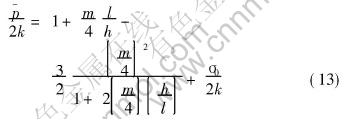
4.2 Parameter b of bulge
By the first equation of Eqn.(1):

where 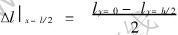 .
.  is the measured length of the forged specimen, which is the difference between the middle and the contact surface along x direction at x=l/2.
is the measured length of the forged specimen, which is the difference between the middle and the contact surface along x direction at x=l/2.
Substitution of Eqn.(14) into Eqn.(11) leads to the value of m. Then substitution of m into Eqn.(12) leads to the minimum upper bound stress effective factor.
5 VALIDATION BY PRESS TEST
The press test was done with 200kN universal material testing machine in the State Key Laboratory of Rolling and Automation NEU. A pure lead specimen was compressed from an initial size of h0=20.27mm, l0=49.73mm, B0=70.12mm to a final size of h1=18.35mm, B1=72.81mm, l1=54.58mm. The ram speed is 30mm/min and the total indicator reading of the machine is 97.2kN.
5.1 Calculated result
The measured dimensions after compression are lm=55.09mm, ls=54.07mm. Therefore, l/h=54.07/18.35=2.9466, h/l=0.3394, Δh=1.92mm. Since Eqn.(15),
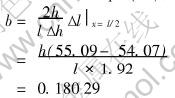
Substitution of these parameters into Eqn.(11) leads to
m=0.177
Substitution of the value of m into Eqn.(12), noticing σ0=0, leads to
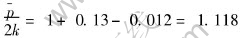
From the measured dimension:
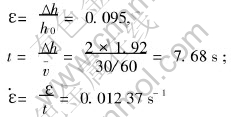
According to ε, 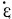 , it can be checked out σs=20.06MPa[12], then the total compression force
, it can be checked out σs=20.06MPa[12], then the total compression force 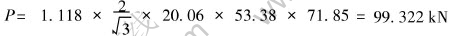 . Notice that the indicator reading of the machine is 97.2kN, so the difference between them is
. Notice that the indicator reading of the machine is 97.2kN, so the difference between them is
Δ=(99.3-97.2)/97.2=2.16%
5.2 Comparison with Avitzurs formula
Substitution of m=0.177 into Eqn.(13) and noticing σ0=0 leads to
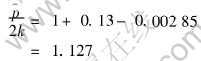
With the same procedure the total forging force is
P=100.12kN
It is proved that the above result is basically in agreement with that of Eqn.(12).
The author of present paper ever deduced a formula to slab forging with bulge by transmission equation[13] as follows:
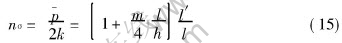
where l′, l are the measured length respectively at the middle y=0 and the surface y=h/2 of the deformed specimen, and l′/l≥1 is the bulge parameter.
Substitution of m=0.177 and other parameter into Eqn.(15) leads to
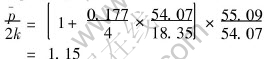
Therefore,
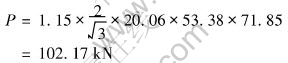
The difference to the indicator reading is
Δ=(102.17-97.2)/97.2
=5.1%
It should be pointed out that in above computation the contact area is a product area of average length and wide of the deformed specimen. In addition Slab[14] and slip-line[15] methods, as well as others[16] available can be used to solve this kind of problems.
Let m=0.1, 0.2, 0.3, 0.4, 0.5 in turn, and calculate stress effective factor nσ=p[DD(-*2]-[DD)]/2k by Eqns.(12), (13) and (15). These results are compared in Table 1 and Fig.2.
Table 1 Comparison of stress effective factor nσ
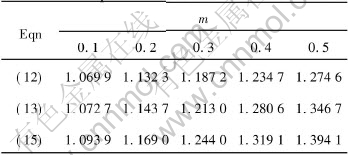
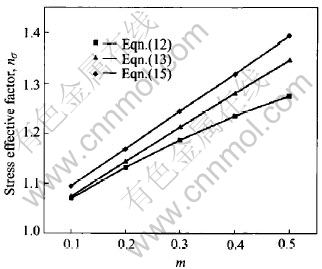
Fig.2 Comparison of stress effective factor by Eqns.(12), (13) and (15)
From Table 1 and Fig.2 a conclusion can be obtained that the value of stress effective factor increases along with the increase of m. The result of Eqn.(15) is higher than the results of Eqns.(12) and (13). The results of Eqns.(12) and (13) are basically consistent.
6 CONCLUSIONS
1) The effective strain rate for slab forging with bulge can be expressed in terms of two-dimensional strain rate vector, and its inner-product integrated term by term. Then the summation of the integrated results yields an analytical solution of deformation power as shown in Eqn.5(c). It is arc-hyperbolic sine function, the same as that of traditional immediate integration.
2) By expanding series and power minimization, the simplified stress effective factor Eqn.(12) is obtained. The corresponding bulge parameter b is shown in Eqn.(11).
3) The calculated results of p[DD(-*2]-[DD)]/2k and total forging force by Eqn.(12) is basically in agreement with those by Eqns.(13) and (15). But all of them are a little higher than the value of indicator reading of the machine.
4) It is indicated that stress effective factor increases along with the increase of the value of friction factor m.
REFERENCES
[1]Tarnovskii I Y. Theory of Metal Forming by Pressure [M]. Moscow: Metallurgizdat, 1963. 55-67. (in Russian)
[2]Kopp R. Some current development trends in metal- forming technology [J]. Journal of Material Processing Technology, 1996, 60: 1-9.
[3]Pittman J F T. Numerical Analysis of Forming Processes [M]. New York: John Wiley & Sons, 1984. 32-33.
[4]Alfozan A, Gunasekera J S. An upper bound element technique approach to the process design of axisymmetric forging by forward and backward simulation [J]. Journal of Material Processing Technology, 2003, 142: 619-627.
[5]Yang H, Zhan M, Liu Y L, et al. Some advanced plastic processing technologies and their numerical simulation [J]. Journal of Material Processing Technology, 2004, 151: 63-69.
[6]ZHAO De-wen. Mathematical Solutions of Continuum Forming Force [M]. Shenyang: Northeastern University Press, 2003. 421-425. (in Chinese)
[7]WANG Guo-dong, ZHAO De-wen. Modern Mechanics of Material Forming [M]. Shenyang: Northeastern University Press, 2004. 66-71. (in Chinese)
[8]Avitzur B. Metal Forming: Processes and Analysis [M]. New York: McGraw-Hill Inc, 1968. 360-369.
[9]ZHAO Zhi-ye. Mechanics of Metal Plastic Forming [M]. Beijing: Metallurgic Industry Press, 1987. 222-223. (in Chinese)
[10]Tarnovskii V I. Variational methods in the mechanics of metal forming by pressure [J]. Journal of Material Processing Technology, 1996, 60: 435-439.
[11]ZHAO De-wen. Mechanics of Material Forming [M]. Shenyang: Northeastern University Press, 2002. 200-202. (in Chinese)
[12]Loizou N, Sims R B. The yield stress of pure lead in compression [J]. Journal of the Mech and Phy Solids, 1953(1): 234-243.
[13]ZHAO De-wen. An engineering calculation formula of slab compression [J]. Engineering Mechanics, 1989, 6(1): 81-87. (in Chinese)
[14]Willianm F H. Metal Forming Mechanics and Metallurgy [M]. Englewood Cliffs: Prentice-Hall Inc, 1983. 123-124.
[15]Johnson W. Plane-strain Slip-line Fields for Metal Deformation Processes [M]. Oxford: Oxford Pergamon Press, 1982. 70-72.
[16]ZHAO De-wen, FANG You-kang. The integral of inverse function of Φ for an analytical solution to the compression of thin workpiece [J]. Trans Nonferrous Met Soc China, 1993, 3(1): 42-45.
Foundation item: Project(50474015) supported by the National Natural Science Foundation of China
Received date: 2004-02-27; Accepted date:2005-05-13
Correspondence: ZHAO De-wen, Professor; Tel: +86-24-83686423; E-mail: cral@mail.neu.edu.cn
(Edited by LI Xiang-qun)