Trans. Nonferrous Met. Soc. China 22(2012) 286-390

Structural, magnetic and electronic properties of FeF₂ by first-principle calculation

YANG Zhen-hua^{1, 2, 3}, WANG Xian-you^{1, 2, 3}, LIU Li^{1, 2, 3}, SU Xu-ping³

1. Faculty of Materials, Optoelectronics and Physics, Xiangtan University, Xiangtan 411105, China;

2. School of Chemistry, Xiangtan University, Xiangtan 411105, China;

3. Key Laboratory of Materials Design and Preparation Technology of Hunan Province, Xiangtan University, Xiangtan 411105, China

Received 8 April 2011; accepted 16 June 2011

Abstract: First-principle calculation was used to investigate the magnetic properties, electronic structure and bonding mechanism of FeF₂. By calculating the lattice parameters and magnetic moment as a function of effective interaction parameter (U_eff), it is found that the optimum value of U_eff is equal to 4 eV, the magnetic moment is 3.752 μB and the value of c/a is 0.704, which are in good agreement with the experiment results. Simultaneously, on the basis of GGA+U method, the electronic structure and bonding mechanism of FeF₂ were investigated by the analysis of electron localization function, Bader charge and total charge density. The results show that the bonding behavior between Fe and F atoms is a combination of ionic and covalent bond.

Key words: magnetic moment; electronic structure; bonding mechanism; FeF₂; lithium-ion battery

1 Introduction

Lithium-ion batteries as power source have been widely used in various energy storage fields due to high energy density and good cycling stability [1, 2]. The commonly used cathode materials for lithium-ion batteries are the layered intercalation compounds, such as LiCoO₂, LiMnO₂, LiFePO₄.

Recently, metal fluorides are considered next generation lithium ion battery cathode materials and enter a prominent space in energy storage [3-5]. The reaction between Li and metal fluorides can be expressed by the following equation:

                (1)

where Me is metal, such as Fe, Co, Ni, Bi; e is the charge of an electron. Due to the high ion bonding character between metal and high electro-negativity of F ions and full use of their valence electrons in charge/discharge process, the chemical energy can be reversibly utilized in metal fluorides through conversion reaction (1), which results in high average voltage and high specific capacity. For example, the theoretical average voltages of CrF₃ and FeF₂ are 2.28 and 2.66 V, respectively [6, 7].

Among all metal fluorides, FeF₂ with theoretical voltage of 2.66 V is considered a promising cathode material for the application of lithium ion battery owing to its low cost and low toxicity. In order to analyze the intrinsic electronic structure of FeF₂, theoretical calculations on FeF₂ have also been carried out. BROWN et al [8] found that the Fe-F interactions presented some covalent bond characters by means of DV-X_α method. The magnetic coupling constants between nearest-neighbor magnetic ions in FeF₂ were calculated using Hartree-Fock method [9]. PHILIPP et al [10] calculated the energy gap and spin-magnetic moments for FeF₂ by using the generalized gradient approximation (GGA) and local-spin-density approximation (LSDA) methods. The result shows that LSDA calculation fails (making them metallic) and GGA calculation yields improvement on the energy gap over LSDA calculation, but the energy gap is very small  (0.4 eV), which cannot describe the wide band gap character state of FeF₂. Besides, the spin-magnetic moment calculated by GGA calculations (3.5 μB) is lower than the experimental result (3.75 μB).

Based on the above discussions, because on-site coulomb interaction exists between Fe 3d and GGA method is not enough to well describe the wide band gap character of the compound, the introduction of a Hubbard-like contribution on the Fe 3d states is necessary. Hence, GGA+U method is put forward. U is the Hubbard parameter, which reflects the strength of the on-site coulomb interaction. Up to date, no attempt was carried out on using GGA+U method to study the structure of FeF₂. In this work, first-principle calculation within GGA+U method was used to investigate the magnetic and electronic properties as well as bonding mechanism of FeF₂.

2 Computational method

The calculations were performed using the ab-initio total-energy and molecular-dynamics program Vienna ab-initio simulation program (VASP) developed at the institut für Materialphysik of the Universit?t Wien [11-14]. The projector augmented wave (PAW) method was implemented in VASP. The approximation used for exchange and correlation energies is GGA. For GGA calculations, the Perdew-Burke-Ernzonhof (PBE) exchange-correlation functional was chosen. To study the strong correlation character of 3d electrons of Fe, GGA+U method was employed. Within the GGA+U approach, the on-site coulomb term U and the exchange term J were considered together. Effective interaction parameter (U_eff) can be concluded by U-J. In order to obtain the appreciate value of U, the electronic structure of FeF₂ was investigated with the U parameters  changing from 1 to 10 eV. The U value was determined through the comparison of equilibrium cell parameters with the available experimental data. The J value was fixed as 1 eV. The cutoff energy of 520 eV and Monkhorst-Pack grid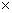 (66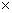9) for k point sampling in the first irreducible Brillouin zone were used to ensure the good convergence for total energy and forces acting on the atoms. All atoms were fully relaxed until the Hellman-Feynman forces on the atoms were converged to less than 1×10^-3 eV/nm by a Quasi Newton (QN) algorithm method.

To obtain the electronic density of states (DOS), the tetrahedron method with Bl?chl corrections was used for the Brillouin-zone integration and a 8×8×12 Monkhorst-Pack k-point mesh was set. In all calculations, spin-polarized calculations were performed.

3 Results and discussion

3.1 Crystal structure of FeF₂

FeF₂ has a tetragonal structure (with two formula units per unit cell) with space group P4₂/mnm. Usually, it can be described by 3 structural parameters: a, c and internal parameter u. a and c are 0.46945 and    0.33097 nm, respectively. The positions of the atoms inside the unit cell are (0, 0, 0) and (1/2, 1/2, 1/2) for the Fe atoms, and (u, u, 0), (1-u, 1-u, 0), (1/2+u, 1/2-u, 1/2) and (1/2-u, 1/2+u, 1/2) for the F atoms, where u is 0.301 [15]. After the structure of FeF₂ is fully relaxed, u is 0.299.

3.2 Ferromagnetic and antiferromagnetic phase of FeF₂

The dependence of the total energies on U_eff for ferromagnetic (FM) and antiferromagnetic (AFM) phase is calculated and shown in Fig. 1. As seen from Fig. 1, with the increase of U values, the energy difference between AFM and FM phases decreases; the     energy difference between AFM and FM phases is negligible when U_eff value is higher than 3.0 eV. Generally speaking, the total energy of AFM phase is lower than that of FM phase, which indicates that AFM phase is more stable than FM phase. Hence, in the following calculations, only the AFM phase is considered in investigating the magnetic and electronic properties of FeF₂.

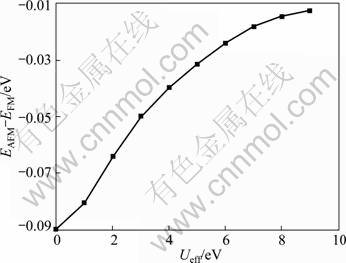
Fig. 1 Energy difference between AFM phase and FM phase (E_AFM-E_FM) within GGA+U as function of U_eff

3.3 Geometry and magnetic properties

The calculated lattice constant a and experimental value are compared in Fig. 2. As seen from Fig. 2, it is clear that the GGA+U method overestimates the lattice constant, and the error increases with the increase of U_eff value. Even though the theoretical error is below 1.5% compared with experimental value, the calculated lattice constant is still in reasonable agreement with the experiment. Figure 3 shows the tendency of c/a value as a function of U_eff. It can be found that the value of c/a decreases with the increase of U_eff value, and it is the closest to the experimental value at U_eff = 4 eV. Moreover, a series of U_eff values are employed to calculate the magnetic moment of Fe²⁺ in FeF₂. The  calculated results are shown in Fig. 4. It is observed from Fig. 4 that the magnetic moment of Fe²⁺ increases with the increase of U_eff, and it is 3.752 μB at U_eff=4 eV, which is in good agreement with the reported experimental value of  3.750 μB [16]. In order to further understand the magnetic properties of FeF₂, the calculated spin density is plotted for the FeF₂ plane using GGA+U (U_eff=4 eV) method, as shown in Fig. 5. According to spin-up and spin-down electrons, Fe atoms are classified as Fe₁ and Fe₂, and F atoms are classified as F₁ and F₂, respectively. As seen from Fig. 5, it is obvious that the magnetic properties of FeF₂ are mainly contributed from the magnetic moment of Fe atoms. As for F atoms, they exhibit very small induced spin magnetic moment by Fe atoms. The calculated spin magnetic moments of Fe and F atoms of FeF₂ are listed in Table 1. Apparently, the spin magnetic moment of Fe is chiefly contributed by Fe 3d state. Moreover, it is interesting that a small spin polarization on the site of F atoms appears, indicating that Fe₁-Fe₂ superexchange interaction occurs in virtue of F atoms.

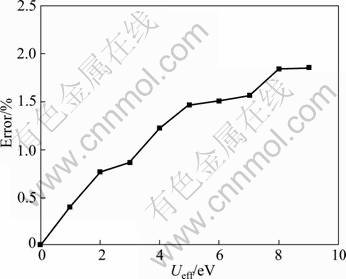
Fig. 2 Errors between calculated lattice constant and experimental value

Fig. 3 Ratio of c and a parameters (c/a) within GGA+U as function of U_eff

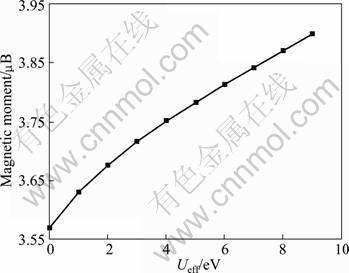
Fig. 4 Magnetic moment within GGA+U as function of U_eff

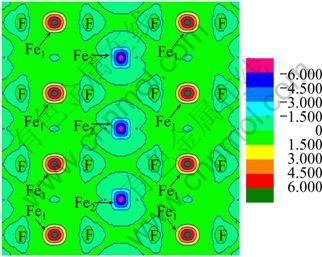
Fig. 5 Spin density of FeF₂ AFM phase in  plane in GGA+U (U_eff =4)

Table 1 Atomic orbit magnetic moments in FeF₂ crystal cell within GGA+U (U_eff =4 eV)

3.4 Electronic structure of FeF₂

The calculated total DOS together with the partial density of states (PDOS) of FeF₂ using the GGA and GGA+U(U_eff =4) methods are compared in Fig.6. It can be seen that the band gap calculated by GGA method is close to 0. The inclusion of correlation effect U_eff=4.0 eV for FeF₂ can push the states at Fermi level away from Fermi level and reproduce the wide band gap character of the compound. The GGA+U calculations show that FeF₂ belongs to Mott-Hubbard materials with a band gap of 2.565 eV. Therefore, the GGA+U calculations can better predict the electronic structure of FeF₂ than GGA calculation. Further analysis on the DOS of FeF₂ is carried out. The valence band is divided into two regions. One is located between -7.34 and -1.05 eV, which shows significant hybridization of Fe3d and F2p. The other is located between -1.05 eV and Fermi level, which is composed of mainly Fe3d and small F2p. Besides, the conduction band is located between 2.57 and 8.28 eV.

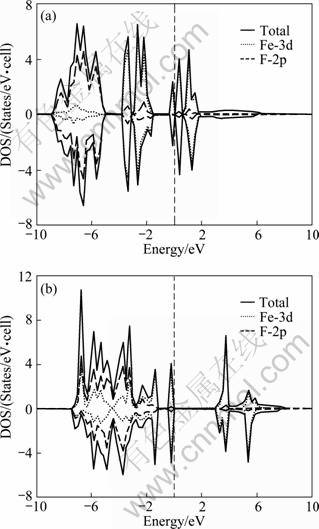
Fig. 6 Total and partial DOS for FeF₂ AFM phase within GGA (a) and GGA+U (b) (U_eff=4 eV) (Fermi level was set 0, positive and negative DOS represents spin up and down DOS, respectively.)

In order to analyze the bonding mechanism of FeF₂, the charge density distribution of FeF₂ is plotted in   Fig. 7. It is found that the charge density around Fe and F ions is spherical distributed with slightly directional character toward the direction to their nearest neighboring atoms, indicating that a little covalent bond exists between Fe and F atoms.

The bonding mechanism can be also further analyzed by electron localization function (ELF) [17, 18]. The value of ELF ranges from 0 to 1.0 with ELF=0.5 corresponding to the free electron gas distribution. An ELF value equal to 1.0 means perfect electron localization. The calculated ELF maps in the  plane of FeF₂ are given in Fig.8. The ELF values of interstitial region between Fe and F atoms are small but none zero, which indicates the bonding between Fe and F atoms processes ionic nature. Hence, the bonding behavior between Fe and F atoms is the combination of covalent bonding and ionic interactions.

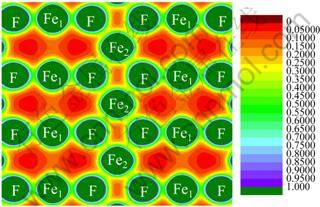
Fig. 7 Calculated total charge density of FeF₂ AFM phase in  plane within GGA+U at U_eff =4 eV

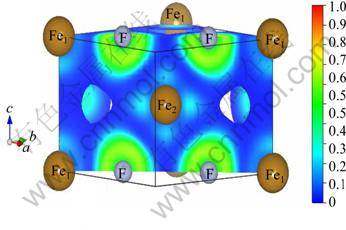
Fig. 8 Calculated plots of ELF of FeF₂ AFM phase within GGA+U at U_eff =4 eV

To describe the covalent and ionic nature quantitatively, the net charges on Fe and F ions are calculated using Bader’s AIM theory [19, 20]. The results are listed in Table 2. As seen from Table 2, it is evident that about 1.5503 electrons transfer from each Fe atom to F atoms. However, net charge on Fe and F atoms are less than nominal charges of the ions (+2 for Fe   and -1 for F). Accordingly, in FeF₂, the bond between Fe and F atom shows evident ionic character and a little covalent bond exists between Fe and F atoms at the same time.

Table 2 Net charge on atoms of Fe and F in FeF₂ calculated using Bader charge analysis

4 Conclusions

1) FeF₂ AFM phase is more stable than FeF₂ FM phase considering the strongly correlated Fe 3d, which is consistent with the experimental results. It is well known that GGA calculations result in a metallic state, while GGA+U method can well describe the wide band gap character of FeF₂ and the calculated band gap is    2.565 eV.

2) The optimum value of U_eff is equal to 4 eV, the magnetic moment is 3.752 μB, and the value of c/a is 0.704, which is in good agreement with the experimental results.

3) It can be concluded that the bond between Fe and F atoms in FeF₂ is a mixture of ionic bond and covalent bond.

References

[1] DO Jing-shan, DAI Rui-feng. Cobalt oxide thin ?lm prepared by an electrochemical route for Li-ion battery [J]. J Power Sources, 2009, 189(1): 204-210.

[2] YAN Feng, LI Ya-li, HOU Feng. Preparation and electrochemical properties of Cr doped LiV₃O₈cathode for lithium ion batteries [J].Mate Lett, 2009, 63(15):1338-1340.

[3] YAMAKAWA N, JIANG M, KEY B, Grey C P. Identifying the local structures formed during lithiation of the conversion material, iron fluoride, in a Li ion battery: A solid-state NMR, X-ray diffraction, and pair distribution function analysis study [J]. J Am Chem Soc, 2009, 131(30): 10525-10536.

[4] LIAO P, McDONALD B L, DUNLAP R A, DAHN J R. Combinatorially prepared [LiF]_1-xFe_x nanocomposites for positive electrode materials in Li-ion batteries [J]. Chem Mater, 2008, 20(2): 454-461.

[5] LI T, LI L, CAO Y L, Ai X P, YANG H X. Reversible three-electron redox behaviors of FeF₃ nanocrystals as high-capacity cathode-active materials for Li-ion batteries [J]. J Phys Chem C, 2010, 114(7): 3190-3195.

[6] LI H, BALAYA P, MAIER J. Li-storage via heterogeneous reaction in selected binary metal fluorides and oxides [J]. Electrochem Soc A, 2004, 151(11): 1878-1885.

[7] AMATUCCI G G, PEREIRA N. Fluoride based electrode materials for advanced energy storage devices [J]. J Fluorine Chem, 2007, 128(4): 243-262.

[8] BROWN P J, FIGGIS B N, REYNOLDS P A. Covalency in FeF₂ from magnetisation density data and from ab initio theory [J]. J Phys: Condens Mat, 1990, 2(24): 5297-5308.

[9] MOREIRA I D P R, DOVESI R, ROETTI C, SAUNDERS V R, ORLANDO R. Ab initio study of MF₂ (M=Mn, Fe, Co, Ni) rutile-type compounds using the periodic unrestricted Hartree-Fock approach [J]. Phys Rev B, 2000, 62(12): 7816-7823.

[10] PHILIPP D, PETER B, VLADIMIR S, KARLHEINZ S. Generalized-gradient-approximation description of band splittings in transition-metal oxides and fluorides [J]. Phys Rev B, 1994, 49(15): 10170-10175.

[11] KRESSE G, HAFNER J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium [J]. Phys Rev B, 1994, 49(20): 14251-14269.

[12] KRESSE G, FURETHM?LLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set [J]. Comput Mater Sci, 1996, 6(1): 15-50.

[13] KRESSE G, FURETHM?LLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Phys Rev B, 1996, 54(16): 11169-11186.

[14] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Phys Rev B, 1999, 59(3): 1758-1775.

[15] BAUR W H, KHAN A A. Rutile-type compounds SiO₂, GeO₂ and a comparison with other rutile-type structures [J]. Acta Crystallographica B, 1971, 27(1): 2133-2139.

[16] DOE R E, PERSSON K A, MENG Y S, CEDER G. First-principles investigation of the Li-Fe-F phase diagram and equilibrium and nonequilibrium conversion reactions of iron fluorides with lithium [J]. Chem Mater, 2008, 20(16): 5274-5283.

[17] MATAR S F, DEMAZEAU G J. Ab initio studies of the electronic structure of the quaternary system LiBC₄N₄ [J]. J Alloys Compd, 2009, 182(1-2): 2678-2679.

[18] OSORIO-GUILL?N J M, SIMAK S I, WANG Y, JOHANSSON B, AHUJA R. Bonding and elastic properties of superconducting MgB₂ [J]. Solid State Commun, 2002, 123(6-7): 257-262.

[19] HENKELMAN G, ARNOLDSSON A, J?NSSON H. A fast and robust algorithm for Bader decomposition of charge density [J]. Comput Mater Sci, 2006, 36(3): 354-360.

[20] DELLE SITE L. A statistical interpretation of Bader’s definition of interatomic surface [J]. Phys Lett A, 2001, 286(1): 61-64.

第一性原理计算FeF₂的磁性、结构及电子性能

杨振华^{1, 2, 3}, 王先友^{1, 2, 3}, 刘 黎^{1, 2, 3}, 苏旭平³

1. 湘潭大学 材料与光电物理学院，湘潭 411105；

2. 湘潭大学 化学学院，湘潭 411105；

3. 湘潭大学 材料设计及制备技术湖南省重点实验室，湘潭 411105

摘  要：采用第一性原理方法研究FeF₂的磁性、电子结构和成键机理。通过计算不同U值下的的晶格参数和磁矩，获得最佳的有效U值(U_eff)为4 eV，此时计算Fe的磁矩和晶格参数c与a 的比值分别3.752 μB和0.704，与实验结果吻合。此外，基于GGA+U方法，利用对电子局域函数，Bader电荷和总电荷的分析来研究FeF₂ 的电子结构和成键机理，结果表明Fe和F之间含有离子键和共价键的特征。

关键词：磁矩；电子结构；成键机理；FeF₂；锂离子电池

 (Edited by FANG Jing-hua)

Foundation item: Project (20871101) supported by the National Natural Science Foundation of China; Project (09C945) supported by the Scientific Research Fund of Hunan Provincial Education Department, China

Corresponding author: WANG Xian-you; Tel: +86-731-58292060; Fax: +86-731-58292061; E-mail: wxianyou@yahoo.com

DOI: 10.1016/S1003-6326(11)61188-6