
Mechanical properties and energy absorption properties of
aluminum foam-filled square tubes
ZHANG Chun-ji (张春基), FENG Yi(凤 仪), ZHANG Xue-bin(张学斌)
Department of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China
Received 25 August 2009; accepted 2 December 2009
Abstract: Longitudinal and transverse mechanical properties and energy absorption properties of foam-filled square tubes under quasi-static loading conditions were studied. The foam-filled thin-walled square tube was fabricated with aluminum tube as its shell and closed-cell Al-Mg alloy foam as its core. The results indicated that the plateau region of the load-displacement curve exhibited a marked fluctuant serration which was clearly related to the formation of folds. The longitudinal deforming mode of foam-filled square tube was the same as that of the empty tube, but the fold number of foam-filled square tube was more than that of the empty tube. The longitudinal compression load and energy absorption value of foam-filled square tube were higher than the sum of that of aluminum foam (alone) and empty tube (alone) due to the interaction between tube and filler. In transverse direction, the compression load and energy absorption ability of foam-filled square tubes were significantly lower than those in longitudinal direction.
Key words: aluminum foam; foam-filled square tube; compression load; energy absorption
1 Introductio
In the past few years, due to the low relative density, high impact energy absorption capacity, high damping capacity and good electromagnetism shield properties, there is an increasing interest in aluminum alloy foams in the automobile, railway and aerospace industries where weight reduction and improvement in safety are needed[1-3]. Metallic foams are excellent impact energy absorber, and they can convert impact energy into deformation energy and absorb more energy than bulk metal at low stress[4-5]. One interesting application of aluminum foams is as filling material to improve the stiffness of hollow sections, rather analogous to the use of aluminum honeycombs[6-8]. Designing for these applications, therefore, demands the full characterization of their mechanical properties, the energy-absorbing capacity and deformation mode[9-11]. There is already evidence that filling aluminum tubes with aluminum foam affects the bucking characteristics. Many studies were carried out in characterizing static mechanical properties of aluminum foams, such as the compression and tensile strength, elastic modulus and fatigue behavior and their relationship of foam density and cell size[12-14]. But less efforts were made on aluminum foam-filled tubes[15-17]. In this work, the foam-filled square tube was fabricated with aluminum tube as its shell and closed-cell Al-Mg alloy foam as its core. The transverse and longitudinal compression properties and energy absorption properties under quasi-static pressing were studied. The effect of sample height on the mechanical properties and energy absorption ability of foam-filled tubes in longitudinal direction was also investigated.
2 Experimental
Al, Mg, Ca particles (adhesion agent) and TiH2 powder (blowing agent) were prepared for the aluminum foam. The production process is shown in Fig.1.
The process started by preparing Al-10%Mg (mass fraction) alloy and melting the Al-Mg alloy at 750 °C. Adding 1.5%Ca (mass fraction) particles to the melt at this temperature and stirring the melt for several minutes to increase its viscosity continuously owing to the formation of CaO, CaAl2O4, or perhaps even Al4Ca intermetallics which thicken the liquid metal[2]. When the temperature dropped to the solid-liquid two-phase coexistence temperature, 1%-2%TiH2 (mass fraction) was added which serves as a blowing agent by releasing

Fig.1 Schematic diagram of production process
H2 in the hot viscous liquid, and the melt was stirred violently for some time. The melt soon started to expand slowly and filled the foaming vessel in the air environment gradually. When the liquid foam expanded to an appropriate volume, the vessel was cooled down at an appropriate cooling rate below the melting point of the alloy and the liquid foam turned into solid aluminum foam. The porosity of aluminum foam varied from 70% to 92% and the cell sizes of aluminum foam varied from 1 to 4 mm.
The aluminum foams with the cross-section of 23 mm×23 mm were prepared using a wire-cutting machine as the filling cores. In order to compare the influence of the height on the longitudinal compression deforming properties, two different heights of 40 and 60 mm were chosen. Aluminum tubes with outer cross-section dimensions of 25 mm×25 mm and wall thickness of 0.8 mm were prepared as the shell materials. Aluminum foam cores and aluminum tubes were combined with epoxy to obtain aluminum foam-filled square tubes. The data were the average value of three samples.
The quasi-statistic compression tests of aluminum foams, empty aluminum tubes and foam-filled tubes were performed in computer controlled electronic universal testing machine (SANS) at a loading speed of 2 mm/min in longitudinal and transverse directions. The load values and the displacement were transmitted to computer by load sensor and displacement sensor to obtain the load-displacement curves automatically.
Corresponding average crushing loads of the samples were calculated using the following relation:
 (1)
(1)
where P and δ are the load and displacement, respectively. In the calculation of the average crushing loads, the initial peak loads of the load-displacement curves were excluded.
3 Results and discussion
3.1 Quasi-static compressive properties of aluminum foam
Fig.2 showed the stress-strain curves of Al-Mg alloy foams with different porosities (ρ). The compression curves of aluminum foams exhibited a typical characteristic of metallic foam and contained three distinct regions: linear elastic region, plateau region and densification region. In the linear elastic region, deformation was controlled by cell walls bending or stretching. This region was followed by a plastic collapse region which proceeded by spreading the local deformation and collapse to non-deformed region of the sample. This region was characterized by a load plateau with either a constant value or slight increase with displacement. In densification region, cell walls started to touch each other and the sample was densified. Fig.2 also showed that the stress of foam increased with the decrease of foam porosity, but the densification point of the foam was slightly lowered.
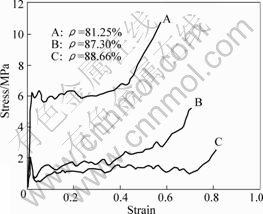
Fig.2 Stress-strain curve of Al-Mg alloy foam with different porosities
Ref.[1] indicated that plastic foam (pure aluminum) exhibited a smooth compressive curve in the plateau region, but referring to brittle foam, the plateau region of the curve appeared marked fluctuant serration. In Fig.2, the plateau region appeared obvious fluctuant serration, which indicated that Al-Mg alloy aluminum foam is a typical brittle material. The development of fluctuant serration is related to the deformation of the framework section (cell wall) which carries the majority load in the loading process. With the increase of the load, the stress on the weak cell wall exceeds the rupture strength and the cell wall starts to yield and collapse, then the load begins to drop. When the compression continues, the unbroken cell walls just above and below the crushed cell wall come into contact with each other and lead to a new rise of the load. The process overlaps ceaselessly until the sample is all densified, so the plateau region of curve develops obvious fluctuant serration.
3.2 Longitudinal crushing of foam-filled tubes
Fig.3 shows the longitudinal load-displacement curves of aluminum foam, empty aluminum tube, foam-filled tube and aluminum foam + empty tube (calculated value) under quasi-static compression with the heights of 40 mm and 60 mm, respectively. In Fig.3, it is found that the load-displacement curves of empty square aluminum tube and foam-filled tube are similar with the curve of aluminum foam and they also contain three regions: linear elastic region, plateau region and densification region. In the linear elastic region, the slope of the line is the macroscopically elastic modulus of the sample. The initial peaks of load of the empty tube and foam-filled tube are followed by a severe load drop and successive oscillations. The crushing curves of empty tube and foam-filled tube also exhibit fluctuant serrations, and the fluctuant degrees and the length of the plateau region increase obviously with the increase of sample height. In the densification region, the load rises sharply with increasing the displacement and the foam-filled tube

Fig.3 Load-displacement curves of different samples with heights of 40 mm (a) and 60 mm (b)
comes into densification region earlier than aluminum foam and empty aluminum tube due to the fact that the filled aluminum foam carried not only the axial crushing but also the transverse pressing by the aluminum tube. Figs.4 and 5 exhibit the compressed empty aluminum tubes and foam-filled tubes. Fig.4(b) and Fig.5(b) show that the empty tube with the height of 60 mm formed three folds and the foam-filled tubes with the height of 60 mm formed four folds. Fig.5 also shows that the number of folds increases with the increasing height of foam-filled tubes.

Fig.4 Photos of empty tube with height of 60 mm after compression: (a) Bottom; (b) Flank
From Figs.4 and 5, we can see that the longitudinal deforming mode of foam-filled tube is the same symmetry folding mode as the empty tube. During the process of crushing, when the sample achieves the yield stress, the aluminum tube starts to yield and a symmetrical square folding is formed in the weak layer. The shape of four corners which join the four flanks changes from beeline to curve shape during folding. In the experiment, the initial folding layer of the foam-filled tube and empty tube with a height of 40 mm formed from the bottom of the sample; but when the height was 60 mm, the initial folding layer formed from the middle part of the sample. With the deformation of the folding, the compressive stiffness and the load declined. When the first symmetrical folding was impacted, the load raised again. With the increase of stress, the second symmetrical square folding formed next to the first folding. The process repeated constantly and the crushing curves correspondingly appeared fluctuant serration. When one folding layer formed, one fluctuant serration appeared in the crushing curve, so the fluctuant degrees in the crushing curves had a corresponding relation with the number of the folding layers. For the foam-filled tube with a height of 60 mm (Fig.5(b)), the total number (four) of folds was equal to the number (four) of fluctuant serration in its crushing curve (Fig.3(b)). The total number (three) of folds in 60 mm high empty tube (Fig.4(b)) was equal to the number (three) of fluctuant serration in its crushing curve (Fig.3(b)).

Fig.5 Photos of foam-filled tube after compression with different heights: (a) 40 mm; (b) 60 mm
From Fig.3 we also found that the displacement among fluctuant serrations of foam-filled tube was shorter than that of empty tube. This can be explained by the interaction effect between the tube wall and foam filler. When the empty tube is compressed, every fold expanded freely outward or inward until all the folds were compacted, so the half-wavelength of fold was long which corresponded to the reduction of the fold number. When the foam-filled tube is compressed, the foam filler and aluminum tube crushed each other and the foam filler which possessed the middle space of aluminum tube restricted the transverse displacement of the folds of tube. Therefore, the half-wavelength of fold was reduced and the number of folds increased.
The simplest approach to predict the crushing load of foam-filled tubes is to add the aluminum foam crushing load to the empty tube crushing load due to the composite structure of foam and tube. In this approach, the foam filler and tube are assumed to deform independently. The sum of the loads of aluminum foam (alone) and empty tube (alone) is shown in Fig.3 and the load of foam-filled tube is obviously higher than the sum of the loads of the empty tube (alone) and aluminum foam (alone) which account for the existence of the interaction effect between the tube and foam filler. The position relationship of curves in Fig.3 indicated that the longitudinal crushing load could be divided into three parts: the load of foam (alone), the load of empty tube (alone) and the load of interaction effect between tube wall and filler. HANSSEN et al[9] presented an equation of the average crushing load (Paf) of foam-filled square tube including contributions of the average crushing load of empty tube (Pae), foam filler plateau stress (σal) and interaction effect between the tube wall and filler:
 (2)
(2)
Where Cavg is a constant which is directly related to the interaction between the tube wall and filling core; σ0, b and t are the yield strength of the aluminum tube, the outer cross-section width of the aluminum tube and the wall thickness of the tube, respectively. The second term of the right hand side in Eq.(2) accounts for the axial compression of the foam and the last term accounts for the interaction effect between tube wall and foam filler. The following formula is deduced from Eq.(2):
Paf > Pae+ σalb2 (3)
Formula (3) shows that the average load of foam-filled tube is higher than the sum of the average loads of foam (alone) and empty tube (alone). According to Eq.(1), the average loads of foam-filled tube, empty tube and aluminum foam with the height of 60 mm are 7.25, 3.60 and 1.5 KN, respectively. The average load values agree fairly well with formula (3).
The strengthening coefficient of the foam-filled tubes can be written as [10]
 (4)
(4)
where Pfoam is the foam-filler plateau load. The strengthening coefficient of foam-filled tube with a height of 60 mm is about 1.76. The structure of foam-filled tube enhances the load carrying capacity through taking full advantage of the interaction between the tube wall and filling core. In the foam-filled tubes, the interaction effect is partly due to the resistance of the filler to the inward and/or outward folding of the tube and partly due to the interfacial friction stress between foam and tube wall.
Aluminum foam is an ideal energy absorption material that the long plateau region enables it to absorb great energy. Thin-walled aluminum tube is an efficient axial energy absorber. As the shell of filling structure, it not only increases the stiffness and strength of foam-filled tube, but also rises the energy absorption ability. Therefore, foam-filled tube structure can be used in packages, protection, structural member and so on[3]. It is important to investigate its energy absorption capability. The energy absorption (E) is simply the area under the load-displacement curve and can be written as:
 (5)
(5)
It is obvious that the higher the load plateau region of the load-displacement curve, the more the capacity for energy absorption.
Fig.6 shows the comparison of energy absorption of aluminum foam, empty aluminum tube, foam-filled tube and aluminum foam+empty tube (calculated value). From Fig.6, we can see that the energy absorption value of foam-filled tube is much higher than the sum of that of aluminum foam (alone) and empty tube (alone). When the displacement is 25 mm, the absorbed energy of foam-filled tube with a height of 40 mm is about 2.13 times that of the empty tube, 7.73 times that of the foams and 1.69 times the sum of empty tube (alone) and aluminum foam (alone). Energy absorption ability of foam-filled tube increases more fleetly with increasing the displacement than empty tube and aluminum foam.

Fig.6 Energy absorption curves of different samples with heights of 40 mm (a) and 60 mm (b)
The above analysis shows that the presence of foam filler dramatically alters the energy absorption behavior compared with the non-filled tube and foam. Ref.[15] indicates that the foam-filled tube absorbed more energy due to the interaction effect between the tube wall and filling core. During the process of the crushing, the foam filler and aluminum tube crush and friction each other and the foam restricts the transverse displacement of the inward and/or outward folding of the tube. The half-wave length of folding is reduced and the number of folding is increased compared with the empty tube, so the tube could absorb more compression energy and the load of foam-filled tube increases obviously. With the combined effect of the longitudinal load and transverse crushing load by tube, the aluminum foam next to the tube develops an extreme densification region (as shown in Fig.7) which has larger stress, more volume change than densification region, therefore, the absorbed energy of aluminum foam was more than that of the foam (alone). The high capacity of energy absorption of the extreme densification region is the main reason for the effect of interaction in the structure of foam-filled tube. Based on the above analysis, foam-filled tube can absorb more energy than the empty tube and foam metal, and can be comprehensively applied in packages, protection, structural member and so on.

Fig.7 Photo of cross section foam-filled tube
3.3 Transverse crushing of foam-filled tubes
The above present results confirmed the advantage of the tube filled with foam in the axial direction. In order to determine whether there was actually any advantage in transverse crushing of the tube filled with foam, the load-displacement experiment was also performed in the transverse direction.
Fig.8 shows transverse load-displacement curves of aluminum foam, empty tube, foam-filled tube and aluminum foam + empty tube (calculated value) with the height of 60 mm. When empty tube and foam-filled tube in the longitudinal direction were compressed, there were four flanks as support surfaces, but when compressed empty tube and foam-filled tube were in the transverse direction, there were only two flanks to carry the crushing load, so the transverse load of empty tube and foam-filled tube was significantly lower than the longitudinal load of them. For aluminum foam, the compressing area (23 mm×60 mm) in the transverse direction was bigger than that in axial direction (23 mm×23 mm), therefore, the load of aluminum foam in the transverse direction was higher than that in the longitudinal direction. Fig.9 shows the transverse compressed photos of empty tube and foam-filled tube. It can be seen that the empty tube formed two inward folds at the upper and lower surface and two outward folds at the flanks. Because there was only one fold at every flank, there was no significant fluctuant serration in the rushing curve.

Fig.8 Transverse load-displacement curves

Fig.9 Photos of samples after transverse compression: (a) Empty tube; (b) Foam-filled tube
The curves of foam-filled tube and aluminum foam both contained three regions: the linear elastic region, the plateau region and the densification region. When the displacement was less than 4 mm, aluminum tube and aluminum foam carried the compression load together, so the load of the foam-filled tube was larger than the load of aluminum foam. During the process of crushing, two outward folds formed in the flanks of the foam-filled tube (Fig.9), and the load reduced dramatically with the increase of displacement. As a result, the foam filler carried the most of the load and the tube almost lost the effect of carrying load, so the load of foam-filled tube was almost equal to the load of aluminum foam (alone). When the sample was all densified, the curve came into the densification region. The crushing curve of the empty aluminum tube consisted of two regions: elastic region and plastic collapse region. When the tube achieved the yield stress, two outward folds and two inward folds formed in the empty tube, so the load of empty tube dropped dramatically with the increase of the displacement and there was no fluctuant serration in the second region.
The crushing load of foam-filled tube in the transverse direction was lower than the sum of the crushing loads of aluminum foam (alone) and empty tube (alone), as shown in Fig.8, which indicated that there was no interaction effect between the tube wall and filling core. When compressed aluminum tube was in transverse direction, the tube always had two opposite surfaces forming inward folds and the two other opposite surfaces forming outward folds. When compressed foam-filled tube was in transverse direction, the upper and lower surfaces of tube had the tendency to form inward folds due to the plasticity of aluminum foam, so the two support flanks must fold outward. As a result of the outward folds at the flanks, there was no interaction effect between the tube flanks and filling core. The number of folds of foam-filled tube (four) was less than that of folds of empty tube and the reduction of fold resulted in the reduction of crushing load of foam-filled tube, so the transverse crushing load of foam-filled tube was lower than the sum of the crushing loads of aluminum foam (alone) and empty tube (alone).
Fig.10 shows the transverse energy absorption curves of aluminum foam, empty tube, foam-filled tube and aluminum foam + empty tube (calculated value) with a height of 60 mm. In the transverse direction, the absorbed energy of foam-filled tube was only 22% that (Fig.6(b)) in the longitudinal direction and its energy absorption ability was significantly lower than that of the foam-filled tubes (Fig.6(b)) in the longitudinal direction. In Fig.10, the transverse energy absorption value of foam-filled tube was much lower than the sum of aluminum foam (alone) and empty tube (alone) due to the reduction of folds of foam-filled tube compared with empty tube.

Fig.10 Transverse energy absorption curves
4 Conclusions
1) In longitudinal direction, the crushing curves of foam-filled tube, empty tube and aluminum foam all contained three regions: linear elastic region, plateau region and densification region. During the crushing process of foam-filled tube and empty tube, when sample formed one folding layer, the rushing curve of sample formed one fluctuant serration, so the folds number of foam-filled tube and empty tube was equal to the fluctuant degree in the crushing curves.
2) The longitudinal deforming mode of foam-filled square tubes and empty tubes was symmetry folding deforming mode, but the number of folds of foam-filled square tube was more than that of empty tube.
3) Due to the interaction effect between tube and filler, the foam-filled tube formed more folds and foam filler formed one new extreme densification region, which resulted in the longitudinal compressive load and energy absorption value of foam-filled tube much higher than the sum of foam (alone) and tube (alone).
4) In transverse direction, the folds number of foam-filled tube reduced and there was no interaction effect between the tube and the filler, so the transverse compressive load and energy absorption value of foam-filled tube were lower than the sum of foam (alone) and tube (alone).
5) The compressive load and energy absorption ability of foam-filled tube and empty tube in the transverse direction were obviously lower than that in the longitudinal direction due to the decrease of support surfaces.
References
[1] GIBSON L J, ASHBY M F. Cellular solids: Structure and properties [M]. Oxford: Pergamon Press, 1997:145-148.
[2] JOHN B. Manufacture, characterization, and application of cellular metals and metal foams [J]. Progress in Materials Science, 2001, 46(6): 559-632.
[3] ASHBY M F, EVANS A G, FLECK N A. Metal foams: A design guide [M]. LIU Pei-sheng, WANG Xi-shu, LI Yan-xiang. Beijng: Metallurgical Industry Press, 2006: 157-162.
[4] KATHRYN A D, JAMES L. High stain rate compression of closed-cell aluminium foams [J]. Materials Science and Engineering A, 2000, 293(1/2): 157-164.
[5] LIU Yu, GONG Xiao-lu. Compressive behavior and energy absorption of metal porous polymer composite with interpenetrating network structure [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: S439-S443.
[6] WANG Song-lin, FENG Yi, XU Yi, ZHANG Xue-bin, SHEN Jian. Transverse and longitudinal crushing of aluminum-foam filled tubes [J]. Transactions of Materials and Heat Treatment, 2007, 28(1): 9-13.
[7] HANSSEN A G, LANGSETH M, HOPPERSTAD M O. Static and dynamic crushing of circular aluminium extrusions with aluminium foam filler [J]. International Journal of Impact Engineering, 2000, 24(5): 475-507.
[8] SIGIT P S, TOMASZ W, ARVE G H, MAGNUS L. Experimental and numerical studies of foam-filled sections [J]. International Journal of Impact Engineering, 2000, 24: 509-534.
[9] HANSSEN A G, LANGSETH M, HOPPERSTAD O S. Static crushing of square aluminium extrusions with aluminium foam filler [J]. Mechanical Sciences, 1999, 41(8): 967-993.
[10] GUDEN M, KAVI H. Quasi-static axial compression behavior of constraint hexagonal and square-packed empty and foam-filled aluminum multi-tubes [J]. Thin-Walled Structures, 2006, 44(7): 739-750.
[11] SHAHBEYK S, VAFAI A, PETRINIC N. Axial crushing of metal foam-filled square columns: Foam density distribution and impactor inclination effects [J]. Thin-Walled Structures, 2005, 43(12): 1818-1830.
[12] YU Hai-jun, YAO Guang-chun, LIU Yi-han. Tensile property of Al-Si closed-cell aluminum foam [J]. Transactions of Nonferrous Metals Society of China, 2006, 16(6): 1335-1340.
[13] AMSTERDAM E, DE HOSSEN J TH M, ONCK P R. Failure mechanics of closed-cell aluminum foam under monotonic and cyclic loading [J]. Acta Materialia, 2006, 54(17): 4465-4472.
[14] PAN Yi, HU Shi-sheng, FENG Yi, ZHU Zhen-gang. Cell size effect on mechanical property of open-cell aluminum alloy foam [J]. Engineering Mechanics, 2003, 20(4): 171-175. (in Chinese)
[15] SONG Hong-wei, YU Gang, FAN Zi-jie, WANG Qing-chun. Interaction effect in energy absorption of porous material filled thin walled structure [J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(6): 697-703. (in Chinese)
[16] LIN Sen, FENG Yi, ZHA Hai-bo, LI Shu, WANG Juan, ZHU Qi-qi. Compression capability and energy absorption of foam aluminum cylinder sandwich with silicone rubber [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(10): 1672-1677.
[17] LI Kun-peng, HE De-ping. Performance of hollow cylindrical sandwich with high specific strength porous Al alloy core under compression [J]. Transactions of Nonferrous Metals Society of China, 2004, 14(3): 385-390.
(Edited by FANG Jing-hua)
Foundation item: Project(200412)supported by the Nippon Sheet Glass Foundation, Japan
Corresponding author: FENG Yi; Tel: +86-551-2902557; Fax: +86-551-2901362; E-mail: fy123@mail.hf.ah.cn
DOI: 10.1016/S1003-6326(09)60308-3