
Simulation of sheet metal extrusion processes with
Arbitrary Lagrangian-Eulerian method
ZHUANG Xin-cun(庄新村), ZHAO Zhen(赵 震), XIANG Hua(向 华), LI Cong-xin(李从心)
National Engineering Research Center of Die and Mold CAD, Shanghai Jiao Tong University, Shanghai 200030, China
Received 17 January 2007; accepted 14 May 2007
Abstract: An Arbitrary Lagrangian-Eulerian(ALE) method was employed to simulate the sheet metal extrusion process, aiming at avoiding mesh distortion and improving the computational accuracy. The method was implemented based on MSC/MARC by using a fractional step method, i.e. a Lagrangian step followed by an Euler step. The Lagrangian step was a pure updated Lagrangian calculation and the Euler step was performed using mesh smoothing and remapping scheme. Due to the extreme distortion of deformation domain, it was almost impossible to complete the whole simulation with only one mesh topology. Therefore, global remeshing combined with the ALE method was used in the simulation work. Based on the numerical model of the process, some deformation features of the sheet metal extrusion process, such as distribution of localized equivalent plastic strain, and shrinkage cavity, were revealed. Furthermore, the differences between conventional extrusion and sheet metal extrusion process were also analyzed.
Key words: sheet metal forming; Arbitrary Lagrangian-Eulerian method; extrusion; mesh smoothing; remapping
1 Introduction
Along with the development of the traditional fine-blanking process[1], the combined forming process, including fine-blanking, forming and stamping(FFS), has been developed rapidly in recent years especially for thick sheet metal. The combined sheet metal extrusion and fine-blanking process is a typical one of them, and applied to reach functional parts for various industry needs. There are two typical characteristics in combined sheet metal extrusion and fine-blanking process: 1) fine-blanking whose deformation mechanism is different from that of the conventional blanking; 2) sheet metal extrusion[2-3], different from the conventional extrusion [4]. It is a further combined process in which the punch penetration and the extrusion take place at the same time. Both of them are large deformation problems where traditional analytical method can not be used to analyze the deformation mechanism. With the continuous development of computer technology and finite element method(FEM), a lot of research[5-8] has been done in the past several decades on the mechanism of fine- blanking process, but fewer research is done on the mechanism of sheet metal extrusion process.
Moreover, Updated Lagrangian(UL) method is generally used to simulate these large deformation problems. Due to the large deformation of the computational domain, the distorted mesh will lead to accuracy loss of the solution and termination of the calculation. Therefore, the UL method is extended with a remeshing procedure, in which the old mesh is replaced by a completely new mesh, and the information on the old mesh is transferred to this new mesh. Since the global remeshing procedure will rapidly increase the total number of degrees of freedom, leading to a prohibitive computational cost and additional computational error, it is not attractive for the problems that need large number of remeshing procedures. An alternative way to simulate these large deformation problems is the Arbitrary Lagrangian-Eulerian(ALE) method[9-10], in which the mesh is not attached to the material particle like Lagrangian method and not fixed in the space like Euler method as well, but can move arbitrarily. Thus, the mesh distortion occurring in large deformation problems can be avoided. The simulation of metal forming processes was done by many researchers, among which LIU et al[11], BENSON[12] and SCHREURS et al[13], WISSELINK et al[14], use fully coupled ALE method[15], semi-coupled one[14] and decoupled one[12-16, 17], respectively.
In this study, the implementation of a decoupled ALE method based on MSC/MARC is discussed and the emphasis is mainly focused on the simulation of sheet metal extrusion process using ALE method. Since it is almost impossible to complete the whole simulation of such a process with only one mesh topology, the remeshing procedure is also combined to counteract the degenerating effect of deformation on the quality of elements in the Lagrangian analysis.
2 Decoupled ALE method
The main idea of ALE method is to separate the material and mesh displacements, which eliminates mesh distortion and entanglement of elements. In ALE method, the mesh can move arbitrarily. Therefore, both the motion of the mesh and the material should be defined. Remapping of state variables is performed with the ALE kinematic formula[18],

where f is an arbitrary function; vi is the material velocity;  is the mesh velocity;
is the mesh velocity;  denotes the time derivative of f with respect to mesh coordinates; and
denotes the time derivative of f with respect to mesh coordinates; and  represents the time derivative of f with respect to material coordinates. The term
represents the time derivative of f with respect to material coordinates. The term  is called the convective velocity.
is called the convective velocity.
The discretized governing equation[12] in the ALE method can be written in a general form as follows:

where Km is stiffness matrix related to material displacement vector; Kr is stiffness matrix related to mesh displacement vector; U is material displacement vector; Ur is mesh displacement vector; R is external load vector; and F is internal force vector. Eqn.(2) shows that the material displacements and the mesh displacements are coupled with material displacements, as a result, the number of equations to be solved is doubled. In this case, supplementary equations are required to solve the equilibrium equation.
Another strategy called the fractional step method has been developed based on the commercial finite element code, MSC/MARC, to decouple mesh displacements and material displacements in the ALE method. To solve the equilibrium equations by this technique, two steps are considered. A Lagrangian step is followed by an Euler step. In the Lagrangian step, the governing equations to fulfill equilibrium and obtain the material displacements are solved. In the Euler step, a new mesh with the same topology is generated for the deformed domain to obtain the mesh displacements. All kinematic and static variables are then transferred from the distorted mesh to the new mesh. The flow chart of this scheme is shown in Fig.1.

Fig.1 Flow chart of decoupled ALE scheme
2.1 Lagrangian step
In Lagrangian step, the configuration at time t is adopted as the reference state for the evaluation of the deformation in the interval (t, t+Δt):

Consequently, the finite-element mesh moves through space with the deforming material. Therefore, the changing shape of the formed product can be followed easily. The history-dependent field variables, such as strain, stress and damage, can be updated in a straight-forward manner.
The Lagrangian step of the decoupled ALE method can be easily implemented in the existing Lagrangian program source code for large deformation problem.
2.2 Euler step
The key issues in the Euler step include mesh smoothing and the remapping of state variables between the two meshes.
2.2.1 Mesh smoothing
After the Lagrangian step, the nodes are moved to limit the element distortion. Unlike the classical remeshing techniques, the mesh smoothing procedure is performed while the topology of the initial mesh can be preserved. It is explicit, cheap and needs less computational efforts[19].
The node positions are determined by using a volume smoothing algorithm. Each node is relocated by computing a volume weighted average of the element centres in the elements surrounding the node, as illustrated in Fig.2.

Fig.2 Node relocation
The location of node n is determined as

where  is the position vector of the eth element centre;
is the position vector of the eth element centre;  is the position vector of the kth node of the eth element; and ne is the node number of the eth element.
is the position vector of the kth node of the eth element; and ne is the node number of the eth element.

where  is the position vector of node n;
is the position vector of node n; 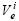 is the volume of the surrounding eth element; ns is the number of surrounding elements.
is the volume of the surrounding eth element; ns is the number of surrounding elements.
2.2.2 Remapping of state variables
After the mesh smoothing, the state variables at the integration point 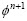 on the new mesh at time
on the new mesh at time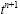 has to be determined from their values at the integration point on the old mesh. The remapping procedure must guarantee the state variable conservation during the mesh motion. Each state variable must remain unchanged during the advection step[20]:
has to be determined from their values at the integration point on the old mesh. The remapping procedure must guarantee the state variable conservation during the mesh motion. Each state variable must remain unchanged during the advection step[20]:

where w is the velocity of the mesh motion; x is the material coordinate.
Generally, the state variables are discontinuous across element boundaries. The Discontinuous Galerkin (DG) method enables the solution of Eqn.(6) by taking into account of the discontinuities in the state variable field before and after transportation. A diffusive smoothing procedure, associated with the construction of a continuous field, is thus avoided. Thus, in this ALE framework of sheet metal extrusion, DG method is used for the numerical advection solution in the following schemes:

where 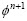 is the value at the integration point after transportation;
is the value at the integration point after transportation; 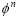 is the value after the Lagrangian step at time
is the value after the Lagrangian step at time 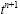 ; u is the mesh nodal displacements;
; u is the mesh nodal displacements;  is the jump term. The discretisation of Eqn.(7) leads to a linear system of equations[17]:
is the jump term. The discretisation of Eqn.(7) leads to a linear system of equations[17]:

This linear system of equations should be solved at each increment step by iteration method.
3 Numerical simulation of sheet metal extrusion process
3.1 FEM model
A schematic view of the model, and geometrical properties and boundary conditions are displayed in Fig.3 and Table 1, respectively. Simulations are performed with different extrusion ratios, in which classical von Mises plasticity with piecewise-linear strain hardening is used. Friction has been described by the Coulomb friction law. The material used in the simulation is SS400 steel, whose detailed properties can be found in Ref.[3]. The model is assumed to be axisymmetric according to the common conditions in production. The tools have been modeled as rigid bodies. Due to the low velocity of punch, the effect of the variance of the strain rate on flow stress is not taken into account[1].

Fig.3 FEM model
Table 1 Simulation parameters

3.2 Results and discussion
3.2.1 Distribution of equivalent strain
Fig.4 shows that a large deformation occurs especially between the edge of the extrusion punch and the edge of the die, where the equivalent plastic strain reaches its maximum.

Fig.4 Distribution of equivalent plastic strain at different stages(D=12 mm, d=8 mm, t=5 mm, material SS400): (a) 30% of thickness; (b) 50% of thickness
By comparing Figs.4(a) with (b), it is clear that the equivalent strain increases gradually when the process continues, which means that the equivalent strain is accumulated during deformation. Furthermore, the equivalent plastic strain in the axis area close to bottom surface of extrusion punch increases severely, which leads to the occurrence of shrinkage cavity. In Fig.4(b), the shrinkage cavity occurs when the extrusion punch penetrates into 50% of material thickness.
Fig.5 shows the distribution of equivalent plastic strain in a conventional forward extrusion with 50% reduction of billet height. In comparison with Fig.4(b), the distribution of equivalent plastic strain in conventional forward extrusion is coincident with sheet metal extrusion in the deformation area except for the area near the edge of extrusion punch and the dead zone. However, in the simulation of conventional forward extrusion, shrinkage cavity does not appear before 50% reduction of billet height, whereas it occurs in sheet metal extrusion with the same process parameters. The reason for this phenomenon may be as follows.

Fig.5 Distribution of equivalent plastic strain (Conventional extrusion, D=12 mm, d=8 mm, t=5 mm, 50% reduction, SS400)
In conventional forward extrusion, due to the circumferential constraint of die, the material can only centralize and flow out through the outlet, which restrains the occurrence of shrinkage cavity. When the remaining height of billet between the extrusion punch and the die shoulder becomes small, there isn’t adequate material near the upper surface of die to flow toward the center. Thus, the lack of the material around the axis has to be replenished by the material close to the center of the bottom surface of the extrusion punch, which makes the shrinkage cavity occur. While in the sheet metal extrusion, the friction force between the material and the die, the subsidiary tensile stress arising from the extrusion punch penetration into the material and the constraint of guide plate will make contribution to the lack of material around the axis. As a result, the material is more difficult to flow toward the center in sheet metal extrusion than in conventional forward extrusion, i.e. the shrinkage cavity is more incidental in the sheet metal extrusion process.
3.2.2 Force—stroke curve prediction
Fig.6 illustrates the force—stroke curves of extru- sion predicted by the decoupled ALE method and UL method with different extrusion ratios (D2/d2). In the meantime, a corresponding curve obtained from the conventional forward extrusion simulation is illustrated as well.

Fig. 6 Force—stroke curves
Fig.6 indicates that the predicted values of the extrusion force using ALE and UL method for the same extrusion ratio are quite close. The curve obtained by UL method is generated by polynomial fit to the numerical data, while the one from ALE method is generated bydata point connection directly. It is clear that the curve obtained by ALE method can well represent the whole extrusion force curve.
For the different extrusion ratios, from the simulation results, it can be concluded that the larger the extrusion ratio, the severer the mesh distortion is and the deeper the shrinkage cavity will be obtained. Furthermore, the larger extrusion force will be acquired. From the force—stroke curve, the tendency for different extrusion ratios is quite similar.
Considering the force—stroke curve of conventional extrusion, the force increases tremendously and reaches a peak value at the first stage. Then it does not change apparently, which means that the steady-state conditions prevail. However, due to the fact that not only extrusion but also penetration occurs in the sheet metal extrusion process, the force value obtained in sheet metal extrusion process is larger than that in the conventional extrusion at the same extrusion ratio. Additionally, different from the tendency of conventional extrusion force—stroke curve, the value continually increases during the whole process.
4 Conclusions
1) The ALE method combined with remeshing technology appears to be capable of handling large, localized deformations occurred in sheet metal extrusion.
2) Based on the distribution of equivalent plastic strain in different stages, large localized deformation is observed between the edge of the extrusion punch and the edge of the die. The area located at the axisymmetric center close to the extrusion punch suffers larger deformation during further deformation.
3) The larger the extrusion ratio, the severer the mesh distortion is and the deeper the shrinkage cavity appears.
4) Due to the occurrence of extrusion and penetration in the sheet metal extrusion process, sheet metal extrusion is different from the conventional extrusion not only in the force—stroke curve, but also in the formation of shrinkage cavity. The shrinkage cavity is incidental in the sheet metal extrusion.
References
[1] LANGE K, BIRZER F, MUKHOTY A, HOFEL P, SINGER H. Cold forming and fineblanking, a handbook on cold processing, material properties, component design [M]. Switzerland: Edelstahlwerke Buderus AG, 1997: 163-174.
[2] CHEN Z H, TANG C Y, CHAN L C, LEE T C. Simulation of the sheet metal extrusion process by the enhanced assumed strain finite element method [J]. Journal of Materials Processing Technology, 1999: 91(1): 250-256.
[3] ZHENG Peng-fei. Finite element analysis of the combined fine blanking and extrusion process [D]. Hong Kong: The Hong Kong Polytechnic University, 2000: 86-116.
[4] MUROTA T, JIMMA T, KATO K. Analysis of axisymmetric extrusion [J]. Bull JSME, 1970, 13: 1366-1381.
[5] LEE T C, CHAN L C, ZHENG P F. Application of the finite-element deformation method in the fine blanking process [J]. Journal of Materials Processing Technology, 1997, 63(1/3): 744-749.
[6] LEE T C, CHAN L C, WU B J. Straining behaviour in blanking process-fine blanking vs conventional blanking [J]. Journal of Materials Processing Technology, 1995, 48(1): 105-111.
[7] KWAK T S, KIM Y J, BAE W B. Finite element analysis on the effect of die clearance on shear planes in fine blanking [J]. Journal of Materials Processing Technology, 2002, 130/131: 462-468.
[8] LI Yu-ming, PENG Ying-hong. Fine-blanking process simulation by rigid viscous-plastic FEM coupled with void damage [J]. Finite Elements in Analysis and Design, 2003, 39(5/6): 457-472.
[9] DONEA J. Arbitrary Lagrangian-Eulerian finite element methods [M]. North-Holland, Amsterdam, 1983: 474-516.
[10] TONG Long-chang. FE simulation of bulk forming processes with a mixed Eulerian-Lagrangian formulation [D]. Zurich: Swiss Federal Institute of Technology, 1995, 18-29.
[11] LIU W K, CHANG H, CHEN J S, BELYTSCHKO T. Arbitrary Lagrangian-Eulerian Petrov-Galerkin finite elements for nonlinear continua [J]. Computer Methods in Applied Mechanics and Engineering, 1988, 68(3): 259-310.
[12] BENSON D J. An efficient, accurate, simple ALE method for nonlinear finite element programs [J]. Computer Methods in Applied Mechanics and Engineering, 1989, 72(3): 305-350.
[13] SCHREURS P J G, VELDPAUS F E, BREKELMANS W A M. Simulation of forming processes using the Arbitrary Eulerian- Lagrangian formulation [J]. Computer Methods in Applied Mechanics and Engineering, 1986, 58(1): 19-36.
[14] WISSELINK H H, HUETINK J. 3D FEM simulation of stationary metal forming processes with applications to slitting and rolling [J]. Journal of Materials Processing Technology, 2004, 148(3): 328-341.
[15] GADALA M S, WANG J I N. Simulation of metal forming processes with finite element methods [J]. International Journal for Numerical Methods in Engineering, 1999, 44(10): 1397-1428.
[16] OLOVSSON L, NILSSON L, SIMONSSON K. An ALE formulation for the solution of two-dimensional metal cutting problems [J]. Computers and Structures, 1999, 72(4/5): 497-507.
[17] BROKKEN D, BREKELMANS W A M, BAAIJENS F P T. Predicting the shape of blanked products: A finite element approach [J]. Journal of Materials Processing Technology, 2000, 103(1): 51-56.
[18] HUGHES T J R, LIU W K, ZIMMERMANN T K. Lagrangian-Eulerian finite element formulation for incompressible viscous flows [J]. Computer Methods in Applied Mechanics and Engineering, 1981, 29(3): 329-349.
[19] YUAN D I, TADANOBU S. Remapping scheme in ALE method for Liquefaction Simulation [C]//16th ASCE Engineering Mechanics Conference. Seattle: University of Washington, 2003: 1-12..
[20] KHADKE A, GHOSH S, LI M. Numerical simulations and design of shearing process for aluminum alloys [J]. Transaction of the ASME, 2005, 127(3): 612-621.
Foundation item: Project(50505027) supported by the National Natural Science Foundation of China; Project(20070248056) supported by the Research Fund for the Doctoral Program of Higher Education of China
Corresponding author: ZHAO Zhen; Tel: +86-21-62813430-8116; E-mail: zzhao@sjtu.edu.cn
(Edited by YANG Bing)