Adomian decomposition method simulation of von Kármán swrling bioconvection nanofluid flow
来源期刊:中南大学学报(英文版)2019年第10期
论文作者:M D SHAMSHUDDIN S R MISHRA O ANWAR BEG A KADIR
文章页码:2797 - 2813
Key words:nanofluids; bioconvection; rotating disk bioreactors; von Kármán swirling flow; Stefan blowing; Adomian decomposition method (ADM)
Abstract: The study reveals analytically on the 3-dimensional viscous time-dependent gyrotactic bioconvection in swirling nanofluid flow past from a rotating disk. It is known that the deformation of the disk is along the radial direction. In addition to that Stefan blowing is considered. The Buongiorno nanofluid model is taken care of assuming the fluid to be dilute and we find Brownian motion and thermophoresis have dominant role on nanoscale unit. The primitive mass conservation equation, radial, tangential and axial momentum, heat, nano-particle concentration and micro-organism density function are developed in a cylindrical polar coordinate system with appropriate wall (disk surface) and free stream boundary conditions. This highly nonlinear, strongly coupled system of unsteady partial differential equations is normalized with the classical von Kármán and other transformations to render the boundary value problem into an ordinary differential system. The emerging 11th order system features an extensive range of dimensionless flow parameters, i.e., disk stretching rate, Brownian motion, thermophoresis, bioconvection Lewis number, unsteadiness parameter, ordinary Lewis number, Prandtl number, mass convective Biot number, Péclet number and Stefan blowing parameter. Solutions of the system are obtained with developed semi-analytical technique, i.e., Adomian decomposition method. Validation of the said problem is also conducted with earlier literature computed by Runge-Kutta shooting technique.
Cite this article as: M D SHAMSHUDDIN, S R MISHRA, O ANWAR BEG, A KADIR. Adomain decomposition method simulation of vonkármán swrling bioconvection nanofluid flow [J]. Journal of Central South University, 2019, 26(10): 2797-2813. DOI: https://doi.org/10.1007/s11771-019-4214-4.

J. Cent. South Univ. (2019) 26: 2797-2813
DOI: https://doi.org/10.1007/s11771-019-4214-4
M D SHAMSHUDDIN1, S R MISHRA2, O ANWAR BEG3, A KADIR3
1. Department of Mathematics, Vaagdevi College of Engineering, Warangal, Telangana, India;
2. Department of Mathematics, Siksha ‘O’Anusandhan Deemed to be University, Khandagiri,Bhubaneswar, Odisha, India;
3. Department of Aeronautical and Mechanical Engineering, University of Salford, Manchester,England, UK
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: The study reveals analytically on the 3-dimensional viscous time-dependent gyrotactic bioconvection in swirling nanofluid flow past from a rotating disk. It is known that the deformation of the disk is along the radial direction. In addition to that Stefan blowing is considered. The Buongiorno nanofluid model is taken care of assuming the fluid to be dilute and we find Brownian motion and thermophoresis have dominant role on nanoscale unit. The primitive mass conservation equation, radial, tangential and axial momentum, heat, nano-particle concentration and micro-organism density function are developed in a cylindrical polar coordinate system with appropriate wall (disk surface) and free stream boundary conditions. This highly nonlinear, strongly coupled system of unsteady partial differential equations is normalized with the classical von Kármán and other transformations to render the boundary value problem into an ordinary differential system. The emerging 11th order system features an extensive range of dimensionless flow parameters, i.e., disk stretching rate, Brownian motion, thermophoresis, bioconvection Lewis number, unsteadiness parameter, ordinary Lewis number, Prandtl number, mass convective Biot number, Péclet number and Stefan blowing parameter. Solutions of the system are obtained with developed semi-analytical technique, i.e., Adomian decomposition method. Validation of the said problem is also conducted with earlier literature computed by Runge-Kutta shooting technique.
Key words: nanofluids; bioconvection; rotating disk bioreactors; von Kármán swirling flow; Stefan blowing; Adomian decomposition method (ADM)
Cite this article as: M D SHAMSHUDDIN, S R MISHRA, O ANWAR BEG, A KADIR. Adomain decomposition method simulation of vonkármán swrling bioconvection nanofluid flow [J]. Journal of Central South University, 2019, 26(10): 2797-2813. DOI: https://doi.org/10.1007/s11771-019-4214-4.
1 Introduction
External heat and/or mass transfer from rotating bodies has received considerable attention in engineering sciences. Such flows feature centrifugal forces which can dramatically modify heat and mass transfer rates at the boundary (solid surface). When strong buoyancy forces are present, the regime becomes a natural convection one. In the absence of buoyancy forces, forced convection is present. Heat transfer is generally analyzed based on the Fourier heat conduction equation and mass transfer via the Fickian diffusion equation. Many different investigations of rotating flows have been communicated over a wide spectrum of geometrical configurations including cones, ellipses, spheres, cylinders and disks and at different rates of rotation from very slow to extremely high speed. MA et al [1] investigated theoretically and experimentally the species diffusion in a rotating cylinder. Further MOHANTY et al [2] studied on cylinders, ANWAR BEG et al [3] on thermo-magnetic free convection boundary layers from a spinning cone in permeable media, SUBHASHINI et al [4] on compressible heat and mass transfer from a spinning sphere (using finite difference methods) and TAKHAR and WHITELAW [5] on asymptotic convection from a rotating sphere. An important geometry in various biochemical and medical processes is the rotating disk apparatus. This is also deployed in petroleum engineering as a mechanism for evaluating the kinetics of heterogeneous reactions [6]. The swirling flow from rotating disks also arises in rotary atomization, photocatalytic fuel cells (RDPFCs) [7] and gas absorption dynamics [8]. The fluid mechanics of rotating disk flow was first evaluated in a monumental study by von KARMAN [9] who introduced his famous set of transformations rendering the Navier-Stokes equations into ordinary differential form. Many studies were communicated subsequently which are summarized in Greenspan [10]. Analyses of heat and mass transfer in von KARMAN flows have been lucidly reviewed more recently by SEHVCHUK [11]. Many interesting studies have been conducted focused on either heat, mass or combined heat and mass transfer for both Newtonian and non- Newtonian fluids with multi-physical and chemical effects present.These studies have been communicated by GAMBARYAN-ROISMAN and STEPHAN [12] (considering wall topography and thermo capillary i.e., surface tension effects), HELCIG and WIESCHE [13] (experimental work considering both air and water).
Recently, nanotechnology is an advanced area of research in engineering. Therefore, CHOI [14] initiated the pioneer work on nanofluids which contribute a emerging role in fluid dynamics due to significant achievements than that of conventional base fluids such as water, kerosene, air, etc, with various nano-particles. The suspensions of these nanoparticles have enhanced properties on thermal conductivity and viscosity. Nowadays, nanofluids have vast use in biomedical technology. Moreover, nanofluid research and development have extensive experimental investigations. Further, BUONGIORNO [15] developed a popular model on nanofluid. This suggests the contribution of dynamic role of thermophoresis and Brownian motion on the enhancement of conductivity. DAS et al [16] proposed advanced diverse applications and simulations of nanofluids. Rotating nanofluid flows have more recently garnered some attention. These combine the theory of rotating fluids with nanofluid properties. Use of similar flows which helps in reduction of maximum coordinates for non-linear coupled PDEs into systems of ODEs and they solved either analytically or numerically. TURKYILMAZOGLU [17] in his proposed study on nanofluid considering water as a base fluid and along with several nanoparticles such as Cu, Ag, CuO, etc. is imposed and for the solution he used spectral Chebyshev collocation method and concluded that copper nanofluids is best for heat transfer. Influence of solutal concentration on swirling disk flow of magnetite ferrous oxide was studied by HAYAT et al [18] and proposed homotopy series solutions. RAZA et al [19] computed magnetized three-dimensional nanofluid flow in a rotating medium using the Buongiorno model.
Bioconvection refers to continuous formation of suspensions of swimming micro-organisms, e.g., algae and bacteria. Steady patterns and also the formation of patterns in gyrotatic bioconvection can be strongly regulated by torques. Very sophisticated hydrodynamic models have been developed for the propulsion of such microorganism. Rotating bioconvection has also received considerable interest in recent years. For example, CHAKRABORTY et al [20] used bvpc function of Matlab to examine impacts of magnetic field and convective boundary conditions. Rotating bio convection in nanofluids is also a rich and emerging area of nano-bio-fluid dynamics which holds some promise for energy systems and medical applications. By suspending micro-organisms in nanofluids, both thermal enhancement benefits and green engineering benefits may be achieved simultaneously. This has inspired some recent activity in mathematical models of nanofluid bio convection in rotating systems. XUN et al [21] used the MATLAB bvp4c ordinary differential equation solver to compute the nanofluid bio convection in a rotating channel with temperature-dependent viscosity and thermal variable conductivity. They observed that local Nusselt number and wall motile microorganisms flux are more significantly modified by thermal conductivity variation parameter and that larger values of bio convection Péclet number result in an accumulation of motile microorganisms in the core region of the channel. They further noted that this accumulation is intensified with thermophoresis but inhibited with Brownian motion.
In the above studies, whether they involve nanofluids or bio convection or both, the boundary walls have generally been rigid. However, deformable boundaries are increasingly featuring in modern biomedical designs. For example, microbial cell engaged in imposing bio convection in nanofluids are exploring stretching (and contracting) walls which can dramatically influence microorganism impacts heavily on fuel cell efficiency and sustainability. Recently, ANWAR BEG et al [22] worked on stretching/shrinking) in a deformable channel as a model for bio convection nanofluid fuel cell. They showed that doping of the base fluid with nanoparticles and suspended gyrotactic microorganisms collectively enhances both nanoparticle and motile microorganism mass wall flux (Sherwood numbers) and generally, a stable mixture (suspension) is attained. Several researcher [23-26] have proposed their work on bio convection nanofluid transport, in various model considering different nanofluids like magnetite- Fe3O4 ferro-nanofluid, CNT nanofluid etc. Other studies include AHMED et al [27] (for magneto-nanofluid squeezed between parallel disk), MUSHTAQ and MUSTAFA [28] (for nanofluids with convective mass wall conditions) and CHEN et al [29] (considering power-law stretching of the disk for gyrotactic bio Nano convection flow). From the aforesaid studies, it is noted that stretching disk is useful for the distribution of temperature, nanoparticle concentration and motile micro-organism density.
In the current study, we re-visit the recent investigation by LATIFF et al [30] to generalize their analysis of time-dependent von Kármán swirl bio convection nanofluid flow from a rotating disk with Stefan blowing (wall mass transfer) and radial disk stretching. Thermophile (“heat loving”) gyrotactic micro-organism bio convection is addressed. Stefan blowing is a more sophisticated mechanism for studying wall mass transfer than conventional transpiration (injection velocity) models. The present nonlinear coupled partial differential equation boundary value problem is normalized with appropriate transformations into ordinary differential form. An optimized Adomian decomposition method based on power-series expansions is utilized to solve the dimensionless governing equations. The results of LATIFF et al [30] are verified. Extensive new computations are also presented which provide a wider insight into the mechanisms of transport in the boundary layer swirl regime. The simulations presented are relevant to biofilm rotating disk reactors modified with nano-particle doping. Furthermore, these studies provide a useful benchmark for more complex computational fluid dynamics analysis with commercial codes (e.g., ANSYS, FLUENT) which will be of benefit to bio-nano-fuel cell designers.
2 Mathematical von Kármán swirl bioconvection nanofluid model
Considered an unsteady 3D bioconvection nanofluid over a rotating disk in a cylindrical polar coordinate system (r, q, z) with velocity components (u, v, w). The nanofluid is assumed to be a dilute suspension with a homogenous distribution of gyrotatic micro- organisms. Gyrotaxis is swimming directed by the balance between the torque due to gravity acting on a bottom-heavy cell and the torque due to viscous forces arising from local shear flows. In the present model, the micro-organisms do not interact with the nano-particles. Similar to nanofluids, in suspensions of motile microorganisms that exhibit spontaneous formation of flow patterns (this phenomenon is called bioconvection) physical laws that govern smaller scales lead to a phenomenon visible on a larger scale. At the disk surface, no-slip boundary conditions are considered with Stefan’s blowing and simulated along axial velocity component. From Figure 1, the species concentration of nanofluid at the disk surface follow Cf>Cw>C∞ to impose mass convective conditions. Due to various nanoparticle concentration near to the disk concentration, wall and ambient states needs mass transfer coefficient hm. From the aforesaid assumptions, the governing equations for continuity, radial, circumferential (azimuthal) and axial momentum, thermal energy (heat), nanoparticle concentration (species volume fraction)and motile microorganism density number, in cylindrical coordinates are as follows [30]:
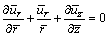 (1)
(1)
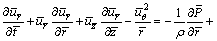
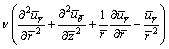 (2)
(2)
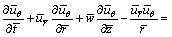
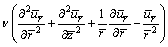 (3)
(3)

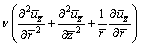 (4)
(4)
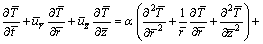
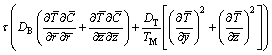 (5)
(5)
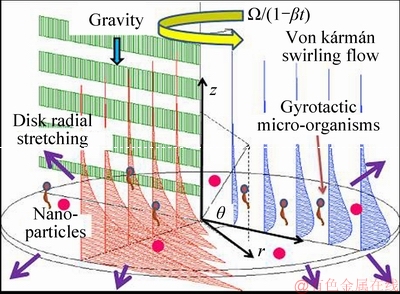
Figure 1 Flow configuration of problem
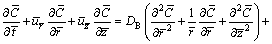
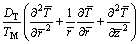 (6)
(6)
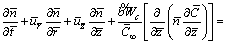
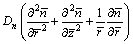 (7)
(7)
Following WATSON and WANG [31], tangential velocity,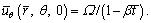 Stretching velocity [23] along the radial direction is
Stretching velocity [23] along the radial direction is 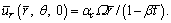 The initial and boundary conditions are [30]:
The initial and boundary conditions are [30]:
 (8)
(8)
where Ω is the angular velocity, β is the unsteadiness parameter (β≠0) and (β=0) is associated to steady state, and αc is the stretching rate in radial direction.
Following LATIFF et al [30], we have adopted the similarity transformations as:
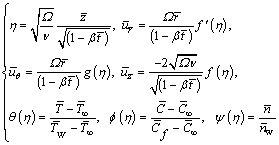 (9)
(9)
Assimilating the similarity variables (9) into Eqs. (2)–(7) and (8) yields the set of ODEs with boundary conditions as:
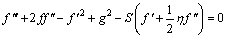 (10)
(10)
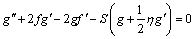 (11)
(11)
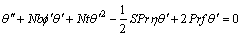 (12)
(12)
 (13)
(13)
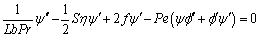 (14)
(14)
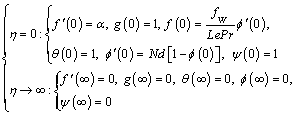 (15)
(15)
where the time dependent parameter, S=β/Ω, Prandtl number, Pr=v/α, Brownian motion, thermophoresis parameter,
thermophoresis parameter, 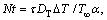 Lewis number, Le=α/DB bio- convection Lewis number, Lb=α/DM, bio-conv-ection Peclet number,
Lewis number, Le=α/DB bio- convection Lewis number, Lb=α/DM, bio-conv-ection Peclet number,  Stefan blowing parameter,
Stefan blowing parameter, 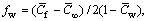 Biot number,
Biot number, 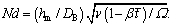
Following the characteristics of engineering coefficients are as follows:
 (16)
(16)
From Eq. (16), the radial 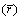 direction shear stress is:
direction shear stress is:
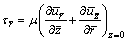 (17)
(17)
Shear stress in tangential (θ) direction:
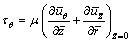 (18)
(18)
Surface heat flux:
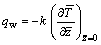 (19)
(19)
Surface mass flux:
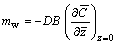 (20)
(20)
Surface motile microorganism flux:
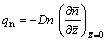 (21)
(21)
Introducing Eqs. (9) and (17)-(21) into Eq. (16), we get:
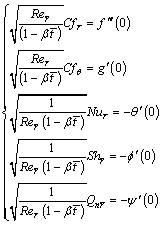 (22)
(22)
Here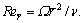
3 Adomian decomposition solution of boundary value problem
The higher order coupled ODEs (10)-(14) with boundary conditions (15) does not admit exact analytical solutions. Many such techniques are available for micro and nano-scale flows including finite element techniques [32] and shooting quadrature [33]. In recent years, another group of semi-numerical methods have also become popular. These power-series expansions use the codes of MAPLE, MATHEMATICA, MATLAB that we can compute numerically, including homotopy methods (DANIEL and DANIEL [34])) and (the successive Taylor series linearization method (STSLM) utilizing Chebyshev interpolating polynomials and Gauss–Lobatto collocation, as employed by BHATTI et al [35]. Finally, ADOMIAN [36] use a polynomial expansion to get higher accuracy result. Adomian decomposition method (ADM) is employed for nanofluid and multi- physical fluid dynamics problems. ADM is an analytical approximation without using linearization, or perturbation methods. ADM gives an infinite series solution and utilizes recursive relations [37, 38]. Eqs. (10)-(14) are first rearranged as:
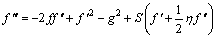 (23)
(23)
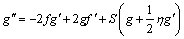 (24)
(24)
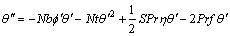 (25)
(25)
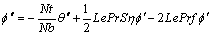 (26)
(26)
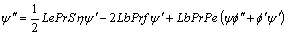 (27)
(27)
Applying ADM, we introduce 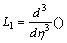 and
and 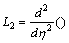 with inverse operators
with inverse operators 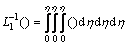 and
and Thus Eqs. (23)-(27) become:
Thus Eqs. (23)-(27) become:
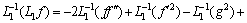
 (28)
(28)
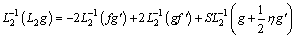 (29)
(29)
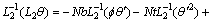
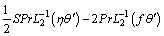 (30)
(30)
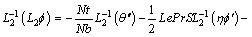
 (31)
(31)
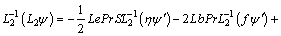
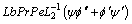 (32)
(32)
The unknown functions f(η), g(η), θ(η), f(η) and ψ(η) can be expressed as infinite series of the form:
 (33)
(33)
The remaining terms of Eqs. (28)-(32) can be expressed as:
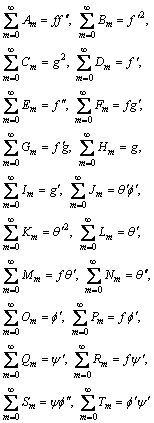 (34)
(34)
Here recursive formula is used to find all the components. The exact solutions of Eqs. (23)-(27) are
 (35)
(35)
Therefore, the RHSs of Eqs. (28)-(32) can be written as:
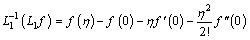 (36)
(36)
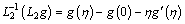 (37)
(37)
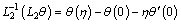 (38)
(38)
 (39)
(39)
 (40)
(40)
From Eq. (15), invoking the boundary conditions:
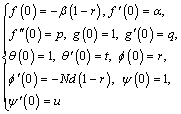 (41)
(41)
The solutions of Eqs. (23)-(27) may therefore be written as

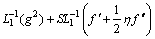 (42)
(42)
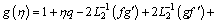
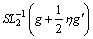 (43)
(43)
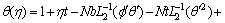
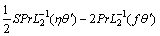 (44)
(44)

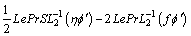 (45)
(45)

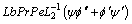 (46)
(46)
Here it is necessary to evaluate the unknowns p, q, r, t, u. Utilizing Eqs. (42)-(46) the initial imposed solutions along with higher order recursive solutions are
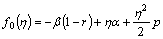 (47)
(47)
 (48)
(48)
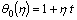 (49)
(49)
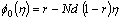 (50)
(50)
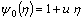 (51)
(51)
and
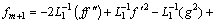
 (52)
(52)
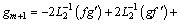
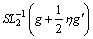 (53)
(53)
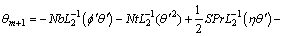
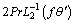 (54)
(54)
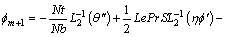
 (55)
(55)
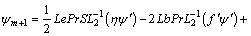
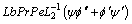 (56)
(56)
Using m=0, 1, 2 in Eqs. (52)-(56) with the aid of Eq. (34), the solutions of Eqs. (23)-(27) expressed in Eq. (33) emerge as follows:

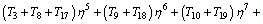
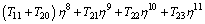 (57)
(57)
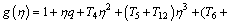
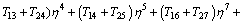
 (58)
(58)
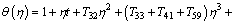
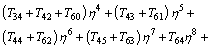
 (59)
(59)
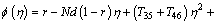

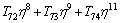 (60)
(60)


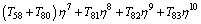 (61)
(61)
The values of the notations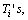 i=1-83 are summarized in the Appendix.
i=1-83 are summarized in the Appendix.
4 Validation of ADM solutions
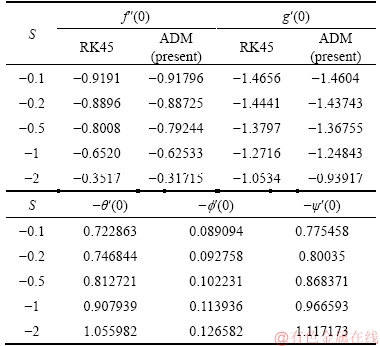
The assumed values f″(0)=p, g′(0)=q, f(0)=r, θ′(0)=t and ψ′(0)=u are calculated by using symbolic software MATLAB [39] with code bvp4c. The conformity of ADM with earlier, the work of LATIFF et al [30] used Runge-Kutta quadrature rule. In the presence of unsteadiness parameter, S (S<0) various cases are taken care of, such as, a non-deformable disk (a=0) and a radially stretching disk (a=1.0). These values are presented in Tables 1 and 2 for the radial local skin friction f″(0), local circumferential skin friction g′(0), local Nusselt number -θ′(0), local Sherwood number or nano-particle wall concentration gradient -f′(0) and motile micro-organism wall mass flux -ψ′(0), i.e., number density gradient function). The confidence of ADM is justified due to good correlation.
Table 1 Comparison of results when α=0

Table 2 Comparison of results when α=1.0
5 ADM results and interpretation
Selected ADM solutions for f ′(η), g(η), θ(η), f(η), ψ(η), f ″(0), g′(0), -θ′(0),-f′(0) and -ψ′(0) are given. For brevity, our discussion restricted to the influences of stretching (S), unsteadiness (a), and Stefan blowing/suction (fw). At the time of computation, we have considered as Nd=0.4, Nb=Nt=10-7, Le=Lb=Pe=1, α=0.2, Pr=0.7. These corresponds to air-based nanofluid with weak Brownian motion, thermophoresis and equal nano- particle, micro-organisms and thermal diffusivities. The current simulations apply to air-based rotating bio-nano rotating disk flows. (Pr=0.7 for the base fluid of air). The data selected for nanofluid properties are based on Ref. [16].
Results are visualized in Figures 2-16 and Tables 3-4.
LATIFF et al [30] rapt principally on the influence of the radial stretching parameter (α) and to a lesser extent on the unsteadiness parameter (S). Herein we address both and consider significantly stronger blowing effects. Figures 2-6 illustrate the collective influence of unsteadiness parameter (S) and Stefan blowing/suction (fw) on radial velocity, circumferential velocity, temperature, nano-particle concentration and motile microorganism density number. It is important to note that suction is not generated by perforations at the disk surface. The suction effect (reverse Stefan blowing) is associated with mass flux from the free stream of the boundary layer to the rotating disk surface. Similarly, the Stefan blowing is caused by the mass flux from rotating disk surface to the free stream. Additionally, it is pertinent to mention that weak radial disk stretching is prescribed (a=0.2). Figure 2 clearly shows that with strong suction (fw<0) radial flow deceleration is induced whereas very strong radial flow acceleration is generated with strong blowing (fw>0). The swirling flow mobilized by the disk rotation acts as a pump drawing fluid inward which spreads radially outwards over the disk face. This assists in momentum development in the radial direction. The presence of suction causes adherence of the boundary layer to disk surface whereas blowing results in the opposite effect. With weak unsteadiness (S=-1), i.e., weak disk deceleration, there is a more gradual evolution in radial velocity profiles from the disk surface (η=0) to the free stream than for strong disk deceleration (S=-10). A very strong overshoot arises for the case of strong disk deceleration with strong blowing (S=-10, fw=2). This generates the maximum radial velocity. With absence of suction or blowing, the peak is reduced and displaced closer to the wall and is in fact almost eliminated with suction (S=-10, fw=2). For the weak disk deceleration case (S=-1), a similar effect is produced although peak radial velocity magnitudes are somewhat lower. Negative radial velocity (back flow) is only induced for a short zone further from the disk surface with strong deceleration. The smoothness of the profile confirms the convergence of the ADM solutions for infinite boundary conditions imposed herewith. Figure 3 depicts the evolution in circumferential (azimuthal) velocity with transverse coordinate and various deceleration, i.e., unsteadiness (S) and blowing/suction (fw) parameters. There is a distinct absence of velocity overshoots for any combination of parameters. With weak disk deceleration, the circumferential velocity decays monotonically from the disk surface to the free stream, whether suction or blowing is present. However, with strong disk deceleration, there is a much sharper decay in circumferential velocity from the disk surface resulting in backflow nearby disk. However, beside further progression into boundary layer, there is a re-surge in circumferential velocity which eventually vanishes in the free stream. The circumferential (and radial velocity) distributions are generally also consistent with numerous other von Kármán swirling flow studies, notably EVANS [40] who did not consider disk deceleration and more recently FANG et al [41], WATSON et al [31]. Furthermore, the presence of nano- particles and micro-organisms therefore does not dramatically alter the classical velocity distributions in von Kármán swirling flow. Figure 4 depicts the response in temperature distribution to unsteadiness (S) and Stefan blowing/suction (fw) effects. Substantially lower values are computed with strong disk deceleration (S=-10) compared with weak disk acceleration (S=-1) indicating that thinner thermal boundary layer. As anticipated, the temperatures are enhanced with Stefan blowing whereas they are reduced with suction.Additionally, there is a greater spread profiles at weaker deceleration compared with stronger deceleration.The diffusion of heat energy in the boundary layer dominion is clearly impacted with retardation in the disk spin and mass transfer conditions. Even though the regime is forced convection and there are no buoyancy effects, there is still significant coupling of the radial momentum (10) and energy Eq. (12) via the term 2Prfθ′ in the latter. The unsteadiness parameter (S) also appears in many terms in all the conservation equations, notably in the radial equation in the term in the azimuthal equation in the term
in the azimuthal equation in the term 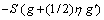 and in the energy equation in the term
and in the energy equation in the term 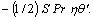 The momenta and temperature fields are therefore very sensitive to adjustment in the unsteadiness parameter and this is reflected in Figures 2-4. A further point of note is shown in Figures 2-4. There is never any intersection of profiles corresponding to a specific unsteadiness value with each other. This trend is not sustained in Figure 5 which displays the influence of unsteadiness and blowing/suction parameter on nano-particle concentration profiles. In addition to that, the profile is partitioned into two distinct layers such as disk region (near and far). In the first region, i.e., 0<η<1, for strong gust, the magnitude of concentration layer is elevated and has a dominating role for weak disk deceleration (S=-1) in comparison with strong disk deceleration (S=-10). Further, in the second region, the effect is opposite, i.e., concentration reduces with the increase in blowing whereas suction slightly enhances it. Again, the profiles deviate for particular value of S when we compare the weak situation with strong situation of disk deceleration. In the present case, we have not discussed the case of S>0. It validates with the mathematical expression presented in Eq. (13),
The momenta and temperature fields are therefore very sensitive to adjustment in the unsteadiness parameter and this is reflected in Figures 2-4. A further point of note is shown in Figures 2-4. There is never any intersection of profiles corresponding to a specific unsteadiness value with each other. This trend is not sustained in Figure 5 which displays the influence of unsteadiness and blowing/suction parameter on nano-particle concentration profiles. In addition to that, the profile is partitioned into two distinct layers such as disk region (near and far). In the first region, i.e., 0<η<1, for strong gust, the magnitude of concentration layer is elevated and has a dominating role for weak disk deceleration (S=-1) in comparison with strong disk deceleration (S=-10). Further, in the second region, the effect is opposite, i.e., concentration reduces with the increase in blowing whereas suction slightly enhances it. Again, the profiles deviate for particular value of S when we compare the weak situation with strong situation of disk deceleration. In the present case, we have not discussed the case of S>0. It validates with the mathematical expression presented in Eq. (13),  and moreover at the time of computation via coupling terms, 2ff′. Figure 6 exhibits the effects of unsteadiness and Stefan blowing/suction on motile micro-organism density profiles for fixed values of various pertinent parameters. Detected that, an increase in blowing inflate micro-organisms effect is reversed in case of suction. Motile micro- organism retards significantly with strong deceleration in comparison with weak disk deceleration. It is also clear from the expression presented in Eq. (14),
and moreover at the time of computation via coupling terms, 2ff′. Figure 6 exhibits the effects of unsteadiness and Stefan blowing/suction on motile micro-organism density profiles for fixed values of various pertinent parameters. Detected that, an increase in blowing inflate micro-organisms effect is reversed in case of suction. Motile micro- organism retards significantly with strong deceleration in comparison with weak disk deceleration. It is also clear from the expression presented in Eq. (14), that micro- organism suppressed directly and via coupling term 2fψ′. Also, notable that there is a hefty mix between the nano-particle species (f) and micro-organism species (y) field via the terms,
that micro- organism suppressed directly and via coupling term 2fψ′. Also, notable that there is a hefty mix between the nano-particle species (f) and micro-organism species (y) field via the terms, 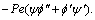
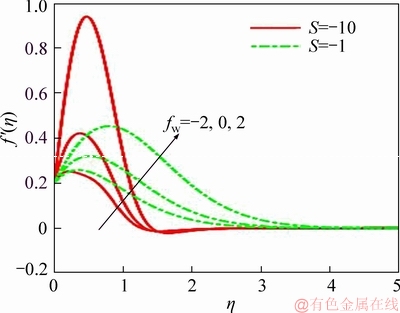
Figure 2 Suction/injection and unsteadiness parameters effect on radial velocity
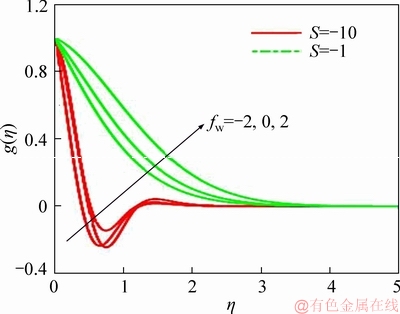
Figure 3 Suction/injection and unsteadiness parameters effect on circumferential velocity
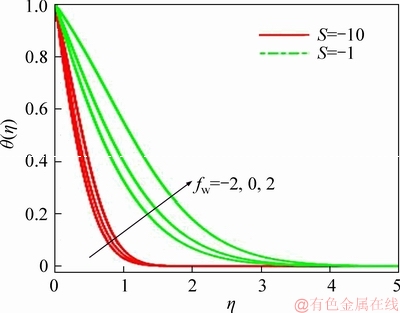
Figure 4 Suction/injection and unsteadiness parameters effect on temperature
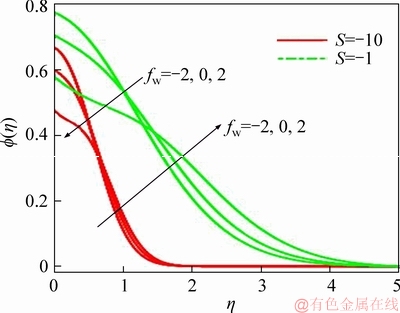
Figure 5 Suction/injection and unsteadiness parameters effect on concentration
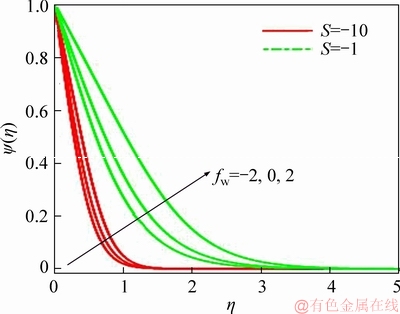
Figure 6 Suction/injection and unsteadiness parameter effect on motile microorganism density number
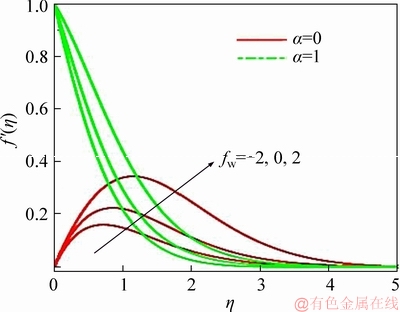
Figure 7 Suction/injection and disk stretching parameters effect on radial velocity
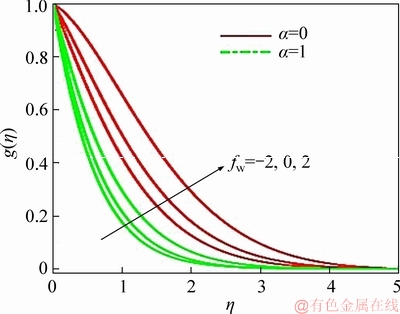
Figure 8 Suction/injection and disk stretching parameters effect on circumferential velocity
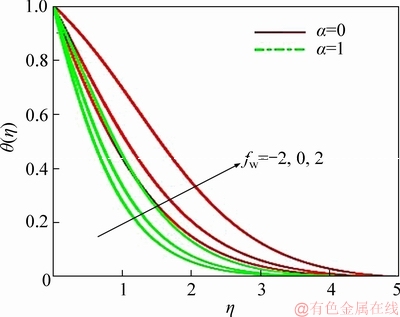
Figure 9 Suction/injection and disk stretching parameters effect on temperature

Figure 10 Suction/injection and disk stretching parameters effect on nanoparticle concentration

Figure 11 Suction/injection and disk stretching parameters effect on motile microorganism
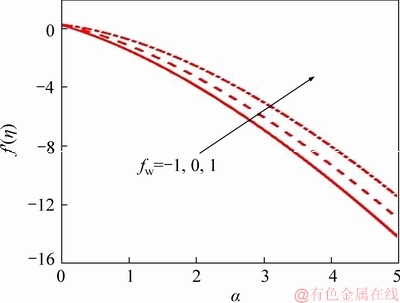
Figure 12 Suction/injection parameter effect on radial skin friction
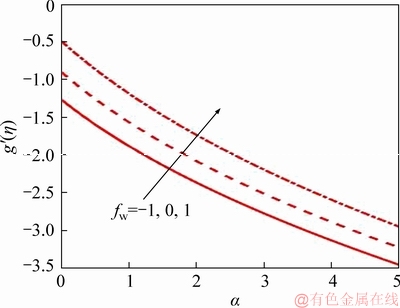
Figure 13 Suction/injection parameter effect on Azimuthal skin friction
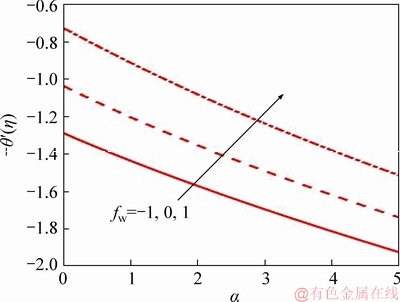
Figure 14 Suction/injection parameter effect on Nusselt number
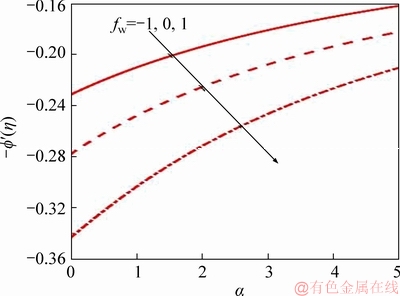
Figure 15 Suction/injection parameter effect on Sherwood number
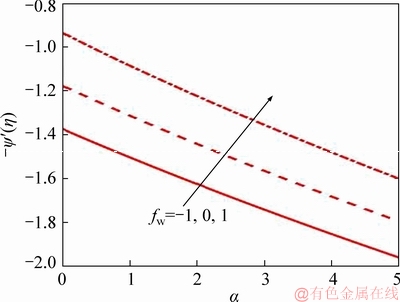
Figure 16 Suction/injection parameter effect on microorganism wall mass flux
Table 3 Values of p, q, t, r and u for Lb=Le=Pe=1, Nt=Nb=10-7, Nd=0.4, α=0.2 and Pr=0.7
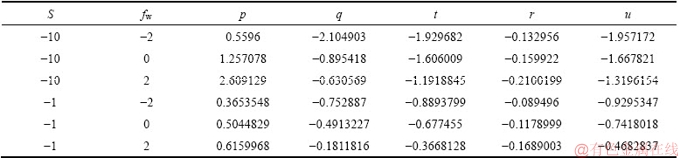
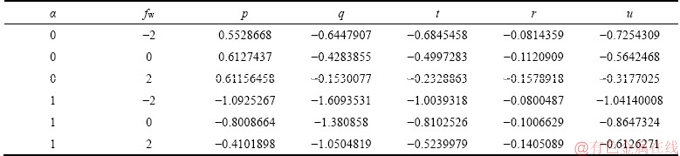
Table 4 Values of p, q, t, r and u for Lb=Le=Pe=1, Nt=Nb=10-7, Nd=0.4, S=-1 and Pr=0.7
Figures 7-11 illustrate the radial velocity, circumferential velocity, temperature, nano-particle concentration and motile micro-organism for various α and fw. A further motivation for the current study was to elaborate in more detail of the findings of LATIFF et al [30] which were limited in interpretation. Radial velocity (Figure 7) is accentuated with disk stretching, i.e., the radial flow is strongly accelerated. However, this is confined to the near-wall zone. The profiles with disk stretching present and absent (α=0) are significantly different. For α>0, the velocity at the surface is non-zero which is presented in Eq. (15). Therefore, the traditional no-slip condition is modified with the particular type of slip condition and suggests decaying in the boundary layer. When α=0, von KARMAN [9] presented their problem with classical no-slip radial velocity boundary condition. This results in the characteristic growth of the radial velocity from zero at the wall to a near-wall peak and subsequent decay into the free stream. In the disk stretching case, Stefan blowing consistently accelerates the radial flow whereas suction decelerates the flow up to considerably large distances from the disk surface; eventually, all profiles converge asymptotically to vanishing radial velocity in free stream. In the non-deformable disk case higher radial velocities are achieved further from the disk surface compared with the stretching case; again, all distributions converge to zero in the free stream. Figure 8 depicts evolution in azimuthal velocity distribution with transverse coordinate, for the case of disk deceleration (S=-0.5). In all cases, decay from the wall to the free stream is maintained. Stretching effect therefore does not influence the topology of circumferential velocity distributions since the parameter a does not arise in the circumferential velocity disk surface (wall) boundary condition in Eq. (15). However, lower circumferential velocity magnitudes are evidently induced with disk stretching. This is attributable to the re-distribution in momentum and the coupling of the radial and azimuthal (circumferential) momentum Eqs. (10) and (11) via the terms +g2 in the former and 2fg′, -2gf′ in the latter. The boost in radial momentum near the disk surface is balanced by depletion in azimuthal momentum, since momentum has to be conserved. The azimuthal flow which is a secondary flow is therefore depleted, which is a predictable quality of swirling flows and studied by many researchers including SHEVCHUK [11], for macroscopic fluids and by TURKYILMAZOGLU [17] for nanofluids. With strong Stefan blowing, the circumferential flow is decelerated owing to assisting momentum development whereas with strong suction it is retarded, irrespective of whether the disk is stretching or not. This pattern is sustained throughout the entire boundary layer regime. Figure 9 illustrates the modification in temperature distribution with the combined effects of blowing/suction parameter (fw) and radial stretching parameter (α). A similar response is computed as with the azimuthal velocity field. Disk stretching is found to reduce temperatures (and thermal boundary layer thickness) whereas without stretching higher temperatures are generated in the boundary layer. The Prandtl number Pr is set as 0.7 (air). Since this parameter represents the ratio of momentum diffusion to thermal diffusion, the latter exceeds the former. This results in greater heat transfer to the disk surface from the body of the nanofluid which manifests in a reduction in temperatures. The disk stretching enhances the radial flow but curtails the azimuthal flow. Therefore, while momentum diffuses faster in the radial field which accelerates the radial flow, this impedes thermal diffusion from the disk surface. Strong blowing however enhances temperatures whereas strong suction decreases them, and this is generally, enforced whether the disk is stretching or not. Figure 10 illustrates the nano-particle concentration profiles for various blowing/suction parameter (fw) and radial stretching parameter (α) values. Significant inter-twining of profiles is observed. With disk stretching and strong Stefan blowing (fw=2), the nano-particle concentrations are initially greater in the vicinity of the disk. Suction (fw=-2) is observed to reduce magnitudes in this zone. However, further from the wall, the absence of disk stretching (α=0) results in enhanced nano- particle concentrations (volume fractions) and furthermore suction is found to boost magnitudes. The nano-particle concentration boundary layer thickness therefore does not exhibit a consistent response to disk stretching or mass transfer effects. Micro-organism density retards with disk stretching whereas in the absence of disk stretching it enhances (Figure 11). The thickness of both the boundary layer for micro-organism density and micro-organism species with greater Stefan blowing consistently since the diffusivity of micro-organism species and nano-particle species equal to momentum diffusivity in Figures 10 and 11.
Figures 12-16 show the variation of different mass transfer parameters (fw) for a=0 on the physical quantities of interest described earlier in Eqs. (17)-(21). It is seen that f″(0) decreases as an increase in α (Figure 12). From Figure 13, azimuthal skin friction g′(0), to diminish with increasing α although upend profiles are computed as compared with f″(0). However, in case of blowing azimuthal skin friction is higher as compared to suction. For the non-deformable disk (a=0), both Figures 12 and 13 radial and azimuthal skin friction are maximum. Figure 14 describes the rate of heat transfer (-θ′(0)) for various disk stretching. Fall in Nusselt number is marked with an increasing disk stretching. It is due to the reason, as increase in stretching in disk thermal diffusion decreases from the boundary layer to the wall. As a result, an increase in suction heat transfer rates retards. Figure 15 displays the Sherwood number which is opposite to that of fluid temperature. Though diffusion of nano-particles is greater which boosts Sherwood number as stretching increases. With no stretching mass transfer rate is minimized and effect is reversed for higher stretching (α=5). However, gust is favorable to reduce Sherwood number whereas suction enhances it. Finally,Figure 16 illustrates the influence of suction or blowing on motile micro-organism wall flux in presence or absence of stretching. The inter- connection is linear between motile micro- organism wall flux and disk stretching rate. In case of α=0, the magnitude is maximum than that of α=5. An increase in fw clearly boosts the -ψ′(0) for all values of the α. Conversely, with strong suction, there is a decrease in -ψ′(0).
Tables 3 and 4 also show the response in f″(0), g′(0), -θ′(0), -f′(0) and -ψ′(0) to a collective variation in respectively, unsteadiness parameter (S) and mass transfer parameter (fw) and stretching rate parameter (α) and mass transfer parameter (fw). Table 4 has already been elaborated via Figures 12-16 and is provided as a benchmark for reader interested in extending the current study. Table 3 shows that with strong disk deceleration, radial skin friction is increased when suction is present whereas it is more dramatically elevated with Stefan blowing. Azimuthal skin friction is however very strongly reduced with disk deceleration and suction and weakly depleted with Stefan blowing. Similarly, -θ′(0), -f′(0) and -ψ′(0) are all reduced more substantially with disk deceleration and suction than with disk deceleration and Stefan blowing.
6 Conclusions
3-dimensional laminar viscous gyrotactic forced bioconvection in swirling dilute nanofluid unsteady mathematical model flow from a rotating disk configuration with convective mass boundary conditions and Stefan blowing. Radial stretching of the disk has been included. The model is inspired by novel developments in nanofluid rotating bio-reactors exploiting specific taxes of thermophile microganisms. Employing the Buongiorno formulation and the Fang-Tao transformations [41], the normalized boundary layer equations for mass, radial and azmiuthal (circumferential) momentum, heat (energy), micro-organism density and nano- particle concentration function derived subject to physically viable wall (disk surface) and free stream boundary conditions. The Adomian decomposition method (ADM) has been implemented with MATLAB symbolic software to solve the emerging high order nonlinear coupled ordinary differential boundary value problem. Verification of solutions has also been included with alidation with earlier Runge-Kutta shooting quadrature solutions. The present analysis has shown that:
1) An increase in stretching parameter along the radial direction decreases all the engineerig coefficients except local Sherwood number of nanoparticles.
2) Thinning in thermal boundary layer is marked due to disk deceleration which accelerates radial flow.
3) Radial and azimuthal flow along with nanoparticle concentration enhances with an increase in Stefan blowing; however, suction causes a reverse effect.
4) An increasein suction is favorable to enhance the local Sherwood number whereas other coefficients. Futher, other physical quantuities of interest redduce.
5) Rapid convergence of the ADM imposed for the said problem shows excellent results in simulating nano-bioconvection fluid dynamics problems.
The Newtonian nanofluids considered in the present problem are taken care of with disk stretching. Future investigations can be obtained by considering various models of non-Newtonian nanofluids. These investigations will also utilize ADM and other numerical techniques (finite element method). Furthermore, wavy geometries for the disk surfaces may be considered [42, 43] as well as thermophysical properties [44] which also constitute interesting extensions to the present work. Porous media [45], onset of bioconvection [46] and specifically water based nanofluid bio convection [47] may also be examined.
Nomenclature
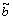
Chemotaxis constant
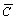
Nanoparticle volume fraction

Fluid concentration

Axial skin friction coefficient
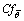
Tangential skin friction coefficient
Cw
Wall concentration
C∞
Free stream concentration
DB
Brownian diffusion coefficient (m2/s)
Dn
Microorganism diffusion coefficient (m2/s)
DT
Thermophoretic diffusion coefficient (m2/s)
f(η)
Axial stream function
fw
Stefan blowing parameter
g(η)
Circumfrential stream function
hm
Convective fluid concentration
Le
Ordinary Lewis number
Lb
Bioconvection Lewis number
mw
Surface mass flux (W/m2)
Nb
Brownian motion parameter
Nd
Biot number
Nt
Thermophoresis parameter

Local Nusselt number
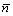
Number of motile microrganism

Motile microorganism at the wall
P
Constant fluid pressure
Pe
Bio convection Peclet number
Pr
Prandtl number
qn
Surface microorganism flux
qw
Wall heat flux (W/m2)
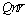
Local wall motile microoganism

Axial coordinate (m)

Local Reynolds number
S
Unsteadiness parameter
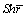
Local Sherwood number
t
Time (s)
T
Nanofluid temperature (K)

Fluid temperature (K)
Tw
Wall temperature (K)
T∞
Free stream temperature (K)
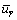
Velocity component along the axis(m/s)
axis(m/s)
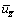
Velocity component along the axis(m/s)
axis(m/s)
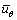
Velocity component along the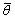 axis(m/s)
axis(m/s)
Wc
Maximum cell swimming speed (m/s)

Coordinate normal to the plate (m)
Greek letters
α
Thermal diffusivity (m2/s)
αc
Strength of disk radial stretching
β
Constant
ψ(η)
Number of motile microrganism
f(η)
Nano particle volume fraction
η
Independent similarity variable
μ
Dynamic viscosity (kg/ms)
θ(η)
Temperature
ρf
Nanofluid density (kg/m3)
τ
Ratio of heat capacity of nanofluid and heat capacity of the fluid
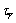
Skin friction in direction (Pa)
direction (Pa)
τθ
Skin friction in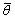 direction (Pa)
direction (Pa)
v
Kinematic viscosity (m2/s)
ψ
Stream function (m2/s)
Ω
Angular velocity
References
[1] MA H T, ZHANG Y F, DENG N. Mass transfer characteristics from a rotating cylinder [C]// HEFAT 2008 6th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics. Pretoria, South Africa, 2008.
[2] MOHANTY A K, TAWFEK A A, PRASAD B V S S. Heat transfer from a rotating cylinder in crossflow [J]. Experimental Thermal and Fluid Science, 1995, 10: 54-61.
[3] ANWAR BEG O, PRASAD V R, VASU B, GORLA R S R. Computational modelling of magnetohydrodynamic convection from a rotating cone in orthotropic Darcian porous media [J]. Journal of Brazilian Society of Mechanical Science Engineering, 2017, 39: 2035-2054.
[4] SUBHASHINI S V, TAKHAR H S, NATH G. Non-uniform mass transfer or wall enthalpy into a compressible flow over a rotating sphere [J]. Heat and Mass Transfer, 2007, 43(11): 1133-1141.
[5] TAKHAR H S, WHITELAW M H. Higher order heat transfer from a rotating sphere [J]. Acta Mechanica, 1978, 30: 101-109.
[6] FRANCESCHINI E A, LACCONI G I, CORTI H R. Kinetics of hydrogen evolution reaction on nickel modified by spontaneous Ru deposition: A rotating disk electrode and impedance spectroscopy approach [J]. International Journal of Hydrogen Energy, 2016, 41(5): 3326-3338.
[7] TANG T, LI K, YING D, SUN T, WANG Y, JAI J. High efficient aqueous-film rotating disk photocatalytic fuel cell (RDPFC) with triple functions: Cogeneration of hydrogen and electricity with dye degradation [J]. International Journal of Hydrogen Energy, 2014, 39(19): 10258-10266.
[8] PEEV G, PESHAV D, NIKOLOVA A. Gas absorption in a thin liquid film flow on a horizontal rotating disk [J]. Heat and Mass Transfer, 2007, 43(8): 843-848.
[9] KARMAN T V. Uber laminare und turbulent Reibung [J]. ZAMM, 1921, 1: 233-252.
[10] GREENSPAN H. The theory of rotating fluids [M]. New York: Cambridge University Press, 1968.
[11] SHEVCHUK I V, Convective heat and mass transfer in rotating disk systems [M]. New York: Springer, 2009.
[12] GAMBARYAN-ROISMAN T, STEPHAN P. Hydrodynamics and heat transfer in a liquid film flowing over a spinning disk with specific wall topography [C]// ASME 2011 9th International Conference on Nanochannels, Microchannels, and Minichannels. Edmonton, Alberta, Canada, 2011.
[13] HELCIG C, WIESCHE S A D. Effect of Prandtl number on the heat transfer from a rotating disk: An experimental study [C]// ASME 2016 Heat Transfer Summer Conference. Washington DC, USA: ASME, 2016.
[14] CHOI S U S, Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian Flows [C]// American Society of Mechanical Engineers. New York, 1995: 99–105.
[15] BUONGIORNO J. Convective transport in nanofluids [J]. ASME Journal of Heat Transfer, 2006, 128(3): 240–250.
[16] DAS S K, CHOI S U S, YU W, PRADEEP T. Nanofluids: Science and Technology [M]. New York: John Wiley, 2007.
[17] TURKYILMAZOGLU M, Nanofluid flow and heat transfer due to a rotating disk [J]. Computers & Fluids, 2014, 94: 139-146.
[18] HAYAT T, IMTIAZ M, ALSAEDI A, ALZAHRANI F. Effects of homogeneous–heterogeneous reactions in flow of magnetite-Fe3O4 nanoparticles by a rotating disk [J]. Journal of Molecular Liquids, 2016, 216: 845-855.
[19] RAZA J, ROHINI A M, OMAR Z, AWAIS M. Heat and mass transfer analysis of MHD nanofluid flow in a rotating channel with slip effects [J]. Journal of Molecular Liquids, 2016, 219: 703-708.
[20] CHAKRABORTY T, DAS K, KUNDU P K. Framing the impact of external magnetic field on bioconvection of a nanofluid flow containing gyrotactic microorganism with convective boundary conditions [J]. Alexandria Engineering Journal, 2016, 57(1): 61-71.
[21] XUN S, ZHAO J, ZHENG L, ZHENG X. Bio convection in rotating system immersed in nanofluid with temperature dependent viscosity and thermal conductivity [J]. International Journal of Heat and Mass Transfer, 2017, 111: 1001-1006.
[22] ANWAR BEG O, BASIR M F M, UDDIN M J, ISMAIL A I M. Numerical study of slip effects on asymmetric bio convective nanofluid flow in a porous microchannel with an expanding/contracting upper wall using Buongiorno’s model [J]. Journal of Mechanics in Medicine and Biology, 2017, 17(5): 17500591.
[23] LI J J, LU H, RAEES A, ZHAO Q K. Unsteady mixed bio convection flow of a nanofluid between two contracting or expanding rotating discs [J]. Zeitschrift für Naturforschung A, 2017, 71(3): 1-12.
[24] IMTIAZ M, HAYAT T, ALSAEDI A, AHMAD B. Convective flow of carbon nanotubes between rotating stretchable disks with thermal radiation effects [J]. International Journal of Heat and Mass Transfer, 2016, 101: 948-957.
[25] HAYAT T, QAYYUM S, IMTIAZ M, ALZAHRANI F, ALSAEDI A. Partial slip effect in flow of magnetite-Fe3O4 nanoparticles between rotating stretchable disks [J]. Journal of Magnetism and Magnetic Materials, 2016, 413: 39-48.
[26] HAYAT T, QAYYUM S, IMTIAZ M, ALZAHRANI F, ALSAEDI A. Radiative flow due to stretchable rotating disk with variable thickness [J]. Results in Physics, 2017, 7: 156-165.
[27] AHMED N, ADNAN, MOHYUD-DIN U S T. Influence of shape factor on flow of magneto-nanofluid squeezed between parallel disk [J]. Alexandria Engineering Journal, 2017. DOI: https://doi.org/10.1016/j.aej.2017.03.031.
[28] MUSHTAQ A, MUSTAFA M. Computations for nanofluid flow near a stretchable rotating disk with axial magnetic field and convective conditions [J]. Results in Physics, 2017, 7: 3137-3144.
[29] CHEN H, CHEN J, GENG Y, CHEN K. Three-dimensional boundary layer flow over a rotating disk with power-law stretching in a nanofluid containing gyrotactic microorganisms [J]. Heat Transfer-Asian Research, 2017, 47(3): 569-582.DOI: https://doi.org/10.1002/htj.21327.
[30] LATIFF N A, UDDIN M J, ISMAIL A I M. Stefan blowing effect on bio convective flow of nanofluid over a solid rotating stretchable disk [J]. Propulsion and Power Research, 2016, 5(4): 267-278.
[31] WATSON L T, WANG C Y. Deceleration of a rotating disk in a viscous fluid [J]. Physics of Fluids, 1979, 22: 2267-2275.
[32] SHAMSHUDDIN M D, ANWAR BEG O, SUNDER RAM M, KADIR A. Finite element computation of multi-physical micropolar transport phenomena from an inclined moving plate in porous media [J]. Indian Journal of Physics, 2017, 92(2): 215-230.
[33] ZOHRA F T, UDDIN M J, ISMAIL A I M, ANWAR BEG O, KADIR A. Anisotropic slip magneto-bio convection flow from a rotating cone to a nanofluid with Stefan blowing effects [J]. Chinese J Phys, 2017, 56(1): 432-448.
[34] DANIEL Y S, DANIEL S K. Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method [J]. Alexandria Engineering Journal, 2015, 54(3): 705-712.
[35] BHATTI M M, SHAHID A, ANWAR BEG O, KADIR A. Numerical study of radiative Maxwell viscoelastic magnetized flow from a stretching permeable sheet with the Cattaneo–Christov heat flux model [M]. Neural Computing & Applic, 2017, 30(11): 3467-3478. DOI: https://doi.org/ 10.1007/ s00521-017-2933-8.
[36] ADOMIAN G. Solving frontier problems in physics: The decomposition method [M]. Dordrecht, USA: Kluwer, 1994.
[37] HAQ F, SHAH, K, GHAUS UR RAHMAN, SHAHZAD M. Numerical solution of fractional order smoking model via Laplace Adomian decomposition method [J]. Alexandria English Journal, 2017, 57(2): 1061-1069. DOI: https://doi. org/10.1016/j.aej. 2017.02.015.
[38] ANWAR BEG O, TRIPATHI D, SOCHI T, GUPTA P K. Adomian decomposition method (ADM) simulation of magneto-bio-tribological squeeze film with magnetic induction effects [J]. Journal of Mechanics Medicine Biology, 2015, 15: 1550072.
[39] AHLERSTEN K. An introduction to MATLAB [M]. Bookboon Publishers, 2015.
[40] EVANS D J. The rotationally symmetric flow of a viscous fluid in the presence of an infinite rotating disc with uniform suction [J]. Quarterly Journal of Mechanics and Applied Mathematics, 1969, 22(4): 467-485.
[41] FANG T, TAO H. unsteady viscous flow over a rotating stretchable disk with deceleration [J]. Communication in Nonlinear Science and Numerical Simulations, 2012, 17(12): 5064-5072.
[42] SIDDIQA S, GUL-E-HINA, BEGUM N, SALEEM S, HOSSAIN M A, GORLA R S R. Numerical solutions of nanofluid bioconvection due to gyrotactic microorganisms along a vertical wavy cone [J]. International Journal of Heat and Mass transfer, 2016, 101: 608-613.
[43] SIDDIQA S, SULAIMAN M, HOSSAIN M A, ISLAM S, GORLA R S R. Gyrotactic bioconvection flow of a nanofluid past a vertical wavy surface [J]. International Journal of Thermal Sciences, 2016, 108: 244-250.
[44] BEGUM N, SIDDIQA S, HOSSAIN M A. Nanofluid bioconvection with variable thermophysical properties [J]. Journal of Molecular Liquids, 2017, 231: 325-332.
[45] SAINI S, SHARMA Y D. Analysis of onset of bio-thermal convection in a fluid containing gravitactic microorganism by the energy method [J]. Chinese Journal of Physics, 2018, 56(5): 2031-2038.
[46] SAINI S, SHARMA Y D. Analysis of onset of bio-thermal convection in a fluid containing gravitactic microorganism by the energy method [J]. Chinese Journal of Physics, 2018, 56(5): 2031-2038.
[47] SAINI S, SHARMA Y D. A bio-thermal convection in waterbased nanofluid containing gyrotactic microorganism: Effect of vertical throughflow [J]. Journal of Applied Fluid Mechanics, 2018, 11(4): 895-903.
(Edited by HE Yun-bin)
中文导读
生物对流纳米流体流动的von Kármán分解法模拟
摘要:本研究分析了纳米流体从旋转圆盘中流过时的三维黏性时变旋流生物对流。圆盘的变形沿径向进行,同时考虑Stefan吹气,通过对Buongiorno纳米流体模型的分析,发现布朗运动和热泳动在纳米尺度上起着主导作用。在适当的壁面(圆盘表面)和自由流边界条件下,建立了原始质量守恒方程、径向动量、切向动量和轴向动量、热量、纳米粒子浓度和微生物密度函数。将这个高度非线性、强耦合的非定常偏微分方程系统用经典的von Kármán和其他变换进行归一化,从而将边值问题转化为一个常微分系统。产生的11阶系统包括多种无量纲流动参数,即生物对流Lewis数、不稳定参数、普通Lewis数、Prandtl数、质量对流Biot数、Peclet数、Stefan吹气参数。利用先进的半解析方法得到了系统的解,即Adomian分解法。利用Runge-Kutta拍摄技术计算的早期文献对上述问题进行了验证。
关键词:纳米流体;生物对流;磁盘旋转生物反应器;von Kármá旋流;Stefan吹气;Adomian分解法
Received date: 2018-06-06; Accepted date: 2019-03-08
Corresponding author: M D SHAMSHUDDIN, PhD; Tel: +98-66826099; E-mail: shammaths@gmail.com; ORCID: 0000-0002-2453- 8492

