Determination of initial cable force of cantilever casting concrete arch bridge using stress balance and influence matrix methods
来源期刊:中南大学学报(英文版)2019年第11期
论文作者:蒋田勇 邓扬 田仲初 彭文平 张建仁
文章页码:3140 - 3155
Key words:concrete arch bridge; cantilever casting; initial cable force; stress balance method; influence matrix method
Abstract: Cantilever casting concrete arch bridge using form traveller has a broad application prospect. However, it is difficult to obtain reasonable initial cable force in construction stage. In this study, stress balance and influence matrix methods were developed to determine the initial cable force of cantilever casting concrete arch bridge. The stress balance equation and influence matrix of arch rib critical section were established, and the buckle cable force range was determined by the allowable stress of arch rib critical section. Then a group of buckle cable forces were selected and substituted into the stress balance equation, and the reasonable initial buckle cable force was determined through iteration. Based on the principle of force balance, the initial anchor cable force was determined. In an engineering application example, it is shown that the stress balance and influence matrix methods for the determination of initial cable force are feasible and reliable. The initial cable forces of arch rib segments only need to be adjusted once in the corresponding construction process, which improves the working efficiency and reduces the construction risk. It is found that the methods have great advantages for determining initial cable force in cantilever casting construction process of concrete arch bridge.
Cite this article as: TIAN Zhong-chu, PENG Wen-ping, ZHANG Jian-ren, JIANG Tian-yong, DENG Yang. Determination of initial cable force of cantilever casting concrete arch bridge using stress balance and influence matrix methods [J]. Journal of Central South University, 2019, 26(11): 3140-3155. DOI: https://doi.org/10.1007/s11771-019- 4242-0.

J. Cent. South Univ. (2019) 26: 3140-3155
DOI: https://doi.org/10.1007/s11771-019-4242-0
TIAN Zhong-chu(田仲初)1, PENG Wen-ping(彭文平)1, ZHANG Jian-ren(张建仁)1,JIANG Tian-yong(蒋田勇)1, DENG Yang(邓扬)2
1. School of Civil Engineering, Changsha University of Science and Technology, Changsha 410114, China;
2. Beijing Advanced Innovation Center for Future Urban Design, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Cantilever casting concrete arch bridge using form traveller has a broad application prospect. However, it is difficult to obtain reasonable initial cable force in construction stage. In this study, stress balance and influence matrix methods were developed to determine the initial cable force of cantilever casting concrete arch bridge. The stress balance equation and influence matrix of arch rib critical section were established, and the buckle cable force range was determined by the allowable stress of arch rib critical section. Then a group of buckle cable forces were selected and substituted into the stress balance equation, and the reasonable initial buckle cable force was determined through iteration. Based on the principle of force balance, the initial anchor cable force was determined. In an engineering application example, it is shown that the stress balance and influence matrix methods for the determination of initial cable force are feasible and reliable. The initial cable forces of arch rib segments only need to be adjusted once in the corresponding construction process, which improves the working efficiency and reduces the construction risk. It is found that the methods have great advantages for determining initial cable force in cantilever casting construction process of concrete arch bridge.
Key words: concrete arch bridge; cantilever casting; initial cable force; stress balance method; influence matrix method
Cite this article as: TIAN Zhong-chu, PENG Wen-ping, ZHANG Jian-ren, JIANG Tian-yong, DENG Yang. Determination of initial cable force of cantilever casting concrete arch bridge using stress balance and influence matrix methods [J]. Journal of Central South University, 2019, 26(11): 3140-3155. DOI: https://doi.org/10.1007/s11771-019- 4242-0.
1 Introduction
Since the concrete arch structure resists the gravity load in compression, the concrete arch bridge can benefit from high compressive strength of concrete [1, 2]. However, with the increase of span, the dead weight of concrete arch bridge increases significantly, which leads to a significant increase in its construction risks and costs [3-6]. Cantilever casting is an important construction method for concrete arch bridge [6-10]. It is suitable for long-span concrete arch bridge with small topographic impact, good overall structure performance and high degree of mechanization. It is a kind of suspension system composed of buckle tower, buckle or anchor cables, form traveller and concrete arch rib. However, during the cantilever casting construction process, the concrete arch bridge is always in the suspension state before the arch rib is closed. Hence, the construction risk is quite large. In addition, in the cantilever casting construction, the buckle cable force greatly affects the state of arch rib. If the buckle cable force is not well controlled, it will easily cause the arch rib section to crack and even affect the safety of arch bridge construction [11-13]. Therefore, it is of great significance to determine the initial buckle cable force and to ensure that the section stress of arch rib is within a reasonable range, thus guaranteeing the safe construction of concrete arch bridge.
With high emphasis of civil structural health monitoring [14-17], the real-time estimate or measurement method of structural forces has received much attention, including fiber optical sensor method [18-21], piezoceramic-based method [22-28], and electro-magnetic impedance method [29-32]. Meanwhile, analytical and numerical methods are also used to determine structural force, and methods proposed in the literature to determine cable force of long-span bridges [33, 34], mainly including optimization method, force equilibrium method, zero displacement method and unit load method. In the optimization method, the cable force is determined based on certain functions that are related to structural efficiency or economy. KASUGA et al [35] proposed some optimized criteria and obtained the optimum adjusting cable force by minimizing the amount of work due to these forces. WU et al [36] presented a method along with its software development to simulate different construction stages of cable-stayed bridge, and provided the initial cable force for each construction stage. WEI et al [37] put forward a method for obtaining the optimum cable force of each segment by setting appropriate objective function. BRUNO et al [38] proposed a new design method to evaluate the optimum configuration of network arch bridge. ELREHIM et al [39] presented a geometrical structural optimization method to study the deck of concrete arch bridge by Genetic Algorithms technique. SUNG et al [40] utilized the constrained minimization method for the optimum solution of cable force of the Mau-Lo Hsi Bridge. WANG et al [41] set up a finite element computation procedure at different erection stages during construction using the cantilever method. The procedure can be successfully applied in determining the initial shape of bridge structures during the erection procedure. Then the initial cable force of bridge can be achieved. GRANATA et al [42] put forward a procedure for determining the initial cable force, considering the geometric nonlinearity of stayed cable through the Dischinger equivalent elastic modulus. FABBROCINO et al [43] developed a procedure for the optimization of cable force in order to achieve the desired bending moment distribution through the application of a self-equilibrated state of stress induced by the optimum pre-tensioning cable force. SONG et al [44] proposed an optimization method to determine the pre-tensioning cable force in long-span bridge considering the counterweight. LI et al [45] determined the initial cable force of long-span concrete-filled steel tube (CFST) arch bridge based on influence matrix and linear programming methods. NAKAMURA et al [46] designed a new type of hybrid bridge (cable-arch bridge) and optimized the cable force status. CARPENTIERI et al [47] developed a procedure for the optimization of cable force according to a given objective function. NEGRAO et al [48] described an analytical sensitivity analysis and optimization implementation for cable-stayed bridge design. KANG et al [49] constructed a model of cable-arch bridge, and investigated its static behavior using the finite element method and experimental test. BALDOMIR et al [50] described an optimization problem of cable cross section of a cable-stayed bridge considering constraints of cable stress and deck displacement. TIAN et al [51] calculated the cable force and pre-camber of each segment of Daning River Bridge using the forward-iteration method. MARTINS et al [52] used an entropy- based optimization algorithm to find the initial cable force of concrete cable-stayed bridge. DAI et al [53] proposed an optimization calculation method to optimize the initial cable force of cable-stayed arch bridge in arch rib cantilever erecting.
In the force equilibrium method, the cable force is determined by utilizing the idea of force equilibrium, which is considered as independent variable for achieving target bending moments along the girder. The approximate influence coefficients are calculated and the pre-tensioning cable forces are obtained iteratively. CHEN et al [54] proposed the force equilibrium method to determine the initial cable force of pre-stressed concrete cable-stayed bridge. In the zero displacement method, the configuration of zero deflection along the girder is taken as the target and the cable forces are obtained by iterative calculation. WANG et al [55] used the zero displacement method to determine the cable forces and the initial configuration of bridge. The method is based on the idea that the stayed cables transform the structural system of girder into a rigidly supported continuous beam. ZHANG et al [56] optimized the zero displacement method using a Kriging surrogate model. The calibration method was used to identify reasonable initial forces in the critical stayed cables. The unit load method (ULM) was used to determine the initial cable force by achieving the desired moment distribution at specific degrees of freedom (DOF). JANJIC et al [57] proposed the ULM for determining the cable force of cable-stayed bridge. The system of linear equations of desired moments was established for each DOF, and the initial cable force was then determined directly by this system. In conclusion, most determination or optimization methods of existing cable force are mainly applied in cable-stayed bridge and concrete-filled steel tubular (CFST) arch bridge. However, few studies on the application of above methods are involved in concrete arch bridge. Only GRANATA et al [58] used the partial elastic scheme method to obtain the initial cable force of cantilever casting concrete arch bridge. However, for the cantilever casting concrete arch bridge, the optimization of initial cable force was less studied.
In this study, a new method was developed for determining the initial cable force of cantilever casting concrete arch bridge by combining stress balance method with influence matrix method. In this method, the stress balance equation and influence matrix of arch rib section are established, and its allowable stress is taken as the constraint condition to determine the cable force. Because the stress influence matrix is a lower triangular matrix, the force of last cable is first determined and then other cable forces are determined one by one. Finally, obtained cable forces are substituted into the stress balance equation of arch rib sections, and stress constraint conditions are used to judge whether they meet requirements. If requirements are not met, the iterative adjustment of cable forces is carried out. Compared with other calculation methods of cable force, this method mainly controls the stress of arch rib sections and does not consider the influence of arch rib alignment, which is particularly suitable for determining the cable force of cantilever casting concrete arch bridge. It is applied to the Shatuo Bridge as a concrete arch bridge for determining the initial cable force during cantilever casting construction process. The initial cable forces of arch rib segments only need to be adjusted once in the corresponding construction stage, which improves the working efficiency and reduces the construction risk.
2 Determination method of initial cable force
2.1 Cantilever casting process of concrete arch bridge
Cantilever casting construction system of concrete arch bridge is a kind of suspension system composed of buckle tower, buckle or anchor cables, form traveller and arch rib. The arch rib segment construction diagram of cantilever casting concrete arch bridges is shown in Figure 1. During the cantilever casting process of concrete arch bridge, the anchor end of anchor cable is installed on the rock and its tensioning end is anchored on the buckle tower; The anchor end of buckle cable is fastened on the poured arch rib segment and its tensioning end is also anchored on the buckle tower. In addition, the buckle tower is built on the top of abutment pier; The abutment pier and arch rib are set on the abutment which transmits the load of superstructure to the foundation. The form traveller is used as the supporting platform of initial casting arch rib segment. When the compressive strength of initial casting concrete arch rib segment meets specification requirements, the buckle cables are installed on the arch rib segment and tensioned by the initial cable force. Then the form traveller is moved for preparing to cast the next arch rib segment. Finally, the arch ribs are closed.
2.2 Initial buckle and anchor cable forces
In this study, the initial cable force was determined by stress balance and influence matrix methods. During the cantilever casting process of concrete arch bridge, in order to ensure the safety of arch rib structure, the critical section stress of concrete arch rib should meet specification requirements. Before the arch rib is closed, the arch rib critical section stress is determined by the arch rib gravity, buckle cable force and temporary load (i.e. form traveller, mechanical equipment and personnel load) during cantilever casting process. Assuming that an arch rib is supported by buckle cables n, critical sections n are selected to calculate the stress, as shown in Figure 1. Stresses at the top and bottom of arch rib critical sections are expressed as vectors {σt} and {σb} respectively as follows.
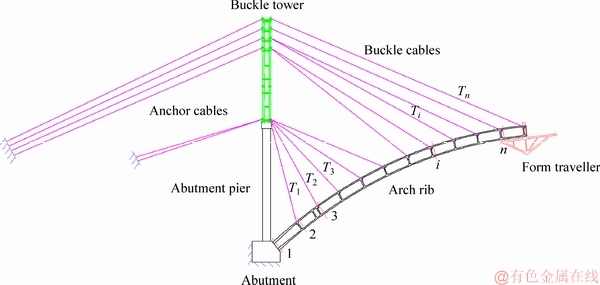
Figure 1 Arch rib construction diagram of cantilever casting concrete arch bridge
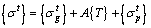 (1)
(1)
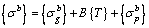 (2)
(2)
where {σt} is a vector of top stress of arch rib critical sections, which can be expressed as 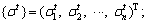 {σb} is a vector of bottom stress of arch rib critical sections, which can be expressed as
{σb} is a vector of bottom stress of arch rib critical sections, which can be expressed as 
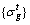 is a vector of top stress of arch rib critical sections caused by the arch rib gravity, which can be expressed as
is a vector of top stress of arch rib critical sections caused by the arch rib gravity, which can be expressed as 
 is a vector of bottom stresses of arch rib critical sections caused by the arch rib gravity, which can be expressed as
is a vector of bottom stresses of arch rib critical sections caused by the arch rib gravity, which can be expressed as 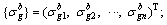 {T} is a vector of buckle cable forces, which can be expressed as
{T} is a vector of buckle cable forces, which can be expressed as 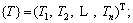 A and B are the stress influence matrices at the top and bottom of critical sections under the action of unit buckle cable force respectively. In particular, typical elements aij and bij of stress influence matrices A and B are defined as stresses at the top and bottom of arch rib critical section No. i caused by a unit tensile stress of buckle cable No. j.
A and B are the stress influence matrices at the top and bottom of critical sections under the action of unit buckle cable force respectively. In particular, typical elements aij and bij of stress influence matrices A and B are defined as stresses at the top and bottom of arch rib critical section No. i caused by a unit tensile stress of buckle cable No. j.  is a vector of top stress of arch rib critical section caused by the temporary load, which can be expressed as
is a vector of top stress of arch rib critical section caused by the temporary load, which can be expressed as 
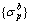 is a vector of bottom stress of arch rib critical section caused by the temporary load, which can be expressed as
is a vector of bottom stress of arch rib critical section caused by the temporary load, which can be expressed as 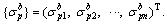
During the cantilever casting construction process of concrete arch bridge, the arch rib gravity and temporary load always result in tensile stress and compressive stress at the top and bottom of arch rib critical sections respectively; The buckle cable force leads to compressive stress and tensile stress at the top and bottom of arch rib critical sections respectively. Therefore, the initial buckle cable force is determined according to the allowable stress of arch rib critical sections in the corresponding specification [59]. In this study, the tensile and compressive allowable stresses of arch rib critical sections are expressed as {f t}and {f c} respectively. When {f t} and {f c} are substituted into the Formulas (1) and (2), they are expressed as follows.
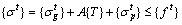 (3)
(3)
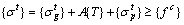 (4)
(4)
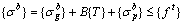 (5)
(5)
 (6)
(6)
where the tensile stress is positive and the compressive stress is negative. It is indicated that the top tensile stress of arch rib critical sections is less than the allowable tensile stress in Eq. (3) while the top compressive stress of arch rib critical sections is greater than the allowable compressive stress in Eq. (4); The bottom tensile stress of arch rib critical sections is less than the allowable tensile stress in Eq. (5) while the bottom compressive stress of arch rib critical sections is greater than the allowable compressive stress in Eq. (6). In the actual calculation process, the minimum buckle cable force is determined by Eqs. (3) and (6). By converting Eqs. (3) and (6), the following expressions can be obtained respectively.
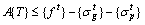 (7)
(7)
 (8)
(8)
Equations (7) and (8) can also be expressed as follows.
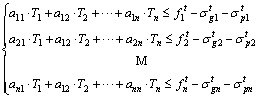 (9)
(9)
 (10)
(10)
In addition, the maximum buckle cable force is determined by Eqs. (4) and (5). By converting Eqs. (4) and (5), the following expressions can be obtained respectively.
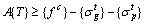 (11)
(11)
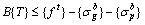 (12)
(12)
Equations (11) and (12) can also be expressed as follows.
 (13)
(13)
 (14)
(14)
Since stress influence matrices A and B are upper triangular matrices, the minimum buckle cable force 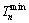 can be easily obtained by Eqs. (9) and (10) , and the maximum buckle cable force
can be easily obtained by Eqs. (9) and (10) , and the maximum buckle cable force 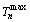 can also be easily determined by Eqs. (13) and (14). If any minimum buckle cable force is negative, the buckle cable force is no longer needed and can be set to zero. The minimum buckle cable force
can also be easily determined by Eqs. (13) and (14). If any minimum buckle cable force is negative, the buckle cable force is no longer needed and can be set to zero. The minimum buckle cable force 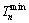 and the maximum buckle cable force
and the maximum buckle cable force 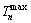 are expressed respectively as follows.
are expressed respectively as follows.
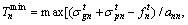
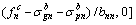 (15)
(15)
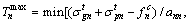
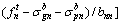 (16)
(16)
where  and
and 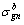 are top and bottom stresses of critical section n of arch rib caused by arch rib gravity respectively;
are top and bottom stresses of critical section n of arch rib caused by arch rib gravity respectively; 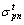 and
and 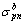 are top and bottom stresses of critical section n of arch rib caused by temporary load respectively;
are top and bottom stresses of critical section n of arch rib caused by temporary load respectively; 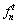 and
and 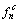 are tensile and compressive allowable stresses of critical section n of arch rib respectively; ann and bnn are defined as top and bottom stresses of critical section n of arch rib caused by unit tension force of buckle cable n. According to the Eqs. (15) and (16), the initial force Tnof buckle cable n can be determined as
are tensile and compressive allowable stresses of critical section n of arch rib respectively; ann and bnn are defined as top and bottom stresses of critical section n of arch rib caused by unit tension force of buckle cable n. According to the Eqs. (15) and (16), the initial force Tnof buckle cable n can be determined as 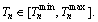 Thus, if the initial force Tn of buckle cable n is substituted into Formulas (9), (10), (13) and (14), the initial force Tn-1 of buckle cable (n-1) also can be obtained according the above analysis method. And the initial force Ti of buckle cable i is determined as
Thus, if the initial force Tn of buckle cable n is substituted into Formulas (9), (10), (13) and (14), the initial force Tn-1 of buckle cable (n-1) also can be obtained according the above analysis method. And the initial force Ti of buckle cable i is determined as 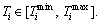 Among them, expressions of
Among them, expressions of  and
and 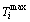 were showed in Eqs. (17) and (18) respectively.
were showed in Eqs. (17) and (18) respectively.
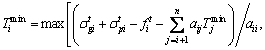
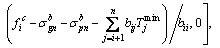
 (17)
(17)
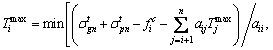

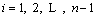 (18)
(18)
where and
and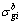 are top and bottom stresses of critical section No. i of arch rib caused by arch rib gravity respectively;
are top and bottom stresses of critical section No. i of arch rib caused by arch rib gravity respectively; and
and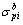 are top and bottom stresses of critical section No. i of arch rib caused by temporary load respectively;
are top and bottom stresses of critical section No. i of arch rib caused by temporary load respectively; 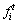 and
and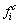 are tensile and compressive allowable stresses of critical section No. i of arch rib respectively; aij and bij are defined as top and bottom stresses of critical section No. i of arch rib caused by unit tension force of buckle cable No. j Equations (17) and (18) can determine the initial force interval of each buckle cable, but in the actual process, a set of optimum cable forces are required during cantilever casting construction process. Assuming that a group of buckle cable forces {T0} are recorded as
are tensile and compressive allowable stresses of critical section No. i of arch rib respectively; aij and bij are defined as top and bottom stresses of critical section No. i of arch rib caused by unit tension force of buckle cable No. j Equations (17) and (18) can determine the initial force interval of each buckle cable, but in the actual process, a set of optimum cable forces are required during cantilever casting construction process. Assuming that a group of buckle cable forces {T0} are recorded as 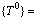
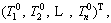
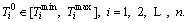 They are substituted into Formulas (1) and (2) to calculate top and bottom stresses of arch rib critical sections. Then, whether these results meet the Eqs. (3)-(6) is checked. If they are satisfied, results of {T0} will be output as the initial buckle cable forces of cantilever casting concrete arch bridge. Otherwise, buckle cable forces {T0} should be adjusted. The solution of cable force adjustment vector {△T} is as follows.
They are substituted into Formulas (1) and (2) to calculate top and bottom stresses of arch rib critical sections. Then, whether these results meet the Eqs. (3)-(6) is checked. If they are satisfied, results of {T0} will be output as the initial buckle cable forces of cantilever casting concrete arch bridge. Otherwise, buckle cable forces {T0} should be adjusted. The solution of cable force adjustment vector {△T} is as follows.
Step 1: Substitute {T0} into Formulas (1) and (2) to determine the top stress {σt0} and bottom stress {σb0} of arch rib critical sections respectively.
Step 2: Transform Formulas (1) and (2) and cable force adjustment vectors {△Tt} and {△Tb} can be determined by Formula (19).
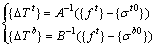 (19)
(19)
Step 3: Select the maximum value of {△Tt} and {△Tb} as {△T}.
Then, substitute {T0+△T} into Eqs. (1) and (2) to re-calculate critical section stress of arch rib and check whether it matches the Eqs. (3)-(6). If not, continue to adjust till these equations are matched.
Solution procedure of initial buckle cable force of cantilever casting concrete arch bridge is shown in Figure 2. In addition, the anchor cable force was calculated according to the force balance principle at anchorage position of buckle and anchor cables, as shown in Figure 3. αi and βi are horizontal inclination angle of buckle and anchor cables at the end of tower respectively; Ti and Pi are buckle and anchor cable forces No. i respectively. Based on the force balance principle, the horizontal component of buckle and anchor cable forces should be the same, as shown in Eq.(20).
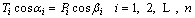 (20)
(20)
Since Ti is buckle cable force No. i, it can be determined by the above solution method; Pi can be easily determined by Eq. (20). Hence, a group of anchor cable forces {P} were obtained and expressed as {P}=(P1, P2, …, Pn)T.
3 Application example
3.1 Bridge description
The Shatuo Bridge, a cantilever casting concrete arch bridge, spans the Wujiang River and is located in Yanhe County, Guizhou Province, China. Its main layout drawing is shown in Figure 4. The arch rib is a concrete catenary structure with box cross section of same height. Its span L, rise height f and rise-span ratio f/L are 240 m, 40 m and 1/6 respectively. It is catenary curve with an arch-axis coefficient m of 1.85. The concrete of arch rib and abutment pier is C60 and C50 respectively. The steel of buckle tower is Q235. The arch rib section of Shatuo Bridge is shown in Figure 5. It is a single box with double chambers, which has a height of 4.5 m and a width of 10 m. The thickness of top and bottom of arch rib section is both 80 cm, and the thickness of three webs is all 65 cm, as shown in Figure 5(a). In the L/4 section of arch rib, the thickness of top and bottom of arch rib section is both 35 cm, and the thickness of three webs is all 40 cm, as shown in Figure 5(b). In the L/2 section of arch rib, the thickness of top and bottom of arch rib section is 50 cm and 35 cm respectively, and the thickness of three webs is all 50 cm, as shown in Figure 5(c).
The arrangement of buckle and anchor cables of Shatuo Bridge is shown in Figure 6. The arch rib was divided into 37 segments longitudinally in which the first segment was constructed with support casting and the closure segment of arch apex was constructed by hanging basket casting. the remaining 34 segments of arch rib were all built by cantilever casting with form travellers. After each arch rib segment was poured, it was tied on the abutment pier or buckle tower by tensioning buckle cables. At the same time, the deviation of abutment pier or buckle tower was adjusted by tensioning anchor cables to ensure its safety. A total of 36 pairs of buckle and anchor cables are needed during the whole cantilever casting construction process. Buckle towers placed at the top of abutment piers, were assembled by steel pipes and connecting rods. Buckle cables No.(1-6) and No. (7-18) were anchored at the abutment pier and buckle tower respectively. The arch rib buckle cables of west bank of Shatuo Bridge were represented by X1 to X18 and the anchor cables were represented by X-MS1 to X-MS18. Buckle cables of arch rib at east bank of Shatuo Bridge were expressed by D1 to D18 and its anchor cables were expressed by D-MS1 to D-MS18. Scene picture of buckle and anchor cables of Shatuo Bridge is shown in Figure 7.
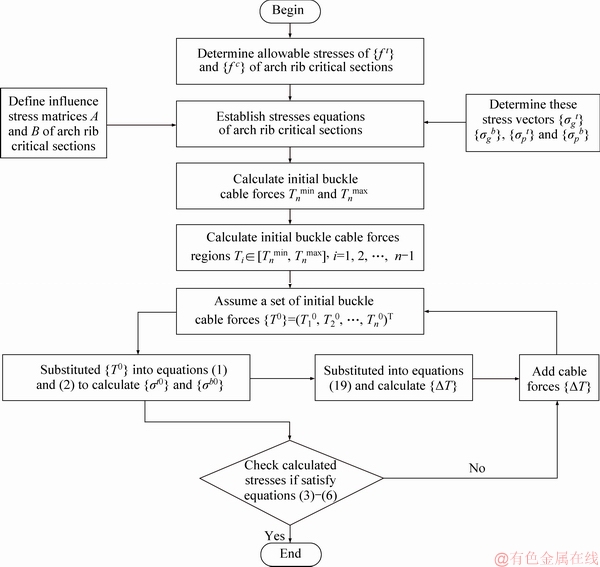
Figure 2 Solution of initial buckle cable forces of cantilever casting concrete arch bridge
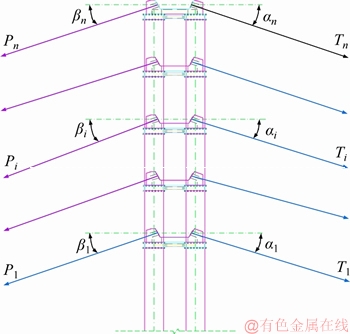
Figure 3 Calculation diagram of anchor cable forces
The form traveller is the main load bearing component, which is mainly composed of load bearing trusses, travel mechanisms, anchoring devices and formworks, as shown in Figure 8. The form traveller of Shatuo Bridge has a length of 16.0 m and a height of 10.0 m. Triangular load bearing truss with a height of 4.30 m was adopted. A set of form traveller weighs about 900 kN (including formworks), and its designed load bearing capacity is 3000 kN.

Figure 4 Main layout drawing of Shatuo Bridge (Unit: m)
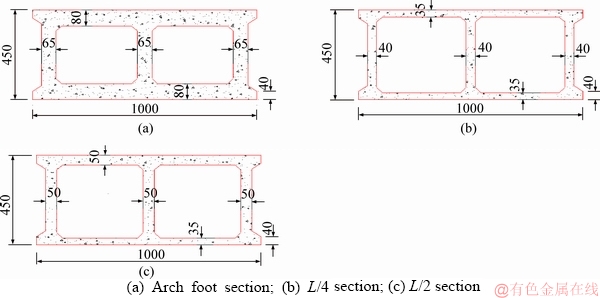
Figure 5 Arch rib sections of Shatuo Bridge (Unit: cm):
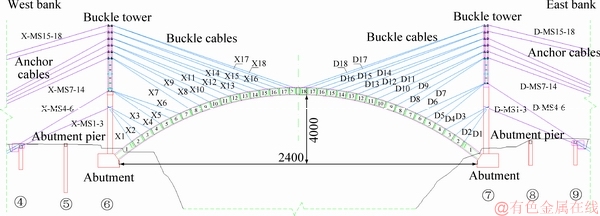
Figure 6 Arrangement of buckle and anchor cables of Shatuo Bridge (Unit: cm)

Figure 7 Scene picture of Shatuo Bridge
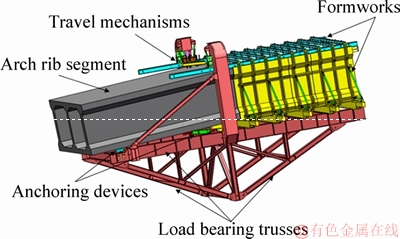
Figure 8 Form traveller of Shatuo Bridge
3.2 Construction monitoring
Buckle and anchor cable forces are important basis for evaluating and judging the internal force status during arch rib segment construction process. Therefore, the force sensor BGK-4900 was used to monitor cable forces, which was installed at the anchorage end of buckle and anchor cables during the cantilever casting construction of arch rib segment. In order to reduce cost, cable force sensors were arranged at critical arch rib segments, as shown in Figure 9(a). Scene picture of cable force sensors is shown in Figure 9(b).
Strain of concrete and steel sections was measured by vibration wire strain sensors BGK-4200 and BGK-4000 respectively. Its test elements were arranged in some critical sections of arch rib, buckle tower and abutment pier, as shown in Figure10.
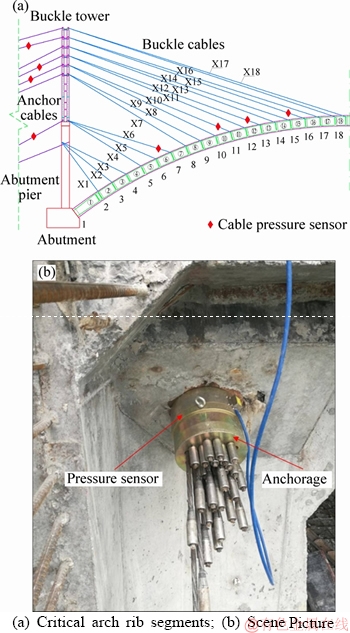
Figure 9 Cable force monitoring sensors of critical arch rib segments:
Cross section arrangement of strain sensors of arch rib, buckle tower and abutment pier is shown in Figure 11. Sixteen strain sensors were embedded in the steel pipe of bottom section of buckle tower, as shown in Figure 11(a). Six strain sensors on concrete were embedded in concrete arch rib section and abutment pier bottom section respectively, as shown in Figures 11(b) and (c). Hence, stresses of critical sections were obtained by the Hooke’s law and whether they were allowable stresses of arch rib critical sections during the construction process was analyzed.
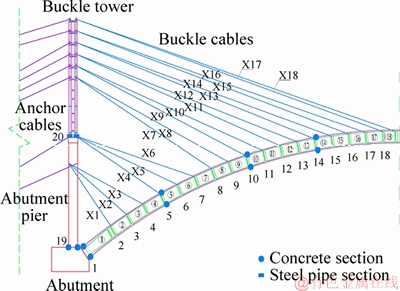
Figure 10 Strain monitoring sections
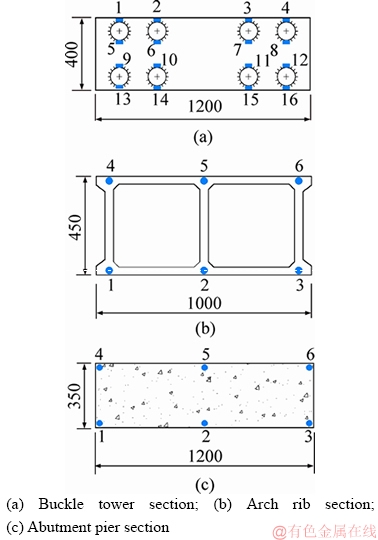
Figure 11 Cross section of strain sensors (Unit: cm):
3.3 Results and analysis
There are eighteen critical segment sections on each half of arch rib. According to requirements of corresponding specification [59, 60], the allowable tensile stress f t of concrete arch rib is 1.96 MPa, and the allowable compressive stress f c of concrete arch rib is 26.50 MPa. The elastic modulus of concrete C60 arch rib, concrete C50 abutment pier and steel Q235 buckle tower is 3.60×104 MPa, 3.45×104 MPa and 2.10×105 MPa respectively. Steel strand with a tensile strength of 1860 MPa and an elastic modulus of 1.95×105 MPa was adopted by buckle and anchor cables. Beam elements were used in arch ribs, buckle towers and abutment piers. Buckle and anchor cables were simulated by the truss element with only tension mode, and the sag effect of cables was taken into account using the elastic modulus modified method by Ernst formula [61]. The form traveller was simulated by equivalent load with node force and bending moment applied to the corresponding section of arch rib. The master-slave technique was used to deal with connections of buckle tower, buckle and anchor cables, and connections between the arch rib and the buckle cable. The finite element model of Shatuo Bridge established by Midas Civil software is shown in Figure 12.
Figure 12 Finite element model of Shatuo Bridge
Based on results of finite element model of Shatuo Bridge, influence matrices A and B, and stress vectors
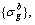
 and
and 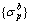 can be obtained. In addition, since it is symmetric for arch rib of Shatuo Bridge, only west bank results are considered in the following analysis. Buckle cable forces {T0} were selected in the allowable ranges of buckle cable forces.
can be obtained. In addition, since it is symmetric for arch rib of Shatuo Bridge, only west bank results are considered in the following analysis. Buckle cable forces {T0} were selected in the allowable ranges of buckle cable forces.
Due to the solution procedure of initial buckle and anchor cable forces of cantilever casting concrete arch bridge, the optimum initial buckle and anchor cable forces were obtained. Initial buckle and anchor cable forces were finally determined, as shown in Figure 13. The maximum initial force of buckle cable X15 is 2260 kN; The minimum initial force of buckle cable X2 is 1280 kN; The maximum initial force of anchor cable X-MS16 is 2260 kN; The minimum initial force of anchor cable X-MS1 is 920 kN.
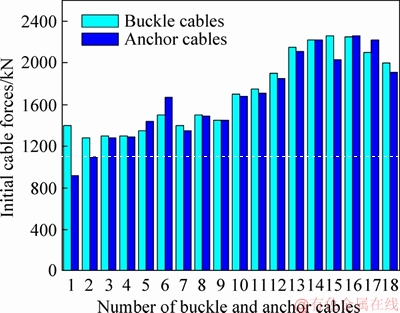
Figure 13 Initial buckle and anchor cable forces
Due to the space limitation in the paper, only buckle and anchor cable forces of arch rib segments in cable tensioning stage and arch rib concrete cantilever casting stage were analyzed. Buckle cable forces in different stages are shown in Table 1. Buckle cable forces in different stages are a 36×18 matrix F. Elements f11, f31, f51, f21, f41, f61are buckle cable X1 forces in the cable tensioning stage of arch rib segment No. 1, No. 2 and No. 3, and concrete cantilever casting stage of arch rib segment No. 2, No. 3 and No. 4 respectively; Elements f32, f52, f42, f62 are buckle cable X2 forces in the cable tensioning stage of arch rib segment No. 2 and No. 3, and concrete cantilever casting stage of arch rib segment No.3 and No.4 respectively; Elements f53 and f63 are buckle cable X3 forces in the cable tensioning stage of arch rib segment No. 3 and concrete cantilever casting stage of arch rib segment No. 4 respectively. It can be seen that the maximum buckle cable force of arch rib segments in different stages is 2658 kN, which is the buckle cable X15 force in the concrete cantilever casting stage of arch rib segment No. 16. From Table 1, it can be found that the buckle cable Xi force reaches the maximum in the concrete cantilever casting stage of arch rib segment No. (i+1) (i=1, 2, 3, …, 18). Among them, the arch rib segment No. 19 is the closure segment of arch apex.
Calculated and tested cable forces in three typical stages are shown in Figure 14. The stage i is the tensioning stage of buckle and anchor cables of arch rib segment No. i; The stage (i+1) is the concrete cantilever casting stage of arch rib segment No. (i+1); The stage (i+2) is the tensioning stage of buckle and anchor cables of arch rib segment No. (i+1) (i=6, 10, 12 and 15). As shown in Figure 14(a), the maximum calculated and tested forces of buckle cable X6 are 1786 and 1761 kN in the concrete cantilever casting stage of arch rib segment No. 7 respectively; The maximum calculated and tested forces of buckle cable X10 are 2018 and 1982 kN in the concrete cantilever casting stage of arch rib segment No.11 respectively; The maximum calculated and tested forces of buckle cable X12 are 2235 and 2275 kN in the concrete cantilever casting stage of arch rib segment No. 13 respectively; The maximum calculated and tested forces of buckle cable X15 are 2658 and 2698 kN in the concrete cantilever casting stage of arch rib segment No.16 respectively. As shown in Figure 14(b), the maximum calculated and tested forces of anchor cable X-MS6 are 1776 and 1742 kN in the concrete cantilever casting stage of arch rib segment No. 7 respectively; The maximum calculated and tested forces of anchor cable X-MS10 are 1898 and 1873 kN in the concrete cantilever casting stage of arch rib segment No. 11 respectively; The maximum calculated and tested forces of anchor cable X-MS12 are 2112 and 2148 kN in the concrete cantilever casting stage of arch rib segment No. 13 respectively; The maximum calculated and tested forces of anchor cable X-MS15 are 2317 and 2366 kN in the concrete cantilever casting stage of arch rib segment No. 16 respectively.
Table 1 Buckle cable forces in different stages (unit: kN)

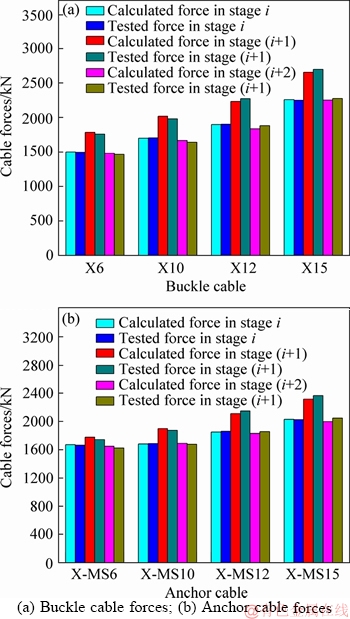
Figure 14 Calculated and tested cable forces in three typical stages:
As shown in Figure 14, calculated and tested cable forces are in good agreement, and their difference is less than 3%. Therefore, stress balance and influence matrix methods for determining the initial cable force of cantilever casting concrete arch bridge in this study are feasible and reliable. From Figure 14, it can be seen that forces of buckle and anchor cables No. i generated by tensioning the arch rib segment No. i reach the maximum force in the concrete cantilever casting stage of arch rib segment No. (i+1) and then decrease in the tensioning stage of arch rib segment No. (i+1).
Top and bottom stress ranges of arch rib critical sections are shown in Figures 15(a) and (b). In the subsequent analysis, the tensile stress is positive and the compressive stress is negative. As shown in Figure 15(a), the maximum top tensile and compressive stresses of arch rib critical sections in arch rib sections No. 1 and No. 2 are 1.56 and -7.42 MPa respectively. As shown in Figure 15(b), the maximum bottom tensile and compressive stresses of arch rib critical sections in arch rib sections No. 3 and No. 9 are 0.80 and -6.67 MPa respectively. From Figure 15, it can be seen that the maximum top and bottom tensile stresses (1.56 and 0.80 MPa) of arch rib critical sections are less than the allowable tensile stress 1.96 MPa; The maximum top and bottom compressive stresses(-7.42 and -6.67 MPa) of arch rib sections are larger than the allowable compressive stress -26.50 MPa. Therefore, they all meet the requirement of codes.
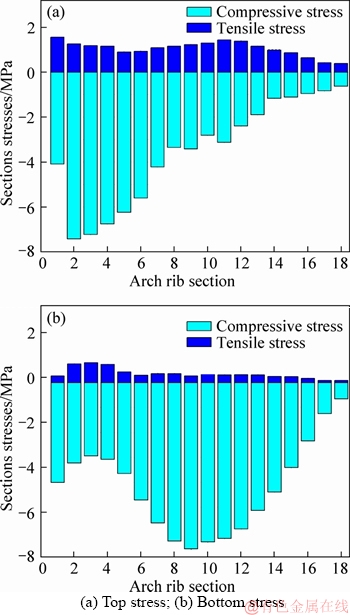
Figure 15 Stress ranges of arch rib critical sections:
Calculated and tested stresses of arch rib critical sections in different stages are shown in Figure 16. Top and bottom tested stresses of arch rib critical sections are the average value of tested stresses at the corresponding test location respectively. Calculated and tested stresses of arch rib section No. 1 are shown in Figure 16(a). It is found that the maximum calculated and tested top tensile stresses of arch rib section No.1 are 1.56 and 1.47 MPa in the concrete cantilever casting stage of arch rib segment No. 7 respectively; The maximum calculated and tested top compressive stresses of arch rib section No. 1 are -4.09 and -3.68 MPa in the tensioning stage of arch rib segment No. 16 respectively; The maximum calculated and tested bottom tensile stresses of arch rib section No. 1 are 0.27 and 0.25 MPa in the tensioning stage of arch rib segment No. 6 respectively; The maximum calculated and tested bottom compressive stresses of arch rib section No. 1 are -4.01 and -3.61 MPa in the concrete cantilever casting stage of arch rib segment No. 11 respectively. Calculated and tested stresses of arch rib section No. 5 are shown in Figure 16(b). It is found that the maximum calculated and tested top tensile stresses of No. 5 arch rib section are 0.90 and 0.87 MPa in the concrete cantilever casting stage of arch rib segment No. 7 respectively; The maximum calculated and tested top compressive stresses of arch rib section No. 5 are -6.24 and -5.62 MPa in the tensioning stage of arch rib segment No. 17 respectively; The maximum calculated and tested bottom tensile stresses of arch rib section No. 5 are 0.43 and 0.38 MPa in the tensioning stage of arch rib segment No. 14 respectively; The maximum calculated and tested bottom compressive stresses of arch rib section No. 5 are -3.65 and -3.25 MPa in the concrete cantilever casting stage of arch rib segment No. 13 respectively.
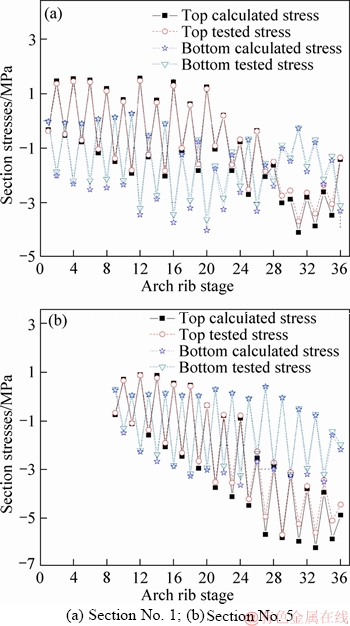
Figure 16 Calculated and tested stresses of arch rib critical sections in different stages:
As shown in Figure 16, calculated and tested stresses are in good agreement, and their maximum difference is 12% and less than 15%. From Figure 16, it can be seen that the maximum top and bottom tensile stresses (1.56 and 0.43 MPa) of arch rib critical sections are less than the allowable tensile stress 1.96 MPa; The maximum top and bottom compressive stresses (-6.24 and -6.39 MPa) of the arch rib critical sections are larger than the allowable compressive stress -26.50 MPa. Therefore, they all meet the requirement of codes.
4 Conclusions
Based on the analysis of cantilever casting construction process of concrete arch bridge, stress balance and influence matrix methods for determining the initial cable force of cantilever casting concrete arch bridge were proposed. During the cantilever casting construction process of concrete arch bridge, stress balance equations and influence matrix of arch rib critical sections were established. The allowable stress of arch rib critical sections as the constraint condition was used to determine the range of buckle cable force. Then a group of buckle cable forces were selected and substituted into stress balance equations, and reasonable initial buckle cable forces were determined by the iteration method. In addition, based on the principle of force balance, initial anchor cable forces were determined.
1) From the engineering example, it is shown that initial buckle and anchor cable forces are utilized in the tensioning stage of current arch rib segment, and reach the maximum forces in the concrete cantilever casting stage of next arch rib segment.
2) Calculated and tested cable forces are in good agreement, and their difference is less than 3%. It is indicated that stress balance and influence matrix methods used for determining the initial cable force of cantilever casting concrete arch bridge in this study is feasible and reliable. In addition, the maximum tensile and compressive stresses of arch rib critical sections are, and their difference is less than 15%. Therefore, they all meet the requirement of codes.
3) From application results, it is shown that initial cable forces of arch rib segments only need to be adjusted once in the corresponding construction stage, which improves the working efficiency and reduces the construction risk.
References
[1] Khan E, SuLLIVAN T J, KOWALSKY M J. Direct displacement-based seismic design of reinforced concrete arch bridges [J]. J Bridge Eng, 2014, 19(1): 44-58.
[2] MOHSENI I, LASHKARIANI H A, KANG J, KANG H T. Dynamic response evaluation of long-span reinforced arch bridges subjected to near-and far-field ground motions [J]. Appl Sci, 2018, 8(8): 1243.
[3] ZHENG Jie-lian, WANG Jian-jun. Concrete-filled steel tube arch bridges in China [J]. Engineering, 2018, 4(1): 143-155.
[4] WEI Jiang-gang, CHEN Bao-chun, WANG Ton-lo. Studies of in-plane ultimate loads of the steel truss web-RC composite arch [J]. J Bridge Eng, 2014, 19(5): 1-8.
[5] YANG Cheng, XIANG Tian-yu, DU Bing. Stochastic long-term behavior of a reinforced concrete arch bridge [J]. Advances in Structural Engineering, 2017, 20(10): 1560-1571.
[6] CHEN Bao-chun, SAVOR Z, HUANG Qing-wei. Material perfor-mance for long span concrete arch bridges:higher is better [C]// ARCH’2016-8th Int Conf on Arch Bridges. Wroclaw, Poland, 2016: 85-102.
[7] Salonga J, Gauvreau P. Comparative study of the proportions, form,and efficiency of concrete arch bridges [J]. J Bridge Eng, 2014, 19(3): 1-12.
[8] ARENAS J J, CAPELLAN G, GARCIA P, MEANA I. Viaduct over River Almonte-conceptual design [C]// ARCH’ 16-8th Int Conf on Arch Bridges. Wroclaw, Poland, 2016: 313-322.
[9] ZDERIC Z, RUNJIC A, HRELJA, G. Design and construction of Cetina river arch bridge [C]// ARCH’07-5th Int Conf on Arch Bridges. Funchal, Madeira, Portugal, 2007: 745-750.
[10] CRUZ J P, CORDEIRO L J. Innovative and contemporary porto bridges [J]. Pract Period Struct Des Constr, 2004, 9(1): 26-43.
[11] PENG D G. Design of the new Mike O’Callaghan Pat Tillman memorial bridge at Hoover Dam [C]// ASCE Structures Congress. 2011: 1806-1815.
[12] AU F T K, WANG J J, LIU G D. Construction control of reinforced concrete arch bridges [J]. J Bridge Eng, 2003, 8(1): 39-45.
[13] CAPELLAN G, MARTINEZ J, MERINO E, GARCIA P, ARRIBAS D, JIMENEZ P. Viaduct over River Almonte-Site control supervision [C]// ARCH’ 16-8th Int Conf on Arch Bridges. Wroclaw, Poland, 2016: 487-496.
[14] SONG Gang-bing, WANG C, WANG B. Structural health monitoring (SHM) of civil structures [J]. Applied Science, 2017, 7(8): 789.
[15] LI H N, REN L, JIA Z G,YI T H, LI D S. State-of-the-art in structural health monitoring of large and complex civil infrastructures [J]. Journal of Civil Structural Health Monitoring, 2016, 6(1): 3-16.
[16] SONG G, LI W, WANG B, HO S. A review of rock bolt monitoring using smart sensors [J]. Sensors, 2017, 17(4): 776.
[17] LI H, OU J. The state of the art in structural health monitoring of cable-stayed bridges [J]. Journal of Civil Structural Health Monitoring, 2016, 6(1): 43-67.
[18] KIM J M, KIM C M, CHOI S Y, LEE B Y. Enhanced strain measurement range of an FBG sensor embedded in seven-wire steel strands [J]. Sensors, 2017, 17(7): 1654.
[19] CHEN D, HUO L, LI H, SONG G. A fiber bragg grating (FBG)-enabled smart washer for bolt pre-load measurement: design, analysis, calibration, and experimental validation [J]. Sensors, 2018, 18(8): 2586.
[20] HEGEDUS G, SARKADI T, CZIGANY T. Self-sensing polymer composite: white-light-illuminated reinforcing fibreglass bundle for deformation monitoring [J]. Sensors, 2019, 19(7): 1745.
[21] CHO K, PARK S, CHO, J R, KIM S, PARK Y H. Estimation of prestress force distribution in the multi-strand system of prestressed concrete structures [J]. Sensors, 2015, 15(6): 14079-14092.
[22] HUO L, CHEN D, LIANG Y, LI H, FENG X, SONG G. Impedance based bolt pre-load monitoring using piezoceramic smart washer [J]. Smart Materials and Structures, 2017, 26(5): 057004.
[23] WANG B, HUO L, CHEN D, LI W, SONG G. Impedance-based pre-stress monitoring of rock bolts using a piezoceramic-based smart washer-A feasibility study [J]. Sensors, 2017, 17(2): 250.
[24] HUO L,WANG B, CHEN D, SONG G. Monitoring of pre-load on rock bolt using piezoceramic-transducer enabled time reversal method [J]. Sensors, 2017, 17(11): 2467.
[25] JIANG T, KONG Q, PATIL D, LUO Z, HUO L, SONG G. Detection of debonding between FRP rebar and concrete structure using piezoceramic transducers and wavelet packet analysis [J]. IEEE Sens J, 2017, 17(7): 1992-1998.
[26] LI Wei-jie, LIU Tie-jun, ZOU Du-jian, WANG Jian-jun, YI Ting-hua. PZT based smart corrosion coupon using electro-mechanical impedance [J]. Mechanical Systems and Signal Processing, 2019, 129: 455-469.
[27] JIANG T, HONG Y, ZHENG J, WANG L, GU H. Crack detection of FRP-reinforced concrete beam using embedded piezoceramic smart aggregates [J]. Sensors, 2019, 19: 1979. DOI: 10.3390/s19091979.
[28] LI Wei-jie, LIU Tie-jun, WANG Jian-jun, ZOU Du-jian. Finite-element analysis of an electro-mechanical impedance- based corrosion sensor with experimental verification [J]. Journal of Aerospace Engineering, 2019, 32(3): 04019012.
[29] DUAN Y F, ZHANG R, DONG C Z, LUO Y Z,OR S W, ZHAO Y, FAN K Q. Development of elasto-magneto-electric (EME) sensor for in-service cable force monitoring [J]. International Journal of Structural Stability and Dynamics, 2016, 16(4): 1640016.
[30] YIM J, WANG M L, SHIN S W, YUN C B, JUNG H J, KIM J T, EEM S H. Field application of elasto-magnetic stress sensors for monitoring of cable tension force in cable-stayed bridges [J]. Smart Structures and Systems, 2013, 12(3): 465-482.
[31] SINGH V, LLOYD G M, WANG M L. Effects of temperature and corrosion thickness and composition on magnetic measure-ments of structural steel wires [J]. NDT & E International, 2004, 37(7): 525-538.
[32] LI W, FAN S, HO, S M, WU J, SONG G. Interfacial debonding detection in FRP rebar reinforced concrete using electro-mechanical impedance technique [J]. Structural Health Monito-ring, 2018, 17(3): 461-471.
[33] HASSAN M M, NASSEF A O, DAMATTY A A. Determination of optimum post-tensioning cable forces of cable-stayed bridges [J]. Eng Struct, 2012, 44: 248-259.
[34] HA M H,VU Q A, TRUONG V H. Optimum design of stay cables of steel cable-stayed bridges using non-linear inelastic analysis and genetic algorithm [J]. Structures, 2018, 16: 288-302.
[35] KASUGA A, ARAI H, BREEN J E, FURUKAWA K. Optimum cable-force adjustments in concrete cable-stayed bridges [J]. J Struct Eng, 1995, 121(4): 685-694.
[36] WU Jie, FRANGOPOL D M, SOLIMAN M. Geometry control simulation for long-span steel cable-stayed bridges based on geometrically nonlinear analysis [J]. Engineering Structures, 2015, 90: 71-82.
[37] WEI Jian-jun, LI Chuan-fu. Optimization analysis of cable tensions for suspension erection of long-span CFST arch bridge [C]// International Conference on Transportation Engi-neering. 2009: 1808-1813.
[38] BRUNO D, LONETTI P, PASCUZZO A. An optimization model for the design of network arch bridges [J]. Computers and Structures, 2016, 170: 13-25.
[39] ELREHIM M Z, EID M A, SAYED M G. Structural optimization of concrete arch bridges using genetic algo-rithms [J]. Ain Shams Engineering Journal, 2019, 10(3): 507-516. DOI: https://doi.org/10.1016/j.asej.2019.01.005.
[40] SUNG Yu-chi, CHANG D W, TEO E H. Optimum post-tensioning cable forces of Mau-Lo Hsi cable-stayed bridge [J]. Engineering Structures, 2006, 28(10): 1407-1417.
[41] WANG P H, TANG T Y, ZHENG H N. Analysis of cable-stayed bridges during construction by cantilever methods [J]. Computers and Structures, 2004, 82(4, 5): 329-346.
[42] GRANATA M F, LONGO G, RECUPERO A, ARICI M. Construction sequence analysis of long-span cable-stayed bridges [J]. Engineering Structures, 2018, 174: 267-281.
[43] FABBROCINO F, MODANO M, FARINA I, CARPENTIERI G, FRATERNALI F. Optimal prestress design of composite cable-stayed bridges [J]. Composite Structures, 2017, 169: 167-172.
[44] SONG Chao-lin, XIAO Ru-cheng, SUN Bin. Optimization of cable pre-tension forces in long-span cable-stayed bridges con-sidering the counterweight [J]. Engineering Structures, 2018,172: 919-928.
[45] LI Yang, WANG Jiang-long, GE Su-su. Optimum calculation method for cable force of concrete-filled steel tube arch bridae in inclined cable-stayed construction [J]. J Highway Transp Res Dev, 2017, 11(1): 42-48.
[46] NAKAMURA S, TANAKA H, KATO K. Static analysis of cable-stayed bridge with CFT arch ribs [J]. Journal of Constructional Steel Research, 2009, 65(4): 776-783.
[47] CARPENTIERI G, MODANO M, FABBROCINO F, FEO L, FRATERNALI F. On the optimal design of cable-stayed bridges [C]// VII European Congress on Computational Methods in Applied Sciences and Engineering. Crete Island, Greece, 2016: 3386-3394.
[48] NEGRAO J H O, SIMOES L M C. Optimization of cable-stayed bridges with three-tuple modelling [J]. Computers and Structures, 1997, 64(1-4): 741-758.
[49] KANG H J, ZHAO Y Y, ZHU H P, JIN Y X. Static behavior of a new type of cable-arch bridge [J]. Journal of Constructional Steel Research, 2013, 81: 1-10.
[50] BALDOMIR A, HERNANDEZ S, NIETO F, JURADO J A. Cable optimization of a long span cable stayed bridge in La Coruna [J]. Advances in Engineering Software, 2010, 41(7, 8): 931-938.
[51] TIAN Wei-fei, ZHANG Liang-liang, AYAD T S. Calculation of cable force and pre-camber for long-span rib arch bridge construction by unstressed state concrol method [C]// International Conference on Transportation Engineering, 2011: 2104-2109.
[52] MARTINS A B, SIMOES L M C, NEGRAO J J O. Optimization of cable forces on concrete cable-stayed bridges including geometrical nonlinearities [J]. Computers and Structures, 2015, 155: 18-27.
[53] DAI Yu-wen, WANG You-yuan. A research to cable force optimizing calculation of cablestayed arch bridge [J]. Procedia Engineering, 2012, 37: 155-160.
[54] CHEN D W, AU F T K, THAM L G, LEE P K K. Determination of initial cable forces in prestressed concrete cable-stayed bridges for given design deck profiles using the force equilibrium method [J]. Computers and Structures, 2000, 74(1): 1-9.
[55] WANG P H, TSENG T C,YANG G G. Initial shape of cable-stayed bridges [J]. Computers and Structures, 1993, 47(1): 111-123.
[56] ZHANG J, AU F T K. Calibration of initial cable forces in cable-stayed bridge based on Kriging approach [J]. Finite Elements in Analysis and Design, 2014, 92: 80-92.
[57] JANJIC D, PIRCHER M, PIRCHER H. Optimization of cable tensioning in cable-stayed bridges [J]. J Bridge Eng, 2003, 8(3): 131-137.
[58] GRANATA M F, MARGIOTTA P, RECUPERO A, ARICI M. Partial elastic scheme method in cantilever construction of concrete arch bridges [J]. J Bridge Eng, 2013, 18(7): 663-672.
[59] JTG 3362-2018. Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts [S]. (in Chinese)
[60] JTG D64-2015. Specifications for design of highway steel bridge [S]. (in Chinese)
[61] SI X, AU T F, LI Z. Capturing the long-term dynamic properties of concrete cable-stayed bridges [J]. Finite Engineering Structures, 2013, 57: 502-511.
(Edited by YANG Hua)
中文导读
基于应力平衡和影响矩阵的混凝土拱桥悬臂浇筑初始索力确定方法研究
摘要:采用挂篮悬臂浇筑法建造混凝土拱桥具有广阔的应用前景,然而确定合理的扣、锚索索力是混凝土拱桥施工过程中的难点问题。本文提出采用影响矩阵和应力平衡法确定悬臂浇筑混凝土拱桥施工阶段的初张索力。在混凝土拱桥悬臂浇筑施工过程中,建立拱肋关键截面的应力影响矩阵和平衡方程,以拱肋关键截面的容许应力为约束条件,确定各扣索的索力范围。进而,选取一组扣索力代入其应力平衡方程,采用迭代法确定合理的施工扣索力。最后,基于力平衡原理确定锚索力。工程应用实例表明,采用影响矩阵和应力平衡法确定悬臂浇筑混凝土拱桥的合理施工索力是可靠的。在施工过程中,拱肋节段的索力只需张拉一次,本文提出的方法提高了工作效率,降低了施工风险。
关键词:混凝土拱桥;悬臂浇筑;初张索力;应力平衡法;影响矩阵法
Foundation item: Projects(51478049, 51778068) supported by the National Natural Science Foundation of China; Project(14JJ2075, 2019JJ40301) supported by the Hunan Natural Science Foundation of China; Project(17A010) supported by the Scientific Research Fund of Hunan Provincial Education Department of China; Project(2017GK4034) supported by the Major Technological Achievements Transformation Program of Hunan Strategic Emerging Industries of China
Received date: 2019-06-10; Accepted date: 2019-10-08
Corresponding author: JIANG Tian-yong, PhD, Associate Professor; Tel: +86-18573105078; E-mail: tianyongjiang@csust.edu.cn; DENG Yang, PhD, Associate Professor; Tel: +86-15011210566; E-mail: dengyang@bucea.edu.cn

