基于序分量提取的无功和谐波电流同步坐标检测方法
牟龙华,吕军,周伟
(同济大学 电气工程系,上海,201804)
摘要:为研究无功补偿和谐波抑制的关键技术中的无功、不对称和谐波电流检测与计算方法,提出基于序分量提取的同步坐标法。研究结果表明:采用无锁相环的广义dq0变换,能准确提取出基波及整数次谐波正、负序以及零序分量;根据不同的无功补偿目标,能准确地检测出基波正序有功电流和基波正序无功电流,分开基波正序无功电流、不对称与谐波电流,实现分别补偿;该法可用于三相三线制和四线制电力系统以及不对称系统;理论推导和仿真结果验证所提方法的正确性。
关键词:序分量提取;同步参考坐标法;检测;不对称系统
中图分类号:TM761 文献标志码:A 文章编号:1672-7207(2011)02-0419-08
Synchronous reference frame method for reactive and harmonics currents detection based on sequence component extraction
MU Long-hua, L? Jun, ZHOU Wei
(Department of Electrical Engineering, Tongji University, Shanghai 201804, China)
Abstract: In order to study the detection method and calculation of reactive power, unbalance and harmonic current, an improved synchronous reference frame method based on sequence component extraction in the time domain was presented. The results show that for the use of general dq0 theory without PLL, the method can accurately extract positive, negative and zero sequence components of both fundamental and integer harmonics, detect fundamental positive sequence active currents and reactive currents, as well as distinguish the fundamental positive sequence reactive current from the sum of unbalanced components and harmonic currents based on different compensating purposes. The proposed method is suitable for the three-phase three-wire or four-wire or unbalanced power system and is verified by theoretical analysis and simulation.
Key words: sequence component extraction; synchronous reference frame method; detection; unbalanced system
非线性负荷及冲击性负荷的增加与广泛使用,使电力系统的谐波和不对称问题日益严重,必须对其进行抑制和补偿。无功、不对称和谐波电流的检测与计算方法一直是无功补偿和谐波抑制技术中的重点研究内容。目前的研究大多是针对三相对称正弦电源系统。基于频域法的主要有快速傅里叶(FFT)算法及其改进算法,其缺点是算法复杂、实时性较差。陈明凯等[1]提出的扇合矢量法将三相电量扇合到一相,从扇合矢量中提取基波正序分量。该方法实质是离散傅里叶(DFT)算法,也存在数据窗问题。在实际中采用较多的是时域检测方法。自适应检测法[2-3]以系统电压波形为模板来获取所需的补偿分量,即使系统电压波形发生畸变仍具有较好的自适应能力,检测精度不受电压波形的影响,然而,动态响应速度较慢。瞬时功率理论结合系统电压波形和负荷电流信息来提取负荷电流中的谐波、无功分量,目前使用较多的是p-q和ip-iq算法[4-5]。在电压波形发生畸变时,不论电压电流是否对称,p-q检测算法都有误差,当电压波形不对称且畸变时,ip-iq算法能检测出基波正序电流,但有功电流的检测存在误差[6]。同时,在实际电网中,三相电压的不对称和非正弦现象普遍存在,同步坐标变换 法[7-10]可较好地实现谐波与无功电流的检测,但因现场工况的复杂性和装置容量的有限性,补偿目标的选择不具有唯一性,使得检测目标也不唯一。在此,本文作者根据矢量分析的通用瞬时功率理论,提出基于序分量提取的无功电流同步坐标检测法。为了获取基波正序电压波形信号,提出了无锁相环的序分量快速提取算法。利用广义dq0变换,能准确提取出基波及整数次谐波正、负序以及零序分量。该法引进基波正序电压波形信息,因而能准确提取出基波正序有功电流,能分开基波正序无功电流、不对称与谐波电流,并实现分别补偿,可方便地用于三相三线制和四线制电力系统。
1 序分量检测原理
根据对称分量法将三相电压、负载电流分解为正序、负序和零序分量,得:
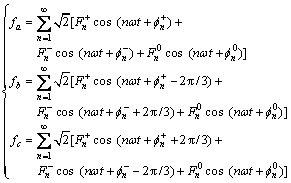 (1)
(1)
式中:fa,fb和fc分别为a,b和c三相电压/电流信号;
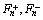 和
和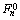 分别为n次谐波的正序、负序及零序的有效值;
分别为n次谐波的正序、负序及零序的有效值;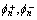 和
和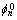 分别为n次谐波的正序、负序及零序的初相角;n=1时表示基波;ω为系统角频率。
分别为n次谐波的正序、负序及零序的初相角;n=1时表示基波;ω为系统角频率。
三相电压/电流通过同步坐标变换到dq0坐标 系[11-13],则有:
 (2)
(2)
其中:
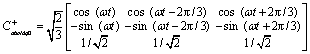 (3)
(3)
将式(1)代入式(2),可得:
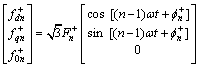 (4)
(4)
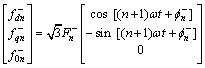 (5)
(5)
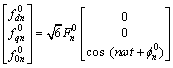 (6)
(6)
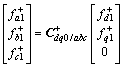 (7)
(7)
其中: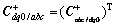 。
。
三相电压(电流)基波正序分量经dq0变换后为直流量,其他各分量仍是交流量。采用低通滤波器(LPF)和式(7)的反变换就能提取出基波正序分量。如图1所示,图中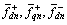 和
和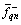 为直流分量。
为直流分量。
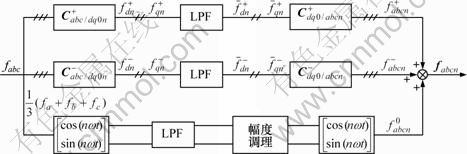
图1 序分量检测框图
Fig.1 Principle diagram of sequence component extraction
当信号中不仅含有基波分量,还含有谐波成分时,为检测谐波正、负序分量,采用式(8)的广义dq0变换矩阵 ,则能提取出m次谐波的正、负序分量,即
,则能提取出m次谐波的正、负序分量,即
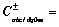
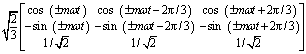 (8)
(8)
基波零序分量常通过截止频率在45~90 Hz的带通滤波器来获取,但因存在对基波信号产生附加相移,中心频率对参数的变化很敏感等因素,不易实现。为此,利用图1所示方法求出谐波零序分量为:
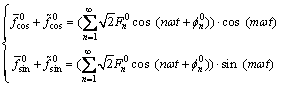 (9)
(9)
其中: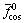 和
和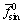 为直流分量;
为直流分量;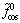 和
和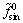 为交流 分量。
为交流 分量。
将式(9)通过低通滤波器滤去交流分量,得到幅值衰减为一半的直流分量。经过幅度调理,幅值扩大2倍再经正余弦变换,得到的直流分量之和即为零序分量。系统仅含有基波分量时,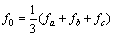 ,不存在任何延时。
,不存在任何延时。
传统的dq0变换法,采用锁相环(PLL)电路获取电压频率和初相角,经正余弦发生器产生正余弦信号,采用倍频电路来获取高频信号。当三相电压不对称时,锁相结果与正序分量存在相差。不难证明因电压不对称引起的相差不影响最终的结果;也不难证明对含任意初相角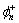 /
/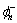 电压/电流序分量的信号进行dq0变换,该变换总是成立的。在电压频率恒为工频时,采用上述方法能检测出任意整数次谐波。但在实际中,电压角频率允许存在偏差。设低通滤波器的截止角频率Ψ,预先指定的电压角频率为工频ab=100π,经dq0变换得到的低频信号角频率为Φ=mω0-nω,则能获取的谐波次数上限为m=Ψ/(ω0-ω)。低通滤波器截止频率、检测到的最高谐波次数和系统频率间的关系如图2所示,图2所示为系统频率低于50 Hz的情况。
电压/电流序分量的信号进行dq0变换,该变换总是成立的。在电压频率恒为工频时,采用上述方法能检测出任意整数次谐波。但在实际中,电压角频率允许存在偏差。设低通滤波器的截止角频率Ψ,预先指定的电压角频率为工频ab=100π,经dq0变换得到的低频信号角频率为Φ=mω0-nω,则能获取的谐波次数上限为m=Ψ/(ω0-ω)。低通滤波器截止频率、检测到的最高谐波次数和系统频率间的关系如图2所示,图2所示为系统频率低于50 Hz的情况。
基波分量经dq0变换后得到的低频信号角频率远远小于低通滤波器的截止角频率,所以,不会影响基波分量的提取。但系统频率波动时,经dq0变换提取的序分量存有相移。为了补偿系统频率波动引起的相移,可采用软件测频方法[14]自适应调整同步坐标的旋转角频率来消除此相移。结合式(1),(2)和(9)可知:dq0变换后信号频率不变,去除了谐波干扰,只含有三相对称基波信号,因而能简洁地测量到系统频率,如图3所示。旋转角频率调整前后的序分量检测误差如表1所示(设调整前预置频率为50 Hz)。
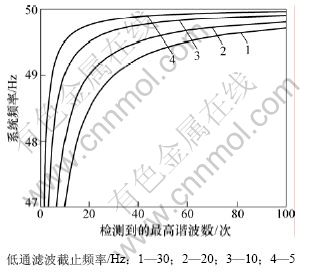
图2 系统频率和低通滤波器截止频率对谐波检测的影响
Fig.2 Relationships among frequency, cutoff frequency of LPF and harmonic

图3 自适应测频
Fig.3 Self-adaptive frequency measurement
表1 系统频率波动下的序分量检测误差
Table 1 Comparison of sequence component with and without error correction in frequency jitter power system

2 改进的同步坐标法
将电源正序电压信号和三相负载电流信号进行αβ0变换,得:
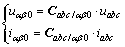 (10)
(10)
其中: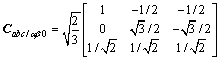
根据右手αβ0坐标系,电流矢量I可分解为2个相互正交的矢量Ip和Iq。在αβ0坐标中,将I投影到电压矢量U方向上,得有功电流Ip各分量为:
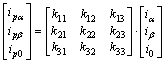 (11)
(11)
其中: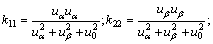
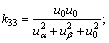
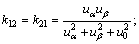
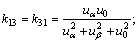
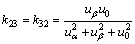 。
。
将Ip从αβ0坐标经式(12)变换到dq0坐标系中,可得:
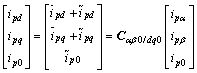 (12)
(12)
其中: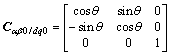 ;θ为同步旋转角。
;θ为同步旋转角。
通过相位补偿、软件查表方法得到式(12)中的同步旋转角θ,存在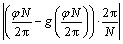 的相位滞后或超前误差(其中:N为工频周期内正余弦表的数据个数;φ为补偿相位;g(·)表示四舍五入取整运算)。采用基波正序电压信号来构造同步旋转正余弦信号,省去了相位补偿误差和锁相环电路。在αβ0坐标系中可知,当电压仅含有基波正序分量时,电压矢量被约束在αβ所确定的平面内旋转,从而有[9]:
的相位滞后或超前误差(其中:N为工频周期内正余弦表的数据个数;φ为补偿相位;g(·)表示四舍五入取整运算)。采用基波正序电压信号来构造同步旋转正余弦信号,省去了相位补偿误差和锁相环电路。在αβ0坐标系中可知,当电压仅含有基波正序分量时,电压矢量被约束在αβ所确定的平面内旋转,从而有[9]:
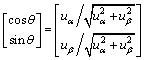 (13)
(13)
可证明
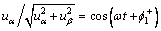 (14)
(14)
式(14)反映了正序电压频率和初相角,其与电压矢量匀速同步旋转。ipd,ipq和ip0通过低通滤波器,滤去谐波分量,得到基波正序电流的直流分量,然后,经过式(15)反变换就可得到广义无功电流(即谐波、不对称分量和无功电流总和)。
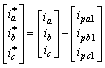 (15)
(15)
其中:ipa1,ipb1和ipc1为基波正序有功电流;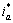 ,
,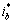 和
和 为各相谐波电流总和;
为各相谐波电流总和;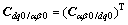 ;
;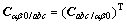 。结合式(10)~(14),可简化无锁相环同步坐标检测法,原理如图4所示。图中简化的dq0变换矩阵为:
。结合式(10)~(14),可简化无锁相环同步坐标检测法,原理如图4所示。图中简化的dq0变换矩阵为:
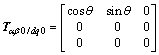 ;
;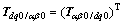
设基波正序无功电流为iqabc1,基波不对称及谐波电流为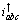 ,则有:
,则有:
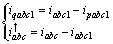 (16)
(16)
其中:ia1,ib1和ic1为基波正序电流。
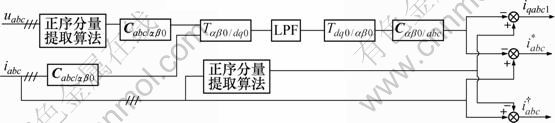
图4 无锁相环同步坐标检测法原理框图
Fig.4 Principle diagram of proposed currents detection
3 补偿方案分析
为防止不对称分量及谐波注入系统,负荷补偿应尽可能使补偿后的电流为正弦对称量,即电流正弦化。基于广义无功电流的补偿目标能使负荷只从电网吸收与电压正序同相位的正弦电流,而无功、不对称和谐波电流则由补偿器吸收,其代价是系统必须提供大于负荷所需的基波正序有功电流。对于不平衡系统,进行dq0变换及低通滤波后,把不对称的基波分量平均分到其他相中去,从而补偿了不平衡负载所需要的零序、负序分量,保证了系统侧三相电流对称。若负序、零序和谐波电流比较大,会使补偿器的输出严重不对称,其中某相电流可能很大,使得装置的容量也加大。为降低装置的补偿容量,可设定为只补偿特定次谐波。在有些应用场合,为了提高装置的利用效率,需要分开基波无功电流、不对称分量与谐波[15]。补偿基波无功时,其变流器可以采用大功率低开关频率的开关器件;补偿高次谐波时,其变流器采用小功率高开关频率的开关器件,从而使二者的优势互补。考虑到不同的补偿目标,给出了如表2所示的补偿方案。
表2 补偿方案
Table 2 Compensation schemes

采用本文提出的算法,计算出的基波有功电流不含零序电流分量,即iα和iβ已不含零序分量。将其和负荷电流相减就能实现对零序分量的补偿,因而适合于三相四线制系统。
设补偿前的电流矢量为i′,其含有零序分量,补偿后的电流矢量为i″。期望电流矢量i″落在αβ0坐标系下αβ组成的平面内,以消除零序的影响。设补偿后电流矢量i″的坐标为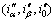 ,则有
,则有
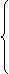
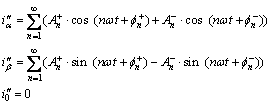 (17)
(17)
当满足式(18)时,得到补偿后电流i″即为基波正序有功电流。其轨迹为图5(a)所示逆时针旋转的圆。
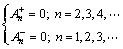 (18)
(18)
谐波抑制及无功补偿的意义可以理解为:在αβ0坐标系中,电流旋转矢量在空间中形成了不规则的三维曲线,通过补偿使三维曲线成为αβ平面内的二维曲线。基于广义无功电流的补偿目标,则是使空间三维曲线光滑成αβ平面内且与基波正序电压同步旋转的半径不同的同心圆,如图5(b)所示。
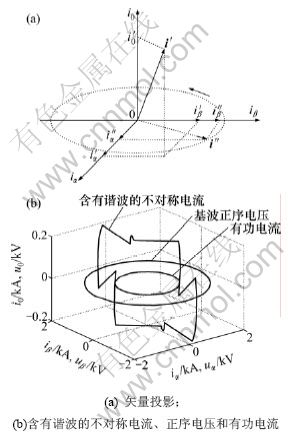
图5 αβ0坐标系下的正弦化电流矢量
Fig.5 Current vectors in αβ0 coordinate system
4 仿真分析
为检验算法的正确性,给出一组信号:
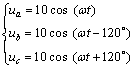
图6所示为根据上述序分量检测法得到的三相电压波形。显然,检测得到的电压波形与已知信号相序一致,幅值相同,相位也相同,说明序分量提取算法能准确提取出所需的信号。
进一步利用仿真软件PSCAD/EMTDC对本文提出的同步坐标法进行仿真计算。仿真系统中,采用线电压为10 kV、内电阻为1 Ω的三相电源,向三相全桥整流电路供电。晶闸管触发角为30°,整流桥负载为电阻10 Ω,滤波电感为50 mH。整流桥交流侧并接Y0型不对称负载,构成三相四线制系统。采样信号取自整流桥交流侧母线电压和母线电流。低通滤波器采用三阶巴特沃斯,截止频率为15 Hz。
图7所示为整流桥交流侧母线电压和电流波形,电压和电流均存在畸变和不对称现象。图8所示为采用序分量提取法得到的基波电流正序分量、基波电流负序分量、基波电流零序分量和基波电流波形图,可见序分量法能提取出所需的基波(谐波)序分量。
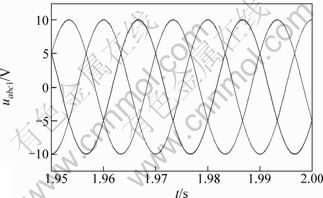
图6 检测到的正序电压信号波形
Fig.6 Waveforms of positive-sequence voltage
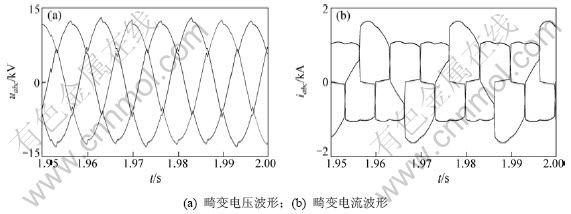
图7 畸变不对称电压和电流波形
Fig.7 Waveforms of three-phase unbalanced distorted voltages and currents
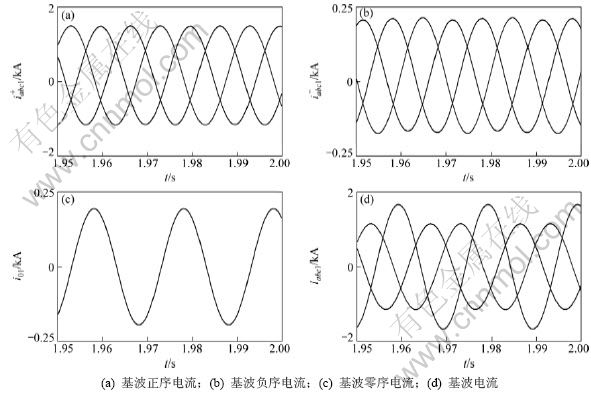
图8 序分量提取的基波电流及各部分分量
Fig.8 Waveforms of fundamental currents and its components
图9所示为基波正序电压、有功电流和无功电流波形图。基波正序有功电流与基波正序电压间存在线性关系,即频率相同,相位一致。
图10所示为基波不对称及谐波电流波形和广义无功电流波形。2种波形可作为特定的补偿基准信号。
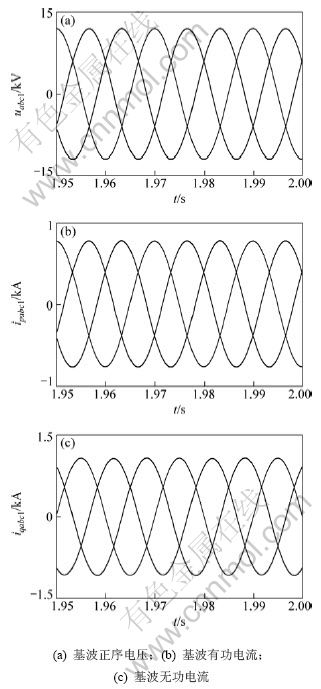
图9 基波正序电压、有功电流和无功电流
Fig.9 Waveforms of positive fundamental voltages, active currents and reactive currents
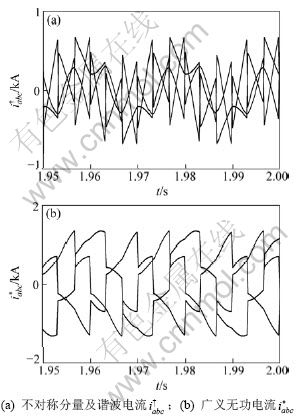
图10 不对称分量及谐波电流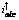 和广义无功电流
和广义无功电流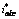
Fig.10 Unbalanced components and harmonic currents 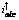 , generalized reactive currents
, generalized reactive currents 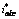
5 结论
(1) 提出无锁相环序分量快速提取算法,可用于获取基波正序电压波形信号,在需补偿特定次谐波的场合,能快速提取所需的谐波电流,不存在原理误差。
(2) 根据矢量分析的通用瞬时功率理论提出的基于序分量提取的同步坐标法,无需锁相环电路,能准确提取出基波正序有功电流,并能把基波正序无功电流和不对称及谐波电流分开以实现分别补偿,可方便地用于三相三线制和四线制电力系统。
参考文献:
[1] 陈明凯, 段小华, 李敏, 等. 扇合矢量法在谐波与无功电流检测中的应用[J]. 中国电机工程学报, 2008, 28(7): 110-115.
CHEN Ming-kai, DUAN Xiao-hua, LI Min, et al. Application of fan-in vector method in detection of harmonics and reactive current[J]. Proceedings of the CSEE, 2008, 28(7): 110-115.
[2] 蔡忠法, 陈隆道, 陈国志. 基于自适应神经网络的谐波分析模型与算法[J]. 电工技术学报, 2008, 23(7): 118-123.
CAI Zhong-fa, CHEN Long-dao, CHEN Guo-zhi. Harmonic analysis model and algorithm based on adaptive neural network[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 118-123.
[3] 李乔, 吴捷. 自适应谐波电流检测方法用于有源电力滤波器的仿真研究[J]. 电工技术学报, 2004, 19(12): 86-90.
LI Qiao, WU Jie. Simulation study of adaptive harmonic current detection method for active power filters[J]. Transactions of China Electrotechnical Society, 2004, 19(12): 86-90.
[4] Akagi H, Kanazawa Y. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Transactions on Industry Applications, 1984, 20(3): 625-630.
[5] 王兆安, 杨君, 刘进军, 等.谐波抑制和无功功率补偿[M]. 2版. 北京: 机械工业出版社, 2006: 220-256.
WANG Zhao-an, YANG Jun, LIU Jin-jun, et al. Harmonic suppression and reactive power compensation[M]. 2nd ed. Beijing: China Machine Press, 2006: 220-256.
[6] 谢运祥, 陈坤鹏, 邓衍平, 等. 改进型谐波与基波有功和无功电流检测法[J]. 华南理工大学学报: 自然科学版, 2005, 33(4): 15-19.
XIE Yun-xiang, CHEN Kun-peng, DENG Yan-ping, et al. Improved detecting method for harmonic and fundamental active and reactive currents[J]. Journal of South China University of Technology: Natural Science, 2005, 33(4): 15-19.
[7] 孙驰, 魏光辉, 毕增军. 基于同步坐标变换的三相不对称系统的无功与谐波电流的检测[J]. 中国电机工程学报, 2003, 23(12): 43-48.
SUN Chi, WEI Guang-hui, BI Zeng-jun. Detection for reactive and harmonics currents of unbalanced three-phase systems based on synchronous reference frame transformation[J]. Proceedings of the CSEE, 2003, 23(12): 43-48.
[8] 杨欢, 赵荣祥, 程方斌. 无锁相环同步坐标变换检测法的硬件延时补偿[J]. 中国电机工程学报, 2008, 28(27): 78-83.
YANG Huan, ZHAO Rong-xiang, CHENG Fang-bin. Delay compensation for harmonics detection based on synchronous reference frame without phase lock loop[J]. Proceedings of the CSEE, 2008, 28(27): 78-83.
[9] 陈东华, 谢少军, 周波. 用于有源电力滤波器谐波和无功电流检测的一种改进同步参考坐标法[J]. 中国电机工程学报, 2005, 25(20): 62-67.
CHEN Dong-hua, XIE Shao-jun, ZHOU Bo. An Improved synchronous reference frame method for harmonics and reactive currents detection of active power filters[J]. Proceedings of the CSEE, 2005, 25(20): 62-67.
[10] 周君求, 陈兰玉, 周沛锋, 等. 同步参考坐标法和正、负序基波提取器在电流检测中的比较[J]. 中南大学学报: 自然科学版, 2008, 39(4): 816-823.
ZHOU Jun-qiu, CHEN Lan-yu, ZHOU Pei-feng, et al. Contrastive research on improved synchronous reference frame method and detecting method based on sequence extractor of positive and negative fundamental wave for detecting current[J]. Journal of Central South University: Science and Technology, 2008, 39(4): 816-823.
[11] 戴列峰, 蒋平, 田大强. 无锁相环d-q谐波电流检测法的实 现[J]. 电网技术, 2003, 27(8): 46-49.
DAI Lie-feng, JIANG Ping, TIAN Da-qiang. Realization of harmonic current detection of d-q transformation without phase lock loop[J]. Power System Technology, 2003, 27(8): 46-49.
[12] 杨柳, 刘会金, 陈允平. 三相四线制系统任意次谐波电流的检测新方法[J]. 中国电机工程学报, 2005, 25(13): 41-44.
YANG Liu, LIU Hui-jin, CHEN Yun-ping. A new algorithm for random harmonic current detection in three phases four wires system[J]. Proceedings of the CSEE, 2005, 25(13): 41-44.
[13] 李亚峰, 李含善, 任永峰. 用于串联型有源电力滤波器的dq0变换[J]. 电工技术学报, 2005, 20(8): 59-63, 73.
LI Ya-feng, LI Han-shan, REN Yong-feng. dq0 transformation used in the series active power filter[J]. Transactions of China Electrotechnical Society, 2005, 20(8): 59-63, 73.
[14] 牟龙华, 邢锦磊. 基于傅里叶变换的精确频率测量算法[J]. 电力系统自动化, 2008, 32(23): 67-70, 94.
MU Long-hua, XING Jin-lei. An accurate frequency measuring algorithm for power systems based on Fourier transform[J]. Automation of Electric Power Systems, 2008, 32(23): 67-70, 94.
[15] 李庚银, 陈志业, 丁巧林, 等. dq0坐标系下广义瞬时无功功率定义及其补偿[J]. 中国电机工程学报, 1996, 16(3): 176-179.
LI Geng-yin, CHEN Zhi-ye, DING Qiao-lin, et al. Definition of generalized instantaneous reactive power in dq0 coordinates and its compensation[J]. Proceedings of the CSEE, 1996, 16(3): 176-179.
(编辑 陈爱华)
收稿日期:2009-11-12;修回日期:2010-03-02
基金项目:浙江省科技计划项目(2007C16034);国家火炬计划项目(2008GH040894)
通信作者:牟龙华(1963-),男,江苏宜兴人,教授,博士生导师,从事电力系统微机保护与电能质量的研究;电话:021-69589871;E-mail:lhmu@vip.163.com