ARTICLE

J. Cent. South Univ. (2019) 26: 2029-2040

DOI: https://doi.org/10.1007/s11771-019-4151-2

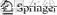
Flow pattern visualization and nonlinear analysis of gas-liquid mixing process with top-blowing gas stirring

YANG Kai(杨凯)^{1, 2}, WANG Shi-bo(王仕博)^{1, 2}, ZHU Xiu-le(朱秀乐)³,XU Jian-xin(徐建新)^{1, 2}, WANG Hua(王华)^{1, 2}

1. State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization, Kunming University of Science and Technology, Kunming 650093, China;

2. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming 650093, China;

3. Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The evaluation of the mixing effect of gas-liquid two-phase flow during the top-blown gas agitation mixing is one of the difficulties in the testing field, especially in the process of using the model method to study the metallurgical top-blowing process. In order to evaluate the effect of gas-liquid two-phase flow mixing, a gas chromatography simulation based on capacitance tomography was used to visualize the flow pattern and analyze the mixed characteristics. A gas top-blown agitation test rig was set up, the gas phase was air-selected, and the liquid phase was selected from synthetic heat-conducting oil. The top-blown stirring test process was measured and imaged by electrical capacitance tomography (ECT) equipment from ECT Instruments Ltd (UK). The MATLAB program was used to identify the mixing areas of the images to obtain the distribution of gas-liquid two-phase. The flow pattern of the gas-liquid mixing region was obtained. The chaotic detection of the gas-liquid mixing process was performed by the three-state test method; the images were processed by the counting box dimension-corrosion method to obtain the mixing uniformity time of gas-liquid flow. Results show that it is feasible to use the capacitance tomography technique to visualize the gas-liquid two-phase distribution. The uniformity time quantification of the gas-liquid mixing process is also achieved.

Key words: top-blowing; electrical capacitance tomography; gas-liquid mixing; visualization; three-state test; mixing uniformity time

Cite this article as: YANG Kai, WANG Shi-bo, ZHU Xiu-le, XU Jian-xin, WANG Hua. Flow pattern visualization and nonlinear analysis of gas-liquid mixing process with top-blowing gas stirring [J]. Journal of Central South University, 2019, 26(8): 2029-2040. DOI: https://doi.org/10.1007/s11771-019-4151-2.

1 Introduction

Mixing is a crucial step for many process technologies [1]. In the physical reaction, the mixing is mainly to obtain the uniformity of mixing, and in the chemical reaction, the mixing is to optimize the reaction process [2]. Metallurgical molten pool agitation is an important means to promote the mass transfer and heat transfer process of metal molten pool and to homogenize the composition and temperature of molten metal [3, 4]. By grasping the agitation state and characteristics of the reactants in the molten pool, we can guide the practice process, thereby increasing the reaction rate of the slag, gas, and molten metal, accelerating the melting rate of the solid material, and making the ingredients in the molten metal more uniform. Due to the high temperature inside the metallurgical bath, the current research on the multi-phase flow effect in the single-hole top-blowing process inside the metallurgical molten pool mainly includes the water model method [5] and the numerical simulation method [6-9]. XU et al [5] studied the quantification of multiphase mixing efficiency in water model and introduced the first Betti number to characterize the heterogeneity of the mixture. However, it uses a high-speed camera to capture the motion of the bubbles, and the imaging has overlap. PENG [6] studied the impact of supersonic oxygen jet on molten steel and slag in the molten pool of top-blown converter, and analyzed the effect of oxygen flow on the flow field of molten steel, but did not study the stirring effect of jet on molten steel and slag.

At present, the most commonly used methods for evaluating the mixing effect are: conductivity method [10], optical method [11], and thermal method [12]. However, the above method has a certain requirement on the selection of the working medium, and can only detect the mixed state of one or several positions in the reactor. There is a large error in using these methods to determine the degree of mixing of the working fluid. Therefore, the visual study and mixed characteristics analysis of the multiphase agitation mixing process are still very important.

Electrical capacitance tomography (ECT) is widely recognized as an effective tool for studying multiphase flow [13, 14], with non-invasive, fast response, real-time imaging and other advantages [15-19]. The basic principle of ECT is that according to the different dielectric constants of the tested substances, when the composition or concentration of the mixture changes, the dielectric constant of the mixture changes, thereby causing the capacitance change of the sensor array. After data acquisition and signal processing, the inverse problem in the electromagnetic field is used to solve the problem, and the media distribution inside the mixture is established. The use of ECT [20-22] allows non-invasive detection of the inner two- phase flow and can be used to understand flow parameters, such as solid concentration, particle velocity and bubble behavior [23]. Other than this, ECT has been used, for example, for imaging the flow of oil and water in the pipeline and for monitoring mixing and drying of wet granules [24-26].

Based on the above, a top-blown agitator based on ECT for measuring gas-liquid two-phase distribution was produced. The feasibility of imaging a gas-liquid mixing process with a capacitance tomography system has been studied; in particular, this work will visualize the gas-liquid mixing process and study whether the gas-liquid mixing behavior has chaotic characteristics under different working conditions, and obtain the earliest mixing time of the gas-liquid mixing process.

2 Electrical capacitance tomography

2.1 Composition of electrical capacitance tomography system

Electrical capacitance tomography (ECT) is a well-established imaging technique [14], which can provide permittivity distribution in a cross section (either circular or square) as images in real time. While its principle is similar to that used in X-ray CT in hospital, ECT is based on measuring capacitance from the boundary of a cross section and then reconstructing tomographic images, using a suitable algorithm. A typical ECT system is shown in Figure 1. The structure of its sensor is shown in Figure 2.

The AC-ECT system designed and developed by ECT Instruments Ltd is based on an AC capacitance measuring circuit with high frequency sine-wave excitation and phase-sensitive demodulation (PSD). It can acquire image data from a 12-electrode ECT sensor at up to 140 frames per second and can reconstruct online images at up to 100 frames per second, with a signal-to-noise ratio (SNR) of 73 dB, in comparison with 40 dB of the charge ECT system, which was developed at UMIST in the last two decades of last century.

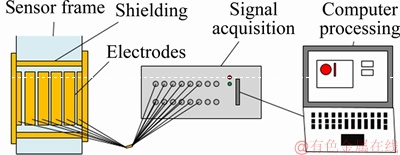
Figure 1 A typical ECT system

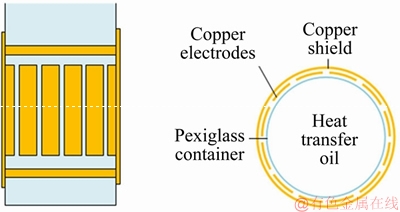
Figure 2 A simple cylindrical bottom blower (left) and simple agitator structure (right)

2.2 Basic principle of ECT system

The ECT image reconstruction system includes both hardware and software. Hardware refers to computers, and software is image reconstruction algorithms. The relationship between the capacitance between the sensitive array electrodes and the dielectric constant distribution e(x, y) can be expressed as

             (1)

An ECT system consisting of n electrodes can provide M independent measured capacitance values [18], resulting in M equations of the same Eq. (1). After finite element splitting, linearization, and discretization, it can be expressed as:

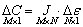                            (2)

where J is the Jacobi matrix, and N is the number of units. In this way, the nonlinear problem is approximated to a linear problem. It meets most occasions where the dielectric constant changes less. Eq. (2) is generally written as a normalized form:

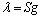                                 (3)

where the value of l composes the normalized capacitance vector; S is the normalized Jacobi matrix; g is the normalized vector of dielectric constant [15, 27].

After the data acquisition system has collected the data, a set of normalized capacitance values is saved. The normalized capacitance values are usually between zero and one. However, some normalized capacitance values may be negative or larger than one because of the soft-field effect. The normalized capacitance is usually calculated by

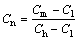                              (4)

where C_m is the measured absolute capacitance; C_l is the capacitance when the ECT sensor is empty, and C_h is the capacitance when the ECT sensor is completely filled with a high permittivity materials. As C_n has been saved and C_l and C_h have been calculated by data acquisition system, C_m can now be worked out.

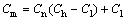                      (5)

As shown in Figure 3, in the measurement process, the 12-electrode ECT sensor adopts the “1P-1E-H” excitation mode, that is, the electrode 1 excites 11 electrodes such as 2, 3, …, 12, and the electrode 2 excites 10 electrodes such as 3, 4, …, 12, respectively. In this way, 66 sets of independent measured capacitance values are obtained, and the image reconstruction is performed by a linear back projection algorithm. The linear back projection algorithm is the earliest simple ECT image reconstruction algorithm. It will accumulate all the projected rays at a point and then inversely estimate the density value of that point. From an imaging perspective, it is an incomplete Rayden inverse.

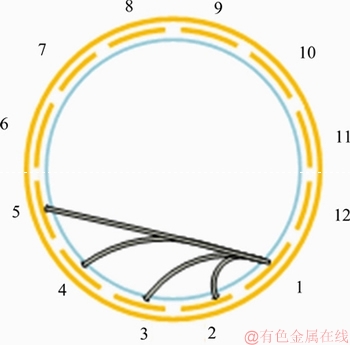
Figure 3 1P-1E-H excitation mode of ECT measuring electrode

3 Experimental method

The top blowing stirring experimental system is shown in Figure 4, including the air pump, the glass rotor flowmeter, the top blowing stirring tank (outer cover sensor), the data collector, and the computer.

The top-blown stirring tank has a height of 0.4 m and a diameter of 0.18 m. It is externally covered with an ECT sensor. The number of electrodes detected by the ECT sensor is 12, the material is 0.2 mm thick copper; the length of the electrode is 0.15 m; the width is 0.04 m; and the distance between each two electrodes is 7 mm. The upper and lower sides of the detection electrode are covered with a copper shield electrode and outer shield. The bottom of the sensor is 0.05 m from the bottom of the agitation tank. The glass rotor flowmeter is connected to the air outlet of the air pump through a rubber tube. The inner diameter of the rubber tube is 8 mm, and the valve of the air outlet of the air pump is adjusted to keep the reading of the glass rotor flow meter at 1.5 m³/h. The top of the glass rotor flowmeter is connected with a rubber tube. The end of the rubber tube is connected to a glass nozzle, and the diameter of the nozzle is 2 mm. During the experiment, the normal-temperature heat-transfer oil was added to the stirred tank until it was as high as the upper part of the sensor. The glass nozzle penetrates the inside of the heat transfer oil from the center of the top of the agitation tank to a depth of 0.02 m.

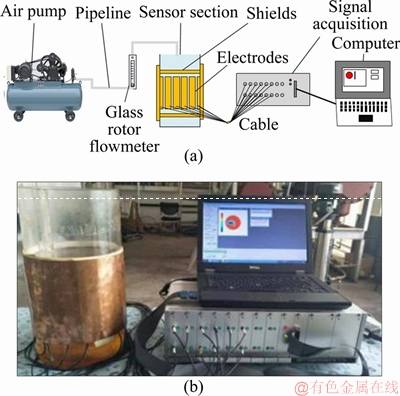
Figure 4 Top-blown stirring experimental system diagram (a) and physical map (b)

During the experiment, air and synthetic heat transfer oil were used as low and high standard materials respectively. The experimental process was as follows. In the initial state of the experiment, there is only air in the agitator, and the ECT system is activated to calibrate it. Next, the normal- temperature heat-transfer oil is added to the top of the top blowing agitation tank to the top of the sensor, and after the working medium is stabilized, it is calibrated. Then click on the “Record” button of the ECT system and start the air pump. The air is sprayed into the top-blown agitation tank through the pipeline to stir the working fluid. The flow rate of the top blowing gas was 1.5, 2 and 2.5 m³/h, respectively. At the same time, the ECT sensor receives the change of the capacitance values of the stirring process and transmits them to the data collector, thereby performing image reconstruction on the computer. The experimental system can acquire 1000 sets of normalized capacitance values within 16 s, that is, 1000 tomographic images can be reconstructed.

In order to verify the accuracy of the reconstructed image, a physical model is established in this paper. Two sealed PVC pipes of 4 cm in diameter were selected and inserted into the heat transfer oil at intervals of 5 cm, as shown in the left part of Figure 5, and the reconstructed image that is presented in the right part of Figure 5 was obtained. Image similarity (S_i) is used as an evaluation index of image reconstruction quality, such as shown in Eq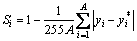. (6):

                   (6)

where A is the number of gray values in the image; y_i is the gray value in the model; y_i^* is the gray value in the experimental image.

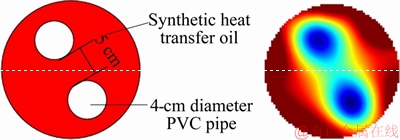
Figure 5 Model (left) and experimental image (right)

It is calculated that the similarity of the two images reaches 94.89%. Therefore, the uncertainty of the experimental process can be considered small. The smaller the uncertainty is, the closer the result is to the measured true value; and because the experimental process of this study is very intense, the focus is on imaging speed. It is acceptable to achieve an image reconstruction accuracy of 94.89% during the experiment.

4 Results and discussion

4.1 Flow pattern visualization and mixed feature extraction

Since the ECT image is tomographic, each set of capacitance value data can be reconstructed into a two-dimensional color map. Among them, red indicates synthetic heat transfer oil, blue indicates air, and yellow indicates gas-liquid mixed zone. Take the “original picture” in Figure 6 as an example, first denoise it, then use Colorpix, MATLAB and other software to identify and image the gas-liquid mixed area, and get the “feature extraction map” to make the gas-liquid mixed area more intuitive. Finally, the “feature extraction map” is grayscaled to make the gas-liquid mixed area clearer.

The synthetic heat transfer oil was stirred under conditions of a top-blowing air flow-rate of 1.5, 2.0 and 2.5 m³/h, respectively. In each case, 1000 sets of normalized capacitance values were obtained in 16 s, and image reconstruction was performed to obtain 1000 images. Taking the condition of the gas flow rate of 1.5 m³/h as an example, the first, 100th, 200th, …, 900th, 1000th images are processed as shown in Table 1.

It can be seen from Table 1 that the stirring effect of air on synthetic heat transfer oil is as follows: the gas-liquid mixing area changes from regular to irregular, and the area increases from small to large. This also shows that the agitation of the gas to the synthetic heat transfer oil is gradually becoming intense. Regardless of the case where the partial normalized capacitance value caused by the soft field effect is greater than one, it can be seen from the normalized capacitance value change of the first to the 1000th pictures in Figure 7, the fluctuation of the normalized capacitance value becomes more and more obvious with the passage of time.

In order to verify this assumption, the standard deviation of the normalized capacitance values of the three different operating conditions is obtained by calculation, as shown in Table 2 and Figure 8. According to this figure, the standard deviation is here used to discriminate the degree of dispersion of each set of data. The results show that under the same working conditions, the standard deviation of the normalized capacitance value becomes larger with time, that is, the degree of dispersion also becomes larger; as the amount of blown gas increases, the degree of dispersion of the normalized capacitance value increases, and the agitation process becomes more intense.

4.2 Chaotic feature extraction and mixing time quantification

Fractal dimension (FD) is a very useful feature in fractal geometry for analysis of digital images [28]. Box-counting dimensions are one of several ways to define fractal dimensions. In fractal geometry, the box-counting dimension, also known as box dimension, Minkowski dimension, is a measure of distance space (X,d) (especially Hausdorff space). Suppose that when the side length of the grid is ε, the space is divided into N grids in total, and then the box-counting dimension is:

                      (7)

where N is the number of boxes and ε is the length of the box.

In the course of the experiment, the three working conditions each obtained 1000 pictures within 16 s, and each graph corresponded to a box-counting dimension value. The 1000 box- counting dimension values constitute a time series, and the time series is processed by the "three-state test" method [29] to determine the chaotic characteristics. The three-state test (3ST) is a method based on ordinal pattern analysis for detecting chaos and determining the period in time series. The 3ST is based on the interpretation of the sign of λ(n): for periodic signals, evidently λ(n)=0 and for chaotic signals, μ(N, n) increases as a function of the observational time, hence λ(n)>0. Based on the assumption made on the definition of quasi-periodic signals, μ(N, n) is decreasing as the observational time evolves, thus implying λ(n)<0.

         (8)

where λ(n) represents the periodicity index;N=(Q-1)P₀+n is the length of the data sequence; P₀ is the integration step; Q is a natural number that is not equal to zero (the number of slopes evaluated); n is the minimum observation duration of the maximum slope to be evaluated,

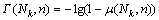                 (9)

The characteristics of the box-counting dimension numerical time series signal of the mixing process are presented in Figure 9. It is difficult to see from the figure what changes in the fractal dimension values over time. The evolution of dynamic systems is often confusing, because small disturbances in the initial state, such as small changes in the initial position of an object, will lead to fundamental changes in its future state [30]. This dynamic system is called a chaotic system. Using the “3ST” method to detect the fractal dimension values of the three working conditions, the signal characteristics of the three operating conditions in this paper are all chaotic.

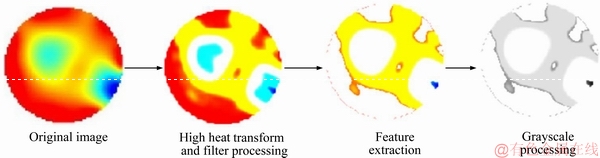
Figure 6 Main steps of obtained image processing (from left to right)

Table 1 ECT images with gas flow rate of 1.5 m³/h

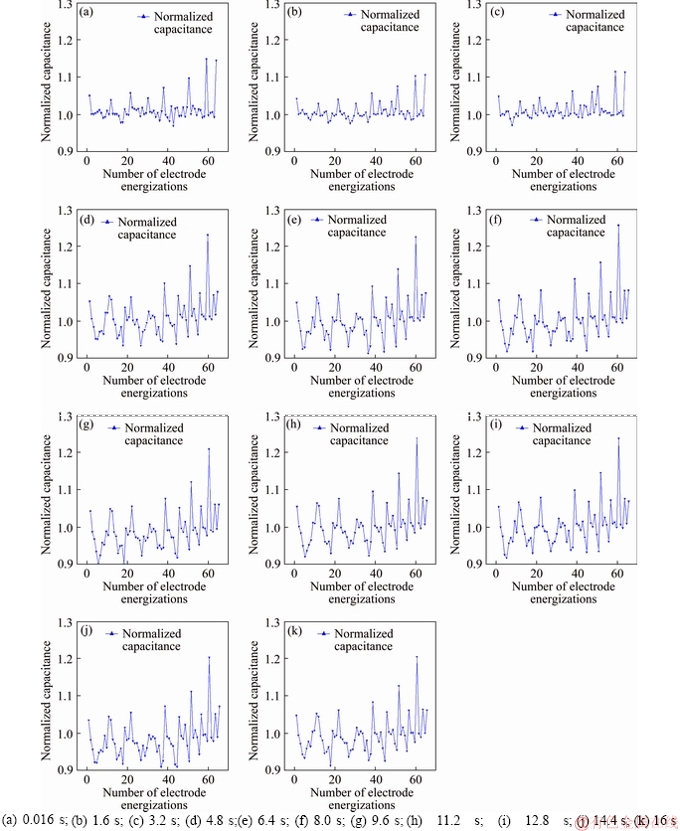
Figure 7 Normalized capacitance when gas flow rate is 1.5 m³/h

Table 2 Standard deviation of normalized capacitance values

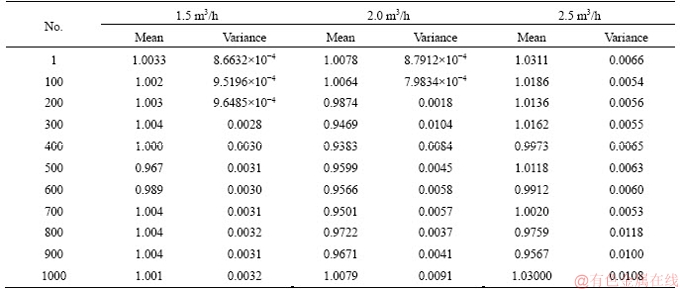
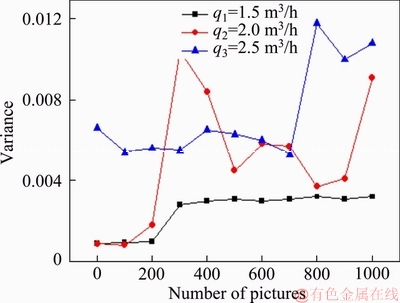
Figure 8 Variance of different working conditions

As shown in Figure 10, the eleven normalized capacitance values of the three operating conditions are selected for comparison. As can be seen from the figure, as time goes by, that is, from the first group to the 1000th group, the fluctuation of the normalized capacitance value becomes more and more obvious. However, for each working condition, the amount of data used for drawing is relatively small, and processing only 11 sets of data does not explain the problem. At the same time, the mixing effect of the gas-liquid two phases cannot be effectively quantified from the figure. Therefore, in the research process, it is necessary to find a way to systematically process the obtained experimental data.

COEN et al [31] conducted a corrosion operation on the same image five times during the prediction of the mixing time. It is found that the fitted curve of lgN and lgr is always a straight line, but the fractal dimension D is constant under any circumstances. This fully demonstrates that the fractal dimension D does not accurately represent the distribution of particles in the pattern. COEN et al [31] then proposed a box-counting dimensional corrosion method to characterize the mixing uniformity time. The method of averaging the slope value of the fractal dimension is adopted to obtain the shortest mixing time t, that is, the evolution curve of the time series is closely mixed with the point of the average value of the P value of the intra-cell oscillation and the closest distance. A more accurate and clear description of multiphase mixing uniformity is obtained here. There are two important indicators to measure the mixing effect: one is the size of the fractal dimension slope P, and the other is the minimum mixing uniform time.

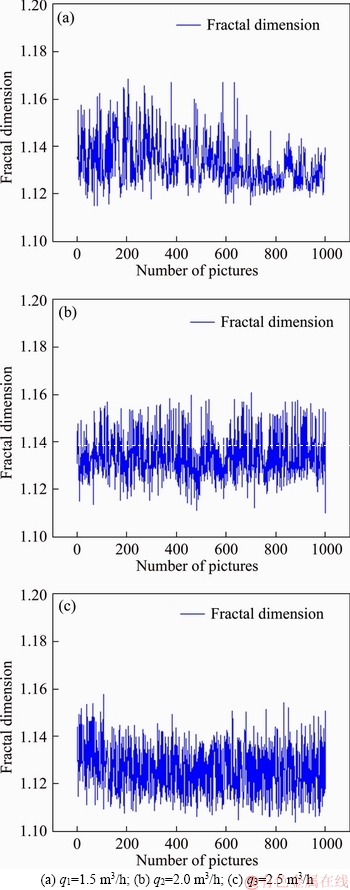
Figure 9 Fractal dimension values of different working conditions:

It can be seen from Figure 11 that at q₁=1.5 m³/h, the change of the P value has a significant increasing trend, and tends to stabilize the fluctuation state after the increase. When q₂=2.0 m³/h, the P value shows an upward trend in the early stage, and immediately rises to a stable fluctuation state. When q₃=2.5 m³/h, the P value is relatively stable at an early stage, but fluctuates greatly in the medium term and then tends to be stable. Considering that q₃ is a large intake air amount under the experimental conditions, the stirring is severe, and some synthetic heat transfer oil will be splashed during the experiment. Therefore, this is the reason why the P value fluctuates in the middle period. The earliest mixing time for the three different working conditions is shown in Table 3.

Figure 10 Capacitance values under different operating conditions:

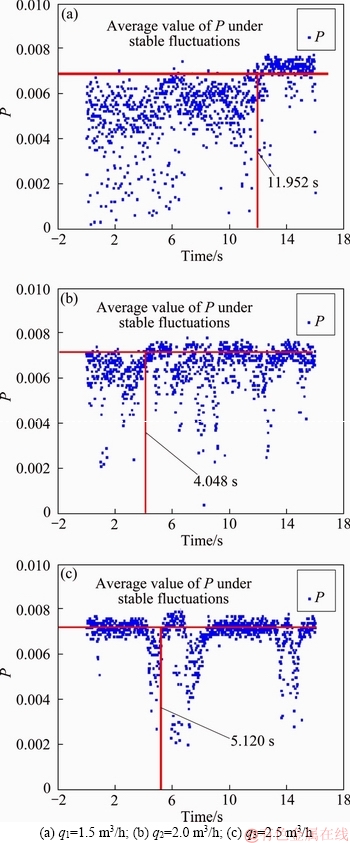
Figure 11 Mixing time of different working conditions:

Table 3 Earliest mixing time of three different working conditions

5 Conclusions

ECT is applied to the model experiment of metallurgical furnace in this work, and a top-blown agitator based on ECT to detect the gas-liquid two-phase mixing effect is designed to realize the visualization of the mixing effect of gas-liquid mixing and to get the earliest time of mixing uniformity. The conclusions drawn from the study may be summarized as follows:

1) It is feasible to use ECT to study gas-liquid mixing. From the experimental ECT image, the flow pattern feature can be extracted, and the image can be processed to obtain gas-liquid mixing characteristics, such as chaotic feature recognition and mixing time quantification.

2) At present, the experimental research on the working state of the working fluid in the metallurgical furnace is mostly the water model method. The method builds the experimental model through the similar principle. This work provides new devices and methods for experimental research of water models. And ECT has the advantages of fast response and non-intrusion.

3) The tomographic imaging of the gas-liquid mixing process is obtained through experiments, which can support the numerical simulation research. The measured results can help mathematical simulation researchers to correctly understand the physical characteristics of the research process, and provide a theoretical basis for metallurgical researchers to optimize the process. For example, researchers can refer to the effect of intake air on mixing time.

4) The gas-liquid mixing effect has a significant impact on the smelting effect in the metallurgical process, which also makes the research on the top blowing more practical. The design concept of the agitator can be used in the model method to study the bottom and side blowing processes of metallurgical baths, hydrometallurgical leaching and agitation processes, and other multiphase flow research fields.

Acknowledgement

The authors wish to especially thank the referees for numerous detailed questions and comments that greatly improved the presentation.

References

[1] BASSING D, BRAEUER A S. The lag between micro- and macro-mixing in compressed fluid flows [J]. Chemical Engineering Science, 2017, 163: 105-113. DOI: 10.1016/ j.ces.2017.01.034

[2] ZAISHA M, CHAO Y. Perspective to study on macro- mixing in chemical reactors [J]. CIESC Journal, 2015, 66(8): 2795-2804. DOI: 10.11949/j.issn.0438-1157.201506 28.

[3] XIAO Q, WANG H, WANG S, YANG P, WU K, XU J. Chaotic characterization of multiphase macromixing efficiency based on modified 0-1 test [J]. Chemical Engineering (China), 2016, 44(2): 46-51. DOI: 10. 3969/j.issn. 1005-9954. 2016. 02. 009. (in Chinese)

[4] WANG S, CHEN Y, LI D, XUE C. Experimental study on three dimensional turbulent flow in a water model of a metallurgical vessel stirred by a eccentric bottom gas injection [J]. Aerodynamic Experiment and Measurement & Control, 1992(1): 17-24. (in Chinese)

[5] XU J, WANG H, FANG H. Multiphase mixing quantification by computational homology and imaging analysis [J]. Applied Mathematical Modelling, 2011, 35(5): 2160-2171. DOI: 10.1016/j.apm.2010.11.028.

[6] PENG Jun, CHEN Zhuo, LIU Si-xuan, CHENG Li-zhen. Numerical simulation and single factor influence analysis of multi-phase flow in copper top-blown furnace [J]. The Chinese Journal of Process Engineering, 2017, 17(5): 926-934. DOI: 10.12034/j.issn.1009-606X.217145.

[7] LOU W, ZHU M Y. Numerical simulation of gas and liquid two-phase flow in gas-stirred systems based on Euler–Euler approach [J]. Metallurgical & Materials Transactions B, 2013, 44(5): 1251-1263. DOI: 10.1007/s11663-013-9897-6.

[8] LI Y, LOU W T, ZHU M Y. Numerical simulation of gas and liquid flow in steelmaking converter with top and bottom combined blowing　[J]. Ironmaking & Steelmaking, 2013, 40(7): 505-514. DOI: 10.1179/1743281212Y.0000000059.

[9] HE C, YANG N, HUANG Q, LIU C, WU L, HU Y, FU Z, GAO Z. A multi-phase numerical simulation of a four-nozzle oxygen lance top-blown convertor [J]. Procedia Earth & Planetary Science, 2011, 2(1): 64-69. DOI: 10.1016/j.proeps.2011.09.011.

[10] WU K, XIAO Q, WANG S, XU J, WANG H, YANG F. A study on the method for RGB color model applied in evaluate the top-blown mixing time [J]. Chemical Industry and Engineering Progress, 2016, 35(9): 2728-2734. DOI:10.16085/j.issn.1000-6613.2016.9.014.

[11] DONG Z. System design of flow velocity measurement gas-solid two-phase flow [D]. Shenyang: Northeastern University, 2014. (in Chinese)

[12] AHMAD R, MUSTAFA M, HAYAT T, ALSAEDI A. Numerical study of MHD nanofluid flow and heat transfer past a bidirectional exponentially stretching sheet [J]. Journal of Magnetism & Magnetic Materials, 2016, 407: 69-74. DOI: 10.1016/j.jmmm.2016.01.038.

[13] PERERA K, PRADEEP C, MYLVAGANAM S, TIME R. Imaging of oil-water flow patterns by Electrical Capacitance Tomography [J]. Flow Measurement & Instrumentation, 2017, 56: 23-34. DOI: 10.1016/j.flowmeasinst.2017.07.002.

[14] ZHANG M, SOLEIMANI M. Imaging floating metals and dielectric objects using electrical capacitance tomography [J]. Measurement, 2015, 74: 143-149. DOI: 10.1016/ j.measurement.2015.07.009.

[15] LIU J, LIU S, ZHOU W, QI X, LEI J, MU H. Sensing flame structure by process tomography [J]. Philos Trans A: Math Phys Eng Sci, 2016, 374(2070): 20150340. DOI: 10.1098/rsta.2015.0340.

[16] AGU C E, TOKHEIM L A, EIKELAND M, MOLDESTAD BM E. Determination of onset of bubbling and slugging in a fluidized bed using a dual-plane electrical capacitance tomography system [J]. Chemical Engineering Journal, 2017, 328: 997-1008. DOI: 10.1016/j.cej.2017.07.098.

[17] DU B, WARSITO W, FAN L S. ECT studies of gas-solid fluidized beds of different diameters [J]. Industrial & Engineering Chemistry Research, 2005, 44(14): 5020-5030. DOI: 10.1021/ie049025n.

[18] SUN J, YANG W, TIAN W. 3D imaging based on fringe effect of an electrical capacitance tomography sensor [J]. Measurement, 2015, 74: 186-199. DOI: 10.1016/ j.measurement.2015.07.018.

[19] LI X, JAWORSKI A J, MAO X. Bubble size and bubble rise velocity estimation by means of electrical capacitance tomography within gas-solids fluidized beds [J]. Measurement, 2018, 117: 226-240. DOI: 10.1016/ j.measurement.2017.12.017.

[20] CHANDRASEKERA T C, LI Y, MOODY D, SCHNELLMANN M A, DENNISJ S, HOLLANE D J. Measurement of bubble sizes in fluidized beds using electrical capacitance tomography [J]. Chemical Engineering Science, 2015, 126: 679-687. DOI: 10.1016/j.ces.2015. 01.011.

[21] QIU G, YE J, WANG H, YANG W. Investigation of flow hydrodynamics and regime transition in a gas–solids fluidized bed with different riser diameters [J]. Chemical Engineering Science, 2014, 116: 195-207. DOI: 10.1016/j.ces.2014.05.006.

[22] JIANG Y, QIU G, WANG H. Modelling and experimental investigation of the full-loop gas–solid flow in a circulating fluidized bed with six cyclone separators [J]. Chemical Engineering Science, 2014, 109(16): 85-97. DOI: 10.1016/ j.ces.2014.01.029.

[23] YANG D, LIU L, FENG W. Experimental investigation of an internally circulating fluidized bed with 32-electrode electrical capacitance volume tomography [J]. Measurement, 2018, 127: 227-237. DOI: 10.1016/j.measurement.2018. 05.076

[24] MOHAMAD E J, RAHIM R A, RAHIMAN M H F, AMERAN H L, MUJI S Z M, MARWAH M P. Measurement and analysis of water/oil multiphase flow using electrical capacitance tomography sensor [J]. Flow Measurement & Instrumentation, 2016, 47: 62-70. DOI: 10.1016/ j.flowmeasinst.2015.12.004.

[25] RIMPILINEN V, POUTIAINEN S, HEIKKINEN L M, SAVOLAINEN T, VAUHKONEN M, KETOLAINEN J. Electrical capacitance tomography as a monitoring tool for high-shear mixing and granulation [J]. Chemical Engineering Science, 2011, 66(18): 4090-4100. DOI: 10.1016/j.ces. 2011.05.044.

[26] RIMPILINEN V, HEIKKINEN L M, VAUHKONEN M. Moisture distribution and hydrodynamics of wet granules during fluidized-bed drying characterized with volumetric electrical capacitance tomography [J]. Chemical Engineering Science, 2012, 75(25): 220-234. DOI: 10.1016/j.ces.2012. 03.028.

[27] YANG W Q, PENG L. Image reconstruction algorithms for electrical capacitance tomography [J]. Journal of Tsinghua University, 2004, 14(4): 478-484. DOI: 10.1088/0957-0233/ 14/1/201.

[28] NAYAK S R, MISHRA J, KHANDUAL A, PALAI G. Fractal dimension of RGB color images [J]. Optik-International Journal for Light and Electron Optics, 2018, 162: 196-205. DOI: 10.1016/j.ijleo.2018.02.066.

[29] FOUDA J S A E, KOEPF W. Efficient detection of the quasi-periodic route to chaos in discrete maps by the three-state test [J]. Nonlinear Dynamics, 2014, 78(2): 1477-1487. DOI: 10.1007/s11071-014-1529-4.

[30] de PAULA A V, MLLER S V. On the chaotic nature of bistable flows [J]. Experimental Thermal and Fluid Science (Exp Therm Fluid Sci), 2018, 94: 172-191. DOI: 10.1016/j.expthermflusci.2018.01.006.

[31] COENT A L L, RIVOIRE A, BRIANCON S, LIETO J. An original image-processing technique for obtaining the mixing time: The box-counting with erosions method [J]. Powder Technology, 2005, 152(1): 62-71. DOI: 10.1016/j.powtec. 2005.01.025.

(Edited by YANG Hua)

中文导读

顶吹气体搅拌气液混合过程流型可视化和非线性分析

摘要：在顶吹气体搅拌混合体系中，气液两相流的混合效果评价是测试领域的难点之一，特别是在使用模型法研究冶金熔池顶吹的过程中。为了评估气液两相流的混合效果，提出基于电容层析成像(ECT)的气相色谱模拟来观察流型并分析混合特征。建立气体顶吹搅拌试验台，气相选择空气，液相选用合成导热油。使用ECT Instruments Ltd(UK)的电容层析成像设备对顶吹搅拌过程进行测量及成像。运用MATLAB程序对气液混合区域进行特征识别，获得气液两相的流型分布。运用“three-state-test(3ST)”方法对气液混合过程进行混沌检测；运用“腐蚀化计盒维数”法处理图像，得到气液搅拌的混均时间。结果表明，利用电容层析成像技术可对气液混合体系进行流型可视化和混匀时间量化。

关键词：顶吹；电容层析成像；气液混合；可视化；three-state-test (3ST)；混匀时间

Foundation item: Project(51666006) supported by the National Natural Science Foundation of China; Project(U1602272) supported by the Joint Funds of the National Natural Science Foundation of China; Project(2015HA019) supported by the Scientific and Technological Leading Talent Projects in Yunnan Province, China

Received date: 2019-05-30; Accepted date: 2019-07-17

Corresponding author: XU Jian-xin, PhD, Professor; Tel: +86-15912469765; E-mail: xujianxina@163.com; ORCID: 0000-0001-5248- 6848; WANG Hua, PhD, Professor; Tel: +86-18810086689; E-mail: wanghua65@163.com