
Microscopic phase-field simulation coupled with elastic strain energy for precipitation process of Ni-Cr-Al alloys with low Al content
LU Yan-li(卢艳丽), CHEN Zheng(陈 铮), LI Yong-sheng(李永胜), WANG Yong-xin(王永欣)
School of Materials Science and Engineering, State Key Laboratory of Solidification Processing,
Northwestern Polytechnical University, Xi’an 710072, China
Received 10 April 2006; accepted 28 November 2006
Abstract: The precipitation process of Ni-Cr-Al alloy with low Al content was studied at atomic scale based on the microscopic phase-field kinetic model coupled with elastic strain energy. The aim is to investigate the effect of elastic strain energy on precipitation mechanism and morphological evolution of the alloy. The simulation results show that in the early stage of precipitation, D022 phase and L12 phase present irregular shape, and they randomly distribute in the matrix. With the progress of aging, L12 phase and D022 phase change into the quadrate shape and their orientations become more obvious. In the later stage, L12 phase and D022 phase present quadrate shape with round corner and align along the [100] and [010] directions, and highly preferential selected microstructure is formed. The mechanism of early precipitation of L12 phase in Ni-17%Cr-7.5%Al (mole fraction) alloy is the mixed style of non-classical nucleation growth and spinodal decomposition and the D022 phase is the spinodal decomposition. The mechanisms of early precipitation of L12 phase and D022 phase in Ni-12.5%Cr-7.5% Al alloy are both the non-classical nucleation and growth. The coarsening process follows the rule of preferential selected coarsening.
Key words: Ni-Cr-Al alloy; elastic strain energy; microscopic phase-field; precipitation process; simulation
1 Introduction
The Ni-Cr-Al system is the most important ternary system for Ni-based superalloys used in the aerospace industry. The precipitation process of metastable ordered phase has drawn a great interest in recent years. PAREIGE et al[1] and PAREIGE-SCHMUCK et al[2] simulated the process of ordering and phase separation of the Ni-Cr-Al alloy at 600 ℃ using Monte Carlo method and compared 3DAP and TEM technologies. BROZ et al[3] calculated the γ+γ′ phase boundary and studied the morphology of Ni-Cr-Al alloys employing the software Thermo-Calc at 850-1 300 ℃. WU et al [4] simulated the microstructure evolution in γ+β/γ diffusion coupled with CALPHAD database. But they all have not quantificationally described precipitation process and transformation mechanism of Ni-Cr-Al alloy with temporal evolution of atom morphology and ordering parameters.
The microscopic phase-field kinetic model has made great success in simulating the morphological evolvement of precipitation[5-8]. However, the elastic strain energy was neglected in the above studies. For many alloys, because of the different lattice parameters between coherent precipitates and matrix phases, elastic strain energy maybe exists around precipitates, which can strongly affect the precipitation process. In this paper, we used the microelasticity theory and the microscopic diffusion kinetic equation that was developed by CHEN[9-10]. The equation was transformed into the Fourier space, so the 3D problem can be solved in the reciprocal space, and intuitionistic atomic configuration through 2D projection can be obtained.
In this paper, the effect of elastic strain energy on the precipitation mechanism and morphological evolution of Ni-Cr-Al alloys with low Al content was first studied. The evolution of atom morphology, concentration and long range order(LRO) parameter of L12 phase and D022 phase before the quadrate precipitation phase forming were mainly studied, and the coarsening process was analyzed, so that precipitation mechanism was predicted.
2 Theory model
2.1 Microscopic phase-field kinetic model of ternary system
Microscopic phase-field kinetic equation was based on the Onsage and Ginzburg-Landu equation[11-13], and the atomic structure and alloy morphology are described by a single-site occupation probability function P(r, t), which is the probability that a given lattice site r is occupied by an atom at time t. The change rate of these probabilities is linearly proportional to the thermodynamics driving force:
 (1)
(1)
where L(r-r′) is the symmetry matrix of the microscopic kinetics related to the probability of an elementary diffusion jump from site r to r′ per unit of time, F is the total free energy including the elastic strain energy contribution.
Microscopic diffusion equation was first put forward by KHACHATURYAN et al[11]. The micro- scopic equation of ternary system was developed by CHEN et al[6, 9]. The kinetic equation is
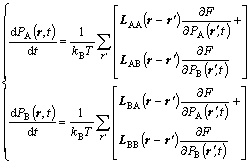 (2)
(2)
where PA(r, t) and PB(r, t) represent the probability of the A, B atoms at a given lattice site r at a given time t. Since for ternary system there are three kinds of atoms, we used PC(r, t) as the occupation probabilities of the C atom. Because PA(r, t)+PB(r, t)+PC(r, t)=1, only the two equations are independent of each other at each lattice site.
F is the total free energy of the system based on the mean-field approximation:
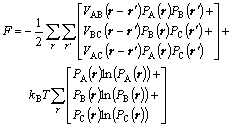 (3)
(3)
where Vαβ(r-r′) is the interaction energies between α and β(α, β=A, B or C) including chemical interaction Vαβ(r-r′)ch and elastic interaction Vαβ(r-r′)el.
Vαβ(r-r′)=Vαβ(r-r′)ch+Vαβ(r-r′)el (4)
2.2 Microelasticity theory
In the microelasticity theory, the strain energy of solid solution was given as two physically distinct terms[11,14]: 1) the configuration-independent term describing the self-energy and image force-induced energy; 2) the configuration-dependent term associated with concentration inhomogeneity. The first term is not affected by spatial redistribution of solute atoms and therefore it can be ignored. The second term however gives a substantially nonlocal strain energy change associated with spatial distribution of solute atoms, which affects the morphology of the precipitation phase.
In a real space, the configuration-dependent strain energy associated with an arbitrary atomic distribution P(r) is
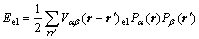 (5)
(5)
The Fourier transformation of Eqn.(5) yields[13]
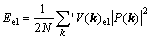 (6)
(6)
where N is the total lattice number. The superscript in the summation (6) implies that the point k=0 is excluded. V(k)el is the Fourier transformation of the density function of elastic energy V(r)el, and the long-wave approximation for V(k)el can be described as
 (7)
(7)
where n=k/k is a unit vector in the k direction, nx and ny are components of the unit vector k along the x and y axes,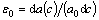 is the concentration coefficient of crystal lattice expansion caused by the atomic size difference, a(c) is the crystal lattice parameter of solute, a0 is the crystal lattice parameter of a solid solution, c is the molar fraction of solute atoms.
is the concentration coefficient of crystal lattice expansion caused by the atomic size difference, a(c) is the crystal lattice parameter of solute, a0 is the crystal lattice parameter of a solid solution, c is the molar fraction of solute atoms.
H(n) is the strain energy parameter that characterizes the elastic properties and the crystal lattice mismatch:
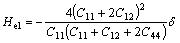 (8)
(8)
where 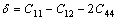 that is the elastic anisotropy constant and Cij are the elastic constants of the studied system. In this study, we choosed C11=212.7 MPa, C12=149.7 MPa, C44=100.0 MPa based on the value of Ni-based alloy at 900 K[15].
that is the elastic anisotropy constant and Cij are the elastic constants of the studied system. In this study, we choosed C11=212.7 MPa, C12=149.7 MPa, C44=100.0 MPa based on the value of Ni-based alloy at 900 K[15].
3 Simulation results and analysis
Ni-17%Cr-7.5%Al (mole fraction) alloy and Ni-12.5%Cr-7.5%Al alloy were aged at 900 K. The occupational probability of atom is represented by a gray scheme on which the black lattices indicate Ni atoms, the white lattices indicate Cr atoms and the gray ones indicate Al atoms. Thus, if the occupation probability of chromium is 1.0, then that site is assigned by the white color, and so on. Therefore, the D022 phase appears to be white, the L12 phase appears to be gray and a black background is formed. The simulation is performed in a square lattice consisting of 128×128 unit cells, periodic boundary conditions are applied along both dimensions, and the time step (t) is 0.000 1.
The morphology evolution of precipitates for Ni-17%Cr-7.5% Al alloy is presented in Fig.1. Many precipitate phases are formed in the disordered solution at 2 000 time steps as shown in Fig.l(a). They distribute randomly and present irregular shape and their atomic arrange is identical to the 2D projection of Ni3Cr order phase (D022 structure), so we regarded the precipitate phase as Ni3Cr[16]. As time proceeding, the D022 phase grows larger. The atomic picture at 3 000 time steps is shown in Fig.1(b). The L12 phase is formed around the D022 phase and in the other region; and they also distribute randomly. The condition at 10 000 time step is presented in Fig.1(c); the L12 precipitate phase and the D022 phase grow larger, and link together. The condition at 100 000 time steps is presented in Fig.1(d); the shape of the L12 and D022 phases changes from initial irregular to quadrate, at the same time, their alignment becomes more regular. With the progress of aging, the orientations of the L12 and D022 phases become more obvious; some precipitates located in particular direction gradually grow and others disappear. In the later stage, the L12 and D022 phases present quadrate shape with round corner and distribute regularly along the particular direction; the quadrate precipitates link together to form rods, as shown in Figs.1(e) and (f); and this behavior is regarded as preferentially selected coarsening process.
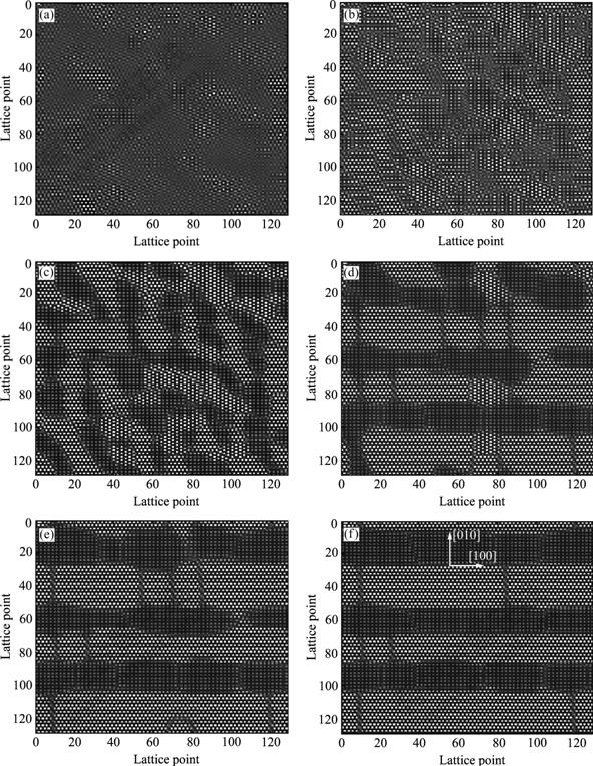
Fig.1 Temporal evolution of occupation probabilities of solute atoms for Ni-17%Cr-7.5%Al alloy: (a) t=2 000; (b) t=3 000; (c) t=10 000; (d) t=100 000; (e) t=150 000; (f) t=400 000
During the precipitation progress of Ni-based alloy, because of the different lattice parameters between coherent precipitate phases and matrix phases, there exist elastic strain fields around precipitates, and their superposition results in long-range elastic interactions, so the phase transformation will be controlled by both the elastic strain energy and the interface energy. Different from interface energy, elastic strain energy is not only proportional to the volume of precipitate phase, but also relates to the appearance of precipitate phase. During initial precipitation, particles prefer to become similar equiaxed or irregular shape in order to reduce interface energy. The contribution of anisotropic elastic energy becomes obvious with the precipitation phase growing up, gradually dominates the precipitation progress, then the precipitate phases develop to quadrate shape in order to reduce the strain energy.
For Ni-based alloy, elastic anisotropic factor is negative[17], and the minimum strain energy is achieved along the <001> direction, so the precipitates arrange along the [100] and [010] directions in the later stage when elastic strain energy dominates precipitation progress.
In order to further identify the precipitation mechanism, the order parameter of typical precipitate phase is calculated and the changing law of order parameter profiles across an ordered phase is obtained, which is difficultly achieved from experiments, so that the advantage of computer simulation is embodied too.
Fig.2 shows the variations of composition and LRO parameters of L12 phase of Ni-17%Cr-7.5%Al alloy. At 3 000, 5 000, 7 000 and 10 000 time steps, the concentra- tion and LRO parameter are both low, which does not reach the equilibrium value. In these stages, precipitate is nonstoichiometric order phase, and its concentration is lower than that of equilibrium order L12. As time proceeds, the center of the curve rises and extends to space at the same time, which indicates that the precipitation process has the doubled characteristic of non-classical nucleation and spinodal decomposition. At 20 000 time steps, the concentration and LRO parameter reach the equilibrium value, and the stoichiometric L12 ordered phase is formed.
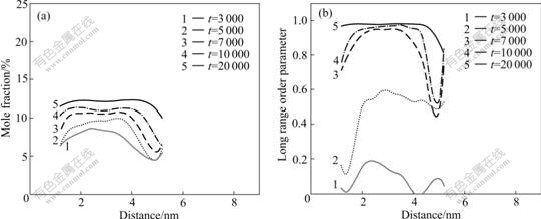
Fig.2 Evolution of concentration (a) and long range order parameter (b) of L12 phase for Ni-17%Cr-7.5%Al alloy
Based on the above analysis, we conclude that the precipitation mechanism of L12 phase in Ni-17%Cr-7.5% Al alloy is the mixed style of non-classical nucleation growth and spinodal decomposition.
The evolution of concentration and LRO parameter of D022 phase is shown in Fig.3. At 1 500 time step, when the concentration presents small fluctuation, the LRO parameter already approaches the equilibrium value, which is corresponded to the congruent order process. The nonstoichiometric order phase is formed. With the progress of aging, the concentration continues to rise. At 5 000 time steps, the concentration and LRO parameter reach the equilibrium value, and the stoichiometric ordered phase is formed.
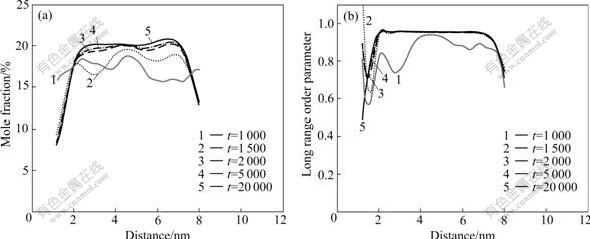
Fig.3 Evolution of concentration (a) and long range order parameter (b) of D022 phase for Ni-17%Cr-7.5%Al alloy
Associated with the characteristic of atomic picture, it is considered that the precipitation mechanism of D022 phase in Ni-17%Cr-7.5%Al alloy is the spinodal decomposition.
The morphology evolution of precipitates for Ni-12.5%Cr-7.5%Al alloy is presented in Fig.4. It is difficult for nucleation at this concentration, so we initially added a certain time steps of thermal fluctuations[18]. The thermal fluctuations are 3 200 time steps. Our simulation indicates that if the thermal fluctuation is less than this value, the system will turn back to the disorder state.
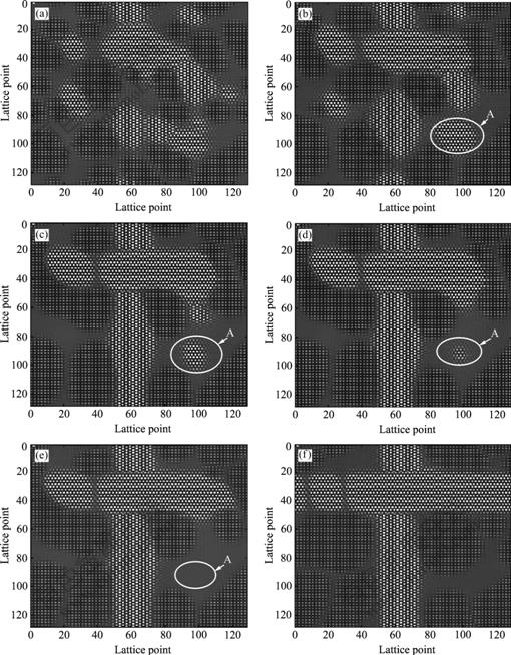
Fig.4 Temporal evolution of occupation probabilities of solute atoms for Ni-12.5%Cr-7.5%Al alloy: (a) t=3 500; (b) t=5 000; (c) t=15 000; (d) t=50 000; (e) t=100 000; (d) t=200 000; (e) t=300 000; (f) t=500 000
The precipitation process of Ni-12.5%Cr-7.5%Al alloy is similar to that of Ni-17%Cr-7.5%Al alloy. In the later stage of aging, L12 and D022 phases present quadrate shape with round corner, and orientate along the [100] and [010] directions regularly. The difference of the size of precipitate is smaller. L12 phase does not merge into rods, and they are segregated by the rod shape D022 phase. Isolated precipitate phases are found from Fig.4. The phase boundary between order phase and disorder phase is diffused. The transition region is about several lattices wide, which is not consistent with the sharp interphase as described in classical theory.
The variation of concentration and LRO parameter of L12 and D022 phases in Ni-12.5%Cr-7.5% Al alloy is respectively presented in Figs.5 and 6. At the beginning, the center of concentration and order parameter are both low, not reaching the equilibrium value. With time proceeding, the center of curve begins to rise and gradually reaches the equilibrium value according to the growth stage of precipitates. We also observed that with the rise of the center of curve, the edge of curve gradually descends, which further shows that the interface of precipitates is diffused. From the atomic configuration and order parameter, we can conclude that the precipitation mechanisms of L12 and D022 phases in Ni-12.5%Cr-7.5%Al alloy are non-classical nucleation growth.
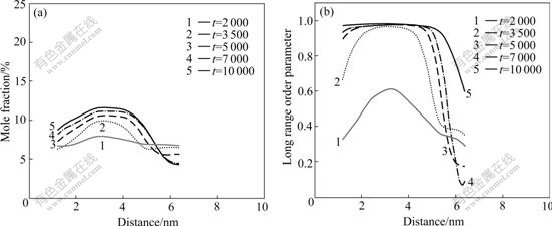
Fig.5 Evolution of concentration (a) and long range order parameter (b) of L12 phase for Ni-12.5%Cr-7.5%Al alloy
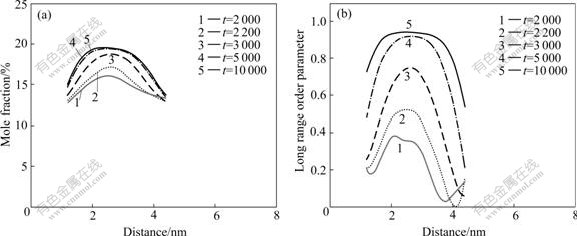
Fig.6 Evolution of concentration (a) and long range order parameter (b) of D022 phase for Ni-12.5%Cr-7.5%Al alloy
During the coarsening process of D022 phase, we also observed that the precipitates lying out of the elastic soft directions ([100] and [010]) gradually dissolve, as shown in Figs.4(b)-(e). At the beginning, the bigger particle A appears in the matrix. With progress of aging, particle A becomes smaller and vanishes in the end.
The variation of concentration and LRO parameter of particle A is presented in Fig.7. The center of curve remains in the equilibrium value at 110 000 time steps. As time proceeds, the curve begins to descend. At 210 000 time steps, the concentration and LRO para- meter return to the initial disordered state, which is because that particle A lies in the unfavorable orientation (out of the elastic soft directions). This indicates that the coarsening process is a preferential elected process. In this process, the particles that temporarily grows large will dissolve due to their unfavorable orientation.
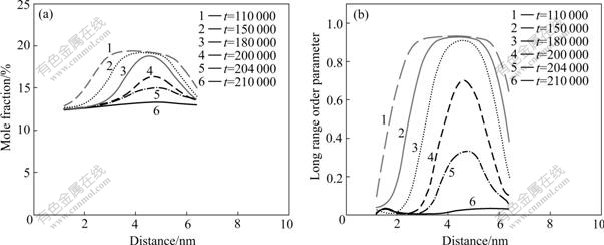
Fig.7 Evolution of concentration (a) and long range order parameter (b) of particle A in later precipitation process
4 Conclusions
1) Ni-17%Cr-7.5% Al and Ni-12.5%Cr-7.5% Al are aged at 900 K. In the early stage of precipitation, L12 and D022 phases present non-directional and irregular shape. With progress of aging, the shape of precipitates changes to quadrate and their orientations become obvious. In the later stage, L12 and D022 phases present quadrate shape with round corner and become regularly aligned along the [100] and [010] directions.
2) The mechanism of early precipitation of L12 phase in Ni-17%Cr-7.5% Al alloy is the mixed style of non-classical nucleation growth and spinodal decomposition and the D022 phase is the spinodal decomposition.
3) The mechanisms of early precipitation of L12 and D022 phases in Ni-12.5%Cr-7.5% Al alloy are both the non-classical nucleation and growth.
4) The coarsening process follows preferential selected rule. The precipitate lying out of the elastic soft directions ([100] and [010]) gradually vanishes and others grow larger and highly preferential selected microstructure is formed.
References
[1] PAREIGE C, SOISSON F, MARTIN G, BLAVETTE D. Ordering and phase separation in Ni-Cr-Al: Monte Carlo simulations vs three-dimensional atom probe [J]. Acta Materialia, 1999, 47(6): 1889-1899.
[2] PAREIGE-SCHMUCK C, SOISSON F, BLAVETTE D. Ordering and phase separation in low supersaturated Ni-Cr-Al alloys: 3D atom probe and Monte Carlo simulation [J]. Mater Sci Eng A, 1998, A250: 99-103.
[3] BROZ P, SVOBODA M, BURSIK J, KROUPA-HAVRANKOVA J. Theoretical and experimental study of the influence of Cr on the γ+γ′ phase field boundary in the Ni-Al-Cr system [J]. Mater Sci Eng A, 2002, A325: 59-65.
[4] WU K, CHANG Y A, WANG Y. Simulating interdiffusion microstructures in Ni-Al-Cr diffusion couples: A phase field approach coupled with CALPHAD database [J]. Scripta Materialia, 2004, 8(50): 1145-1150.
[5] LI Xiao-ling, CHEN Zheng, LIU Bing, WANG Yong-xin. Transition from metastablity to instability in dynamics for the precipitation of δ(Al3Li) [J]. Rare Metals, 2001, 20(4): 240-247.
[6] POUDRI R, CHEN L Q. Computer simulation of atomic ordering and compositional clustering in the pseudobinary Ni3Al-Ni3V system [J]. Acta Mater, 1998, 46(5): 1719-1729.
[7] ZHAO Yu-hong, CHEN Zheng, LI Xiao-ling. Computer simulation of strain-induced morphological transformation of coherent precipitates [J]. Journal of University of Science and Technology Beijing, 2003, 10(4): 55-60.
[8] LI yong-sheng, CHEN Zheng, LU Yan-li, WANG Yong-xin. Simulation of interphase boundary of Ni75AlxV25-x alloys using microscopic phase-field method [J]. Trans Nonferrous Met Soc China, 2006, 16(1): 91-97.
[9] CHEN L Q. Computer simulation of spinodal decomposition in ternary systems [J]. Acta Metall Mater, 1994, 42(10): 3503-3513.
[10] CHEN L Q. A computer simulation technique spinodal decomposition and ordering in ternary [J]. Scripta Metallurgica ET Materialia, 1993, 29: 683-688.
[11] KHACHATURYAN A G. Theory of Structural Transformation in Solids [M]. New York: Wiley, 1983: 129-136.
[12] PODURI R, CHEN L Q. Computer simulation of the kinetics of order-disorder and phase separation during precipitation of δ(Al3Li) in Al-Li alloys [J]. Acta Mater, 1997, 45(1): 245-255.
[13] MIYAZAKI T, KOYAMA T, KOZAKAI T. Computer simulation of the phase transformation in real alloy systems based on the phase field method [J]. Mater Sci Eng A, 2001, A312: 38-49.
[14] WANG Y, CHEN L Q, KHACHATURYAN A G. Kinetics of strain-induced morphological transformation in cubic alloys with a miscibility gap [J]. Acta Metal Mater, 1993, 41(1): 279-296.
[15] PRIKHODKO S V, CARNES J D, ISAAK D G, ARDELL A J. Elastic constants of a Ni-12.69%Al alloy from 295 to 1 300 K [J]. Scr Mater, 1998, 38(1): 67-72.
[16] DUVAL S, CHAMBRLAND S, CARON P. Phase composition and chemical order in the single crystal Nickel base superalloy MC2 [J]. Acta Metal Mater, 1994, 42(1): 185-194.
[17] VAITHYANATHAN V, CHEN L Q. Coaserning of ordered intermetallic precipitates with coherency stress [J]. Acta Mater, 2002, 50: 4061-4073.
[18] LI Xiao-ling, CHEN Zheng, WANG Yong-xin, LIU Bing. Computer simulation for early precipitation of δ(Al3Li) [J]. Progress in Natural Science, 2002, 12(1): 74-78. (in Chinese)
Foundation item: Projects(50671084, 50071046) supported by the National Natural Science Foundation of China; Project(2002AA331051) supported by the National Hi-Tech Research Development Program of China
Corresponding author: CHEN Zheng; Tel: +86-29-88460502; E-mail: chenzh@nwpu.edu.cn
(Edited by LI Xiang-qun)