Article ID: 1003-6326(2005)03-0686-05
Mass transfer mathematical model for
one-side plate steady-state ultrafiltration
QIU Yun-ren(邱运仁)1, ZHANG Qi-xiu(张启修)2
(1. School of Chemistry and Chemical Engineering, Central South University,
Changsha 410083, China;
2. Metallurgical Separation Science and Technology Laboratory, Central South University,
Changsha 410083, China)
Abstract: A mass transfer mathematical model was developed based on one-side plate steady-state ultrafiltration(UF), and the numerical solution was obtained by Crank-Nicolson finite difference method. The effects of the feed concentration, channel length, axial velocity, and diffusion coefficient on the concentration at membrane surface and the concentration profiles were investigated. Furthermore, the operation parameters and the parameters of membrane module were all transformed into dimensionless ones, and the parameter rejection was included in the mass transfer model, therefore, it can be used to calculate the steady-state ultrafiltration with different rejections. The model was used for the calculation of the ultrafiltration of metal-cutting oil emulsion. The results show that the concentration polarization can be reduced by increasing the axial velocity to some extent, but the reduction of concentration polarization is very small when the resistance of ultrafiltration is very great.
Key words: cross-flow ultrafiltration; emulsion; concentration polarization; mass transfer; mathematical model CLC
number: TQ028.8 Document code: A
1 INTRODUCTION
Ultrafiltration(UF) is a pressure-driven membrane separation process widely used for separation of macromolecules, colloidal particles from liquid, and the treatment of oil emulsion. Many mathematical models describing the steady-state ultrafiltration have been developed based on concentration polarization and membrane fouling in ultrafiltration[1-13], but they are almost based on hollow fiber membranes or tubular membranes[1-10]. The fouling index can also be applied in a model to predict fouling during ultrafiltration[14], both Navier-Stokes and Darcys law may be used for the calculation of filtration with tubular membranes[15].
However, up to know, there are few models on cross-flow plate ultrafiltration. The distribution of concentration is symmetrical because of the symmetry of the membrane module, for example, the concentration profile of hollow fiber is symmetrical on the axis, and the concentration of two-side plate cross-flow UF is symmetrical on the central plane. Furthermore, the rejection of the solute is not considered in most UF models, that is to say, the default value of rejection is 100%. In fact, the rejection of the solute is not complete in most circumstances. Thus, the parameter rejection is essential to be considered in a mathematical model so that the models can be used to solve the practical problems. However, there have been few mathematical models reported for one-side plate cross-flow ultrafiltration. In this paper, a mass transfer mathematical model for one-side plate steady-state ultrafiltration is developed, and numerical results are obtained by application of Crank-Nicolson finite difference according to the boundary conditions and experimental conditions[16]. The calculated results can be used for the design of the membrane module and the selection of the operation conditions.
2 MODEL
The mass transfer mathematical model for one-side plate steady-state ultrafiltration can be deduced according to the principles of transfer as
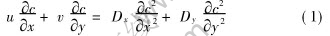
where u and v are the axial velocity and transverse velocity, respectively, c is the concentration, Dx and Dy are the axial diffusion coefficient and the transverse diffusion coefficient, m2/s, respectively.
Boundary conditions are given by
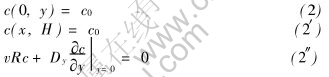
where c0 and cp are the concentration of the feed and the permeate, respectively, H is the height of the channel, L is the length of the channel, as shown in Fig.1, R is the rejection of the solute.

Then Eqn.(1) can be non-dimensionalized as
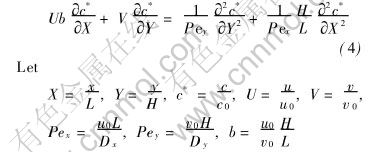
where Pex and Pey are the axial Peclet number and the transverse Peclet number, respectively.
Because PexPey, [SX(]H[]L[SX)]〈1, Eqn.(4) can be written as
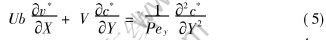
And the boundary conditions Eqns.(2), (2′), and (2″) become
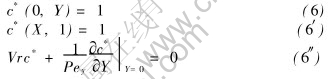
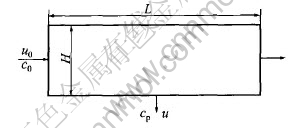
Fig.1 Schematic of one-side plate cross-flow UF
3 RESULTS AND DISCUSSION
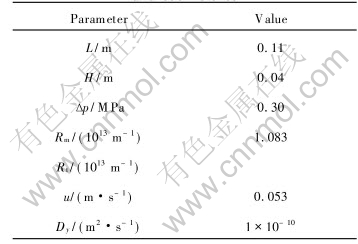
Eqn.(5) can be solved by using Crank-Nicolson finite difference method[16]. The parameters used in this model are determined by the membrane module and the operating conditions. Unless specifically stated, the parameters are given in Table 1, where Δp is transmembrane pressure, Rm and Rt are the intrinsic membrane resistance and the total resistance of membrane process, u is the axial velocity.
3.1 Effects of rejection on concentration at membrane surface
The metal-NaCl modified PVA-CA blend UF membrane were used to treat the O/W cutting oil emulsion, and the average concentration at the membrane surface was calculated at the steady state at transmembrane pressure 0.30MPa, the results are shown in Fig.2, where J is steady-state
Table 1 Values of model parameters and coefficients
permeate flux, L·m-2·h-1, w is the mass fraction of cutting oil, R is the rejection, and the value to which the dash line pointed is the experimental value, c*m is the dimensionless concentration at the membrane surface, which is defined as c*m=cm/c0, here cm is the concentration at the membrane surface.
Fig.2 shows that the concentration at the membrane surface increases with the rejection of oil under a certain operation condition, when the concentration of the emulsion increases the steady-state flux decreases and also the dimensionless concentration at the membrane surface at the same rejection.
3.2 Effects of channel length on concentration at membrane surface
Fig.3 shows the correlation of the concentration at membrane surface and the channel length at transmembrane pressure 0.30MPa and the feed velocity 0.053m/s. It illustrates that the concentration at membrane surface increases with the distance from the entrance of the module, the concentration at membrane surface is small but it increases greatly within one fifth of the length. The concentration polarization also increases with the length of the channel. Thus, the long channel does not help to prevent concentration polarization and the fouling of the membrane.
3.3 Effects of distance from membrane surface on concentration
Fig.4 shows the correlation between concentration and the distance from the surface of the membrane at transmembrane pressure 0.30MPa and the feed velocity 0.053m/s, where the mass concentrations of the emulsion in Figs.4(a) and (b) are 0.5% and 1.0%, respectively. Fig.4 shows that the closer the distance from the surface of the membrane, the greater the concentration, and the increment of the concentration is in the range Y≤0.025.
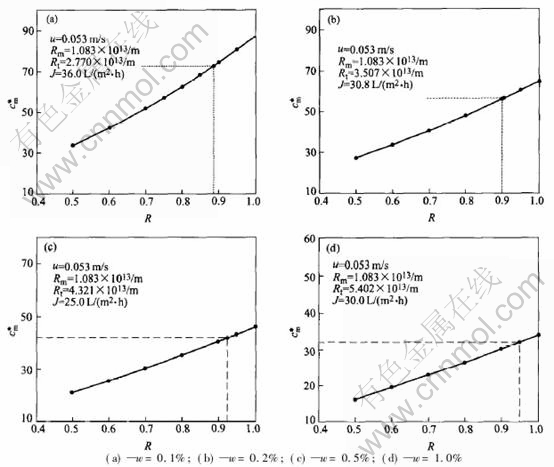
Fig.2 Curves of concentration vs rejection at membrane surface
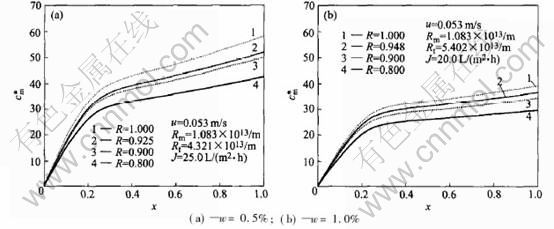
Fig.3 Curves of concentration at membrane surface vs distance to entrance of channel
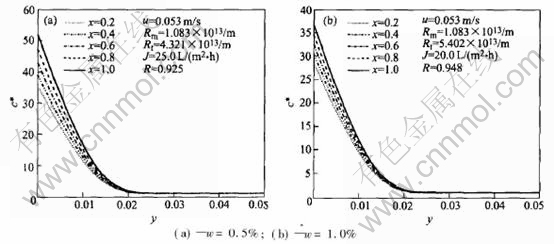
Fig.4 Vertical concentration profiles along x-axis
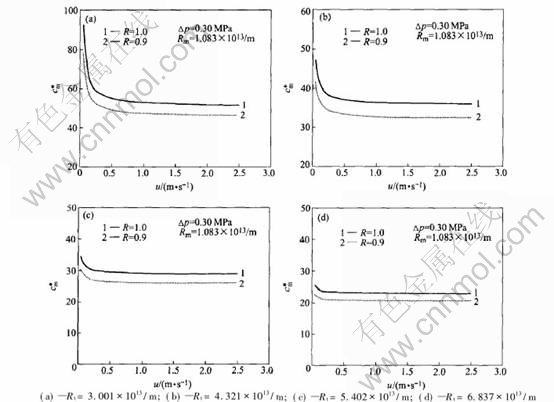
Fig.5 Curves of concentration at membrane surface vs axial velocity
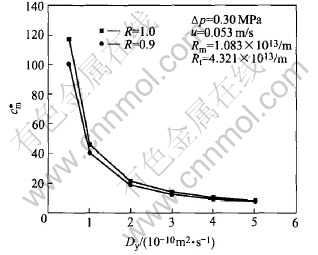
Fig.6 Curves of diffusion coefficient vs concentration at membrane surface
3.4 Effects of velocity on concentration at membrane surface
Fig.5 shows that the concentration at membrane surface decreases with the increase of the axial velocity of the fluid. When the axial velocity is small (u〈0.25m/s), the concentration decreases greatly with increment of the velocity, when the velocity is greater than 1.0m/s, the concentration decreases very slowly with the increment of the velocity, and the increment of the velocity contributes little to the reduction of concentration polarization. Furthermore, it illustrates that the reduction to concentration polarization is very little if only by increasing the velocity, when the total resistance of the ultrafiltration is great (Fig.5(c) and (d)). It also shows that the fouling of the membrane is heavy and the resistance of concentration polarization is far less than the fouling resistance, in order to eliminate the fouling of membrane, cleaning is needed. Indeed, great velocity has active action on the elimination of concentration polarization, and the turbulent fluid may take some effects on the cleaning of the surface of the membrane. But great velocity may bring about the increase of the energy consumption.
3.5 Effects of diffusion coefficient on concentration at membrane surface
Fig.6 shows that the concentration at membrane surface decreases with the increase of the diffusion coefficient under the same operation conditions. When R=0.9, diffusion coefficient increase from 0.5×10-10 to 1.0×10-10m2/s,the dimensionless concentration at membrane surface decreases from 100.49 to 40.48, but when diffusion coefficient is greater than 2.0×10-10m2/s, the concentration at membrane surface decreases very slowly with the increase of the diffusion coefficient. Diffusion coefficient increases from 2.0×10-10 to 5.0×10-10m2/s,the dimensionless concentration at the membrane surface decreases from 18.66 to 7.62 at R=0.9.
Thus, the improvement of diffusion coefficient is needed to reduce the concentration polarization. The total diffusion coefficient is only the molecular diffusion coefficient under laminar flow, but the shear-induced diffusion coefficient is not neglected under transition and turbulent region, and it becomes predominant among the total diffusion coefficient under turbulent flow. Thus, in order to reduce the concentration polarization and the fouling of the membrane, measures may be taken to improve the turbulence of the fluid in the module.
4 CONCLUSIONS
1) A mass transfer mathematical model is developed based on one-side plate steady-state ultrafiltration(UF), and the numerical solution is obtained by Crank-Nicolson finite difference method. The parameter rejection is included in the model, which can be used to calculate the steady-state ultrafiltration with different rejections.
2) The operation parameters and the parameters of membrane module are all transformed into dimensionless ones in the model, so it is convenient for application, the calculated results can be used for the design of membrane module and the selection of operation conditions.
3) The model is used for the calculation of the ultrafiltration of metal-cutting oil emulsion, the results show that the concentration polarization can be reduced by increasing the axial velocity to some extent, but the reduction of concentration polarization is very small when the resistance of ultrafiltration is very great. In addition, the concentration polarization can be greatly reduced by increasing the diffusion coefficient of solute, the measures to increase the intension of turbulence may increase the shear-induced diffusion coefficient, and decrease concentration polarization.
REFERENCES
[1]Bader M S H, Veenstra J N. Analysis of concentration polarization phenomenon in ultrafiltration under turbulent flow conditions[J]. J Membr Sci, 1996, 114(2): 139-148.
[2]Perkins T W, Saksena S, Reis V R. Dynamic film model for ultrafiltration[J]. J Membr Sci, 1999, 158(1): 243-256.
[3]Harri N, Seppo P. Flowsheet simulation of ultrafiltration and reverse osmosis processes[J]. J Membr Sci, 1994, 91(1-2): 111-124.
[4]Tansel B, Bao W Y, Tansel I N. Characterization of fouling kinetics in ultra-filtration systems by resistances in series model[J]. Desalination, 2000, 129(1): 7-14.
[5]Bellara S R, Cui Z F. Maxwell-Stefan approach to modelling the cross-flow ultrafiltration of protein solutions in tubular membranes[J]. Chem Eng Sci, 1998, 53(12): 2153-2166.
[6]Cumming I W, Holdich R G, Smith I D. Rejection of oil by microfiltration of a stabilized kerosene/water emulsion[J]. J Membr Sci, 2000, 169(1): 147-155.
[7]Dong S X, Zhang J Y. Mathematical simulation of oil-containing waste water treatment by low pressure hollow fiber ultrafiltration membrane[J]. J Chem Ind Eng, 2000, 51(3): 320-324. (in Chinese)
[8]Sanchayita G, Anirudha P, Siddhartha D, et al. Numerical simulation of an unstirred batch ultrafiltration process based on the boundary layer concept[J]. Separation and Purification Techology, 1999, 16(1): 75-81.
[9]Lee Y H, Clark M M. A numerical model of steady-state permeate flux during cross-flow ultrfiltration[J]. Desalination, 1997, 109(3): 241-251.
[10]Belkacent M, Hadjiev D, Aurelle Y. A model for calculating the steady state flux of organic ultrafiltration membranes for the case of cutting oil emulsions[J]. Chem Eng J, 1995, 56(2): 27-32.
[11]Lee Y H, Clark M M. Modeling of flux decline during crossflow ultrafiltration of colloidal suspensions[J]. J Membr Sci, 1998, 149(2): 181-202.
[12]Karode S K. A new unsteady-state model for macromolecular ultrafiltration[J]. Chem Eng Sci, 2000, 55(10): 1769-1773.
[13]Arnot T C, Field R W, Koltuniewicz A B, et al. Cross-flow and dead-end microfiltration of oily-water emulsions. Part Ⅱ. Mechanisms and modelling of flux decline[J]. J Membr Sci, 2000, 169(1): 1-15.
[14]Boerlage S F, Kennedy M, Tarawneh Z, et al. Development of the MFI-UF in constant flux filtration[J]. Desalination, 2004, 161(2): 103-113.
[15]Damak K, Ayadi A, Zeghmati B, et al. A new Navier-Stokes and Darcys law combined model for fluid flow in crossflow filtration tubular membranes[J]. Desalination, 2004, 161(1): 67-77.
[16]ZHOU Ai-yue. Mathematics in Chemical Engineering[M]. Beijing: Chemical Industry Press, 1993. (in Chinese)
(Edited by LONG Huai-zhong)
Received date: 2004-05-31; Accepted date: 2004-12-26
Correspondence: QIU Yun-ren, Associate professor, PhD; Tel:+86-731-8836309; E-mail: qiu_yunren@yahoo.com.cn