J. Cent. South Univ. (2020) 27: 1965-1980

DOI: https://doi.org/10.1007/s11771-020-4423-x

Stability analysis method of geogrid reinforced expansive soil slopes and its engineering application

ZHANG Rui(张锐)^{1, 2}, LONG Ming-xu(龙明旭)², LAN Tian(兰天)²,ZHENG Jian-long(郑健龙)^{1, 2}, GEOFF Chao³

1. National Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology, Changsha 410114, China;

2. School of Traffic & Transportation Engineering, Changsha University of Science & Technology,Changsha 410114, China;

3. Department of Geotechnical and Earth Resources Engineering, Asian Institute of Technology, Klong Luang, Pathumthani 12120, Thailand

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: The traditional stability analysis method of geogrid reinforced slopes does not consider the effect of lateral swelling, so it is not applicable to reinforced expansive soil slopes. This paper reports a new stability analysis method for geogrid reinforced expansive soil slopes. The additional pullout force of the free zone due to the lateral swelling and the anti-pullout safety factor of each geogrid layer were obtained by ensuring the overall stability of the reinforced slope. The optimum design was carried out to treat an expansive soil cut slope in Hubei Province, China, by changing the spacing and length of geogrid reinforcement. Calculation results show that the additional pullout force caused by lateral swelling has a great influence on the anti-pullout stability of geogrids, and the local stability of the reinforced slope will be overestimated if the swelling effect of soil in the free zone is not considered.

Key words: expansive soil; lateral swelling pressure; geogrid-soil interaction; stability analysis; engineering application

Cite this article as: ZHANG Rui, LONG Ming-xu, LAN Tian, ZHENG Jian-long, GEOFF Chao. Stability analysis method of geogrid reinforced expansive soil slopes and its engineering application [J]. Journal of Central South University, 2020, 27(7): 1965-1980. DOI: https://doi.org/10.1007/s11771-020-4423-x

1 Introduction

Expansive soil is rich in hydrophilic minerals, such as montmorillonite, and its volume changes after water absorption or loss. In the natural state, an expansive soil slope swells and shrinks continuously under cyclic wetting and drying, which brings out numerous cracks. Further rainfall infiltration causes the soil strength to decline, resulting in progressive shallow slope failures [1-4]. When a rigid retaining structure is adopted, the swelling deformation of the slope is completely limited. In this case, expansive soil produces great lateral swelling pressures on the retaining structure, which eventually leads to structural damages. Therefore, it is necessary to take into account the effect of lateral swelling pressure in the design of retaining structures [5, 6]. For geosynthetic reinforced soil retaining walls, non-cohesive soil is generally recommended as backfill material. However, expansive soil is also considered in some areas to avoid too much abandoned soil. When expansive soil is used as backfill material, it is often reinforced by geosynthetics and a special waterproofing and drainage design is incorporated [7-9]. When geogrids is used to reinforce expansive soil slopes, the lateral swelling pressure of expansive soil can be effectively reduced due to the tensile deformation of geogrids, and the pullout force caused by soil sliding is resisted at the same time. Therefore, the large deformation of expansive soil can be avoided and the shallow failure of the expansive soil slope can be prevented. This technique, which is of high economic and environmental benefits, has been widely used in expansive soil slopes along highways, railways and water conservancy facilities [10, 11]. Nevertheless, when expansive soil and other cohesive soils are used as fillers, the infiltration of rainwater through cracks on the slope surface can reduce the stability of the reinforced body. Moreover, the heterogeneity of backfill materials has a great influence on the stability of the reinforced body in practice [12]. Thus, there remains a need to study the interaction mechanism between expansive soil and geogrids.

To date, related previous researches have focused mainly on the interface friction by laboratory tests and numerical analyses. The interface parameters of reinforced soil are often obtained by direct shear tests and pullout tests. Boundary conditions of these two test methods have great influences on test results. Increasing the test scale can reduce the boundary effect, but it is difficult to implement the field test because of its complexity and high cost. Alternatively, numerical analysis methods, such as the finite element method and discrete element methods, are effective to study the interaction between soil and geogrids [13, 14]. Because the interaction mechanism between soil and geogrids is complex, some limitations exist in the establishment of numerical models, and the accuracy of results is difficult to guarantee. Although there are many test methods for the study of the interaction between soil and geogrids, test results vary a lot due to different test mechanisms and influencing factors. Currently, the available test technique is still an approximate simulation of the behavior of geomaterials in the field [15].

There are few application cases of geogrid reinforcement in expansive soil slopes. In relevant cases, the workability and failure modes of expansive soil slopes were mainly studied by the model test, and the slope stability was analyzed by the limit equilibrium method. The deformation and failure mechanisms are examined by the finite element method or finite difference method [16-18]. The service limit-state design of geosynthetic reinforced soil retaining walls requires an accurate estimation of short-term and long-term lateral displacements [19]. Existing numerical methods focused on the study of swelling deformation of expansive soils based on assumed input parameters. Especially, expansive soils are often regarded as isotropic and linear elastic in the calculation. However, experimental studies have shown that expansive soils is of significant anisotropy; and the swelling pressure presents a highly non-linear characteristic with the change of swelling strain. The assumption is inconsistent with the actual situation of expansive soil slope [20]. At present, there is no commonly agreed simulation method for the deformation behavior of reinforced areas [21]. When the expansive soil is used as filler, the deformation behavior of the reinforced area is more complex. There is no special correlation for expansive soil in the current design and calculation method of reinforced soil slopes in the United States [22]. In order to ensure the stability of reinforced retaining wall in expansive soil areas, the additional pullout force caused by soil swelling should be considered in the designing phase.

For this reason, a stability analysis method of geogrid reinforced expansive soil slopes was developed considering actual working conditions in this study. Then, an engineering case of geogrid reinforced expansive soil slope was taken to verify the rationality of the analysis method. Based on the engineering data, the reinforcement scheme was proposed. By means of lateral swelling pressure test and tensile test, the lateral swelling property of the local expansive soil and the tensile property of geogrids were determined, respectively. According to the deformation compatibility between reinforced expansive soil and geogrids, the pullout force of geogrids in the equilibrium state was obtained, and the anti-pullout stability of each layer of geogrids was analyzed. The optimum design scheme was identified by changing the reinforcement spacing and length, and the relevant construction process was introduced.

2 Geogrid reinforced structure and calculation hypothesis

The geogrid reinforced soil retaining wall is often used to reinforce the cut or embankment slope. It is basically composed of filling and reinforcement materials. Horizontal reinforcement layers are formed by layering the reinforcement materials into the soil (Figure 1). To prevent the shallow collapse caused by the local deformation of the slope, geogrids are generally back-folded and wrapped around the soil. The back-wrapped part of the lower geogrid is connected with the upper geogrid by a connecting rod to enhance the constraint of lateral deformation. To facilitate the stress analysis of geogrids, their back-wrapped parts are not shown in Figure 1. In order to study the local stability of reinforced expansive soil slopes, a back-wrapped reinforced soil unit is taken as the research object.

In the calculation of unit model, influencing factors are various and the effect is relatively complex. For the sake of simplicity, the following assumptions are made when analyzing the reinforced soil based on the results of laboratory tests and field monitoring:

1) The stability of geogrid reinforced expansive soil slopes is a plane strain problem.

2) The soil in the free zone of a geogrid (i.e., the area significantly influenced by cyclic drying and wetting in the reinforced soil unit) is fully saturated. ZHAN et al [23] monitored the performance of a vegetable expansive soil slope under artificial rainfall in situ. It was found that the suction of soil in the depth of 2 m decreased down to approximately zero after rainfall; and this means that the soil was in the saturated state within this depth. Therefore, it is reasonable to assumed that the area affected by drying-wetting cycles is completely saturated and the shallow slope is in the most disadvantageous state.

3) In the process of humidification, the swelling deformation of soil in the reinforced soil unit is in accordance with the tensile deformation of geogrid, and the friction between reinforcement materials and soil in the free zone of geogrid is not considered. Because of the back-wrapping effect of geogrids in reinforced soil unit, the soil in the free zone is firmly confined in the interior of geogrids. When the balance state is reached, the total deformation is the same as the final deformation of upper and lower geogrids. The cohesion of soil is almost zero when the soil in the free zone is saturated. Because the surface of geogrids is smooth, the friction between the geogrid and the wet soil is very small and not considered in this study.

4) The water content of the anchorage zone is close to the equilibrium water content, and plastic limit is the most disadvantageous situation. Crack is the most important index for dividing the area affected by drying-wetting cycles. It has no or less influence on the soil in the anchorage area. The permeability coefficient of expansive soil is low. Therefore, it is difficult for water to migrate between the soil layers, and the water content has little change.

5) In the anchorage zone, the tensile stress of reinforcement materials is considered while the displacement is neglected. The water content of the soil in the anchorage zone is quite different from that in the free zone, and the overburden pressure is also different because of the free surface of slope. Therefore, the friction between the geogrid and the soil in the anchorage zone is much larger than that in the free zone. The geogrid in the anchorage zone can hardly produce displacement or only produce micro-displacement, which is not considered in this study.

Figure 1 Schematic diagram of geogrid reinforced structure:

3 Stability analysis method of geogrid reinforced expansive soil slope

The reinforced soil unit consists of the free zone and the anchorage zone. The interaction calculation methods of soil and geogrids are selected separately according to different interface states of soil. The calculation model of reinforced soil interaction is shown in Figure 1. In the calculation of the anti-pullout stability of geogrids, the total pullout force includes pullout forces caused by sliding and lateral swelling. The total anchorage force is produced by anchorage zone. Finally, according to the results of the total pullout force and the total anchorage force, the pullout resistance safety factor of each layer of geogrid is calculated.

3.1 Pullout force in free zone caused by soil swelling

The lateral swelling of expansive soil after humidification results in lateral pullout force in the back-wrapped area of geogrids. The lateral swelling pressure of reinforced soil unit in different layers is affected by the overburden pressure. When the swelling deformation reaches the equilibrium state, the pullout force of expansive soil is borne entirely by the upper and lower geogrids of reinforced soil unit, and each geogrid layer bears half the pullout force. Because the deformation of soil in the free zone of reinforced soil unit is in accordance with that of the geogrid, the strains of the geogrid and expansive soil are identical after swelling deformation. When the reinforced soil reaches the equilibrium state after humidification and swelling, the following equations are obtained:

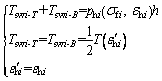                 (1)

where p_hi(σ_fi, ε_hi) is the lateral swelling pressure corresponding to the strain ε_hi of the soil in the free zone of the reinforced soil unit of layer i when the overburden pressure is σ_fi; T(ε′_hi) is the pullout force of upper and lower geogrids of the reinforced soil unit of layer i produced by swelling of expansive soil; T_swi-T and T_swi-B are the pullout forces of upper and lower geogrids of the reinforced soil unit of layer i produced by swelling, respectively; h is the reinforcement spacing; ε_hi and ε′_hi are the lateral strains of expansive soil and geogrid in the free zone of the reinforced soil unit of layer i, respectively.

3.2 Pullout force in free zone caused by soil sliding

According to the method recommended by Technical Specification for Application of Geosynthetics in Highway (JTG/T D32 2012) [24], the total tensile force of reinforcement materials in non-expansive soil reinforced slope meeting the design requirements is calculated by:

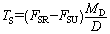                        (2)

where T_S is the sum of the required tensile force per unit width of a reinforcement; F_SR is the target minimum safety factor of a slope, which is 1.3; F_SU is the safety factor of a unreinforced slope; D is the moment arm of T_S with respect to the center of the failure circle (when the geogrid is used as reinforced material); D equals the radius of the failure circle; M_D is the driving moment with respect to the center of the failure circle, which is expressed by the following equation:

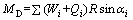                     (3)

where W_i is the gravity of slice i; Q_i is the external force acting on the vertical direction of strip i; R is the radius of the failure circle; α_i is the angle between the bottom sliding plane and the horizontal plane of slice i.

According to the statement in the specification [24], if the slope height is not more than 6 m, The total tensile force is evenly distributed to each reinforcement layer, the tensile force in each reinforcement layer and its reinforcement spacing are equal. When the slope height is more than 6 m, the slope can be divided into two reinforced areas of equal height. The total tensile force of the reinforced area is equal to the sum of the tensile forces of the two reinforced areas. The tensile forces of upper and lower parts of the reinforced area are calculated by:

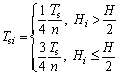                       (4)

where H_i is the height from the geogrid to the slope bottom; H is the height of the anchorage zone; n is the number of geogrid layers; T_si is the tensile force of the geogrid.

3.3 Anchorage force in anchorage zone

The maximum anchorage force produced by the friction between reinforcement materials and soil is called the ultimate anchorage force, which can be determined by the interface strength and related to the overburden pressure:

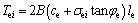                    (5)

where B is the width of the reinforced soil unit, which is 1 m; l_e is the length of the anchorage zone; c_e is the interface cohesion; φ_e is the interface friction angle; σ_ei is the overburden pressure on the geogrid reinforced anchorage zone of layer i.

3.4 Anti-pullout safety factor of each geogrid layer

The total pullout force of each geogrid layer includes the pullout forces caused by soil swelling and sliding. Because the pullout forces of the upper and lower interfaces of a single-layer geogrid are different, it is assumed that half pullout force of each geogrid layer is provided by adjacent reinforced soil unit. The anti-pullout safety factor of each geogrid layer is calculated by:

            (6)

where F_si is the anti-pullout safety factor of the geogrid of layer i; T_ei is the allowable anchorage force of the anchorage zone of layer i; θ_i is the angle between the sliding plane and the horizontal direction.

As can be seen from Eq. (6), the local stability of the reinforced slope will be overestimated if the swelling effect of soil in the free zone is not considered. The key of the above calculation method is to obtain the calculation parameters, including: 1) the lateral swelling parameter p_hi(σ_fi, ε_hi) of soil and the tensile parameter T(ε′_hi) of the geogrid required by Eq. (1); 2) the interface parameters c_e and φ_e required by Eq. (5).

4 Determination of key parameters

4.1 Lateral swelling parameters of soil

When used as backfill material, expansive soil shows swelling anisotropy. In order to obtain the variation law of actual lateral swelling pressure with lateral swelling strain, a test device of lateral swelling pressure considering the effect of different overburden pressures was developed, as shown in Figure 2. The test device includes a main component, a loading system, and a monitoring and acquisition system. The main component consists of an inner box, a lateral displacement adjusting lever and an outer box. The left side wall of the inner box is equipped with a water inlet hole, and a porous stone is placed between the left side wall and the specimen. The right side of the specimen is equipped with a concave block, and the pressure sensor and cushion block are placed in the concave groove of the concave block. The conventional three-phase high-pressure consolidometer is used as the loading system. The monitoring and acquisition system includes a lateral pressure sensor, vertical and lateral dial gauges, a data acquisition device and a computer. The pressure sensor is a high precision resistance strain pressure sensor with a thickness of 12 mm, a diameter of 20 mm, a range of 0-1000 kPa, and a precision of 0.05% FS.

As shown in Figure 2, the lateral pressures of the fully lateral restrained expansive soil after immersion could be determined by the apparatus under different vertical swelling conditions. Moreover, the variation law of the lateral pressure with the lateral swelling strain was obtained by controlling the lateral displacement. However, the measured lateral pressure contains the component caused by overburden pressure so that it is difficult to distinguish the lateral swelling pressure effectively. Therefore, it is necessary to improve the test method. Considering that the anisotropy of swelling pressure is attributed to the directional arrangement of platy montmorillonite particles in expansive soil, the lateral swelling pressure could be directly measured by the vertical loading swelling test method. Thus, the problems caused by the conventional test method are avoided. In order to change the arrangement direction of platy montmorillonite particles in the test, the specimen preparation device and method were improved, as shown in Figure 3. In this way, the original lateral side of the specimen was upward during the test.

The main steps for a lateral swelling test are as follows:

1) Intact or remolded specimens are prepared according to the requirement. The specimen preparation device is used to mold the soil specimen with the desired water content by hydrostatic compaction according to the desired dry density.

2) The prepared specimen is placed into the swelling box. The dial gauges are reset and the time interval is set.

3) The specimen is immersed in water. If the specimen swells in the horizontal direction, the horizontal load is increased immediately. When the change of vertical pressure is less than 1.0 kPa within 2 h, it is considered stable. The vertical and horizontal pressures are the original vertical swelling pressure and lateral swelling pressure, respectively. The horizontal load decreases till 0.001 mm swelling occurs in the horizontal direction.

4) The horizontal displacement of the concave block is slowly adjusted so that the vertical stress can decrease to the preset value and be stabilized. The initial lateral swelling pressure is measured by the unloading method in Step 3.

5) The vertical strain is kept constant and the original lateral swelling pressure is gradually reduced to 0. After unloading at each stage, the reading of the vertical dial gauge is not more than 0.01 mm within 2 h, which means that the swelling deformation is stable; the horizontal strain is the original lateral swelling strain when it is stable. The variation law of lateral swelling pressure with lateral swelling strain under initial lateral swelling pressure can be obtained in this step.

6) By changing the vertical load in Step 5 and then repeating Steps 1-5, the variation law of lateral swelling pressure with lateral strain under different overburden pressures can be obtained.

Figure 2 Structure diagram of two-dimensional swelling pressure test apparatus:(Unit: mm)

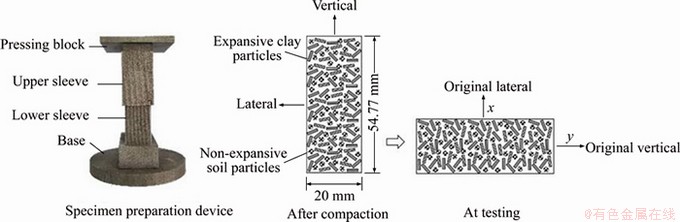
Figure 3 Specimen preparation device and specimen in preparation and testing stages

4.2 Tensile parameters of geogrid

When the geogrid is used as reinforcement material in reinforced soil structures, it mainly bears the load transferred from the soil through its tensile strength. The tensile strength is expressed by the tensile force per unit width, which can be measured by tensile tests according to the Specification for Test and Measurement of Geosynthetics (SL 235-2012) in China [25]. The lowest tensile strength of geogrids is only considered under the most disadvantageous condition. The smaller the tensile strength of reinforcement is used in the design and calculation, the safer the reinforced soil structure is. Therefore, it is suggested that test results at a tensile rate of 0.05 mm/min are selected for parameter calculation. The effect of tensile strain on the tensile strength of geogrids can be measured by experiments [26]. Then the relationship between the tensile strength and the tensile strain of geogrids can be fitted. Then, the fitting equation can be used to predict the relationship between the tensile strength and the tensile strain of geogrids at a given tensile rate.

4.3 Interface parameters between geogrid and soil

The interface cohesion c_e and friction angle φ_e are key factors in the design of reinforced soil retaining walls. The shear strength of reinforced soil interface is directly defined, and the rationality of reinforced soil structure design and the safety of engineering are determined. Pullout tests can be used to determine the parameters of interaction between the geogrid and soil. The interfacial shear stress-displacement curves under different normal stresses can be obtained by applying different normal stresses to the geogrid reinforced soil specimen. The interface cohesion and friction angle under different normal stresses can be determined by fitting the data points. They are then applied to calculate the anchorage force of geogrids under different overburden pressures. The shear strength of reinforced soil interface is linearly correlated with the normal stress; the relationship can be expressed by the Mohr-Coulomb strength theory.

5 Engineering applications

5.1 Engineering background

Anxiao Road is a class I highway of two-way four lanes located in Zhijiang City, Hubei Province, China. It has a total length of 7.3 km, in which 4 km is covered by expansive soil. Its design speed is 80 km/h and subgrade width is 22.5 m. The landform of the working area of the road mainly belongs to the denudation accumulation type. Most of the road is situated in the river terrace, only a part is in the structural denudation hilly area. The groundwater level is relatively shallow and is mainly supplied by atmospheric rainfall. The buried depth of groundwater level is generally 1-3 m, and its dynamic change is greatly affected by the seasons.

The test slope of 8.5 m high is at the left side of the section between K5+448 and K5+558 of Anxiao Road. After the excavation at a slope ratio of 1(V):1.5(H), groundwater seeped out from the slope surface and a collapse occurred later. When the slope ratio was modified into 1(V):2.5(H), another collapse took place, as shown in Figure 4. In both cases, the soil slid out at the foot of the slope, which is characterized by shallow and progressive sliding.

Figure 4 Failure of expansive soil cut slope at different slope ratios:

Through the field investigation, it was found that the distance from the sliding surface to the slope surface was about 1.5 m. An obvious weak layer with a thickness of about 0.15 m was found. The soil surface was gray white and wet with water overflown, as shown in Figure 5. Through the field investigation, it was found that the distance from the sliding surface to the slope surface was about 1.5 m. An obvious weak layer with a thickness of about 0.15 m was found. The soil surface was gray white and wet with water overflown, as shown in Figure 5. According to the statistical data, the local atmospheric impact depth (the area significantly impacted by drying-wetting cycles) is 2.0 m. The continuous collapses of the slope was resulted from the weak expansive soil with the characteristics of swelling and shrinkage. Due to the effect of atmospheric drying-wetting cycles, cracks developed in the shallow layer (2 m) of the slope. Dense crack networks were distributed on the surface of the slope, and many large cracks occurred on the top of the slope. Rainwater infiltrated along the cracks, which led to the formation of the upper stagnant water area under rainfall. On the one hand, the shallow soil swelled after humidification. Consequently, the shear strength was reduced, and the effective cohesion was completely lost. The effective internal friction angle was slightly reduced because of the soil swelling. Meanwhile, the pore water pressure in the shallow soil increased and the effective stress decreased after rainwater infiltration. Therefore, the expansive soil slope eventually showed shallow collapses compared with a general soil slope. Even if the slope ratio was adjusted to 1(V):2.5(H), the slope still collapsed. In order to reduce the construction cost, the expansive soil was not replaced but reinforced with geogrids.

Figure 5 Field investigation of sliding surfaces:

The natural water content that determined by laboratory tests was 26%. The natural density and dry density were 2.0 and 1.6 g/cm³, respectively. The liquid limit (LL) and the plasticity index (PI) were 54.3% and 29.9%, respectively. The specific gravity (Gs) of soil was 2.73. According to the Test Methods of Soils for Highway Engineering (JTG E40-2007) [27] in China, the free swelling rate (FSR) of the expansive soil was 40%, so the soil was classified as weak potential expansive soil. Referring to the wet compaction standard, the maximum dry density and the optimum water content of the soil were 1.75 g/cm³ and 20.8%, respectively. The physical properties of the expansive soil are shown in Table 1.

5.2 Initial design and stability analysis of geogrid reinforced structure

The reinforcement design was carried out following the method recommended in the Chinese specification [24]. The height of the reinforced soil retaining wall was 6 m. The slope ratio was 1(V):1.5(H), and the reinforcement spacing was 0.5 m. The length of the free zone determined based on the local atmospheric influence depth and slope rate was 3.0 m. A length of 1.0 m was considered for the anchorage zone. Therefore, the reinforcement length was 4.0 m. When expansive soils in the free zone were assumed to be nearly saturated, the cohesion and friction angle were 2.5 kPa and 20°, respectively. Expansive soils in the anchorage zone were not affected by atmospheric circulation and rainfall. They were regarded as unsaturated state, the cohesion and friction angle were 18 kPa and 20°. In order to calculate the anti-pullout stability of the top geogrid, a 0.5 m planting layer was considered as the overburden pressure. The anchorage force of reinforcement in the anchorage zone and the swelling force of soil in the free zone were taken into account. The calculation steps are presented in the following subsections.

5.2.1 Determination of calculation parameters

1) Lateral swelling parameters of soil

Five specimens with the same initial water content and density were prepared. The initial dry density was 93% of the maximum dry density, and the initial water content was the optimum water content. The vertical loads applied to the specimens were controlled at 86.5, 52.5, 25.3, 12.5 and 0 kPa, respectively, so that the specimens swelled vertically under different stresses. The lateral swelling pressure under completely lateral restrained conditions was obtained by the lateral swelling pressure test. In the test, the lateral swelling pressure was 74.3 and 22.8 kPa, when the vertical swelling strain was 0 and the maximum, respectively. Thus, the lateral swelling pressures could be calculated by the following equation:

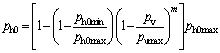         (7)

where p_h0 is the lateral swelling pressure under completely lateral restrained conditions; p_h0max is the lateral swelling pressure without vertical swelling; p_h0min is the lateral swelling pressure when the vertical stress is 0; p_v is the vertical stress; p_vmax is the vertical swelling pressure; m is the fitting parameter, which reflects the effect of vertical swelling on the change of lateral swelling pressure. Fitting results showed that m=2.28 with the coefficient of determination of 0.98.

Similarly, the initial lateral swelling pressure and the corresponding final lateral strain were plotted in Figure 6. It can be seen that within a certain range of lateral swelling pressure, there is a good linear relationship between the initial lateral swelling pressure and the final lateral strain, which is expressed by:

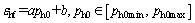             (8)

where ε_hf is the final lateral strain when the lateral swelling pressure decreases to zero with the lateral swelling deformation; a and b are fitting parameters.

Table 1 Physical properties of expansive soil

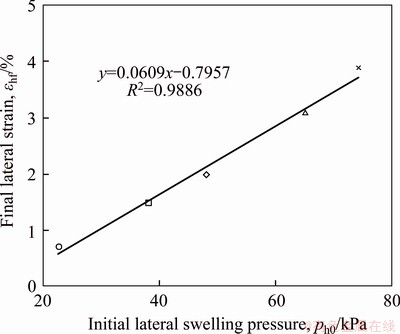
Figure 6 Relationship between final lateral strain and initial lateral swelling pressure

Fitting results showed that a and b are 0.061 and -0.796, respectively (the coefficient of determination is 0.99).

In order to characterize the variation of different initial lateral swelling pressures with lateral strain, the obtained lateral swelling pressures together with the lateral strains are fitted by a power function (Figure 7):

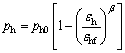                      (9)

where p_h is the lateral swelling pressure varying with the lateral strain ε_h; β=0.421 is the fitting parameter, which reflects the effect of lateral swelling deformation on the attenuation of lateral swelling pressure.

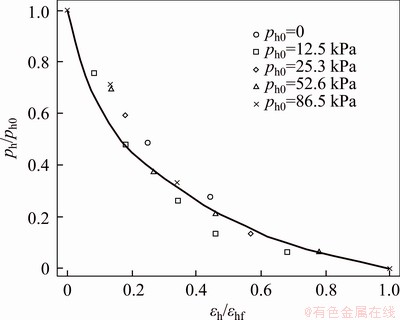
Figure 7 Variation of normalized lateral swelling pressure with normalized lateral strain under different initial lateral swelling pressures

2) Tensile parameters of the geogrid

The polypropylene geogrid of type TGDG-35 was selected for tensile test at a tensile rate of 0.05 mm/min. The relationship between the tensile strength and strain of geogrids used in the test is shown in Figure 8 and expressed by the following equation:

                          (10)

where k and q are fitting parameters related to the tensile rate and material (k=6.121 and q=0.689 in this study).

Figure 8 Relationship between tensile strength and strain of geogrid

3) Interface parameters between geogrid and soil

The pullout test was carried out by a large-scale digital control pullout test system (CS-LB01) at a constant pullout rate of 1 mm/min [28]. The interface shear stress-shear displacement curve under different normal stresses is plotted in Figure 9. The interface parameters between reinforcement and soil were as follows: c_e=7.0 kPa, φ_e=6.2°.

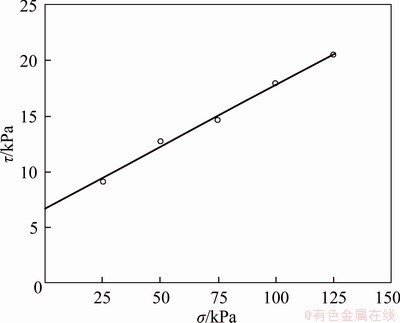
Figure 9 Relationship between shear strength and normal stress of pullout test

5.2.2 Calculation of pullout force in free zone caused by swelling

The following equation was derived based on Eqs. (1) and (8)-(10):

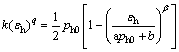              (11)

By substituting experimental parameters (i.e., k, q, a, b and β) into Eq. (9), one could determine P_h0. The lateral swelling pressure and pullout strength of each layer of geogrid corresponding to different overburden pressures were obtained. However, because ε_h is in both sides of Eq. (11), the formula must be solved by the iteration method. When the residual value is less than 0.01, it is considered that the calculation requirements can be satisfied. The lateral strains of layers 1-9 of geogrids were all 0.99%, and those of layers 10-12 were 0.97%, 0.90% and 0.78%, respectively. The lateral swelling forces of corresponding layers 1-9 of the reinforced soil unit were all 6.1 kN, and those of layers 10-12 were 6.0, 5.7 and 5.3 kN, respectively.

The pullout force in the free zone caused by the swelling of soils in different layers was obtained by substituting the corresponding strains of geogrids in different reinforced soil units into the Eq. (1) and Eq. (10). The pullout forces of geogrids of layers 1-8 caused by soil swelling are 6.1 kN, and those of layers 9-12 were 6.0, 5.9, 5.4 and 2.6 kN, respectively.

5.2.3 Calculation of pullout force in free zone caused by sliding

Firstly, the module Slope/W of GeoStudio software was used to calculate the stability of an unreinforced slope, and the Bishop method was selected as the calculation method. The whole slope was divided into two areas: 1) green area, which represents the unsaturated soil, and 2) yellow area, which represents the saturated soil. The shallow sliding of the slope was considered and the sliding earth mass was represented by orange, and it can be known that the third part of the sliding earth mass belongs to the saturated area. The safety factor, the maximum vertical depth under the most disadvantageous condition and the position of the center of the corresponding failure circle were obtained, as shown in Figure 10. The safety factor (F_su) of the unreinforced slope is 0.890 and the maximum vertical depth (D_v) of the sliding surface is 1.72 m under the most unfavorable condition.

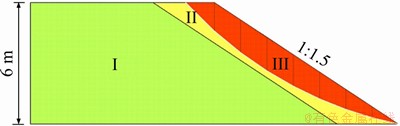
Figure 10 Safety factor and the maximum vertical sliding depth of unreinforced expansive soil slope (I: Unsaturated area; II: Saturated area; III: Sliding earth mass)

According to Eqs. (2) and (3), the total tensile force of geogrids was calculated as follows:

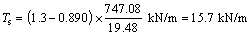    (12)

When the slope height was less than 6 m, geogrids were arranged at equal spacing in 8 layers, as shown in Figure 11. The average tensile force of different geogrid layers was evenly distributed by the standard method as follows:

               (13)

Thus, the pullout force on each layer of geogrids can be determined based on the average tensile force and its angle to the horizontal direction. The pullout forces of geogrids of layers 1-3 were 1.2 kN, those of layers 4-6 were 1.1 kN, those of layers 7-9 were 1.0 kN, those of layers 10-11 were 0.9 kN, and that of layer 12 was 0.8 kN.

Figure 11 Reinforcement layout of reinforced expansive soil slope (I: Unsaturated area; II: Saturated area; III: Sliding earth mass; IV: Planting layer)

5.2.4 Calculation of allowable anchorage force in anchorage zone

The working environment of reinforcement materials has a great influence on their strengths. Because of creep characteristics and construction damage, their performance is difficult to fully play. Reinforcement materials, filling material types and environmental conditions should be considered in the design of reinforcement. According to the Chinese specification [24], the durability reduction coefficient is 1.2; the construction damage reduction coefficient is 1.1; and the creep reduction coefficient is 1.5. Therefore, the total reduction coefficient is 2.0. According to Eq. (5), the ultimate anchorage forces of geogrids of layers 1-9 were 24.2 kN, and those of layers 10-12 were 22.7, 18.4 and 16.2 kN, respectively. The allowable anchorage forces after reduction of geogrids of layers 1-8 are 12.2 kN, and those of 9-12 layers are 11.5, 10.4, 9.3 and 8.2 kN, respectively.

5.2.5 Calculation of anti-pullout safety factor of each geogrid layer

The parameters obtained from Sections 5.2.2-5.2.4 were substituted into Eq. (6). The results are presented in Table 2, the safety factors of geogrid layers 1-8 were 1.7, and those of geogrid layers 9-12 were 1.6, 1.5, 1.5 and 2.4, respectively.

Table 2 Calculation results of safety factors of different geogrid layers

5.2.6 Discussion of results

It can be found that the anti-pullout safety factor of geogrids at the top layer is the highest because the geogrid there only bears the lateral force produced by the swelling of the next reinforced expansive soil unit. The upper arable soil is non-expansive soil, which cannot swell laterally. Therefore, the lateral swelling pressure of the geogrid at the top layer is about half of that of the geogrid at a lower layer.

The safety factors of geogrids at layers 10 and 11 are low. Because it is close to the top of the slope, the anchorage force of geogrid is limited under small overburden pressure. Geogrid layers from 11 to 1, each layer of geogrids has to bear the lateral swelling pressure of reinforced expansive soil unit in upper and lower layers, which produces a larger pullout force; thus, there is a pullout risk for geogrids.

The safety factor of the geogrid at the middle of the slope changes less. With the increase of overburden pressure, geogrids can produce enough anchorage force. When the overburden pressure of the reinforced soil unit close to the bottom of the slope does not change, the pullout force caused by lateral swelling remains unchanged. However, the proportion of pullout force caused by sliding is smaller than that of total pullout force, which results in less change. It can be seen that the lateral swelling of expansive soil plays a dominant role in the analysis of anti-pullout stability of expansive soil slope.

The safety factor of geogrid layers near the bottom of the slope tends to decrease because the overlying load of reinforced soil unit does not change any more. Therefore, the pullout force caused by the lateral swelling remains unchanged. The pullout force caused by sliding tends to increase, resulting in the increase of total pullout force. The anchorage force generated by the anchorage zone also does not changed. Thus, the anti-pullout safety factor of geogrid layers decreases.

According to the Technical Specifications for Application of Geosynthetics in Highway (JTG/T D32 2012) [24], when the clay is used as filler, the anti-pullout safety factor of geogrids should reach 2.0. In the case studied, except that the geogrids at the top layer meet the requirements, other geogrid layers do not meet the requirements of specification. Therefore, a new design scheme is needed.

5.3 Structural optimization design

The optimum scheme consisted in changing the reinforcement spacing and length. For each scheme, the reinforcement spacing and length increase by 0.25 and 0.5 m, respectively, and other parameters remain unchanged. The reinforcement spacing can be set to 0.5, 0.75 and 1.0 m, and the reinforcement length can be set to 4.0 and 4.5 m. There are six schemes, as shown in Table 3.

Table 3 Reinforcement sizes of different schemes

The calculation results of each scheme are given in Table 4. It can be found that with the increase of reinforcement spacing, the number of geogrid layers decreases correspondingly. In schemes I, III and V, the anti-pullout safety factor of each layer of geogrid does not meet the requirements of the specification [24]. When the length of reinforcement is set to 4.0 m, the length of the anchorage zone is only 1.0 m, which cannot provide sufficient anchoring force. When the length and spacing of reinforcement are 4.5 and 0.5 m respectively, the minimum safety factor is 2.3. The safety factor of each geogrid layer is greater than 2.0. Therefore, the scheme II is feasible. If the reinforcement spacing is 0.75 m, the minimum safety factor is 2.0. The safety factor of each geogrid layer is greater than 2.0. Therefore, the scheme IV is also feasible. If the reinforcement spacing is 1.0 m, the minimum safety factor is 1.9. The safety factor of one geogrid layer does not meet the requirements of the specification. This means that scheme VI is unfeasible. Compared with scheme IV, scheme II needs more geogrids and the geogrid strength is not fully developed, which leads to higher construction costs and a longer construction period. Therefore, scheme IV is chosen as the optimum scheme.

5.4 Application of geogrid reinforced structure

According to the above analysis, the length and spacing of reinforcement were 4.5 and 0.75 m, respectively. Eight layers of geogrids were laid. Each layer of geogrid was filled with three layers of soils. The compaction thickness of each layer was 0.25 m. The upper and lower layers of geogrids were connected by connection rods in the back- wrapped part, and the length of the back-wrapped part was 1.5 m. Three U-shaped steel nails with diameters of 6 mm were used to fix the end of each geogrid to the compacted soil. The original slope was 8.5 m high; the slope ratio was 1(V):2.5(H); the reinforced slope ratio was 1(V):1.5(H); and the reinforced body was 6 m high. The base was over-excavated by 0.5 m and backfilled with lime-treated soil. The top slope was backfilled with non-expansive soil and the slope ratio was adjusted to 1:6. The TDGD-35 geogrids with a width of 2.5 m were used. The minimum tensile strength was 35 kN/m, and the maximum elongation was 8%. The cross section at K5+537 was taken as an example, and the specific design size of reinforcement was shown in Figure 12.

After the base was excavated and backfilled with lime-treated soil, a layer of waterproof geotextile was laid, and a gravel layer with a thickness of 0.5 m was set for drainage. After the backfilling of expansive soil, another layer of waterproof geotextile was laid on the top of the slope to protect the geogrid from rainwater erosion. The backfilled arable soil and the plants planted subsequently of the slope plays the role of rainwater erosion prevention and greening. The base treatment had been finished since July 28, 2019. Due to the impact of several days of rainfall on the construction progress, the construction of the arable layer was completed on August 12, 2019, and the subsequent constructions of intercepting ditch and grass seed spraying were completed successively. The construction of reinforced soil retaining wall lasted for about two weeks with simple construction steps and low cost. Figure 13 shows the photographs taken in the construction process.

Table 4 Safety factors of geogrid layers in different reinforcement schemes

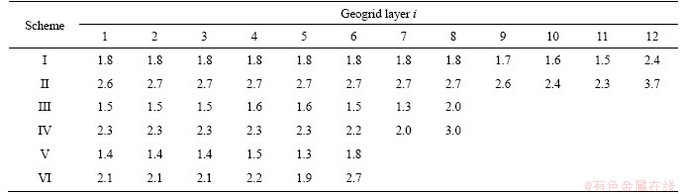
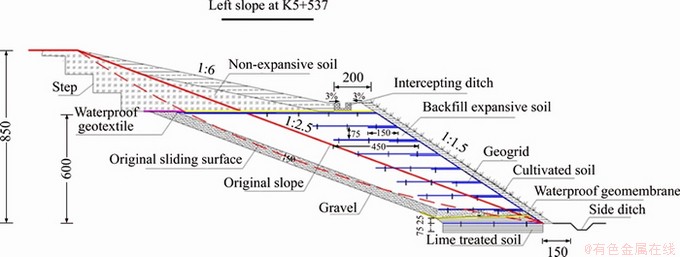
Figure 12 Structural design diagram of geogrid reinforced cut slope (unit: cm)

Figure 13 Photographs taken in construction process:

6 Conclusions

Based on the laboratory test results of expansive soils in Hubei Province, China, the interaction between expansive soil and geogrid incorporated with the failure characteristics of expansive soil slope were considered in the stability analysis. The determination method of key parameters was introduced, and the stability calculation method was then used in the treatment of a failed expansive soil cut slope. The stability of the slope was rechecked by changing the reinforcement spacing and length so as to determine the optimal reinforcement scheme. The engineering case of geogrid reinforced expansive soil cut slope was successfully constructed. The following conclusions were drawn:

1) The reinforced soil unit is composed of the free zone and the anchorage zone. In calculating the anti-pullout stability of geogrids, the additional pullout force caused by lateral swelling should be considered. Therefore, the total pullout force includes the component caused by sliding and that caused by lateral swelling. The total anchorage force is produced by the anchorage zone; it is related to the overburden pressure and interface friction parameters.

2) The key parameters to be determined in the calculation include the lateral swelling parameters of expansive soil, the tensile parameters of geogrid and the interface parameters of reinforced soil, which can be determined by the lateral swelling pressure test, tensile test and pullout test, respectively.

3) The pullout stability of geogrid layers is verified by the calculation method in this study. By analyzing the anti-pullout safety factor of geogrid of each layer in initial reinforced structure, one can note that the safety factor of geogrid at the top layer is the highest, those of geogrid layers below the top of slope are smaller. Moreover, there is a little difference in the safety factor of geogrid layers in the middle of slope, and those of the geogrid layers closer to the foot of the slope tend to decrease. The lateral swelling pressure of expansive soil is the main source of pullout force on the geogrid.

4) The method proposed in this study can be used to optimize the reinforcement design. On the premise of ensuring the overall stability of the reinforcement body, the size of reinforcement can be adjusted continuously, and the optimum reinforcement scheme can be determined considering the economic and construction factors.

5) In order to verify the rationality of the calculation method, a cut slope engineering case of geogrid reinforced expansive soil was constructed. In this construction, expansive soil was directly used, which enabled to reduce the cost and shorten the construction period. This technique also has the advantages of good workability and environmental friendliness.

References

[1] HOU Tian-shun, XU Guang-li, SHEN Yan-jun, WU Yan-jun, ZHANG Ning-ning, WANG Rui. Formation mechanism and stability analysis of the Houba expansive soil landslide [J]. Engineering Geology, 2013, 161: 34-43. DOI: 10.1016/ j.enggeo.2013.04.010.

[2] ZHAN T L T, CHEN R, NG C W W. Wetting-induced softening behavior of an unsaturated expansive clay [J]. Landslides, 2014, 11: 1051-1061. DOI: 10.1007/s10346- 013-0449-6.

[3] DONG Jun-gui, XU Guo-yuan, LV Hai-bo, YANG Jun-yan. Prediction of expansive soil strength based on micro-scale properties [J]. Geotechnical and Geological Engineering, 2019, 37: 869-882. DOI: 10.1007/s10706-018-0657-x.

[4] KHAN M S, HOSSAIN S, AHMED A, FAYSAL M. Investigation of a shallow slope failure on expansive clay in Texas [J]. Engineering Geology, 2017, 219: 118-129. DOI: 10.1016/j.enggeo.2016.10.004.

[5] LIU Yun-long, VANAPALLI S K. Influence of lateral swelling pressure on the geotechnical infrastructure in expansive soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2017, 143(6): 04017006. DOI: 10.1061/(ASCE)GT.1943-5606.0001651.

[6] ZHANG Rui, LIU Zheng-nan, ZHENG Jian-long, ZHANG Jun-hui. Experimental evaluation of lateral swelling pressure of expansive soil fill behind a retaining wall [J]. Journal of Materials in Civil Engineering, 2020, 32: 04019360. DOI: 10.1061/(ASCE)MT.1943-5533.0003032.

[7] ZHENG Jian-long, ZHANG Rui, YANG He-ping. Highway subgrade construction in expansive soil areas [J]. Journal of Materials in Civil Engineering, 2009, 21: 154-162. DOI: 10.1061/(ASCE)0899-1561(2009)21:4(154).

[8] WANG Liu-jiang, LIU Si-hong, ZHOU Bin. Experimental study on the inclusion of soilbags in retaining walls constructed in expansive soils [J]. Geotextiles and Geomembranes, 2015, 43: 89-96. DOI: 10.1016/ j.geotexmem.2014.11.002.

[9] LIU Si-hong, LU Yang, WENG Li-ping, BAI Fu-qing. Field study of treatment for expansive soil/rock channel slope with soilbags [J]. Geotextiles and Geomembranes, 2015, 43: 283-292. DOI: 10.1016/j.geotexmem.2015.04.004.

[10] ZHANG Rui, LONG Ming-xu, ZHENG Jian-long. Comparison of environmental impacts of two alternative stabilization techniques on expansive soil slopes [J]. Advances in Civil Engineering, 2019: 9454929. DOI: 10.1155/2019/9454929.

[11] XIAO Jie, YANG He-ping, ZHANG Jun-hui, TANG Xian- yuan. Surficial failure of expansive soil cutting slope and its flexible support treatment technology [J]. Advances in Civil Engineering, 2018: 1609608. DOI: 10.1155/2018/ 1609608.

[12] CHEHADE H A, DIAS D, SADEK M, JENCK O, CHEHADE F H. Seismic analysis of geosynthetic-reinforced retaining wall in cohesive soils [J]. Geotextiles and Geomembranes, 2019, 47: 315-326. DOI: 10.1016/ j.geotexmem.2019.02.003.

[13] RAHMOUNI O, MABROUKI A, BENMEDDOUR D, MELLAS M. A numerical investigation into the behavior of geosynthetic-reinforced soil segmental retaining walls [J]. International Journal of Geotechnical Engineering, 2016, 10: 435-444. DOI: 10.1080/19386362.2016.1158443.

[14] STAHL M, KONIETZKY H, KAMP L T, JAS H. Discrete element simulation of geogrid-stabilised soil [J]. Acta Geotechnica, 2014, 9: 1073-1084. DOI: 10.1007/s11440- 013-0265-0.

[15] PALMEIRA E M. Soil-geosynthetic interaction: Modelling and analysis [J]. Geotextiles and Geomembranes, 2009, 27: 368-390. DOI: 10.1016/j.geotexmem.2009.03.003.

[16] WON M S, KIM Y S. Internal deformation behavior of geosynthetic-reinforced soil walls [J]. Geotextiles and Geomembranes, 2007, 25: 10-22. DOI: 10.1016/ j.geotexmem.2006.10.001.

[17] PATHAK Y P, ALFARO M C. Wetting-drying behaviour of geogrid reinforced clay under working load conditions [J]. Geosynthetics International, 2010, 17: 144-156. DOI: 10.1680/gein.2010.17.3.144.

[18] Al-OMARI R R, FATTAH M Y, ALI H A. Treatment of soil swelling using geogrid reinforced columns [J]. Italian Journal of Geosciences, 2016, 135: 83-94. DOI: 10.3301/ IJG.2014.54.

[19] LIU Hua-bei. Long-term lateral displacement of geosynthetic-reinforced soil segmental retaining walls [J]. Geotextiles and Geomembranes, 2012, 32: 18-27. DOI: 10.1016/j.geotexmem.2011.12.001.

[20] ZHANG Rui, ZHANG Bo-ya, ZHENG Jian-long, LIU Zheng-nan. Modified lateral confined swelling tests on an expansive soil [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2223-2230. DOI: 10.11779/ CJGE201812009. (in Chinese)

[21] SCOTLAND I, DIXON N, FROST M, FOWMES G, HORGAN G. Modelling deformation during the construction of wrapped geogrid reinforced structures [J]. Geosynthetics International, 2016, 23: 219-232. DOI: 10.1680/jgein.15. 00049.

[22] Federal Highway Association. FHWA-NHI-10-025: Design and construction of mechanically stabilized earth walls and reinforced soil slopes [R]. 2009.

[23] ZHAN Liang-tong, NG Wang-wai Charles, BAO Cheng- gang, GONG Bi-wei. Artificial rainfall infiltration tests on a well-instrumented unsaturated expansive soil slope [J]. Rock and Soil Mechanics, 2003, 24(2): 151-158. DOI: 10.1142/ S0252959903000104. (in Chinese)

[24] Ministry of Transport of the People’s Republic of China. JTG/T D32: Technical specifications for application of geosynthetics in highway [R]. 2012. (in Chinese)

[25] Ministry of Water Resources of the People’s Republic of China. SL 235: Specification for test and measurement of geosynthetics [R]. 2012. (in Chinese)

[26] YANG Guang-qing, PANG Wei, LV Peng, ZHOU Qiao- yong. Experimental study of tensile properties of Geogrids [J]. Rock and Soil Mechanics, 2008, 29(9): 2387-2391. DOI: 10.3969/j.issn.1000-7598.2008.09.015. (in Chinese)

[27] Ministry of Water Resources of the People’s Republic of China [S]. JTG E40: Test methods of soils for highway engineering. Beijing, 2007. (in Chinese)

[28] YANG He-ping, WANG Liang, ZHENG Jian-long. Development and application of large scale numerical control pullout test system [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(7): 129-133. DOI: 10.3321/j.issn:1000-4548.2007.07.019. (in Chinese)

(Edited by ZHENG Yu-tong)

中文导读

土工格栅加筋膨胀土边坡稳定性的分析方法及工程应用

摘要：传统土工格栅加筋边坡稳定性分析方法忽略了侧向膨胀作用对加筋体局部稳定性的影响，并不适用于膨胀土加筋边坡。本文提出了一种土工格栅加筋膨胀土边坡稳定性分析的新方法，在保证加筋边坡整体稳定的前提下，得到了自由区因侧向膨胀而产生的附加拔出力和各土工格栅层的抗拔安全系数。通过改变土工格栅加筋间距和长度，对湖北省某膨胀土路堑边坡进行了优化设计。结果表明，膨胀土侧向膨胀引起的附加拔出力对土工格栅的抗拔稳定性有很大影响，若不考虑自由区土体的膨胀效应，将高估加筋边坡的局部稳定性。

关键词：膨胀土；侧向膨胀力；筋土相互作用；稳定性分析；工程应用

Foundation item: Project(51978085) supported by the National Natural Science Foundation of China; Project(201808430102) supported by the China Scholarship Council; Project(JTG-201507) supported by the Highway Industry Standard Compilation Project of Ministry of Transportation, China; Project(kfj180102) supported by the Open Fund of Changsha University of Science & Technology, China

Received date: 2020-03-13; Accepted date: 2020-04-03

Corresponding author: ZHANG Rui, PhD, Associate Professor; Tel: +86-18508428180; Email: zr@csust.edu.cn; ORCID: 0000-0003-2451-7103