DOI: 10.11817/j.issn.1672-7207.2015.01.045

双车道公路弯道驾驶人模糊优选决策模型与实验验证

王婉秋¹，陈雨人²，钱宇彬¹

 (1. 上海工程技术大学 汽车工程学院，上海，201620；

2. 同济大学 道路与交通工程教育部重点实验室，上海，201804)

摘要：研究驾驶人在前方弯道线形影响下的驾驶特性、视觉特性，引入驾驶行为的控制因素。针对驾驶行为中客观存在的模糊性和主观性问题，利用多目标模糊优选决策理论研究模糊性和主观性对驾驶行为的影响规律，提出一种将驾驶人的模糊感知决策能力引入到速度控制和轨迹跟踪的数学建模方法，给出一种基于灰色理论的主观和客观相结合的权重确定方法。研究结果表明：驾驶行为是一种相对意义上的模糊优选决策行为。最后，通过现场实验验证该建模方法的合理性和可行性。

关键词：双车道公路弯道; 速度控制模型; 轨迹跟踪模型; 多目标模糊优选决策; 权重

中图分类号：U491.25             文献标志码：A         文章编号：1672-7207(2015)01-0332-10

Driver’s fuzzy optimal decision-making models in curves of two-lane highway and experimenta validation

WANG Wanqiu¹, CHEN Yuren², QIAN Yubing¹

 (1. School of Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China;

2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University,

Shanghai 201804,China)

Abstract: Driver’ s driving characteristics and visual features influenced by curves alignments ahead were studied and the control factors of steering behavior and speed decision-making behavior were presented. The objective existence of fuzziness and subjectivity was given in driving behavior, the influence rules of fuzziness and subjectivity on driving behavior were studied by adopting the multi-target fuzzy optimization decision theory, a mathematical modeling method involving driver’s capacity of fuzzy perception and decision-making in the models of speed controlling and trajectory tracking was established, and based on gray theory, a solution combined subjectivity and objectivity to determinate weight was presented. The results show that the driving behavior in curves can be described as relative optimal fuzzy decision-making behavior. Finally, through field experiments, the modeling methods were verified to be reasonable and feasible.

Key words: curves of two-lane highway; speed decision-making model; trajectory tracking model; multi-objective fuzzy optimal decision-making behavior; weight

双车道公路弯道因其线形条件的特殊性和驾驶行为的复杂性，往往成为交通事故的高发路段。弯道驾驶行为受前方道路线形、驾驶人生理心理因素、车辆动力性能及行车稳定性等因素影响。驾驶人作为复杂的生物，其具有的模糊性、主观性也支撑着驾驶行为。如何从驾驶行为发生的机理和影响因素入手建立双车道公路弯道驾驶人模型，是研究该路段交通事故发生机理的重要基础工作之一。驾驶人模型的研究初衷是为了在闭环实验中分析车辆的操作稳定性，驾驶行为只涉及轨迹跟踪部分，模型建立采用补偿跟踪和预瞄跟随策略。MacAdam^[1]以驾驶人前方固定的一点作为输入，建立线性预测模型，Reddy等^[2]也提出类似的预瞄控制模型；Sharp等^[3]使用线性预瞄最优控制模型模拟赛车的驾驶行为；Guo等^[4]提出“预瞄最优曲率模型”。该类模型的重要特点是对理想轨迹的跟随，较适宜模拟真实道路条件下，自由流状态的轨迹跟踪行为。然而，在这些研究中，驾驶人的前视预瞄点被视为定值，不符合驾驶人在实际驾驶过程中依据前方线形变化动态确定前视预瞄点的动态特性，同时驾驶人的模糊性、主观性对轨迹跟踪行为的影响也未考虑。之后，为了实现车辆智能驾驶中的自动巡航功能，研究者开始从事车辆速度自动控制算法的探索。ADAMS软件的IPD速度控制模型被应用于赛道驾驶行为模拟^[5]，尽管赛道的驾驶行为与公路具有相似之处，然而赛车手追求车辆动力学性能和路面附着性能的最大程度利用，追求极速车速的现象在公路驾驶中甚少出现。高振海等^[6]研究智能街道的最优加速度控制算法，关注前后车辆、路侧行为对速度控制的影响。考虑公路驾驶行为主要受线形因素的影响，该算法不宜用于公路驾驶环境。通过以上分析，应用于双车道公路弯道驾驶环境的驾驶人模型有待进行算法结构上的调整。本文作者采用预瞄跟随策略，在研究驾驶人受前方道路线形因素影响的驾驶特性、视觉特性的基础上，引入驾驶行为的控制因素，以这些控制因素作为目标集，考虑驾驶人在决策中具有的模糊优选、主观特性，建立基于多目标模糊优选决策的驾驶人模型，并针对模型中的若干关键技术：决策集、目标集、目标距优相对隶属度、目标特征值、目标权重进行研究。最后选择8处实验曲线路段标定和验证模型的有效性。

1  驾驶行为控制因素的引入

1.1  转向驾驶行为控制因素的引入

当驾驶行为只受线形因素影响时，文献[7]提出，驾驶人在长时间驾驶过程中具有某种驾驶倾向性：驾驶人倾向于选用较长的前视时间追随目标轨迹，以减少驾驶操作强度。该驾驶倾向性的数学描述如图1所示。图1中AA为驾驶人的瞬时位置，BB为曲线段视距范围，假设方向盘转角的可行范围为，由Acklman几何关系(其中i为转向系传动比；L为轴距)，对应的一系列轨迹圆弧的曲率范围为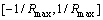，与行车道中心线的交点为[m₁, m₂, m₃, …]，每一交点对应驾驶人的1个前视预瞄点。若仅从驾驶人倾向于选择较长前视时间的倾向性出发，弧长中的最大者max(l₁, l₂, l₃, …,  l_n)对应的方向盘转角即为驾驶人下一时刻倾向的转向操纵行为。该最大弧长定义为最大行驶轨迹弧长。

图1　转向驾驶行为的数学描述

Fig. 1  Mathematical description of steering driving behavior

然而驾驶人在维持该驾驶倾向性的过程中，安全因素至关重要。国内外研究表明，公路曲线路段的车辆实际行驶轨迹与行车道中心线并不完全匹配，文献[8]采集公路曲线段的行驶轨迹发现，进入曲线路段，行驶轨迹向曲线内侧偏移，而离出曲线时，行驶轨迹向曲线外侧偏移，轨迹偏移如图2所示。依据文献[8]的研究，若驾驶人在驶入曲线路段时选择较远的前视点，将引起行驶轨迹侧向偏移d的增大，如图3所示。此时，方向盘转角也相应增大，由Acklman几何关系，行驶轨迹曲率1/R增大，在相同车速下，由横向力系数计算式，横向力系数也增大。轨迹侧向偏移d、横向力系数是与行车安全密切相关，并且能被驾驶人所直接感知的因素。于是，驾驶人在追求较长行驶轨迹弧长l的同时，不得不考虑其对行车安全带来的不利影响，从而进行相对意义上的优选决策。行驶轨迹弧长l、侧向偏移d和横向力系数成为转向驾驶行为的控制因素。

图2　行驶轨迹与行车道中心线的关系

Fig. 2  Relationship between trajectory and centerline of lane

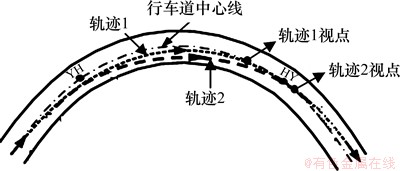
图3　不同前视点的轨迹关系

Fig. 3  Relationships between trajectories derived from different preview points

1.2  速度决策行为控制因素的引入

众所周知，驾驶人控制车速的根本目的是在保障行车安全的条件下，力求快速抵达目的地。由驾驶人的视觉特性研究表明^[9]，随着速度的提高，驾驶人的有效视野越来越窄，主要注意力被用于观测前方较远路段的线形情况。随着驾驶人前视点的前移，进入曲线时，驾驶人转向操作对应的行驶轨迹弧长比低速时产生的轨迹弧长的长(如图3所示)。因此，从某种程度上而言，驾驶人对速度的追求也是驾驶人对行驶轨迹弧长的追求，期望通过速度的提高，前移前视点，达到较大的行驶轨迹弧长，实现快速的通达性。与转向驾驶行为的控制因素类似，驾驶人对速度的追求，受行驶轨迹侧向偏移d和横向力系数的制约，也是驾驶人的一种优选决策行为。

2  基于多目标模糊优选决策的速度控制模型

驾驶人速度控制模型采用预瞄跟随策略。每个仿真步长，驾驶人调整当前车速v₀追随期望车速v_A行驶。算法中的关键节点是期望车速v_A的计算。

2.1  模糊性与主观性的客观存在性分析

通过1.2节分析，当车速只受弯道线形因素影响时，驾驶人的速度选择涉及优选决策思想，而且受车辆动力性能的制约，车速不能无限增大，存在一个决策集，因此，期望车速v_A的产生可以视为驾驶人的多目标优选决策过程。在此过程中，驾驶人对目标集的感知、判断完全依靠于驾驶人自身的驾驶经验和对行驶状态的实时感知、判断，不存在完全精确的计算和测量，驾驶人的模糊感受一直支撑着驾驶行为，另外，驾驶人对目标集权重的确定也不是恒定不变，随着驾驶环境的改变而动态变化，既具有客观性的一面，又包含了驾驶人的主观感受。目标集权重的确定具有因人而异的特点。鉴于驾驶人的模糊性和主观性便随着驾驶行为，期望车速v_A的决策过程更应视为驾驶人的多目标模糊优选决策过程。

2.2  多目标模糊优选决策模型的关键技术

多目标模糊优选理论模型^[10]的计算步骤如下：

1) 将目标特征值矩阵变换为目标相对隶属度矩阵； i=1, 2, …, m；j=1, 2, …, n；

2) 建立优等决策、劣等决策的相对隶属度，；

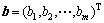3) 计算目标之间的权重：；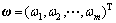                 

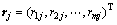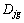4) 决策以相对隶属度隶属于模糊概念—优，加权距优距离和加权距劣距离为；

         (1)

       (2)

5) 建立优化准则：决策j的加权距优距离平方与加权距劣距离平方之总和为最小，目标函数为

(3)

6) ，得到决策j相对隶属度的最优值：

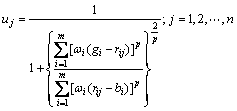   (4)

7) 即为最优决策。

将多目标模糊优选理论模型应用于期望车速v_A决策模型的构建，需解决如下关键技术：决策集、目标集、目标距优相对隶属度、目标特征值以及目标之间权重关系。

2.3  决策集

弯道行驶时，速度变化受减速度值、加速度值控制。Fambro等^[11]研究得出驾驶人在未知情况下的平均制动减速度为-0.55g(1g=9.806 65 m/s²)，该情况可以理解为驾驶人面对前方突然出现的弯道时所采取的最大制动强度，借鉴Fambro等^[11]的结论，减速度变化范围定为。车辆弯道中行驶，进入曲线的速度下降量明显大于离开曲线的速度增加量^[12]，美国交通工程师学会认为^[8]：非紧急情况下的车辆加速度约为最大加速度的65％，大约为1 m/s²，本文最大加速度采用非紧急情况下的最大加速度，加速度变化范围为: 。弯道期望车速v_A的决策集由加、减速度变化范围计算得到，其中△t为仿真步长。

加速过程：

；

减速过程：

。

2.4  目标集

驾驶人模糊优化决策的目标集为：{侧向偏移d、横向力系数、行驶轨迹弧长l}。这些控制因素对驾驶行为的影响因车辆行驶位置的不同而不同。当车辆驶入前缓和曲线过程中，驾驶人的速度控制行为主要受轨迹侧向偏移d、横向力系数因素的控制，追求较长行驶轨迹弧长l的需求处于较次要的位置，尤其当曲线半径较小时，这种趋势尤为显著；当车辆驶离圆曲线进入后缓和曲线时，缓和曲线曲率变化率逐渐减小，车辆行驶轨迹向曲线外侧偏移，驾驶人在兼顾侧向偏移d和横向力系数的基础上，采取适当加速行为，前移前视点，追求较长的行驶轨迹弧长l。

2.5  目标集距优相对隶属度的确定

在驾驶过程中，驾驶人通过模糊感知对目标集进行模糊优劣判断：对横向力系数的感知是越小越好；对侧向偏移d的感知是越靠近中线越好；对行驶轨迹弧长l的判断是越长越好。

模糊概念“越…，越…”用模糊数学概念，即相对隶属度进行客观描述^[10]。依据目标特征值的变化幅度，采用两套公式，其中目标特征值变化范围小时，宜采用第二套公式。两套“越…，越…”的相对隶属度计算公式如下。

1) 越大越好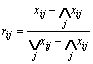：；越小越好：。

2) 越大越好：；越小越好：。

式中：和分别为决策集j=1, 2, …, n对目标i的特征值取大和取小。

鉴于驾驶人对横向力系数的模糊感知的量化范围为0~0.4，而曲线内侧向偏移d的变化幅度为0~1.875 m或0~1.750 m，相比而言，行驶轨迹弧长l的变化幅度比较大。因此，横向力系数和侧向偏移采用第二套公式计算相对隶属度，行驶轨迹弧长采用第一套公式，以反映各个目标特征值实际的变化情况。

2.6  目标特征值的计算

目标特征值的计算与前方线形影响区域有关。根据文献[13]研究，3.0 s行程点是前方线形前后注视区域的分界点，其中后视区域([1.5, 3.0] s行程范围)是驾驶人用以轨迹跟踪的前方线形影响范围，而前视区域的最远注视点，考虑弯道设计要保证一定的停车视距，出于一般性考虑，取6.0 s行程作为驾驶人最远端注视点。前视区域[3.0, 6.0] s的行程范围具有超前性，适合于驾驶人驶入弯道前，对弯道进行预判断的阶段。而驾驶人在弯道内部行驶时，速度控制行为便随着轨迹跟踪同步进行，此时，用以速度控制的前方线形影响范围为后视区域[1.5, 3.0] s行程范围。因此，本文  速度控制的前方线形影响区域定义如下：进入弯道前：前方[3.0, 6.0] s行程的线形影响范围；弯道中：前方 [1.5, 3.0] s行程的线形影响范围。

设速度决策集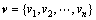，在速度决策对应的前方线形影响范围内，驾驶人可以有m个方向盘转角选择，其中转角(k=1, 2, …, m)产生目标值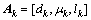，则速度决策v_i对应一系列目标值，及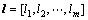。本文采用质心法计算决策v_j下目标的综合值，计算步骤如下。

步骤1  首先计算速度决策v_j条件下转角(k=1, 2, …, m)产生的目标值：侧向偏移d_k，横向力系数和行驶轨迹弧长l_k。

1) 侧向偏移d_k为

               (5)

式中：dl为微段弧长；m(l)为微段弧长的侧向偏移。

图4所示为侧向偏移计算示意图。微段弧长的侧向偏移m(l)的求解在直线段和圆曲线段能通过较为简单的数学公式加以求解，对于缓和曲线，由于无法获得缓和曲线反函数的显示表达，本文采用二分搜索法进行数值求解。计算出微段弧长dl的侧向偏移m(l)，需对dl进行积分计算。考虑自适应积分法是一种比较经济而且快速的求积分的方法，本文采用自适应辛普森数值积分法。

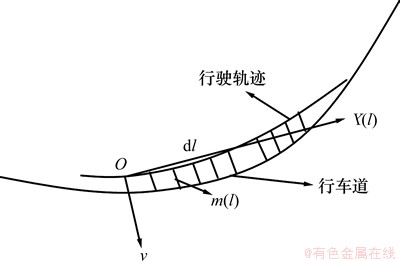
图4　侧向偏移计算示意图

Fig. 4  Illustration of lateral deviation calculation

2) 横向力系数为

               (6)

3) 行驶轨迹弧长l_k。为了求解方向盘转角对应的行驶轨迹弧长l_k，首先求转角下的圆弧曲线与前方影响区域线形l_l的交点，然后求交点与驾驶人所在位置之间的圆弧弧长，即为行驶轨迹弧长l_k。

曲线与曲线的求交运算有区间搜索法和二分法，均采用逼近的方法求交。鉴于公路线形复杂，将其应用于公路线形与圆弧曲线的求交运算，存在收敛速度过慢，计算效率不高的缺点。于是，本文采用将曲线离散为点集再求交的方法计算交点，以提高计算速度。

步骤2  由速度决策v_j对应的一系列目标值 ，及，计算速度决策v_j产生的目标综合效应值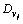，和，其中积分算法选用自适应辛普森数值积分法。

；；

2.7  主客观结合的目标权重的确定方法

目标集的权重既具有客观性，又包含驾驶人的主观性，本文的权重确定采用主客观相结合的方法，以客观权重确定方法为主，通过重新建立目标特征值的无量纲化方法，将驾驶人的主观特性融入至客观权重的确定方法中。

2.7.1  客观权重的确定方法

期望车速v_A的模糊优选决策过程应视为灰色的系统状态，客观权重的确定采用灰色理论的灰色关联法。灰色关联法确定权重^[14]的计算步骤如下。

1) 首先为了消除量纲和量纲单位不同所带来的不可公度性，对各因素序列进行无量纲化处理；

2) 计算母因素序列与子因素序列之间的关联系数：

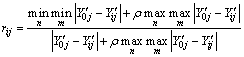     (7)

式中：r_ij为子因素(i=1, 2, …, n; j=1, 2, …, m)关于母因素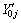(j=1, 2, …, m)的灰色关联度；

3) 由关联系数计算指标的关联度。由于(r_1j, r_2j, …, r_nj)反映了第i(i=1, 2, …, n)个子因素的第j个指标值与理想值的关联程度，故其平均值反映了第j个指标与理想值的关联度，即反映了第j个指标在整个指标空间中所占的比重：

，j=1, 2, …, m           (8)

2.7.2  驾驶人的主观倾向性建模分析

灰色关联法确定权重的首要步骤是将因素进行无量纲化。无量纲方法通常有^[15]：效益型指标的无量纲化法和成本型指标的无量纲化法。然而已有的无量纲化方法并不适合目标：侧向偏移d、横向力系数特征值的无量纲化。就其原因，当行车轨迹位于行车道中线附近，侧向偏移d的特征值变化幅度小，若按已有无量纲化方法进行无量纲化，无量纲值将接近1，这将夸大侧向偏移d与理想值的灰色关联度，从而夸大侧向偏移d的权重。这与驾驶人的主观倾向性不符，在此情况下，驾驶人通常不会对侧向偏移d给予过多的关注，关注行驶轨迹弧长l或横向力系数将更有意义。类似分析也适合横向力系数。

因此，新的无量纲化方法需要建立，以将驾驶人的主观倾向性考虑进去。本文尝试建立驾驶人主观倾向性曲线模型，模型形式为

   (9)

式中：m_max为边界因子，可以是侧向偏移d和横向力系数的最大值d_max和；a为主观倾向因子，是表征驾驶人主观倾向性的主要因子。

主观倾向性曲线模型在m≤m_max范围内的曲线形式如图5所示。

图5　m≤m_max主观倾向性曲线图

Fig. 5  Driver’s preference curves of m≤m_max

以行车轨迹侧向偏移d为例进行主观倾向性分析，主观倾向性曲线具有如下特点：1) W位于[0, 1]之间，符合无量纲化需求。2) d_max可以代表行车道边界，侧向偏移越接近d_max，W越接近1。当d＞d_max时，W为1。3) 主观倾向因子a对W的影响反映了驾驶人的主观倾向性。

从图5可见：主观倾向因子a越大，曲线斜率越大，即W在d_max范围内的变化趋势越剧烈，侧向偏移d还未接近d_max而将其设置为1的趋势越强；主观倾向因子a越小，曲线斜率越缓，即W在d_max范围内逐渐增大，而且边界附近的W的特殊处理程度越小。因此，从某种意义上而言，主观倾向因子a代表了驾驶人对侧向偏移d的一种主观态度。

在此必须指出，主观倾向因子a取值不能太小，如图6所示，此时驾驶人对侧向偏移值的判别出现偏差，认为在d＜d_max范围内的侧向偏移差别不大，这与实际不符。因此，主观倾向因子a存在一个限制范围 ＞1/16。

主观倾向性曲线模型的参数d_max和需通过实验进行标定。

以上内容即是期望车速v_A的多目标模糊优选决策模型的关键技术。通过多目标模糊优选决策模型确定下一仿真时段的期望车速v_A，计算当前车速v₀与下一仿真时段期望车速v_A的偏差△v，调整速度，推进车辆追随期望车速v_A向前行驶。

图6　a=1/16主观倾向性曲线图图

Fig. 6　Driver’s preference curve of a=1/16

3  基于多目标模糊优选决策的轨迹跟踪模型

驾驶人在某一决策速度下，转动方向盘进行后视区域[1.5, 3.0] s行程范围的轨迹跟踪。轨迹跟踪模型仍然采用预瞄跟随策略。每个仿真步长，驾驶人根据前方线形影响范围的信息和汽车的实时运动状态，判断一个相对最优圆弧轨迹，保证车辆跟随目标路径行驶。目标路径本文定义为行车道中心线。算法中的关键节点是相对最优圆弧轨迹的确定，仍然采用多目标模糊优选决策方法构建，其中关键技术：目标距优相对隶属度、目标集特征值的计算、目标之间权重的确定方法参见速度决策模型的相关内容。

3.1  决策集

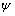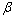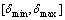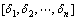驾驶人总是以与自身(车辆)方向相一致的相对坐标(x, y)来观测前方道路与车辆位置的关系，如图7所示，此时，车辆重心的绝对坐标为(X, Y)，相对坐标为(x, y)，车辆方向角为，重心侧偏角为，为此时车辆速度方向。随着方向盘转角在内变化，轨迹圆弧与前方线形影响范围相交形成一系列弧长，该系列弧长对应的方向盘转角即为轨迹跟踪决策集。

图7  轨迹跟踪决策集示意图

Fig. 7  Illustration of decision set of trajectory tracking

3.2  目标集

在轨迹跟踪决策集中，驾驶人选择侧向偏移d相对小，而行驶轨迹弧长l较长的方向盘转角作为最终决策，目标集为：{侧向偏移d、行驶轨迹弧长l}。在此，驾驶人的另一感知因素：横向力系数未考虑。这是因为在速度控制模型中，驾驶人通过控制速度行为已将横向力系数控制在较为舒适的状态。目标特征值的计算方法参见速度决策模型的相关内容。

以上即为模糊优选决策理论构建轨迹跟踪模型的关键技术。

4  驾驶人模型有效性验证和参数标定

4.1  实验路段的选取

为了检验本文提出的理论模型的完整性和有效性，以及标定主观倾向性曲线模型参数，本文选取8处自由流状态下的双车道公路曲线段进行实地实验，采集过往车辆的车速和行驶轨迹。观测断面的编号如图8所示。

4.2  实验数据筛选

鉴于本文是为了研究弯道驾驶人行为特征，对实验路段进行一定的筛选处理，即选取半径R＜500 m的实验路段，该类路段的车速受弯道影响变化显著(见表1)。将位于选取路段的观测断面(直缓点ZH、缓圆点HY、圆缓点YH和缓直点HZ)的特征车速v₈₅作为速度控制模型验证和参数标定的数据来源。

表1  特征断面运行车速特征值

  Table 1  Speed values in characteristic sections   km/h

实验路段观测断面(缓圆点HY和缓直点HZ)附近的行车轨迹侧向偏移△d达到最大值(见表2)，该值反映了平曲线对轨迹侧向偏移的影响程度。将半径R＜

500 m的实验路段的轨迹侧向偏移最大值△d_max作为轨迹跟踪模型验证和参数标定的数据来源。

图8　实验观测断面编号示意图

Fig. 8  Illustration of characteristic sections in experimental curves

表2  特征断面行车轨迹特征值D₈₅

                              Table 2  Trajectory data in characteristic sections                             cm

4.3  模型标定结果

4.3.1  速度控制模型中主观倾向性曲线模型的参数标定

选取R为160，280和480 m的实验路段的线形资料作为实际道路输入，以观测断面1的车速特征值v₈₅作为初始车速，仿真试算被选实验路段其余观测断面的特征车速，使之与该处的实验特征值v₈₅尽可能接近(见图9)，以此方法标定模型参数。

图9  各曲线车速实验值与仿真值对比研究结果

Fig. 9  Comparison of speed values in curves by experiment and simulation

1) 行车轨迹侧向偏移d的主观倾向性曲线模型标定结果。

对R＜500 m的曲线段，d_max=0.4~0.5，a_d=2，取d_max的平均值为0.45，

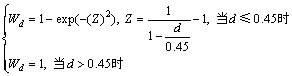  (10)

2) 横向力系数的主观倾向性曲线模型标定结果。

图10  各曲线行驶轨迹实验值与仿真值对比研究结果

Fig. 10  Comparison of trajectory values in curves by experiment and simulation

图11  各曲线运行车速、行驶轨迹实验值与仿真值对比研究结果

Fig. 11  Comparison of speed values and trajectory values in curves by experiment and simulation

对R＜500 m的曲线段，，a_u=2，

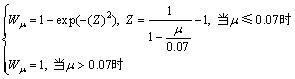     (11)

4.3.2  轨迹跟踪模型中主观倾向性曲线模型的参数标定

类似地，以R为160，280和480 m实验路段线形资料作为实际道路输入，对观测断面：缓圆点HY和缓直点HZ附近的行车轨迹侧向偏移进行仿真试算，标定模型参数如图10所示。

对R＜500 m的曲线段，d_max=0.3~0.5, a_d=2。

取d_max的平均值为0.4，行车轨迹侧向偏移d的主观倾向性曲线模型标定结果为

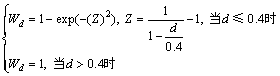 (12)

4.4  模型预测

以标定的模型，对其余实验路段R=240 m和R=320 m进行仿真计算，仿真结果与实验特征值的对比如图11所示。

通过误差分析和秩和检验，仿真结果与实验统计结果无显著性差异，从而验证了文中提出的模型和方法的可行性及有效性，应用文中提出的模型能反映实验路段车辆的行车特性。

5  结论

1) 研究驾驶人在前方弯道线形影响下的驾驶特性，视觉特性，给出转向驾驶行为、速度决策行为的控制因素。通过研究各控制因素在驾驶行为中作用，提出驾驶行为是一种相对意义上的优选决策行为。

2) 实现了驾驶人的模糊优选决策能力在速度控制模型和轨迹跟踪模型的构建，针对模糊优选决策模型中的若干关键技术：决策集、目标集、目标距优相对隶属度、目标特征值、目标权重进行研究。

3) 提出了一种将主观和客观相结合的权重确定方法，其中运用灰色关联分析确定目标集权重，并通过构建驾驶人主观倾向性曲线模型，提出应用主观倾向性曲线模型对目标进行无量纲化的方法，以融入驾驶人对目标权重的主观倾向性。

4) 选择实验路段，进行实地实验，对模型的有效性和参数进行检验和标定。

参考文献：

[1] MacAdam C C. An optimal preview control for linear systems[J]. Journal of Dynamic Systems, Measurement and Control, 1980, 102(3): 188-190.

[2] Reddy R N, Ellis J R. Contribution to the simulation of driver-vehicle-road system[J]. SAE Paper 810513, 1981.

[3] Sharp R S, Casanova D, Symonds P. A mathematical model for driver steering control, with design, turning and performance results[J]. Vehicle System Dynamics, 2000, 33(5): 289-326.

[4] GUO Konghui, GUAN Hsin. Modeling of driver/vehicle directional control system[J]. Vehicle System Dynamics, 1993, 22(1): 141-184.

[5] 徐进. 道路几何设计对车辆行驶特性的影响机理研究[D]. 成都: 西南交通大学土木工程学院, 2009: 70-72.

XU Jin. Effects of change in road geometry design on vehicle driving dynamics[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2009: 70-72.

[6] 高振海, 管欣, 李谦, 等. 驾驶员最优预瞄纵向加速度模型[J]. 汽车工程, 2002, 24(5): 434-437.

GAO Zhenhai, GUAN Xin, LI Qian, et al. Driver optimal preview longitudinal acceleration model[J]. Automotive Engineering, 2002, 24(5): 434-437.

[7] 郭孔辉. 汽车操纵动力学原理[M]. 南京: 江苏科学技术出版社, 2011: 499-506.

GUO Konghui. Vehicle handling dynamics theory[M]. Nanjing: Jiangsu Science Press, 2011: 499-506.

[8] 杨轸. 行车动力学仿真模型研究[D]. 上海: 同济大学交通运输工程学院, 2004: 16-34.

YANG Zhen. Research on driving dynamic simulation model[D]. Shanghai: Tongji University. School of Transportation Engineering, 2004: 16-34.

[9] 范士儒. 交通心理学教程[M]. 北京: 中国人民公安大学出版社, 2005: 15-16.

FANG Shiru. Course of traffic psychology[M]. Beijing: People’s Public Security University of China Press, 2005: 15-16.

[10] 张哲, 王会利, 石磊, 等. 桥梁方案多层多目标模糊优选模型及其应用[J]. 哈尔滨工业大学学报, 2006, 38(9): 1567-1571.

ZHANG Zhe, WANG Huili, SHI Lei, et al. Application of multi-levels and multi-objectives fuzzy optimization model of bridge type selection[J]. Journal of Harbin Institute of Technology. 2006, 38(9): 1567-1571.

[11] Fambro D B, Fitzpatrick K, Koppa R J. New stopping sight distance model for use in highway geometric design[J]. Transportation Research Record, 2000, 1701: 1-8.

[12] 徐进, 彭其渊. 运行车速预测新方法及其应用[J]. 西南交通大学学报, 2010, 45(2): 238-248.

XU Jin, PENG Qiyuan. New prediction method of operating speed and its application to highway alignment evaluation[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 238-248.

[13] 林涛. 山区公路曲线段车辆加速度及轨迹研究[D]. 上海: 同济大学交通运输工程学院, 2008: 42-43.

LIN Tao. Vehicle acceleration and driving track research of sharp curves in mountainous highway[D]. Shanghai: Tongji University. School of Transportation Engineering, 2008: 42-43.

[14] 王婉秋, 方守恩, 孙道成. 基于灰色关联度的道路交通安全管理设施多层模糊综合评价[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(4): 652-656.

WANG Wanqiu, FANG Shouen, SUN Daocheng. A multi-level fuzzy comprehensive evaluation of road traffic safety management facilities based on grey relation degree analysis[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2010, 34(4): 652-656.

[15] 江文奇. 无量纲化方法对属性权重影响的敏感性和方案保序性[J]. 系统工程与电子技术, 2012, 34(12): 2520-2523.

JIANG Wenqi. Sensibility and alternative COP analysis of dimensionless methods on effect of attribute weight[J]. Systems Engineering and Electronics, 2012, 34(12): 2520-2523.

(编辑  杨幼平)

收稿日期：2014-02-13；修回日期：2014-04-20

基金项目(Foundation item)：国家自然科学基金资助项目(51078270) (Project(51078270) supported by the National Natural Science Foundation of China)

通信作者：王婉秋，博士研究生，讲师，从事道路交通安全研究；E-mail: tutu_net@163.com