A mixed stochastic user equilibrium model considering influence of advanced traveller information systems in degradable transport network
来源期刊:中南大学学报(英文版)2018年第5期
论文作者:楼小明 程琳 周静 马捷
文章页码:1182 - 1194
Key words:mixed stochastic user equilibrium model; degradable transport network; advanced traveler information systems (ATIS); drivers’ behavioral adaptability; multiple equilibrium behaviors; fixed point problem
Abstract: Advanced traveler information systems (ATIS) can not only improve drivers’ accessibility to the more accurate route travel time information, but also can improve drivers’ adaptability to the stochastic network capacity degradations. In this paper, a mixed stochastic user equilibrium model was proposed to describe the interactive route choice behaviors between ATIS equipped and unequipped drivers on a degradable transport network. In the proposed model, the information accessibility of equipped drivers was reflected by lower degree of uncertainty in their stochastic equilibrium flow distributions, and their behavioral adaptability was captured by multiple equilibrium behaviors over the stochastic network state set. The mixed equilibrium model was formulated as a fixed point problem defined in the mixed route flows, and its solution was achieved by executing an iterative algorithm. Numerical experiments were provided to verify the properties of the mixed network equilibrium model and the efficiency of the iterative algorithm.
Cite this article as: CHENG Lin, LOU Xiao-ming, ZHOU Jing, MA Jie. A mixed stochastic user equilibrium model considering influence of advanced traveller information systems in degradable transport network [J]. Journal of Central South University, 2018, 25(5): 1182–1194. DOI: https://doi.org/10.1007/s11771-018-3817-5.

J. Cent. South Univ. (2018) 25: 1182-1194
DOI: https://doi.org/10.1007/s11771-018-3817-5
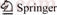
CHENG Lin(程琳)1, LOU Xiao-ming(楼小明)2, ZHOU Jing(周静)3, MA Jie(马捷)1
1. School of Transportation, Southeast University, Nanjing 210096, China;
2. Zhejiang Development & Planning Research Institute, Hangzhou 310012, China;
3. Zhejiang Institute of Communications, Hangzhou 311112, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Advanced traveler information systems (ATIS) can not only improve drivers’ accessibility to the more accurate route travel time information, but also can improve drivers’ adaptability to the stochastic network capacity degradations. In this paper, a mixed stochastic user equilibrium model was proposed to describe the interactive route choice behaviors between ATIS equipped and unequipped drivers on a degradable transport network. In the proposed model, the information accessibility of equipped drivers was reflected by lower degree of uncertainty in their stochastic equilibrium flow distributions, and their behavioral adaptability was captured by multiple equilibrium behaviors over the stochastic network state set. The mixed equilibrium model was formulated as a fixed point problem defined in the mixed route flows, and its solution was achieved by executing an iterative algorithm. Numerical experiments were provided to verify the properties of the mixed network equilibrium model and the efficiency of the iterative algorithm.
Key words: mixed stochastic user equilibrium model; degradable transport network; advanced traveler information systems (ATIS); drivers’ behavioral adaptability; multiple equilibrium behaviors; fixed point problem
Cite this article as: CHENG Lin, LOU Xiao-ming, ZHOU Jing, MA Jie. A mixed stochastic user equilibrium model considering influence of advanced traveller information systems in degradable transport network [J]. Journal of Central South University, 2018, 25(5): 1182–1194. DOI: https://doi.org/10.1007/s11771-018-3817-5.
1 Introduction
Nowadays, with the development of modern science and technology, intelligent traffic systems (ITS) has emerged as one of the most effective tool to solve the current urban traffic problems. As an important component of ITS, the advanced traveler information systems (ATIS) are generally believed to be beneficial in several aspects such as improving individuals’ travel efficiency, alleviating road congestion, and enhancing network performance. A number of researches have been undertaken on the modeling and effect evaluation of ATIS [1–10].
ATIS can potentially improve drivers’ accessibility to real-time traffic information through a range of communication technologies. With this traffic information, drivers can conduct both pre-trip path selection and en-route path adjustment to avoid unexpected traffic congestion [11–17]. ATIS plays its role in influencing driver’s individual travel choice, and the corresponding road congestion as well as network performance at an aggregate level. To assess the effect of ATIS, therefore, the key is to investigate drivers’ choice behaviors under the influence of dynamic or real-time traffic information.
In existing literatures, a mixed assignment model incorporating the user equilibrium and stochastic user equilibrium routing criteria is widely adopted to reflect the multiple equilibrium routing behaviors under the influences of ATIS information [18–24]. In this model, the effect of ATIS are reflected by the reduced variations of the travel time perceptions for equipped drivers through provision of travel information, and thus the benefits of ATIS are mainly measured based upon the ultimate equilibrium flow distributions with less random error. We argue that this measurement method is insufficient because ATIS not only helps drivers to select faster routes at the stable equilibrium state, but also assist them to make adaptive dynamic adjustments during the disequilibrium transient of transport network, which is probably caused by the intra-day link capacity degradation.
In degradable transport network, link and route travel times are always fluctuant because of the stochastic link capacity reductions [25–27]. Such travel time variability reduces drivers’ travel reliability and induces their unexpected travel time delays. For ATIS equipped drivers, they can receive more real-time information about the present network condition, and make dynamic travel adjustments against the potential link capacity degradations. This dynamic routing adjustment effects supported by ATIS service obviously cannot be evaluated in the abovementioned equilibrium models. Some studies [28–31] modeled route choice behaviors of ATIS equipped drivers under a dynamic evolution framework, and investigated the effects of ATIS on some specific dynamic system properties such as network flow convergence and stability. Still, these works only analyzed the effects of ATIS based upon idealized transport network and did not consider the influence of stochastic link capacity degradations.
This work makes efforts to establish an analytical framework, to quantify the effects of ATIS on drivers’ route choices in the presence of degradable link capacities. It is believed that ATIS can not only improve drivers’ accessibility to the more accurate route travel time information, but also can improve drivers’ adaptability to the potential network capacity degradations. In the context of analytical model, the information accessibility can be reflected by lower degree of uncertainty in the stochastic equilibrium flow distribution, and the behavioral adaptability can be embodied by readjustments of equipped drivers’ route choices to fit with different link capacity conditions.
To reflect the network degradation situation, link capacity will be randomized as finite number of possible discrete values associating with corresponding occurring probabilities. The combination of all these discrete link capacities constitutes the set of all possible network states. For any change of the network state, ATIS equipped drivers is supposed to be able to adjust their route choices in time to adapt to the current situation. As a consequence, equipped drivers will perform different equilibrium flow distributions according to different network states. Following this idea, we formulate multiple flow equilibriums of equipped drivers over the whole network state set, to capture the behavioral adaptability supported by ATIS.
In this work, we propose a mixed stochastic user equilibrium model to describe the interactive choice behaviors between ATIS equipped and unequipped drivers over a degradable transport network. Following the previous works [19, 20, 23, 24], drivers in this paper are also supposed to be heterogeneous in terms of their values of time (VOT) which follows a certain continuous probability distribution. The concurrent service charge and the information benefit as well as the continuously distributed VOT jointly influence the attractiveness of ATIS for drivers. The final stationary equilibrium level of ATIS market penetration is so determined that the value of the information provided will decline to the point at which no new drivers will find it advantageous to purchase that service.
This study advances previous work by making the following specific contributions. First, this study proposes a mixed stochastic user equilibrium model to describe the interactive choice behaviors between ATIS equipped and unequipped drivers over a degradable transport network. Different from previous studies, the proposed model considers a more comprehensive utility of ATIS on both drivers’ information accessibility and their behavioral adaptability. Second, this study applies multiple equilibrium behaviors of ATIS equipped drivers, to capture their behavioral adaptability without resorting to a complicated dynamic route choice adjustment process. Third, this study formulates the mixed network equilibrium as a fixed point problem (FPP) defined in the mixed route flows, and proposes an iterative algorithm for its solution. Finally, this study also adopts the traditional mixed equilibrium model as comparison, to investigate the effects of additional consideration about drivers’ behavioral adaptability in the proposed model.
The remainder of this work is organized as follows: Section 2 describes the degradable transport network in question and provides relevant notion definitions. Section 3 proposes the mixed network equilibrium model and formulates it as a FPP to describe the interactive choice behaviors between ATIS equipped and unequipped drivers. Section 4 investigates the existence of equilibrium route flows and proposes an iterative algorithm for solving the equilibrium model. Section 5 conducts numerical experiments on the Nugyen Dupuis’s network to verify the properties of the mixed network equilibrium model and the efficiency of the iterative algorithm. The conclusion and future work are summarized in Section 6.
2 Degradable transport network and relevant notion definitions
A traffic network is a directed graph (N, L) where N represents the node set and L corresponds to the link or road set. The actual capacity of each degradable link can be obviously regarded as stochastic variable, which is further randomized as finite number of possible discrete values associating with corresponding occurring probabilities. Then all possible states of the transport network can be enumerated by combining these discrete link capacities. The notations that will be used in this paper are all defined following such degradation situation and they are listed as appendix.
Some other parameters and notations will be defined when first introduced. In this paper, the set of possible network states V, and their corresponding probability distributions Ω are both assumed to be known and unchanged. This means that capacity degradations of the transport network are exogenous information and independent of the loaded traffic flows. Note that when the set Ul contains only one element, namely |Ul|=1, this actually refers to the special case that link l always maintains its idealized capacity and never suffers degradation. Therefore, the idealized network condition can be regarded as a special situation of the degradable transport network considered here.
For a degradable transportation network, the following relationships are valid: Cw(x(vj),vj)= 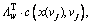
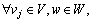 which represents the relationship between actual route travel time and link travel time;
which represents the relationship between actual route travel time and link travel time; 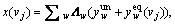
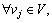 which represents the relationship between link flow and route flow; and
which represents the relationship between link flow and route flow; and 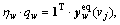
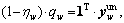
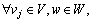 which express, respectively, the total flow conservation of equipped and unequipped drivers, the notation ‘1’ denotes unit vector.
which express, respectively, the total flow conservation of equipped and unequipped drivers, the notation ‘1’ denotes unit vector.
3 Description of mixed behavior equilibrium model
This section applies static, multiple route strategies to model the different routing behaviors and interactions of the two groups of equipped and unequipped drivers in degradable transport network.
3.1 Stochastic equilibrium flow of equipped drivers
Consider a specific scenario in which the network state is happen to be 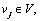 the actual route travel time is calculated based on the actual link travel time, which further depends on all drivers’ route choice results. This means that the actual route travel time can be formulated as a function of all route flows conducted by both equipped and unequipped drivers:
the actual route travel time is calculated based on the actual link travel time, which further depends on all drivers’ route choice results. This means that the actual route travel time can be formulated as a function of all route flows conducted by both equipped and unequipped drivers:

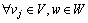 (1)
(1)
With the received route travel time information, the route flow distribution of equipped drivers can be estimated in turn according to their route choice behaviors, which is usually modelled through a random utility model assuming that each driver perceives the route utility values and chooses the maximum perceived utility route. The random factor is adopted to account for the effect of imperfect information provided by ATIS. In general, driver’s perceived route utility value can be set as the opposite of the perceived travel time, and then drivers’ route choice probabilities are obtained according to the perceived route time, leading to a route choice probability model φ(·) expressed as below.
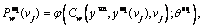
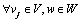 (2)
(2)
where the positive dispersion parameter θeq is related to the variation of travel time perceptions of equipped drivers. Obviously, larger value of θeq reflects higher sensitivity of route choices to travel time and thus corresponds to more accurate ATIS information. This dispersion parameter measures the travel time information quality of ATIS.
In the following the positive dispersion parameter θeq is assumed common to all equipped drivers. Furthermore, if the perception errors are assumed to be identically and independently Gumbel distributed random variables with mean zero and identical standard deviations, then the route choice probability model φ(·) can be specified as the following Logit-based formula.
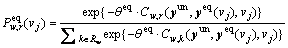 ,
,
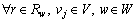 (3)
(3)
According to the weak law of large numbers, the route flow distributions of equipped drivers can be estimated as below.
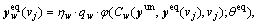
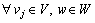 (4)
(4)
In Eq. (4), the route choice results 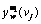 of ATIS equipped drivers are not always stable but will evolve according to the occurring network state vj, which is clearly different from the traditional stochastic user equilibrium state in which drivers’ route choices are assumed to be stable over the whole network state set V. Actually, Eq. (4) implies that ATIS assists equipped drivers to quickly realize which state is prevailing, and to adjust their previous route choices in time to adapt the current network state. Therefore, the correlation between
of ATIS equipped drivers are not always stable but will evolve according to the occurring network state vj, which is clearly different from the traditional stochastic user equilibrium state in which drivers’ route choices are assumed to be stable over the whole network state set V. Actually, Eq. (4) implies that ATIS assists equipped drivers to quickly realize which state is prevailing, and to adjust their previous route choices in time to adapt the current network state. Therefore, the correlation between 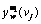 and vj reflects equipped drivers’ behavioral adaptability under the influence of real-time traffic information provided by ATIS.
and vj reflects equipped drivers’ behavioral adaptability under the influence of real-time traffic information provided by ATIS.
3.2 Stochastic equilibrium flow of unequipped drivers
Due to the inaccessibility of real-time information, unequipped drivers are almost impossible to make travel adjustments in time to adapt to stochastic route travel time caused by network degradations. With this consideration, we assume that unequipped drivers make route choices based merely on their estimated route travel time. We further assume that unequipped drivers are risk neutral decision makers, who estimate the stochastic route travel time to be its expected value by accounting for all possible network states and relevant occurrence probabilities. Define Sw,r to represent the estimated travel time of route  According to the aforementioned assumption,Sw,r can be formulated as below:
According to the aforementioned assumption,Sw,r can be formulated as below:
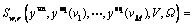
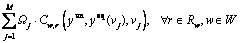 (5)
(5)
For ease of presentation, we further define Sw to represent the vector of the estimated route travel time on OD pair w, 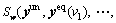
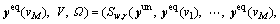

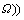 ,
, 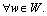 Now the route choice behaviors of unequipped drivers can be described by the same probability model φ(·) but with different degree of uncertainty:
Now the route choice behaviors of unequipped drivers can be described by the same probability model φ(·) but with different degree of uncertainty:
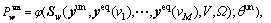
 (6)
(6)
where the positive dispersion parameter θun is related to the variation of travel time perceptions of unequipped drivers. In reality, equipped drivers usually know route travel time better and thus have less variability of perceived travel time than those traveling without ATIS. Therefore, the value of θun is always less than θeq, or θeq >θun. The relative value of θeq in relation to θun dictates the information accessibility of equipped drivers supported by ATIS in improving their route choice decisions.
The route flow distributions of unequipped drivers can now be formulated based on their route choice probabilities:

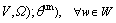 (7)
(7)
For the unequipped drivers, they can acquire the occurrence probabilities of possible network states through studying their past travel experiences; however, they cannot quickly realize the prevailing network state in the absence of ATIS information. Under this situation, the unequipped drivers make route choices according to the estimated route travel time Sw and their choice results  are stable on the whole network state set V.
are stable on the whole network state set V.
3.3 Determination of ATIS market penetration level
Note that in Eqs. (4) and (7), the level of ATIS market penetration ηw is a endogenous variable which is determined jointly by the daily service charge of ATIS device γeq and the probability distribution of drivers’ VOT f(τ) as well as the information benefit perceived by drivers. Specifically, each driver evaluates the potential net benefits of AITS device in terms of the monetary value of time saving minus service charge according to individual value of time. Let ΔCw represent the average travel time saving of every equipped driver and its value can be calculated as the individual travel time difference between equipped and unequipped drivers, that is,
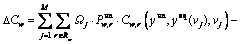

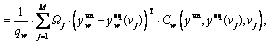
 (8)
(8)
Drivers have the motivation to purchase ATIS service only when they can get positive net benefits of this system. To determine the level of ATIS market penetration, we should first calculate the critical value of time τ′ which corresponds to the break-even point. Namely,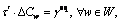 and therefore,
and therefore, 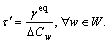
It is obviously that only the drivers whose VOT is larger than τ′ will purchase ATIS service (see Figure 1). Following this thought, the level of ATIS market penetration on each OD pair can be determined as follows:
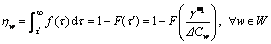 (9)
(9)
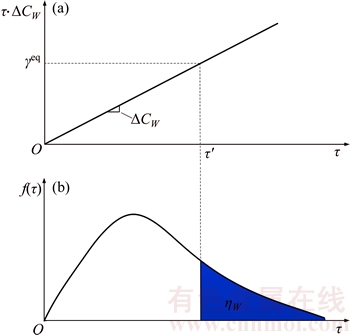
Figure 1 Information benefits (a) and ATIS market penetration level (b)
Equation (9) can reveal non-uniform market penetrations among OD pairs when the average travel time savings ΔCw are different from these OD pairs.
3.4 Mixed stochastic user equilibrium model
By now, we have modeled the route choice behaviors of equipped and unequipped drivers as well as the endogenous ATIS market penetration level in the above subsections 3.1–3.3, we can now integrate them together to formulate the mixed stochastic user equilibrium model as below.
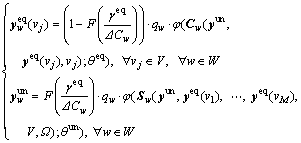 (10)
(10)
In this work, the set of possible network states V, and their corresponding probability distributions Ω are both assumed to be known and unchanged. Besides of these, the OD travel demand qw, the daily service charge of ATIS device γeq, the cumulative distribution function of drivers’ VOT F(τ) and the dispersion parameters θun, θeq are all given in advance and independent on the loaded network flow. In such situation, the proposed mixed network equilibrium model Eq. (10) is actually equivalent to a FPP which defines a map of 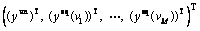 to itself.
to itself.
For every variable in the FPP, the superscript * is marked to represent its stationary value at the ultimate equilibrium solution. Then the equilibrium route flows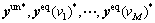 can be achieved through solving the FPP (10). On this basis, the final travel time saving of equipped driver
can be achieved through solving the FPP (10). On this basis, the final travel time saving of equipped driver 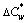
 and then the stationary ATIS market penetration level
and then the stationary ATIS market penetration level 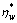
 can also be calculated according to Eqs. (8) and (9).
can also be calculated according to Eqs. (8) and (9).
ATIS assist drivers to make dynamic travel adjustments to adapt to different network states caused by link capacity degradations. In the proposed mixed equilibrium model, these dynamic adjustment behaviors are assumed to contribute to multiple flow equilibriums of equipped drivers. The multiple equilibrium behaviors can be roughly interpreted as such a phenomenon that equipped drivers make route choices to form stationary route flow pattern 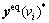 with probability
with probability 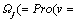
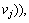 to adapt to the occasional network state vj. In other words, the actual dynamic route choice adjustments made by equipped drivers are approximated by their multiple equilibrium behaviors in the static mixed network equilibrium model to reflect their behavioral adaptability supported by ATIS.
to adapt to the occasional network state vj. In other words, the actual dynamic route choice adjustments made by equipped drivers are approximated by their multiple equilibrium behaviors in the static mixed network equilibrium model to reflect their behavioral adaptability supported by ATIS.
4 Iterative algorithm for model solution
As stated previously, the mixed network equilibrium model Eq. (10) can be regarded as a FPP defined in 
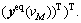 We reformulate this model in an abstract way,
We reformulate this model in an abstract way,
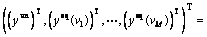
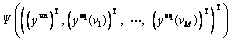 (11)
(11)
where Ψ(·) covers all the function relations presented in model Eq. (10). Before the introduction of solution algorithm, we should first investigate the existence of equilibrium route flows for the mixed equilibrium model Eq. (10), or equivalently the existence of fixed-point for the FPP Eq. (11).
Sufficient conditions for fixed-point existence can be easily derived through Brouwer’s fixed point theorem, requiring a continuous function mapping a compact convex set into itself. Since the OD traffic demand is positive and can be assumed with no loss of generality upper bounded, feasible route flows are non-negative and upper bounded, that is, they belong to a closed, compact, and convex set. Moreover, if each OD pair is connected by at least one route, the feasible route flow set is non-empty. On this basis, if the adopted travel time function c(·) and the probabilistic route choice model φ(·) both meet continuity condition, then the continuity condition of the self-mapping about route flows is also guaranteed, and thus all the hypotheses of the Brouwer existence theorem for the FPP Eq.(11) are satisfied.
For the convenience of description, we define vector Y to denote the mixed route flows, namely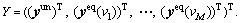 By inspection, we can find the fixed-point
By inspection, we can find the fixed-point 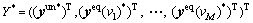 of FPP Eq. (11) is identical to the stable point of a dynamic system established as follows:
of FPP Eq. (11) is identical to the stable point of a dynamic system established as follows:
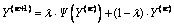 (12)
(12)
where the parameter λ (0<λ≤1) measures iterative step length and the superscript κ (κ=0, 1, 2, …) represents iterative time. If the stable point of dynamic system Eq. (12) satisfies the asymptotic stability condition, then the fixed-point Y* can be achieved by executing dynamic system Eq. (12) from arbitrary feasible initial vector Y(0) belonging to the domain of attraction of Y*. A generalized condition to assure asymptotic stability is assigning sufficiently small value for the iterative step length λ.
In the following, we will propose an iterative algorithm based on the dynamic system Eq. (12) to solve the mixed network equilibrium model.
Iterative algorithm procedure
Step 0
Initialization. Assign value for the iterative step length λ. Set κ=0.
Step 1
Choose the feasible initial vector of route flows  where H represents the feasible set which satisfies both the nonnegative constraint of route flows and the total flow conservation on each OD pair.
where H represents the feasible set which satisfies both the nonnegative constraint of route flows and the total flow conservation on each OD pair.
Step 2
Renew the route flow vector using the following iterative formula:

Step 3
Check the iterative convergence:
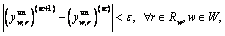
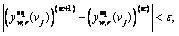
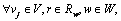
where ε represents convergence criteria. If the convergence condition is met, go to Step 4; otherwise set κ=κ+1 and go to Step 2.
Step 4
Treat the newest route flows Y(κ+1) as the final equilibrium solution, namely Y*= Y(κ+1), and then calculate the stationary ATIS market penetration level 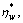
 according to Eq. (9), stop.
according to Eq. (9), stop.
5 Numerical experiments
The proposed network equilibrium model is applied to Nugyen Dupuis’s network with 13 nodes and 19 links, whose topology is illustrated in the left side of Figure 2. There are four OD pairs in the network, 1-2, 1-3, 4-2 and 4-3 and the numbers of routes between these OD pairs are 8, 6, 5 and 6 respectively. The fundamental OD travel demands are given as: q12=1500 veh/h, q13=2200 veh/h, q42=1800 veh/h, q43=1000 veh/h. Every link is assumed to suffer some stochastic degradation from its design capacity 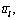
 1, 2, …, 19.
1, 2, …, 19.
In this work, in order to simplify the formulation of the mixed equilibrium model, link stochastic degradable capacity is processed into a finite number of discrete values, rather than a specific continuous distribution curve. If the occurrences of link capacity degradations are independent of each other, then we can enumerate the possible network states by combining all links’ discrete capacity values. Obviously, the numbers of discrete link capacity values and then the possible network states will increase with the simulation precision of capacity degradation issue in question. In the following example, we introduce a simplified situation to reduce the number of possible network states. Specifically, we assume that all links are affected by some common factors to cause the same capacity decreasing extent with the same probability. Following this assumption, we can design four possible network states, namely 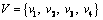 , to reflect degradable transport network in this experiment. These four network states are respectively defined as: v1=
, to reflect degradable transport network in this experiment. These four network states are respectively defined as: v1=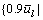 for all l=1, 2, …, 19}, v2=
for all l=1, 2, …, 19}, v2= for all l=1, 2, …, 19}, v3=
for all l=1, 2, …, 19}, v3= for all l=1, 2, …, 19}, v4=
for all l=1, 2, …, 19}, v4=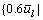 for all l=1, 2, …, 19} and their corresponding occurrence probabilities are given as: Ω1=Pro(v=v1)=0.2,Ω2=Pro(v=v2)=0.3,Ω3=Pro(v=v3)=0.3 and Ω4=Pro(v=v4)=0.2.
for all l=1, 2, …, 19} and their corresponding occurrence probabilities are given as: Ω1=Pro(v=v1)=0.2,Ω2=Pro(v=v2)=0.3,Ω3=Pro(v=v3)=0.3 and Ω4=Pro(v=v4)=0.2.
The link cost function is of BPR type:
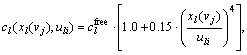

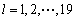 (13)
(13)
where 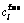 is the free flow travel time of link l. The values of
is the free flow travel time of link l. The values of 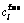 and
and 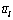 are given in the right side of Figure 2. The Logit model as formulated by Eq. (3) is applied to describe drivers’ stochastic route choices. In addition, following the previous works [19, 20, 23], the continuously distributed VOT f(τ) is represented by a log-normal distribution:
are given in the right side of Figure 2. The Logit model as formulated by Eq. (3) is applied to describe drivers’ stochastic route choices. In addition, following the previous works [19, 20, 23], the continuously distributed VOT f(τ) is represented by a log-normal distribution:

0<τ<∞, β>0 (14)

Figure 2 Topology and link parameters for experiment network
where α and β are the mean and the standard deviation of lnτ, respectively, and are related to the mean μ and the standard deviation σ of τ by the following equations:
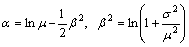 (15)
(15)
where the values of μ and σ are given as: μ=2.0 RMB¥/min, σ=1.5 RMB¥/min, and the other model parameters are set as: γeq=5.0 RMB¥, θeq=0.1 min–1, θun=0.05 min–1.
5.1 Multiple equilibrium behaviors of equipped drivers
We first execute the mixed equilibrium model to investigate equipped drivers’ multiple equilibrium behaviors caused by their behavioral adaptability. For graph simplicity, we select six routes on the network and only use their loaded flows to reflect the equilibrium states of the network. These six routes are respectively labeled as r1 (node order: 1→12→6→7→8→2), r2 (node order: 1→5→6→7→11→3), r3 (node order: 1→ 5→6→10→11→3), r4 (node order: 1→12→6→ 7→11→3), r5 (node order: 1→12→6→10→11→3) and r6 (node order: 4→9→10→11→3). The equilibrium route flows conducted by equipped drivers are compared with that conducted by unequipped drivers in Figure 3.
Figure 3(a) reveals four distinct route choice patterns as the equilibrium route flow distributions of the equipped drivers, in which each flow pattern 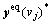 is associated to a specific network state
is associated to a specific network state 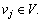 This multiple equilibrium behavior differs significantly from the route choices of unequipped drivers which lead to a sole equilibrium flow distribution, as shown in Figure 3(b). This difference surely reflects the utility of ATIS to assist drivers in making adaptive travel choices as considered in our model. In the following, we will compare the proposed model Eq. (10) with the traditional mixed equilibrium model appearing in the existing literatures, to investigate the effect of additional consideration about drivers’ behavioral adaptability.
This multiple equilibrium behavior differs significantly from the route choices of unequipped drivers which lead to a sole equilibrium flow distribution, as shown in Figure 3(b). This difference surely reflects the utility of ATIS to assist drivers in making adaptive travel choices as considered in our model. In the following, we will compare the proposed model Eq. (10) with the traditional mixed equilibrium model appearing in the existing literatures, to investigate the effect of additional consideration about drivers’ behavioral adaptability.
5.2 Comparison with traditional mixed network equilibrium model
In most traditional mixed equilibrium models, the decreasing of travel uncertainty is thought to be the only benefit of ATIS for drivers, and the effect of AITS in disseminating real-time information for drivers’ adaptive travel adjustments is usually neglected. In such a situation, ATIS equipped drivers is also assumed to be insensitive to the stochastic network degradations and they will make route choices based on the estimated route travel time as same as that adopted by unequipped drivers. Now the only behavioral difference between these two driver groups is reflected by the variations of travel time perceptions, namely the values of parameters θeq and θun (θeq>θun) in the probabilistic route choice model.
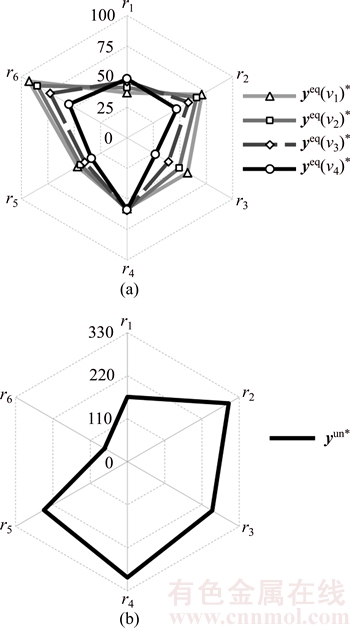
Figure 3 Comparison of route flows between equipped (a) and unequipped (b) drivers
The traditional mixed equilibrium model without considering equipped drivers’ behavioral adaptability can be formulated as below.
 (16)
(16)
where 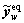 represents |Rw|×1 vector of equipped route flows on OD pair
represents |Rw|×1 vector of equipped route flows on OD pair 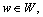 which is stationary over the whole network state set V in the traditional mixed equilibrium model,
which is stationary over the whole network state set V in the traditional mixed equilibrium model, 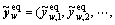
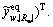
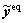 represents |R|×1 vector of equipped route flows on all OD pairs, and
represents |R|×1 vector of equipped route flows on all OD pairs, and 
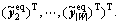 Similarly,
Similarly,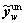 and
and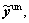 respectively, represent the vectors of unequipped route flows on OD pair
respectively, represent the vectors of unequipped route flows on OD pair 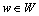 and on the whole network in the traditional mixed equilibrium model.
and on the whole network in the traditional mixed equilibrium model. 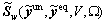 represents the vector of the estimated route travel time,
represents the vector of the estimated route travel time, 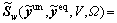
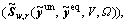 and its element
and its element 
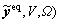 can be expressed as following:
can be expressed as following:
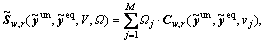
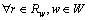 (17)
(17)
In addition, the level of ATIS market penetration ηw in the traditional mixed equilibrium model is determined by the average travel time saving of equipped drivers 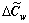 :
:
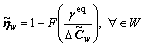 (18)
(18)
and the average travel time saving  is further defined by the following formula:
is further defined by the following formula:
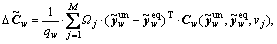
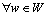 (19)
(19)
The traditional model is solved by following the same iterative algorithm as introduced in Section 4. For the purpose of comparison, the parameter values for model Eq.(16) are set to be the same as that for the previous model Eq. (10). Figure 4 shows the equilibrium route flow distributions achieved from the traditional model Eq. (16).
As we can see, whether equipped or unequipped drivers, they make route choices together to form a unique flow distribution pattern at the final stable state of the traditional mixed equilibrium model. Due to the neglect of multiple equilibrium behaviors, the reduced travel time variation of equipped drivers (reflected by the relative value of θeq in relation to θun) is regarded as the only advantage of ATIS to contribute to individual travel time saving.
Now, the difference between our model Eq. (10) and the traditional one Eq. (5) can be further investigated by comparing their resultant travel time savings 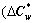 vs.
vs.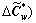 and stationary ATIS market penetration levels
and stationary ATIS market penetration levels  vs
vs  The comparison result is shown in Figure 5. Obviously, the proposed model Eq. (10) predicts more travel time savings of equipped drivers and therefore higher ATIS market penetration levels than the traditional model (16). The increased predictions are entirely owing to the additional consideration of drivers’ behavioral adaptability or their multiple equilibrium behaviors in our mixed model.
The comparison result is shown in Figure 5. Obviously, the proposed model Eq. (10) predicts more travel time savings of equipped drivers and therefore higher ATIS market penetration levels than the traditional model (16). The increased predictions are entirely owing to the additional consideration of drivers’ behavioral adaptability or their multiple equilibrium behaviors in our mixed model.

Figure 4 Stationary route flow distributions conducted by equipped (a) and unequipped (b) drivers in traditional mixed equilibrium model
5.3 Efficiency of iterative algorithm
The proposed iterative algorithm contains a sole parameter λ to control its iterative step length and thus its efficiency depends critically on the value of this parameter. Here we can execute the iterative algorithm with different λ-values to check its influence on the convergence. Figure 6 shows the ATIS unequipped flow iteration processes on route r3 according to three different values of parameter λ. It is found that a larger λ-value will lead to some greater fluctuations of route flows at the early iterations, but at the same time it contributes to a faster process for the iteration process to converge to the final stationary state.
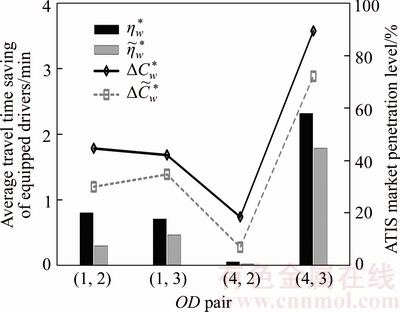
Figure 5 Effects of drivers’ behavioral adaptability on their average travel time savings and stationary levels of ATIS market penetration
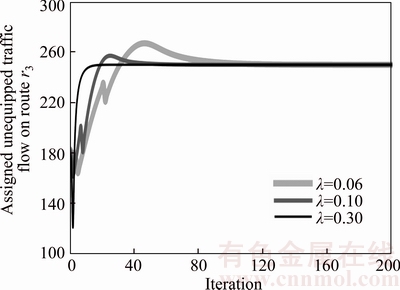
Figure 6 Traffic flow iteration processes on route r3 with different λ-values
There exists an upper limit value for the parameter λ to assure convergence of the iteration process. That is, as long as the value of λ is not larger than this upper limit, we can always find the solution of the proposed mixed equilibrium model by applying the iterative algorithm. On the other hand, when the parameter λ is assigned too large, the resultant route flows will always fluctuate along the iteration procedure and never converge to the stable state. For the numerical experiment considered here, the upper limit of λ is found to be about 0.45. Note that the upper limit value is jointly determined by the other model parameters including γeq, θeq, θun, μ, σ, the structure and scale of the transport network, as well as the occurrence situation of the capacity degradations.
6 Conclusion and future work
This work investigates the comprehensive effects of ATIS on both drivers’ information accessibility and their behavioral adaptability in the presence of degradable link capacities, and on this basis proposes a mixed network equilibrium model to describe the interactive route choice behaviors between ATIS equipped and unequipped drivers. This paper shows that the formulated mixed network equilibrium model can be regarded as a FPP defined in the mixed route flows, and its equilibrium solution is identical to the stable point of a relevant dynamic system. According to this dynamic system, this paper proposes an iterative algorithm to solve the mixed equilibrium model. Short of empirical data, this paper conducts numerical experiments on Nguyen Dupuis’s network, to verify the properties of the mixed network equilibrium model and the efficiency of the iterative algorithm. Under the situation of degradable transport network, this paper also compares the proposed model with the traditional one, to investigate the effect of additional consideration about drivers’ behavioral adaptability.
Our study may benefit the evaluation and design of the advanced traveler information systems. Further studies should be carried out with collection of empirical data for model calibration and validation in practice. In the proposed model, both the service charge and the information accuracy of ATIS are treated as exogenous variables which are changeless and independent on the network traffic flows. This may not conform to the actual case that the information services are provided by competitive ATIS firms which adaptively adjust the service charge and service quality according to drivers’ choice behaviors to maximize their respective profits. Therefore, it is meaningful to incorporating more realistic market-oriented ATIS services into the mixed equilibrium model in the future work.
Nomenclature
Link index
O
Origin set, o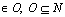
D
Destination set,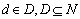
W
Set of OD pairs, W={o,d}
w
OD pair index, 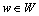
Rw
Set of routes on OD pair w
R
Set of all routes, R=UwRw
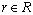
Route index
Λlrw
Link-route index for OD pair w: if link l belongs to route 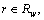
 otherwise, Λlrw=0
otherwise, Λlrw=0
Λw
|L|×|Rw| link-route incidence matrix for OD pair w, Λw=(Λlrw)
qw
Travel demand on OD pair w
q
|W|×1 vector of OD demands, q=(q1, q2, …, q|W|)T
Pro(E)
Probability of occurrence of event E
ul
Stochastic capacity of degradable link l
Ul
Set of all possible capacity values for link l, Ul={ul1, ul2, …, ulm}, in which m=|Ul| denotes the number of elements in Ul, and obviously, 
v
Stochastic network state, which is combined by stochastic link capacities, namely v={ul|for all 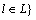
V
Set of all possible network states, V={v1, v2, …, vM}, in which M=|V| denotes the number of elements in V
Ωj
Occurrence probability of a possible network state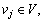 namely Ωj= Pro(v=vj), and
namely Ωj= Pro(v=vj), and 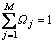
Ω
Probability distribution of all possible network states, Ω={Ω1, Ω2, …, ΩM}
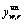
Number of ATIS unequipped drivers (namely unequipped traffic flow) on route 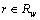

|Rw|×1 vector of unequipped route flows on OD pair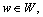
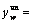
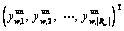
yun
|R|×1 vector of unequipped route flows on all OD pairs, yun= 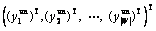
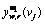
Number of ATIS equipped drivers (namely equipped traffic flow) on route  under the network state
under the network state 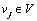
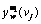
|Rw|×1 vector of equipped route flows on OD pair w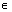 W under the network state vj
W under the network state vj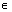 V,
V, 
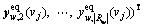
yeq(vj)
|R|×1 vector of equipped route flows on all OD pairs under the network state vj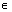 V,
V, 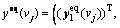
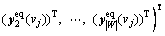
xl(vj)
Mixed (equipped and unequipped drivers) flow on link 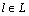 under the network state vj
under the network state vj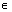 V
V
x(vj)
|L|×1 vector of mixed link flows under the network state vj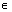 V, x(vj)=
V, x(vj)= 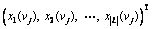
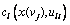
Actual travel time of link 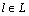 under the network state vj
under the network state vj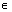 V, as a function of the mixed link flows x(vj) and the occurred link capacity
V, as a function of the mixed link flows x(vj) and the occurred link capacity 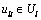

|L|×1 vector of actual link travel time under the network state vj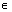 V,
V, 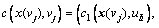
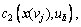
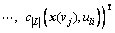
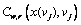
Actual travel time of route  under the network state
under the network state 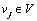
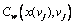
|Rw|×1 vector of actual route travel time on OD pair 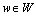 under the network state
under the network state 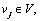
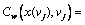

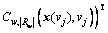

Probability unequipped drivers select route 
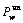
|Rw|×1 vector of route choice probabilities of unequipped drivers on OD pair w, 
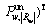
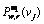
Probability equipped drivers select route  under the network state
under the network state 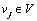

|Rw|×1 vector of route choice probabilities of equipped drivers under the network state 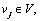
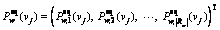
ηw
Level of ATIS market penetration on OD pair 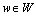
γeq
Daily system service charge of ATIS
f(τ)
Probability density function of the continuously distributed VOT τ (0<τ< ∞) across the drivers
F(τ)
Cumulative distribution function of drivers’ VOT, 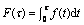
References
[1] WATLING D, van VUREN T. The modeling of dynamic route guidance systems [J]. Transportation Research Part C-Emerging Technologies, 1993, 1(2): 159–182. DOI: 10.1016/0968-090X(93)90012-5.
[2] WATLING D. Urban traffic network models and dynamic driver information system [J]. Transport Reviews, 1994, 14(3): 219–246. DOI: 10.1080/01441649408716881.
[3] EMMERINK R H, AXHAUSEN K W, NIJKAMP P, RIETVELD P. Effects of information in road transport networks with recurrent congestion [J]. Transportation, 1995, 22(1): 21–53. DOI: 10.1007/BF01151617.
[4] EMMERINK R H, AXHAUSEN K W, NIJKAMP P, RIETVELD P. The potential of information provision in a simulated road transport network with non-recurrent congestion [J]. Transportation Research Part C-Emerging Technologies, 1995, 3(5): 293–309. DOI: 10.1016/0968- 090X(95)00012-8.
[5] AL-DEEK H M, KHATTAK A J, THANANJEYAN P. A combined traveler behavior and system performance model with advanced travel information systems [J]. Transportation Research Part A-Policy and Practice, 1998, 32(7): 479–493. DOI: 10.1016/S0965-8564(98)00010-X.
[6] CHORUS C G, MOLIN E J, VAN WEE B. Use and effects of advanced traveler information services (ATIS): A review of the literature [J]. Transport Reviews, 2006, 26(2): 127–149. DOI: 10.1080/01441640500333677.
[7] ZHANG Rong, VERHOEF E T. A monopolistic market for advanced traveler information systems and road use efficiency [J]. Transportation Research Part A-Policy and Practice, 2006, 40(5): 424–443. DOI: 10.1016/j.tra.2005.08. 010.
[8] FERNANDEZ E J, de CEA J, VALVERDE G G. Effect of advanced traveler information systems and road pricing in a network with non-recurrent congestion [J]. Transportation Research Part A-Policy and Practice, 2009, 43(5): 481–499. DOI: 10.1016/j.tra.2008.12.001.
[9] YAO Xue-heng, ZHAN F B, LU Yong-mei, YANG Min-hua. Effects of real-time traffic information systems on traffic performance under different network structures [J]. Journal of Central South University, 2012, 19(2): 586–592. DOI: 10.1007/s11771-012-1043-0.
[10] HAGHANI M, SHAHHOSEINI Z, SARVI M. Quantifying benefits of traveler information systems to performance of transport networks prior to implementation: A double-class structured-parameter stochastic trip assignment approach [J]. Transportation Letters: The International Journal of Transportation Research, 2016, 8(1): 1–12. DOI: 10.1179/ 1942787515Y.0000000013.
[11] KHATTAK A, POLYDOROPOULOU A, BEN-AKIVA M. Modeling revealed and stated pretrip travel response to advanced traveler information systems [J]. Transportation Research Record: Journal of the Transportation Research Board, 1996, 1537: 46–54. DOI: 10.3141/1537-07.
[12] MAHMASSANI H S, LIU Y H. Dynamics of commuting decision behavior under advanced traveler information systems [J]. Transportation Research Part C-Emerging Technologies, 1999, 7(2, 3): 91–107. DOI: 10.1016/S0968- 090X(99)00014-5.
[13] ABDEL-ATY M, ABDALLA M F. Modeling drivers’ diversion from normal routes under ATIS using generalized estimating equations and binomial probit link function [J]. Transportation, 2004, 31(3): 327–348. DOI: 10.1023/ B:PORT.0000025396.32909.dc.
[14] PEETA S, YU J W. A hybrid model for driver route choice incorporating en-route attributes and real-time information effects [J]. Networks and Spatial Economics, 2005, 5(1): 21–40. DOI: 10.1007/s11067-005-6660-9.
[15] TSIRIMPA A, POLYDOROPOULOU A, ANTONIOU C. Development of a mixed multi-nomial logit model to capture the impact of information systems on travelers’ switching behavior [J]. Journal of Intelligent Transportation System, 2007, 11(2): 79–89. DOI: 10.1080/15472450701293882.
[16] GAO S, HUANG H J. Real-time traveler information for optimal adaptive routing in stochastic time-dependent networks [J]. Transportation Research Part C-Emerging Technologies, 2012, 21(1): 196–213. DOI: 10.1016/j.trc. 2011.09.007.
[17] LOU X M, CHENG L, CHU Z M. Modeling travelers’ en-route path switching in a day-to-day dynamical system [J]. Transportmetrica B: Transport Dynamics, 2017, 5(1): 15–37. DOI:10.1080/21680566.2016.1147001.
[18] YANG H. Multiple equilibrium behaviors and advanced traveler information systems with endogenous market penetration [J]. Transportation Research Part B-Methodological, 1998, 32(3): 205–218. DOI: 10.1016/ S0191-2615(97)00025-8.
[19] YANG H, MENG Q. Modeling user adoption of advanced traveler information systems: Dynamic evolution and stationary equilibrium [J]. Transportation Research Part A-Policy and Practice, 2001, 35(10): 895–912. DOI: 10.1016/S0965-8564(00)00030-6.
[20] YANG H, ZHANG X. Modeling competitive transit and road traffic information services with heterogeneous endogenous demand [J]. Transportation Research Record: Journal of the Transportation Research Board, 2002, 1783: 7–18. DOI: 10.3141/1783-02.
[21] LO H K, SZETO W Y. A methodology for sustainable traveler information services [J]. Transportation Research Part B-Methodological, 2002, 36(2): 113–130. DOI: 10.1016/S0191-2615(00)00040-0.
[22] YIN Y, YANG H. Simultaneous determination of the equilibrium market penetration and compliance rate of advanced traveler information systems [J]. Transportation Research Part A-Policy and Practice, 2003, 37(2): 165–181. DOI: 10.1016/S0965-8564(02)00011-3.
[23] YANG H, HUANG H J. Modeling user adoption of advanced traveler information systems: A control theoretic approach for optimal endogenous growth [J]. Transportation Research Part C-Emerging Technologies, 2004, 12(3): 193–207. DOI: 10.1016/j.trc.2004.07.004.
[24] HUANG H J, LI Z C. A multiclass, multicriteria logit-based traffic equilibrium assignment model under ATIS [J]. European Journal of Operational Research, 2007, 176(3): 1464–1477. DOI: 10.1016/j.ejor.2005.09.035.
[25] LO H K, TUNG Y K. Network with degradable links: Capacity analysis and design [J]. Transportation Research Part B-Methodological, 2003, 37(4): 345–363. DOI: 10.1016/S0191-2615(02)00017-6.
[26] LO H K, LUO X W, SIU B W Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion [J]. Transportation Research Part B-Methodological, 2006, 40(9): 792–806. DOI: 10.1016/ j.trb.2005.10.003.
[27] SIU B W Y, LO H K. Doubly uncertain transportation network: Degradable capacity and stochastic demand [J]. European Journal of Operational Research, 2008, 191(1): 166–181. DOI: 10.1016/j.ejor.2007.08.026.
[28] FRIESZ T L, BERNSTEIN D, MEHTA N J, TOBIN R L, GANJALIZADEH S. Day-to-day dynamic network disequilibria and idealized traveler information systems [J]. Operations Research, 1994, 42(6): 1120–1136. DOI: 10.1287/opre.42.6.1120.
[29] HUANG H J, LIU T L, YANG H. Modeling the evolutions of day-to-day route choice and year-to-year ATIS adoption with stochastic user equilibrium [J]. Journal of Advanced Transportation, 2008, 42(2): 111–127. DOI: 10.1002/atr. 5670420202.
[30] CANTARELLA G E. Day-to-day dynamic models for intelligent transportation systems design and appraisal [J]. Transportation Research Part C-Emerging Technologies, 2013, 29: 117–130. DOI: 10.1016/j.trc.2012.03.005.
[31] BIFULCO G N, CANTARELLA G E, SIMONELLI F, VELONA P. Advanced traveler information systems under recurrent traffic conditions: Network equilibrium and stability [J]. Transportation Research Part B-Methodological, 2016, 92: 73–87. DOI: 10.1016/j.trb.2015.12.008.
(Edited by YANG Hua)
中文导读
通行能力退化路网中考虑ATIS信息影响的混合随机用户均衡模型研究
摘要:先进的出行者信息系统(简写ATIS)不仅能帮助出行者获取更准确的交通时间信息,还能提高出行者在面对路网通行能力下降等随机事件时的应急和实时调整能力。本文提出了一类新的混合随机用户均衡模型,用以描述在通行能力随机退化的路网中,装备ATIS和未装备ATIS两类出行者各自的路径选择行为和由此形成的路网交通流均衡状态。在提出的模型中,ATIS向出行者提供交通信息的优势体现在路网流量均衡分布状态的随机性更低,而ATIS对出行者适应路网能力随机退化的强化优势,则通过路网流量的多均衡态加以体现。论文将该混合随机用户均衡模型表示成一个关于混合路径流量的不动点问题,并设计了一类迭代求解算法。通过数值算例,论文分析了模型的相关数学特性,并验证了迭代算法的求解效率。
关键词:混合随机用户均衡模型;可退化交通网络;先进的出行者信息系统(ATIS);出行者行为适应性;多均衡行为;不动点问题
Foundation item: Projects(51378119, 51578150) supported by the National Natural Science Foundation of China
Received date: 2016-10-17; Accepted date: 2016-12-08
Corresponding author: LOU Xiao-ming, PhD, Engineer; Tel: +86-15088767309; E-mail: xiaoming-lou@hotmail.com; ORCID: 0000- 0002-5582-5582

