J. Cent. South Univ. Technol. (2011) 18: 1780-1788

DOI: 10.1007/s11771-011-0902-4

Simulation of faceted dendrite growth of non-isothermal alloy

in forced flow by phase field method

CHEN Zhi(陈志)¹, HAO Li-mei(郝丽梅)², CHEN Chang-le(陈长乐)¹

1. Department of Applied Physics, School of Science, Northwestern Polytechnical University, Xi’an 710129, China;

2. Department of Applied Physics, School of Science, Xi′an University of Science & Technology,

Xi’an 710054, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Numerical simulation based on a new regularized phase field model was presented to simulate the dendritic shape of a non-isothermal alloy with strong anisotropy in a forced flow. The simulation results show that a crystal nucleus grows into a symmetric dendrite in a free flow and into an asymmetry dendrite in a forced flow. As the forced flow velocity is increased, both of the promoting effect on the upstream arm and the inhibiting effects on the downstream and perpendicular arms are intensified, and the perpendicular arm tilts to the upstream direction. With increasing the anisotropy value to 0.14, all of the dendrite arms tip velocities are gradually stabilized and finally reach their relative saturation values. In addition, the effects of an undercooling parameter and a forced compound flow on the faceted dendrite growth were also investigated.

Key words: phase field method; forced flow; strong anisotropy; faceted dendrite; steady state tip velocity

1 Introduction

Dendrites are common shapes in the melt solidification, and they influence the physical properties of cast materials. Therefore, it is important to understand the dendrite growth rules [1-3]. In addition, melt flow is not prevented in the process of solidification, and it greatly changes the distribution of the concentration and the thermal field near the solid/liquid interface, which has a significant effect on the dendritic shape. The presence of a melt flow makes it complex to analyze dendrite growth rules both in theory and in practice [4-6]. Therefore, the use of numerical simulation to study the laws of dendrite growth in forced flow is becoming an important means.

In the last two decades, numerical simulation method has become an effective research means for the prediction of the dendrite growth in the presence of a forced flow. Many simulation methods, such as lattice Boltzmann method [3], phase field method [7], the level set method [8] and explicit interface tracking method  [9], were performed to model the dendrite growth. In the phase field method, f is introduced to represent the phase field parameter: f = 1 denotes the solid phase, f = -1 denotes the liquid phase, and the phase field varies smoothly within the solid/liquid interface region [10-11]. The merits of phase field method are that interface curvature, anisotropy and kinetics effects are implicitly incorporated in the phase field equation, and the explicit tracking of the interface is unnecessary [12]. The phase field method becomes one of the main numerical simulation methods. In 1996, the interface thickness in KARMA and RAPPEL model [10] was released to an order of microstructures, and then phase field method made a great progress. In 2001, TONG et al [5] introduced the forced flow to the phase field model, and obtained an asymmetry dendrite growth shape. After then, LI and BECKERMANN [13] and LAN et al [14] studied the dendrite growth of the pure substance and binary alloy in the presence of a forced flow. However, these researches were mainly focused on a non-faceted dendrite growth with the anisotropy value in the range from 0 to 1/15 (critical value). On the contrary, the literatures on a faceted dendrite growth with the anisotropy greater than 1/15 are rare. Until 2001, EGGLESTON et al [15] proposed a modification phase field method for the interfacial energy including the missing orientations, and originally studied a faceted dendrite growth. In 2003, KASAJIMA et al [16] simulated the silicon growth of faceted dendrite. In 2007, SUZUKI et al [17] modeled the faceted dendrite growth of the Si-Ni binary alloy, and their simulation results were similar to the experimental observations. SEKERKA [18] and KIM et al [19] also made lots of researches on a facet dendrite with strong anisotropy. In 2008, CHEN et al [20] modeled directional solidification interface shapes using a regularized faceted model. In 2009, TORABI et al [21] presented a new regularized anisotropic Cahn-Hilliard phase field equation. In 2010, WANG and INATOMI [22] further researched three dimensional faceted directional solidification micro- structure. Similarly, in 2011, LIN et al [23] modeled three dimensional faceted free dendrite growths based on the idea of EGGLESTON. In the above researches, a faceted dendrite growth with the strong anisotropy is in the absence of the forced flow. However, the study on facet dendrite growth at a strong anisotropy in the present of a forced flow was never reported.

In this work, based on the model by EGGLESTON et al [15], a new regularized phase field model for a non- isothermal facet binary alloy with a strong anisotropy value in a forced flow was presented, and the effects of anisotropy parameters, flow velocity, undercooling and compound flow on the faceted dendrite shape were investigated.

2 Phase field model

Usually, an anisotropy parameter reflects the dependence of both the average bonding energy and the attach kinetics on the local interface orientation and controls the dendrite growth direction. In undercooling melt, the equilibrium condition at the solid/liquid interface is obtained using the Gibbs-Thomson equation [16, 24]:

             (1)

where R(φ) is a curvature radius of solid/liquid interface;  is the dimensionless anisotropy parameter; f ^L and f ^S are the free energy densities of the liquid and solid phases, respectively. When ≤1/15, two sides of the equation are positive, and the crystal shape is smooth and continuous. When >1/15, the left side of the equation is negative as a result of the missing orientations, and the interface becomes discontinuous, which occurs as concave parts similar to “ears”. These “ears” parts enlarge with the increase of the anisotropy value, which makes it difficult to simulate the faceted dendrite shape with a strong anisotropy [19]. To simulate the dendrite growth of a non-isothermal binary alloy with a strong anisotropy value, these “ears” must be removed, and the phase field model should be regularized.

In this work, the two-phase system was described by a phenomenological free energy [25-26]:

                 (2)

where f (f, C, θ) is the bulk free energy density, and it is used here in the form of

with minima at f  = -1 and f  = 1 which correspond to the liquid and solid phases, respectively. It obeys the first order kinetic equation,

                                                             (3)

Meanwhile, a new regularized interface energy coefficient for the whole crystal nucleus was based on the quarter regularized idea of EGGLESTON and KIM [15, 19]:

      (4)

where W(n)=W₀a_s(n) is the interface thickness; n=  is the unit vector normal to the interface;  is the surface energy function; φ= arctan(?_yf/?_xf) is the angle of the horizontal axis and the direction normal to the interface; φ_m is the corner angle of the equilibrium shape [18, 27].

Further combining Eqs.(3) and (4), a new regularized phase field equation is presented to model the entire facet dendrite shape of a non-isothermal binary alloy in a forced flow:

For  i=0, 1, 2, 3

     (2)

For  i=0, 2

(3)

For  i=1, 3

                                      (4)

where  is an orientation-dependent relaxation time of phase field; λ is a coupling parameter; α is a dimensionless thermal diffusion parameter.

Here, it is assumed that all material properties are constant, the solute diffusivity in the solid is neglected, thermal diffusion coefficients of the solid and liquid are equal, and the melt flow is incompressible [5, 7]. The solute field, the thermal field, the mass conservation and the momentum equations are given, respectively, by

                                        (5)

                           (6)

                                                       (7)

                                    (8)

where U is a dimensionless solute diffusion parameter; D is a dimensionless solute diffuse parameter;

is a dissipative interfacial stress, and h is 2.757 as in Ref.[5]; P, ρ and υ are density, pressure and kinematics viscosity, respectively; t is the dimensionless time.

The chemical capillary length d₀ and the interface kinetic coefficient β are related to the phase-field parameters by asymptotic analysis [10]:

                                                            (12)

                             (13)

The expressions for the coefficients a₁=0.883 9 and a₂=0.626 7 are identical to those derived by KARMA and RAPPLE [10] and the interface kinetics can be eliminated by choosing .

The dimensionless solute concentration, the supersaturating, the scaled magnitude of liquids slope and the thermal undercooling are given by [25]:

                                       (9)

                                                (10)

                                                 (11)

                                         (12)

where C is a mixture concentration in the interface region; C_∞ is an initial alloy concentration apart from the solidification front;  is a liquid balance concentration, m is the slope of liquidus; L is the solidification latent heat; c_p is the heat capacity as constant.

3 Numerical simulations

3.1 Initial condition and boundary condition

An initial crystal radius was assumed to be r, and the small spherical seed existed at the center of a square domain. Undercooling melt entered the domain from the left boundary with a forced flow velocity Vd₀/α, flowed past the crystal, and exited at the right boundary with a velocity gradient of zero. The top and bottom domain surfaces were treated as symmetrical closed boundaries [5, 8]. The initial phase field, the solute field and the thermal field were taken as f =1, U=0, θ=0 in the solid, and f =-1, U=-Ω, θ=-Δ elsewhere in the domain. The results in the initial crystal with four axes of symmetry were aligned with x and y axis [14].

3.2 Calculation method

Equations (5)-(11) were solved using the standard finite difference method on a uniform square mesh, time step was solved using the explicit Euler scheme, and  was solved using a nine-point formula with the nearest and next nearest neighbors, which reduces the grid anisotropy [10]. For convenience, the following conditions were chosen: mesh grid 800×800, time step ?t=0.008, space step ?x=?y=0.4, τ₀=1, d₀=0.277, W₀=1, α=2, Δ=0.25, λ=3.192, k=0.1, C_∞=0.1. Prandtl number is the ratio of dynamic viscosity to temperature diffusion coefficient [28-29], and p_r=0.011,  ρ=2.53, t=35 000?t were chosen. Unless otherwise stated, these parameters were not varied.

4 Results and discussion

4.1 Effect of heat latent

Figure 1 shows the phase field shapes with Vd₀/α= 0.10 and at t=25 000Δt. It can be seen that the dendrite size under the isothermal condition is larger than that of the non-isothermal condition. Furthermore, the perpendicular arm in the side of the upstream direction obviously appears a secondary dendrite under the isothermal condition, while that under the non-isothermal condition is smooth. The reason [4] is that the heat latent, released in the process of dendrite growth under the non-isothermal condition, weakens the undercooling near the dendrite arm tip. In other words, the heat latent increases the temperature in the interface front, and then the undercooling of the interface decreases the driving force of dendrite growth.

4.2 Effect of anisotropy

Figure 2 depicts the phase field shape with Vd₀/α= 0.10 and various anisotropy values. It is shown that the growth of the upstream arm is the fastest, the perpendicular arm takes the second place, and the downstream arm is the slowest. As the anisotropy value in the range of 0.07-0.12 is increased, the sizes of both the upstream-arm and downstream-arm become smaller, while the perpendicular arm is larger. However, when the anisotropy value increases from 0.12 to 0.14, the upstream-arm size keeps invariant, the perpendicular- arm size slowly increases, but the downstream-arm is shortened into a facet without dendrite arm. In addition, as seen from Fig.3, with increasing the anisotropy value, the steady state tip velocities of the downstream and upstream arms decrease, while those of the perpendicular arm increase. Notice that the steady state tip velocities in three directions finally reach their own saturation values. It is thought that with the increase of the anisotropy value, the missing orientation enhances, and it results in the decrease and then saturation of the upstream arm steady state tip velocity. The lower upstream tip velocity reduces the release of the latent heat around perpendicular arms, and promotes the growth of perpendicular arms. The reason of the decrease in downstream tip velocity is that the range of missing orientations is increased and more latent heat in the perpendicular direction is released. In addition, when the anisotropy value is 0.15, the growth of the upstream arm becomes unstable, and a bifurcation phenomenon occurs in the upstream direction, which is similar to the result in Ref.[30].
 

Fig.1 Phase field shapes with Vd₀/α=0.10 and at t=25 000 Δt: (a) Under isothermal condition; (b) Under non-isothermal condition

Fig.2 Phase field shapes with Vd₀/α=0.10 and various anisotropy values: (a) 0.07; (b) 0.10; (c) 0.12; (d) 0.13; (e) 0.14; (f) 0.15
 

Fig.3 Time evolution of tip velocities at various anisotropy values

4.3 Effect of forced flow

Figure 4 demonstrates the phase field shapes at the various forced flow velocities. Notice that the crystal grows into an equiaxial dendrite in the absence of a forced flow, whereas dendrite shape is asymmetrical in the presence of a forced flow. The upstream arm size in a forced flow is larger than that of a free flow. Conversely, the growth of downstream arm is suppressed, but the perpendicular arm has no significant change, namely, has a slight decrease. As the forced flow velocity is increased, both of the promoting effect on the upstream arm and the inhibiting effects on the downstream and perpendicular arms are intensified. Furthermore, the downstream arm is shortened into a facet without dendrite arm, and the perpendicular arm in the side of the upstream direction obviously appears a secondary dendrite, tilting to the upstream direction.
 

Fig.4 Phase field shapes at various forced flow velocity: (a) 0.00; (b) 0.10; (c) 0.30; (d) 0.40

The curves of tip steady state velocities versus flow velocity for dendrite arms in various directions are plotted in Fig.5. A further analysis can be obtained from Fig.5 that with the increase of the flow velocity, the arm growth velocity increases in the upstream direction; on the contrary, it decreases in the downstream and perpendicular directions.

Fig.5 Curves of tip steady state velocities versus flow velocity for dendritic arms in various directions

Figure 6 shows the plot of the solute concentration profiles in the solid along the central dendrite axis grid at various flow velocities. As can be seen, when the flow velocity is increased, the solute accumulation of the solid/liquid interface descends in the upstream direction, whereas that of the downstream and perpendicular direction enhances. Therefore, it is suggested that a dendrite shape is asymmetrical in the presence of a forced flow from this aspect, which agrees with the rule of a non-facet dendrite growth.

On the other hand, the arm tip undercooling as a function of time is summarized in Fig.7. With the increase of the flow velocity, the undercooling of the upstream arm tip gradually increases; on the contrary, those of the downstream and perpendicular arms gradually decrease. In addition, the curves are in a state of fluctuation, resulting from the released latent heat and the redistribution solute, and then the fluctuation is intensified with the increase of the flow velocity.

Fig.6 Solute concentration profiles in solid along central dendritic axis grid at various flow velocities: (a) Upstream arm; (b) Perpendicular arm; (c) Downstream arm

4.4 Effect of undercooling parameter

The undercooling parameter has a significant influence on the facet dendrite shape in the non-isothermal condition of binary alloy. Figure 8 shows the isotherms around phase field dendrite shapes at various undercooling parameters with Vd₀/α=0.10 and t=18 000Δt. The contours in the upstream direction are the densest, while those of the perpendicular direction take the second place, and those of the downstream direction are the thinnest. As the undercooling parameter increases, the contours in three directions become denser, and the temperature gradient becomes higher. Thus, the dendrite arm growth velocities in three directions increase, and then the dendrite size lengthens. When the undercooling parameter is increased to -0.45, a crystal nucleus grows into a developed dendrite, that is, the perpendicular arm in the side of the upstream direction obviously appears secondary dendrites.

Fig.7 Dendritic arm tip undercooling as function of time:    (a) Upstream arm; (b) Perpendicular arm; (c) Downstream arm

Fig.8 Isotherms around phase field dendrite shapes at various undercooling parameters with Vd₀/α=0.10 and t=18 000Δt:   (a) -0.05; (b) -0.25; (c) -0.45

The relation between the arm tip steady state velocity and the square undercooling is given in Fig.9. When the undercooling square increases, all the arm tip steady state velocities in three directions enhance, where the velocity increment of the upstream direction is the largest, while that of the perpendicular direction takes the second place, and that of the downstream direction is the smallest.

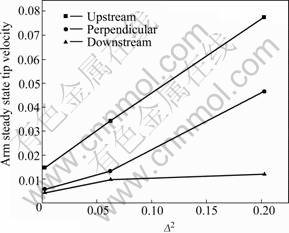
Fig.9 Relation between arm steady state tip velocity and square undercooling
 

4.5 Effect of compound flow

The effect of the compound flow, consisting of the right-horizontal flow and the above-vertical flow, on the facet binary alloy was investigated.

Figure 10 shows the isotherms around phase field dendrite shapes at various V₁d₀/α and V₂d₀/α. When the values of V₁d₀/α and V₂d₀/α are equal and the flow velocity increases, the size of both number 1 and 4 dendrite arms lengthens, and increased second dendrites appear between their main stems. However, those of number 2 and 3 arms shorten into the 2-3 facet. When the values of V₁d₀/α and V₂d₀/α are not equal, a crystal grows into an asymmetry facet dendrite, as shown in Figs.10(d) and (e).
 

Fig.10 Isotherms around phase field dendrite shapes at various V₁d₀/α and V₂d₀/α: (a) 0.10, 0.10; (b) 0.20, 0.20; (c) 0.30, 0.30;  (d) 0.30, 0.10; (e) 0.30, 0.20
 

5 Conclusions

1) An asymmetry facet dendrite shape of a non-isothermal binary alloy in the presence of a forced flow has been successfully achieved by a new modified phase field model, and it is similar to a non-facet dendrite shape.

2) Different from non-faceted dendrite, with the increase of the anisotropy value, the upstream and downstream dendrite arms are both inhibited, while the perpendicular arm is promoted. But all of the dendrite arms tip velocities are gradually stabilized and finally reach their own relative saturation values when the anisotropy value is increased to 0.14.

3) As the forced flow velocity is increased, all of the promoting effect on the upstream arm and the inhibiting effects on the downstream and perpendicular arms are intensified, and the perpendicular arm tilts to the upstream direction.

4) When the undercooling value is increased, all of the arm tip steady state velocities in three directions enhance. When a compound forced flow is introduced, the facet dendrite shape becomes more complicated.

References

[1] BECKERMANN C, DIEPERS H J, STEINBACH I, KARMA A, TONG X. Modeling melt convection in phase-field simulations of solidification [J]. Journal of Computational Physics, 1999, 154(2) 468-496.

[2] LAN C W, LIU C C, HSU C M. An adaptive finite volume method for incompressible heat flow problems in solidification [J]. Journal of Computational Physics, 2002, 178(2): 464-497.

[3] MEDVEDEV D, KASSNER K. Lattice-Boltzmann scheme for dendrite growth in presence of convection [J]. Journal of Crystal Growth, 2005, 275(1/2): 1495-1500.

[4] AL-RAWAHI N, TRYGGVASON G. Numerical simulation of dendrite solidification with convection: Two-dimensional geometry [J]. Journal of Computational Physics, 2002, 180(2): 471-496.

[5] TONG X, BECKERMANN C, KARMA A, LI Q. Phase-field simulations of dendrite crystal growth in a forced flow [J]. Physical Review E, 2001, 63(6): 061601.

[6] ZHU M F, LEE S Y, HONG C P. Modified cellular automaton model for the prediction of dendrite growth with melt convection [J]. Physical Review E, 2004, 69(6): 061610.

[7] LAN C W, CHANG Y C, SHIH C J. Adaptive phase field simulation of non-isothermal free dendrite growth of a binary alloy [J]. Acta Materialia, 2003, 51(7): 1857-1869.

[8] KIM Y T, GOLDENFELD N. Computation of dendrite microstructures using a level set method [J]. Physical Review E, 2000, 62(2): 2471-2474.

[9] UDAYKUMAR H S, MARELLA S, KRISHNAN S. Sharp-interface simulation of dendrite growth with convection: Benchmarks [J]. International Journal of Heat and Mass Transfer, 2003, 46(14): 2615-2627.

[10] KARMA A, RAPPEL W J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics [J]. Physical Review E, 1996, 53(4): 3017-3020.

[11] KARMA A, RAPPEL W. J. Quantitative phase-field modeling of dendrite growth in two and three dimensions [J]. Physical Review E, 1998, 57(4): 4323-4349

[12] TAN L J, ZABARAS N. A level set simulation of dendrite solidification with combined features of front-tracking and fixed-domain methods [J]. Journal of Computational Physics, 2006, 211(1): 36-63.

[13] LI Q, BECKERMANN C. Modeling of free dendrite growth of succinonitrile acetone alloys with thermosolutal melt convection [J]. Journal of Crystal Growth, 2002, 236(1/2/3): 482-498.

[14] LAN C W, HSU C M, LIU C C. Efficient adaptive phase field simulation of dendrite growth in a forced flow at low supercooling [J]. Journal of Crystal Growth, 2002, 241(3): 379-386.

[15] EGGLESTON J J, MCFADDEN G B, VOORHEES P W. A phase-field model for highly anisotropic interfacial energy [J]. Physica D, 2001, 150(1/2): 91-103.

[16] KASAJIMA H, NAGANO E, SUZUKI T, KIM S G, KIM W T. Phase-field modeling for facet dendrite growth of silicon [J]. Science and Technology of Advanced Materials, 2003, 4(6): 553-557.

[17] SUZUKI T, KIM S G, KIM W T. Two-dimensional facet crystal growth of silicon from undercooled melt of Si-Ni alloy [J]. Materials Science and Engineering A, 2007, 449-451: 99-104.

[18] SEKERKA R F. Equilibrium and growth shapes of crystals: How do they differ and why should we care? [J]. Crystal Research and Technology, 2005, 40(4/5): 291-306.

[19] KIM S G, KIM W T. Phase field modeling of dendrite growth with high anisotropy [J]. Journal of Crystal Growth, 2005, 275(1/2): 355- 360.

[20] CHEN P, TSAI Y L, LAN C W. Phase field modeling of growth competition of silicon grains [J]. Acta Materialia, 2008, 56(15): 4114-4122.

[21] TORABI S, LOWENGRUB J, VOIGT A, WISE S. A new phase-field model for strongly anisotropic systems [J]. Proceedings of the Royal Society A, 2009, 465(2105): 1337-1359.

[22] WANG J C, INATOMI Y K. Three-dimensional phase field modeling of the faceted cellular growth [J]. ISIJ International, 2010, 50 (12): 1901-1907.

[23] LIN H K, CHEN C C, LAN C W. Adaptive three-dimensional phase-field modeling of dendrite crystal growth with high anisotropy [J]. Journal of Crystal Growth, 2011, 39(1): 51-54.

[24] lEZ-CINCA R G, RAM?REZ-PISCINA L, CASADEMUNT J, HERN?NDEZ-MACHADO A, T? TH-KATONA T, B? RZS? NYI T, BUKA?. Heat diffusion anisotropy in dendrite growth: Phase field simulations and experiments in liquid crystals [J]. Journal of Crystal Growth, 1998, 193(4): 712-719.

[25] ROSAM J, JIMACK P K, MULLIS A M. An adaptive, fully implicit multigrid phase-field model for the quantitative simulation of non-isothermal binary alloy solidification [J]. Acta Materialia, 2008, 56(17): 4559-4569.

[26] KARMA A. Phase-field formulation for quantitative modeling of alloy solidification [J]. Physical Review Letters, 2011, 87(11): 115701

[27] TAKAKI T, HASEBE T, TOMITA Y. Two-dimensional phase-field simulation of self-assembled quantum dot formation [J]. Journal of Crystal Growth, 2006, 287(2): 495-499.

[28] ZHANG T, WANG G X, ZHANG H, LADEINDE F, PRASAD V. Turbulent transport of oxygen in the Czochralski growth of large silicon crystals [J]. Journal of Crystal Growth, 1999, 198/199(1): 141-146.

[29] GORBUNOV L, PEDCHENKO A, FEODOROV A, TOMZIG E, VIRBULIS J. AMMON W V. Physical modeling of the melt flow during large-diameter silicon single crystal growth [J]. Journal of Crystal Growth, 2003, 257(1/2): 7-18.

[30] DEBIERRE J M, KARMA A, CELESTINI F, GU?RIN R. Phase-field approach for faceted solidification [J]. Physical Review E, 2003, 68(4): 041604.

(Edited by HE Yun-bin)

Foundation item: Project(11102164) supported by the National Natural Science Foundation of China; Project(G9KY101502) supported by NPU Foundation for Fundamental Research, China

Received date: 2010-11-18; Accepted date: 2011-02-19

Corresponding author: CHEN Zhi, PhD; Tel: +86-13228039957; E-mail: c2002z@nwpu.edu.cn